Multiscale Modelling of Hydrogen Transport and Segregation in Polycrystalline Steels
Abstract
1. Introduction
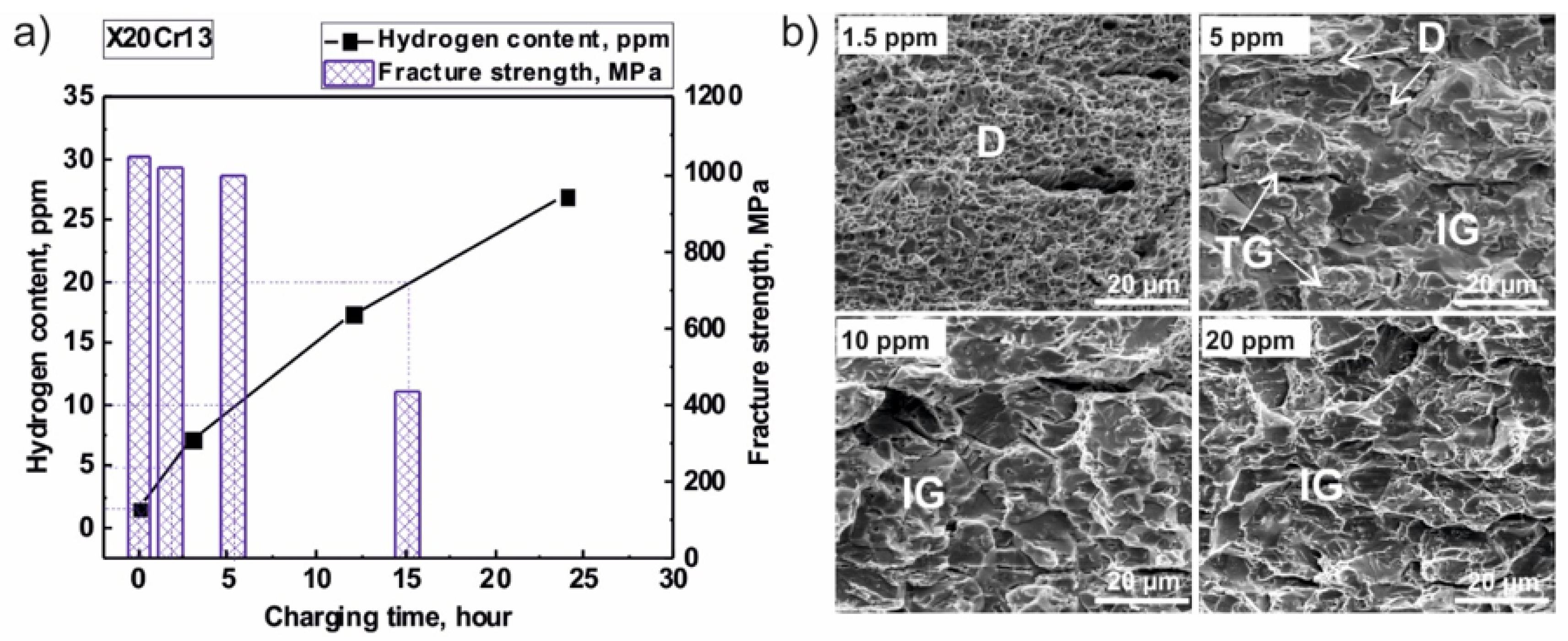
2. Experimental Findings
3. Model Formulation
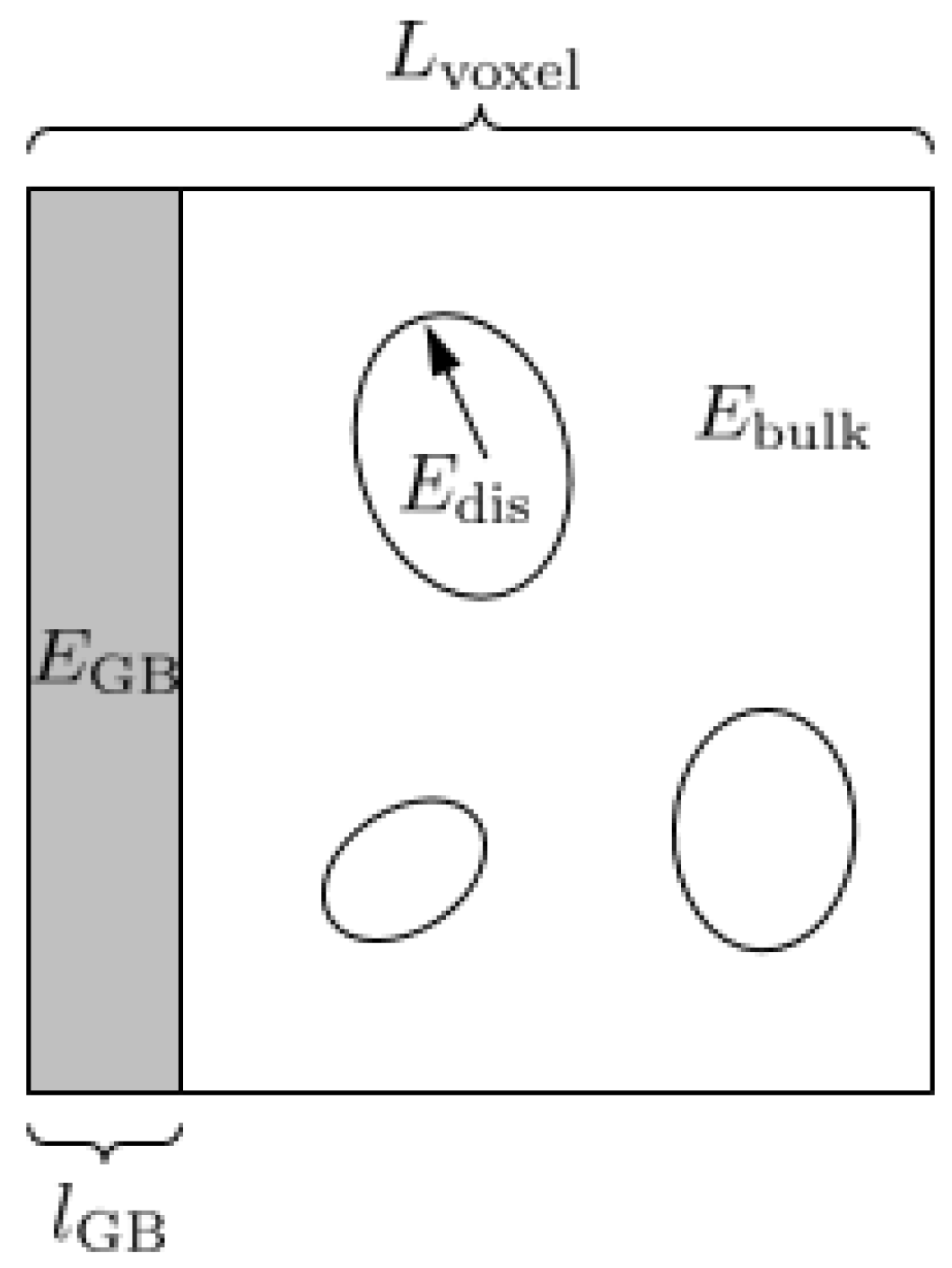
3.1. Continuum Model Formulation
3.2. Numerical Implementation of the Continuum Model
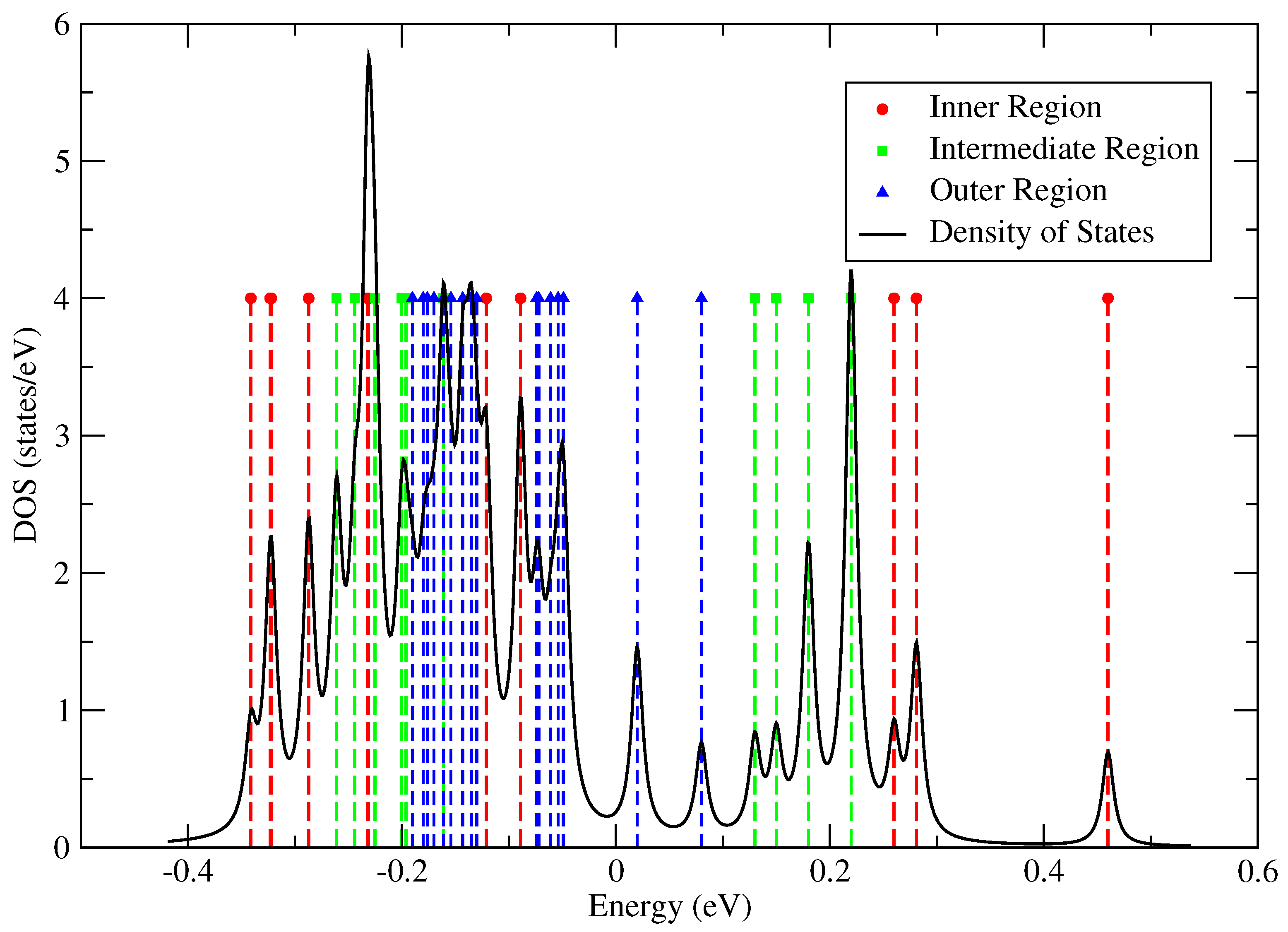
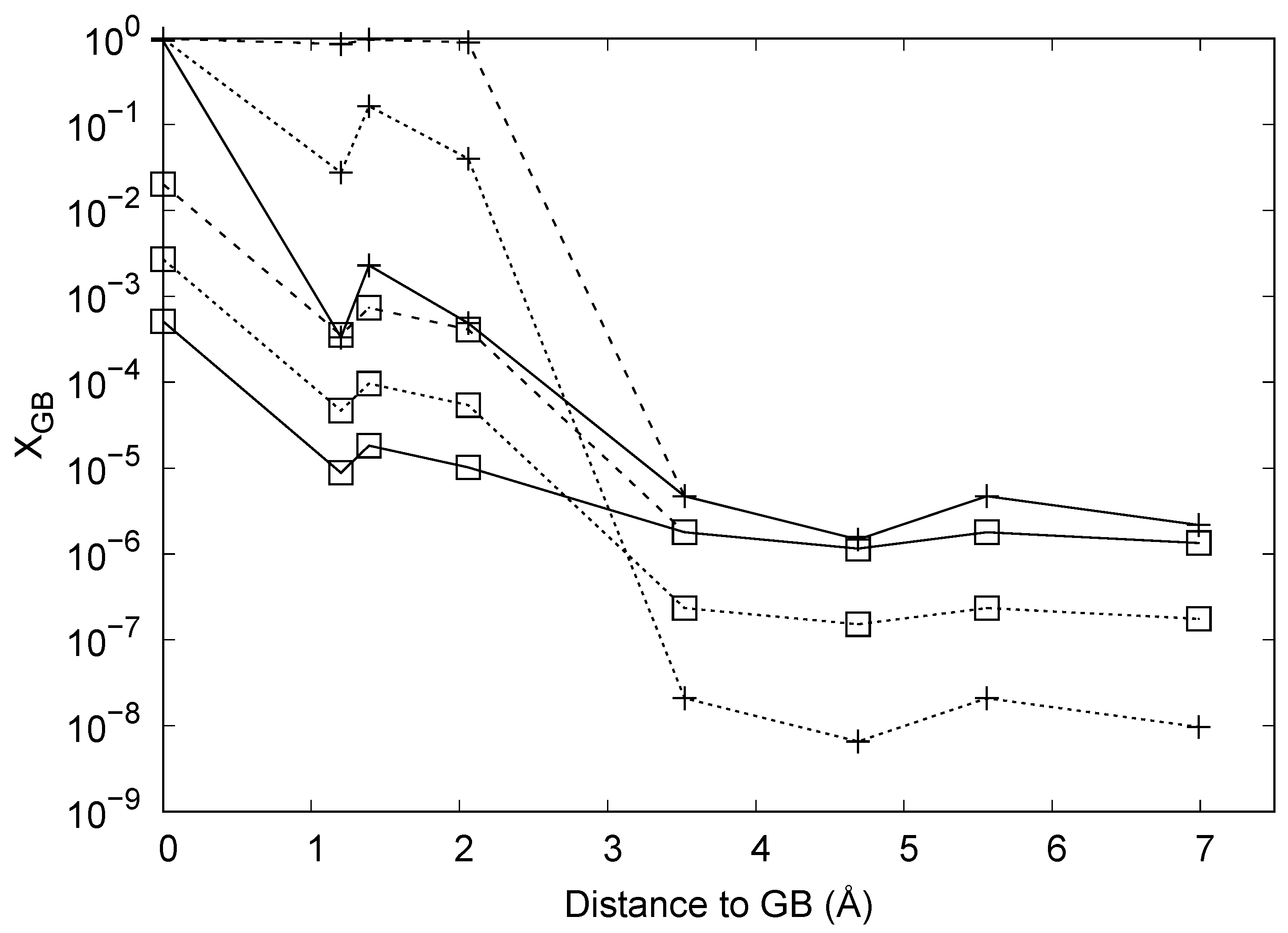
3.3. Atomistic Parameterisation
4. Results and Discussion
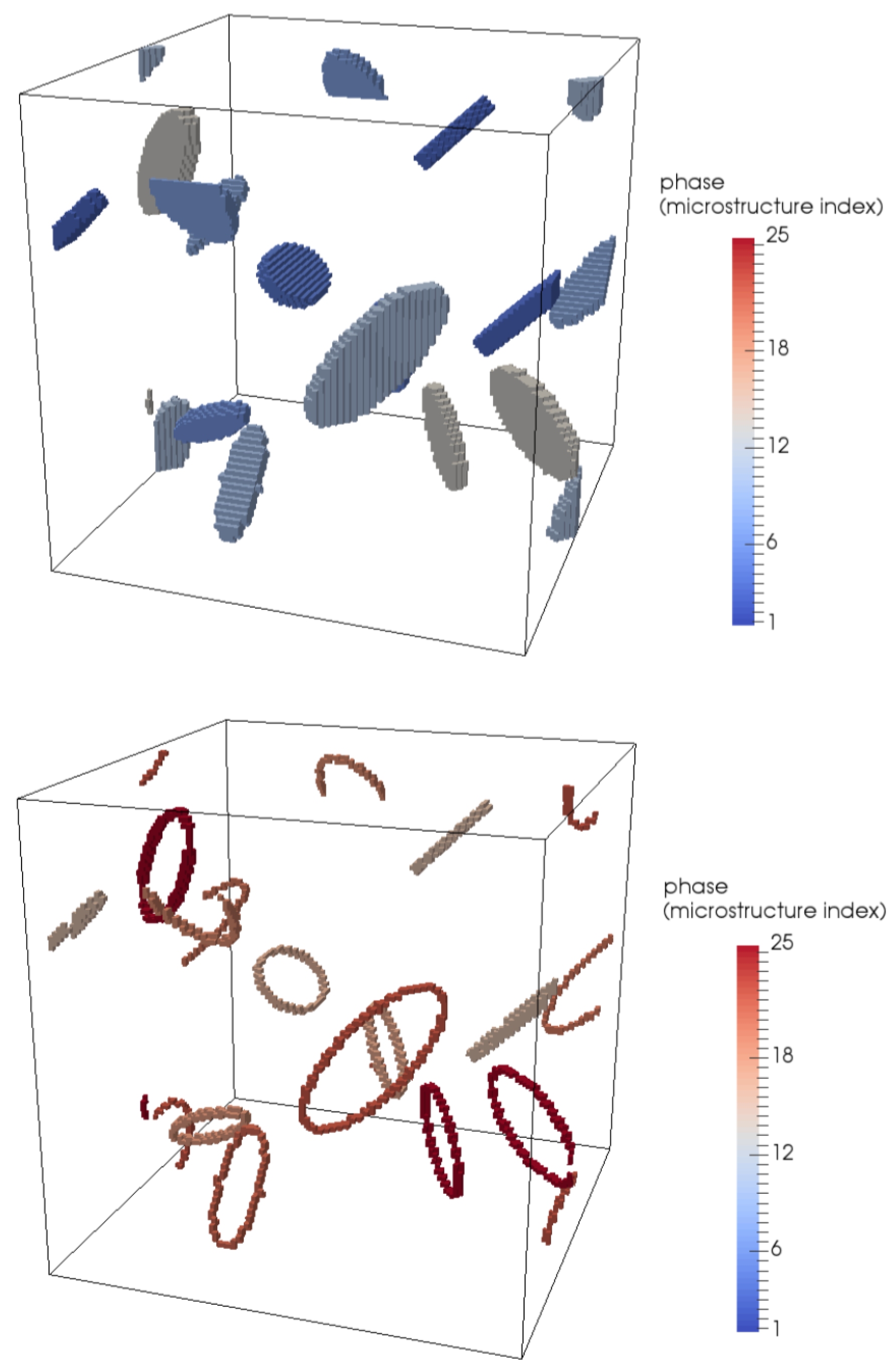
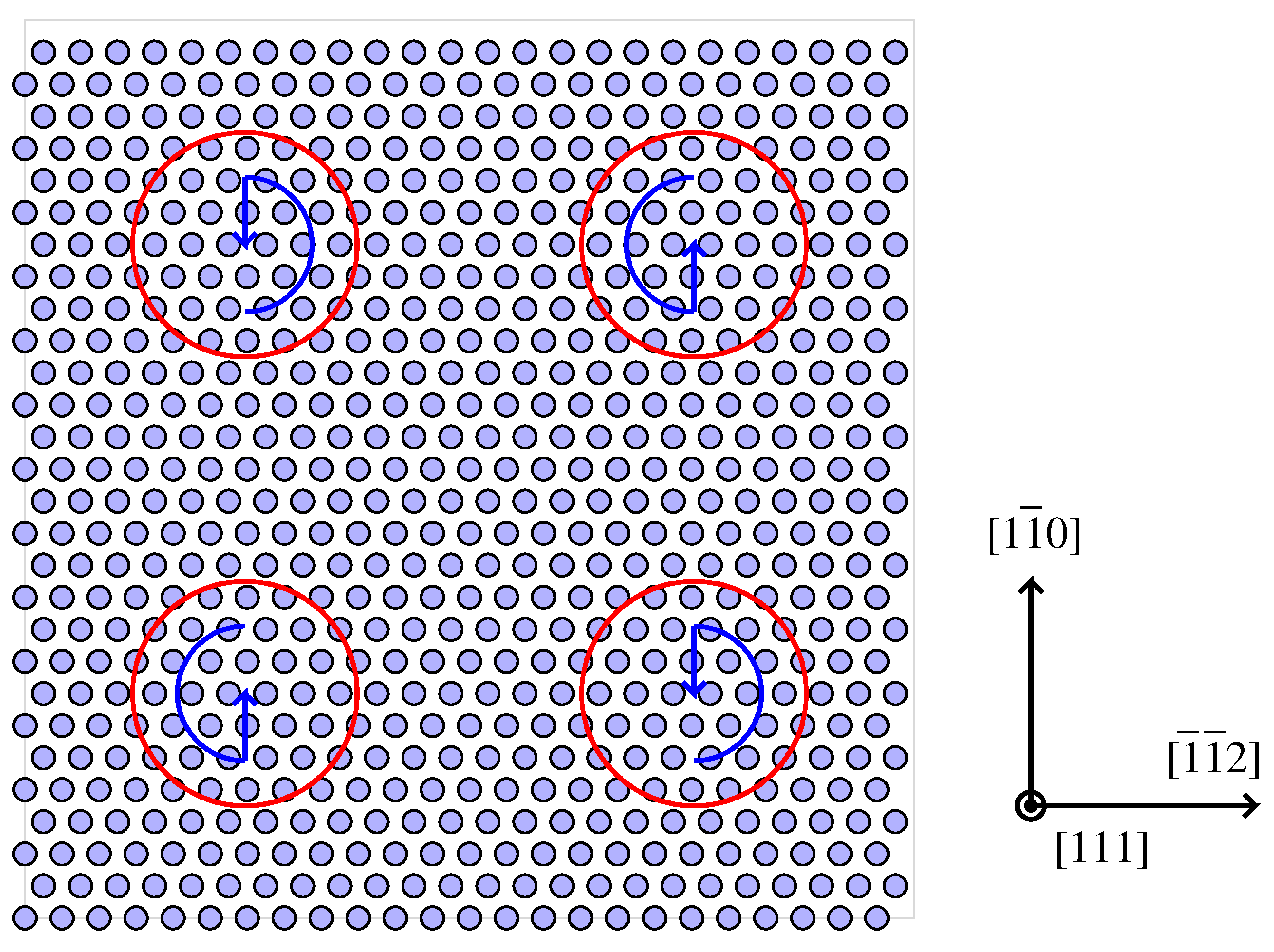
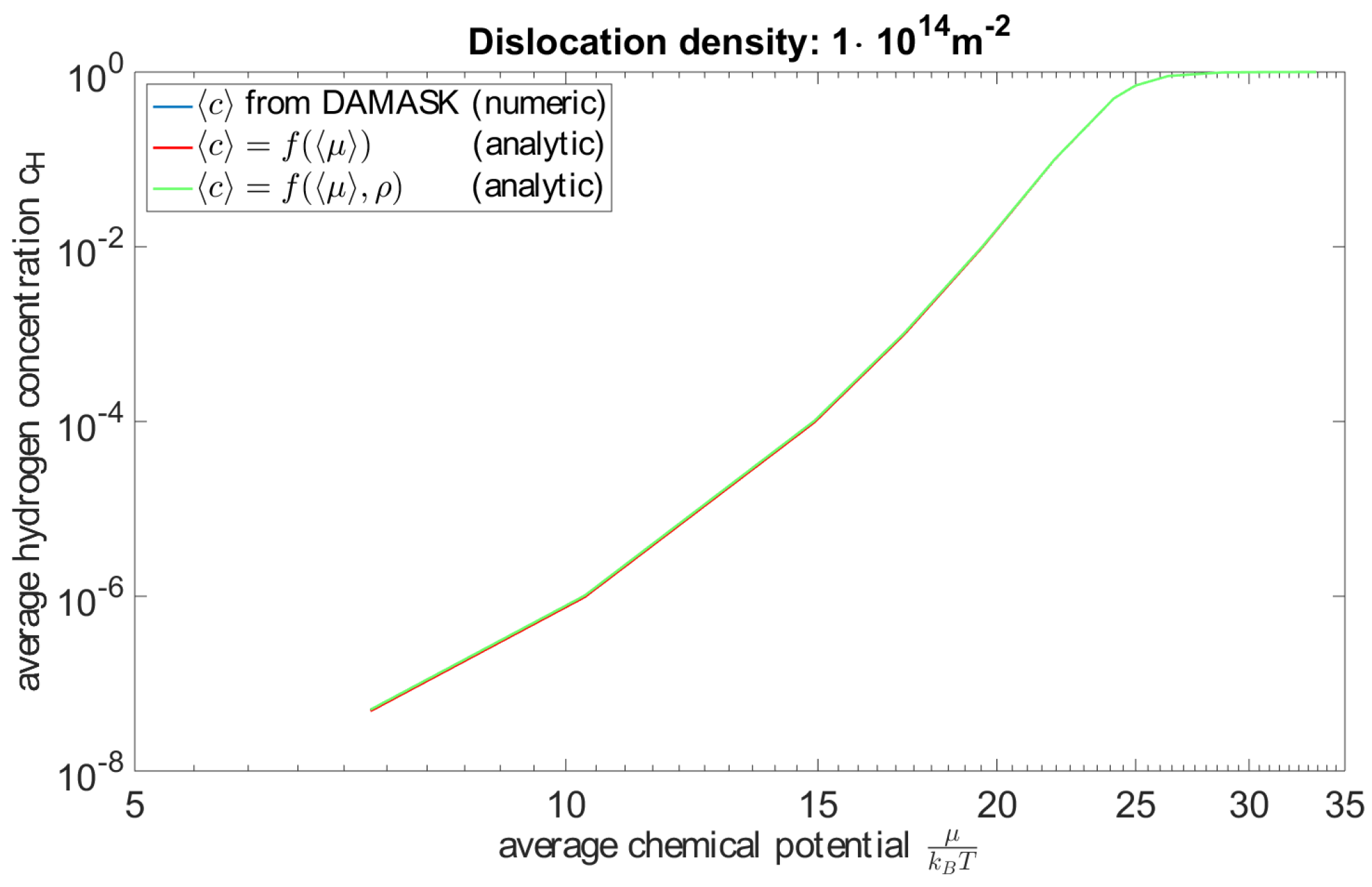
4.1. Modelling Hydrogen Aggregation Considering Dislocation Effects
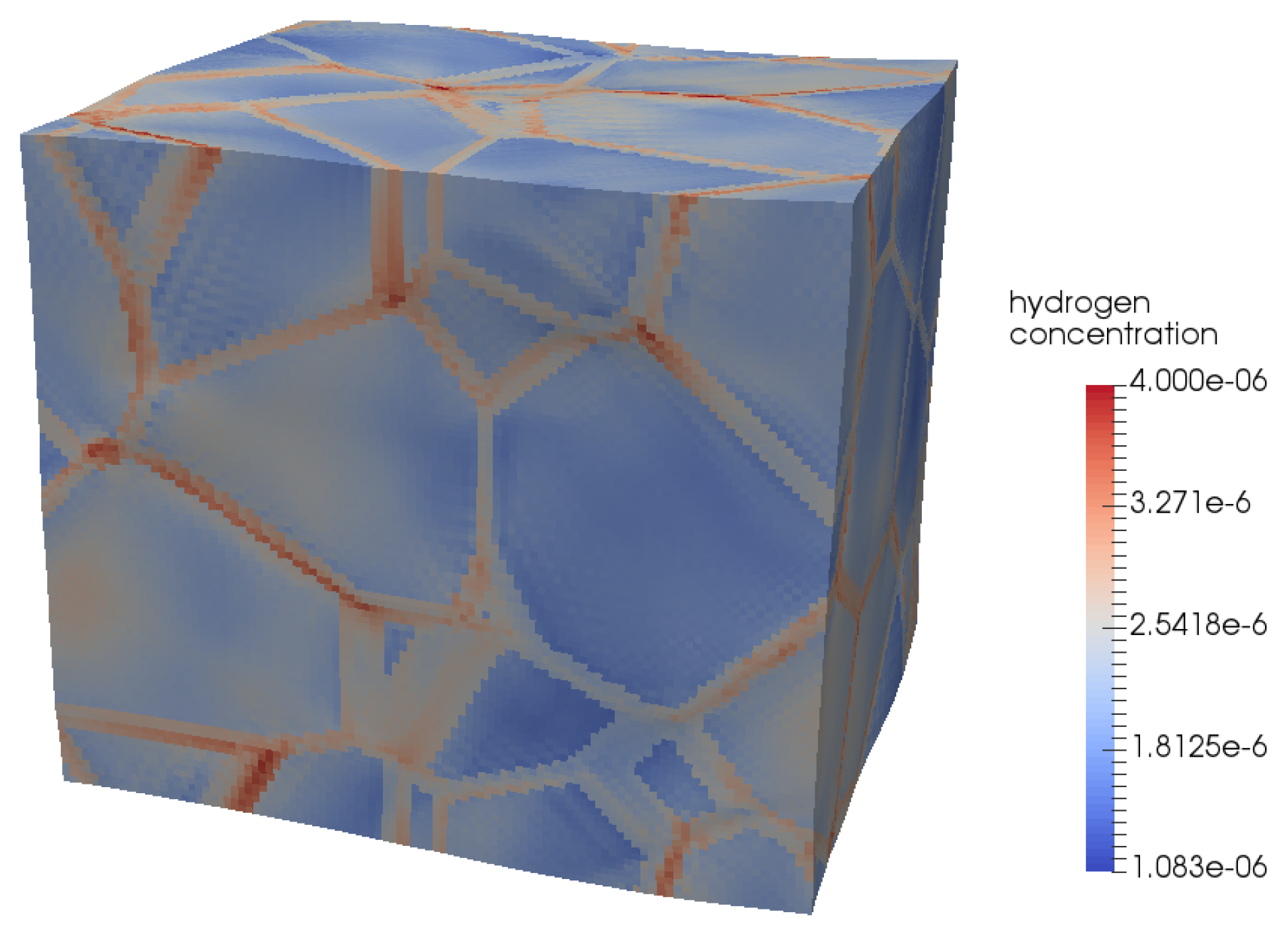
4.2. Modelling Hydrogen Aggregation Considering Dislocation and Grain Boundary Effects
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Petch, N.J. The lowering of fracture-stress due to surface adsorption. Philos. Mag. 1956, 1, 331–337. [Google Scholar] [CrossRef]
- Birnbaum, H.K.; Sofronis, P. Hydrogen-enhanced localized plasticity—A mechanism for hydrogen-related fracture. Mater. Sci. Eng. A 1994, 176, 191–202. [Google Scholar] [CrossRef]
- Kirchheim, R. Reducing grain boundary, dislocation line and vacancy formation energies by solute segregation. I. Theoretical background. Acta Mater. 2007, 55, 5129–5138. [Google Scholar] [CrossRef]
- Kirchheim, R. Reducing grain boundary, dislocation line and vacancy formation energies by solute segregation: II. Experimental evidence and consequences. Acta Mater. 2007, 55, 5139–5148. [Google Scholar] [CrossRef]
- Lynch, S. Environmentally assisted cracking: Overview of evidence for an adsorption-induced localised-slip process. Acta Metall. 1988, 36, 2639–2661. [Google Scholar] [CrossRef]
- Nagumo, M. Hydrogen related failure of steels—A new aspect. Mater. Sci. Technol. 2004, 20, 940–950. [Google Scholar] [CrossRef]
- Takai, K.; Shoda, H.; Suzuki, H.; Nagumo, M. Lattice defects dominating hydrogen-related failure of metals. Acta Mater. 2008, 56, 5158–5167. [Google Scholar] [CrossRef]
- Crabtree, G.W.; Dresselhaus, M.S.; Buchanan, M.V. The hydrogen economy. Phys. Today 2004, 57, 39–44. [Google Scholar] [CrossRef]
- Turner, J.A. Sustainable hydrogen production. Science 2004, 305, 972–974. [Google Scholar] [CrossRef] [PubMed]
- Figueroa, D.; Robinson, M. The effects of sacrificial coatings on hydrogen embrittlement and re-embrittlement of ultra high strength steels. Corros. Sci. 2008, 50, 1066–1079. [Google Scholar] [CrossRef]
- Rhodes, P. Environment-assisted cracking of corrosion-resistant alloys in oil and gas production environments: A review. Corrosion 2001, 57, 923–966. [Google Scholar] [CrossRef]
- Barrera, O.; Bombac, D.; Chen, Y.; Daff, T.; Galindo-Nava, E.; Gong, P.; Haley, D.; Horton, R.; Katzarov, I.; Kermode, J.; et al. Understanding and mitigating hydrogen embrittlement of steels: A review of experimental, modelling and design progress from atomistic to continuum. J. Mater. Sci. 2018, 53, 6251–6290. [Google Scholar] [CrossRef]
- Jemblie, L.; Olden, V.; Akselsen, O.M. A review of cohesive zone modelling as an approach for numerically assessing hydrogen embrittlement of steel structures. Philos. Trans. R. Soc. A 2017, 375, 20160411. [Google Scholar] [CrossRef] [PubMed]
- Koyama, M.; Akiyama, E.; Lee, Y.K.; Raabe, D.; Tsuzaki, K. Overview of hydrogen embrittlement in high-Mn steels. Int. J. Hydrogen Energy 2017, 42, 12706–12723. [Google Scholar] [CrossRef]
- Du, Y.A.; Ismer, L.; Rogal, J.; Hickel, T.; Neugebauer, J.; Drautz, R. First-principles study on the interaction of H interstitials with grain boundaries in α- and γ-Fe. Phys. Rev. B 2011, 84, 144121. [Google Scholar] [CrossRef]
- Troiano, A.R. The role of hydrogen and other interstitials in the mechanical behavior of metals. Trans. ASM 1960, 52, 54–80. [Google Scholar] [CrossRef]
- Oriani, R. A mechanistic theory of hydrogen embrittlement of steels. Ber. Bunsengesellsch. Phys. Chem. 1972, 76, 848–857. [Google Scholar]
- Oriani, R.; Josephic, P. Equilibrium aspects of hydrogen-induced cracking of steels. Acta Metall. 1974, 22, 1065–1074. [Google Scholar] [CrossRef]
- Baechem, C. A New Model for Hydrogen-Assisted Cracking. Met. Trans. 1972, 3, 437–451. [Google Scholar]
- Von Pezold, J.; Lymperakis, L.; Neugebeauer, J. Hydrogen-enhanced local plasticity at dilute bulk H concentrations: The role of H–H interactions and the formation of local hydrides. Acta Mater. 2011, 59, 2969–2980. [Google Scholar] [CrossRef]
- Leyson, G.; Grabowski, B.; Neugebauer, J. Multiscale description of dislocation induced nano-hydrides. Acta Mater. 2015, 89, 50–59. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Kords, C.; Tjahjanto, D.; Diehl, M.; Raabe, D. DAMASK: The Duesseldorf Advanced Material Simulation Kit for studying crystal plasticity using an FE based or a spectral numerical solver. Procedia IUTAM 2012, 3, 3–10. [Google Scholar] [CrossRef]
- Hirth, J. Effects of hydrogen on the properties of iron and steel. Metall. Trans. A 1980, 11, 861–890. [Google Scholar] [CrossRef]
- Shanthraj, P.; Sharma, L.; Svendsen, B.; Roters, F.; Raabe, D. A phase field model for damage in elasto-viscoplastic materials. Comput. Methods Appl. Mech. Eng. 2016, 312, 167–185. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Hori, M. Micromechanics: Overall Properties of Heterogenous Materials; Elsevier North-Holland: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Peirce, D.; Asaro, R.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- McEniry, E.J.; Drautz, R.; Madsen, G. Environmental tight-binding modeling of nickel and cobalt clusters. J. Phys. Condens. Matter 2013, 25, 115502. [Google Scholar] [CrossRef] [PubMed]
- McEniry, E.J.; Hickel, T.; Neugebauer, J. Hydrogen behaviour at twist {110} grain boundaries in α-Fe. Philos. Trans. A 2017, 375, 20160402. [Google Scholar] [CrossRef] [PubMed]
- Clouet, E.; Ventelon, L.; Willaime, F. Dislocation core field. II. Screw dislocation in iron. Phys. Rev. B 2011, 84, 224107. [Google Scholar] [CrossRef]
- Lejcek, P. Grain Boundary Segregation in Metals; Springer: Berlin, Germany, 2010. [Google Scholar]
- Psiachos, D.; Hammerschmidt, T.; Drautz, R. Ab initio study of the modification of elastic properties of alpha-iron by hydrostatic strain and by hydrogen interstitials. Acta Mater. 2011, 59, 4255–4263. [Google Scholar] [CrossRef]
- Peisl, H. Topics in Applied Physics: Hydrogen in Metals I; Springer: Berlin, Germany, 1978. [Google Scholar]
- Tehranchi, A. Atomistic Mechanisms of Hydrogen Embrittlement; EPFL: Lausanne, Switzerland, 2017; p. 165. [Google Scholar]
- Tehranchi, A.; Curtin, W. Atomistic study of hydrogen embrittlement of grain boundaries in nickel: II. Decohesion. Model. Simul. Mater. Sci. Eng. 2017, 25, 075013. [Google Scholar] [CrossRef]
- Tehranchi, A.; Curtin, W. Atomistic study of hydrogen embrittlement of grain boundaries in nickel: I. Fracture. J. Mech. Phys. Solids 2017, 101, 150–165. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hüter, C.; Shanthraj, P.; McEniry, E.; Spatschek, R.; Hickel, T.; Tehranchi, A.; Guo, X.; Roters, F. Multiscale Modelling of Hydrogen Transport and Segregation in Polycrystalline Steels. Metals 2018, 8, 430. https://doi.org/10.3390/met8060430
Hüter C, Shanthraj P, McEniry E, Spatschek R, Hickel T, Tehranchi A, Guo X, Roters F. Multiscale Modelling of Hydrogen Transport and Segregation in Polycrystalline Steels. Metals. 2018; 8(6):430. https://doi.org/10.3390/met8060430
Chicago/Turabian StyleHüter, Claas, Pratheek Shanthraj, Eunan McEniry, Robert Spatschek, Tilmann Hickel, Ali Tehranchi, Xiaofei Guo, and Franz Roters. 2018. "Multiscale Modelling of Hydrogen Transport and Segregation in Polycrystalline Steels" Metals 8, no. 6: 430. https://doi.org/10.3390/met8060430
APA StyleHüter, C., Shanthraj, P., McEniry, E., Spatschek, R., Hickel, T., Tehranchi, A., Guo, X., & Roters, F. (2018). Multiscale Modelling of Hydrogen Transport and Segregation in Polycrystalline Steels. Metals, 8(6), 430. https://doi.org/10.3390/met8060430




