Tensile–Shear Fracture Behavior Prediction of High-Strength Steel Laser Overlap Welds
Abstract
1. Introduction
2. Experimental Procedure
3. Results and Discussion
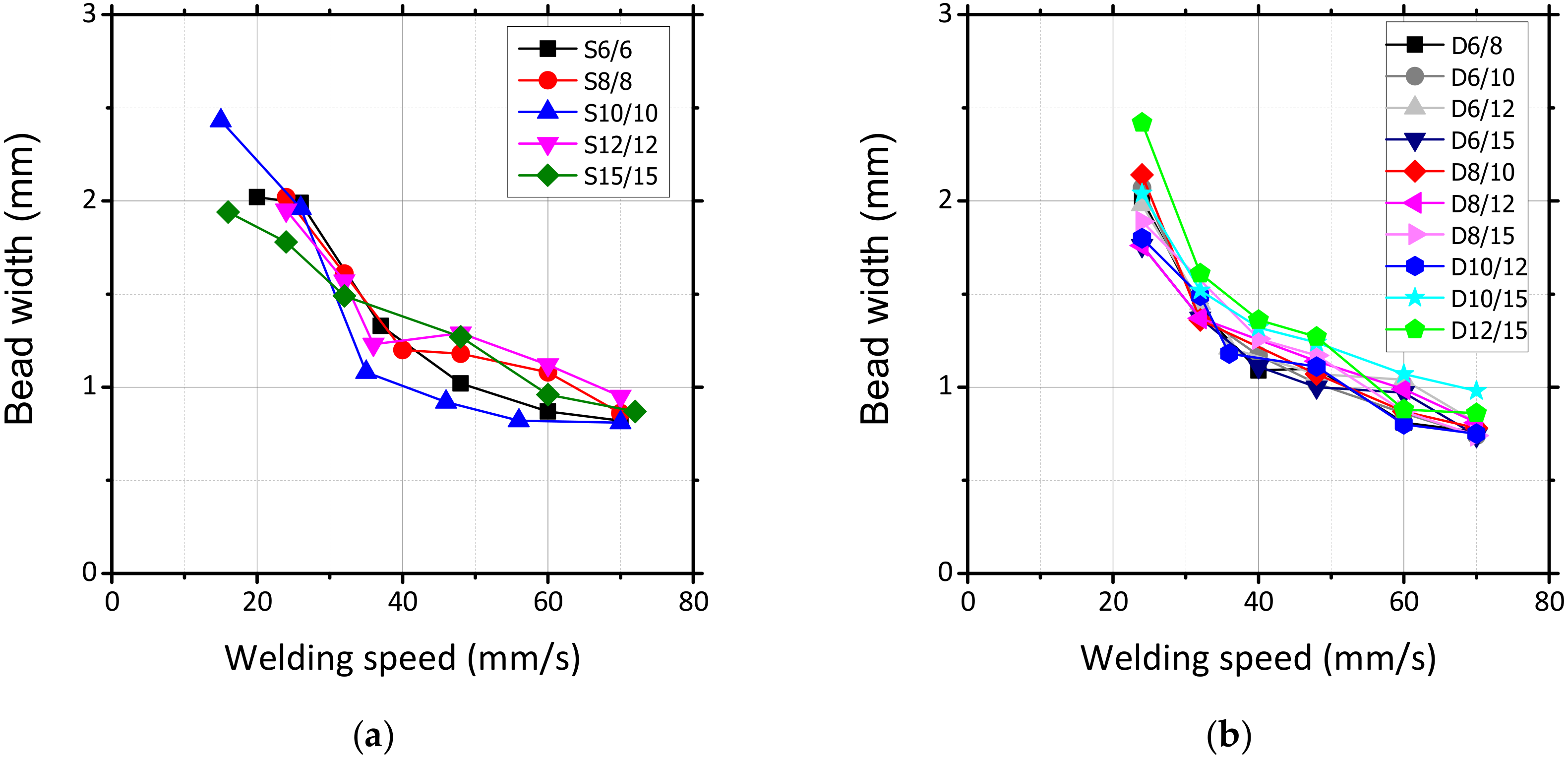
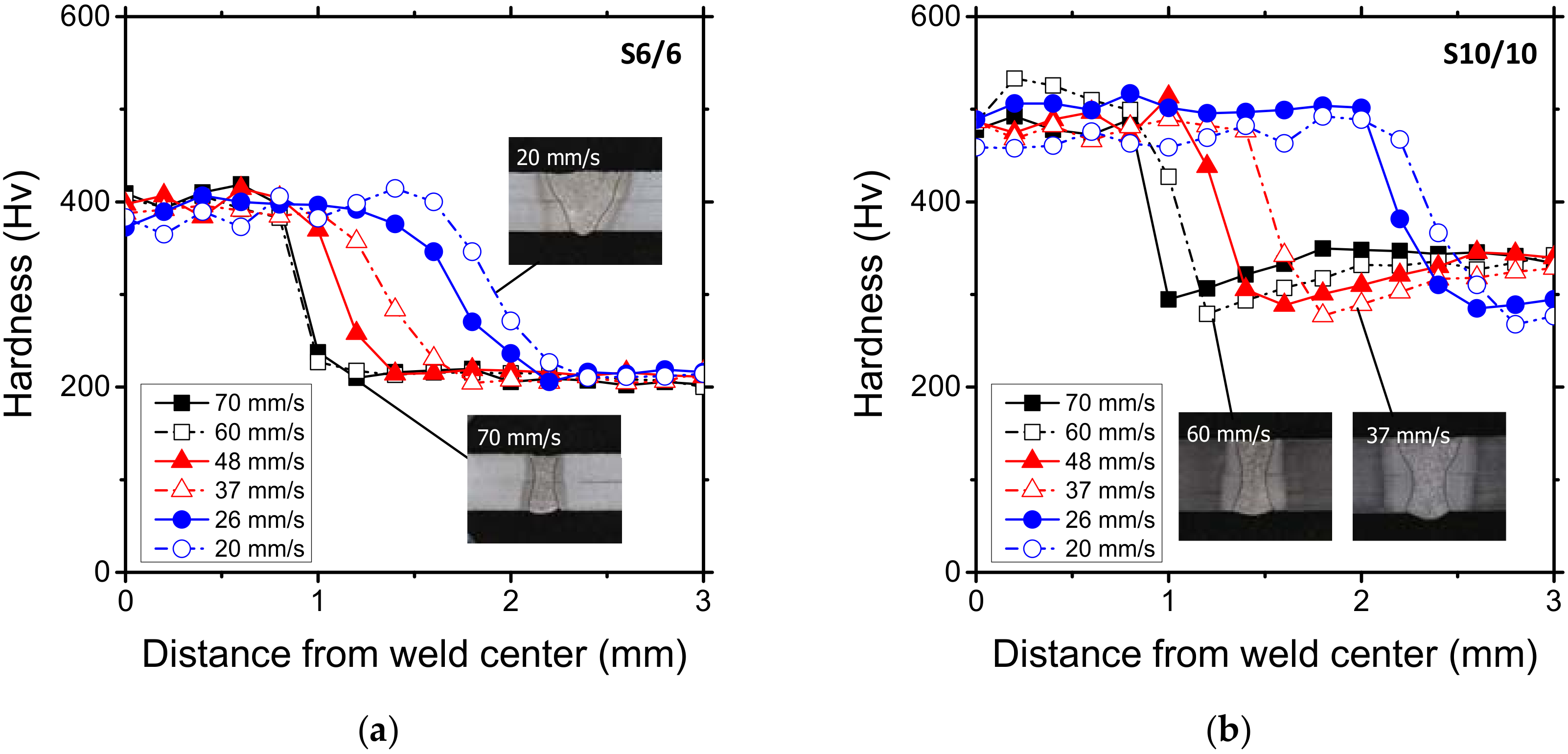
3.1. Laser Weld Characteristics under Various Welding Conditions
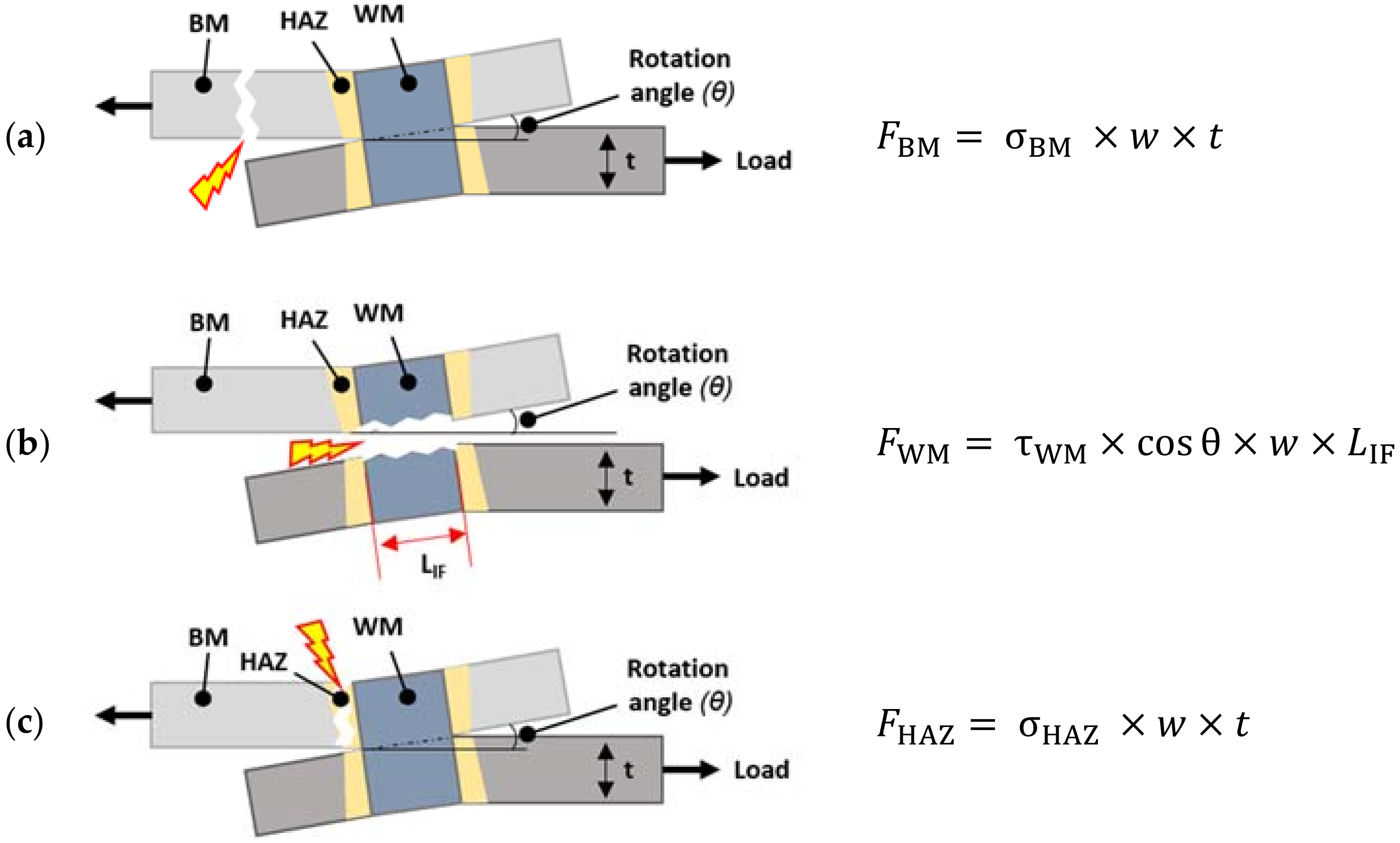
3.2. Fracture Mode Definitions for Overlap Welds
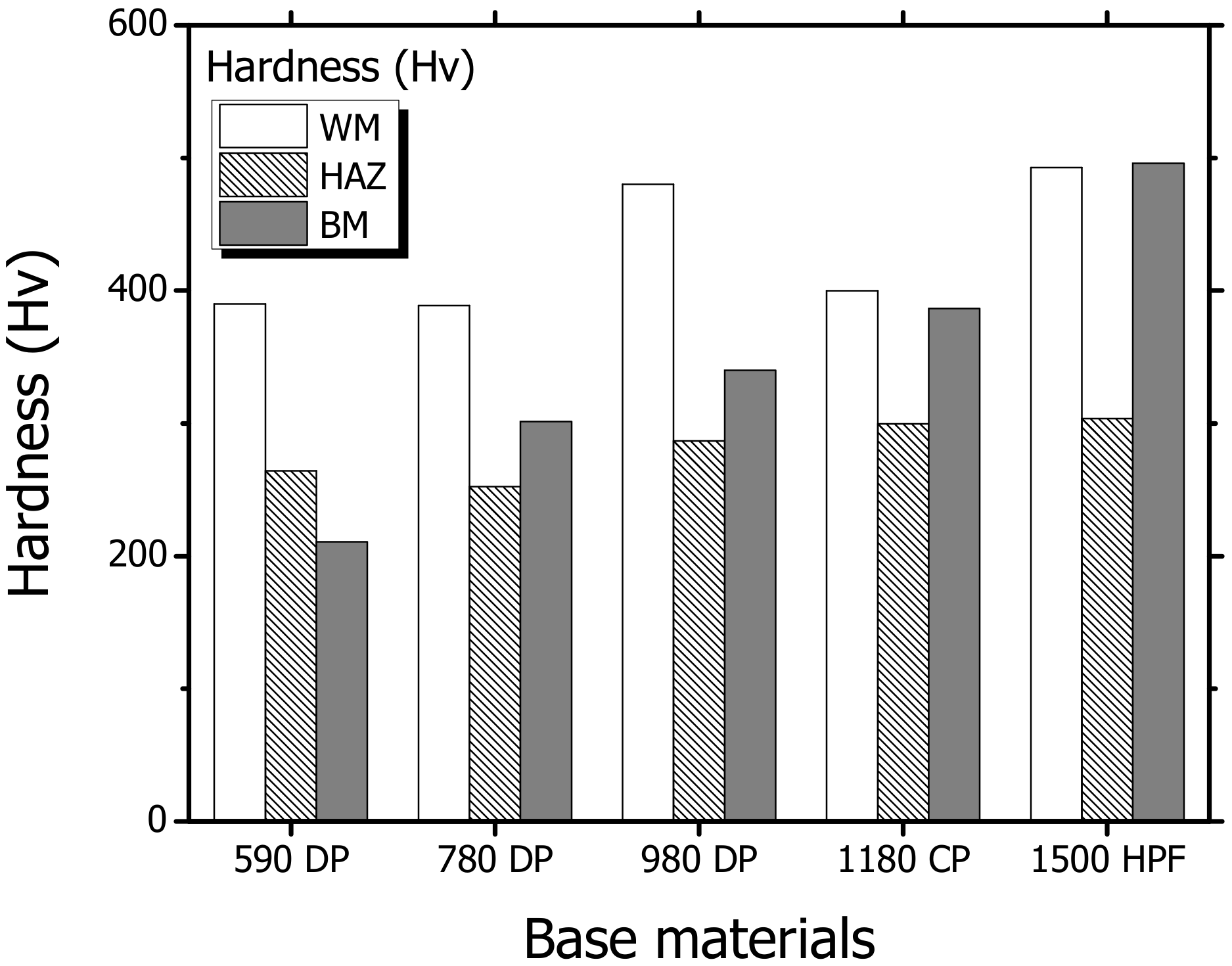
3.3. Estimation of Hardness with Carbon Equivalent
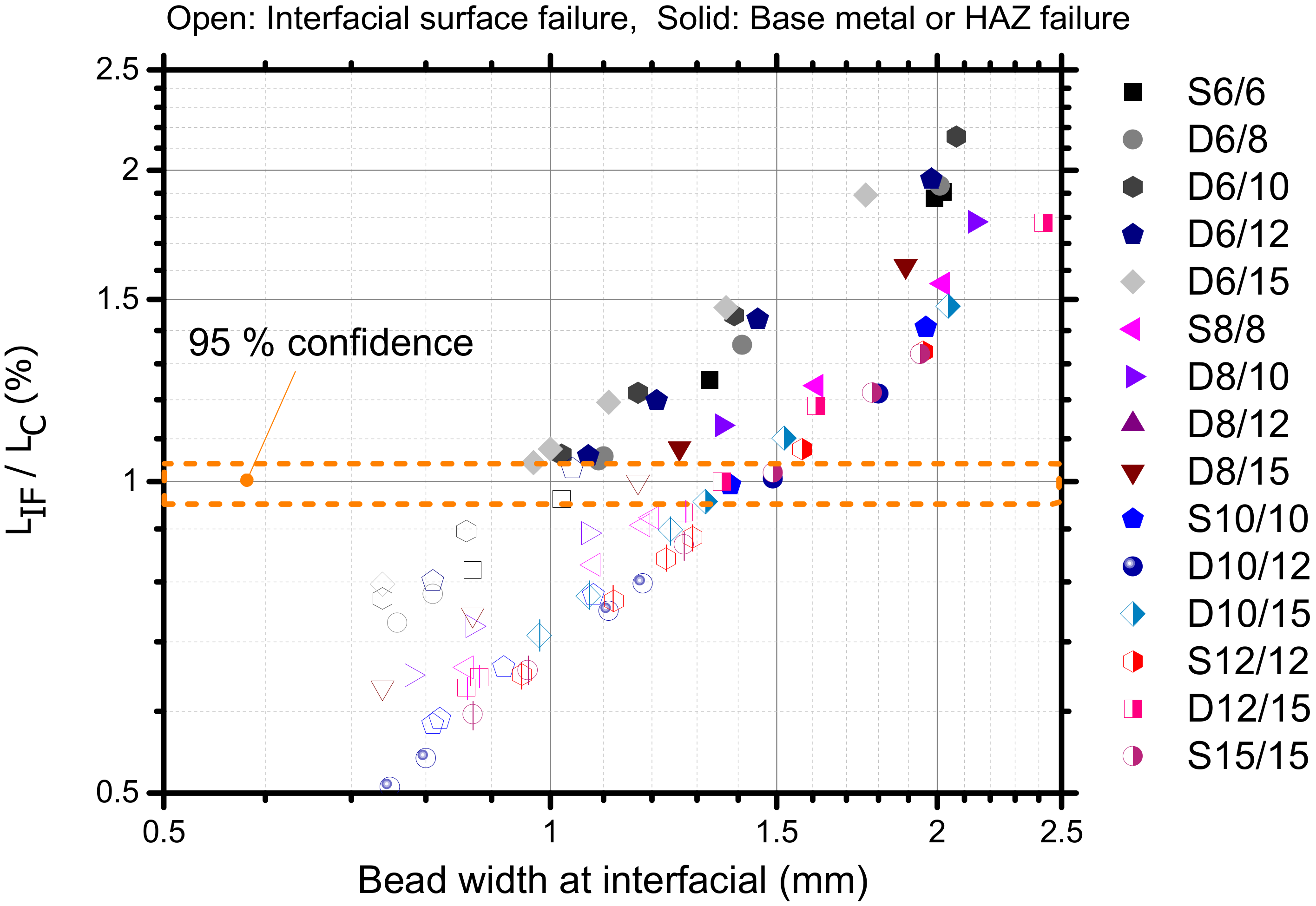
3.4. Critical Interface Bead Width (LIF)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| BM | base metal |
| WM | metals-08-00365 |
| HAZ | weld metal |
| IF | interface fracture |
| DIC | digital image correlation |
| tensile load on BM | |
| tensile stress on BM | |
| tensile load on HAZ | |
| tensile stress on HAZ | |
| shear load on the IF | |
| shear stress on IF | |
| θ | angle of the rotation |
| width of the specimen | |
| thickness of the specimen | |
| measured interface bead width | |
| critical bead width to change the fracture mode | |
| carbon equivalent proposed in [21] | |
| predicted hardness value of WM | |
| predicted hardness value of HAZ | |
| as received tensile strength of the BM | |
| calculated tensile strength of the HAZ | |
| calculated tensile strength of the WM | |
| calculated shear strength of WM |
References
- Lagneborg, R. New steels and steel applications for vehicles. Mater. Des. 1991, 12, 3–14. [Google Scholar] [CrossRef]
- Senuma, T. Physical metallurgy of modern high strength steel sheets. ISIJ Int. 2001, 41, 520–532. [Google Scholar] [CrossRef]
- Takahashi, M. Development of high strength steels for automobiles. Nippon Steel Tech. Rep. 2003, 88, 2–6. [Google Scholar]
- Fan, D.W.; Kim, H.S.; De Cooman, B.C. A review of the physical metallurgy related to the hot press forming of advanced high strength steel. Steel Res. Int. 2009, 80, 241–248. [Google Scholar]
- Karbasian, H.; Tekkaya, A.E. A review on hot stamping. J. Mater. Process. Technol. 2010, 210, 2103–2118. [Google Scholar] [CrossRef]
- Uchihara, M. Joining technologies for automotive steel sheets. Weld. Int. 2011, 25, 249–259. [Google Scholar] [CrossRef]
- Han, T.-K.; Park, B.-G.; Kang, C.-Y. Hardening characteristics of CO2 laser welds in advanced high strength steel. Met. Mater. Int. 2012, 18, 473–479. [Google Scholar] [CrossRef]
- Xia, M.; Biro, E.; Tian, Z.; Zhou, Y.N. Effects of heat input and martensite on HAZ softening in laser welding of dual phase steels. ISIJ Int. 2008, 48, 809–814. [Google Scholar] [CrossRef]
- Mohandas, T.; Reddy, G.M.; Kumar, B.S. Heat-affected zone softening in high-strength low-alloy steels. J. Mater. Process. Technol. 1999, 88, 284–294. [Google Scholar] [CrossRef]
- Biro, E.; McDermid, J.; Embury, J.; Zhou, Y. Softening kinetics in the subcritical heat-affected zone of dual-phase steel welds. Metall. Mater. Trans. A 2010, 41, 2348–2356. [Google Scholar] [CrossRef]
- Kim, C.; Choi, J.-K.; Kang, M.; Park, Y.-D. A study on the CO2 laser welding characteristics of high strength steel up to 1500 MPa for automotive application. J. Achiev. Mater. Manuf. Eng. 2010, 39, 79–86. [Google Scholar]
- Dearden, J.; O’Neill, H. A Guide to the Selection and Welding of Low Alloy Structural Steels; Welding Research Council of the Institute of Welding: Cambridge, UK, 1940. [Google Scholar]
- Ito, Y.; Bessyo, K. Weldability Formula of High Strength Steels: Related to Heat-Affected Zone Cracking; IIW Document IX-567-568; IIW: Warsaw, Poland, 1968. [Google Scholar]
- Yurioka, N.; Suzuki, H. Determination of necessary preheating temperature in steel welding. Weld. J. 1983, 62, 147–153. [Google Scholar]
- Yurioka, N. Physical metallurgy of steel weldability. ISIJ Int. 2001, 41, 566–570. [Google Scholar] [CrossRef]
- Kasuya, T.; Yurioka, N.; Okumura, M. Methods for predicting maximum hardness of heat-affected zone and selecting necessary preheat temperature for steel welding. Nippon Steel Tech. Rep. 1995, 65, 7–14. [Google Scholar]
- Kasuya, T.; Hashiba, Y. Carbon equivalent to assess hardenability of steel and prediction of HAZ hardness distribution. Nippon Steel Tech. Rep. 2007, 95, 53–61. [Google Scholar]
- Kaizu, S.; Shinbo, Y.; Ono, M. Relationship between Vickers hardness of laser weld and chemical composition of steel sheets. Prepr. Natl. Meet. JWS 1994, 55, 118–119. [Google Scholar]
- Taka, T.; Yamamoto, T. The hardness of laser welded metal in steel sheets. In Proceedings of the 34th Material Processing Conference; Japan Laser Processing Society: Osaka, Japan, 1995; pp. 113–122. [Google Scholar]
- Den Uijl, N.J.; Nishibata, H.; Smith, S.; Okada, T.; van der Veldt, T.; Uchihara, M.; Fukui, K. Prediction of post weld hardness of advanced high strength steels for automotive application using a dedicated carbon equivalent number. Weld. World 2008, 52, 18–29. [Google Scholar] [CrossRef]
- Jeon, I.-H.; Kim, C.; Kim, J.-D. Hardness estimation of laser welded boron steel welds with the carbon equivalent. J. Weld. Join. 2016, 34, 1–5. (In Korean) [Google Scholar] [CrossRef]
- Ono, M.; Yoshitake, A.; Ohmura, M. Laser weldability of high-strength steel sheets in fabrication of tailor welded blanks. Weld. Int. 2004, 18, 774–784. [Google Scholar] [CrossRef]
- Miyazaki, Y.; Furusako, S. Tensile shear strength of laser welded lap joints. Nippon Steel Tech. Rep. 2007, 95, 28–34. [Google Scholar]
- Kang, M.; Kim, C.; Lee, J. Weld strength of laser-welded hot-press-forming steel. J. Laser Appl. 2012, 24, 022004. [Google Scholar] [CrossRef]
- Benasciutti, D.; Lanzutti, A.; Rupil, G.; Haeberle, E.F. Microstructural and mechanical characterisation of laser-welded lap joints with linear and circular beads in thin low carbon steel sheets. Mater. Des. 2014, 62, 205–216. [Google Scholar] [CrossRef]
- Furusako, S.; Miyazaki, Y.; Hashimoto, K.; Kobayashi, J. Establishment of a model predicting tensile shear strength and fracture portion of laser-welded lap joints. In Proceedings of the International Congress on Laser Advanced Materials Processing, Osaka, Japan, 27–31 May 2002; pp. 197–202. [Google Scholar]
- Ono, M.; Kabasawa, M.; Omura, M. Static and fatigue strength of laser-welded lap joints in thin steel sheet. Weld. Int. 1997, 11, 462–467. [Google Scholar] [CrossRef]
- Terasaki, T.; Kitamura, T. Prediction of static fracture strength of laser-welded lap joints by numerical analysis. Weld. Int. 2004, 18, 524–530. [Google Scholar] [CrossRef]
- Asim, K.; Lee, J.; Pan, J. Failure mode of laser welds in lap-shear specimens of high strength low alloy (HSLA) steel sheets. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 219–237. [Google Scholar] [CrossRef]
- Lee, J.; Asim, K.; Pan, J. Modeling of failure mode of laser welds in lap-shear specimens of HSLA steel sheets. Eng. Fract. Mech. 2011, 78, 374–396. [Google Scholar] [CrossRef]
- Ha, J.; Huh, H. Failure characterization of laser welds under combined loading conditions. Int. J. Mech. Sci. 2013, 69, 40–58. [Google Scholar] [CrossRef]
- Ma, J.; Kong, F.; Liu, W.; Carlson, B.; Kovacevic, R. Study on the strength and failure modes of laser welded galvanized DP980 steel lap joints. J. Mater. Process. Technol. 2014, 214, 1696–1709. [Google Scholar] [CrossRef]
- Yang, Y.-P.; Cao, Z.; Gould, J.; McGaughy, T.; Jennings, J. Develop an excel-based modeling tool to predict weld and HAZ cooling rate and hardness for pipeline welding. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015. [Google Scholar]
- Miyazaki, Y.; Sakiyama, T.; Kodama, S. Welding techniques for tailored blanks. Nippon Steel Tech. Rep. 2007, 95, 2–10. [Google Scholar]
- Ion, J.; Easterling, K.E.; Ashby, M. A second report on diagrams of microstructure and hardness for heat-affected zones in welds. Acta Metall. 1984, 32, 1949–1962. [Google Scholar] [CrossRef]
- Pavlina, E.; Van Tyne, C. Correlation of yield strength and tensile strength with hardness for steels. J. Mater. Eng. Perform. 2008, 17, 888–893. [Google Scholar] [CrossRef]

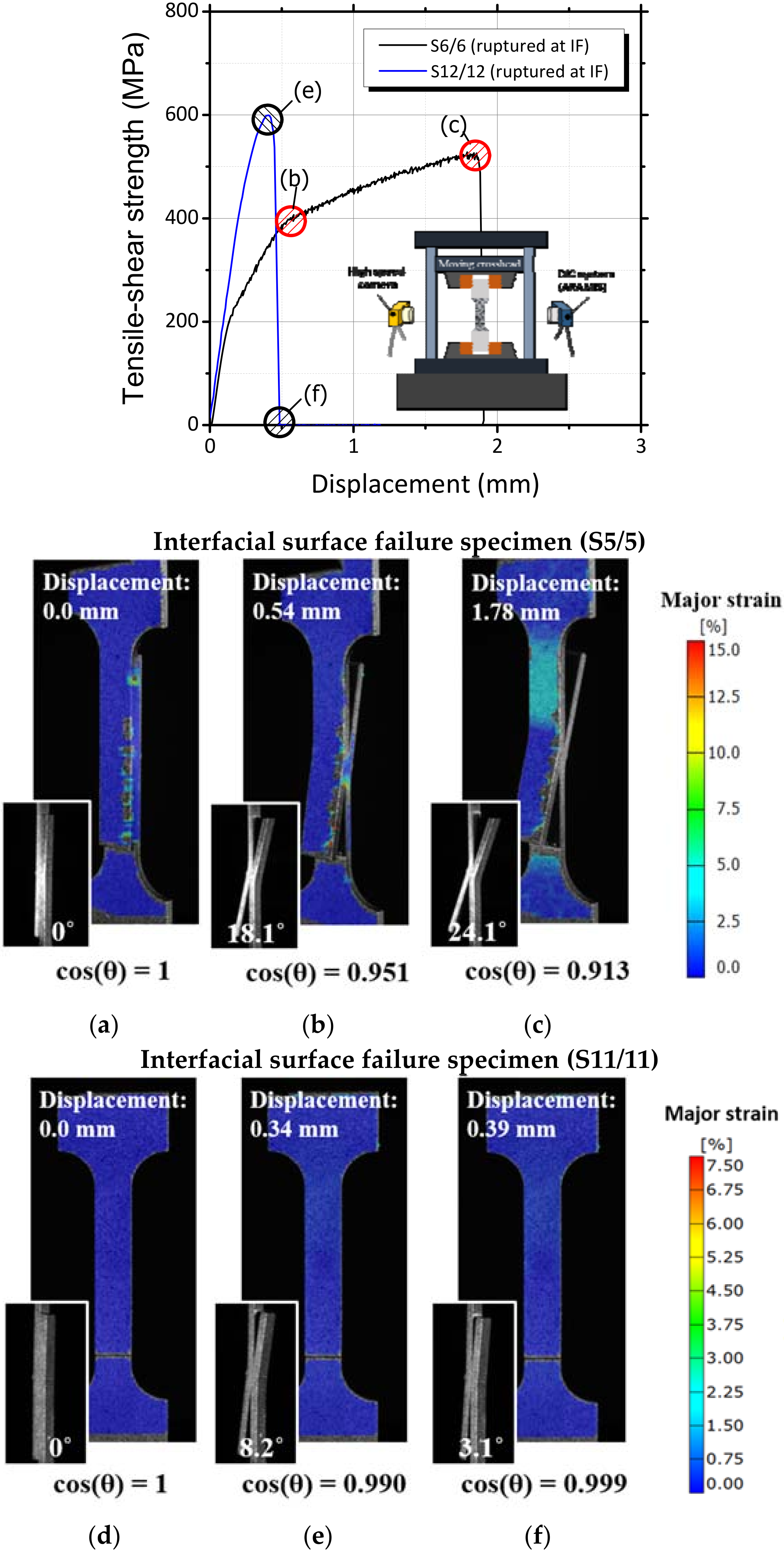
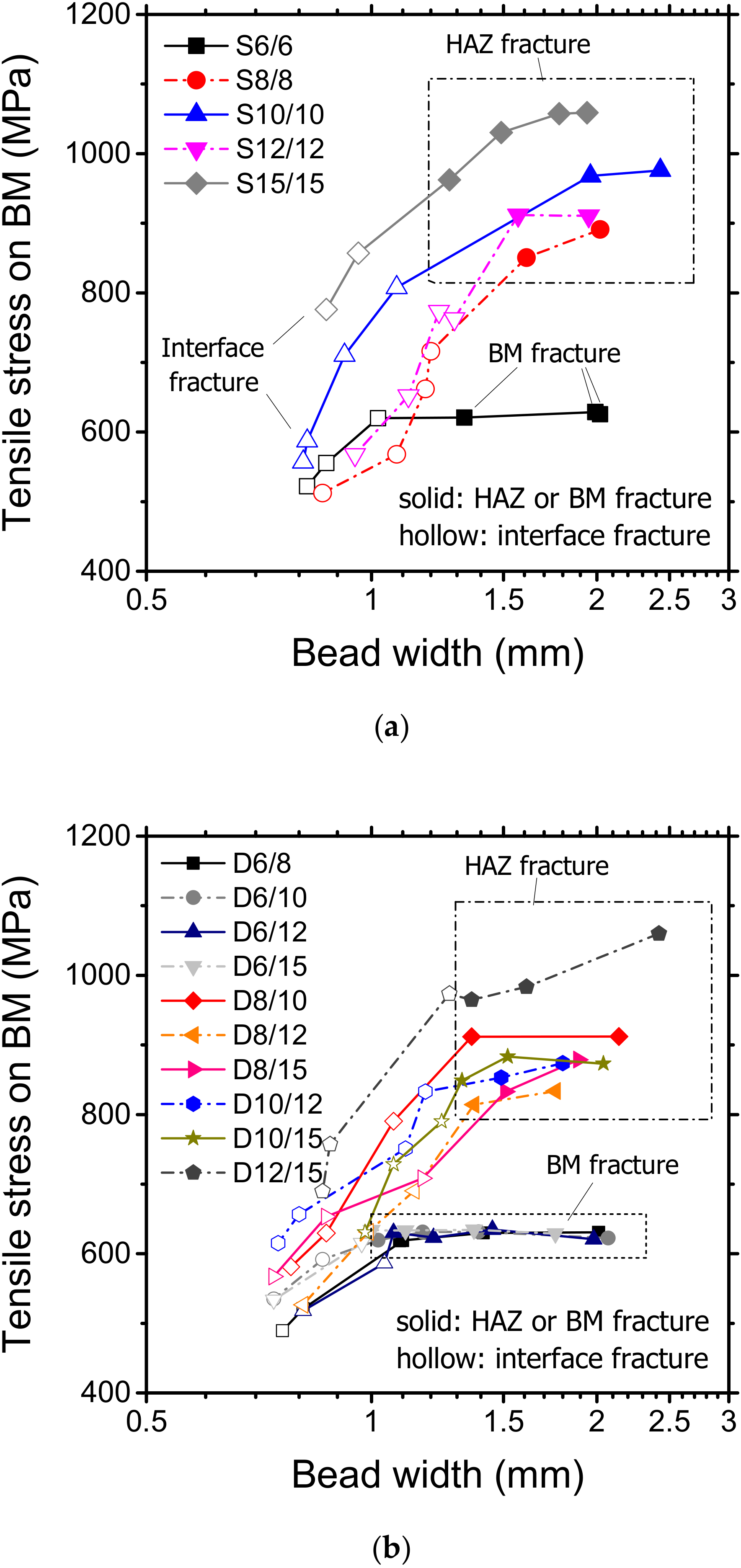
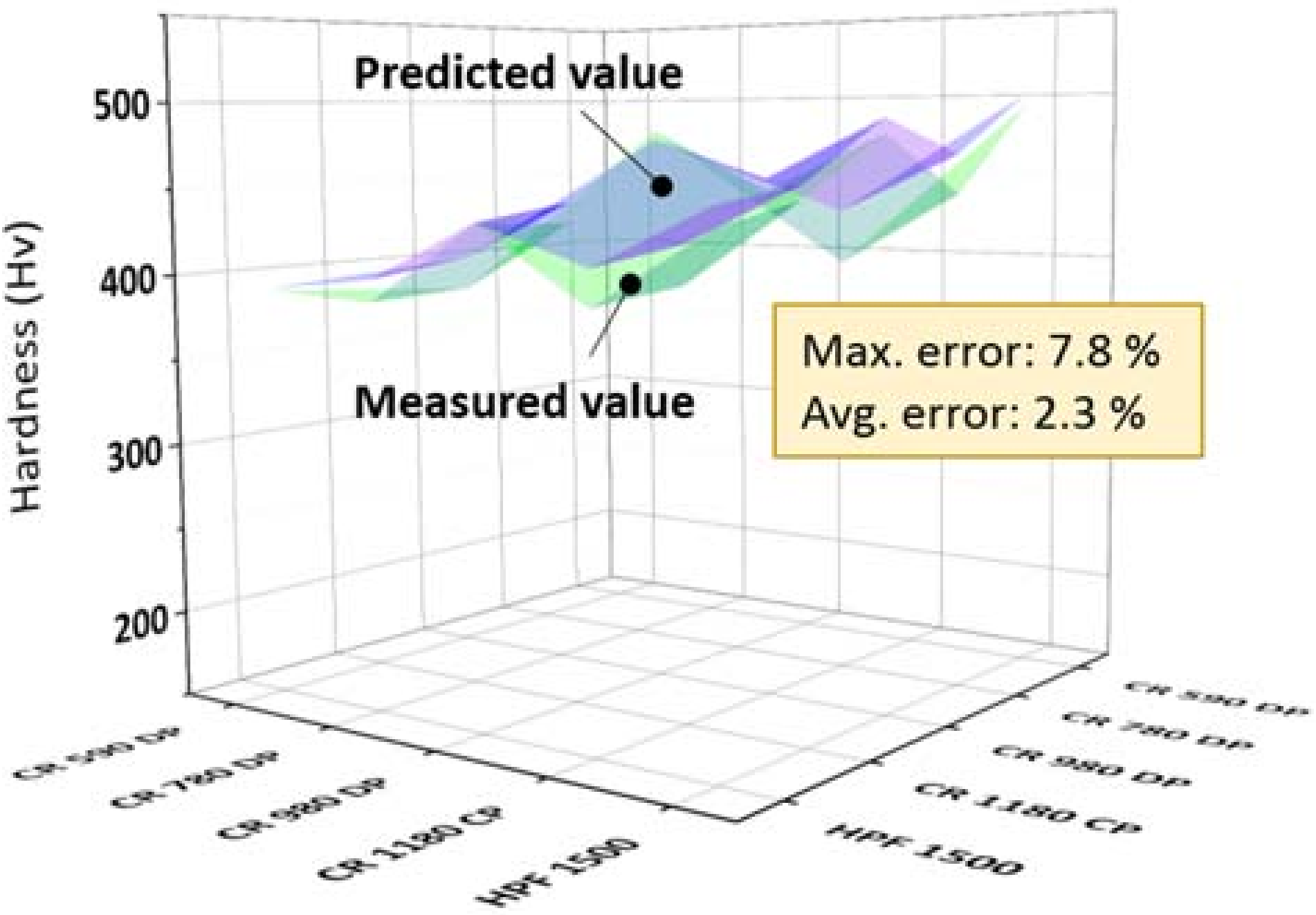
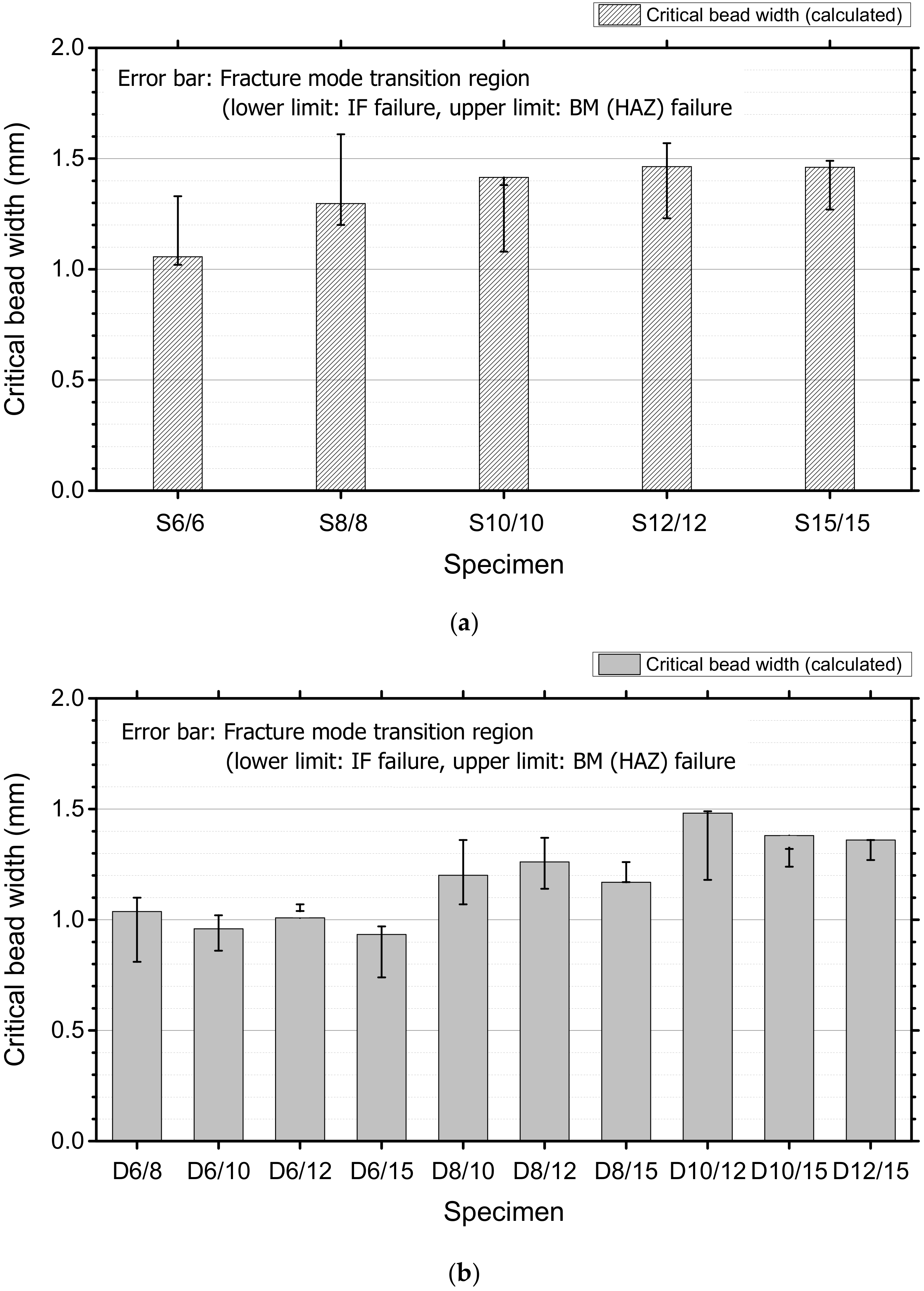
| Base Materials | C | Si | Mn | P | S | Cr | B |
|---|---|---|---|---|---|---|---|
| 590 DP (1.2 mm) | 0.078 | 0.363 | 1.808 | 0.011 | 0.001 | - | - |
| 780 DP (1.2 mm) | 0.070 | 0.977 | 2.264 | 0.010 | 0.015 | - | - |
| 980 DP (1.2 mm) | 0.170 | 1.340 | 2.000 | 0.016 | 0.001 | - | - |
| 1180 CP (1.2 mm) | 0.110 | 0.110 | 2.790 | 0.019 | 0.004 | 1.040 | - |
| 1500 HPF (1.1 mm) | 0.216 | 0.240 | 1.255 | 0.002 | 0.002 | 0.001 | 0.003 |
| (a) | ||
| Specimen. | Top Plate | Top Plate |
| S6/6 | CR 590 DP | CR 590 DP |
| S8/8 | CR 780 DP | CR 780 DP |
| S10/10 | CR 980 DP | CR 980 DP |
| S12/12 | CR 1180 CP | CR 1180 CP |
| S15/15 | HPF 1500 | HPF 1500 |
| (b) | ||
| Specimen. | Top Plate | Bottom Plate |
| D6/8 | CR 590 DP | CR 780 DP |
| D6/10 | - | CR 980 DP |
| D6/12 | - | CR 1180 CP |
| D6/15 | - | HPF 1500 |
| D8/10 | CR 780 DP | CR 980 DP |
| D8/12 | - | CR 1180 CP |
| D8/15 | - | HPF 1500 |
| D10/12 | CR 980 DP | CR 1180 CP |
| D10/15 | - | HPF 1500 |
| D12/15 | CR 1180 CP | HPF 1500 |
| Parameters | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | Level 6 |
|---|---|---|---|---|---|---|
| Focal position (mm) | 0 | 5 | 10 | 10 | 15 | 20 |
| Laser spot size (mm) | 0.3 | 0.34 | 0.46 | 0.46 | 0.55 | 0.65 |
| Apparent power density (W/mm2) | 13,440 | 10,463 | 5716 | 5716 | 3999 | 2863 |
| Welding speed (mm/s) | 70 | 60 | 48 | 37 | 26 | 20 |
| Heat input per unit length (J/mm) | 54.3 | 63.3 | 79.2 | 102.7 | 146.2 | 190.0 |
| (a) | ||||||||||
| Specimen | S6/6 | S8/8 | S10/10 | S12/12 | S15/15 | |||||
| Measured hardness (Hv) | 390.0 | 388.8 | 480.0 | 399.9 | 492.7 | |||||
| Predicted hardness (Hv) | 391.4 | 407.1 | 475.0 | 431.0 | 499.7 | |||||
| CELB | 0.157 | 0.180 | 0.277 | 0.214 | 0.312 | |||||
| Error (%) | 0.4 | 4.7 | 1.0 | 7.8 | 1.4 | |||||
| (b) | ||||||||||
| Specimen | D6/8 | D6/10 | D6/12 | D6/15 | D8/10 | D8/12 | D8/15 | D10/12 | D10/15 | D12/15 |
| Measured hardness (Hv) | 386.6 | 432.2 | 390.4 | 434.0 | 429.4 | 396.4 | 445.6 | 446.0 | 478.4 | 442.2 |
| Predicted hardness (Hv) | 399.3 | 433.2 | 411.2 | 445.5 | 441.1 | 419.0 | 453.4 | 453.0 | 487.4 | 465.3 |
| Error (%) | 3.3 | 0.2 | 5.3 | 2.6 | 2.7 | 5.7 | 1.8 | 1.6 | 1.9 | 5.2 |
| (a) | ||||||||||
| Phase fraction | Hm | Hb | Hf | Vm | Vb | Vfp | ||||
| 590 DP | 357.95 | 290.27 | 151.67 | 0.44 | 0.06 | 0.50 | ||||
| 780 DP | 371.86 | 292.97 | 125.34 | 0.47 | 0.03 | 0.50 | ||||
| 980 DP | 473.84 | 337.26 | 117.19 | 0.55 | 0.02 | 0.43 | ||||
| 1180 CP | 383.16 | 321.56 | 201.17 | 0.53 | 0.01 | 0.46 | ||||
| 1500 HPF | 479.80 | 349.89 | 173.57 | 0.54 | 0.04 | 0.42 | ||||
| (b) | ||||||||||
| Base metal | 590 DP | 780 DP | 980 DP | 1180 CP | 1500 HPF | |||||
| Measured hardness (Hv) | 264.2 | 252.2 | 286.8 | 299.7 | 303.6 | |||||
| Predicted hardness (Hv) | 250.2 | 247.2 | 317.7 | 298.2 | 345.8 | |||||
| Error (%) | 5.3 | 2.0 | 10.8 | 0.5 | 13.9 | |||||
| (a) Similar Material Combination | ||||||||||
| Specimen | S6/6 | S8/8 | S10/10 | S12/12 | S15/15 | |||||
| 609.0 | 816.5 | 1023.3 | 1272.7 | 1545.0 | ||||||
| 817.4 | 807.4 | 1037.8 | 974.0 | 1129.5 | ||||||
| 738.2 | 767.8 | 895.9 | 812.9 | 942.4 | ||||||
| (b) Dissimilar Material Combinations | ||||||||||
| Specimen | D6/8 | D6/10 | D6/12 | D6/15 | D8/10 | D8/12 | D8/15 | D10/12 | D10/15 | D12/15 |
| 609.0 | 816.5 | 1023.3 | 1272.7 | |||||||
| 817.4 | 807.4 | 1037.8 | 974.0 | |||||||
| 753.1 | 817.0 | 775.5 | 840.2 | 831.9 | 790.4 | 855.1 | 854.4 | 919.2 | 877.6 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, M.; Jeon, I.-H.; Han, H.N.; Kim, C. Tensile–Shear Fracture Behavior Prediction of High-Strength Steel Laser Overlap Welds. Metals 2018, 8, 365. https://doi.org/10.3390/met8050365
Kang M, Jeon I-H, Han HN, Kim C. Tensile–Shear Fracture Behavior Prediction of High-Strength Steel Laser Overlap Welds. Metals. 2018; 8(5):365. https://doi.org/10.3390/met8050365
Chicago/Turabian StyleKang, Minjung, In-Hwan Jeon, Heung Nam Han, and Cheolhee Kim. 2018. "Tensile–Shear Fracture Behavior Prediction of High-Strength Steel Laser Overlap Welds" Metals 8, no. 5: 365. https://doi.org/10.3390/met8050365
APA StyleKang, M., Jeon, I.-H., Han, H. N., & Kim, C. (2018). Tensile–Shear Fracture Behavior Prediction of High-Strength Steel Laser Overlap Welds. Metals, 8(5), 365. https://doi.org/10.3390/met8050365






