1. Introduction
Laser beam welding (LBW) is a material-joining technique that applies laser radiation to melt the base material and create the welding joint. LBW process is related to other traditional welding methods, such as electron beam welding (EBW), tungsten plasma arc welding (PAW), or inert gas tungsten arc welding (TIG). LBW applies a high power industrial laser to create a narrow and deep melt pool between the parts to be welded. Laser is a highly concentrated heat source that can be easily automated and installed on industrial welding cells, providing high welding speeds for many industrial applications. Nevertheless, factors such as the laser beam quality or the processed materials have a great influence on the resulting geometry, microstructure, and residual stress distribution. Therefore, final results are directly dependent on the process input parameters [
1], which means that process parameters must be carefully selected for achieving the desired quality [
2].
LBW modeling represents a basic tool for predicting the temperature field and giving accurate information about shape of the melt pool and final shape of the bead, depending on the process parameters (welding speed, laser power, workpiece geometry, etc.) [
3,
4,
5]. This fact has a direct impact on reducing the costs derived from experimental tests [
6].
Modern aircraft engines require materials capable of withstanding high temperatures without lowering their mechanical properties. In order to fulfil this task, nickel-based alloys comprise about 50% of the total weight of the engines used in aerospace industry, providing high temperature strength and good resistance against wear or corrosion, thanks to their chemical stability [
7]. Aeronautical structures design and fabrication searches for minimum weight models that may put up with several flight work conditions. Since Ni alloys’ machinability is relatively low, and the cost of the material is high, welding techniques present high advantages over machining. On the one hand, welding can be used for building complex structures from smaller parts and, on the other hand, wasted material and chip formation is drastically reduced.
Inconel 718 superalloy is widely used in gas turbine components, such as tail bearing housings (TBH), which have to deal with high temperature gradients and corrosive environments. The strength of the material comes mainly from small γ′ and γ′′ precipitates that are high in Ni content [
8]. On the other hand, despite that the Inconel 718 alloy has a reasonably good resistance against weld solidification cracking, it is slightly prone to the appearance of microfissures in the heat affected zone (HAZ) [
9], so LBW is an appropriate joining method, as it affects just a narrow zone.
Regarding this fact, modeling and study are needed in order to check weld integrity, as LBW is an innovative assembling method both for dispensing rivets and for its good qualities compared to other conventional welding techniques [
10]. LBW is also suitable for joining both similar and dissimilar metal alloys. This last case is given the possibility to benefit from the properties that each welded part can offer for different working conditions [
11], giving an increasing value to the dissimilar metal alloys’ welding process in the aerospace industry, due to its direct impact on cost reduction and design flexibility [
12].
Furthermore, LBW has arisen as an alternative to electron beam welding (EBW), which can only be used in a vacuum chamber, and requires a more complex fixturing, which results in a much more expensive process.
In terms of pores formation, nickel-based alloys with chromium (as Inconel 718) are susceptible to this phenomenon during the welding process, having to resort to protective gases in order to avoid pores [
13].
The laser power level that materials absorb can be reasonably predicted, so the effects of the heat input may be accurately estimated by a numerical model [
14]. The absorptivity of the material represents the ratio of the energy that the workpiece absorbs, it is one of the bases for any heat transfer calculation [
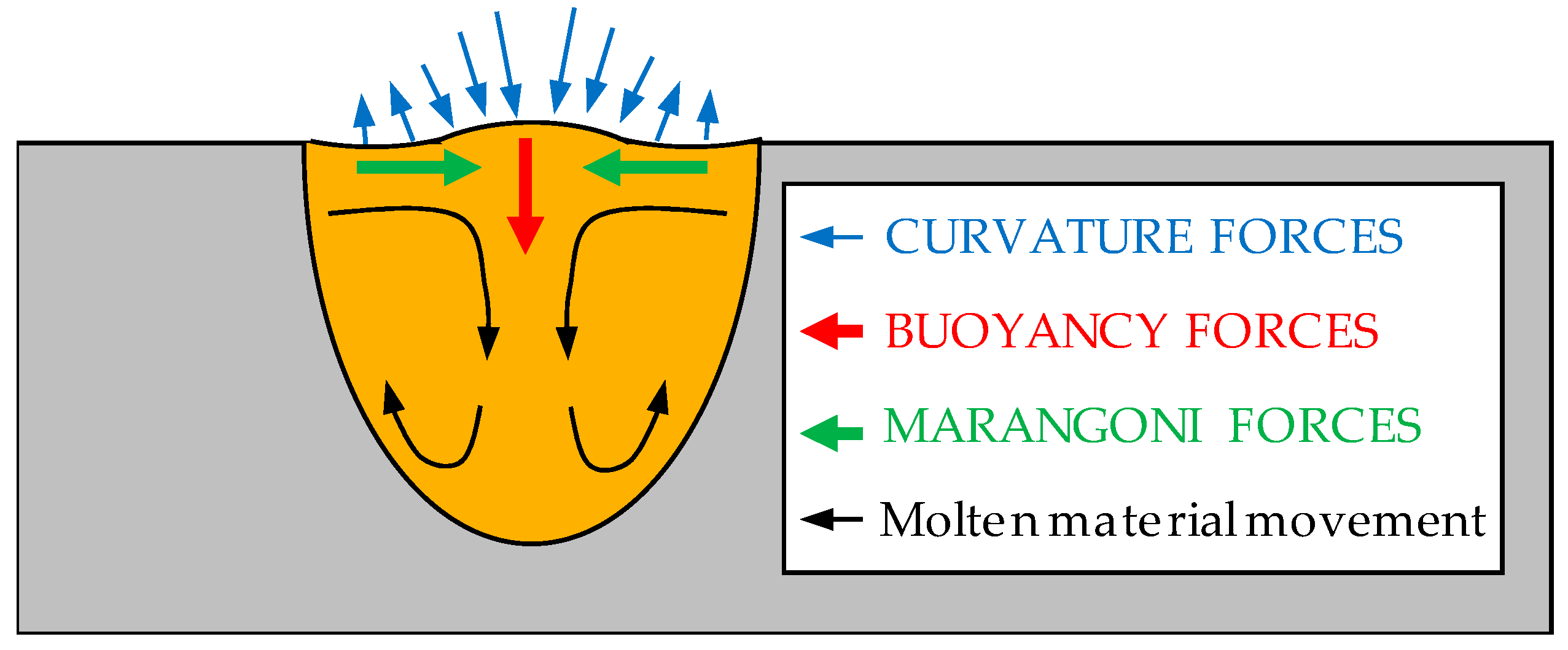
15], and hence, modeling must consider this characteristic for any reliable result. Moreover, other effects need to be considered in laser welding processes, such as convective and thermocapillary forces that cause deformations during solidification after the melting phase. These forces are generated due to a decrease of the surface tension of the molten material as temperature increases, which leads to material flow between hot and cold regions [
16]. This phenomenon, named as the Marangoni effect, has a direct impact on the weld bead geometry [
17]. Therefore, the model must consider this effect in order to achieve the desired accuracy and predict the welding profile.
At the beginning of the LBW technology, Swift-Hook and Gick stated that lasers opened a wide range of possibilities according to deep welds [
18], and Klemens declared that many factors, such as heat, vapor flow, gravity, or surface tension, are directly connected with the final shape of the seam. Moreover, the need for experimental tests for validating the theoretical heat models took force for identifying unknown factors [
19].
In the 1980s, Mazumder praised the importance of better understanding the melt pool generation and fluid flow, in order to improve the potential of the mathematical models, making them predictive powerful tools [
15]. In the same way, Goldak et al. asserted that the prediction of aspects such as the strength of the welded structures, which is directly related to residual stress or distortions, called for precise analysis of the thermal cycles for further modeling [
20].
Afterwards, Bonollo et al. assured that the laser welding dynamics were not entirely understood, despite that theoretical evaluation and subsequent experimental validation had enabled development of the comprehension of the LBW technique [
21]. This statement was confirmed by Kaplan et al., who placed value on modeling for improving the physical understanding of the LBW process [
22]. Ducharme et al., for their part, pointed out that modeling allowed for demonstration of the relationship between the keyhole and the melt pool [
23].
Sudnik et al. alleged the need for new theoretical work, in order to better the laser welding process, as well as its control and the description of the defects. This was grounded on the fact that many heat conduction models did not achieve the desired accuracy when predicting the weld bead geometry [
24]. Nevertheless, Tsirkas et al. pointed the difficulty of modeling the welding process, as thermal, mechanical, and metallurgical phenomena take place at the same time [
25]. Furthermore, Gery et al. concluded that the experimental work is mandatory for determining relations between heat source models and subsequent empirical testing [
26].
Later, Kazemi and Goldak continued maintaining the idea that modeling the laser keyhole welding was still challenging, and defended the idea of simplifying the models for describing the temperature fields [
6]. In turn, Zhao et al. affirmed that the coexistence of three different phases (plasma, liquid, and solid) added to the complex keyhole behavior and the forces acting in the weld pool made modeling still difficult [
27].
Likewise, Kubiak et al. underlined the necessity of an innovative focusing on the theory and numerical solution techniques used for LBW, as this process offers characteristic heat distributions compared to traditional welding methods [
28]. However, Zhang et al. pointed out that despite the advances in laser deep penetration knowledge due to numerical simulation, many issues still remain unexplored [
29].
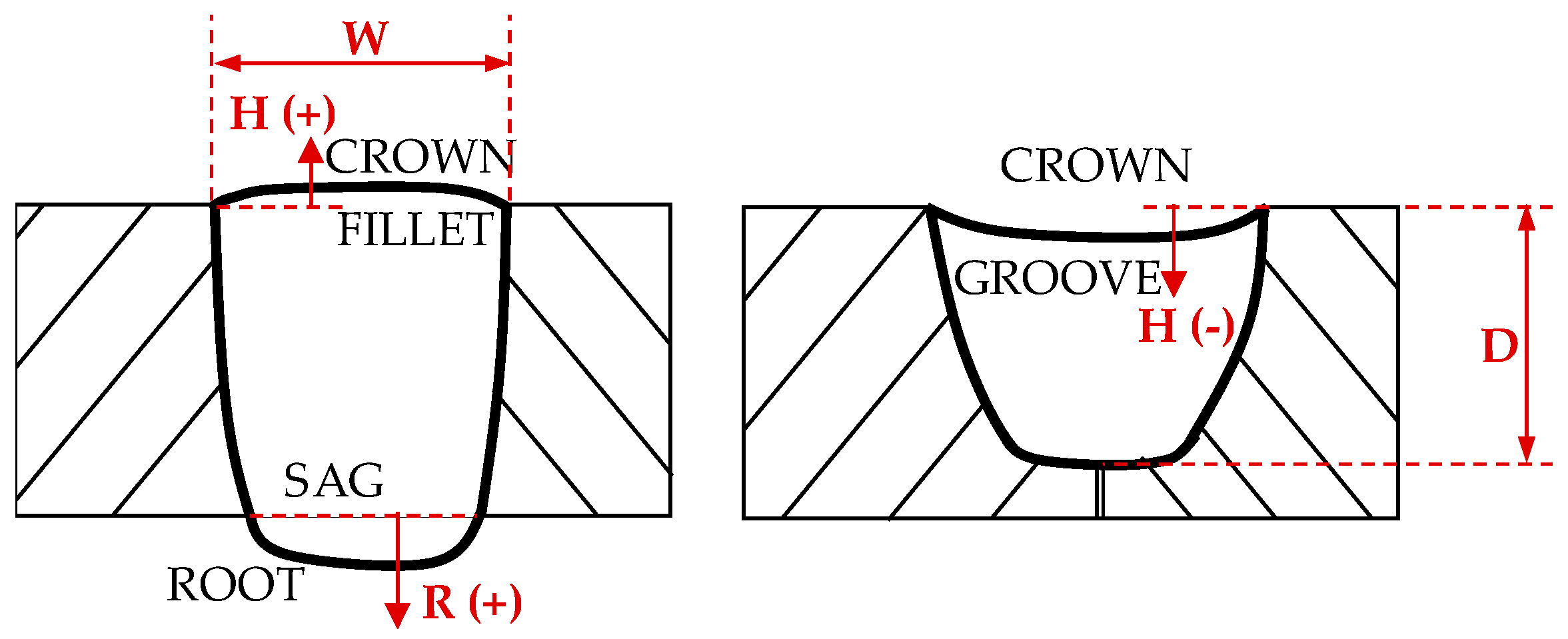
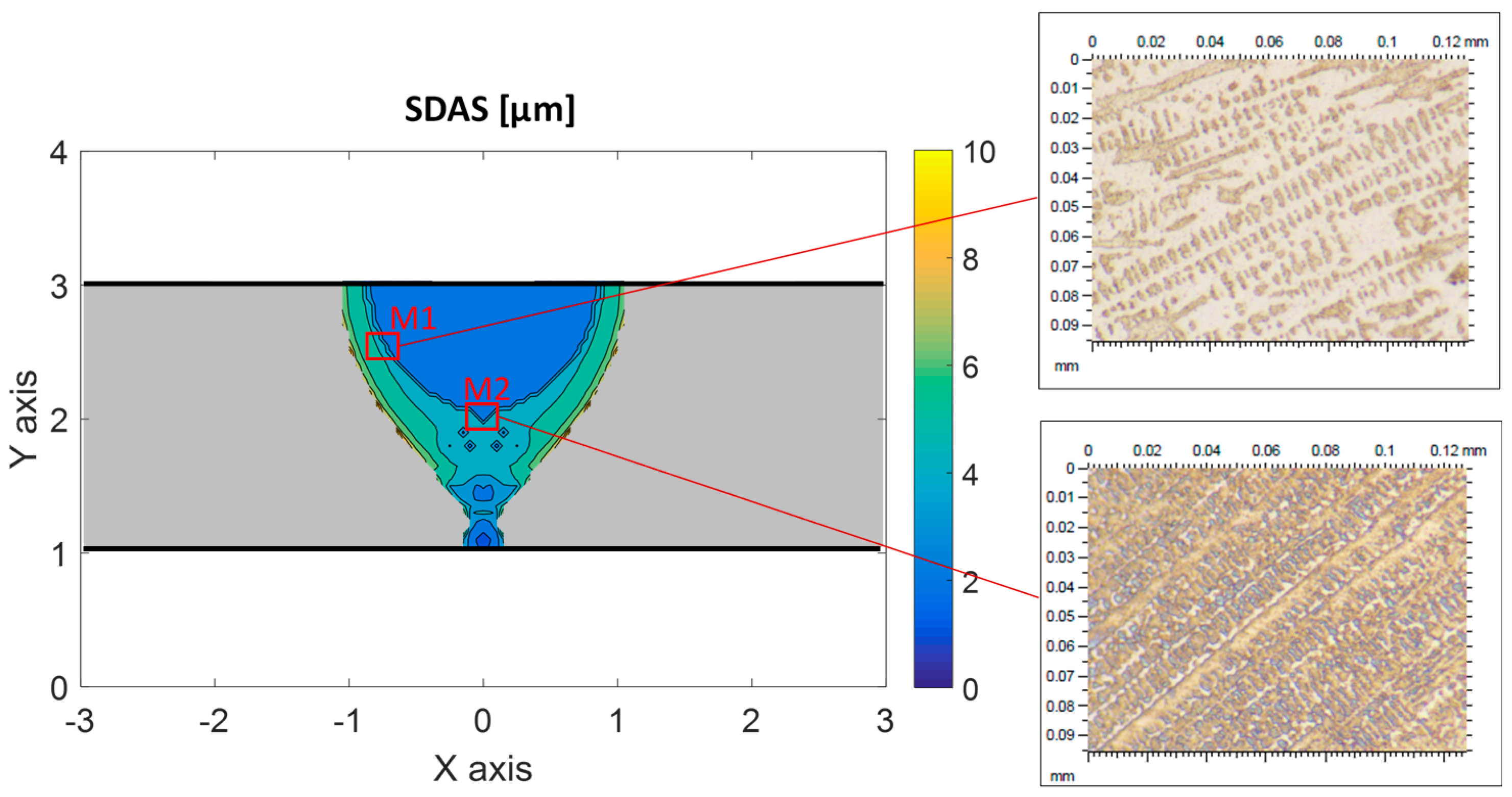
For this reason, it is concluded that there is a need, in the aerospace industry, to develop a model that predicts the geometry of the resulting joint when welding thin Inconel 718 plates. Therefore, a model that considers the melt pool dynamics during the welding process is developed. The model takes into account gravity, Marangoni, and surface forces caused by the curvature developed by the weld bead. Moreover, the numeric tool is capable of predicting the generated secondary dendrite arm spacing based on the thermal field variations during the process. In addition, the obtained results are experimentally validated under different conditions. Employed nomenclature is detailed in
Table 1.