Determination of the Critical Stress Associated with Dynamic Phase Transformation in Steels by Means of Free Energy Method
Abstract
:1. Introduction
2. Materials and Methods
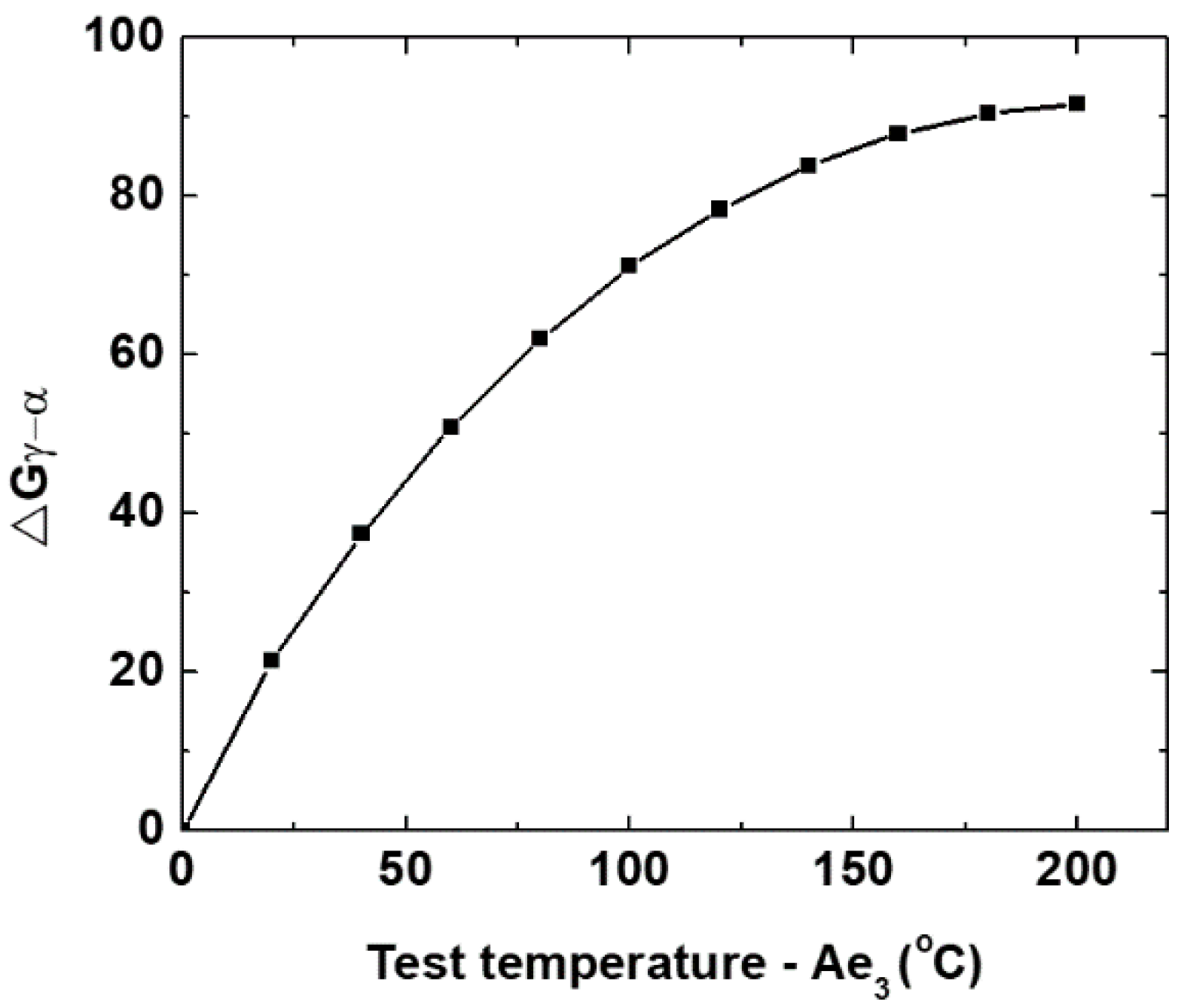
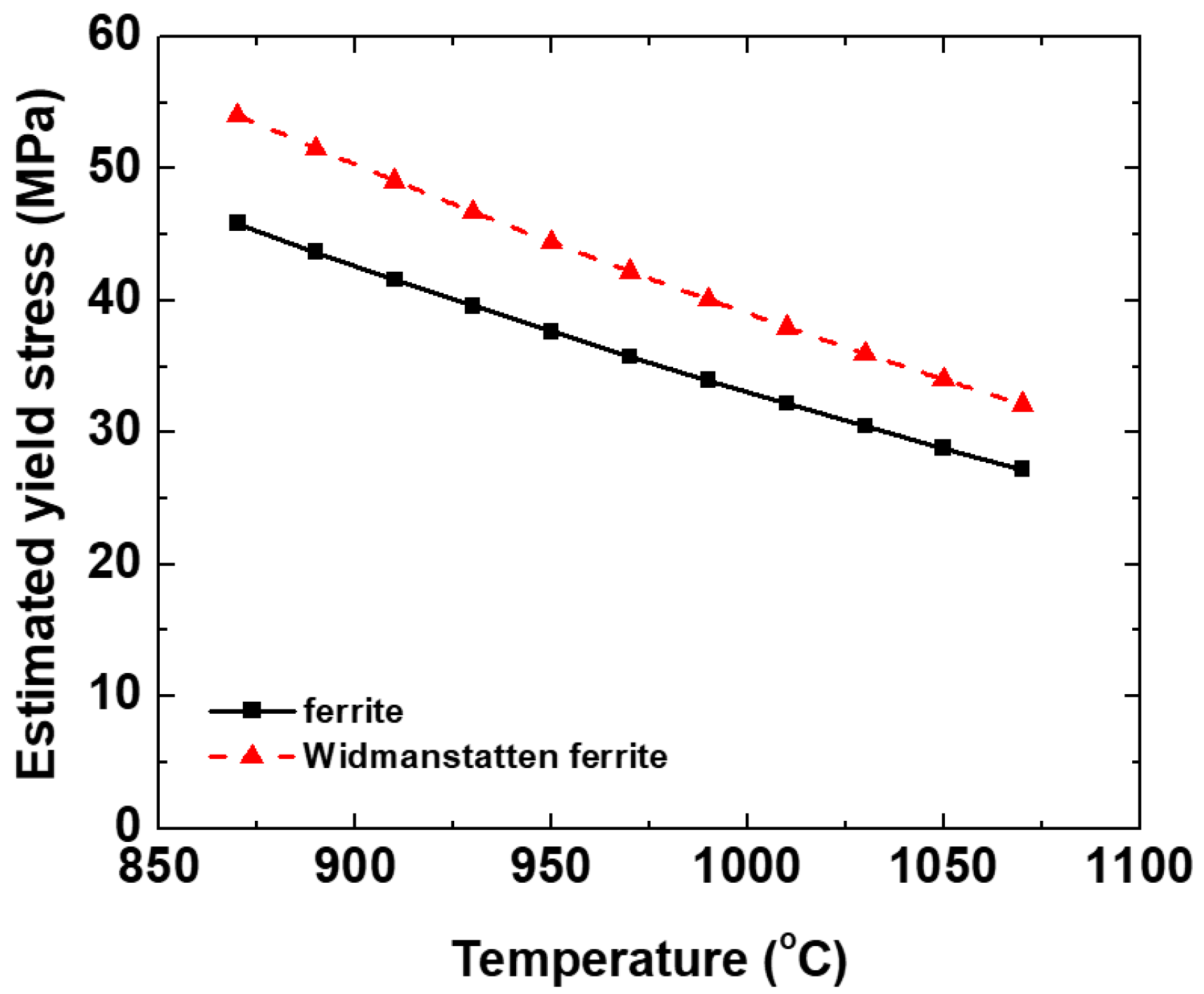
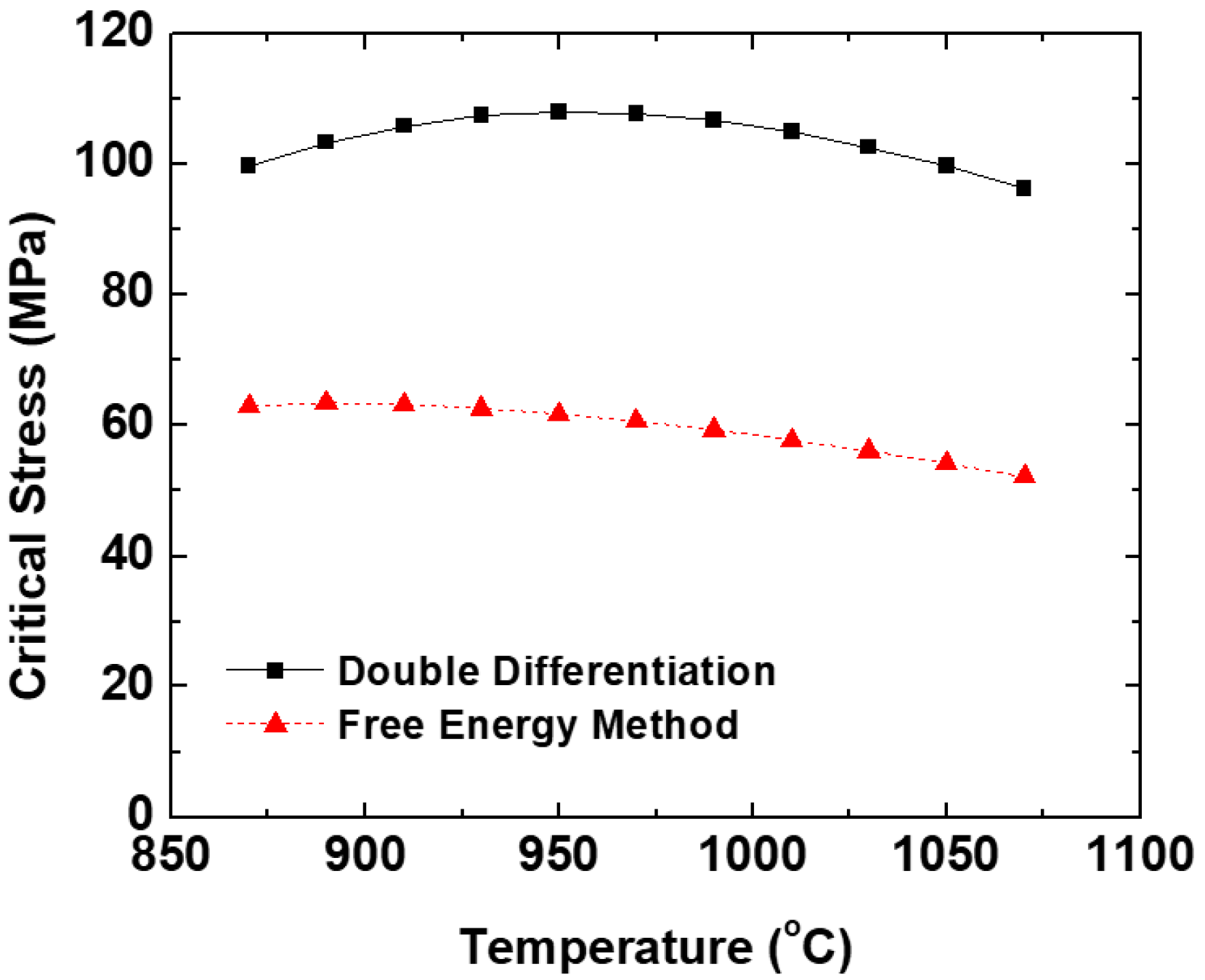
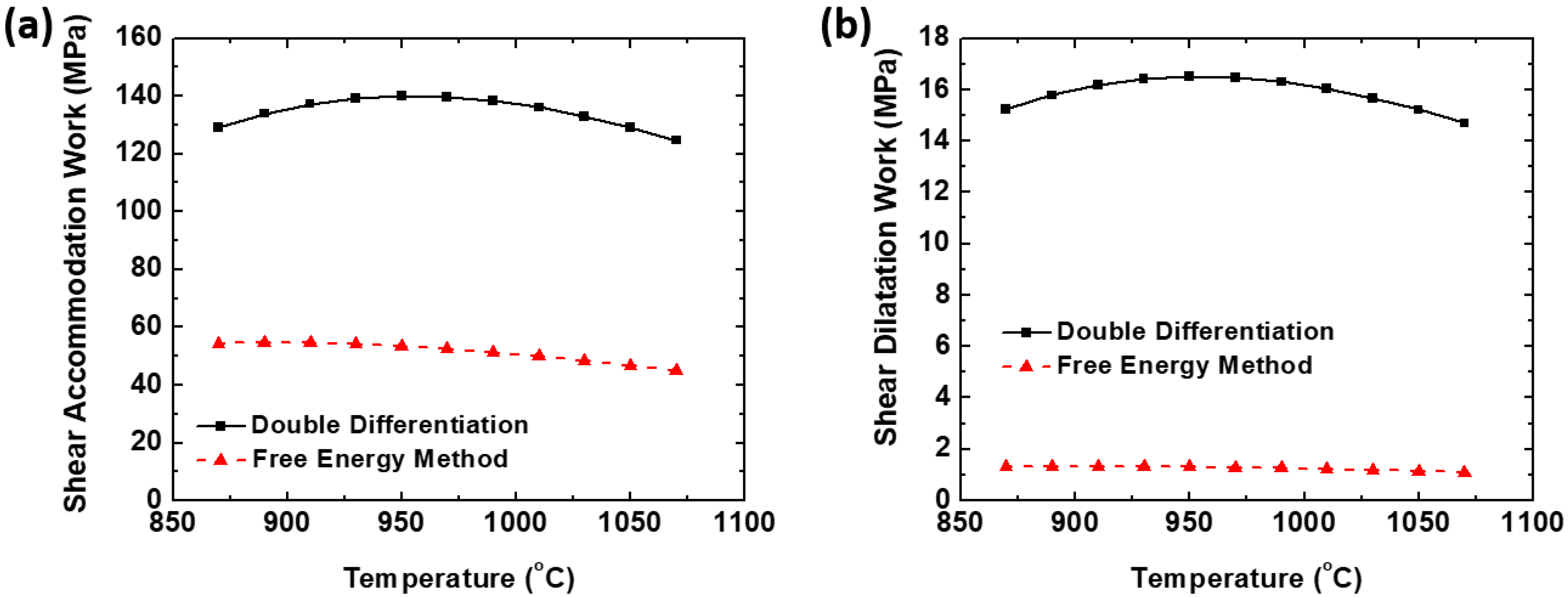
3. Results and Discussion
4. Conclusions
- An alternative method is proposed to calculate the critical stress for dynamic transformation in steels by using the free energy difference between the austenite and ferrite, and the yield stress of the freshly formed ferrite, referred to here as the free energy method. A simple equation was generated for this purpose by assuming that the driving force is equal to that of the energy obstacle at the exact initiation point of dynamic transformation.
- The critical stress obtained from the free energy method is always lower than that of the values calculated using the double differentiation method. The latter overestimates the critical stress as it requires a substantial volume fraction of softening for it to be detectable.
- The present approach can potentially be used to model the occurrence of dynamic transformation above the Ae3 during thermomechanical processing without performing hot deformation experiments.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Poliak, E.; Jonas, J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta Mater. 1996, 44, 127–136. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Najafizadeh, A. Prediction of the critical conditions for initiation of dynamic recrystallization. Mater. Des. 2010, 31, 1174–1179. [Google Scholar] [CrossRef]
- Momeni, A.; Dehghani, K.; Ebrahimi, G.R. Modeling the initiation of dynamic recrystallization using a dynamic recovery model. J. Alloys Compd. 2011, 509, 9387–9393. [Google Scholar] [CrossRef]
- Grewal, R.; Aranas, C.; Chadha, K.; Shahriari, D.; Jahazi, M.; Jonas, J.J. Formation of Widmastatten ferrite at very high temperatures in the austenite phase field. Acta Mater. 2016, 109, 23–31. [Google Scholar] [CrossRef]
- Rodrigues, S.F.; Aranas, C.; Wang, T.; Jonas, J.J. Dynamic transformation of an X70 steel under plate rolling conditions. ISIJ Int. 2017, 57, 162–169. [Google Scholar] [CrossRef]
- Jonas, J.J.; Aranas, C.; Basabe, V.V.; Ghosh, C. Dynamic transformation during the torsion simulation of strip rolling. Mater. Sci. Forum 2014, 783, 39–44. [Google Scholar] [CrossRef]
- Beladi, H.; Kelly, G.L.; Shokouchi, A.; Hodgson, P.D. The evolution of ultrafine ferrite formation through dynamic strain-induced transformation. Mater. Sci. Eng. A 2004, 371, 343–352. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, R. Formation of ultra-fine grain structure of plain low carbon steel through deformation induced ferrite transformation. ISIJ Int. 2003, 43, 761–766. [Google Scholar] [CrossRef]
- Xiong, Z.P.; Saleh, A.A.; Kostryzhev, A.G.; Pereloma, E.V. Strain-induced ferrite formation and its effect on mechanical properties of a dual phase steel produced using laboratory simulated strip casting. J. Alloys Compd. 2017, 721, 291–306. [Google Scholar] [CrossRef]
- Zhao, L.; Park, N.; Tian, Y.; Shibata, A.; Tsuji, N. Combination of dynamic transformation and dynamic recrystallization for realizing ultrafine-grained steels with superior mechanical properties. Sci. Rep. 2016, 6, 39127. [Google Scholar] [CrossRef] [PubMed]
- Park, N.; Shibata, A.; Terada, D.; Tsuji, N. Flow stress analysis for determining the critical condition of dynamic ferrite transformation in 6Ni-0.1C steel. Acta Mater. 2013, 61, 163–173. [Google Scholar] [CrossRef]
- Aranas, C.; Shen, Y.J.; Rodrigues, S.F.; Jonas, J.J. Microstructural evolution of a C-Mn steel during hot compression above the Ae3. Metall. Mater. Trans. A 2016, 47, 4357–4361. [Google Scholar] [CrossRef]
- Ghosh, C.; Basabe, V.V.; Jonas, J.J.; Kim, Y.M.; Jung, I.H.; Yue, S. The dynamic transformation of deformed austenite at temperatures above the Ae3. Acta Mater. 2013, 61, 2348–2363. [Google Scholar] [CrossRef]
- Aranas, C.; Foul, A.; Guo, B.; Fall, A.; Jahazi, M.; Jonas, J.J. Determination of the critical stress for the initiation of dynamic transformation in commercially pure titanium. Scr. Mater. 2017, 133, 83–85. [Google Scholar] [CrossRef]
- Aranas, C.; Jung, I.H.; Yue, S.; Rodrigues, S.F.; Jonas, J.J. A metastable phase diagram for the dynamic transformation of austenite at temperatures above the Ae3. Int. J. Mater. Res. 2016, 107, 881–886. [Google Scholar] [CrossRef]
- Aranas, C.; Jonas, J.J. Effect of Mn and Si on the dynamic transformation of austenite above the Ae3 temperature. Acta Mater. 2015, 82, 1–10. [Google Scholar] [CrossRef]
- Aranas, C.; Rodrigues, S.F.; Shen, Y.J.; Zhang, Z.; Jonas, J.J. Time-Temperature-Reverse Transformation behaviors of a C-Mn and a Nb microalloyed steel after dynamic transformation above the Ae3. Steel Res. Int. 2017, 88, 1700006. [Google Scholar] [CrossRef]
- Rodrigues, S.F.; Aranas, C.; Jonas, J.J. Retransformation behavior of dynamically transformed ferrite during the simulated plate rolling of a low C and an X70 Nb steel. ISIJ Int. 2017, 57, 929–936. [Google Scholar] [CrossRef]
- Ghosh, C.; Aranas, C.; Jonas, J.J. Dynamic transformation of deformed austenite at temperatures above the Ae3. Prog. Mater. Sci. 2016, 82, 151–233. [Google Scholar] [CrossRef]
- Bale, C.W.; Belisle, E.; Chartrand, P.; Decterov, S.A.; Eriksson, G.; Hack, K.; Jung, I.H.; Kang, Y.Y.; Melancon, J.; Pelton, A.D.; et al. FactSage thermochemical software and databases—Recent developments. Calphad 2009, 33, 295–311. [Google Scholar] [CrossRef]
- Basabe, V.V.; Jonas, J.J.; Ghosh, C. Formation of Widmastätten ferrite in a 0.036% Nb low carbon steel at temperatures above the Ae3. Steel Res. Int. 2013, 85, 8–15. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aranas, C., Jr.; Rodrigues, S.; Fall, A.; Jahazi, M.; Jonas, J. Determination of the Critical Stress Associated with Dynamic Phase Transformation in Steels by Means of Free Energy Method. Metals 2018, 8, 360. https://doi.org/10.3390/met8050360
Aranas C Jr., Rodrigues S, Fall A, Jahazi M, Jonas J. Determination of the Critical Stress Associated with Dynamic Phase Transformation in Steels by Means of Free Energy Method. Metals. 2018; 8(5):360. https://doi.org/10.3390/met8050360
Chicago/Turabian StyleAranas, Clodualdo, Jr., Samuel Rodrigues, Ameth Fall, Mohammad Jahazi, and John Jonas. 2018. "Determination of the Critical Stress Associated with Dynamic Phase Transformation in Steels by Means of Free Energy Method" Metals 8, no. 5: 360. https://doi.org/10.3390/met8050360
APA StyleAranas, C., Jr., Rodrigues, S., Fall, A., Jahazi, M., & Jonas, J. (2018). Determination of the Critical Stress Associated with Dynamic Phase Transformation in Steels by Means of Free Energy Method. Metals, 8(5), 360. https://doi.org/10.3390/met8050360




