An Investigation on the Adiabatic Shear Bands in Depleted U-0.75 wt % Ti Alloy under Dynamic Loading
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Materials and Microstructural Characterization
2.2. Impact Testing and Microstructural Characterization
2.3. Split-Hopkinson Pressure Bar (SHPB) Testing and Microstructural Characterization
3. Results and Discussions
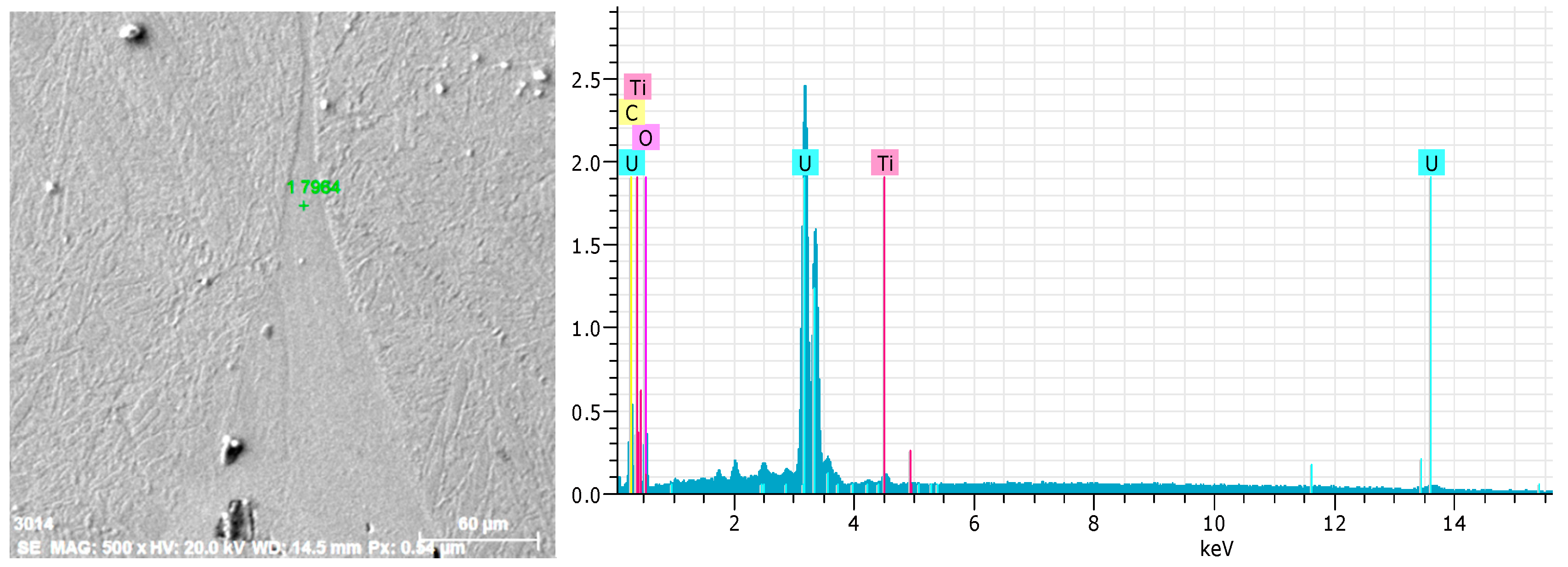
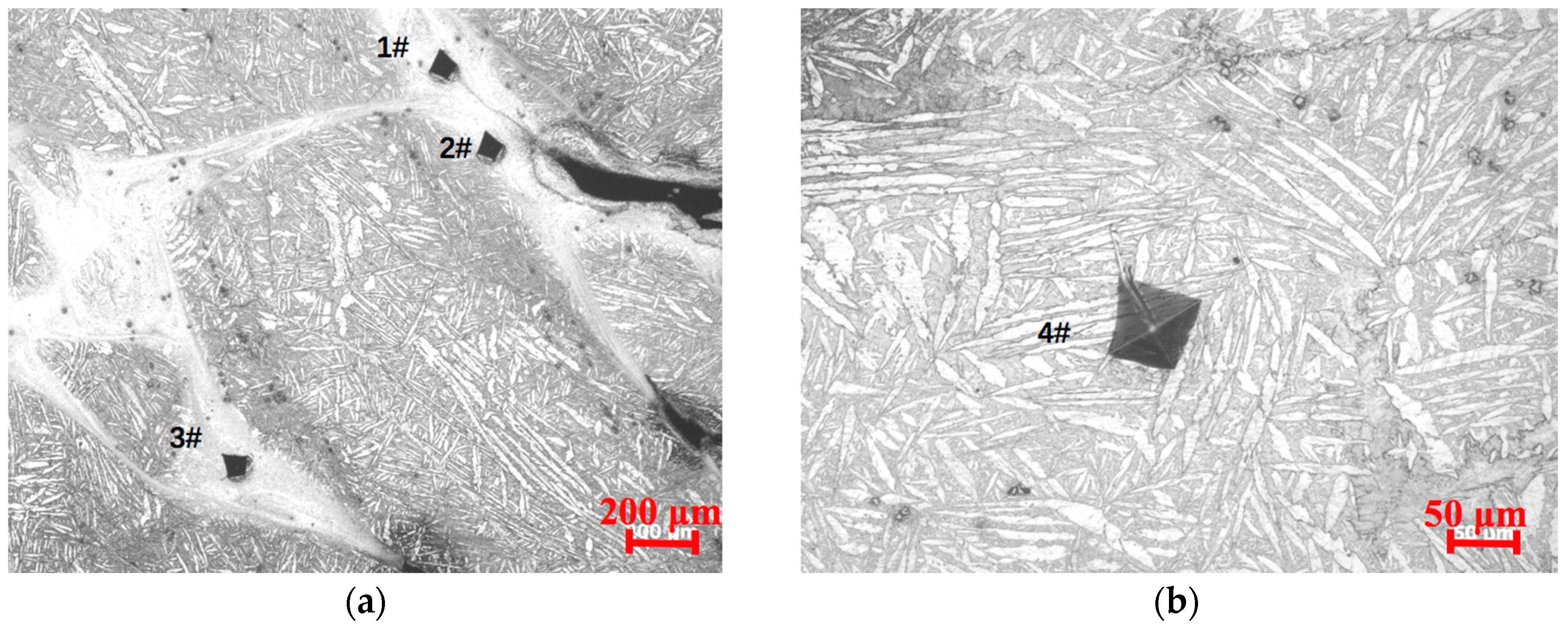
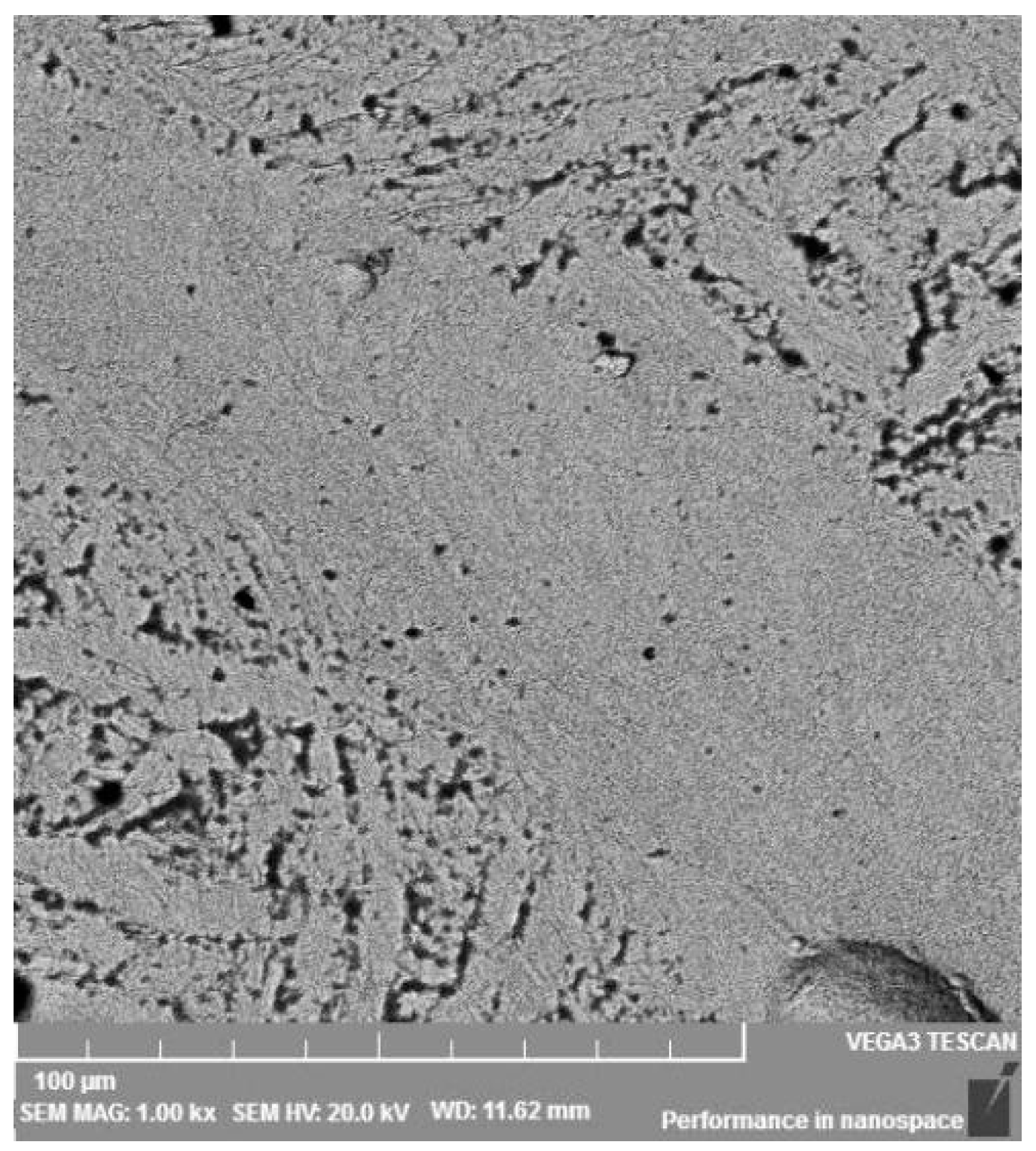
3.1. Microstructure after Impacting
3.2. Scanning Electron Microscope and Vickers Micro-Hardness Results on Shear Bands
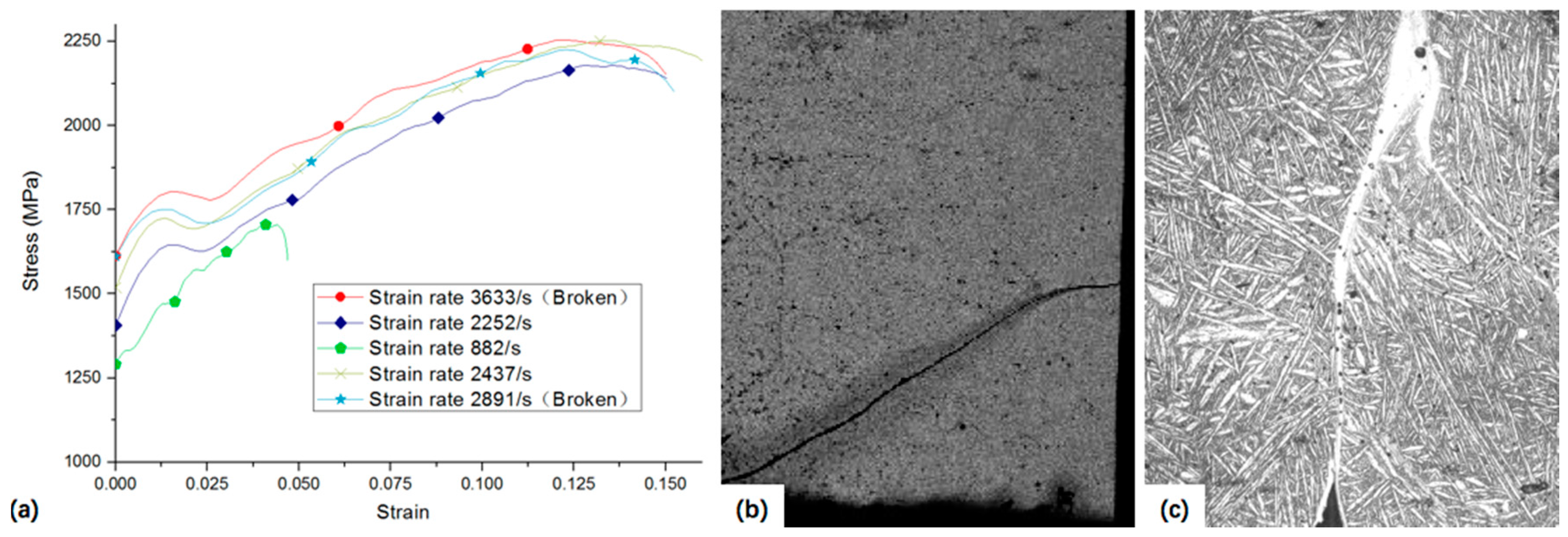
3.3. Dynamic Mechanical Characterization and Microstructure after SHPB
4. Conclusions
- (1)
- Clear shear bands concentrated in an angle were observed in the microstructure of the uranium alloy after impact. These findings are the direct evidence of the so-called “self-sharpening” mechanism that was confirmed by the shear band distribution formed after impact.
- (2)
- The Vickers micro-hardness test results showed that the micro-hardness in the adiabatic shear zone was 18% lower than that in the matrix. Based on the theoretical calculations, the Vickers micro-hardness, and SEM results, we deduced that the shear bands experienced a process of phase change, with average impact temperature rises of 796.75 °C at an impact speed of 1300 m/s.
- (3)
- A strain rate of around 2891 s−1 was determined to be the threshold value required to trigger the appearance of adiabatic shear bands for the U-0.75 wt % Ti alloy.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hu, N.; Molinari, J.F. Shear bands in dense metallic granular materials. J. Mech. Phys. Solids 2004, 52, 499–531. [Google Scholar] [CrossRef]
- Maaß, R.; Löffler, J.F. Shear-band dynamics in metallic glasses. Adv. Funct. Mater. 2015, 25, 2353–2368. [Google Scholar] [CrossRef]
- Wei, Q.; Jia, D.; Ramesh, K.T.; Ma, E. Evolution and microstructure of shear bands in nanostructured Fe. Appl. Phys. Lett. 2002, 81, 1240–1242. [Google Scholar] [CrossRef]
- Olmsted, P.D. Perspectives on shear banding in complex fluids. Rheol. Acta 2008, 47, 283–300. [Google Scholar] [CrossRef]
- Rosenberg, Z.; Dekel, E. On the role of nose profile in long-rod penetration. Int. J. Impact Eng. 1999, 22, 551–557. [Google Scholar] [CrossRef]
- Magness, L.S. Properties and performance of KE penetrator materials. In Proceedings of the Tungsten and Tungsten Alloys Conference, Arlington, TX, USA, 15–18 November 1992; Bose, A., Dowding, R., Eds.; Metal Powder Industries Federation: Princeton, NJ, USA, 1993; pp. 15–22. [Google Scholar]
- Zurek, A.K.; Follansbee, P.S. A comparison of shear localization susceptibility in U-0.75 wt pct Ti and W–Ni–Fe during high strain rate deformation. Metall. Mater. Trans. A 1995, 26, 1483–1490. [Google Scholar] [CrossRef]
- Batra, R.; Stevens, J. Adiabatic shear bands in axisymmetric impact and penetration problems. Comput. Methods Appl. Mech. Eng. 1998, 151, 325–342. [Google Scholar] [CrossRef]
- Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. B 1949, 62, 676. [Google Scholar] [CrossRef]
- Asay, J.R.; Shahinpoor, M. High-Pressure Shock Compression of Solids; Springer: New York, NY, USA, 2012. [Google Scholar]
- Chen, W.W.; Song, B. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Zhao, H.; Elnasri, I.; Li, H.J. The mechanism of strength enhancement under impact loading of cellular materials. Adv. Eng. Mater. 2006, 8, 877–883. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, P.; He, L. Dynamic mechanical properties of U–Ti alloy. Atom. Energy Sci. Technol. 2009, 43, 1095–1099. [Google Scholar]
- Liu, T.; Zhang, P.; He, L.; Bai, B. Dynamic compression performances and adiabatic shearing characters of U–Ti alloys. Rare Met. Mater. Eng. 2010, 39, 800–803. [Google Scholar]
- He, L.; Xiao, D.; Wu, X.; Liu, T.; Jiang, C. Deformation and failure mechanism of U–Ti alloy by SHPB. Rare Met. Mater. Eng. 2013, 42, 1382–1386. [Google Scholar]
- ASM Handbook. Properties and Selection: Nonferrous Alloys and Special-Purpose Materials; ASM International: Almere, The Netherlands, 1990; Volume 2, pp. 889–896. [Google Scholar]
- Starikov, S.; Kolotova, L. Features of cubic and tetragonal structures of U-Mo alloys: Atomistic simulation. Scr. Mater. 2016, 113, 27–30. [Google Scholar] [CrossRef]
- Clark, D.L.; Keogh, D.W.; Neu, M.P.; Runde, W. Uranium and uranium compounds. In Kirk-Othmer Encyclopedia of Chemical Technology; Whitlock, J., Ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Kimmel, G.; Landau, A.; Sariel, J.; Admon, U. Phase transformations in dilute U–Ti alloys. J. Less Common Met. 1986, 121, 483–486. [Google Scholar] [CrossRef]
- Peehs, M.; Walter, T.; Walter, S.; Zemek, M. Uranium, uranium alloys, and uranium compounds. In Ullmann’s Encyclopedia of Industrial Chemistry; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- McDiarmid, M.A.; Gaitens, J.M.; Squibb, K.S. Uranium and thorium. In Patty’s Toxicology; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Sunwoo, A.; Goto, D. Effects of processing on microstructure and properties of α-uranium formed parts. Scr. Mater. 2002, 47, 261–266. [Google Scholar] [CrossRef]
- Timothy, S. The structure of adiabatic shear bands in metals: A critical review. Acta Metall. 1987, 35, 301–306. [Google Scholar] [CrossRef]
- Meyers, M.A. Dynamic Behavior of Materials; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, A.; Qiao, L.; Zhang, J.; Zhang, Y.; Guan, Z. Experimental study on impact-initiated characters of multifunctional energetic structural materials. J. Appl. Phys. 2013, 113, 083508. [Google Scholar] [CrossRef]
- Feng, S.; Wang, C.; Huang, G. Experimental study on the reaction zone distribution of impact-induced reactive materials. Propellants Explos. Pyrotech. 2017, 42, 896–905. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.; Yu, Q.; Liu, Z.; Yu, W. Impact-induced initiation and energy release behavior of reactive materials. J. Appl. Phys. 2011, 110, 074904. [Google Scholar]
- Zurek, A. Preshock-induced phase transition in spalled U-0.75 wt % Ti. J. Nucl. Mater. 1999, 264, 155–160. [Google Scholar] [CrossRef]




| Material | Test Temperature | Diameter | Yield Stress (σs) | Tensile Strength (σb) | Elongation |
|---|---|---|---|---|---|
| U-0.75 wt % Ti | 27 °C | 5.02 mm | 1122.9 MPa | 1519.4 MPa | 16.6% |
| No. | Test Location | Vickers Micro-Hardness | Average Value |
|---|---|---|---|
| #1 | Shear band | 365 HW | 368 HW |
| #2 | Shear band | 396 HW | (18% decline) |
| #3 | Shear band | 345 HW | - |
| #4 | Sample matrix | 445 HW | 449 HW |
| #5 | Sample matrix | 455 HW | - |
| #6 | Sample matrix | 449 HW | - |
| No. | Materials | ρ (g/cm3) | a (mm/μs) | b | γ | Cv J/(g·K) |
|---|---|---|---|---|---|---|
| 1 | DU | 18.95 | 2.49 | 2.20 | 2.1 | 0.12 |
| 2 | Steel | 7.85 | 3.57 | 1.92 | 1.8 | 0.45 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Dong, Y.; Huang, G. An Investigation on the Adiabatic Shear Bands in Depleted U-0.75 wt % Ti Alloy under Dynamic Loading. Metals 2018, 8, 145. https://doi.org/10.3390/met8020145
Wang B, Dong Y, Huang G. An Investigation on the Adiabatic Shear Bands in Depleted U-0.75 wt % Ti Alloy under Dynamic Loading. Metals. 2018; 8(2):145. https://doi.org/10.3390/met8020145
Chicago/Turabian StyleWang, Bo, Yongxiang Dong, and Guangyan Huang. 2018. "An Investigation on the Adiabatic Shear Bands in Depleted U-0.75 wt % Ti Alloy under Dynamic Loading" Metals 8, no. 2: 145. https://doi.org/10.3390/met8020145
APA StyleWang, B., Dong, Y., & Huang, G. (2018). An Investigation on the Adiabatic Shear Bands in Depleted U-0.75 wt % Ti Alloy under Dynamic Loading. Metals, 8(2), 145. https://doi.org/10.3390/met8020145





