Finite Element Analysis of Surface Integrity in Deep Ball-Burnishing of a Biodegradable AZ31B Mg Alloy
Abstract
:1. Introduction
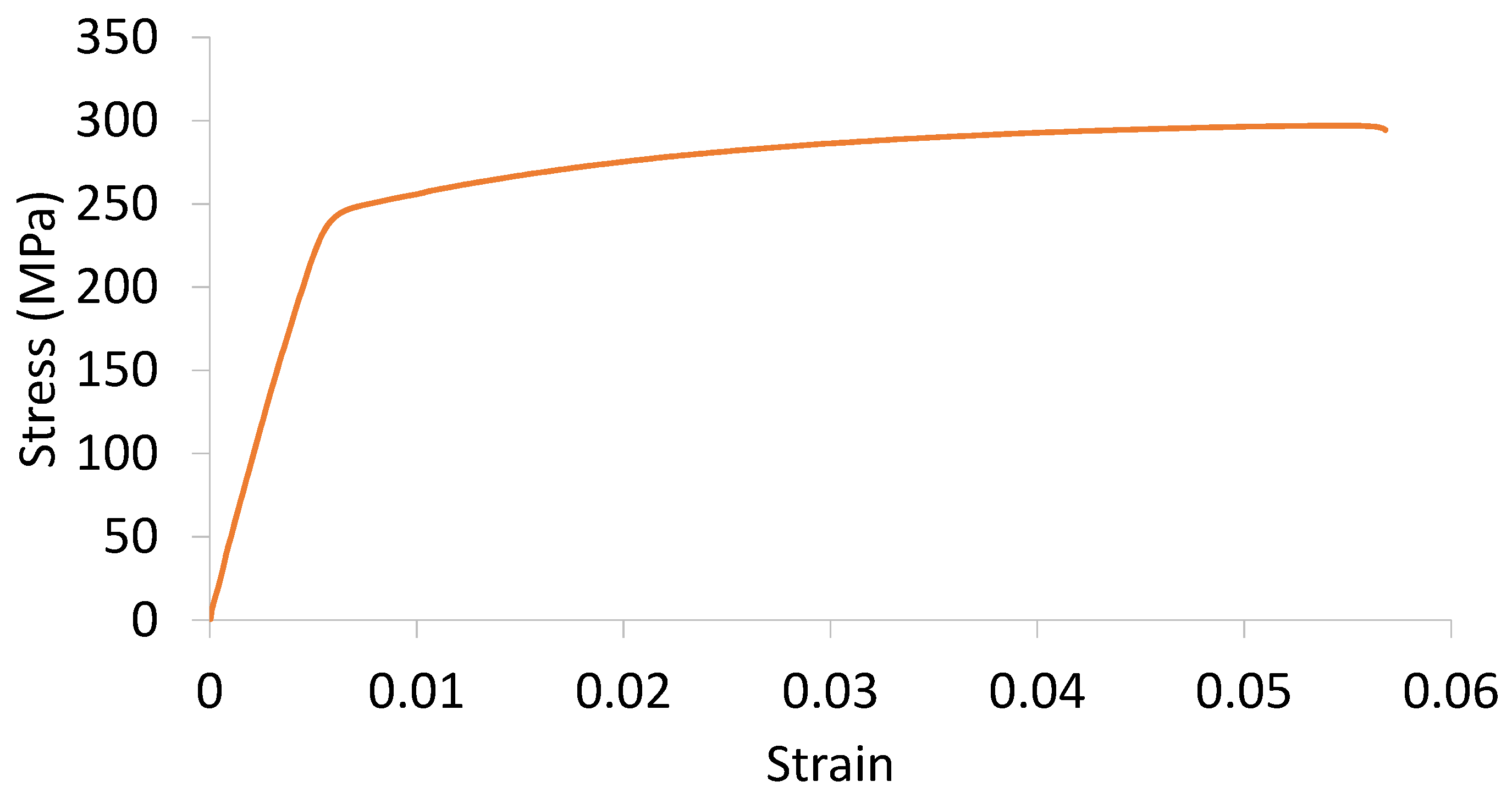
2. Materials and Methods
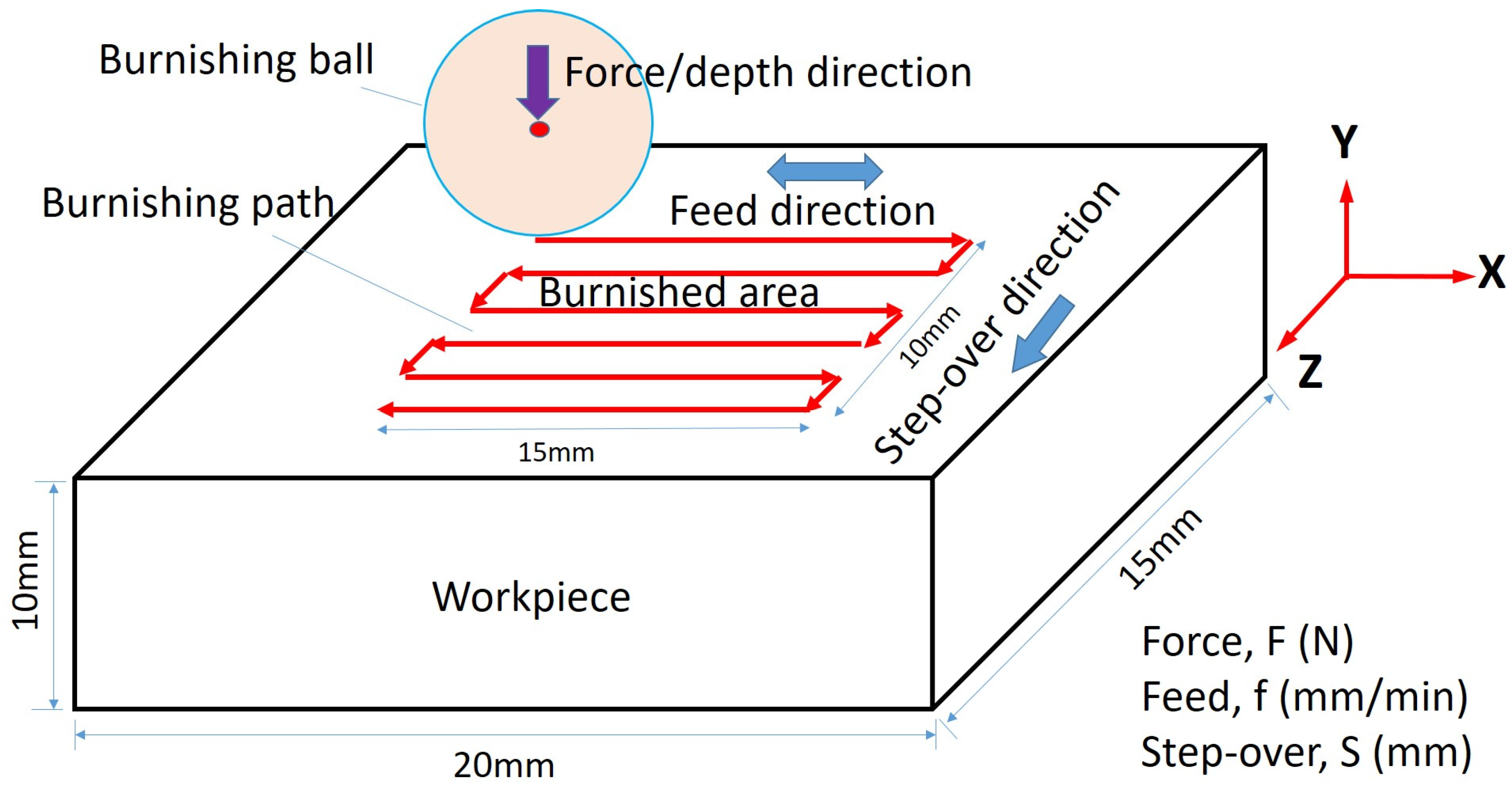
2.1. Burnishing Experiments
2.2. Finite Element Modelling
3. Results
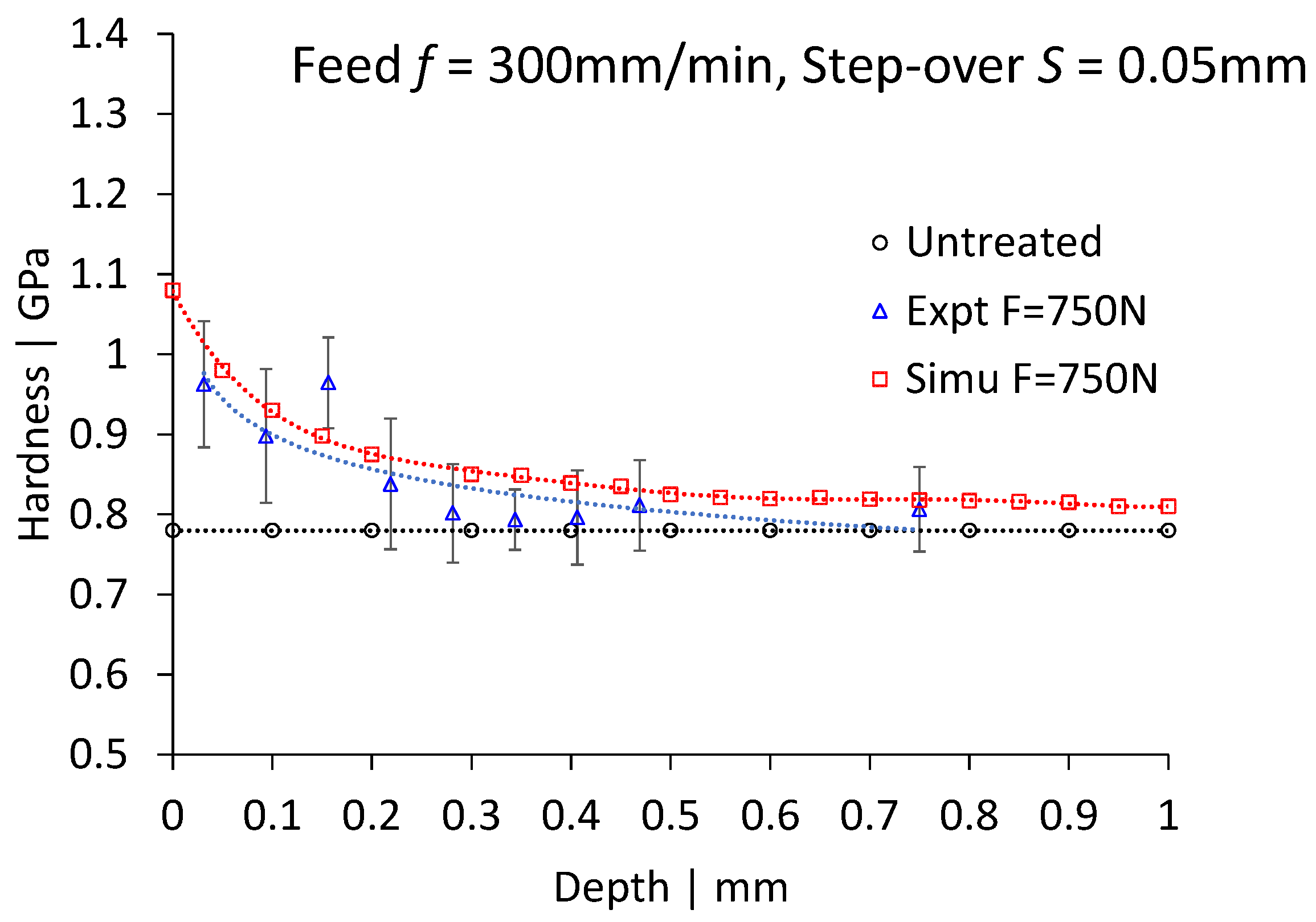
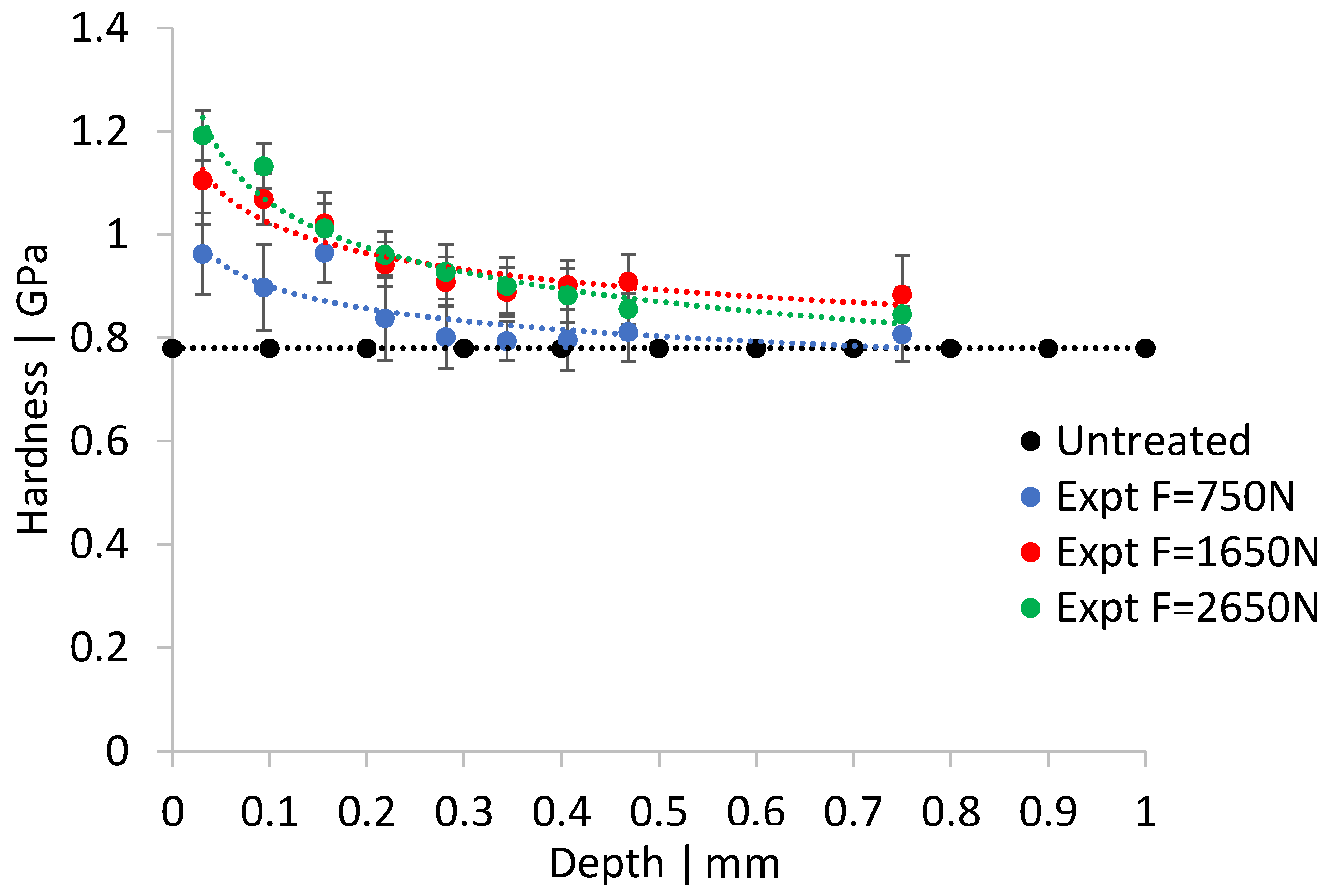
3.1. Comparison between Experiment and the Finite Element Model
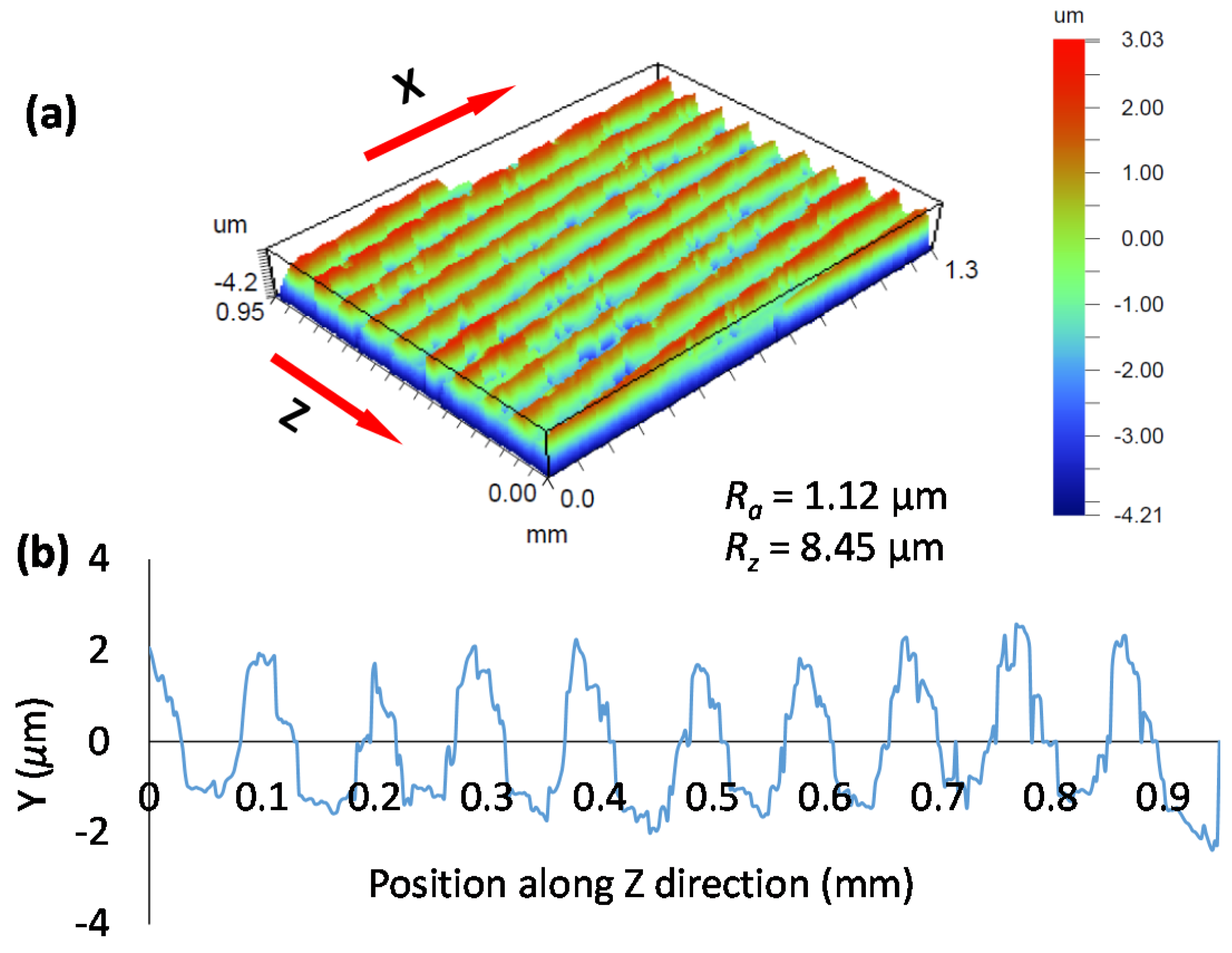
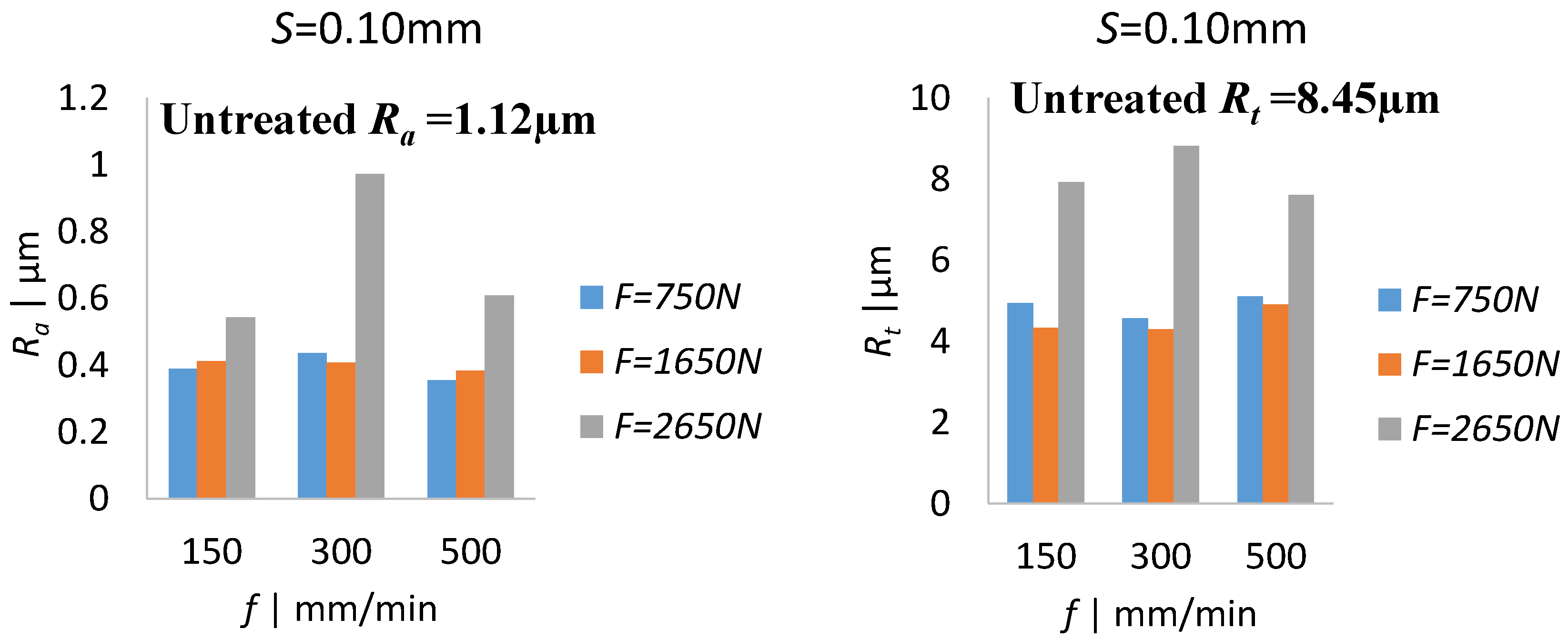
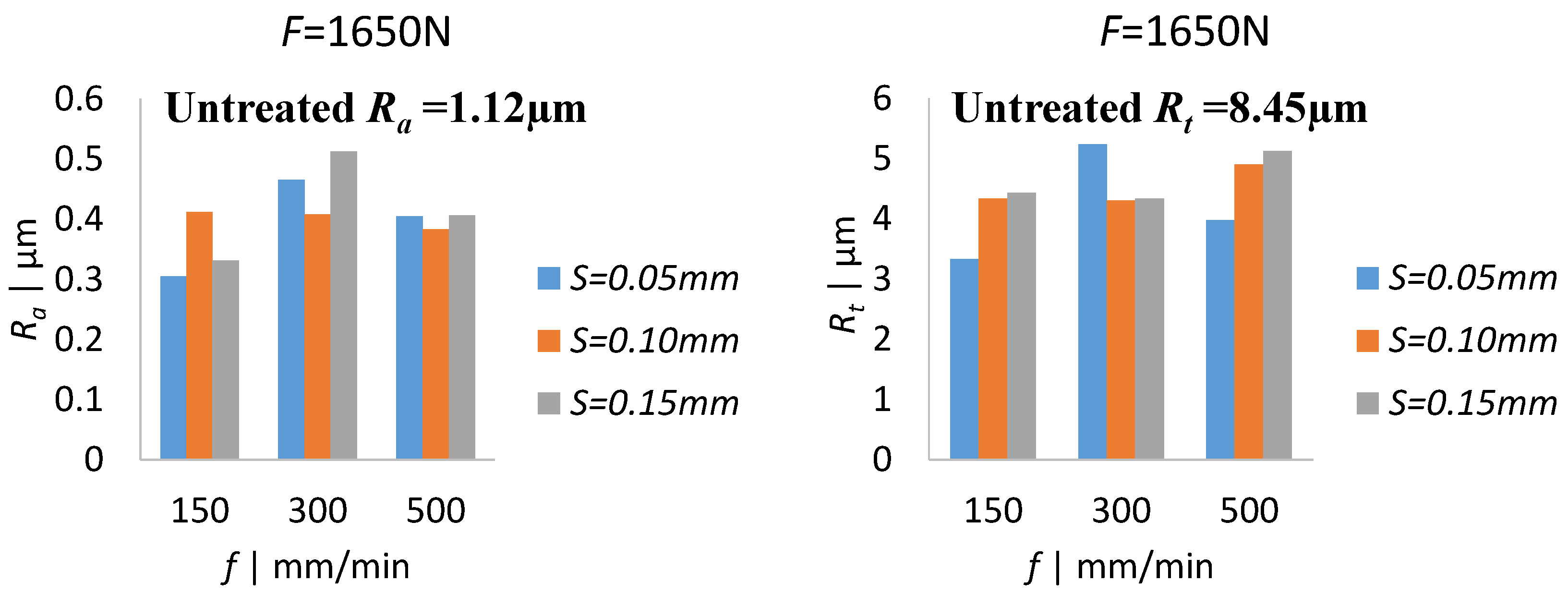
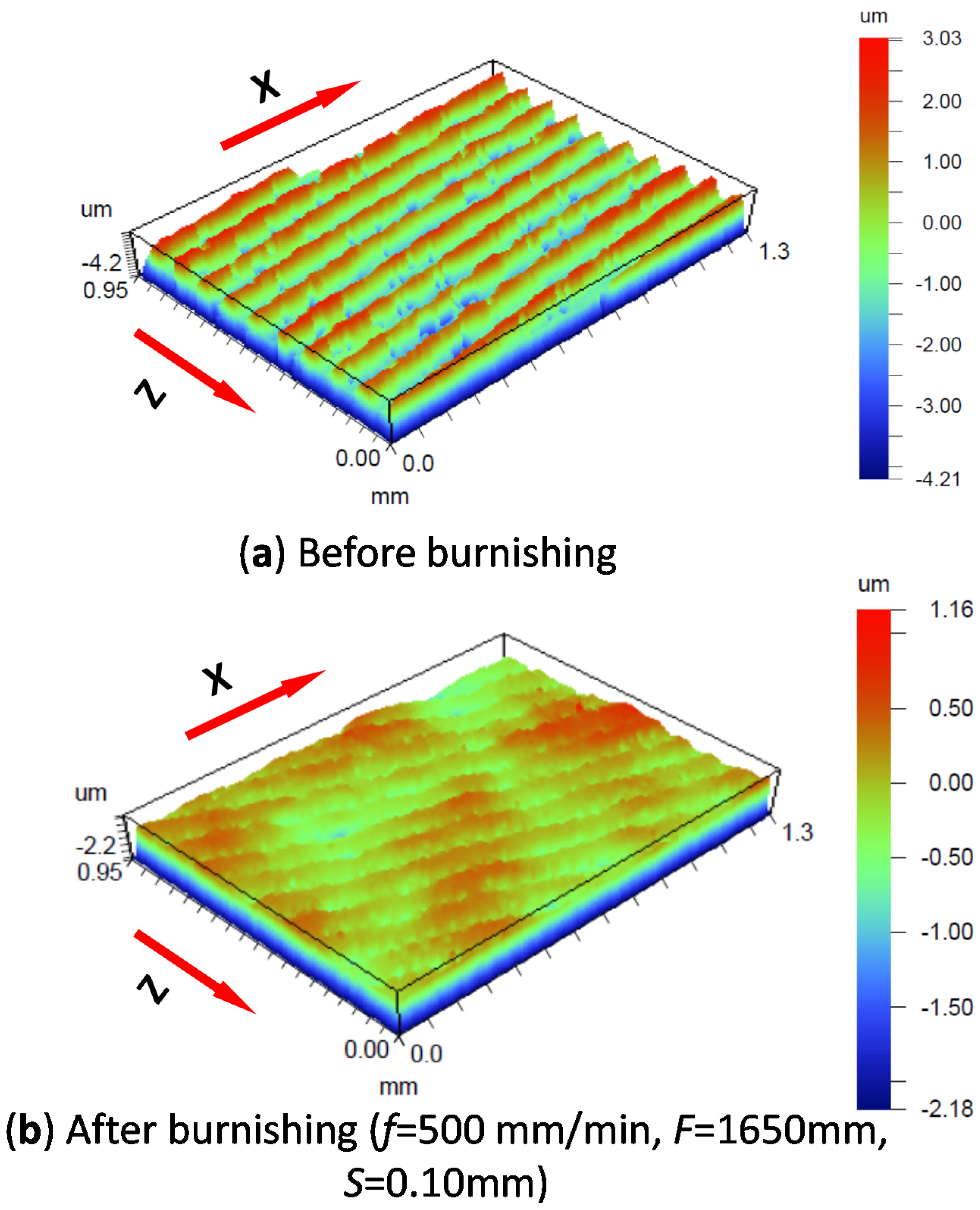
3.2. Analysis of Experimental Surface Roughness and Topography
3.3. Sensitivity Study via Finite Element Modelling
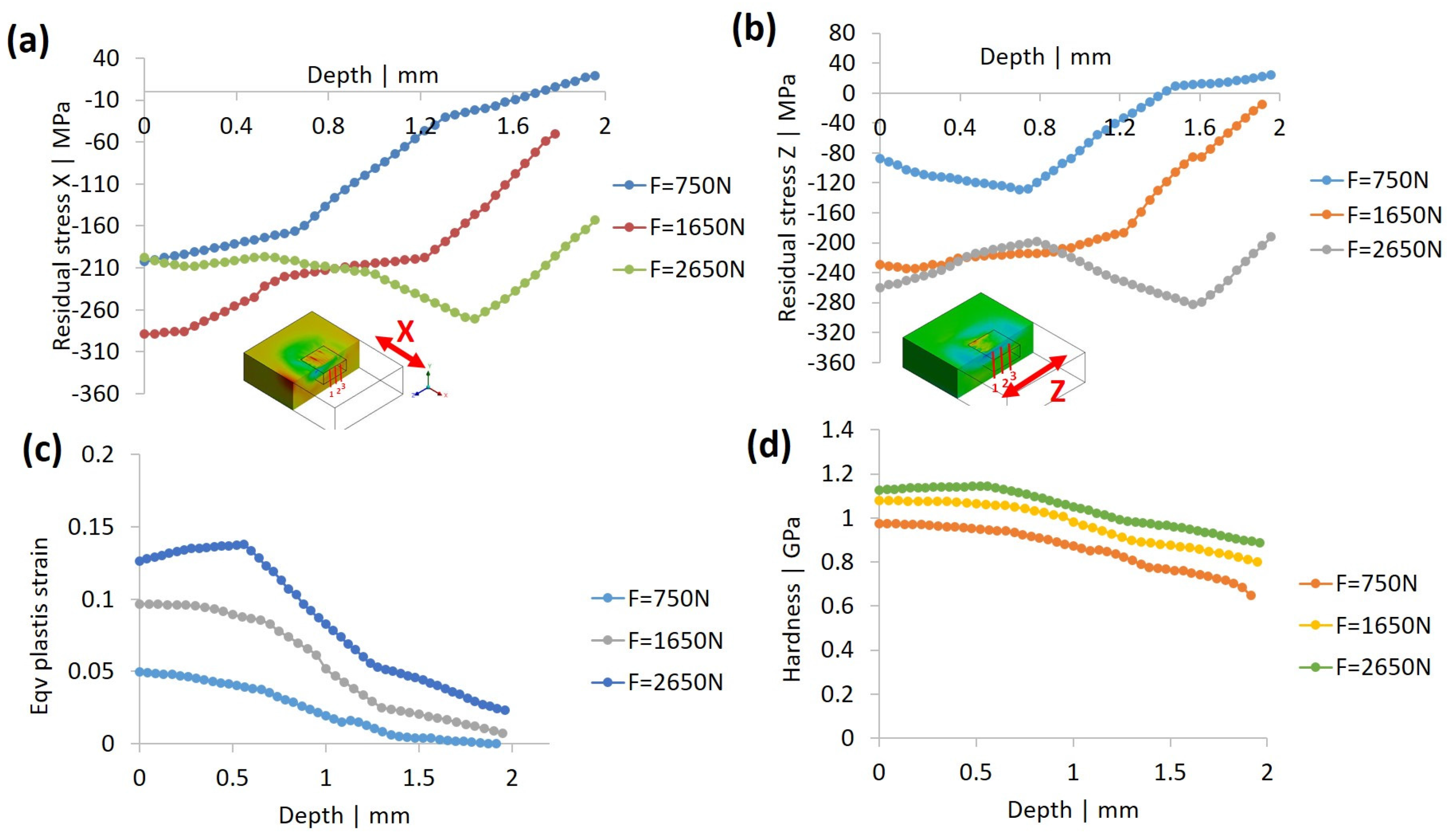
3.3.1. Effect of Burnishing Force
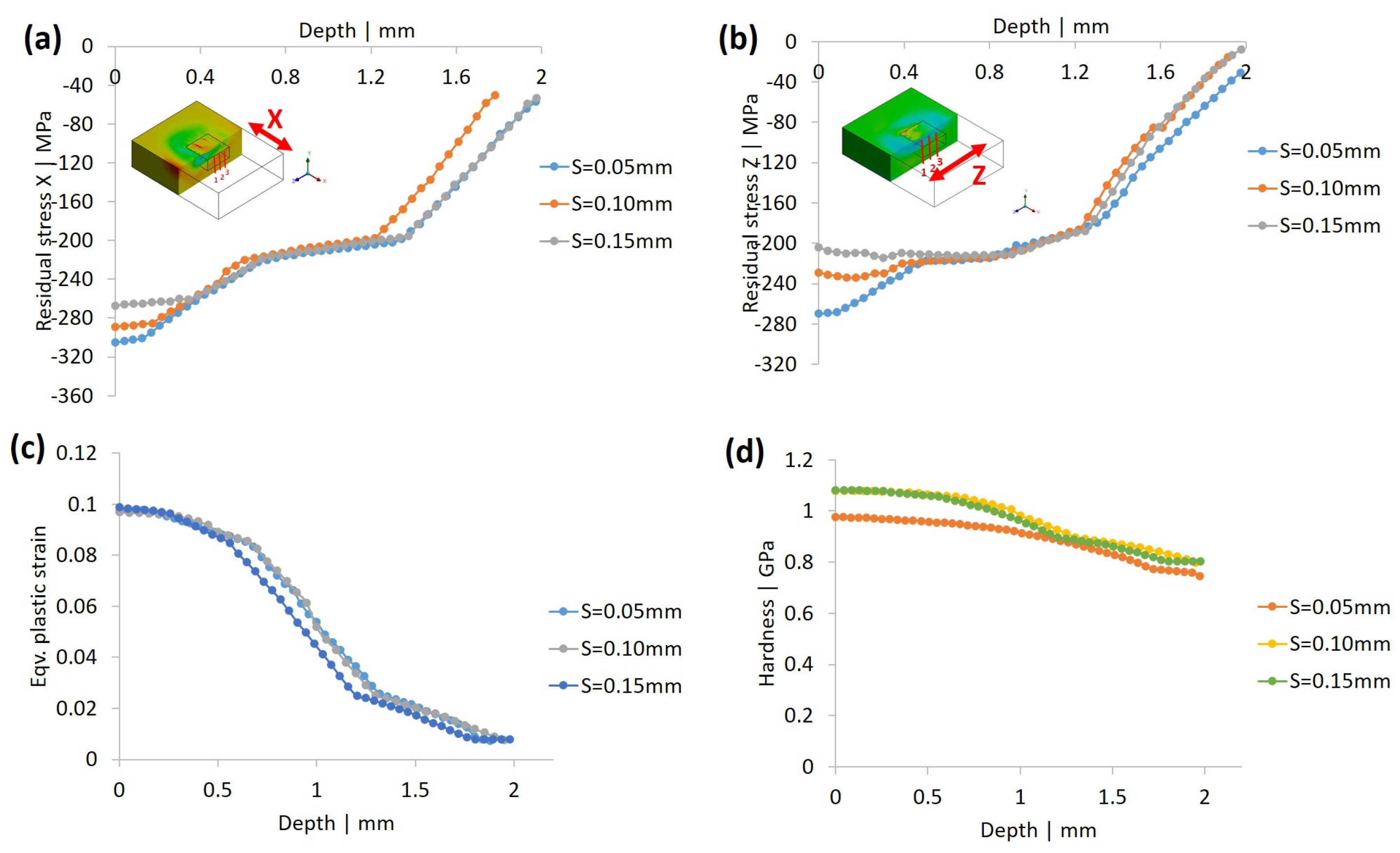
3.3.2. Effect of Burnishing Step
3.3.3. Effect of Burnishing Feed Rate
4. Discussion
5. Conclusions
- Experimental results indicate that compared to untreated specimens, burnishing distinctively improved hardness at the top, to a maximum, which decreases and reaches the bulk hardness (0.78 GPa) as the depth increases.
- The FE model satisfactorily agrees with the experiment, with a maximum error of 10%, in hardness at burnishing force of 750 N, a feed rate of 300 mm/min, and a step-over of 0.05 mm, hence validating the reliability of the model.
- Experimental surface topography results indicate that while all burnishing conditions improve roughness compared to the untreated surface, a lower burnishing force (of up to 1650 N) and step-over (of up to 0.10 mm) are shown to significantly reduce surface roughness (Ra and Rt) for a given feed, while feed has minimal effect. A smooth surface is expected to minimize pitting corrosion of Mg alloys.
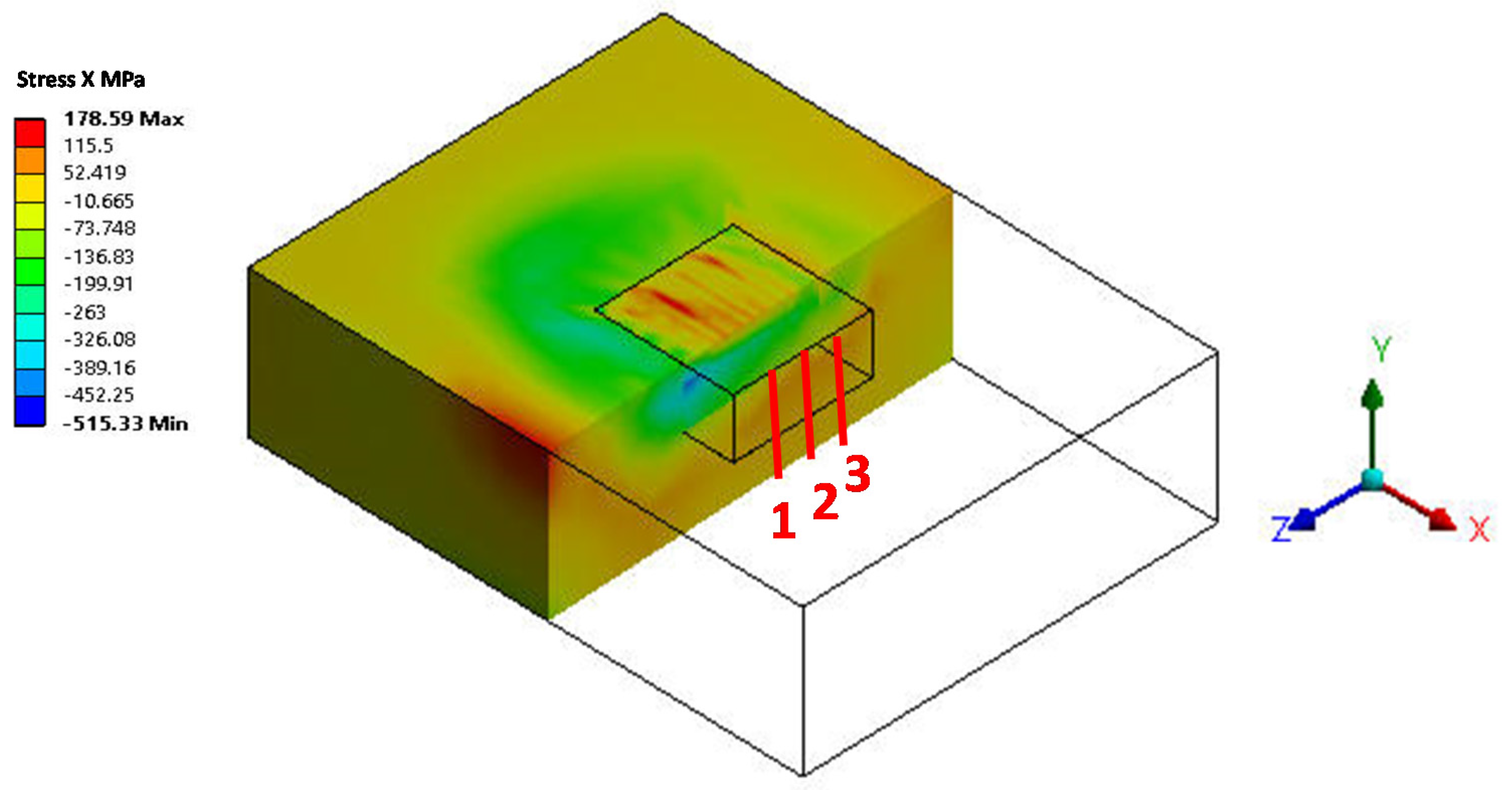
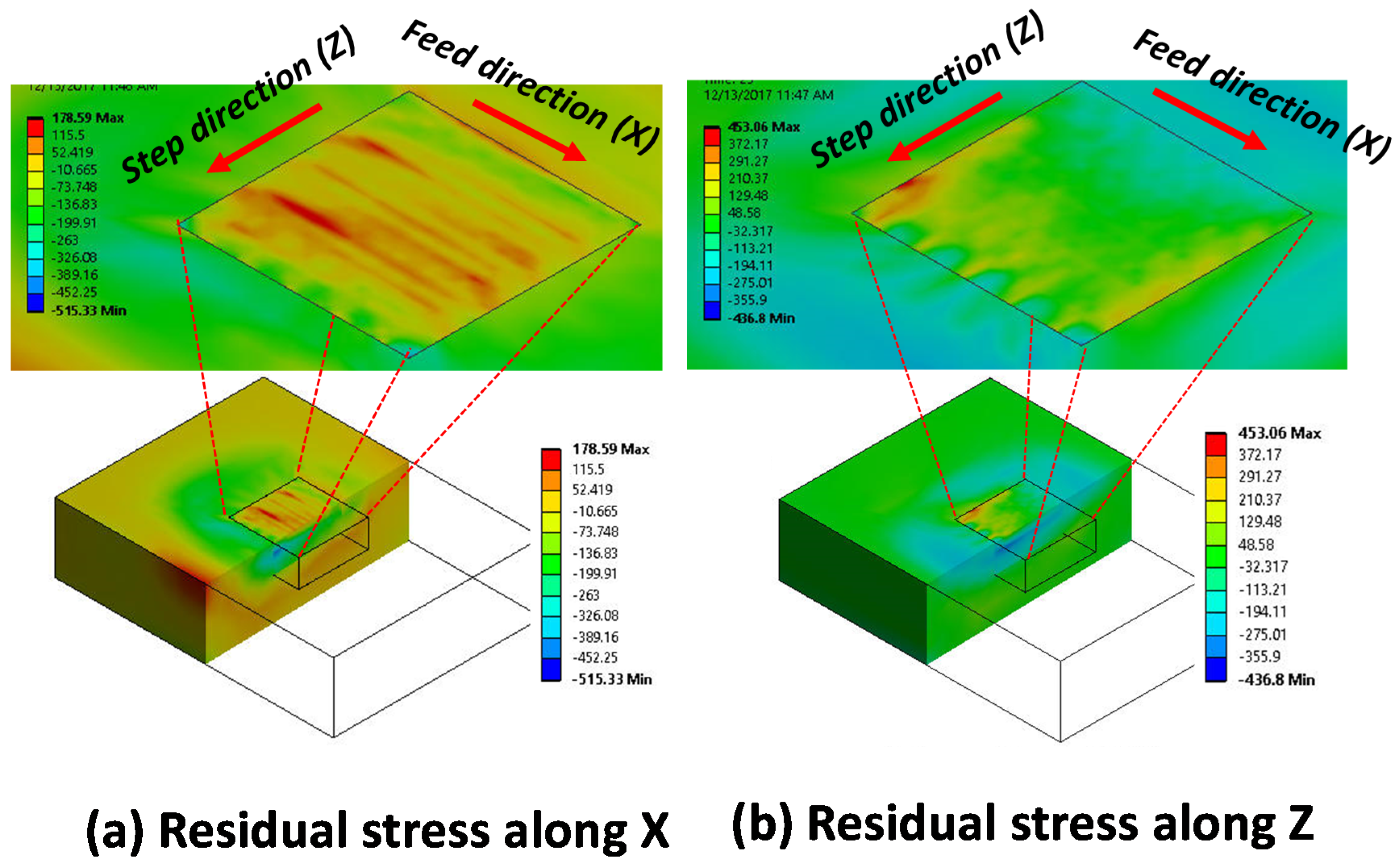
- The FE analysis shows that the higher the burnishing force, the larger the residual stress, at a depth of as much as 1.2 mm. Stress is high (as high as −300 MPa) at the top surface, and decreases as the depth increases. Residual stress in the feed direction (X) is always found to be larger than that in the step-over direction (Z). Plastic strain and hardness follow the same trend, with the change of force, while hardness increases up to 1.1 GPa at the top surface at a force of 2650 N. Caution, however, must be taken, as a very large burnishing force may cause negative effects, i.e., lower compressive stress, high roughness, and surface damage.
- The smaller the burnishing step-over, the higher the residual stress; however, such improvement is noticed at a shallow depth of 0.40 mm, after which changes in the step-over amount has minimal effect. Plastic strain and hardness, though, behave slightly in the opposite way, where hardness increases with a larger step-over. A trade-off between residual stress and hardness may need to be taken into consideration.
- While a lower feed rate seems to increase residual stress, that stress’ variation across depth is relatively small when the feed rate goes up to 300 mm/min; afterwards, the effect is negative, i.e., stress drops drastically. Therefore, a smaller feed rate may be selected, to avoid potential surface or sub-surface cracks/damage, which can generate tensile stress. Plastic strain and hardness are not much affected by feed.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Uddin, M.S.; Hall, C.; Murphy, P. Surface treatments for controlling corrosion rate of biodegradable Mg and Mg-based alloy implants. Sci. Technol. Adv. Mater. 2015, 16, 053501. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, S.; Curtin, J.; Duffy, B.; Jaiswal, S. Biodegradable magnesium alloys for orthopaedic applications: A review on corrosion, biocompatibility and surface modifications. Mater. Sci. Eng. C 2016, 68, 948–963. [Google Scholar] [CrossRef] [PubMed]
- Cha, P.-R.; Han, H.-S.; Yang, G.-F.; Kim, Y.-C.; Hong, K.-H.; Lee, S.-C.; Jung, J.-Y.; Ahn, J.-P.; Kim, Y.-Y.; Cho, S.-Y.; et al. Biodegradability engineering of biodegradable Mg alloys: Tailoring the electrochemical properties and microstructure of constituent phases. Sci. Rep. 2013, 3, 2367. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.S.; Rosman, H.; Hall, C.; Murphy, P. Enhancing the corrosion resistance of biodegradable Mg-based alloy by machining-induced surface integrity: Influence of machining parameters on surface roughness and hardness. Int. J. Adv. Manuf. Technol. 2016, 1–14. [Google Scholar] [CrossRef]
- Schulze, V.; Bleicher, F.; Groche, P.; Guo, Y.B.; Pyun, Y.S. Surface modification by machine hammer peening and burnishing. CIRP Ann. Manuf. Technol. 2016, 65, 809–832. [Google Scholar] [CrossRef]
- Sealy, M.P.; Guo, Y.B.; Caslaru, R.C.; Sharkins, J.; Feldman, D. Fatigue performance of biodegradable magnesium-calcium alloy processed by laser shock peening for orthopedic implants. Int. J. Fatigue 2016, 82, 428–436. [Google Scholar] [CrossRef]
- Zhang, T.; Bugtai, N.; Marinescu, I.D. Burnishing of aerospace alloy: A theoretical-experimental approach. J. Manuf. Syst. 2015, 37, 472–478. [Google Scholar] [CrossRef]
- Chomienne, V.; Valiorgue, F.; Rech, J.; Verdu, C. Influence of ball-burnishing on residual stress profile of a 15-5PH stainless steel. CIRP J. Manuf. Sci. Technol. 2016, 13, 90–96. [Google Scholar] [CrossRef]
- Lim, A.; Castagne, S.; Cher Wong, C. Effect of deep cold rolling on residual stress distributions between the treated and untreated regions on Ti-6Al-4V alloy. J. Manuf. Sci. Eng. 2016, 138, 111005. [Google Scholar] [CrossRef]
- Salahshoor, M.; Guo, Y.B. Biodegradation control of magnesium-calcium biomaterial via adjusting surface integrity by synergistic cutting-burnishing. Procedia CIRP 2014, 13, 143–149. [Google Scholar] [CrossRef]
- Salahshoor, M.; Guo, Y.B. Process mechanics in ball-burnishing biomedical magnesium-calcium alloy. Int. J. Adv. Manuf. Technol. 2013, 64, 133–144. [Google Scholar] [CrossRef]
- Salahshoor, M.; Guo, Y.B. Surface integrity of magnesium-calcium implants processed by synergistic dry cutting-finish burnishing. Procedia Eng. 2011, 19, 288–293. [Google Scholar] [CrossRef]
- Hering, B.; Wippermann, A.; Mörke, T.; Grove, T.; Denkena, B. Manufacturing of osteosynthesis systems made of magnesium alloy AZ91. In Magnesium Technology 2016; Singh, A., Solanki, K., Vnuel, M., Neelameggham, N.R., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2016; pp. 317–322. ISBN 978-1-119-27480-3. [Google Scholar]
- Pu, Z.; Song, G.-L.; Yang, S.; Dillon, O.W.; Puleo, D.A.; Jawahir, I.S. Cryogenic burnishing of AZ31B Mg alloy for enhanced corrosion resistance. In Magnesium Technology 2011; Sillekens, W.H., Agnew, S.R., Neelameggham, N.R., Mathaudhu, S.N., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2011; pp. 513–518. ISBN 978-1-118-06202-9. [Google Scholar]
- Pu, Z.; Yang, S.; Song, G.-L.; Dillon, O.W., Jr.; Puleo, D.A.; Jawahir, I.S. Ultrafine-grained surface layer on Mg-Al-Zn alloy produced by cryogenic burnishing for enhanced corrosion resistance. Scr. Mater. 2011, 65, 520–523. [Google Scholar] [CrossRef]
- Coules, H.E.; Horne, G.C.M.; Kabra, S.; Colegrove, P.; Smith, D.J. Three-dimensional mapping of the residual stress field in a locally-rolled aluminium alloy specimen. J. Manuf. Process. 2017, 26, 240–251. [Google Scholar] [CrossRef]
- Virtanen, S. Surface modification and coating of biodegradable magnesium. Meet. Abstr. 2016, 10, 1206. [Google Scholar]
- Yen, Y.C.; Sartkulvanich, P.; Altan, T. Finite element modeling of roller burnishing process. CIRP Ann. Manuf. Technol. 2005, 54, 237–240. [Google Scholar] [CrossRef]
- Sonmez, F.O.; Demir, A. Analytical relations between hardness and strain for cold formed parts. J. Mater. Process. Technol. 2007, 186, 163–173. [Google Scholar] [CrossRef]
- Ahmad, I.R.; Shu, D.W. Experimental and constitutive study of tensile behavior of AZ31B wrought magnesium alloy. ASCE J. Eng. Mech. 2015, 141. [Google Scholar] [CrossRef]
- Trdan, U.; Skarba, M.; Grum, J. Laser shock peening effect on the dislocation transitions and grain refinement of Al-Mg-Si alloy. Mater. Charact. 2014, 97, 57–68. [Google Scholar] [CrossRef]
- De Lacalle, L.N.L.; Lamikiz, A.; Sánchez, J.A.; Arana, J.L. The effect of ball-burnishing on heat-treated steel and Inconel 718 milled surfaces. Int. J. Adv. Manuf. Technol. 2007, 32, 958–968. [Google Scholar] [CrossRef]
- Revankar, G.D.; Shetty, R.; Rao, S.S.; Gaitonde, V.N. Wear resistance enhancement of titanium alloy (Ti-6Al-4V) by ball-burnishing process. J. Mater. Res. Technol. 2017, 6, 13–32. [Google Scholar] [CrossRef]




| Element | Mg | Al | Zn | Si | Mn | Cu | Ca | Fe | Ni |
|---|---|---|---|---|---|---|---|---|---|
| Composition (wt %) | 96.3 | 2.5 | 0.8 | 0.10 | 0.20 | 0.050 | 0.04 | 0.005 | 0.005 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uddin, M.S.; Hall, C.; Hooper, R.; Charrault, E.; Murphy, P.; Santos, V. Finite Element Analysis of Surface Integrity in Deep Ball-Burnishing of a Biodegradable AZ31B Mg Alloy. Metals 2018, 8, 136. https://doi.org/10.3390/met8020136
Uddin MS, Hall C, Hooper R, Charrault E, Murphy P, Santos V. Finite Element Analysis of Surface Integrity in Deep Ball-Burnishing of a Biodegradable AZ31B Mg Alloy. Metals. 2018; 8(2):136. https://doi.org/10.3390/met8020136
Chicago/Turabian StyleUddin, Mohammad Sharif, Colin Hall, Ryan Hooper, Eric Charrault, Peter Murphy, and Vincent Santos. 2018. "Finite Element Analysis of Surface Integrity in Deep Ball-Burnishing of a Biodegradable AZ31B Mg Alloy" Metals 8, no. 2: 136. https://doi.org/10.3390/met8020136
APA StyleUddin, M. S., Hall, C., Hooper, R., Charrault, E., Murphy, P., & Santos, V. (2018). Finite Element Analysis of Surface Integrity in Deep Ball-Burnishing of a Biodegradable AZ31B Mg Alloy. Metals, 8(2), 136. https://doi.org/10.3390/met8020136






