Evolution of Microstructure and Mechanical Properties of a CoCrFeMnNi High-Entropy Alloy during High-Pressure Torsion at Room and Cryogenic Temperatures
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
- (1)
- HPT processing at room temperature results in the formation of in inhomogeneous severely deformed microstructure with (sub)grains of ~50 nm already after the rotation for 180°. The microstructure evolution was associated with intensive deformation-induced twinning, and substructure development resulted in a gradual microstructure refinement.
- (2)
- HPT at 77 K produced more heterogeneous structure in comparison with the room-temperature deformation. The dislocation density was much higher after cryogenic deformation.
- (3)
- Tensile strength of the alloy after HPT at 293 K was found to be strongly dependent on HPT strain. The ultimate tensile strength increased from 981 to 2069 MPa when the rotation angle at HPT increased from 90° to 720°. In all examined conditions, the alloy exhibited limited ductility.
- (4)
- A decrease of HPT temperature from 293 to 77 K resulted in higher tensile strength. A rotation for 180° resulted in the ultimate tensile strength of 1193 MPa and 1596 MPa after processing at room and cryogenic temperature, respectively.
- (5)
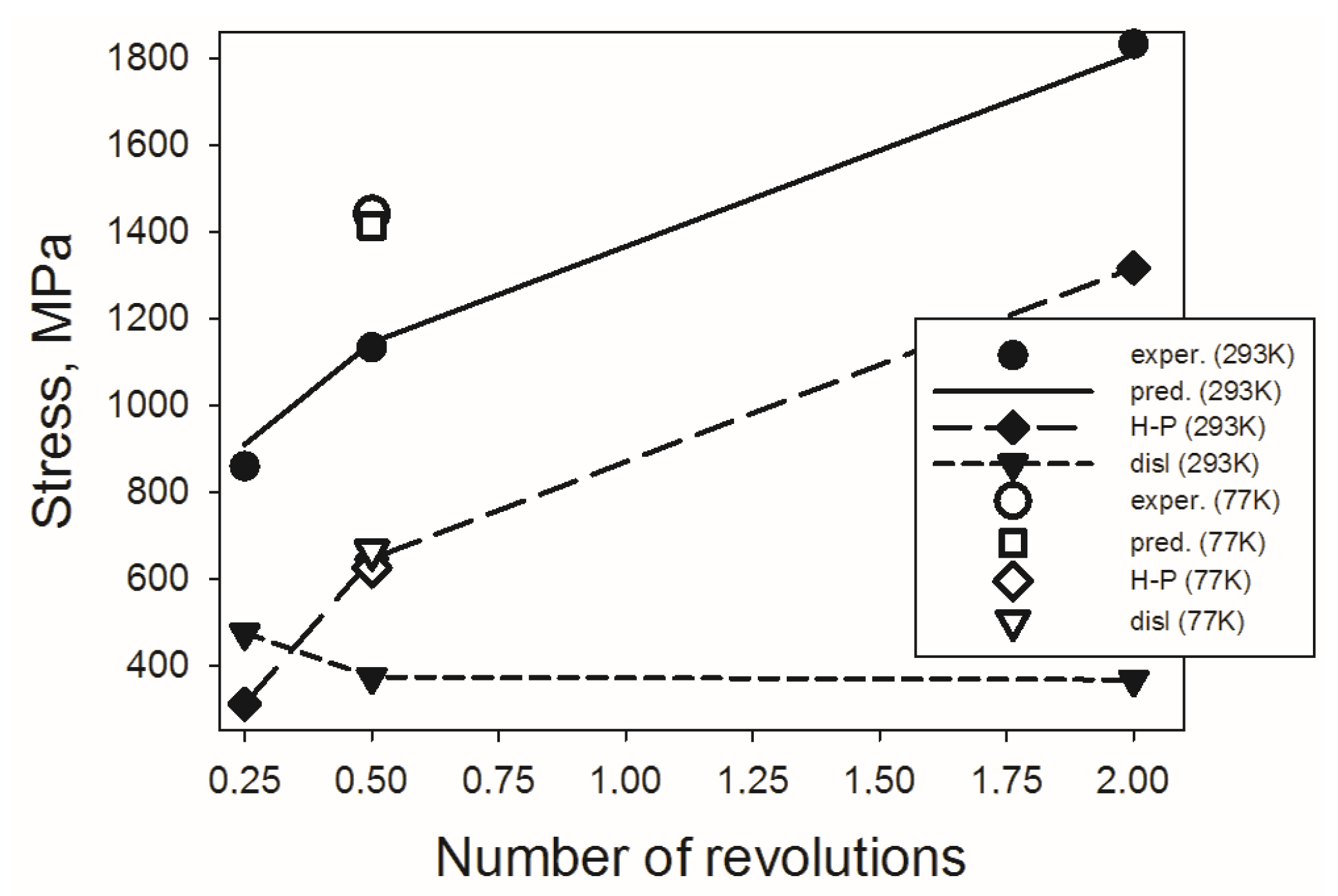
- An increase of yield strength of the alloy with an increase of the angle of rotation can mostly be ascribed to a contribution of Hall–Petch strengthening. In turn, higher strength of the alloy after HPT at 77 K was attributed to substructure (dislocation) hardening.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yeh, J.-W.; Chen, S.-K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Otto, F.; Yang, Y.; Bei, H.; George, E.P.P. Relative effects of enthalpy and entropy on the phase stability of equiatomic high-entropy alloys. Acta Mater. 2013, 61, 2628–2638. [Google Scholar] [CrossRef]
- Laurent-Brocq, M.; Akhatova, A.; Perrière, L.; Chebini, S.; Sauvage, X.; Leroy, E.; Champion, Y. Insights into the phase diagram of the CrMnFeCoNi high entropy alloy. Acta Mater. 2015, 88, 355–365. [Google Scholar] [CrossRef]
- Otto, F.; Dlouhý, A.; Somsen, C.; Bei, H.; Eggeler, G.; George, E.P. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater. 2013, 61. [Google Scholar] [CrossRef]
- Gali, A.; George, E.P. Tensile properties of high- and medium-entropy alloys. Intermetallics 2013, 39, 74–78. [Google Scholar] [CrossRef]
- Schuh, B.; Mendez-Martin, F.; Völker, B.; George, E.P.P.; Clemens, H.; Pippan, R.; Hohenwarter, A.; Völker, B.; George, E.P.P.; Clemens, H.; et al. Mechanical properties, microstructure and thermal stability of a nanocrystalline CoCrFeMnNi high-entropy alloy after severe plastic deformation. Acta Mater. 2015, 96, 258–268. [Google Scholar] [CrossRef]
- Lee, D.-H.; Choi, I.-C.; Seok, M.-Y.; He, J.; Lu, Z.; Suh, J.-Y.; Kawasaki, M.; Langdon, T.G.; Jang, J. Nanomechanical behavior and structural stability of a nanocrystalline CoCrFeNiMn high-entropy alloy processed by high-pressure torsion. J. Mater. Res. 2015, 30, 2804–2815. [Google Scholar] [CrossRef]
- Heczel, A.; Kawasaki, M.; Lábár, J.L.; Jang, J.; Langdon, T.G.; Gubicza, J. Defect structure and hardness in nanocrystalline CoCrFeMnNi High-Entropy Alloy processed by High-Pressure Torsion. J. Alloy. Compd. 2017, 711, 143–154. [Google Scholar] [CrossRef]
- Laplanche, G.; Kostka, A.; Horst, O.M.M.; Eggeler, G.; George, E.P.P. Microstructure evolution and critical stress for twinning in the CrMnFeCoNi high-entropy alloy. Acta Mater. 2016, 118, 152–163. [Google Scholar] [CrossRef]
- Stepanov, N.; Tikhonovsky, M.; Yurchenko, N.; Zyabkin, D.; Klimova, M.; Zherebtsov, S.; Efimov, A.; Salishchev, G. Effect of cryo-deformation on structure and properties of CoCrFeNiMn high-entropy alloy. Intermetallics 2015, 59, 8–17. [Google Scholar] [CrossRef]
- Zherebtsov, S.V.; Dyakonov, G.S.; Salem, A.A.; Sokolenko, V.I.; Salishchev, G.A.; Semiatin, S.L. Formation of nanostructures in commercial-purity titanium via cryorolling. Acta Mater. 2013, 61, 1167–1178. [Google Scholar] [CrossRef]
- Zherebtsov, S.V.; Dyakonov, G.S.; Salishchev, G.A.; Salem, A.A.; Semiatin, S.L. The Influence of Grain Size on Twinning and Microstructure Refinement during Cold Rolling of Commercial-Purity Titanium. Metall. Mater. Trans. A 2016, 47, 5101–5113. [Google Scholar] [CrossRef]
- Salishchev, G.A.; Tikhonovsky, M.A.; Shaysultanov, D.G.; Stepanov, N.D.; Kuznetsov, A.V.; Kolodiy, I.V.; Tortika, A.S.; Senkov, O.N. Effect of Mn and V on structure and mechanical properties of high-entropy alloys based on CoCrFeNi system. J. Alloy. Compd. 2014, 591, 11–21. [Google Scholar] [CrossRef]
- Stepanov, N.D.; Shaysultanov, D.G.; Salishchev, G.A.; Tikhonovsky, M.A.; Oleynik, E.E.; Tortika, A.S.; Senkov, O.N. Effect of V content on microstructure and mechanical properties of the CoCrFeMnNiVx high entropy alloys. J. Alloy. Compd. 2015, 628, 170–185. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Langdon, T.G. Using high-pressure torsion for metal processing: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 893–979. [Google Scholar] [CrossRef]
- Stepanov, N.D.; Shaysultanov, D.G.; Chernichenko, R.S.; Yurchenko, N.Y.; Zherebtsov, S.V.; Tikhonovsky, M.A.; Salishchev, G.A. Effect of thermomechanical processing on microstructure and mechanical properties of the carbon-containing CoCrFeNiMn high entropy alloy. J. Alloy. Compd. 2017, 693, 394–405. [Google Scholar] [CrossRef]
- Smallman, R.E.; Westmacott, K.H. Stacking faults in face-centred cubic metals and alloys. Philos. Mag. 1957, 2, 669–683. [Google Scholar] [CrossRef]
- Williamson, G.K.; Hall, W.H. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Klimova, M.; Zherebtsov, S.; Stepanov, N.; Salishchev, G.; Haase, C.; Molodov, D.A. Microstructure and texture evolution of a high manganese TWIP steel during cryo-rolling. Mater. Charact. 2017, 132, 20–30. [Google Scholar] [CrossRef]
- Odnobokova, M.; Tikhonova, M.; Belyakov, A.; Kaibyshev, R. Development of S3n CSL boundaries in austenitic stainless steels subjected to large strain deformation and annealing. J. Mater. Sci. 2017, 52, 4210–4223. [Google Scholar] [CrossRef]
- Zherebtsov, S.; Kudryavtsev, E.; Kostjuchenko, S.; Malysheva, S.; Salishchev, G. Strength and ductility-related properties of ultrafine grained two-phase titanium alloy produced by warm multiaxial forging. Mater. Sci. Eng. A 2012, 536, 190–196. [Google Scholar] [CrossRef]
- Tang, Q.H.; Huang, Y.Y.; Huang, Y.Y.; Liao, X.Z.; Langdon, T.G.; Dai, P.Q. Hardening of an Al0.3CoCrFeNi high entropy alloy via high-pressure torsion and thermal annealing. Mater. Lett. 2015, 151, 126–129. [Google Scholar] [CrossRef]
- Shahmir, H.; He, J.; Lu, Z.; Kawasaki, M.; Langdon, T.G. Effect of annealing on mechanical properties of a nanocrystalline CoCrFeNiMn high-entropy alloy processed by high-pressure torsion. Mater. Sci. Eng. A 2016, 676, 294–303. [Google Scholar] [CrossRef]
- Moon, J.; Qi, Y.; Tabachnikova, E.; Estrin, Y.; Choi, W.-M.; Joo, S.-H.; Lee, B.-J.; Podolskiy, A.; Tikhonovsky, M.; Kim, H.S. Deformation-induced phase transformation of Co20Cr26Fe20Mn20Ni14 high-entropy alloy during high-pressure torsion at 77 K. Mater. Lett. 2017, 202, 86–88. [Google Scholar] [CrossRef]
- Joo, S.-H.; Kato, H.; Jang, M.J.; Moon, J.; Tsai, C.W.; Yeh, J.W.; Kim, H.S. Tensile deformation behavior and deformation twinning of an equimolar CoCrFeMnNi high-entropy alloy. Mater. Sci. Eng. A 2017, 689, 122–133. [Google Scholar] [CrossRef]
- Jang, M.J.; Ahn, D.-H.; Moon, J.; Bae, J.W.; Yim, D.; Yeh, J.-W.; Estrin, Y.; Kim, H.S. Constitutive modeling of deformation behavior of high-entropy alloys with face-centered cubic crystal structure. Mater. Res. Lett. 2017, 5, 350–356. [Google Scholar] [CrossRef]
- Zherebtsov, S.; Lojkowski, W.; Mazur, A.; Salishchev, G. Structure and properties of hydrostatically extruded commercially pure titanium. Mater. Sci. Eng. A 2010, 527, 5596–5603. [Google Scholar] [CrossRef]
- Salishchev, G.; Mironov, S.; Zherebtsov, S.; Belyakov, A. Changes in misorientations of grain boundaries in titanium during deformation. Mater. Charact. 2010, 61, 732–739. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Templeman, Y.; Ben Hamu, G.; Meshi, L. Friction stir welded AM50 and AZ31 Mg alloys: Microstructural evolution and improved corrosion resistance. Mater. Charact. 2017, 126, 86–95. [Google Scholar] [CrossRef]
- Meyers, M.A.; Vöhringer, O.; Lubarda, V.A. The onset of twinning in metals: A constitutive description. Acta Mater. 2001, 49, 4025–4039. [Google Scholar] [CrossRef]
- Hull, D.; Bacon, D.J. Introduction to Dislocations; Butterworth-Heinemann: Oxford, UK, 2011; ISBN 9780080966724. [Google Scholar]
- Laplanche, G.; Gadaud, P.; Horst, O.; Otto, F.; Eggeler, G.; George, E.P.P. Temperature dependencies of the elastic moduli and thermal expansion coefficient of an equiatomic, single-phase CoCrFeMnNi high-entropy alloy. J. Alloy. Compd. 2015, 623, 348–353. [Google Scholar] [CrossRef]
- Hughes, D.; Hansen, N. Microstructure and strength of nickel at large strains. Acta Mater. 2000, 48, 2985–3004. [Google Scholar] [CrossRef]
- Fu, Z.; Chen, W.; Wen, H.; Zhang, D.; Chen, Z.; Zheng, B.; Zhou, Y.; Lavernia, E.J. Microstructure and strengthening mechanisms in an FCC structured single-phase nanocrystalline Co25Ni25Fe25Al7.5Cu17.5 high-entropy alloy. Acta Mater. 2016, 107, 59–71. [Google Scholar] [CrossRef]
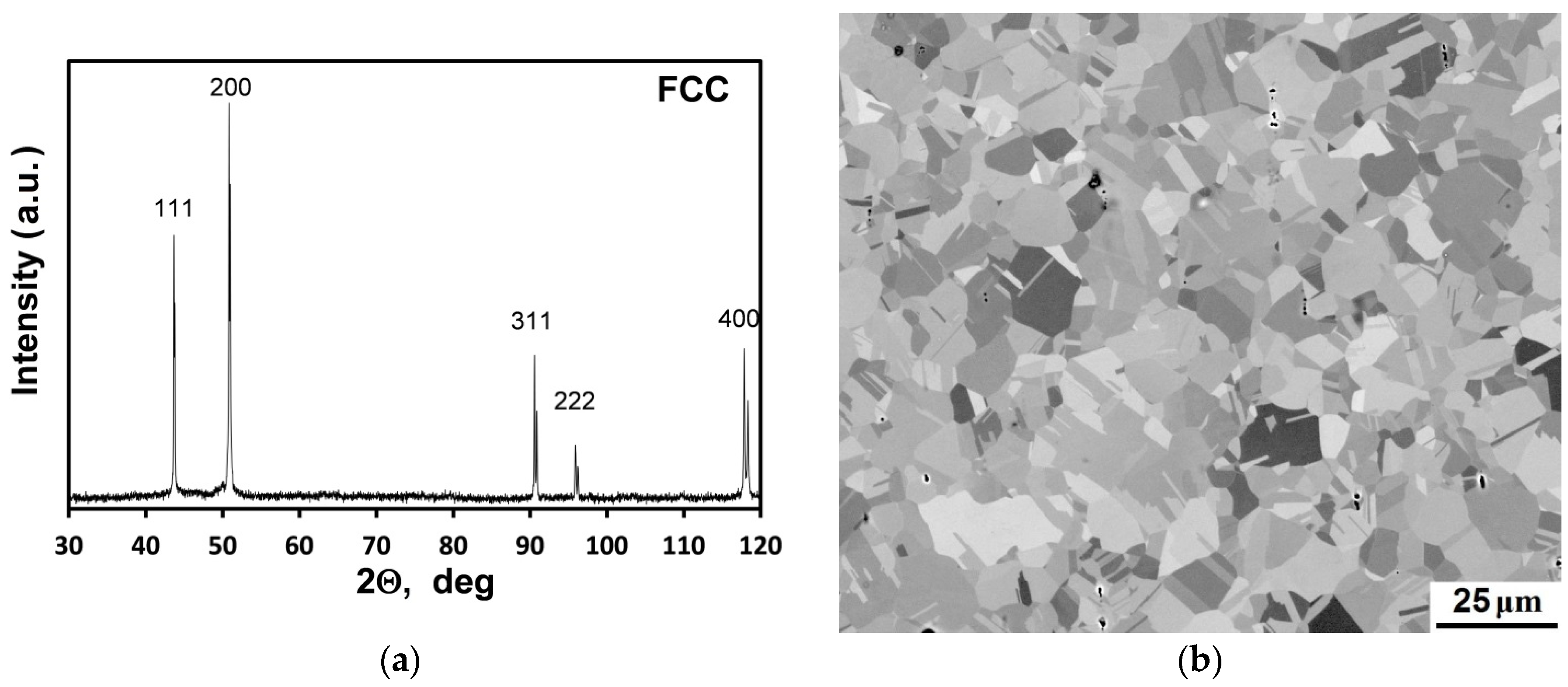




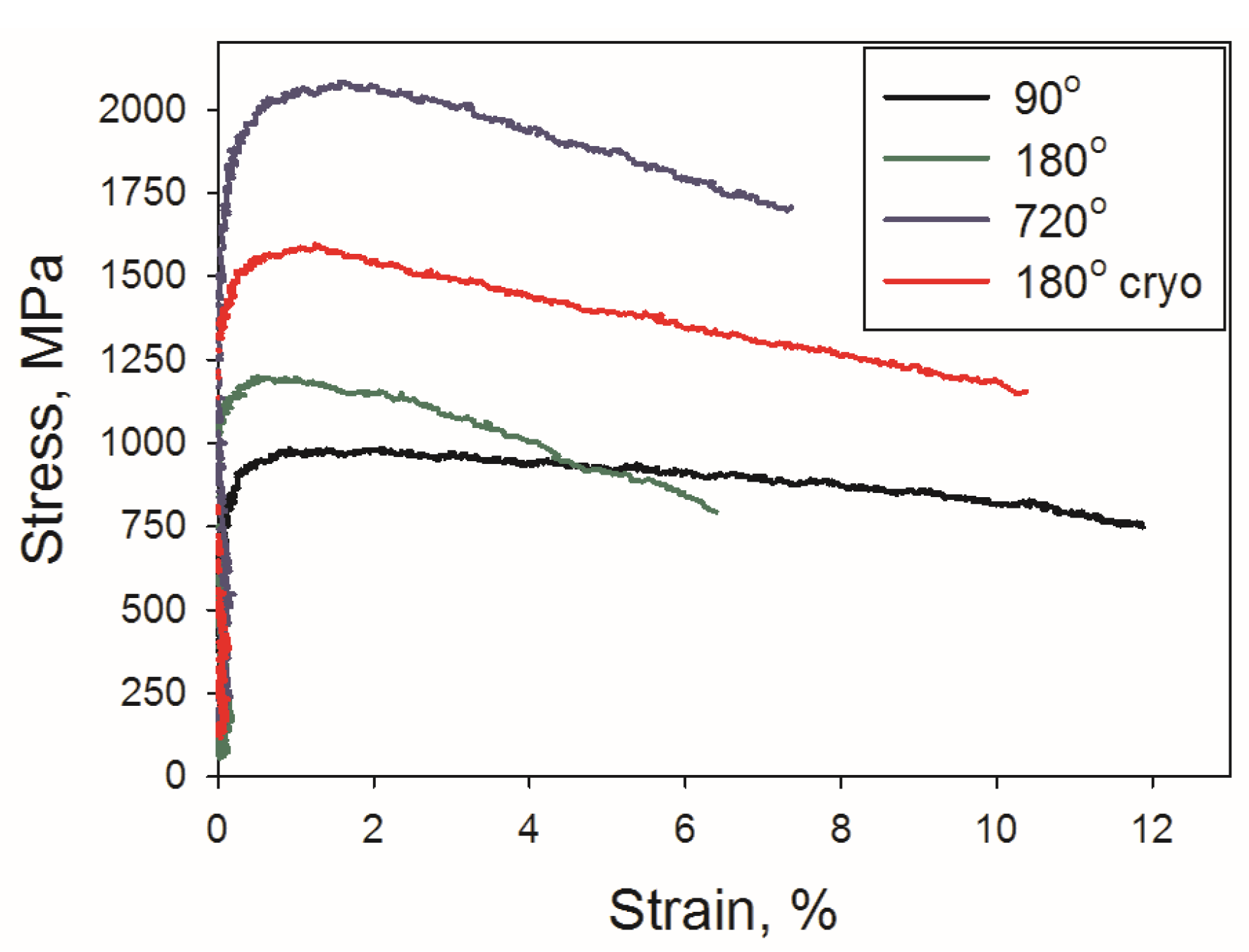
| HPT Condition | YS, MPa | UTS, MPa | UE, % | TE, % | |
|---|---|---|---|---|---|
| Temperature, K | Rotation, ° | ||||
| 293 | 90 | 860 | 981 | 1.4 | 11.9 |
| 180 | 1134 | 1197 | 0.5 | 6.4 | |
| 720 | 1834 | 2069 | 1.4 | 7.4 | |
| 77 | 180 | 1442 | 1596 | 1.3 | 10.4 |
| Strain, ° (Temperature, K) | Dislocation Density, m−2 | Calculated Grain Size, nm | σH−P, MPa | σρ, MPa | Predicted YS, MPa |
|---|---|---|---|---|---|
| 90 (293) | 1.48 × 1015 | 2500 | 311 | 475 | 911 |
| 180 (293) | 9.14 × 1014 | 580 | 646 | 373 | 1144 |
| 720 (293) | 8.86 × 1014 | 140 | 1317 | 367 | 1809 |
| 180 (77) | 2.9 × 1015 | 625 | 625 | 664 | 1414 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zherebtsov, S.; Stepanov, N.; Ivanisenko, Y.; Shaysultanov, D.; Yurchenko, N.; Klimova, M.; Salishchev, G. Evolution of Microstructure and Mechanical Properties of a CoCrFeMnNi High-Entropy Alloy during High-Pressure Torsion at Room and Cryogenic Temperatures. Metals 2018, 8, 123. https://doi.org/10.3390/met8020123
Zherebtsov S, Stepanov N, Ivanisenko Y, Shaysultanov D, Yurchenko N, Klimova M, Salishchev G. Evolution of Microstructure and Mechanical Properties of a CoCrFeMnNi High-Entropy Alloy during High-Pressure Torsion at Room and Cryogenic Temperatures. Metals. 2018; 8(2):123. https://doi.org/10.3390/met8020123
Chicago/Turabian StyleZherebtsov, Sergey, Nikita Stepanov, Yulia Ivanisenko, Dmitry Shaysultanov, Nikita Yurchenko, Margarita Klimova, and Gennady Salishchev. 2018. "Evolution of Microstructure and Mechanical Properties of a CoCrFeMnNi High-Entropy Alloy during High-Pressure Torsion at Room and Cryogenic Temperatures" Metals 8, no. 2: 123. https://doi.org/10.3390/met8020123
APA StyleZherebtsov, S., Stepanov, N., Ivanisenko, Y., Shaysultanov, D., Yurchenko, N., Klimova, M., & Salishchev, G. (2018). Evolution of Microstructure and Mechanical Properties of a CoCrFeMnNi High-Entropy Alloy during High-Pressure Torsion at Room and Cryogenic Temperatures. Metals, 8(2), 123. https://doi.org/10.3390/met8020123







