High Quality Steel Casting by Using Advanced Mathematical Methods
Abstract
1. Introduction
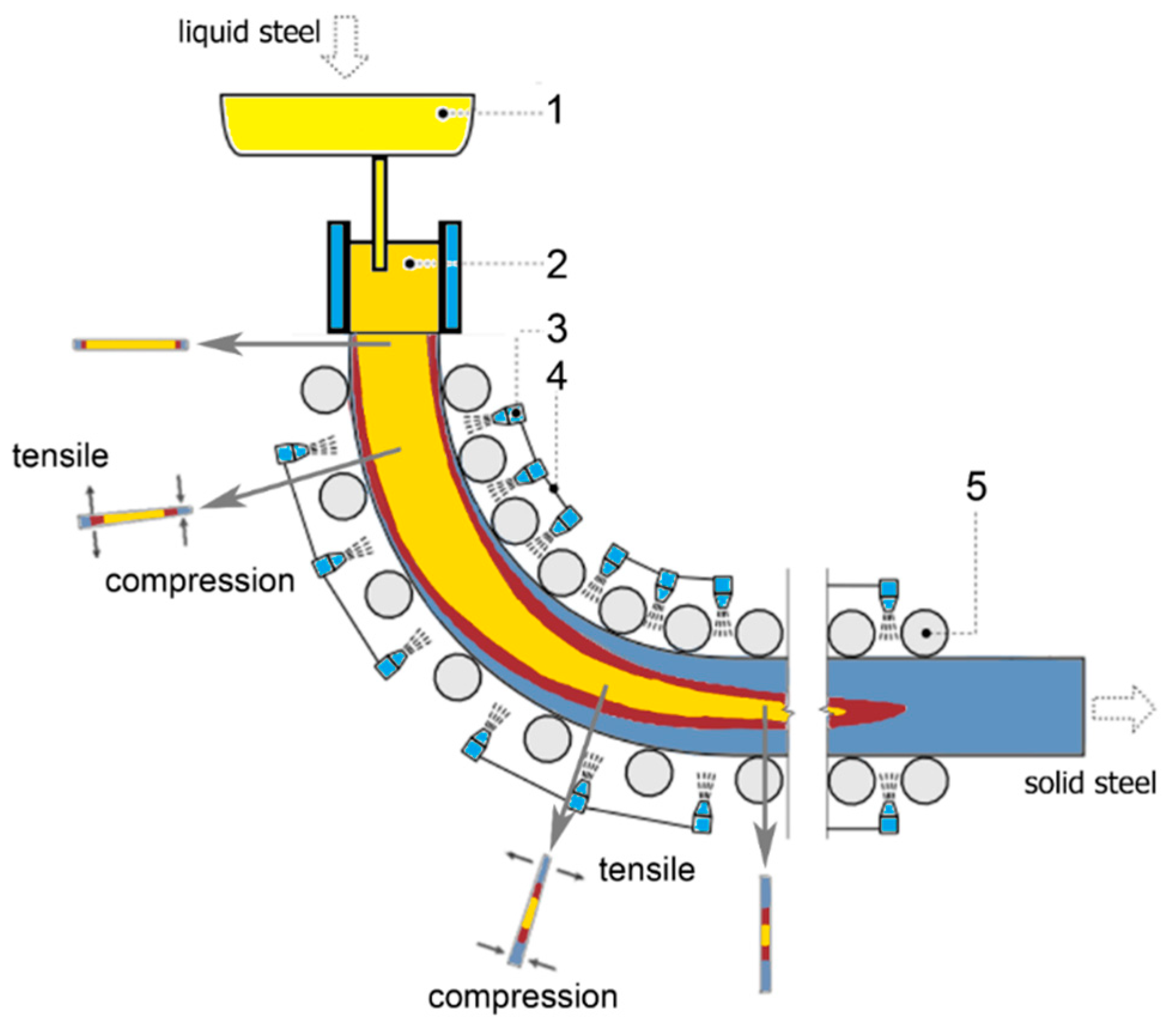
2. Solidification Model—BrDSM
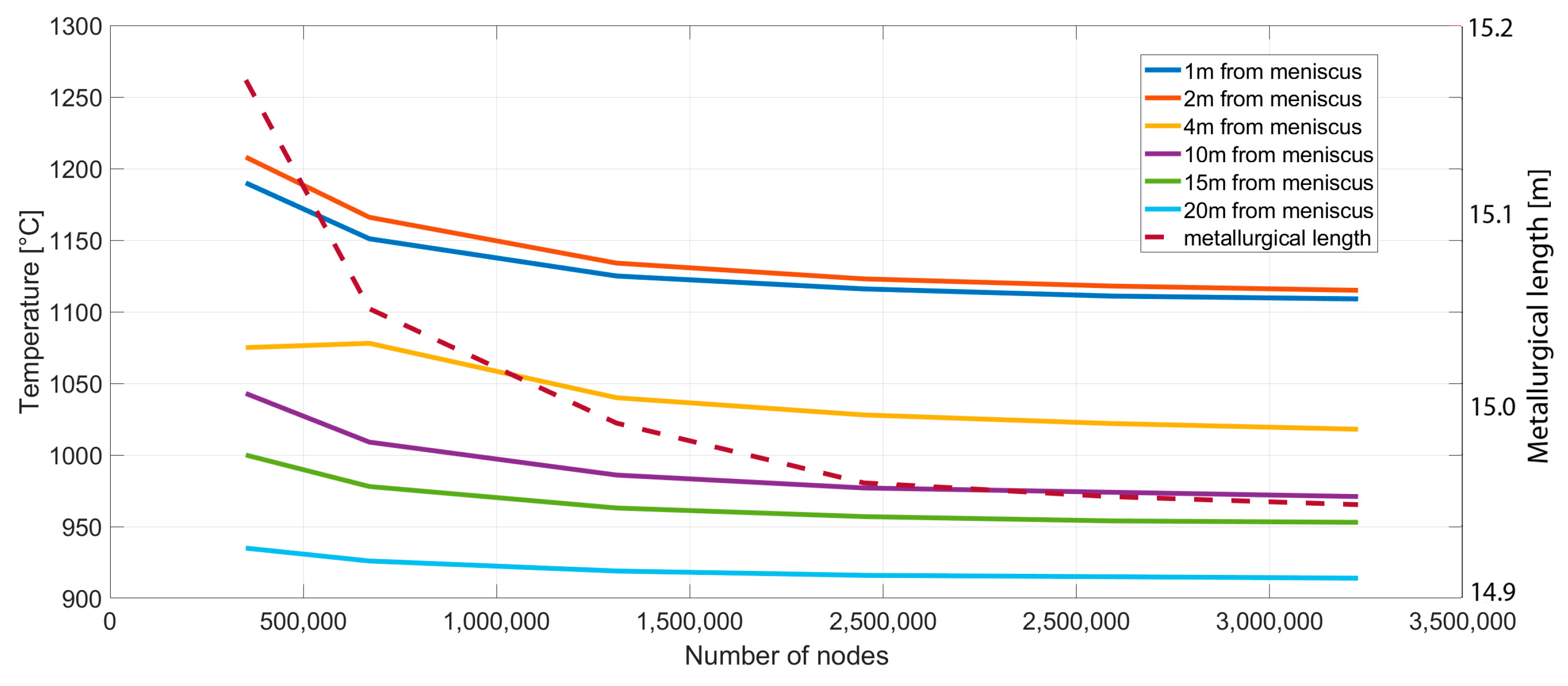
3. Numerical Formulation and Massive Parallelization
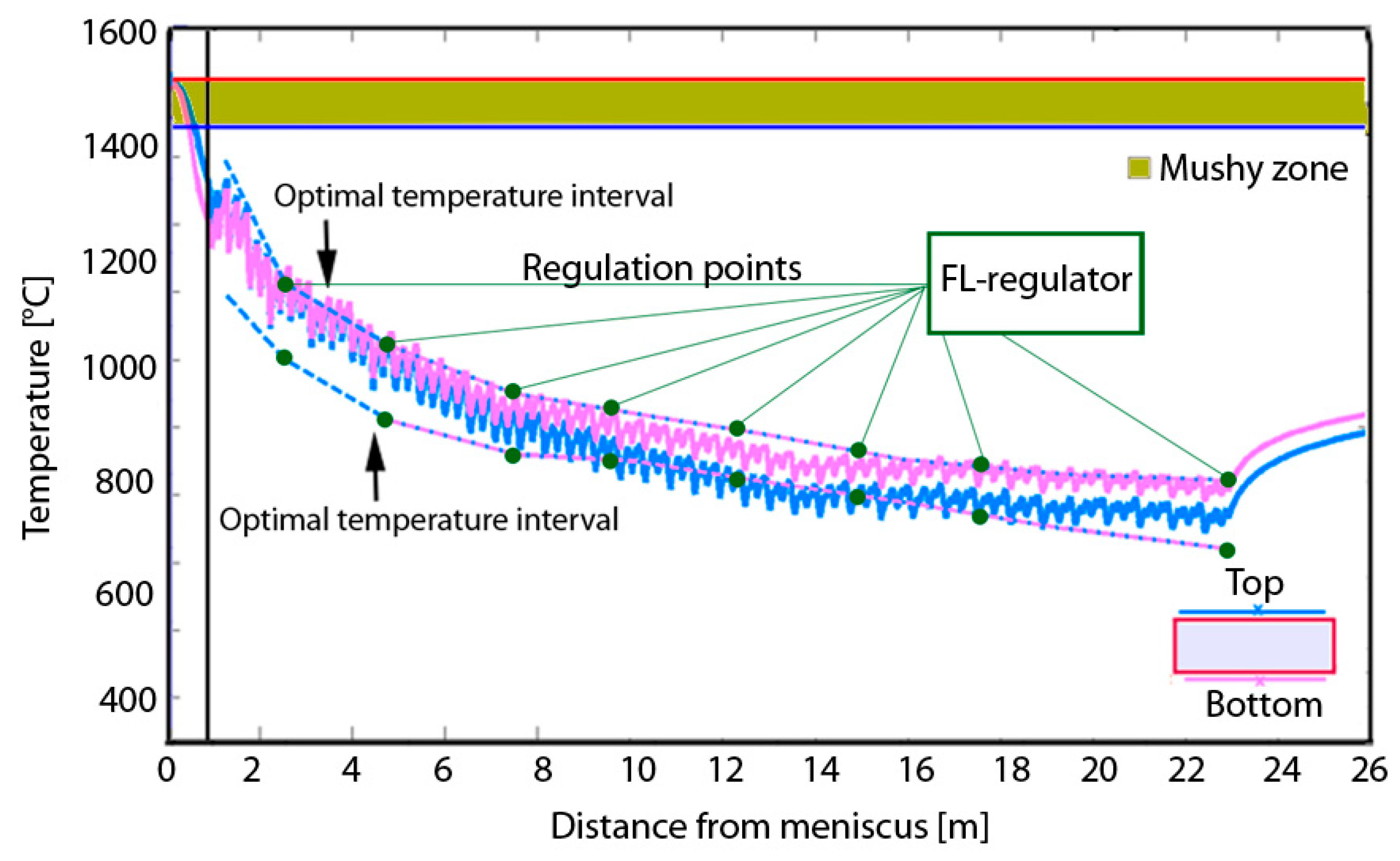
4. Fuzzy Logic Regulator—FL-BrDSM
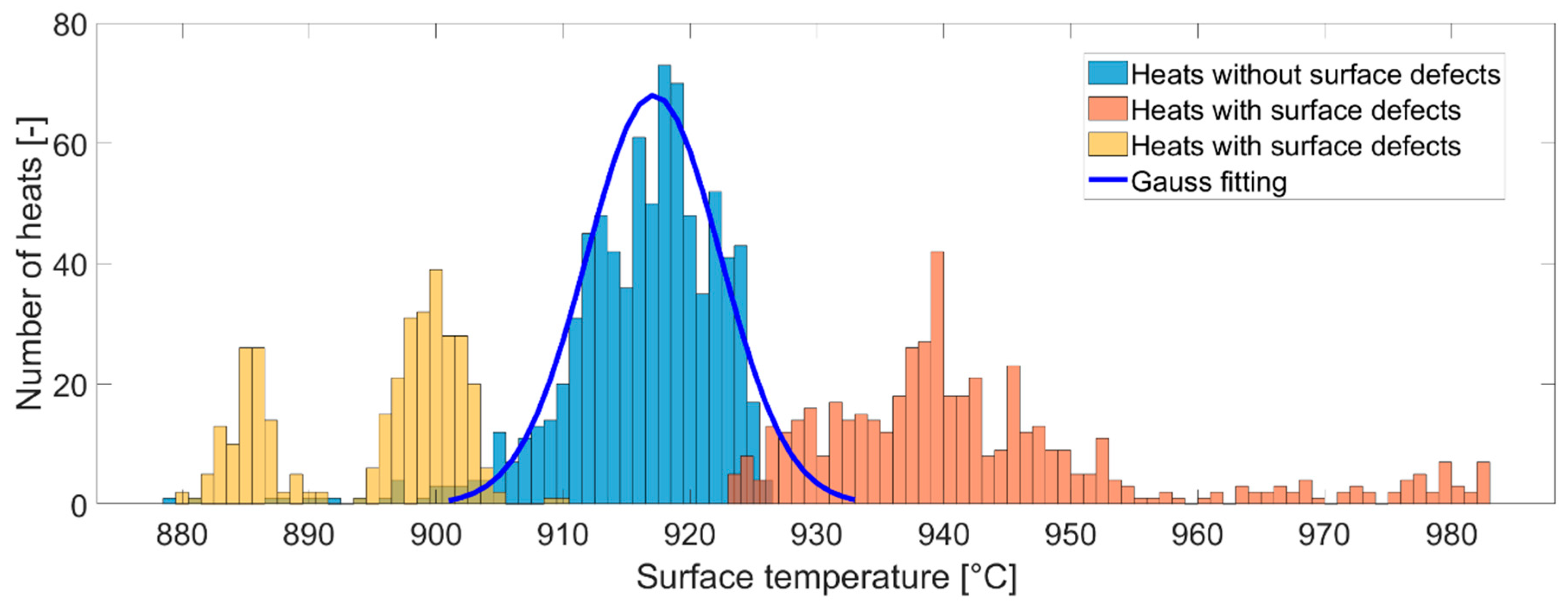
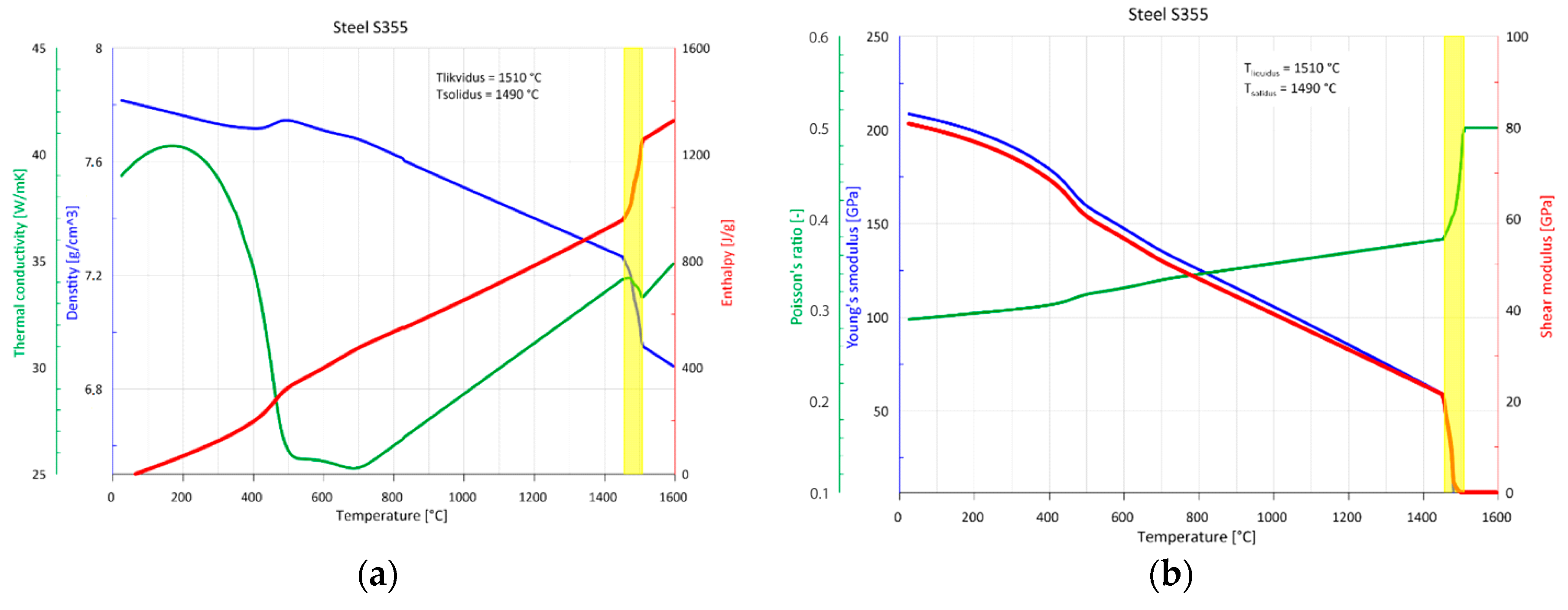
5. Steel S355 and Real Casting Data
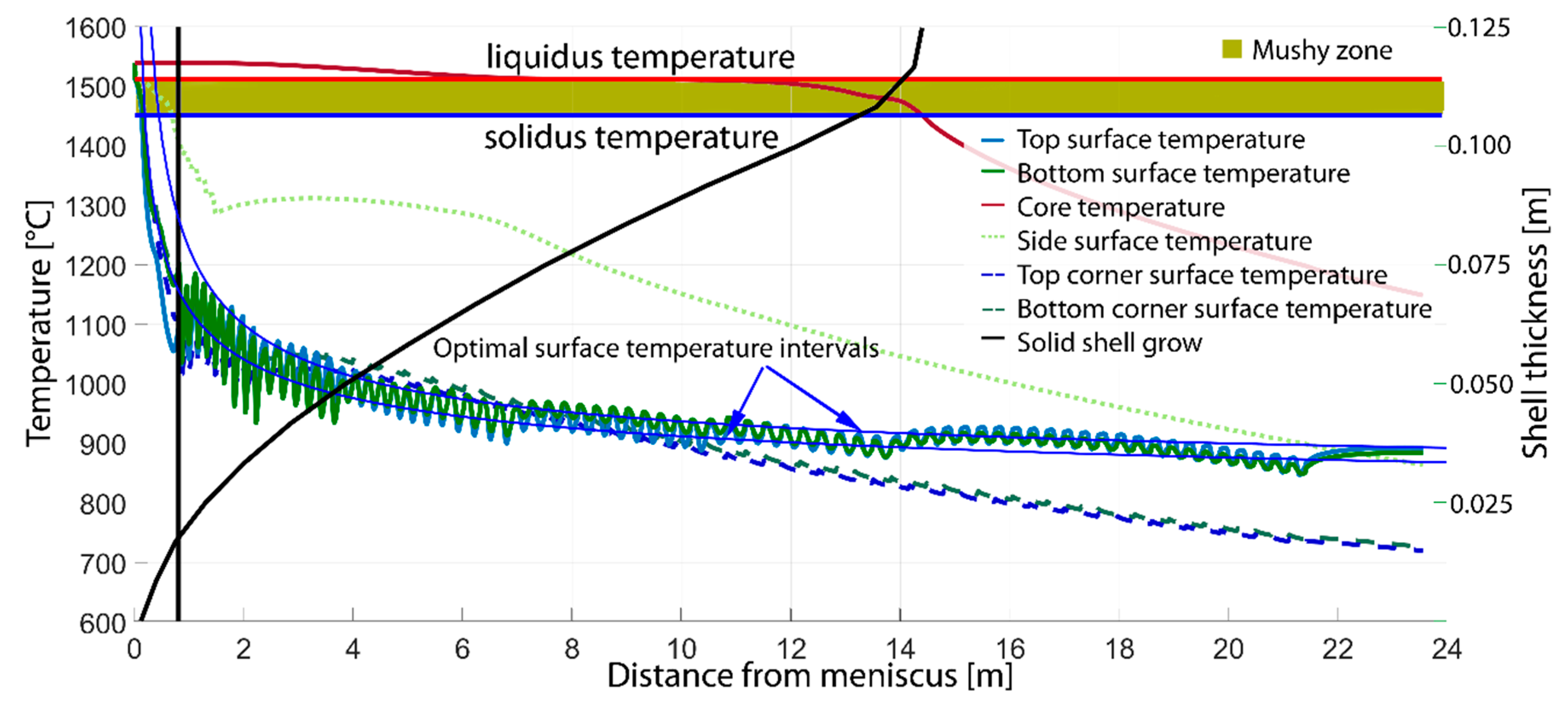
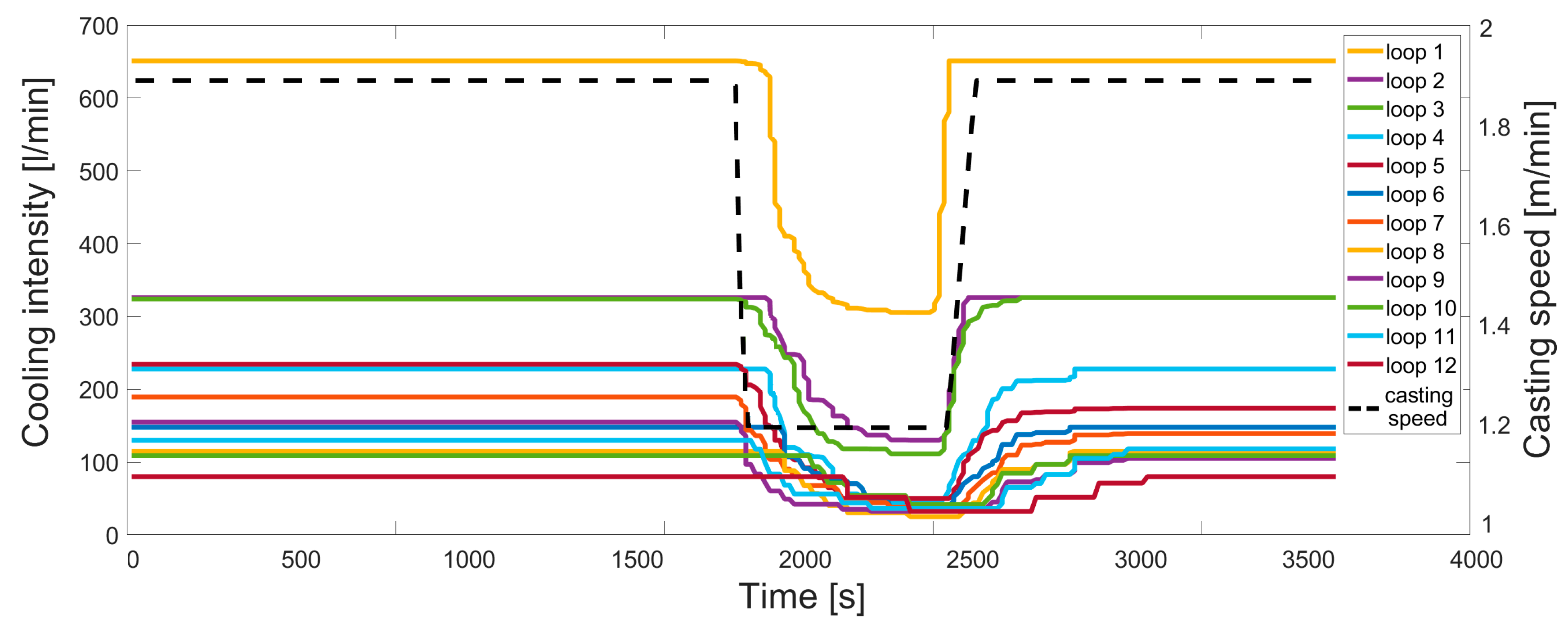
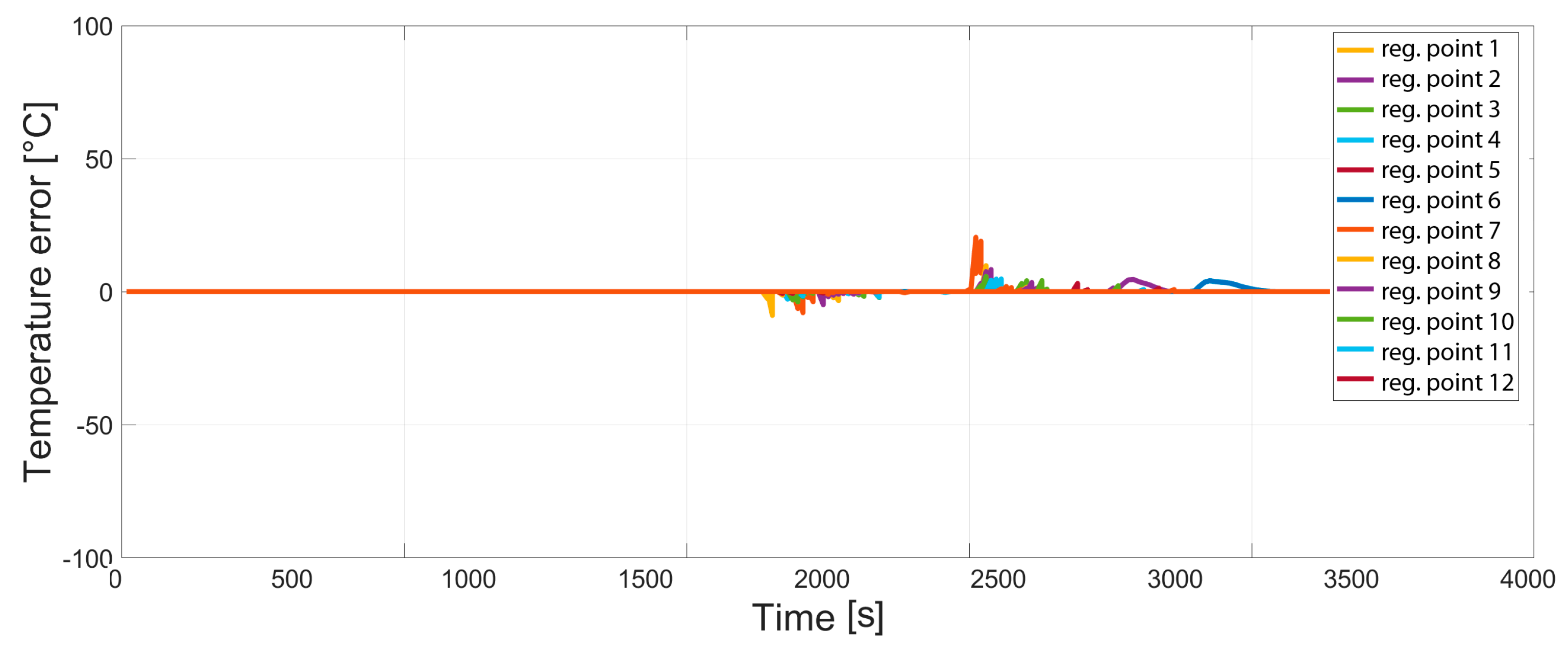
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flick, A.; Stoiber, C. Trends in continuous casting of steel: Yesterday, today and tomorrow. In Proceedings of the METEC InSteelCon, Düsseldorf, Germany, 27 June–1 July 2011; pp. 80–91. [Google Scholar]
- Birat, P.; Chow, C.; Emi, T.; Emling, W.H.; Fastert, H.P.; Fitzel, H.; Flemings, M.C.; Gaye, H.R.; Gilles, H.L.; Glaws, P.C.; et al. The Making, Shaping and Treating of Steel: Casting Volume, 11th ed.; The AISE Steel Foundation: Pittsburgh, PA, USA, 2003; p. 1000. ISBN 978-0-930767-04-4. [Google Scholar]
- Santos, C.A.; Spim, J.A.; Garcia, A. Mathematical modeling and optimization strategies (genetic algorithm and knowledge base) applied to the continuous casting of steel. Eng. Appl. Artif. Intell. 2003, 16, 511–527. [Google Scholar] [CrossRef]
- Zhemping, J.; Wang, B.; Xie, Z.; Lai, Z. Ant Colony Optimization Based Heat Transfer Coefficient Identification for Secondary Cooling Zone of Continuous Caster. In Proceedings of the IEEE International Conference Industrial Technology, Shenzhen, China, 20–24 March 2007; pp. 558–562. [Google Scholar] [CrossRef]
- Zheng, P.; Guo, J.; Hao, X.-J. Hybrid Strategies for Optimizing Continuous Casting Process of Steel. In Proceedings of the IEEE International Conference Industrial Technology, Hammamet, Tunisia, 8–10 December 2004; pp. 1156–1161. [Google Scholar] [CrossRef]
- Mauder, T.; Novotny, J. Two mathematical approaches for optimal control of the continuous slab casting process. In Proceedings of the Mendel 2010—16th International Conference on Soft Computing, Brno, Czech Republic, 26–28 June 2010; pp. 395–400, ISBN 978-80-214-4120-0. [Google Scholar]
- Ivanova, A.A. Predictive Control of Water Discharge in the Secondary Cooling Zone of a Continuous Caster. Metallurgist 2013, 57, 592–599. [Google Scholar] [CrossRef]
- Rao, R.V.; Kalyankar, V.D.; Waghmare, G. Parameters optimization of selected casting processes using teaching-learning-based optimization algorithm. Appl. Math. Modell. 2014, 38, 5592–5608. [Google Scholar] [CrossRef]
- Mosayebidorcheh, S.; Bandpy, M.G. Local and averaged-area analysis of steel slab heat transfer and phase. change in continuous casting process. Appl. Thermal Eng. 2017, 118, 724–733. [Google Scholar] [CrossRef]
- Mauder, T.; Charvat, P.; Stetina, J.; Klimes, L. Assessment of Basic Approaches to Numerical Modeling of Phase Change Problems-Accuracy, Efficiency, and Parallel Decomposition. J. Heat Transf. 2017, 139, 5. [Google Scholar] [CrossRef]
- Miettinen, J. IDS Solidification Analysis Package for Steels: User Manual of DOS Version 2.0.0; Helsinki University of Technology: Helsinki, Finland, 1999; p. 22. ISBN 9512246600. [Google Scholar]
- Zhang, J.; Chen, D.F.; Zhang, C.Q.; Wang, S.G.; Hwang, W.S.; Han, M.R. Effects of an even secondary cooling mode on the temperature and stress fields of round billet continuous casting steel. J. Mater. Process. Technol. 2015, 222, 315–326. [Google Scholar] [CrossRef]
- Javurek, M.; Ladner, P.; Watzinger, J.; Wimmer, P. Secondary cooling: Roll heat transfer during dry casting. In Proceedings of the METEC ESTAD, Düsseldorf, Germany, 15–19 June 2015; p. 8. [Google Scholar]
- Totten, G.E.; Bates, C.E.; Clinton, N.A. Handbook of Quenchants and Quenching Technology; Haddad, M.T., Ed.; ASM International: Materials Park, OH, USA, 1993; p. 507. ISBN 0-87170-448-X. [Google Scholar]
- Ramírez-López, A.; Muñoz-Negrón, D.; Palomar-Pardavé, M.; Romero-Romo, M.A.; Gonzalez-Trejo, J. Heat removal analysis on steel billets and slabs produced by continuous casting using numerical simulation. Int. J. Adv. Manuf. Technol. 2017, 93, 1545–1565. [Google Scholar] [CrossRef]
- Raudensky, M.; Hnizdil, M.; Hwang, J.Y.; Lee, S.H.; Kim, S.Y. Influence of Water Temperature on The Cooling Intensity of Mist Nozzles in Continuous Casting. Mater. Tehnol. 2012, 46, 311–315. [Google Scholar]
- Stetina, J.; Mauder, T.; Klimeš, L. Utilization of Nonlinear Model Predictive Control to Secondary Cooling during Dynamic Variations. In Proceedings of the AISTech, Pittsburgh, PA, USA, 16–19 May 2016; p. 14. [Google Scholar]
- Mauder, T.; Sandera, C.; Stetina, J. Optimal control algorithm for continuous casting process by using fuzzy logic. Steel Res. Int. 2015, 86, 785–798. [Google Scholar] [CrossRef]
- Louhenkilpi, S.; Laine, J.; Miettinen, J.; Vesanen, R. New Continuous Casting and Slab Tracking Simulators for Steel Industry. Mater. Sci. Forum 2013, 762, 691–698. [Google Scholar] [CrossRef]


| Numerical Scheme | Computational Time (s) | ||
|---|---|---|---|
| Coarse mesh | Fine-mesh | Very-fine mesh | |
| SE—1 CPU | 11.54 | 887.14 | 54,362.12 |
| SE—12 CPU | 135.28 | 1122.13 | 35,124.54 |
| ADI—1 CPU | 41.81 | 714.73 | 36,210.41 |
| ADI—12 CPU | 58.61 | 824.32 | 32,416.32 |
| SE—GPU | 18.67 | 97.72 | 972.49 |
| Weight Fraction | Ni | Mn | Mo | Si | Nb | Ti | Cu |
| wt% | max 0.300 | 1.400–1.550 | max 0.080 | 0.5 | max 0.060 | max 0.020 | max 0.200 |
| Weight Fraction | V | Al | P | C | Cr | S | Ca |
| wt% | max 0.020 | 0.020–0.060 | 0.030 | 0.160–0.180 | max 0.200 | 0.020 | 0.002 |
| Casting Speed (m/min) | Loop 1 (L/min) | Loop 2 (L/min) | Loop 3 (L/min) | Loop 4 (L/min) | Loop 5 (L/min) | Loop 6 (L/min) |
| 1.5 | 96.6 | 125.4 | 103.9 | 124.6 | 65.3 | 98.5 |
| 1.9 | 98.1 | 132.6 | 109.5 | 146.3 | 98.3 | 103.3 |
| Casting Speed (m/min) | Loop 7 (L/min) | Loop 8 (L/min) | Loop 9 (L/min) | Loop 10 (L/min) | Loop 11 (L/min) | Loop 12 (L/min) |
| 1.5 | 32.0 | 65.7 | 22.0 | 34.7 | 31.2 | 43.7 |
| 1.9 | 46.9 | 85.7 | 26.7 | 58.3 | 99.5 | 106.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mauder, T.; Stetina, J. High Quality Steel Casting by Using Advanced Mathematical Methods. Metals 2018, 8, 1019. https://doi.org/10.3390/met8121019
Mauder T, Stetina J. High Quality Steel Casting by Using Advanced Mathematical Methods. Metals. 2018; 8(12):1019. https://doi.org/10.3390/met8121019
Chicago/Turabian StyleMauder, Tomas, and Josef Stetina. 2018. "High Quality Steel Casting by Using Advanced Mathematical Methods" Metals 8, no. 12: 1019. https://doi.org/10.3390/met8121019
APA StyleMauder, T., & Stetina, J. (2018). High Quality Steel Casting by Using Advanced Mathematical Methods. Metals, 8(12), 1019. https://doi.org/10.3390/met8121019





