Fatigue and Fracture Resistance of Heavy-Section Ferritic Ductile Cast Iron
Abstract
:1. Introduction
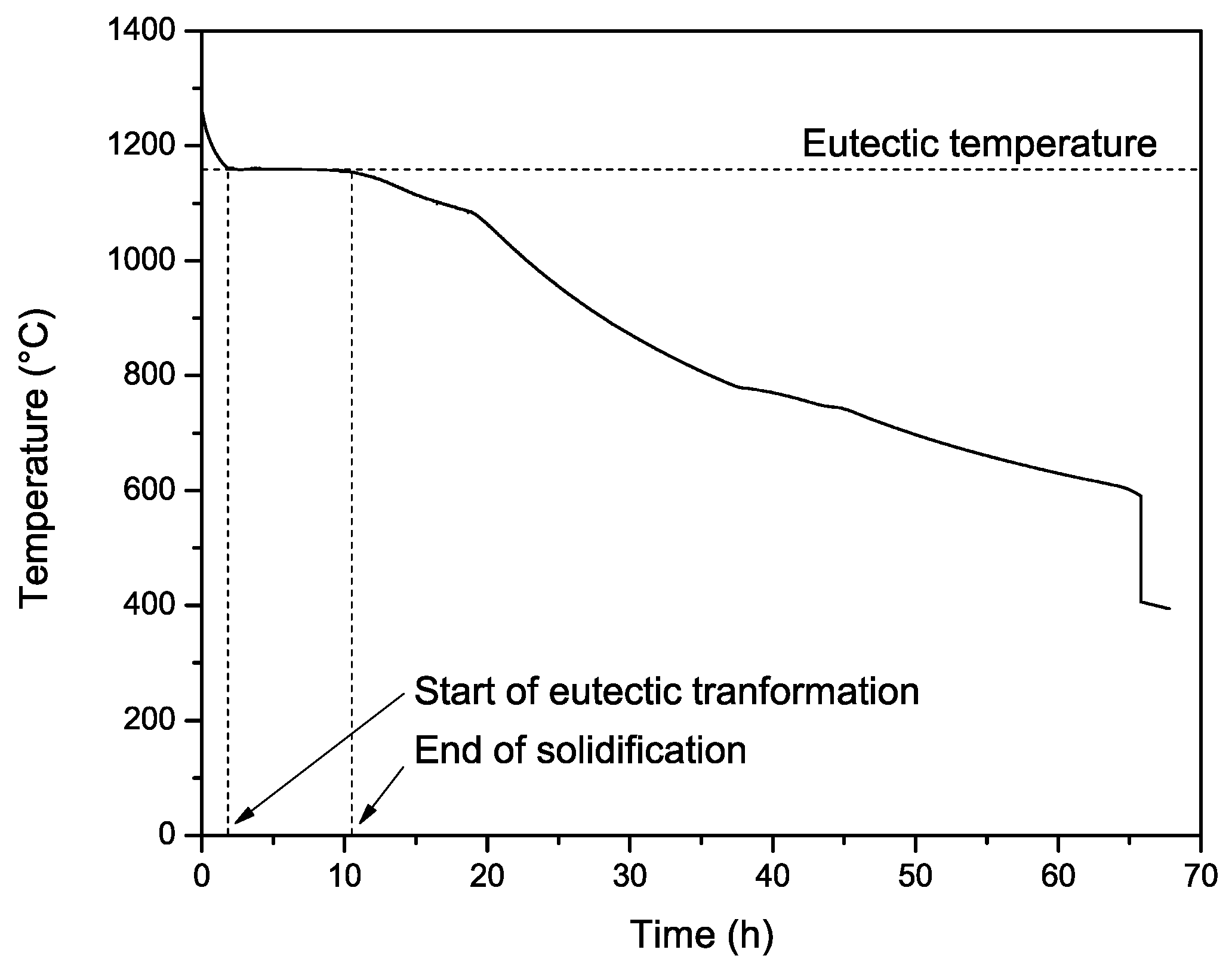
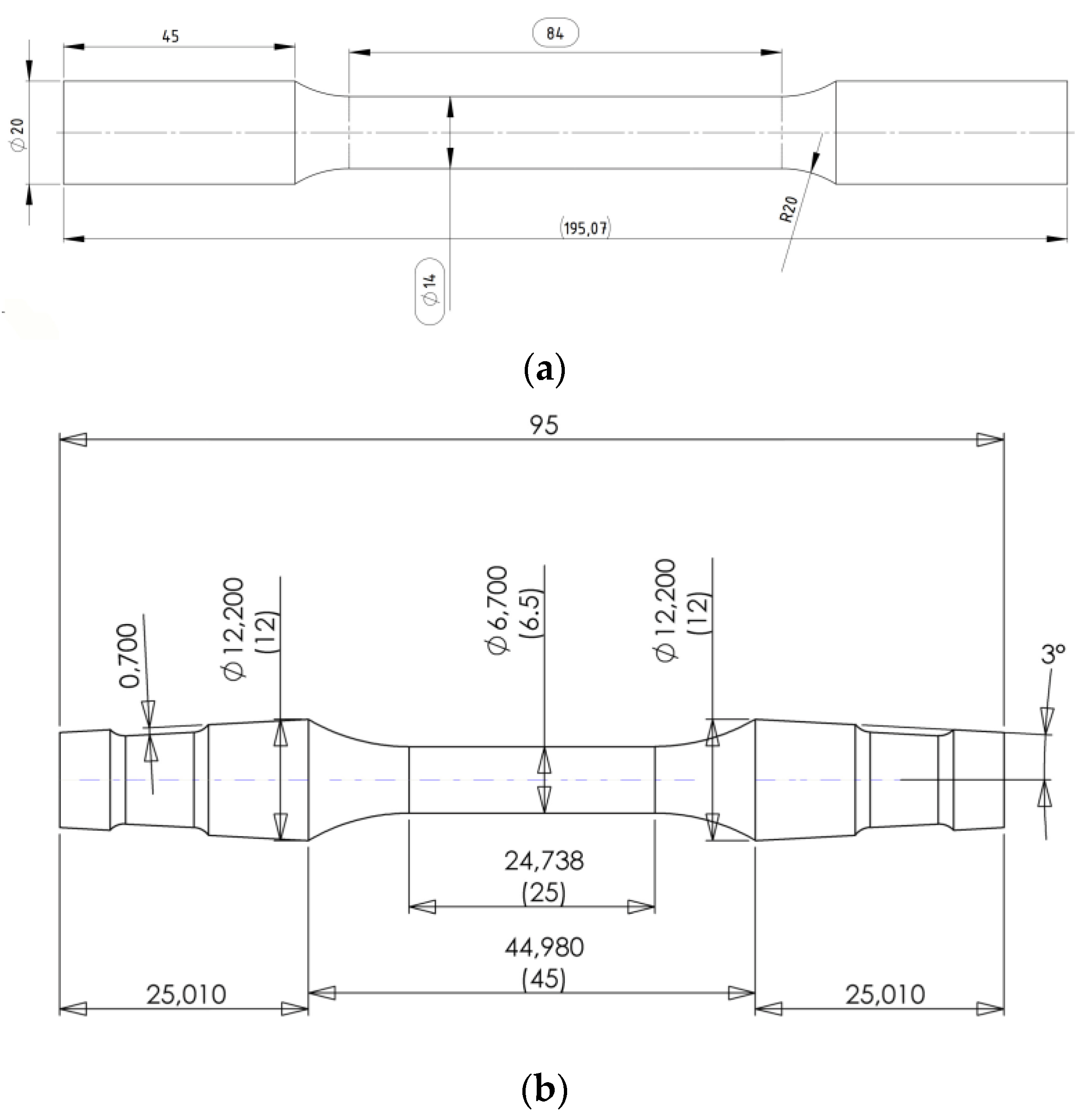
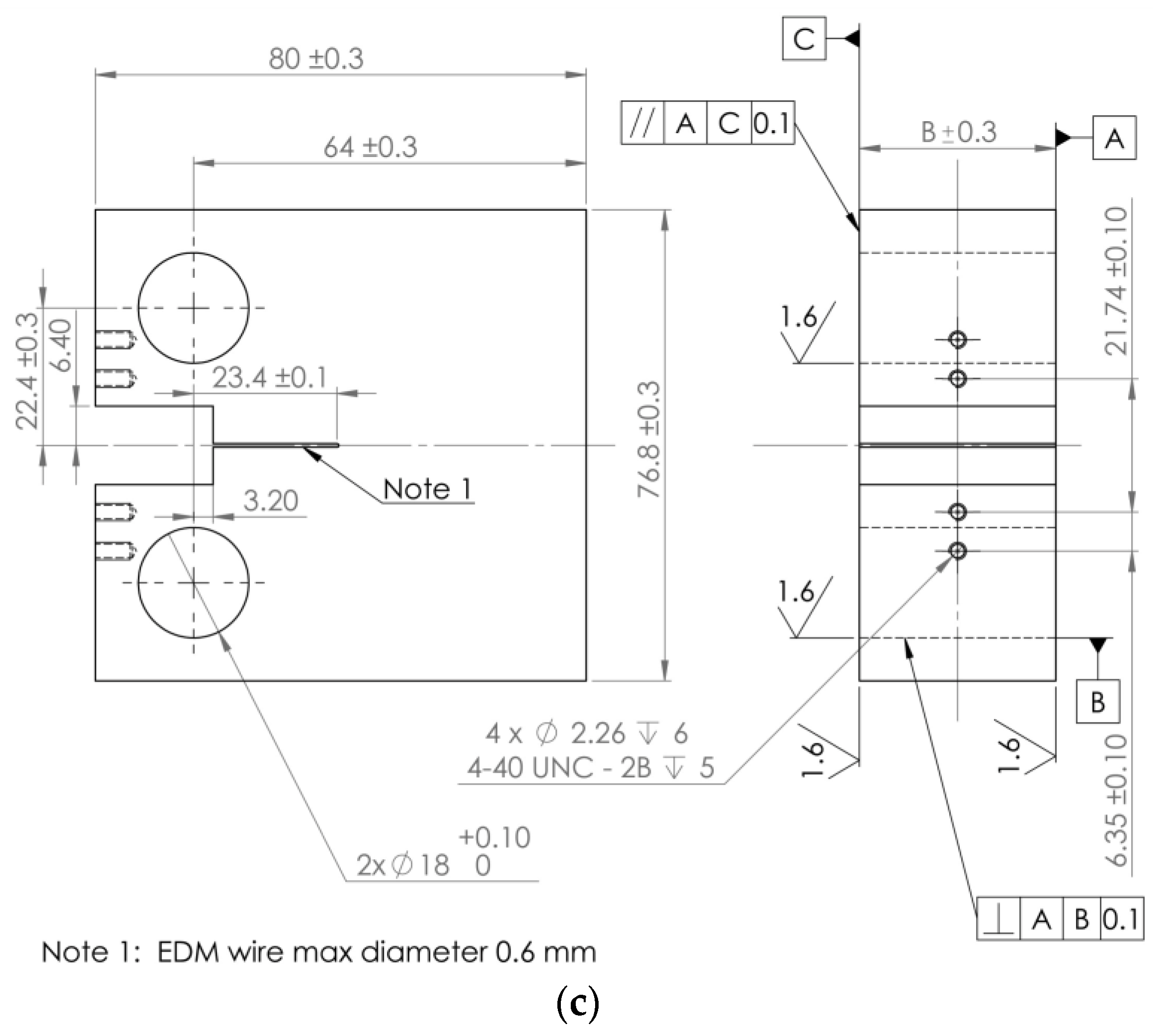
2. Material and Experimental Procedures
3. Results and Discussion
3.1. Microstructure
3.2. Monotonic and High-Cycle Fatigue Properties
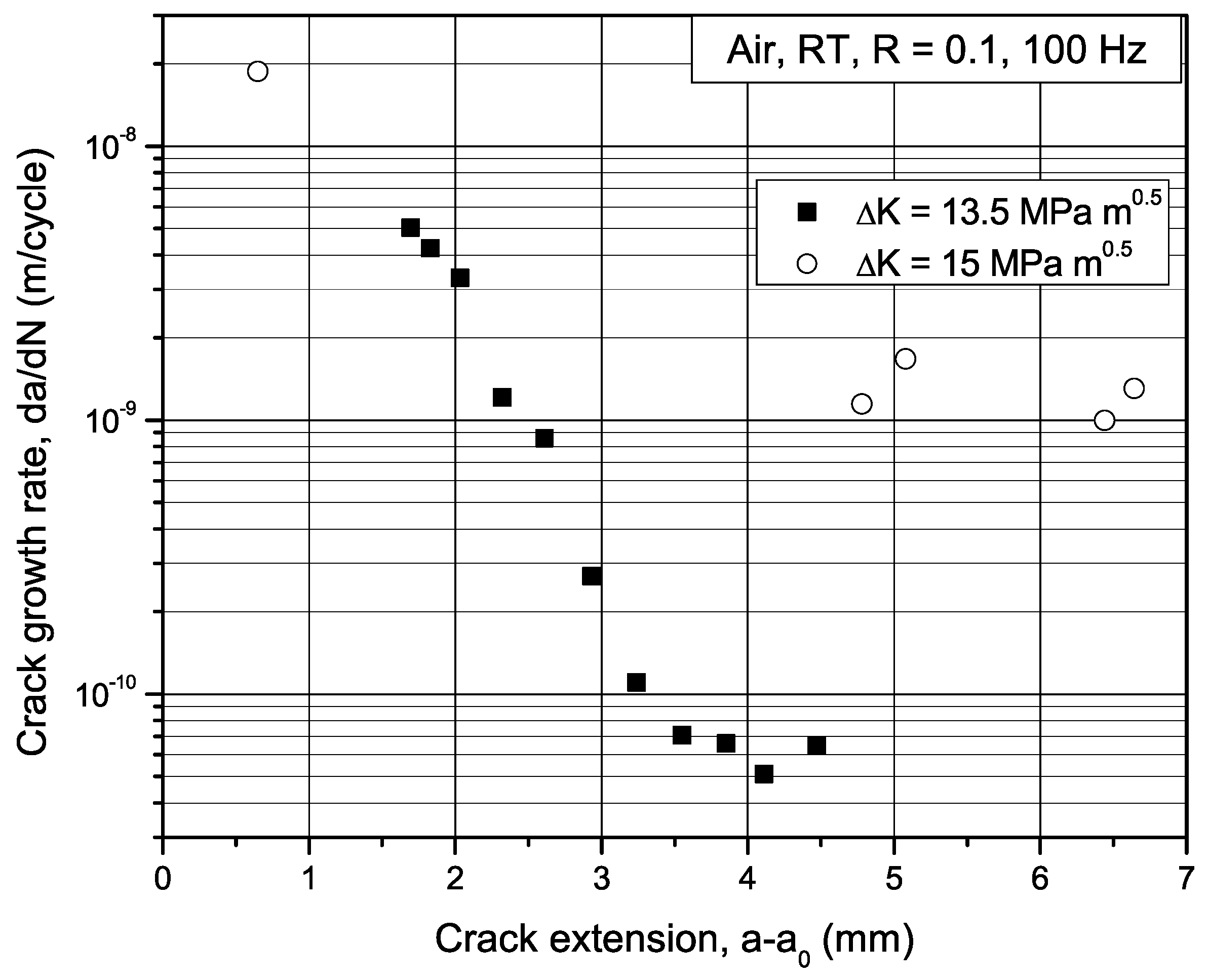
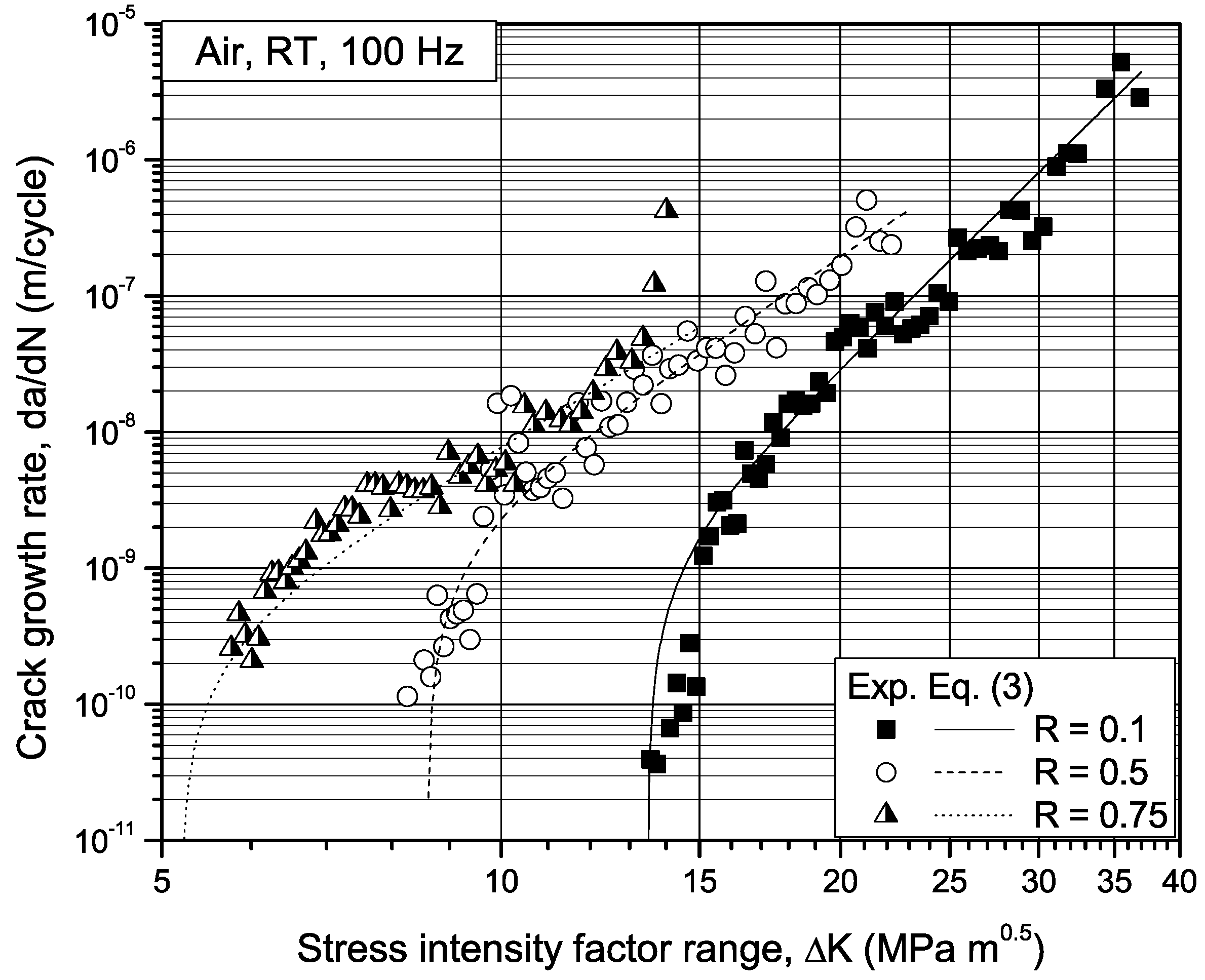
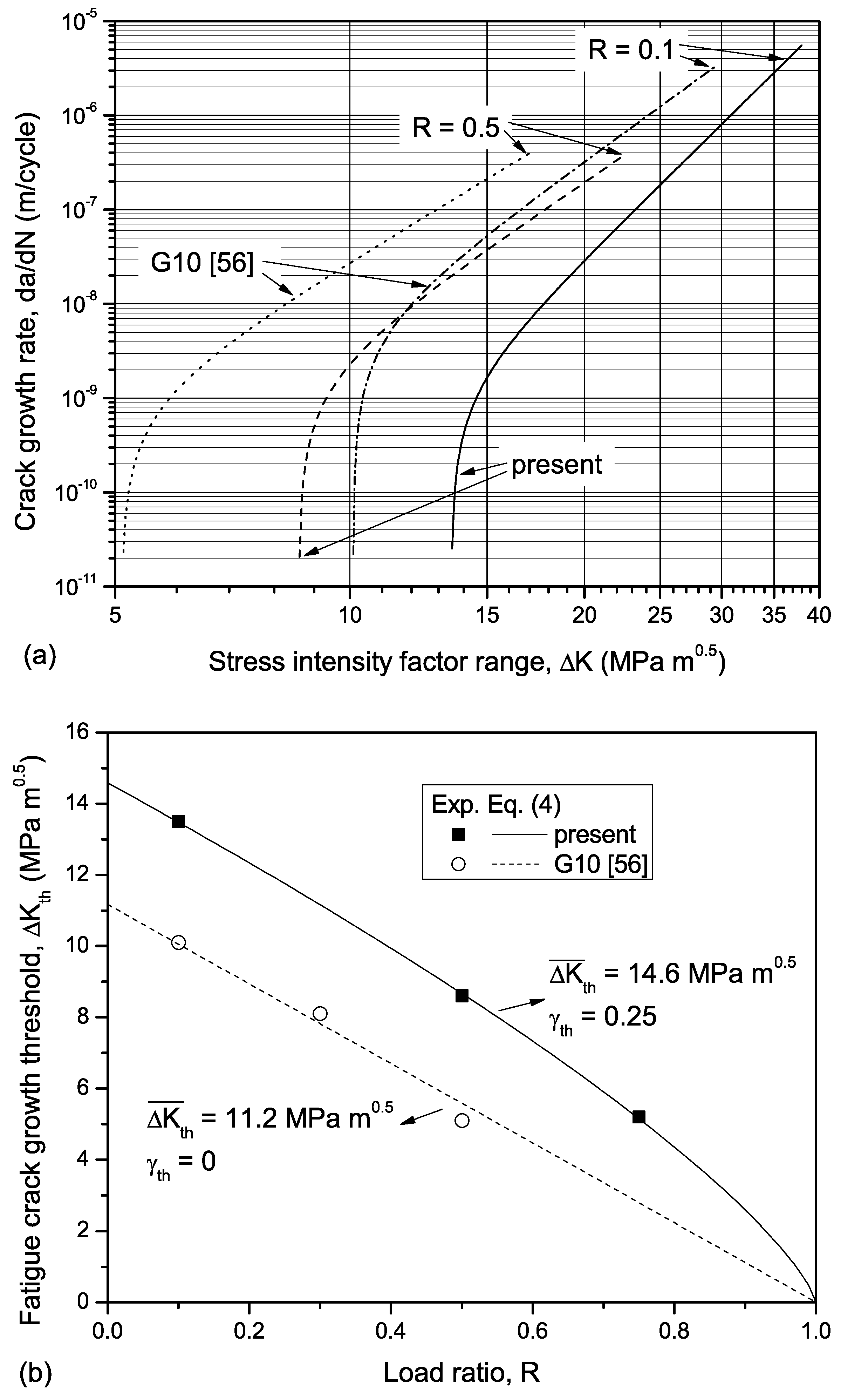
3.3. Fatigue Crack Growth Curves
3.4. Fracture Toughness
4. Conclusions
- (1)
- The microstructure consists of a prevailing ferritic matrix, in which 2/3 of graphite is interspersed in form of overgrown spheroidal nodules and the rest in form of chunky graphite.
- (2)
- The tensile strength and the total elongation are reduced by 20% and 75% with respect to thick-walled (t > 60 mm) EN-GJS-400-15.
- (3)
- The rotating bending fatigue limit at five million cycles is reduced by 30% with respect to the standard EN-1563 reporting the results of fatigue tests employing laboratory samples extracted from thin-walled castings. The fatigue limit is strongly correlated to the dimension of the largest shrinkage pore found on the fracture surface. Nevertheless, shrinkage pores are not the only defects involved in the fatigue damage, as also degenerated chunky graphite can be site of crack nucleation.
- (4)
- The material displays a higher fatigue crack growth resistance, especially in the near-threshold regime, with respect to DCI subject to normal solidification conditions. This has been attributed, at least partially, to crack front geometry effects and crack closure phenomena induced by the high roughness and interlocking crack mating surfaces in the neighborhood of chunky graphite.
- (5)
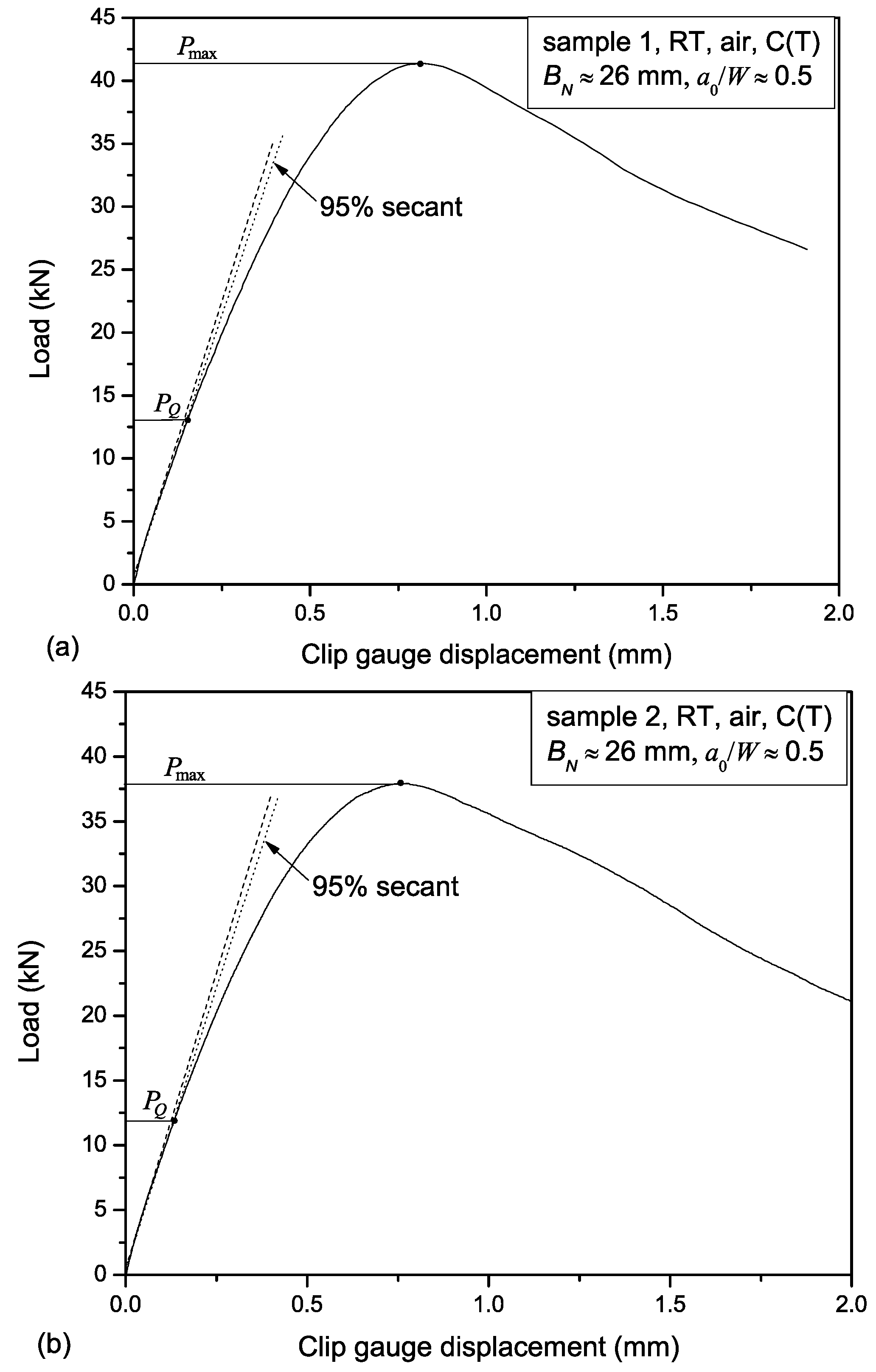
- The fracture toughness is 14% lower than that reported for DCI obtained under normal solidification conditions. On the other hand, the thickness of the samples used in the present experimentation is three times larger than that of specimens usually tested in the literature. The highly nonlinear stress–strain behavior displayed by cast irons makes very difficult to meet the ASTM prescription on the PQ load.
Author Contributions
Conflicts of Interest
References
- Luo, J.; Hardning, R.A.; Bowen, P. Evaluation of the fatigue behavior of ductile irons with various matrix microstructures. Metall. Mater. Trans. A 2002, 33A, 3719–3729. [Google Scholar] [CrossRef]
- Di Cocco, V.; Iacoviello, F.; Rossi, A.; Cavallini, M.; Natali, S. Graphite nodules and fatigue crack propagation micromechanisms in a ferritic ductile cast iron. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 893–902. [Google Scholar] [CrossRef]
- Kaufmann, H.; Wolters, D.B. Zyklische Beanspruchbarkeit dickwandiger Bauteile aus ferritischem Gusseisen mit Kugelgraphit. Konstr. Giess. 2002, 27, 4–27. [Google Scholar]
- Minnebo, P.; Nilsson, KF.; Blagoeva, D. Tensile, compression and fracture properties of thick walled ductile cast iron components. J. Mater. Eng. Perform. 2007, 16, 35–45. [Google Scholar] [CrossRef]
- Kobayashi, M.; Yamabe, J. Influence of casting surfaces on fatigue strength of ductile cast iron. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 403–415. [Google Scholar]
- Meneghetti, G.; Ricotta, M.; Masaggia, S.; Atzori, B. Comparison of the los cycle and medium cycle fatigue behaviour of ferrtic, pearlitic, isothermed and austempered ductile irons. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 913–929. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Bathias, C. Fatigue characterization of a spheroidal graphite cast iron under ultrasonic loading. J. Mater. Sci. 2004, 39, 687–689. [Google Scholar] [CrossRef]
- Caldera, M.; Chapetti, M.; Massone, J.M.; Sikore, J.A. Influence of nodule count on fatigue properties of ferritic thin wall ductile iron. Mater. Sci. Technol. 2007, 23, 1000–1004. [Google Scholar] [CrossRef]
- Andreiko, I.M.; Ostash, O.P.; Popovych, V.V. Influence of microstructure on the strength and cyclic crack resistance of cast irons. Mater. Sci. 2002, 38, 659–671. [Google Scholar] [CrossRef]
- Greno, G.L.; Otegui, J.L.; Boeri, R.E. Mechanisms of fatigue crack growth in austempered ductile Iron. Int. J. Fatigue 1999, 21, 35–43. [Google Scholar] [CrossRef]
- Borsato, T.; Ferro, P.; Berto, F.; Carollo, C. Mechanical and fatigue properties of heavy section solution strengthened ferritic ductile iron castings. Adv. Eng. Mater. 2016, 18, 2070–2075. [Google Scholar] [CrossRef]
- Borsato, T.; Ferro, P.; Berto, F.; Carollo, C. Fatigue strength improvement of heavy-section pearlitic ductile iron castings by in-mould inoculation treatment. Int. J. Fatigue 2017. [Google Scholar] [CrossRef]
- Taylor, D.; Hughes, M.; Allen, D. Notch fatigue behavior in cast irons explained using a fracture mechanics approach. Int. J. Fatigue 1996, 18, 439–445. [Google Scholar] [CrossRef]
- Davis, J.R. Cast Irons, 1st ed.; ASM International: Materials Park, OH, USA, 1996; p. 65. [Google Scholar]
- Karsay, S.I. Control of Graphite Structure in Heavy Ductile Iron Castings. AFS Trans. 1970, 78, 85–92. [Google Scholar]
- Strizik, P.; Jeglitsch, F. Contribution to the Mechanism of Formation of Chunky Graphite. AFS Int. Cast Met. J. 1976, 1, 23–30. [Google Scholar]
- Liu, P.C.; Li, C.L.; Wu, D.H.; Loper, C.R. SEM Study of Chunky Graphite in Heavy Section Ductile Iron. AFS Trans. 1983, 91, 119–126. [Google Scholar]
- Hoover, H.W., Jr. A literature survey on degenerate graphite in heavy section ductile iron. Trans. Am. Foundrym. Soc. 1986, 94, 601–608. [Google Scholar]
- Stefanescu, D.M.; Alonso, G.; Larrañaga, P.; De la Fuente, E.; Suarez, R. On the crystallization of graphite from liquid iron-carbon-silicon melts. Acta Mater. 2016, 107, 102–126. [Google Scholar] [CrossRef]
- Itofuji, H.; Uchikawa, H. Formation mechanism of chunky graphite in heavy-section ductile cast irons. AFS Trans. 1990, 90, 429–448. [Google Scholar]
- Gagné, M.; Argo, D. Heavy section ductile cast iron castings part I and part II. In Proceedings of the an International Conference on Advanced Casting Technology, Kalamazoo, MI, USA, 12–14 November 1989; ASM International: Materials Park, OH, USA, 1989; pp. 231–256. [Google Scholar]
- Nakae, H.; Junk, S.; Shin, H.-C. Formation mechanism of chunky graphite and its preventive measures. J. Mater. Sci. Technol. 2008, 24, 289–295. [Google Scholar]
- Udroiu, A. Wedge theory: new approach to explain the formation of “chunky graphite” in ductile iron. In Proceeding of the 70th World Foundry Congress, Monterrey, Mexico, 25–27 April 2012; pp. 614–631.
- Källbom, R.; Hamberg, K.; Wessén, M.; Björkegren, L.-E. On the solidification sequence of ductile iron castings containing chunky graphite. Mater. Sci. Eng. A 2005, 413–414, 346–351. [Google Scholar] [CrossRef]
- Riposan, I.; Chisamera, M.; Stan, A. Control surface graphite degeneration ductile iron windmill applications. Int. J. Metalcast. 2013, 7, 9–20. [Google Scholar] [CrossRef]
- Nakae, H.; Fukami, M.; Kitazawa, T.; Zou, Y. Influence of Si, Ce, Sb and Sn on chunky graphite formation. China Foundry 2011, 8, 96–100. [Google Scholar]
- Lacaze, J.; Armendariz, S.; Larrañaga, P.; Asenjo, I.; Sertucha, J.; Suarez, R. Effect of carbon equivalent on graphite formation in heavy-section ductile iron parts. Mater. Sci. Forum 2010, 636–637, 523–530. [Google Scholar] [CrossRef]
- Riposan, I.; Chisamera, M.; Uta, V.; Stan, S. The importance of rare earth contribution from nodulizing alloys and their subsequent effect on the inoculation of ductile iron. Int. J. Metalcast. 2014, 8, 65–80. [Google Scholar] [CrossRef]
- Onsøien, M.I.; Grong, Ø.; Skaland, T.; Jørgensen, K. Mechanisms of graphite formation in ductile cast iron containing rare earth metals. Mater. Sci. Technol. 1999, 15, 253–259. [Google Scholar] [CrossRef]
- Choi, J.O.; Kim, J.Y.; Choi, C.O.; Kim, J.K.; Rohatgi, P.K. Effect of rare earth element on microstructure formation and mechanical properties of thin wall ductile iron castings. Mater. Sci. Eng. A 2004, 383, 323–333. [Google Scholar] [CrossRef]
- Zhe, L.; Weiping, C.; Yu, D. Influence of cooling rate and antimony addition content on graphite morphology and mechanical properties of a ductile iron. China Foundry 2012, 9, 114–118. [Google Scholar]
- Diao, X.G.; Ning, Z.L.; Cao, F.Y.; Ren, S.Z.; Sun, J.F. Effects of antimony addition and section size on formation of chunky graphite in ductile iron. Mater. Sci. Technol. 2011, 27, 834–838. [Google Scholar] [CrossRef]
- Gorny, M.; Tyrala, E. Effect of cooling rate on microstructure and mechanical properties of thin-walled ductile iron castings. J. Mater. Eng. Perform. 2013, 22, 300–305. [Google Scholar] [CrossRef]
- Ferro, P.; Fabrizi, A.; Cervo, R.; Carollo, C. Effect of inoculant containing rare earth metals and bismuth on microstructure and mechanical properties of heavy-section near-eutectic ductile iron castings. J. Mater. Process. Technol. 2013, 213, 1601–1608. [Google Scholar] [CrossRef]
- Zhang, Z.; Flower, H.M.; Niu, Y. Classification of degenerate graphite and its formation processes in heavy section ductile iron. Mater. Sci. Technol. 1989, 5, 657–664. [Google Scholar] [CrossRef]
- Skaland, T.; Grong, Ø.; Grong, T. A model for the graphite formation in ductile cast iron. Metall. Mater. Trans. A 1993, 24A, 2321–2345. [Google Scholar] [CrossRef]
- Asenjo, I.; Larrañaga, P.; Sertucha, J.; Suárez, R.; Gómez, J.-M.; Ferrer, I.; Lacaze, J. Effect of mould inoculation on formation of chunky graphite in heavy section spheroidal graphite cast iron parts. Int. J. Cast Met. Res. 2007, 20, 319–324. [Google Scholar] [CrossRef]
- Kallbom, R.; Hamberg, K.; Bjӧrkegren, L.-E. Chunky graphite—Formation and influence on mechanical properties in ductile cast iron. In Competent Design by Castings—Improvements in a Nordic Project; Samuelson, J., Marquis, G., Solin, J., Eds.; VTT: Helsinki, Finland, 2005; pp. 63–86. [Google Scholar]
- Endo, M.; Yanase, K. Effects of small defects, matrix structures and loading conditions on the fatigue strength of ductile cast irons. Theor. Appl. Fract. Mech. 2014, 69, 34–43. [Google Scholar] [CrossRef]
- Mourujärvi, A.; Widell, K.; Saukkonen, T.; Hänninen, H. Influence of chunky graphite on mechanical and fatigue properties of heavy-section cast iron. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 379–390. [Google Scholar] [CrossRef]
- Ferro, P.; Lazzarin, P.; Berto, F. Fatigue properties of ductile cast iron containing chunky graphite. Mater. Sci. Eng. A 2012, 554, 122–128. [Google Scholar] [CrossRef]
- Foglio, E.; Lusuardi, D.; Pola, A.; La Vecchia, G.M.; Gelfi, M. Fatigue design of heavy section ductile irons: Influence of chunky graphite. Mater. Des. 2016, 111, 353–361. [Google Scholar] [CrossRef]
- Nadot, Y.; Mendez, J.; Ranganathan, N.; Beranger, A.S. Fatigue life assessment of nodular cast iron containing casting defects. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 289–300. [Google Scholar] [CrossRef]
- Collini, L.; Pirondi, A. Fatigue crack growth analysis in porous ductile cast iron microstructure. Int. J. Fatigue 2014, 62, 258–265. [Google Scholar] [CrossRef]
- Collini, L.; Pirondi, A.; Bianchi, R.; Cova, M.; Milella, P.P. Influence of casting defects on fatigue crack initiation and fatigue limit of ductile cast iron. Procedia Eng. 2011, 10, 2898–2903. [Google Scholar] [CrossRef]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions, 1st ed.; Elsevier: Oxford, UK, 2002. [Google Scholar]
- Hübner, P.; Schlosser, H.; Pusch, G.; Biermann, H. Load history effects in ductile cast iron for wind turbine components. Int. J. Fatigue 2007, 29, 1788–1796. [Google Scholar] [CrossRef]
- Benedetti, M.; Fontanari, V.; Zonta, D. Structural health monitoring of wind towers: Remote damage detection using strain sensors. Smart Mater. Struct. 2011, 20, 055009. [Google Scholar] [CrossRef]
- Benedetti, M.; Fontanari, V.; Battisti, L. Structural health monitoring of wind towers: Residual fatigue life estimation. Smart Mater. Struct. 2013, 22, 045017. [Google Scholar] [CrossRef]
- Foglio, E.; Gelfi, M.; Pola, A.; Goffelli, S.; Lusuardi, D. Fatigue Characterization and Optimization of the Production Process of Heavy Section Ductile Iron Castings. Int. J. Metalcast. 2017, 11, 33–43. [Google Scholar] [CrossRef]
- European Standard EN 1563:2011. Founding—Spheroidal Graphite Cast Iron; CEN: Brussels, Belgium, 2011. [Google Scholar]
- Murakami, Y.; Endo, M. Effects of hardness and crack geometries on ∆Kth of small cracks emanating from small defects. In The Behaviour of Short Fatigue Cracks; Miller, K.J., de los Rios, E.R., Eds.; Institution of Mechanical Engineers: London, UK, 1986; pp. 275–293. [Google Scholar]
- Ritchie, R.O. Mechanisms of fatigue-crack propagation in ductile and brittle solids. Int. J. Fract. 1999, 100, 55–83. [Google Scholar] [CrossRef]
- Benedetti, M.; Heidemann, J.; Peters, J.O.; Lütjering, G. Influence of sharp microstructural gradients on the fatigue crack growth resistance of α+β and near-α titanium alloys. Fatigue Fract. Eng. Mater. Struct. 2005, 28, 909–922. [Google Scholar] [CrossRef]
- Zambrano, H.R.; Härkegård, G.; Stärk, K.F. Fracture toughness and growth of short and long fatigue cracks in ductile cast iron EN-GJS-400-18-LT. Fatigue Fract. Eng. Mater. Struct. 2011, 35, 374–388. [Google Scholar] [CrossRef]
- Mottitschka, T.; Pusch, G.; Biermann, H.; Zybell, L.; Kuna, M. Influence of overloads on the fatigue crack growth in nodular cast iron: Experiments and numerical simulation. Procedia Eng. 2010, 2, 1557–1567. [Google Scholar] [CrossRef]
- Čanžar, P.; Tonković, Z.; Kodvanj, J. Microstructure influence on fatigue behaviour of nodular cast iron. Mater. Sci. Eng. A 2012, 556, 88–99. [Google Scholar] [CrossRef]
- Klesnil, M.; Lukáš, P. Influence of strength and stress history on growth and stabilisation of fatigue cracks. Eng. Fract. Mech. 1972, 4, 77–92. [Google Scholar] [CrossRef]
- Walker, E.K. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum. In Effect of Environment and Complex Load History on Fatigue Life; American Society for Testing and Materials: West Conshohocken, PA, USA, 1970; pp. 1–14. [Google Scholar]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]




| C | Si | Mn | Cu | Sn | S | Mg | Cr | P |
|---|---|---|---|---|---|---|---|---|
| 3.59 | 2.51 | 0.23 | 0.11 | 0.0031 | 0.0109 | 0.0462 | 0.043 | 0.044 |
| Total Graphite Content (%) | Fraction of Spheroidal Graphite (%) | Fraction of Chunky Graphite (%) | Diameter of Spheroidal Graphite (µm) | Shape Factor Spheroidal Graphite f0 |
|---|---|---|---|---|
| 9.3 ± 2.1 | 71 ± 15 | 29 ± 15 | 310 ± 110 | 0.49 ± 0.19 |
| σYS (MPa) | σU (MPa) | σYS/σU | T.E. (%) | HB | σlim,−1 (MPa) |
|---|---|---|---|---|---|
| 275 ± 4 | 295 ± 8 | 0.93 | 2.9 ± 0.2 | 144 ± 2 | 138 ± 4 |
| Sample Number | Stress Amplitude, σa (MPa) | Number of Cycles to Failure, Nf | Remarks |
|---|---|---|---|
| 5 | 130 | 8,396,603 | Run-out |
| 6 | 140 | 5,181,473 | Run-out |
| 7 | 150 | 3,870,378 | |
| 8 | 140 | 3,535,376 | |
| 9 | 130 | 8,110,087 | Run-out |
| 10 | 140 | 1,253,313 | |
| 11 | 130 | 24,732,626 | Run-out |
| 12 | 140 | 2,483,398 | |
| 13 | 130 | 8,143,060 | Run-out |
| 14 | 140 | 1,347,937 | |
| 15 | 130 | 6,989,257 | Run-out |
| 16 | 140 | 7,653,654 | Run-out |
| 17 | 150 | 2,851,237 | |
| 18 | 140 | 2,443,680 | |
| 20 | 130 | 8,891,424 | Run-out |
| Load Ratio R | ΔKth (MPa m0.5) | C | m |
|---|---|---|---|
| 0.1 | 13.5 | 7.72 × 10−19 | 8.1 |
| 0.5 | 8.6 | 9.48 × 10−15 | 5.6 |
| 0.75 | 5.2 | 9.59 × 10−14 | 4.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benedetti, M.; Torresani, E.; Fontanari, V.; Lusuardi, D. Fatigue and Fracture Resistance of Heavy-Section Ferritic Ductile Cast Iron. Metals 2017, 7, 88. https://doi.org/10.3390/met7030088
Benedetti M, Torresani E, Fontanari V, Lusuardi D. Fatigue and Fracture Resistance of Heavy-Section Ferritic Ductile Cast Iron. Metals. 2017; 7(3):88. https://doi.org/10.3390/met7030088
Chicago/Turabian StyleBenedetti, Matteo, Elisa Torresani, Vigilio Fontanari, and Danilo Lusuardi. 2017. "Fatigue and Fracture Resistance of Heavy-Section Ferritic Ductile Cast Iron" Metals 7, no. 3: 88. https://doi.org/10.3390/met7030088
APA StyleBenedetti, M., Torresani, E., Fontanari, V., & Lusuardi, D. (2017). Fatigue and Fracture Resistance of Heavy-Section Ferritic Ductile Cast Iron. Metals, 7(3), 88. https://doi.org/10.3390/met7030088








