Very High Cycle Fatigue of Butt-Welded High-Strength Steel Plate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Dynamic Young’s Modulus
- Suspend the bar-shaped original FB steel with a thread for free motion;
- Place a piezoelectric element at the end of the bar with wax to provide the excitation frequency;
- Measure the displacement using the LDV on the other side of the piezoelectric element; and
- Measure the resonant frequency by analyzing the excitation frequency and displacement with the DSA.
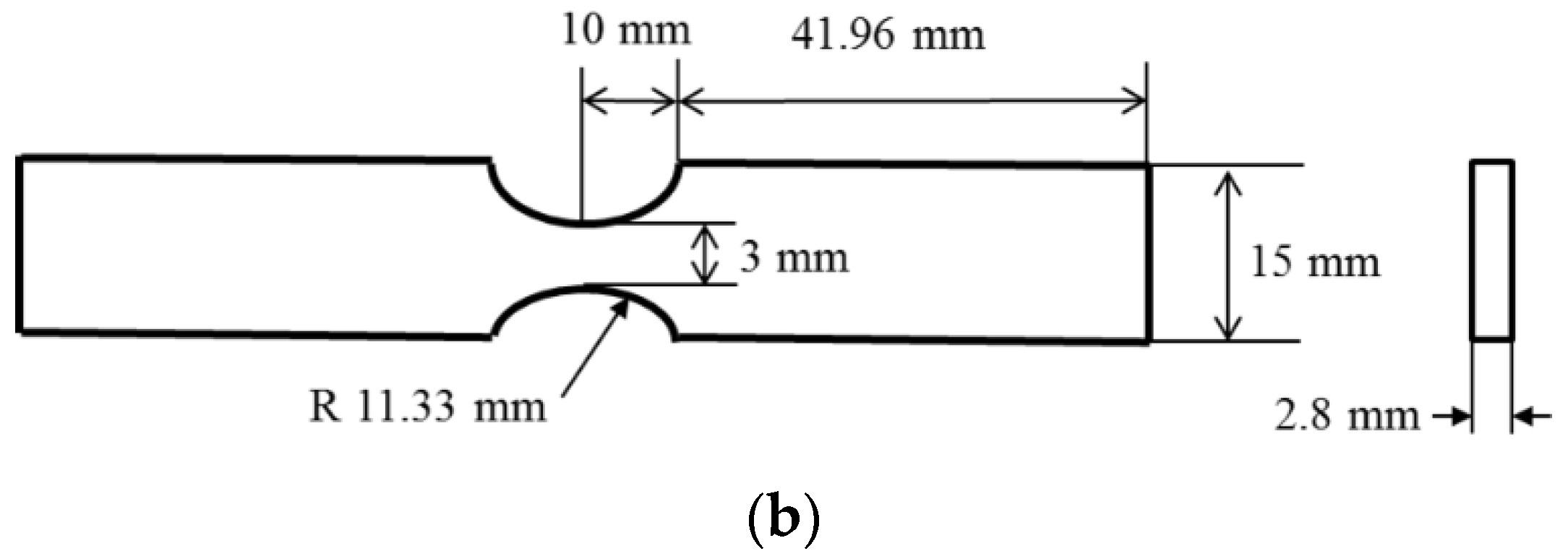
2.3. Design of Plate Specimen
2.4. Welded Fatigue Specimen
3. Results
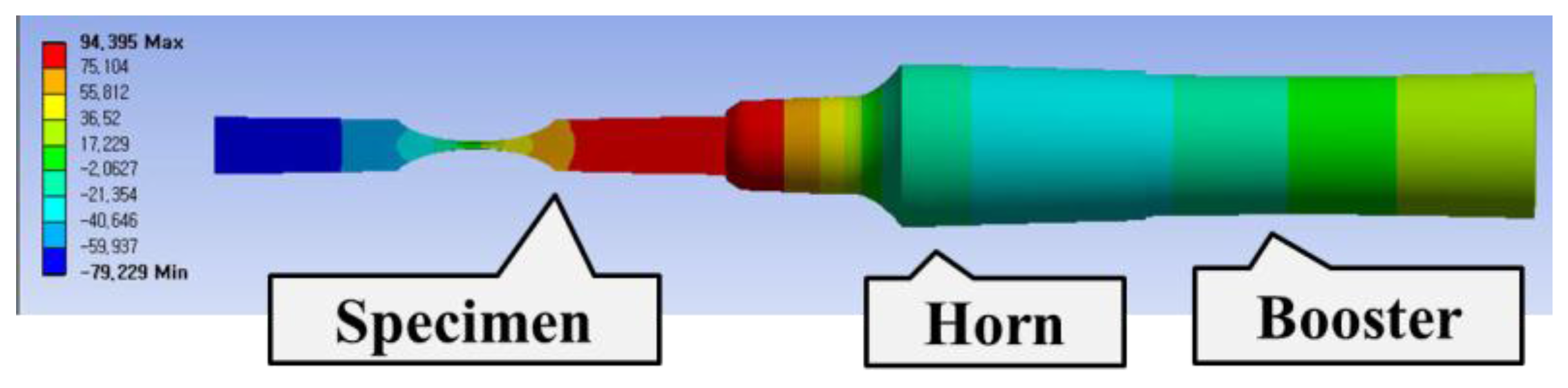
3.1. Finite Element Method (FEM) Simulation for Specimen Resonance
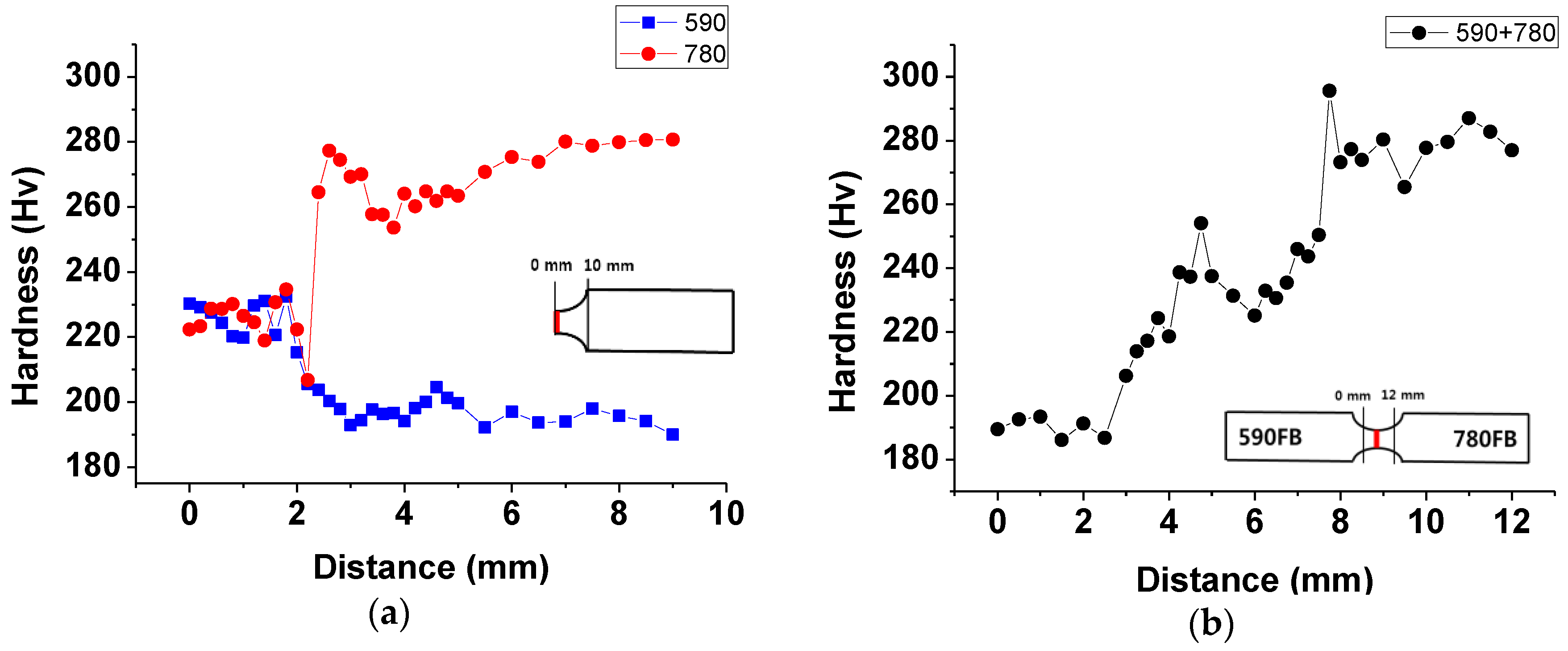
3.2. Hardness Tests
3.3. Ultrasonic Fatigue Test
3.4. Fracture Surface
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bathias, C.; Paris, P.C. Gigacycle Fatigue in Mechanical Practice; Marcel Dekker: New York, NY, USA, 2005; pp. 9–50. [Google Scholar]
- Kazymyrovych, V. Very High Cycle Fatigue of Tool Steels. Ph.D. Thesis, Karlstad University, Karlstad, Sweden, 10 September 2010. [Google Scholar]
- Crupi, V.; Epasto, G.; Guglielmino, E.; Risitano, G. Analysis of temperature and fracture surface of AISI4140 steel in very high cycle fatigue regime. Theor. Appl. Fract. Mech. 2015, 80, 22–30. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Bathias, C.; Kawagoishi, N.; Chen, Q. Effect of inclusion on subsurface crack initiation and gigacycle fatigue strength. Int. J. Fatigue 2002, 24, 1269–1274. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Berard, J.Y.; Dubarre, A.; Baudry, G.; Rathery, S.; Bathias, C. Gigacycle fatigue of ferrous alloys. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 667–672. [Google Scholar] [CrossRef]
- Gu, Y.; Tao, C.; He, Y.; Liu, C. The effect of frequency and sample shape on fatigue behaviors of DZ125 superalloy. Theor. Appl. Mech. Lett. 2012, 2. [Google Scholar] [CrossRef]
- Jiang, Q.; Sun, C.; Liu, X.; Hong, Y. Very-high-cycle fatigue behavior of a structural steel with and without induced surface defects. Int. J. Fatigue 2016, 93, 352–362. [Google Scholar] [CrossRef]
- Heinz, S.; Eifler, D. Crack initiation mechanisms of Ti6Al4V in the very high cycle fatigue regime. Int. J. Fatigue 2016, 93, 301–308. [Google Scholar] [CrossRef]
- Müller-Bollenhagen, C.; Zimmermann, M.; Christ, H.J. Very high cycle fatigue behaviour of austenitic stainless steel and the effect of strain-induced martensite. Int. J. Fatigue 2010, 32, 936–942. [Google Scholar] [CrossRef]
- Mayer, H.; Papakyriacou, M.; Zettl, B.; Stanzl-Tschegg, S.E. Influence of Porosity on the Fatigue Limit of Die Cast Magnesium and Aluminium Alloys. Int. J. Fatigue 2003, 25, 245–256. [Google Scholar] [CrossRef]
- Majumdar, S.; Roy, S.; Ray, K.K. Fatigue performance of dual-phase steels for automotive wheel application. Fatigue Fract. Eng. Mater. Struct. 2016, 40, 315–332. [Google Scholar] [CrossRef]
- Ellwood, R.D. Fatigue Performance of Downgauged High Strength Steel Automotive Suspension Component. Ph.D. Thesis, University of Wales Swansea, Swansea, UK, 2003. [Google Scholar]
- Potukutchi, R.; Agrawal, H.; Perumalswami, P.; Dong, P. Fatigue Analysis of Steel MIG Welds in Automotive Structures; SAE International: Warrendale, PA, USA, 2004. [Google Scholar]
- Takaoka, Y.; Shimoda, T.; Hara, J.; Seki, N.; Deguchi, T.; Koshio, K. Application of the latest technologies to fatigue strength improvement. In Proceedings of the TSCF2010 Shipbuilders’ Meeting, Todyo, Japan, 28 October 2010.
- Zhao, Z.P.; Qiao, G.Y.; Li, G.P.; Yang, W.W.; Liao, B.; Xiao, F.R. Fatigue properties of ferrite/bainite dual-phase X80 pipeline steel welded joints. Sci. Technol. Weld. Join. 2016, 22, 1–10. [Google Scholar] [CrossRef]
- Shrama, Kadhum. Fatigue of Welded High Strength Steels for Automotive Chassis and Suspension Applications. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2016. [Google Scholar]
- Zhang, M.; Wang, W.; Wang, P.; Liu, Y.; Li, J. Fatigue behavior and mechanism of FV520B-I welding seams in a very high cycle regime. Int. J. Fatigue 2016, 87, 22–37. [Google Scholar] [CrossRef]
- Zhu, M.L.; Liu, L.L.; Xuan, F.Z. Effect of frequency on very high cycle fatigue behavior of a low strength Cr-Ni-Mo-V steel welded joint. Int. J. Fatigue 2015, 77, 166–173. [Google Scholar] [CrossRef]
- Zhao, X.; Dongpo, W.; Deng, C.; Liu, Y.; Zongxian, S. The fatigue behaviors of butt welds ground flush in the super-long life regime. Int. J. Fatigue 2012, 36, 1–8. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, R.; He, C. Gigacycle fatigue behaviors in fusion zone and heat affected zone of Q345 LA steel welded joints. In Proceedings of the ICF13, Beijing, China, 16–21 June 2013.
- Matlock, D.K.; John, G.S. Third generation of AHSS: Microstructure design concepts. In Microstructure and Texture in Steels; Springer: London, UK, 2009; pp. 185–205. [Google Scholar]
- Rojas, J.I.; Daniel, C. Onset Frequency of Fatigue Effects in Pure Aluminum and 7075 (AlZnMg) and 2024 (AlCuMg). Metals 2016, 6, 50. [Google Scholar] [CrossRef]
- Buehler. The Science behind Materials Preparation a Guide to Materials Preparation & Analysis; Buehler Ltd.: Lake Bluff, IL, USA, 2007. [Google Scholar]
- Westgate, S. The resistance spot welding of high and ultra-high strength steels. In Proceedings of the 3rd International Seminar on Advances in Resistance Welding, Berlin, Germany, 16–17 November 2004.
- Seon, S.W.; Yi, W.; Park, H.D.; Hwang, Y.T. Characteristics of welds of pure titanium plate using ultrasonic attenuation. J. Korean Soc. Nondestruct. Test. 2013, 33, 205–211. [Google Scholar] [CrossRef]
- Stille, S.; Tilmann, B.; Lorenz, S. Very high cycle fatigue (VHCF) behavior of structured Al 2024 thin sheets. In Proceedings of the 13th International Conference on Fracture, Beijing, China, 16–21 June 2013.











| Materials | C Max. (wt %) | Mn Max. (wt %) | Si Max. (wt %) | P Max. (wt %) | S Max. (wt %) | Fe |
|---|---|---|---|---|---|---|
| 590 FB | 0.090 | 1.550 | 0.150 | 0.030 | 0.003 | balance |
| 780 FB | 0.050 | 1.800 | 1.250 | 0.015 | 0.003 | balance |
| Materials | Density (g/cm3) | Dynamic Young’s Modulus (GPa) |
|---|---|---|
| 590 FB | 7.91 | 221.28 |
| 780 FB | 8.01 | 221.98 |
| Current (A) | Voltage (V) | Feed (cm/min) | Shield Gas Ratio (%) | Shield Gas Injection Quantity (L/min) | Contact Tip to Work Distance (mm) | Torch Degree (°) |
|---|---|---|---|---|---|---|
| 210 | 24.5 | 76 | 80(Ar):20(CO2) | 20 | 15 | 90 |
| Part | Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Specimen | FB590 | 8170 | 221 | 0.3 |
| Horn, Booster | Titanium Alloy | 4620 | 96 | 0.36 |
| Stress Ratio (R) | Frequency (kHz) | Temperature (°C) | On/Off Time (s) |
|---|---|---|---|
| −1 | 19.914 | 25 | 5/2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeom, H.; Choi, B.; Seol, T.; Lee, M.; Jeon, Y.
Very High Cycle Fatigue of Butt-Welded High-Strength Steel Plate
. Metals 2017, 7, 103.
https://doi.org/10.3390/met7030103
Yeom H, Choi B, Seol T, Lee M, Jeon Y.
Very High Cycle Fatigue of Butt-Welded High-Strength Steel Plate
. Metals. 2017; 7(3):103.
https://doi.org/10.3390/met7030103
Yeom, Hyunho, Byungjoo Choi, Taeho Seol, Moongu Lee, and Yongho Jeon.
2017. "Very High Cycle Fatigue of Butt-Welded High-Strength Steel Plate
" Metals 7, no. 3: 103.
https://doi.org/10.3390/met7030103
Yeom, H., Choi, B., Seol, T., Lee, M., & Jeon, Y.
(2017). Very High Cycle Fatigue of Butt-Welded High-Strength Steel Plate
. Metals, 7(3), 103.
https://doi.org/10.3390/met7030103






