A Practical 1D Approach for Real-Time Prediction of Argon Flow and Pressure in Continuous Casting of Steel
Abstract
1. Introduction
- Pressure loss in argon line.
- Impact of thermal expansion on gas flow in argon line.
- Amount of air aspiration/argon leakage.
- Actual gas volume flow rate injected to the system.
- Influence of argon line design factors on the argon line pressure.
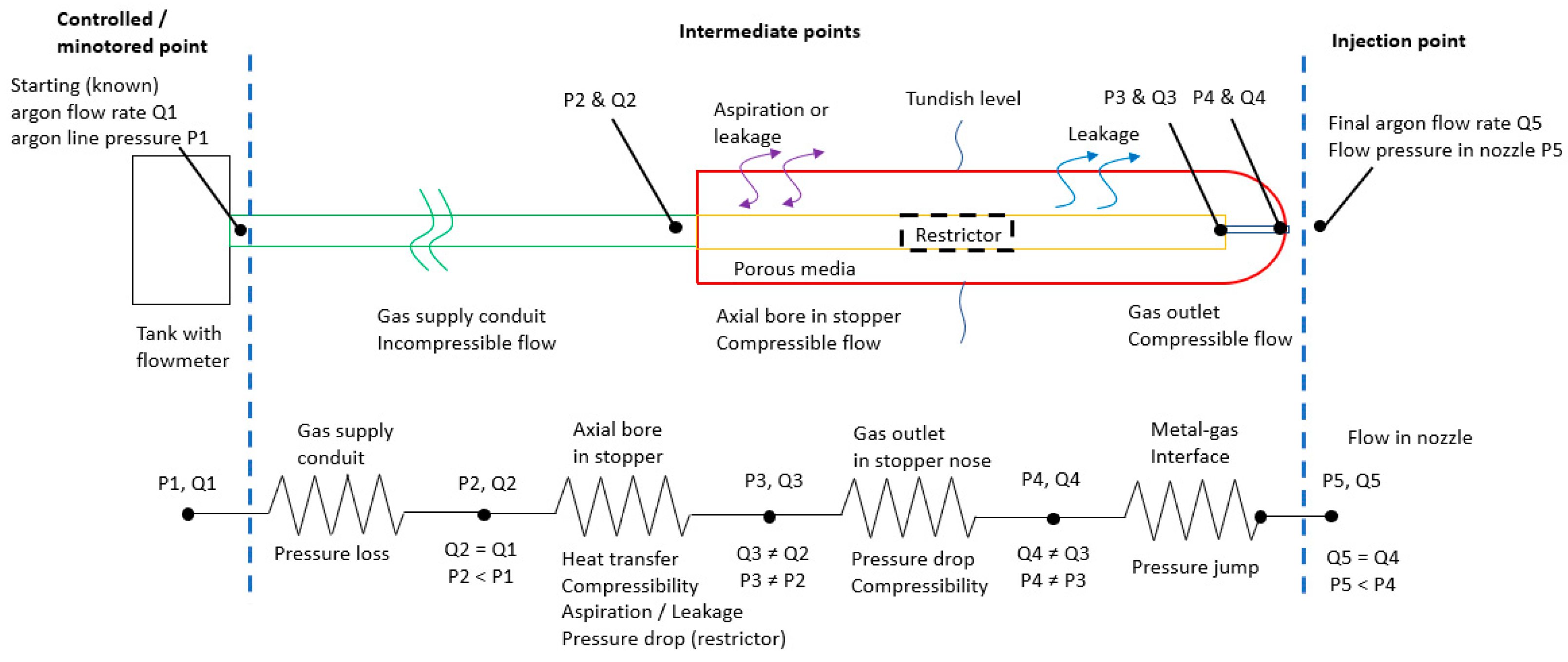
2. Model Description: 1D Argon Line Model
2.1. Gas Supply Conduit Before Entering the Stopper (P1–P2 Section in Figure 1)
2.2. Axial Bore in Stopper (P2–P3 Section in Figure 1)
2.3. Restrictor in Stopper (P2–P3 Section in Figure 1)
2.4. Air Aspiration and Argon Leakage in Stopper (P2–P3 Section in Figure 1)
2.5. Gas Outlet of Stopper (P3–P4 Section in Figure 1)
2.6. Gas Bubbling at the Metal–Argon Interface (P4–P5 Section in Figure 1)
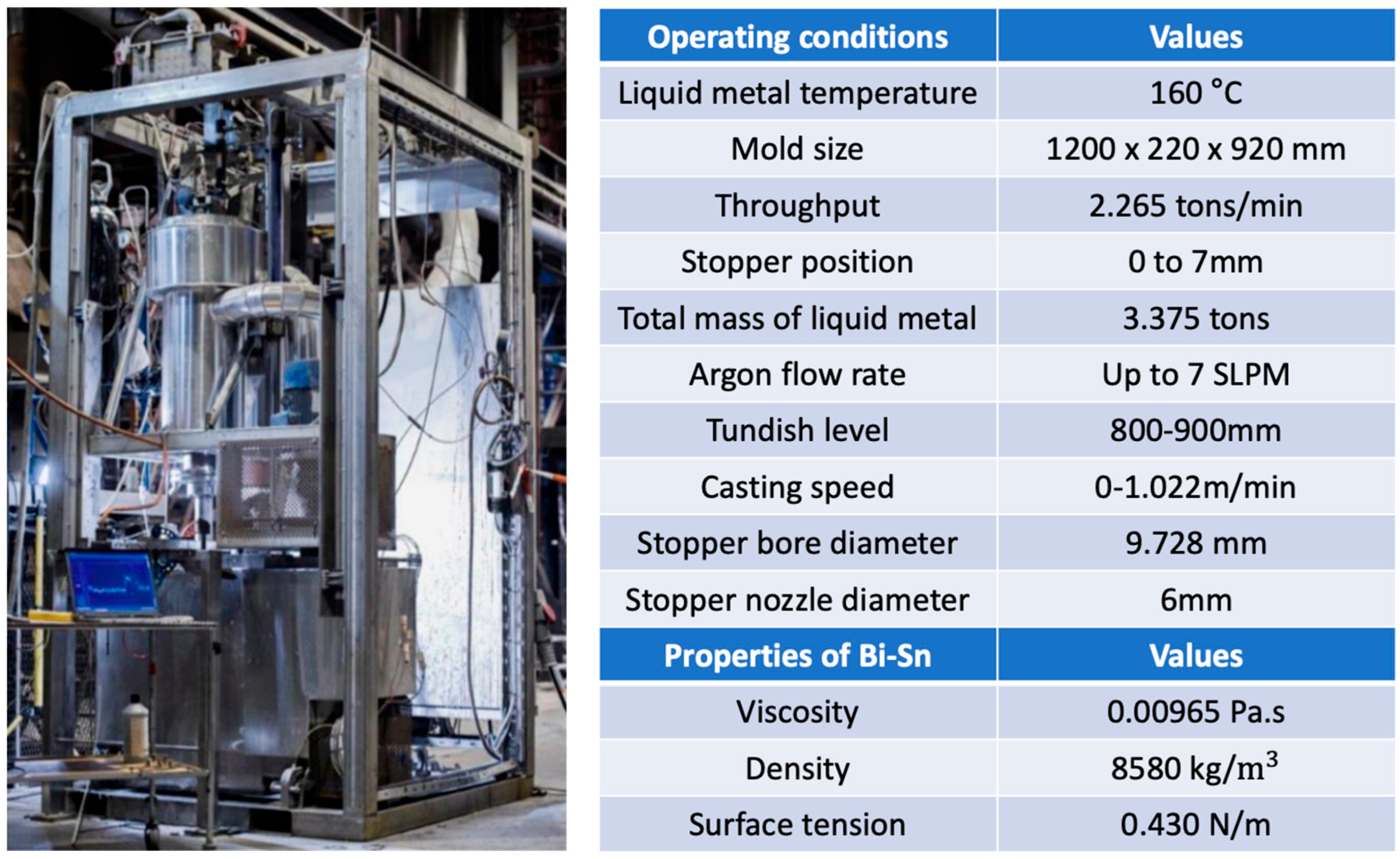
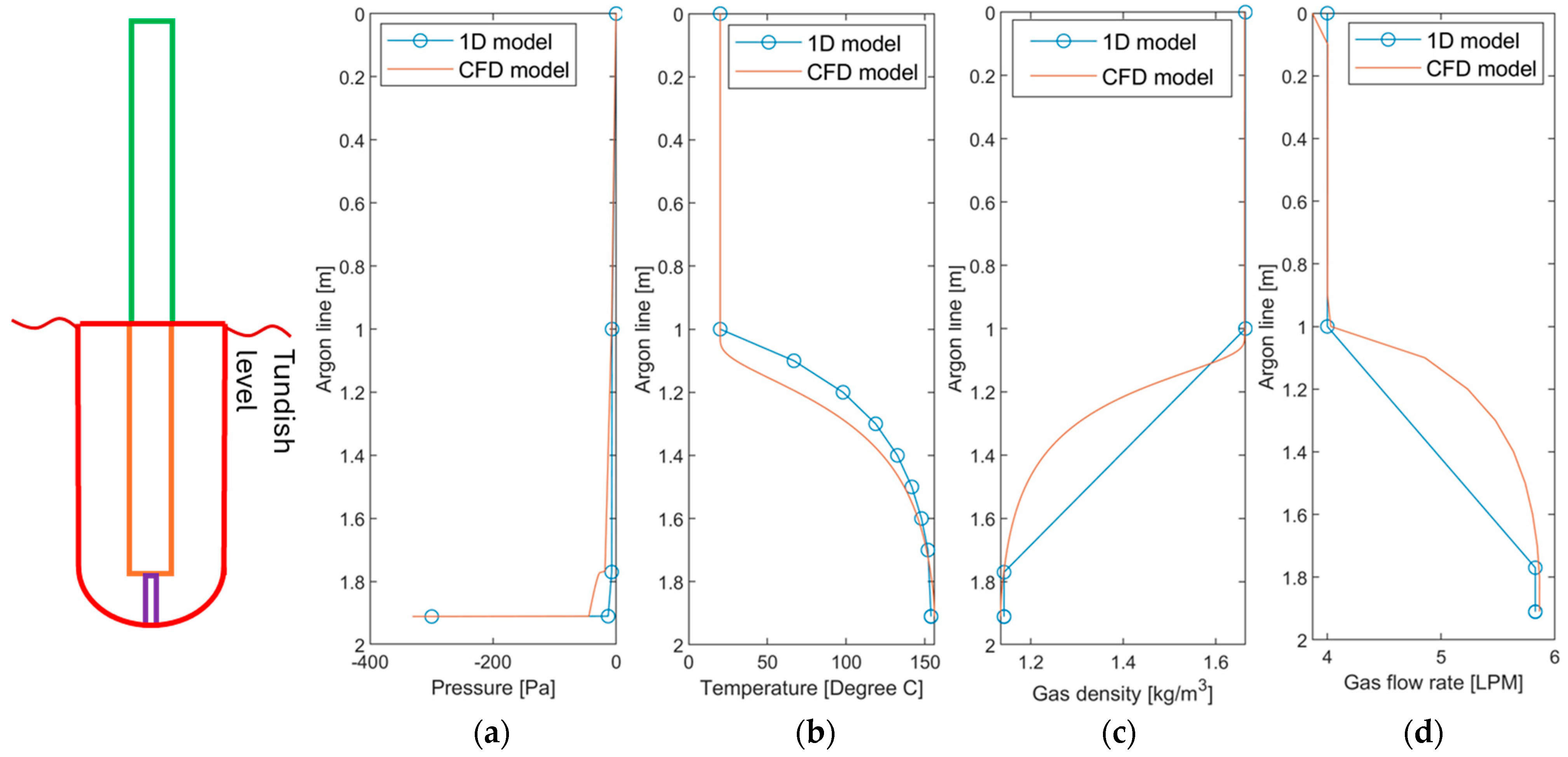
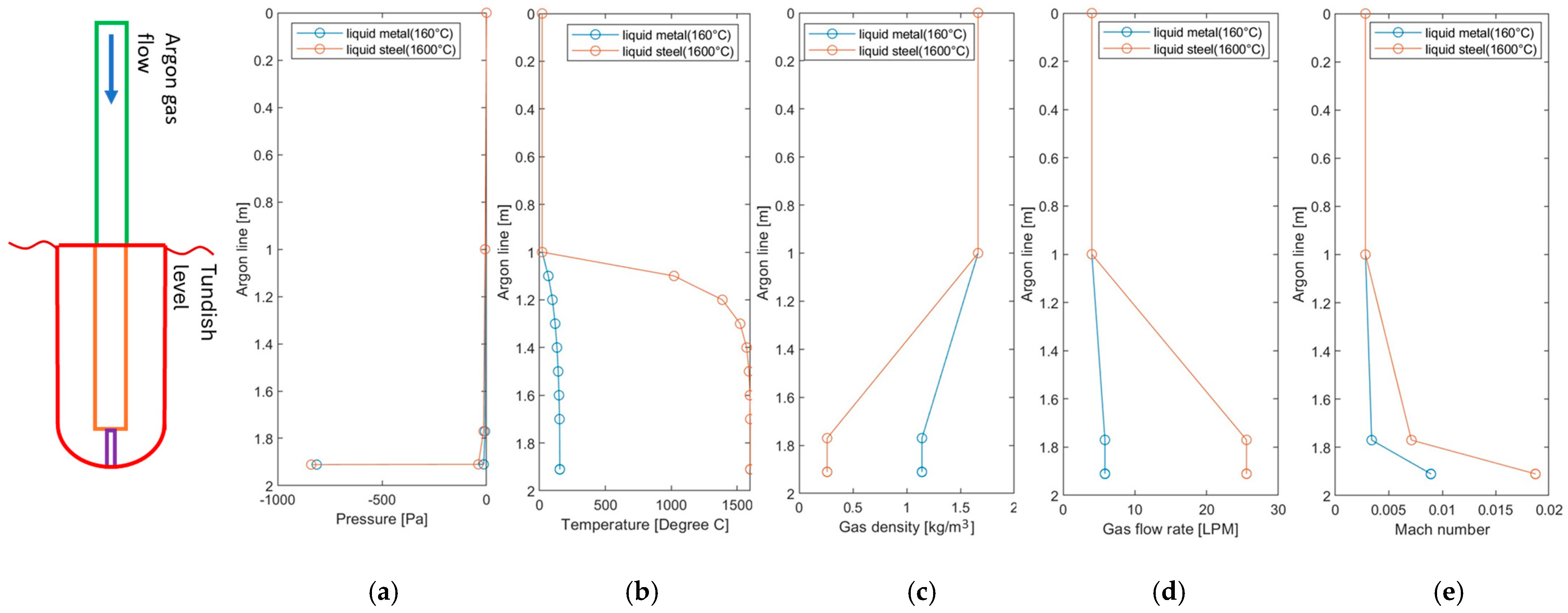
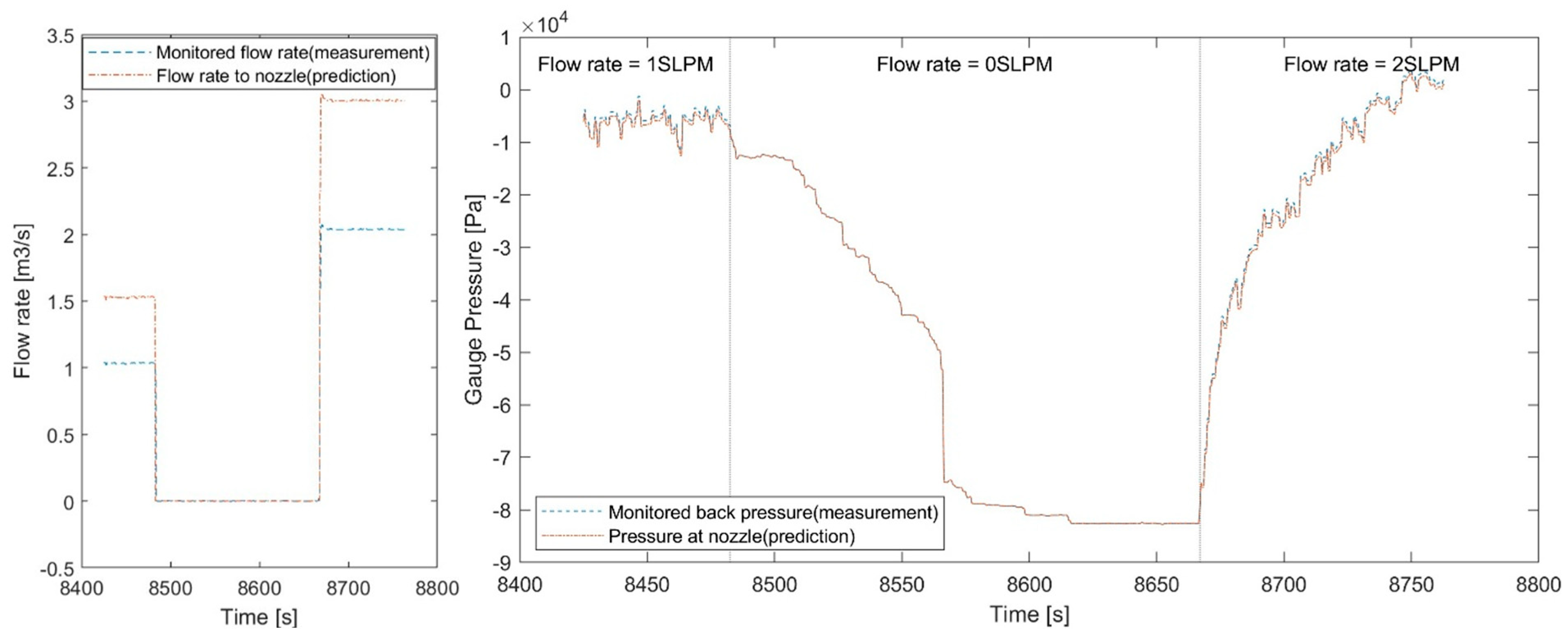
3. Validation of the 1D Model
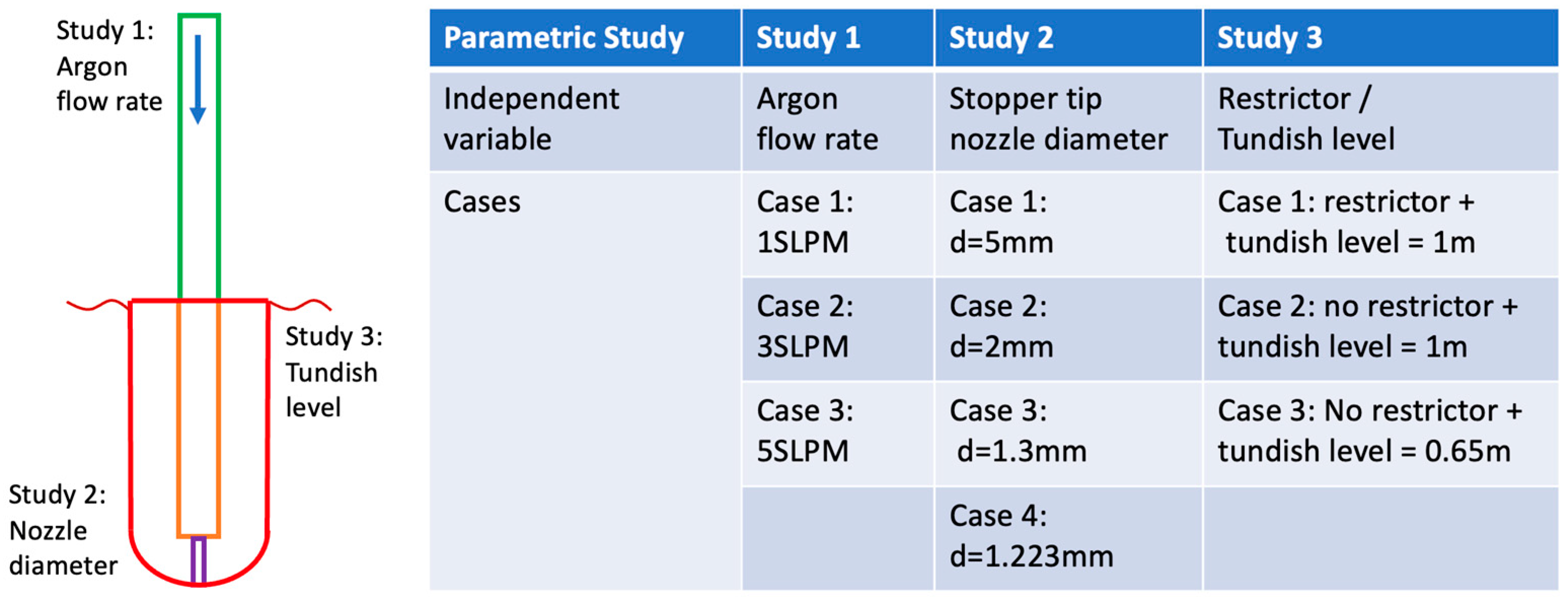
4. Parametric Study Using the 1D Argon Line Model
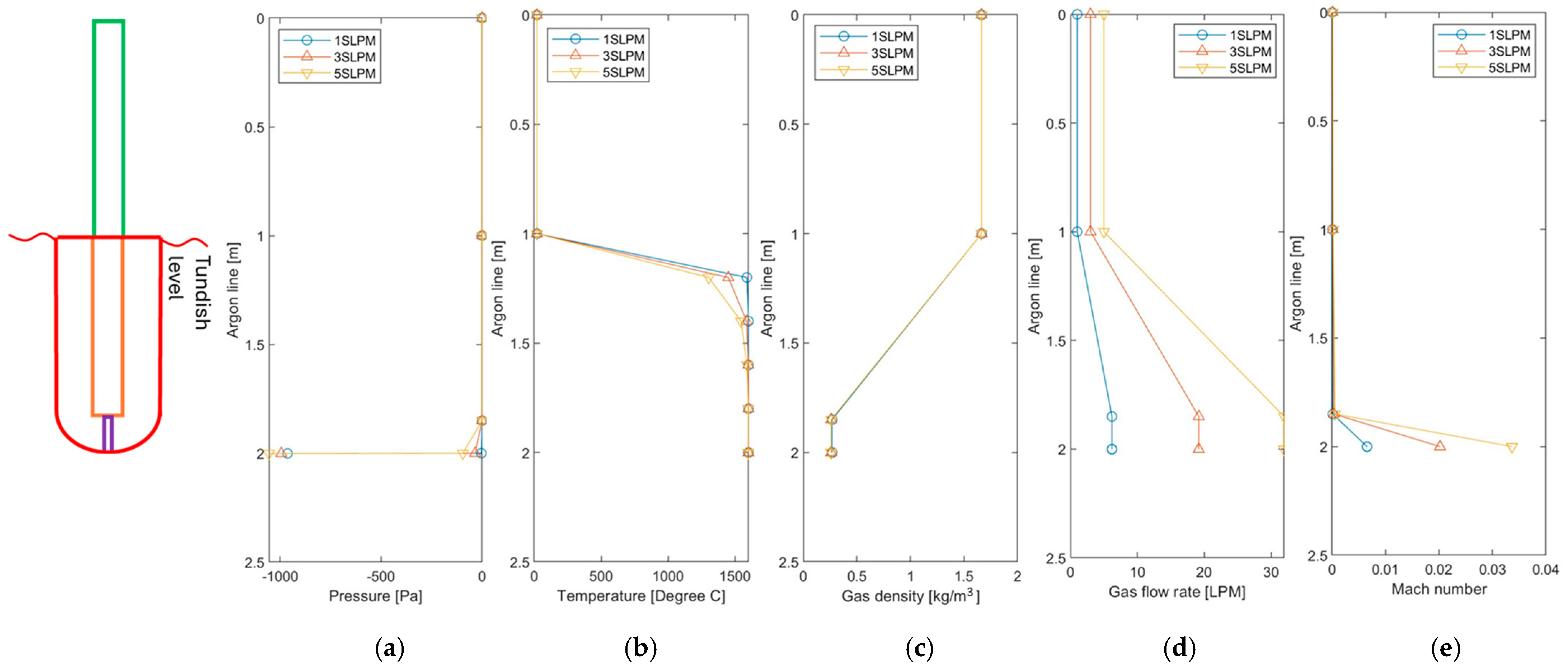
4.1. Effect of Gas Flow Rate
4.2. Effect of Stopper Tip Nozzle Diameter
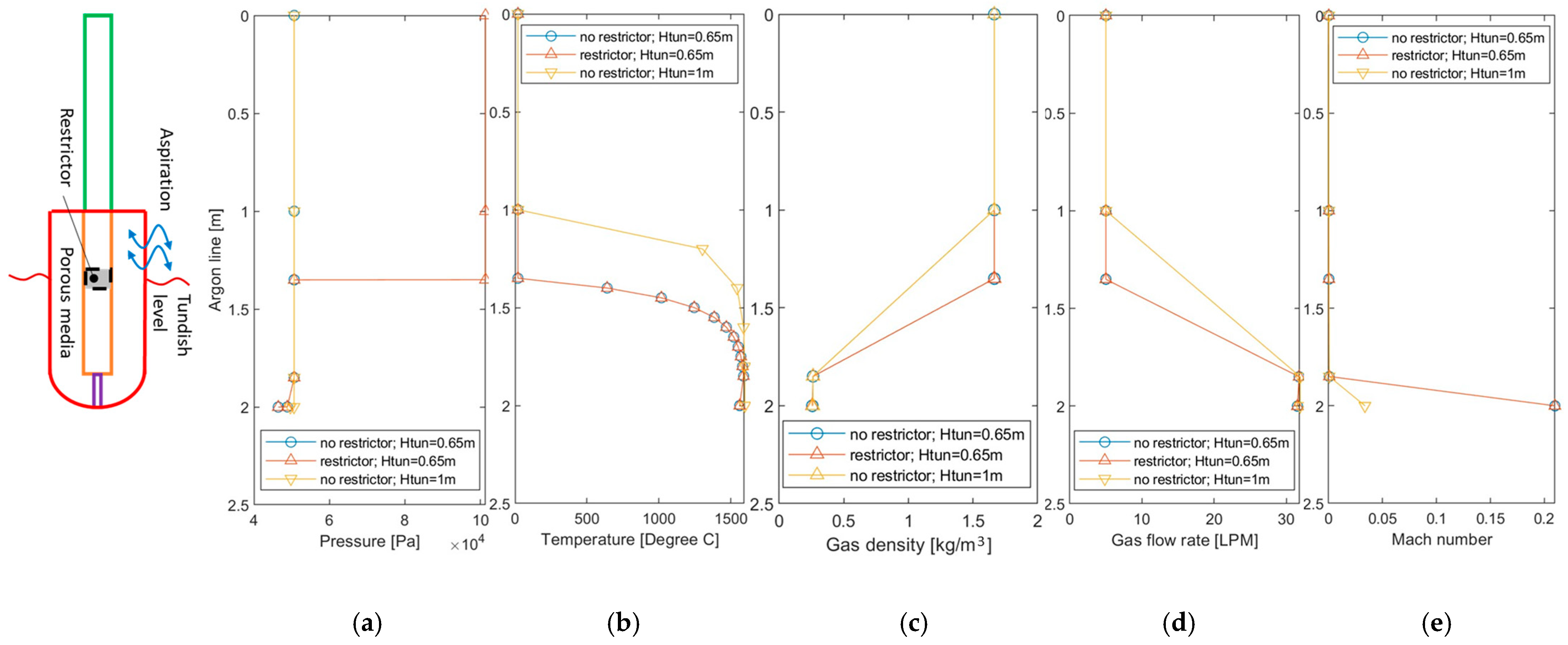
4.3. Effect of Restrictor and Tundish Level
4.4. Demonstration of Real-Time Operation Using Continuous Caster Simulator (CCS)
5. Conclusions
- Under a fixed argon line design (diameter > 5 mm), variations in argon flow rate (1, 3, and 5 SLPM) do not significantly affect pressure loss but influence gas heating rates; lower flow rates result in quicker temperature increases. Argon gas expands approximately six-fold due to thermal expansion upon heating, confirming thermal expansion as the primary factor of increased volumetric flow. Compressibility effects remain minimal (Mach number < 0.3), indicating insignificant impact at the tested argon line diameters.
- Reducing the stopper tip nozzle diameter significantly increases compressibility effects, causing higher Mach numbers, gas expansion, temperature drops, and pressure losses. A critical nozzle diameter (1.223 mm) corresponds to choked flow, limiting the maximum achievable gas flow rate to 5 SLPM and making the flow rate independent of downstream pressure conditions. This choking characteristic can be effectively utilized as a passive method to prevent excessive argon injection, thus ensuring mold flow stability during continuous casting.
- Introducing a restrictor effectively prevents negative pressure from propagating upstream within the argon line, eliminating significant air aspiration through the porous stopper. Without a restrictor, negative pressure can lead to considerable air aspiration (~3 SLPM) under given conditions, but this can also be mitigated by maintaining a sufficiently high tundish level, ensuring the stopper remains fully submerged. Additionally, the tundish level influences argon heating, impacting gas density and flow rate, a behavior accurately captured by the proposed 1D model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Gas density at point i [kg/m3] | Gas temperature at point i [K] | Inner radius [m] | |||
| Cross-section averaged gas velocity at point i [m/s] | Perimeter of bore [m] | Outer radius [m] | |||
| Friction factor | Average heat transfer coefficient [W/m2·K] | Ideal gas constant [J/mol.K] | |||
| Absolute roughness [m] | Average Nusselt number | Interfacial tension [N/m] | |||
| Length of conduit [m] | Prandtl number | Radius of the nozzle outlet [m] | |||
| Conduit diameter [m] | Gas thermal conductivity [W/m.K] | Gas velocity field [m/s] | |||
| Reynolds number | Mach number at point i | Shear stress tensor [Pa] | |||
| Gas viscosity [Pa.s] | Specific heat ratio | Gravitational acceleration [m/s2] | |||
| Gas mass flow rate [kg/s] | Gas flow rate at point i [m3/s] | Time [s] | |||
| Pressure at point i [Pa] | Cross-sectional area [m2] | Dimensionless wall distance | |||
| Heat capacity [J/kg.K] | Permeability [m2] |
References
- Bai, H.; Thomas, B.G. Effects of clogging, argon injection, and continuous casting conditions on flow and air aspiration in submerged entry nozzles. Metall. Mater. Trans. B 2001, 32, 707–722. [Google Scholar] [CrossRef]
- Yang, H.; Vanka, S.P.; Thomas, B.G. Modeling Argon Gas Behavior in Continuous Casting of Steel. JOM 2018, 70, 2148–2156. [Google Scholar] [CrossRef]
- Park, J.H.; Kang, Y.-B. Reoxidation Phenomena of Liquid Steel in Secondary Refining and Continuous Casting Processes: A Review. Steel Res. Int. 2024, 95, 2300598. [Google Scholar] [CrossRef]
- Yang, H.; Olia, H.; Thomas, B.G. Modeling Air Aspiration in Steel Continuous Casting Slide-Gate Nozzles. Metals 2021, 11, 116. [Google Scholar] [CrossRef]
- Yang, H.; Eck, J.; Lopez, P.E.R. Analysis of a Full-Scale Bi–Sn Liquid Metal Model for the Continuous Casting of Steel. Met. Mater. Int. 2024, 30, 1370–1386. [Google Scholar] [CrossRef]
- Olia, H.; Palmer, D.; Jebellat, E.; Thomas, B.G. Investigation of Multiphase Flow in Continuous-Casting Water Model with Measurements and Computational Modeling. Fluids 2025, 10, 113. [Google Scholar] [CrossRef]
- Liu, R.; Thomas, B.G. Model of gas flow through porous refractory applied to an upper tundish nozzle. Metall. Trans. B 2015, 46, 388–405. [Google Scholar] [CrossRef]
- Nitzl, G. Stopper Rod. US Patent 9168586 B2, 27 October 2015. [Google Scholar]
- Nitzl, G. Ceramic Refractory Stopper. US Patent 9302321B2, 5 April 2016. [Google Scholar]
- Cho, S.-M.; Thomas, B.G.; Kim, S.-H. Bubble Behavior and Size Distributions in Stopper-Rod Nozzle and Mold during Continuous Casting of Steel Slabs. ISIJ Int. 2018, 58, 1443–1452. [Google Scholar] [CrossRef]
- Liu, R.; Forman, B.; Yin, H.; Lee, Y. A New Insight into the Flow and Pressure Behavior of a Stopper Rod Flow Control System. Steel Res. Int. 2023, 94, 2200626. [Google Scholar] [CrossRef]
- Eck, J.; Lopez, P.E.R.; Cervantes, M.J. Investigation of Pressure Distribution during Flow Regulation with a Stopper and Associated Mould Level Stability in a Continuous Cast-ing Simulator based on Liquid Metal. Metall. Ital. 2022, 114, 42–51. [Google Scholar]
- Hackl, G. A Stopper Rod and a Method for Providing a Uniform Gas Curtain Around a Stopper Rod. EU Patent 3705204A1, 28 January 2020. [Google Scholar]
- Takahashi, S. Stopper for Continuous Casting. US Patent 6478201B2, 12 November 2002. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 2011. [Google Scholar]
- NIST. NIST Chemistry Webbook SRD69; NIST: Gaithersburg, MD, USA, 2005.
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer: New York, NY, USA, 2012. [Google Scholar]
- Erhard, P.; Etling, D.; Muller, U.; Riedel, U.; Sreenivasan, K.; Warnatz, J. Prandtl-Essentials of Fluid Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 158. [Google Scholar]
- Suzuki, M.; Yamaoka, Y.; Kubo, N.; Suzuki, M. Oxidation of molten steel by the air permeated through a refractory tube. ISIJ Int. 2002, 42, 248–256. [Google Scholar] [CrossRef]
- Zucker, R.D. Fundamentals of Gas Dynamics, 2nd ed.; Zucker, R.D., Biblarz, O., Eds.; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
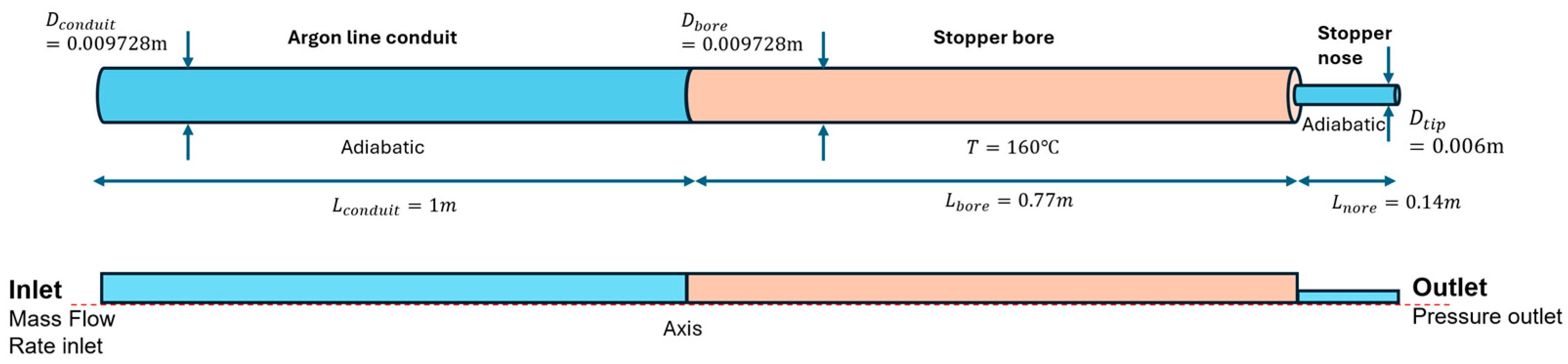

| Operating Condition | |
|---|---|
| Operating temperature | 1600 °C (liquid steel) |
| Argon flow rate | 5 SLPM (Parametric study 1: 1, 3, 5 SLPM) |
| Tundish level | 1 m (Parametric study 3: 0.65, 1 m) |
| Argon line design | |
| Argon conduit diameter | 50 mm |
| Stopper bore diameter | 40 mm |
| Stopper tip nozzle diameter | 5 mm (Parametric study 2: 5, 2, 1.3, 1.223 mm) |
| Stopper bore length | 0.85 m |
| Stopper nose length | 0.15 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Jin, B.-M.; Kim, H.; Seo, S.; Sim, S. A Practical 1D Approach for Real-Time Prediction of Argon Flow and Pressure in Continuous Casting of Steel. Metals 2025, 15, 978. https://doi.org/10.3390/met15090978
Yang H, Jin B-M, Kim H, Seo S, Sim S. A Practical 1D Approach for Real-Time Prediction of Argon Flow and Pressure in Continuous Casting of Steel. Metals. 2025; 15(9):978. https://doi.org/10.3390/met15090978
Chicago/Turabian StyleYang, Hyunjin, Bong-Min Jin, Hyeonjin Kim, Seungwon Seo, and Seunghyun Sim. 2025. "A Practical 1D Approach for Real-Time Prediction of Argon Flow and Pressure in Continuous Casting of Steel" Metals 15, no. 9: 978. https://doi.org/10.3390/met15090978
APA StyleYang, H., Jin, B.-M., Kim, H., Seo, S., & Sim, S. (2025). A Practical 1D Approach for Real-Time Prediction of Argon Flow and Pressure in Continuous Casting of Steel. Metals, 15(9), 978. https://doi.org/10.3390/met15090978







