Gradient-Based Calibration of a Precipitation Hardening Model for 6xxx Series Aluminium Alloys

Abstract

Precipitation hardening is the primary mechanism for strengthening 6xxx series aluminium alloys. The characteristics of the precipitates play a crucial role in determining the mechanical properties. In particular, predicting yield strength (YS) based on microstructure is experimentally complex and costly because its key variables, such as precipitate radius, spacing, and volume fraction (VF), are difficult to measure. Physics-based models have emerged to tackle these complications utilising advancements in simulation environments. Nevertheless, pure physics-based models require numerous free parameters and ongoing debates over governing equations. Conversely, purely data-driven models struggle with insufficient datasets and physical interpretability. Moreover, the complex dynamics between internal model variables has led both approaches to adopt heuristic optimisation methods, such as the Powell or Nelder–Mead methods, which fail to exploit valuable gradient information. To overcome these issues, we propose a gradient-based optimisation for the Kampmann–Wagner Numerical (KWN) model, incorporating CALPHAD (CALculation of PHAse Diagrams) and a strength model. Our modifications include facilitating differentiability via smoothed approximations of conditional logic, optimising non-linear combinations of free parameters, and reducing computational complexity through a single size-class assumption. Model calibration is guided by a mean squared error (MSE) loss function that aligns the YS predictions with interpolated experimental data using L2 regularisation for penalising deviations from a purely physics-based modelling structure. A comparison shows that the gradient-based adaptive moment estimation (ADAM) outperforms the gradient-free Powell and Nelder–Mead methods by converging faster, requiring fewer evaluations, and yielding more physically plausible parameters, highlighting the importance of calibration techniques in the modelling of 6xxx series precipitation hardening.

1. Introduction

The 6xxx series aluminium alloys are commonly used in various industrial applications due to their unique properties, such as lightweight, corrosion resistance, and strength [1,2]. The strengthening of these alloys is attributed to a combination of factors, including solid solution strengthening, work hardening, grain structure control, and precipitate hardening [3,4].

Work hardening has a minor effect, and solid solution strengthening and grain boundary strengthening have a moderate impact, while precipitation hardening is the primary mechanism for strengthening aluminium alloys [5,6]. In this process, finely dispersed precipitates obstruct the dislocation motion and improve the yield strength (YS). The process involves multiple stages, including supersaturation, nucleation, growth and coarsening, and phase transformation, all of which are influenced by temperature, time, and composition [5,7].

Early-stage precipitates, such as β″ (forming at the nanometre scale), are challenging to detect using transmission electron microscopy (TEM) and are often invisible in X-ray diffraction (XRD) or differential scanning calorimetry (DSC) at a low volume fraction (VF) [8,9].

Building on the insights obtained from in-situ TEM, physics-based modelling (PBM) offers a next step by enabling the prediction and systematic exploration of precipitate evolution. The scalability of PBM allows for the simulation of multiple alloy chemistries and processes simultaneously. By contrast, in-situ microscopy is limited to examining a single sample condition during each session [10]. Additionally, PBM has a lower computational cost compared to the high expenses associated with sample preparation, time, and microscope usage. In terms of time efficiency, PBM can provide results in a matter of minutes to hours, while typical in-situ scanning transmission electron microscopy (STEM) experiments, in spite of superior fidelity, can take several days to yield results [11]. The repeatability of PBM is also high, as it is deterministic with well-defined parameters [10]. By contrast, in-situ techniques can be affected by user variability and sample artifacts [10]. Furthermore, physics-based methods allow us to expand the alloy design space by exploring a wide range of compositions [11,12]. By comparison, in-situ STEM is often restricted to reference alloys.

In industrial applications, such as automotive crash alloys, the strength and bendability of the alloy must meet stringent specifications [2]. Therefore, adopting physics-based models, such as the Kampmann–Wagner Numerical (KWN) model, cluster dynamics, or CALPHAD (CALculation of PHAse Diagrams) combined with kinetics, is essential for process optimisation and alloy design. However, implementing these models is often hindered by a lack of experimental visibility and difficulties in tracking the key phenomena that influence the strengthening processes.

These processes are influenced by various factors, including the composition of the alloy, thermal cycles, and levels of impurities, such as Fe, Si, and Mn. The need for physics-based models can be summarised through the following points: (1) predicting precipitate evolution, at which modelling helps to understand how particles nucleate, grow, and coarsen under various heat treatment or processing schedules [10]; (2) replacing trial-and-error heat treatments to avoid costly and time-consuming experimental campaigns [10]; (3) enabling process optimisation, where the physics-based approach can predict the strength based on the processing history (such as quench rate and ageing time), thereby saving energy [10]; (4) support alloy development from scrap, enabling the simulation of the effects of impurities, such as Fe, Mn, or Zn, on precipitate interactions and kinetics while reducing material waste [10].

One of the earliest models of phase transformations is the JMAK model by Johnson and Mehl [13], which describes bulk transformation kinetics but lacks the microstructural detail needed for accurate precipitation modelling. The subsequent model by Shercliff and Ashby introduced distinct stages for nucleation and growth and coarsening [14], while Wagner et al. later unified these stages in the KWN model, enabling the simultaneous simulation of all subprocesses and bringing PBM closer to the actual ageing behaviour of alloys [15]. Although the KWN model improves agreement with experimental data [16], it introduces greater complexity, requiring over 10 fitting parameters compared to the 3–4 parameters used in earlier models. More recent work has expanded the KWN framework to incorporate additional features, such as non-spherical precipitates and the integration of CALPHAD thermodynamics and mechanical strength models [17].

Incorporating industrial needs, such as cold forming between non-isothermal heat treatments, introduces yet further complexity to precipitation modelling. This is primarily due to the requirement for temperature-dependent diffusion coefficients and strain-modulated nucleation kinetics, each necessitating new calibration constants for every ageing stage. Furthermore, accounting for clustering during natural ageing adds another layer of parameterisation, as the interfacial energy of clusters becomes size-dependent. Alloying elements, such as magnesium, further influence clustering kinetics, thereby increasing the number of variables that must be calibrated to accurately reflect the evolving microstructure and mechanical properties [18]. These requirements on the PBM of precipitation hardening brings serious challenges shared across alloy systems despite its established foundations. While the details of PBM vary depending on theoretical assumptions and industrial requirements, they are ultimately governed by a shared set of physical equations, such as those represented in the KWN model, and therefore face common calibration challenges. It is important to note that, in its present form, our work applies to the precipitation response during artificial ageing of the solution-treated and quenched alloys. Other manufacturing processes, such as cold forming, welding, or non-isothermal treatments, introduce additional microstructural complexities (e.g., recovery, recrystallisation, strain-modulated nucleation) that are beyond the scope of this work.

One of the major complexities of pure physics-based models is their dependence on manual calibration. These models often require the expert-driven fitting of parameters through iterative trial-and-error, relying heavily on metallurgists’ subjective judgment and prior domain expertise [19]. For example, Lu et al. established a detailed PBM framework based on TEM measurements and stress–strain curves to assess individual strengthening contributions, including the minor but necessary work-hardening effect, and to calibrate a yield-strength model against tensile data [20]. Hell et al. further nuanced the same physics-based strength modelling framework by explaining the double-peak behaviour observed during artificial ageing of 6082 alloys under no-ramp treatment [21]. However, the calibration of the free parameters in this model was still carried out empirically and manually, rather than through automated optimisation. These studies highlight the typical manual calibration approach used in precipitation hardening models, where physically guided parameter values (e.g., interfacial energy, coarsening constants) are iteratively adjusted to reproduce experimental curves.

Additionally, disagreements among the experts about governing physics, simplifications, or approximations introduce structural uncertainties into the models. These uncertainties necessitate further calibration, requiring the need for expert intervention [22]. For instance, the NaMo model assumes spherical, volume-equivalent precipitates, which simplifies the mathematics but ignores the elongated rod- or lath-shaped morphology of real β″ precipitates [23]. This geometric simplification underestimates the density of effective dislocation obstacles in overaged conditions and creates a systematic bias that must be corrected with calibration. The Esmaeili model captures the rod-like geometry more realistically but reduces the precipitate distribution to mean cross-sectional values. This assumption overlooks the tail of the size distribution, where a few large precipitates can disproportionately strengthen the alloy, and thus the model often under- or over-predicts yield strength unless recalibrated against experimental data [22]. By contrast, the Holmedal model integrates the full-size distribution and accounts for the multiple slip planes intersected by long precipitates, providing a closer match to the experimental data. However, even this more advanced framework carries uncertainties, such as assuming a single critical shearable-to-non-shearable transition size for all precipitate phases. This approximation fails to capture phase-specific interactions with dislocations without careful calibration [24,25]. This makes model calibration an inevitable and important step in all PBM approaches.

Computational intensity is yet another obstacle. Detailed physics-based simulations are resource-demanding, involving time-consuming calculations and significant computational costs. Efforts to add uncertainty quantification [26], an essential component for reliable predictions, further increases the burden, sometimes to impractical levels for complex systems [27].

For aluminium alloys, PBM faces particularly steep challenges due to two key factors. Firstly, a vast design space governs the development of age-hardenable aluminium alloys, encompassing not only a wide range of processing parameters and alloy chemistries but conflicting performance objectives. High yield strength is essential to resist deformation; however, sufficient ductility and work-hardening capacity are equally critical to ensure energy absorption and formability. Thermal stability becomes a decisive factor for alloys exposed to elevated service temperatures, while additional requirements, such as corrosion resistance, fracture toughness, and electrical conductivity, further complicate optimisation [25]. As noted by [28], the wide and largely unexplored compositional space of aluminium alloys, combined with their intricate precipitation mechanisms, makes it difficult to construct accurate microstructure–property models. While addressing these broader design trade-offs is of great importance, it lies beyond the scope of this paper. Instead, we turn to a second major challenge: parameter calibration.

The current form of manual calibration causes inconsistency across expert studies and reduces overall confidence in purely physics-based predictions [29]. Coupling precipitation hardening models with other physics-based modules brings about additional integration challenges. Multiphysics interactions introduce hierarchical dependencies and cascading uncertainties, which make the simultaneous calibration of parameters extremely difficult. Notably, Li et al. highlighted that, for strength models, the lack of a direct mapping between the composition and the strength model parameters severely limits the ability of PBM to predict the properties [30]. As another inseparable part in modelling the precipitation hardening, calibrating CALPHAD models presents another formidable obstacle, as it requires tackling a complex, high-dimensional optimisation problem involving multiple objectives [31]. In a practical design scenario without limiting assumptions or case-specific settings, the number of trainable parameters can rise to the hundreds within a multivariate, multi-objective design space.

By contrast, relatively newer data-driven models offer the advantage of automated calibration via techniques like automatic differentiation, reducing reliance on expert intervention. They can capture complex, nonlinear relationships between composition, processing, and properties, which enable a high-throughput alloy design, as demonstrated by Juan et al. and Tamura et al. [28,32]. However, their effectiveness depends on the availability of large, high-quality datasets, often lacking rare or unexplored alloys. Without detailed compositional or microstructural features, predictive accuracy and extrapolation capability diminish. Furthermore, their black-box nature limits physical interpretability, making it difficult to extract mechanistic insights.

Hybrid modelling offers a promising solution by combining the strengths of physics-based and data-driven approaches. Martinsen et al. exemplified this by integrating a simplified physics-based precipitation model using Gaussian process regression. By learning the residuals between the physics-based predictions and the experimental measurements, they effectively corrected the discrepancies between the experimental data and the physics-based model, improving predictive accuracy even when including cold-forming processes [33]. However, their approach still inherits data-driven limitations, as the learned Gaussian process parameters remain uninterpretable from a metallurgic point of view.

Between all the ways that data can be integrated with physics in a complex model, direct model calibration offers the best physical interpretability [34], and gradient-free optimisers are particularly easier, though not necessarily better to apply than gradient-based ones. This is because, without careful implementation, the valuable gradient information is lost in complex systems due to recursive behaviour on the time axis, complicated correlations in the parameter space, and discontinuities caused by intrinsic if–else branching logic [35].

The KWN model contains all these sources of complexity, which persuaded Yu et al. to calibrate model parameters using the Nelder–Mead and Powell algorithms, both being gradient-free [36]. However, the lack of sufficient training data in their work highlights the necessity of gradient-based methods. Another limitation of these heuristic methods is their tendency to propose physically implausible values during a full simulation trial, as seen in their work. We believe this also causes the physics-based model to collapse, often within just a few iterations if performed without careful modifications on the physics-based model. Furthermore, a critical limitation in their approach lies in the use of extremely limited training data, sometimes as few as three points, or even a single data point per trial, without any indication of interpolation or data smoothing to guide the optimisation. In such data-scarce environments, the absence of interpolation raises concerns about the robustness of the parameter fitting process and its ability to generalise across ageing durations. Equally concerning is the lack of documented modifications to the physics-based model to ensure numerical stability. Given the known discontinuities and recursive dependencies in KWN-type models, it is unclear how convergence was achieved in the absence of constraints on free parameters. These omissions underscore the importance of making targeted, case-specific changes to the model structure before applying gradient-based or heuristic optimisation methods for a complicated physics-based model.

Regarding gradient-based calibration of physics-based models, Kreikemeyer and Andelfinger addressed the discontinuities by combining smooth interpretation (a probabilistic execution model that approximates the program’s convolution with a Gaussian kernel) with automatic differentiation. Their approach enables the computation of smoothed gradients for imperative programs with input-dependent control flow, allowing for gradient-based methods to be applied effectively. Empirical evaluations across several high-dimensional, non-convex optimisation problems show that their estimators offer smoother and more informative gradient signals even in the presence of discontinuities [35]. Given the characteristics of precipitation hardening, a broadly generalised solution for smoothing the model discontinuities is unnecessary for the time-being. Instead, we resolve the discontinuities through tailored, case-specific modifications to maintain model tractability.

Moreover, while PBM of precipitation hardening has achieved significant progress, driven by advances in computational power and data availability, the present work does not aim to further develop the physics formulations or to generate high-fidelity experimental datasets. Instead, our focus is narrowed to the problem of automatic calibration, demonstrated here on a simplified physics-based model trained with a single alloy composition and processing condition. This approach serves as a first step toward addressing the broader challenge of parameter calibration that is common to both simple and advanced mechanistic models, regardless of whether they are trained with limited or highly accurate experimental data.

Among the fitting parameters, the choice of interfacial energy and coarsening factor is particularly important yet challenging, as these parameters are difficult to measure experimentally [26,36]. They appear in multiple equations within the KWN model and influence the output with varying degrees of sensitivity. Furthermore, the underlying physical formulations of these parameters remain a topic of ongoing debate in the literature [27]. Thus, the hosting equations of these parameters are of particular interest in this work.

These studies underscore the limitations of relying solely on physics-based or data-driven models, while highlighting the potential and nuances of hybrid approaches to balance physical interpretability and predictive power. In this work, we propose an alternative approach: a gradient-based calibration of the physics-based parameters in a simplified KWN model integrated with machine learning (ML) for the evolution of precipitate hardening in aluminium 6xxx series. The main contributions of this work include (1) a differentiable simplistic KWN implementation, (2) a gradient-based calibration using the ADAM optimiser, and (3) a comparative analysis against the gradient-free Powell and Nelder–Mead optimisers.

The remainder of this paper is organised as follows: Section 2 presents the proposed methodology, including a dependency graph of the ML-integrated, physics-based equations acquired from the literature underlying the precipitation hardening model and the required adjustments to a purely physics-based method that are offered by this work. We propose trainable coefficients within the network of equations for ML integration. Section 3 describes a gradient-based optimisation algorithm applied to the model and demonstrates its effectiveness in automatically calibrating the YS evolution for a 6xxx series aluminium alloy. In addition, a performance comparison between a gradient-based method and two gradient-free methods is presented. Section 4 concludes this paper and outlines directions for future research. In this work, scalars are written in italic (e.g. $R$, $t$), vectors in bold italic (e.g. $\mathit{N}\mathit{D}$), and abbreviations in plain text (e.g. YS, TEM). Elements of vectors are scalars and written in italics (e.g. $ND\left[i\right]$). This notation is applied consistently throughout the paper.

2. Methods

We apply trainable coefficients $P_k, k\in \left\{0,\dots ,5\right\}$ to treat each equation that hosts an occurrence of a functional form of free parameters (rather than optimising each free parameter directly). Before showing where they appear throughout the KWN model, we start by defining the sigmoid function that is used to make the model end-to-end differentiable. To implement this, different definitions for positive and negative input domains are used as follows:

$$\sigma \left(a,x\right)=\left\{\begin{array}{c}{\displaystyle \frac{1}{1+e^{-ax}}} for x\ge 0,\\ {\displaystyle \frac{e^{ax}}{1+e^{ax}}} for x<0.\end{array}\right..$$

(1)

The above implementation mitigates the risk of overflow that appears in a well-known version of the sigmoid function: $\sigma \left(a,x\right)=1/(1+e^{-ax})$. In this version, there is a risk of overflow for values of $x$ that are significantly negative. Although introducing the sigmoid function adds a hyperparameter, its steepness coefficient $a$, it is commonly chosen from practical values, such as 1, $10$, or $100$. These values control the smoothness of the transition and can be tuned to balance between physical realism and numerical smoothness.

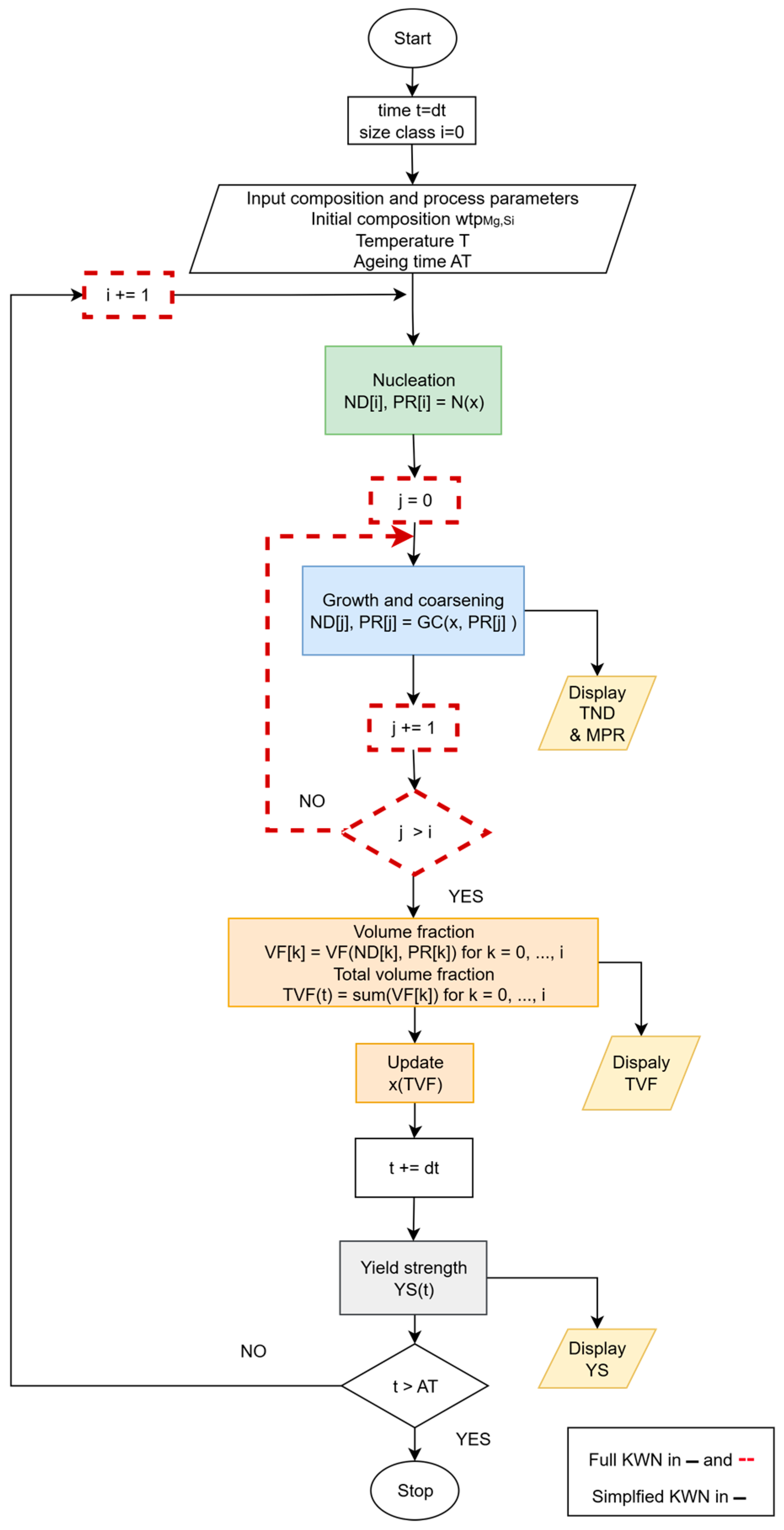
Figure 1 shows a flowchart of the common full KWN model found in the literature [18,37,38], with the redundant blocks for a simplified implementation in dashed red lines for this work. Following the full implementation, time $t$ and size class counters $i$ and $j$ are set to zero in the Initialisation block. Then, the process and composition parameters, temperature $T$, and initial composition $x\left(0\right)$, are specified. In the Nucleation block, $ND\left[i\right]$ new precipitates with radius $PR\left[i\right]$ nucleate. Next, the $\mathrm{G}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}$ block updates all the size classes j ($0<j<=i$) in $ND\left[j\right]$ and $PR\left[j\right]$ according to the input arguments ($x, PR\left[j\right]$). The updated vectors are passed on to the $\mathrm{Volume\; Fraction}$ block to calculate the vector $VF\left[i\right]$, in which the $i$’th array represents the contribution of size class $i$ to the total volume fraction (TVF) as a function of the $i$’th array in vectors $\mathit{N}\mathit{D}$ and $\mathit{P}\mathit{R}$. The $\mathrm{Y}\mathrm{i}\mathrm{e}\mathrm{l}\mathrm{d} \mathrm{S}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}$ block calculates $YS\left(t\right)$ based on the vectors $\mathit{N}\mathit{D}$, $\mathit{P}\mathit{R}$, and scalar $TVF\left(t\right)$ at time $t$. The $\mathrm{U}\mathrm{p}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}$ block renews the concentrations $x$ of leftover Mg and Si in the matrix as a function of $TVF$. The concentrations x play an important role in the system state and affects the $\mathrm{N}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$ and $\mathrm{G}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}$ for the next iteration. The size class counter $i$ is increased by $1$ to allow for the creation of a newer i’th size class, and the time $t$ is increased by $\mathrm{d}\mathrm{t}$ at the end of each iteration. The outputs, such as total number density (TND), mean particle radius (MPR), TVF, and YS, are some of the outputs that can be measured experimentally; therefore, the physics-based model’s performance, with respect to the choice of the fitting parameters, can be evaluated by how much the model predictions agree with the experimental data.

A simplified version of the KWN model can be derived from Figure 1 by removing the blocks outlined by dashed red lines. In this proposed formalisation, $\mathrm{N}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$ is assumed to occur only once at the beginning of the simulation, as most of the nucleation events take place during the early stages of the ageing process, which is not far from the reality. Subsequent particle growth and coarsening take place only for this initial size class throughout the rest of the ageing process. By restricting nucleation to a single event, the number of iterative loops in the model is reduced from two to one, thereby simplifying the integration of the gradient-based optimiser with the $\mathrm{N}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$ and Growth and Coarsening blocks (more on this in Appendix A). A more comprehensive KWN model incorporating detailed physics and multiple size classes will be the subject of future work.

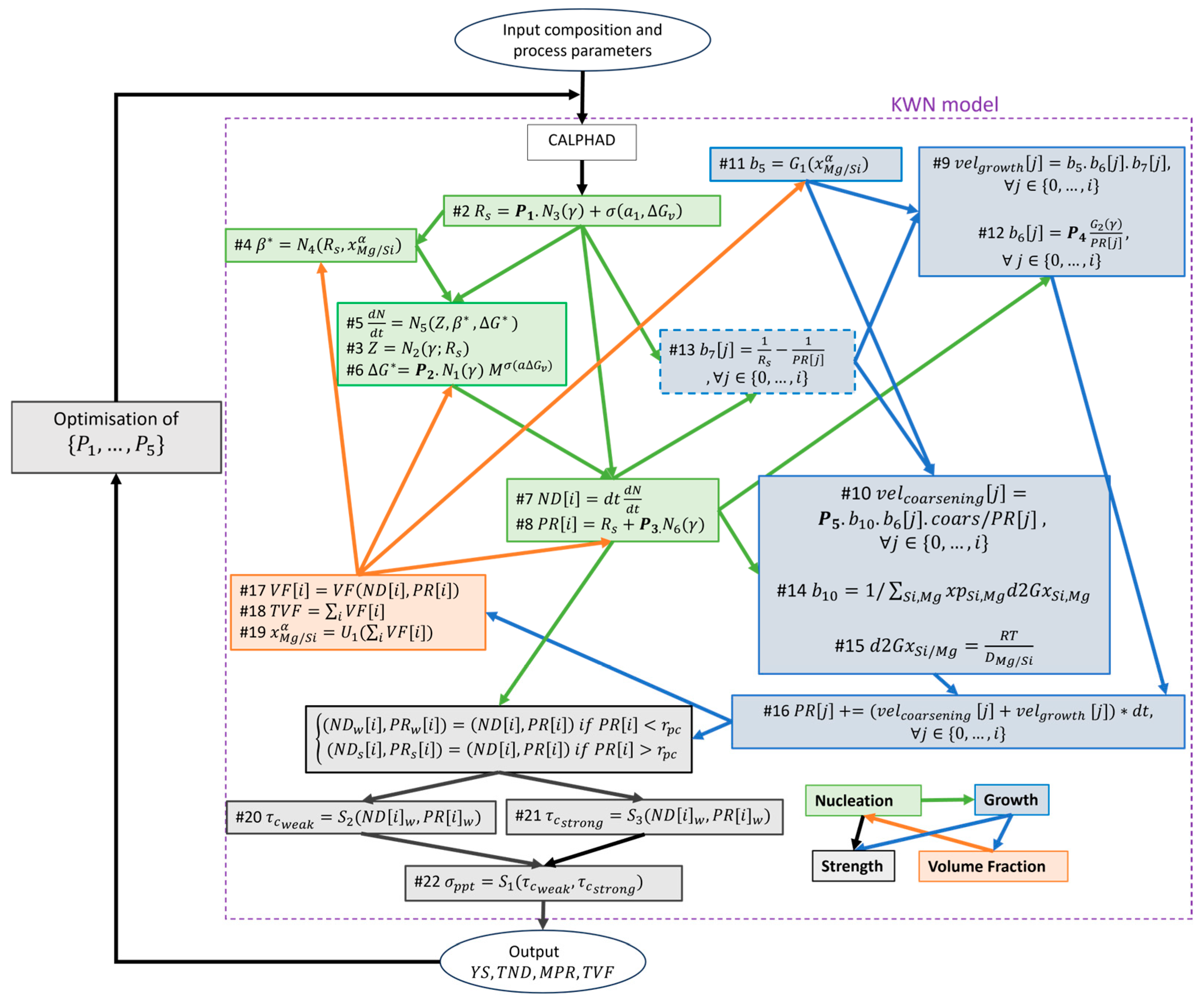
Figure 2 presents a compilation of the abovementioned KWN module as a network of equations. It also illustrates the dependency structure among nucleation (green), growth and coarsening (blue) and their overall connection to the optimisation block. The KWN model is driven by input composition and processing parameters (namely, temperature and solute concentrations in this work) which appear throughout the formulation. These quantities contribute to loop-based calculations of particle number density (ND) and particle radius (PR), which are the core variables of the KWN framework and evolve in array size and value over time. The outputs of the microstructural evolution feed into a mechanical $\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}$ model used to predict the YS, which in turn guides the iterative optimisation of the model’s trainable coefficients $\left\{P_1,\dots ,P_5\right\},$ proposed by this work. Please note that the simplified KWN model is derived once the $(i,j)$ size class counters are both assumed to be zero across all time steps $t$. The complete forms of the equations in Figure 2 are provided in

Table A2. Abbreviated forms of the equation components shown in Figure 2 and their corresponding expanded mathematical expressions.

Equation Ref. (Figure 2)	Abbreviated Form	Expanded Equation Part
(1)	$R_s=N_3\left(\gamma \right)$	$R_s={\displaystyle \frac{-2\gamma }{\Delta G_v}}{\displaystyle \frac{2\varnothing }{3\varnothing -1}}$
(3)	$Z=N_2(\gamma ;R_s)$	$Z={\displaystyle \frac{v_{at}^{\beta }}{(3\varnothing -1)\pi R_s}}\sqrt{{\displaystyle \frac{\varnothing \gamma }{k_{b}T}}}$
(4)	${\beta }^{*}=N_4(R_s,x_{Mg/Si}^{\alpha })$	${\beta }^{*}={\displaystyle \frac{4\pi \varnothing {R_s}^2}{a_{\beta }^4}}{({\displaystyle \frac{{(x_{Si}^{\beta }-x_{Si}^{\alpha })}^2}{{D_{Si}x}_{Si}^{\alpha }}}+{\displaystyle \frac{{(x_{Mg}^{\beta }-x_{Mg}^{\alpha })}^2}{{D_{Mg}x}_{Mg}^{\alpha }}})}^{-1}$
(5)	${\displaystyle \frac{dN}{dt}}=N_5\left(Z{,\beta }^{*}{,\Delta G}^{*}\right)$	${\displaystyle \frac{dN}{dt}}=N_{0}Z{\beta }^{*}\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{{\Delta G}^{*}}{k_{b}T}})$
(6)	${\Delta G}^{*}=N_1\left(\gamma \right)$	${\Delta G}^{*}={\displaystyle \frac{16\pi {\gamma }^3}{3{\left(\Delta G_v\right)}^2}}{\displaystyle \frac{4{\varnothing }^3}{{(3\varnothing -1)}^2}}$
(8)	$N_6\left(\gamma \right)$	$N_6\left(\gamma \right)={\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{KT}{\pi \varnothing \gamma }}}$
(11)	$b_5=G_1\left(x_{Mg/Si}^{\alpha }\right)$	$b_5={\left\{{\displaystyle \frac{{({rp}_{Si}-x_{Si}^{\alpha })}^2}{{{d2Gx}_{Si}x}_{Si}^{\alpha }}}+{\displaystyle \frac{{({rp}_{Mg}-x_{Mg}^{\alpha })}^2}{{{d2Gx}_{Mg}x}_{Mg}^{\alpha }}}\right\}}^{-1}$
(12)	$G_2\left(\gamma \right)$	$G_2\left(\gamma \right)={\displaystyle \frac{4\gamma \varnothing v_m}{(3\varnothing -1)R_{g}T}}$
(14)	$b_{10}$	$b_{10}=1/{\sum }_{Si, Mg}{xp}_{Si,Mg}{d2Gx}_{Si,Mg}$
(17)	$VF\left[i\right]=VF\left(ND\left[i\right], PR\left[i\right]\right)$	$VF\left[i\right]=\left(2\varnothing -{\displaystyle \frac{2}{3}}\right)\pi {PR}^3\left[i\right]ND\left[i\right]$
(18)	${VF}_{total}$	${VF}_{total}={\sum }_{i}VF\left[i\right]$
(19)	${x_{Mg/Si}^{\alpha }=U}_1\left(TVF\right)$	$x_{Mg/Si}^{\alpha }={\displaystyle \frac{f\left(wt{p}_{Mg/Si}\right)-\epsilon TVF{.rp}_{Mg/Si}}{1-\epsilon TVF}}$
(19)	$x_{Mg/Si}=\mathrm{f}$$(wt{p}_{Mg/Si}$)	$x_{Mg/Si}^0={\displaystyle \frac{wt{p}_{Mg/Si}/m{w}_{Mg/Si}}{x_{denom}}}, x_{denom}=\sum _{e\in Mg,Si, Al}{\displaystyle \frac{wt{p}_e}{m{w}_e}}$
(20)	${{\tau }_c}_{weak}=S_2({ND\left[i\right]}_w,{PR\left[i\right]}_w)$	${{\tau }_c}_{weak}={\displaystyle \frac{\sqrt{\sum {ND\left[i\right]}_{w}2\varnothing {PR\left[i\right]}_w}}{\sqrt{2\sqrt{3}\Gamma }b}}{\left({\displaystyle \frac{\sum {ND\left[i\right]}_w\sqrt{2}\delta G{b}^2{PR\left[i\right]}_w/{PR}_c}{\sum {ND\left[i\right]}_w}}\right)}^{3/2}$
(21)	${{\tau }_c}_{strong}=S_3({ND\left[i\right]}_w,{PR\left[i\right]}_w)$	${{\tau }_c}_{strong}=\sqrt{2}\delta Gb\sqrt{\sum {ND\left[i\right]}_{s}2\varnothing {PR\left[i\right]}_s}$

in Appendix C.

It is important to note that assuming a value of unity for all instances, i.e., $P1=P2=P3=P4=P5$, results in the purely physics-based KWN model formulation commonly used in the literature. However, in this work, we deliberately allow for each instance to vary independently, enabling the optimisation algorithm to explore a five-dimensional parameter space. It is intuitional to conclude that the optimiser will obtain this solution in the extreme scenario when all the physics-based formulations are ideal. This added flexibility allows us to investigate whether improved model fidelity or new physical insights can emerge from differentiating between instances of the same physical variable.

Starting from the $\mathrm{N}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$ block, the temperature $T$ and compositions $x$ are input to the CALPHAD module to determine the driving force $\mathsf{\Delta }G$. The volumetric driving force $\mathsf{\Delta }{G}_v$ (normalised by the molar volume $v_m$) is then used in the definition of the critical radius $R_s$. It determines the minimum value for the radius $PR\left[i\right]$ of a newly formed size class $i$ to be able to grow larger rather than dissolve back to the matrix. The original critical radius $R_s$, defined by classical nucleation theory [39], is modified with the trainable coefficient $P_1$ and a smoothing term as follows:

$$R_s=P_1{\displaystyle \frac{-2\gamma }{\Delta G_v}}{\displaystyle \frac{2\varnothing }{3\varnothing -1}}+\sigma \left(a_1,\Delta G_v\right),$$

(2)

where $\gamma$ is the interfacial energy between the precipitate and the matrix, The sigmoid function $\sigma \left(.\right)$ guarantees the physics-based definition (the first term) is only used when the driving force is negative. Once the composition and temperature conditions turn unfavourable for nucleation, the driving force becomes positive. Hence, the critical radius is smoothly set to a large value (close to 1) by including the second term in its calculations. A $R_s\cong 1$ signals to the rest of the downstream equations a thermodynamically unstable condition for the nucleation of new precipitates without imposing discontinuity on the model. The shape parameter $\varnothing$ is simply a constant that depends on the shape of the precipitates. $P_1$ is a coefficient for the original interfacial energy that is optimised by automatic calibration. The critical radius $R_s$, whether in the order of $O\left({10}^{-9}\right)$ in nucleating conditions or $O\left(1\right)$ for non-nucleating conditions, is then passed on to the equation of the Zeldovich factor $Z$ and the attachment rate ${\beta }^{*}$. We maintain their original form for Mg₅Si₆ precipitates as defined by [18]:

$$Z={\displaystyle \frac{v_{at}^{\beta }}{(3\mathit{\varnothing }-1)\pi R_s}}\sqrt{{\displaystyle \frac{\varnothing \gamma }{k_{b}T}}},$$

(3)

$${\beta }^{*}={\displaystyle \frac{4\pi \varnothing {R_s}^2}{a_{\beta }^4}}{({\displaystyle \frac{{({xp}_{Si}-x_{Si})}^2}{D_{Si}{x}_{Si}}}+{\displaystyle \frac{{({xp}_{Mg}-x_{Mg})}^2}{D_{Mg}{x}_{Mg}}})}^{-1},$$

(4)

Regarding the Zeldovich factor (which accounts for the probability of a nucleus reaching the critical size), $v_{at}^{\beta }$, and $k_b$ represent the atomic volume of the precipitates and the Boltzmann factor, respectively. For the attachment rate, $a_{\beta }$, $D_{Si/Mg}$, $x_{Si/Mg}^{\beta }$ define the interatomic distance in the precipitate, diffusion rate of Mg/Si atoms, and precipitate concentrations $x$ of Mg/Si atoms. The Zeldovich factor and the attachment rate are passed on to the nucleation rate defined by classical nucleation theory as follows [39]:

$${\displaystyle \frac{dN}{dt}}=N_{0}Z\beta \mathit{exp}\left(-{\displaystyle \frac{{\Delta G}^{*}}{k_{b}T}}\right).$$

(5)

where ${\Delta G}^{*}$ is the critical Gibbs free energy [40]. We modify this key parameter of the $\mathrm{N}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$ block by the addition of $P_2$ and a factor $M$ as follows:

$${\Delta G}^{*}=P_2{\displaystyle \frac{16\pi {\mathit{\gamma }}^3}{3{\left(\Delta G_v\right)}^2}}{\displaystyle \frac{4{\varnothing }^3}{{(3\varnothing -1)}^2}}{M}^{\sigma (a_2,\Delta G_v)},$$

(6)

Here, $M^{\sigma \left(\Delta G_v\right)}$ sets the critical Gibbs free energy ${\Delta G}^{*}$ to an infinitely large number when the driving force is positive. This smoothing mechanism is required for the addition of the ML optimiser. Consequently, the ND of the newly formed class will also be smoothly set to zero by Equation (5). The $\mathrm{N}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$ block is concluded by defining the number density $ND\left[i\right]$ and particle radius $PR\left[i\right]$ of the current size class $i$ as follows [39]:

$$ND\left[i\right]=dt.{\displaystyle \frac{dN}{dt}},$$

(7)

$${PR\left[i\right]=r}_p^{*}=\left(R_s+{\displaystyle \frac{P_3 }{2}}\sqrt{{\displaystyle \frac{KT}{\pi \varnothing \gamma }}}\right).$$

(8)

It is worth mentioning that the PR will be set to a value close to $1^{+}$ by combining Equations (2) and (8) when the driving force is positive. However, in the calculation of VF, which we will see later, this large value will be multiplied by $ND\left[i\right]\cong 0$ and the calculations of VF, and new concentrations will not be affected.

In the $\mathrm{G}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}$ block, velocity of growth $ve{l}_{growth}$ and velocity of coarsening $ve{l}_{coarsening}$ are the most centric equations, and for each size class up to and including the current size class $i$, their original form can be found in [18]. Here, however, we introduce two trainable coefficients $P_4$ and $P_5$ to account for the fitting parameters that they contained:

$$ve{l}_{growth}\left[j\right]=P_4. b_5.b_6\left[j\right].b_7\left[j\right], \forall j\in \left\{0,\dots ,i\right\},$$

(9)

$$ve{l}_{coarsening}\left[j\right]=P_5. b_{10}.b_6\left[j\right].{\displaystyle \frac{coars}{PR\left[j\right]}}, \forall j\in \{0,\dots ,i\}$$

(10)

where $coars$ is the coarsening parameter. The fitting parameters $P_4$ and $P_5$ modify the interfacial energy $\gamma$ (from inside $b_6$), and the product $\gamma \ast coars$, respectively. The parameter groups $b_5$, $b_6$, $b_7$, and $b_{10}$ are defined as follows [18]:

$$b_5={\left\{{\displaystyle \frac{{(x_{Si}-x_{Si})}^2}{{{d2Gx}_{Si}x}_{Si}^{\alpha }}}+{\displaystyle \frac{{(x_{Mg}-x_{Mg})}^2}{{{d2Gx}_{Mg}x}_{Mg}^{\alpha }}}\right\}}^{-1},$$

(11)

$$b_6\left[j\right]={\displaystyle \frac{1}{PR\left[j\right]}}{\displaystyle \frac{4\gamma \varnothing v_m}{\left(3\varnothing -1\right)RT}}, \forall j\in \{0,\dots ,i\},$$

(12)

$$b_7\left[j\right]={\displaystyle \frac{1}{R_s}}-{\displaystyle \frac{1}{PR\left[j\right]}}, \forall j\in \left\{0,\dots ,i\right\},$$

(13)

$$b_{10}=1/\sum _{Si, Mg}{xp}_{Si,Mg}{d2Gx}_{Si,Mg}.$$

(14)

Here, $R$ represents the gas constant, and ${d2Gx}_{Si,Mg}$ is defined as follows [18]:

$${d2Gx}_{Si/Mg}={\displaystyle \frac{RT}{D_{Mg/Si}}}.$$

(15)

Combining the above equations, the PR of the size class up to and including $i$ updates with Equation (16):

$$PR\left[j\right]=ra{d}_{total}\left[j\right]=PR\left[j\right]+\left(ve{l}_{coarsening}\left[j\right]+ve{l}_{growth}\left[j\right]\right)\ast dt, \forall j\in \{0,\dots ,i\}.$$

(16)

According to Ostwald ripening, the ND of the precipitates should also be modified since bigger precipitates grow larger by consuming smaller ones [18]:

$$ND\left[j\right]=ND\left[j\right]\times {\left({\displaystyle \frac{ra{d}_{growth}\left[j\right]}{ra{d}_{total}\left[j\right]}}\right)}^3, \forall j\in \left\{0,\dots ,i\right\},$$

(17)

where $ra{d}_{growth}\left[j\right]=PR\left[j\right]+\left(ve{l}_{growth}\left[j\right]\right)\times dt$.

The ND and PR are input to the $\mathrm{U}\mathrm{p}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}$ block. The VF of all the size classes up to and including $i$ is readily available as follows:

$$VF\left[j\right]=\left(2\varnothing -{\displaystyle \frac{2}{3}}\right)\pi {PR}^3\left[j\right]ND\left[j\right], \forall j\in \left\{0,\dots ,i\right\}.$$

(18)

As mentioned above, $\mathit{P}\mathit{R}$ array values close to one will not affect the computations of the update block (hence upcoming time steps) because they will be masked by the multiplication of zero values in $ND$. The TVF is calculated by a summation over all the arrays of $\mathit{V}\mathit{F}$ as follows:

$$TVF={\sum }_{i}VF\left[i\right].$$

(19)

The $\mathrm{U}\mathrm{p}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}$ block receives its name by updating the concentrations of Mg and Si as follows:

$$x_{Mg/Si}={\displaystyle \frac{f\left(wt{p}_{Mg/Si}\right)-TVF{.x}_{Mg/Si}}{1-TVF}}$$

(20)

The function $f(.)$ converts the initial composition from weight percent to initial molar concentration.

Finally, the $\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}$ block divides the size classes to weak/sheared ${(ND\left[i\right]}_w,{PR\left[i\right]}_w)$ and strong/bypassed ${(ND\left[i\right]}_s,{PR\left[i\right]}_s)$ size classes based on the critical threshold $r_{pc}$. The weak size classes contribute to the strength as follows [37]:

$${{\tau }_c}_{weak}={\displaystyle \frac{\sqrt{\sum {ND\left[i\right]}_{w}2\varnothing {PR\left[i\right]}_w}}{\sqrt{2\sqrt{3}{\Gamma }_{dis}}{b}_{dis}}}{({\displaystyle \frac{\sum {ND\left[i\right]}_w\sqrt{2}{\delta }_{dis}{G}_{mod}{b_{dis}}^2{PR\left[i\right]}_w/{PR}_c}{\sum {ND\left[i\right]}_w}})}^{3/2}.$$

(21)

where ${\Gamma }_{dis}=\left({\displaystyle \frac{2}{\sqrt{3}}}\right){\delta }_{dis}{G}_{mod}{b_{dis}}^2$. The parameters ${\delta }_{dis},G_{mod}$, and $b_{dis}$ represent the dislocation parameter (depending on the shape and nature of dislocations) [37], the shear modulus of the aluminium matrix, and the magnitude of the Burgers vector, respectively. The strong size classes $({ND\left[i\right]}_s,{PR\left[i\right]}_s)$ contribute to the strength as follows [37]:

$${{\tau }_c}_{strong}=\sqrt{2}{\delta }_{dis}.G_{mod}.b_{dis}\sqrt{\sum {ND\left[i\right]}_{s}2\varnothing {PR\left[i\right]}_s}.$$

(22)

The Strength block is concluded by superposition of these two mechanisms which gives the precipitation’s contribution to the overall YS as follows [37]:

$${\sigma }_{ppt}=M_{ppt}\sqrt[q]{({{{\tau }_c}_{weak}}^q+{{{\tau }_c}_{strong}}^q)}$$

(23)

where $q$ and $M_{ppt}$ are the Taylor exponent and the Taylor factor, respectively.

To clarify, the variables of the KWN model mentioned so far are divided into five groups (G1–5):

G1. The independent physical constants, such as the Boltzmann constant K.

G2. The independent experimental parameters, such as temperature $T$.

G3. The dependent parameters, such as the Gibb’s free energy that depend on other variables.

G4. The outputs, such as the $YS\left(t\right)$, $V{F}_{total}\left(t\right)$, $TND\left(i\right)$, and $MPR\left(i\right)$.

G5. The fitting parameters, such as the interfacial energy $\gamma$.

This work aims to calibrate the functional forms of the fitting parameters of Group 5 indirectly via the coefficients $P_i$ (as presented in

Table 1. Summary of the trainable coefficients, the corresponding physics-based variables and fitting parameter instance, and the governing equations in which they appear.

Trainable Coefficients	Variables (Parameter Instance)	The Hosting Equation
$P_1$	$R_s\left(\gamma \right)$	(2)
$P_2$	${\Delta G}^{*}\left({\gamma }^3\right)$	(6)
$P_3$	$R_p\left(\sqrt{{\displaystyle \frac{1}{\gamma }}}\right)$	(8)
$P_4$	$Ve{l}_{growth}\left(\gamma \right)$	(12)
$P_5$	$Ve{l}_{coarsening}(\gamma \times coar{s}_{coeff})$	(10) and (12)

). To address the discontinuities and to ensure compatibility with gradient-based optimisation, we introduced modifications to the traditional KWN model. Theoretically speaking, nucleation occurs only when this driving force is negative. However, in conventional implementations, once the solute concentration falls below a threshold, the driving force becomes positive, leading to an abrupt stop in nucleation, causing a discontinuity that propagates to model outputs. To mitigate this, we employed a smooth approximation using a sigmoid function, as often found in activation functions in neural networks.

As a second instance of discontinuity, the equation for the critical nucleation radius (see Equation (2) in Methods) contains the driving force in the denominator. A positive driving force would mathematically result in a nonphysical, negative radius. As a replacement to truncating or zeroing the radius (which introduces non-differentiability), we applied a large softening term via a sigmoid, effectively assigning a large nucleation radius. These radii correspond to near-zero number densities from Equation (5), ensuring that such precipitates do not affect the overall evolution of the system. It is worth mentioning that, although traditional precipitation hardening models often distinguish between small and large particles, potentially introducing further discontinuities, we circumvent this issue by using a single size class in our current work, which is justified in Appendix A. Nevertheless, we acknowledge that additional discontinuities may emerge when expanding the model or applying it to more complex case studies. Table 1 summarises the trainable coefficients and the corresponding equations that have appeared in this section.

3. Results

This section presents the findings of applying a gradient-based calibration framework to the differentiable KWN model for predicting YS in a 6xxx series aluminium alloy. We begin by examining how the ADAM optimiser progressively refines the model’s trainable coefficients to match an interpolated version of the raw experimental data borrowed from [41]. Convergence behaviour, parameter trajectories, and loss function evolution are thoroughly examined for the ADAM optimiser to assess the optimisation performance, followed by a comparative analysis against the gradient-free Powell and Nelder–Mead optimisers. A brief Monte Carlo analysis of the parameter initialisation reveals insights into the robustness and variance of the fitted coefficients. Finally, a benchmark table summarises the advantages of gradient-based optimisation in terms of convergence time, parameter stability, physical plausibility, and computational complexity.

The ADAM optimiser of TensorFlow (version 2.14.0) trains the trainable coefficients in a multivariable optimisation task, with a unique learning rate for each trainable coefficient $\{{LR}_{p1}=0.01, {LR}_{p2}=0.001,{LR}_{p3}= 0.1,{LR}_{p4}= 0.01, {LR}_{p5}=0.01\}$ and a communal ADAM learning rate of $0.001$. The learning rates have been chosen empirically based on visual assessments on the sensitivity of each parameter. Due to the higher sensitivity of the KWN model on parameter $P_2$, a smaller initialisation variance of 0.01 has been chosen for it while the rest of the parameters use an initialisation variance of 0.1. A mean initialisation value of unity has been chosen for all the trainable coefficients, meaning the optimisation starts with the purely physics-based knowledge and leaves further refinement to the optimiser. The loss criterion is the mean squared error (MSE) plus the L2 regularisation terms on the trainable coefficients that penalise their divergence from unity and thus the physics-based assumptions. This condition on the loss function defines how far the optimiser can explore from the purely physics-based equations.

Moreover, a one-on-one comparison is made between the ADAM, Powell, and Nelder–Mead optimisers. The Powell settings in SciPy version 1.11.2 include a function tolerance of $ftol=1\times {10}^{-4}$, a strict parameter tolerance of $1\times {10}^{-12}$, and a strict maximum function evaluation of $maxfev=\mathrm{10,000}$ to ensure that successful termination is only based on the function tolerance. To prevent the physics-based model from collapsing due to unrealistically large or small parameter values during line searches, the bounds were restricted to the range $[0, 5]$. The Nelder–Mead optimiser is set up with a similar optimisation package and values: a “function absolute tolerance” of $fatol=1\times {10}^{-4}$ and a “strict absolute error in parameter space” of $xatal=1\times {10}^{-10}$ to ensure convergence is only based on the improvements in function values. The loss function for the Powell and Nelder–Mead optimisers is defined in the same way as the ADAM optimiser to ensure a fair comparison: MSE with L2 regularisation with a weight of $1\times {10}^{-4}.$.

The training data is sourced from [41]. In their work, the commercial Al-Mg-Si alloy was acquired in the form of extruded rods with a diameter of 16.5 mm. Its chemical composition, determined using atomic emission spectroscopic analysis, includes 0.50 wt.% Mg, 0.43 wt.% Si, 0.18 wt.% Fe, 0.08 wt.% Mn, along with minor quantities of Cu, Cr, Zn, and Ti, with the balance being Al. Hardness and tensile samples, with a gauge length of 25 mm and a diameter of 6.25 mm, underwent solution treatment at 525 °C for two hours, followed by rapid quenching in ice water and subsequent artificial ageing at 150 °C. Uniaxial tensile tests were conducted on a servo-hydraulic universal testing machine (Model: 8801, Instron, Norwood, MA, USA) under a nominal strain rate of ${10}^{-3} {\mathrm{s}}^{-1}$ at room temperature (298 K). For each ageing time, three samples were tested, and the average tensile properties were reported.

The PBM is implemented using Python 3.11.5 and the thermodynamic library of Kawin (version 0.3.0).

Table A1. The parameters for the simulation of the differentiable simplified KWN model.

Type	Name	Parameter	Value (Unit) [Reference]
Independent physical constant	Boltzmann constant	$K$	$1.380649{ \times 10}^{-23}\left(\mathrm{j}·{\mathrm{K}}^{-1}\right)$
Independent physical constant	As-quenched strength	${\sigma }_0$	$55{ \times 10}^6 \left(\mathrm{P}\mathrm{a}\right)$
Independent physical constant	Gas constant	$R$	8.31 (j·K−1.mol−1)
Independent physical constant	Mg’s ppt concentration	$x{p}_{Mg}$	$5/11$
Independent physical constant	Si’s ppt concentration	$x{p}_{Si}$	$6/11$
Independent physical constant	Average volume of ppt atoms	$v$	$1.92{ \times 10}^{-29}\left({\mathrm{m}}^3\right)$
Independent physical constant	Interatomic distance	$a$	$2.86{ \times 10}^{-10}$$\left(\mathrm{m}\right)$
Independent physical constant	Precipitation sites	$N_0$	$5.8{ \times 10}^{28}$
Independent physical constant	Molar volume of precipitates	$v_m$	$3.95{ \times 10}^{-5}\left({\mathrm{m}}^3\right)$
Independent physical constant	Shear modulus of Al matrix	$G_{mod}$	$2.7{ \times 10}^{10} (\mathrm{N}·{\mathrm{m}}^2)$
Independent physical constant	The magnitude of the Burgers vector	$b_{dis}$	$2.84{ \times 10}^{-10}$
Independent physical constant	Mg’s molar weight	$m{w}_{Mg}$	$24.305 (\mathrm{g}/\mathrm{m}\mathrm{o}\mathrm{l})$
Independent physical constant	Si’s molar weight	$m{w}_{Si}$	$28.09 (\mathrm{g}/\mathrm{m}\mathrm{o}\mathrm{l})$
Independent physical constant	Al’s molar weight	$m{w}_{Al}$	$26.98 (\mathrm{g}/\mathrm{m}\mathrm{o}\mathrm{l})$
Independent physical constant	Scaling factor for Mg solid solution hardening	$k_{Mg}$	$21.1{ \times 10}^6 (\mathrm{P}\mathrm{a}/\mathrm{w}\mathrm{t}\%)$ [37]
Independent physical constant	Scaling factor for Si solid solution hardening	$k_{Si}$	$10.5{ \times 10}^6 (\mathrm{P}\mathrm{a}/\mathrm{w}\mathrm{t}\%)$ [42]
Independent physical constant	Critical threshold	$r_{pc}$	$2.4{ \times 10}^{-9} \left(\mathrm{m}\right)$ [37]
Independent physical constant	Mg’s diffusion coefficient	$D{0}_{Mg}$	$2.2{ \times 10}^{-4}$ (m2/s) [38]
Independent physical constant	Mg’s activation energy	$Q_{Mg}$	$\mathrm{115,000} (\mathrm{j}/\mathrm{m}\mathrm{o}\mathrm{l})$
Independent physical constant	Si’s diffusion coefficient	$D{0}_{Si}$	$2.2{ \times 10}^{-4}$(m2/s) [38]
Independent physical constant	Si’s activation energy	$Q_{Si}$	$\mathrm{115,000} (\mathrm{j}/\mathrm{m}\mathrm{o}\mathrm{l})$
Independent physical constant	Time step	dt	3600 (s)
Independent experimental parameter	Time	$t$	$1$ (s)
Independent experimental parameter	Mg’s weight percent	$wt{p}_{Mg}$	$0.5$
Independent experimental parameter	Si’s weight percent	$wt{p}_{Si}$	$0.43$
Independent experimental parameter	Temperature	$T$	$(150+273)$ (K)
Independent experimental parameter	Ageing time	$AT$	$170 \left(\mathrm{h}\right)$
Fitting	Shape factor	$\varphi$	7
Fitting	Total volume fraction coefficient	$\epsilon$	1
Fitting	Coarsening coefficient	$coar{s}_{coeff}$	$1{ \times 10}^{-3}$
Fitting	Taylor factor	$M_{ppt}$	$3.1$
Fitting	Taylor exponent	$q$	$2$
Fitting	A parameter depending on the shape and nature of dislocations	${\delta }_{dis}$	$0.5$
Fitting	Strength-to-yield’s parameter	$c_{02}$	$500$ [37]
Fitting	Strength-to-yield’s parameter	$c_{03}$	$10$ [37]
Fitting	A parameter in the growth and coarsening equations	$\xi$	$0.3$
Fitting	Interfacial energy	$\gamma$	$0.042$ (j/m2)
Dependent parameter	Critical radius	$R_s$	Variable
Dependent parameter	Volumetric Gibbs free energy	$\Delta G_v$	Variable
Dependent parameter	Strain energy	$\Delta G_s$	Variable
Dependent parameter	Critical Gibbs free energy	${\Delta G}^{*}$	Variable
Dependent parameter	-	${d2Gx}_{Si/Mg}$	Variable
Dependent parameter	Diffusion coefficient	$D_{Mg/Si}$	Variable
Dependent parameter	-	$b_5$	Variable
Dependent parameter	-	$b_6$	Variable
Dependent parameter	-	$b_7$	Variable
Dependent parameter	-	$b_{10}$	Variable
Dependent parameter	Mg/Si molar concentration	$x_{Si,Mg}$	Variable
Dependent parameter	Velocity of growth	$ve{l}_{growth}$	Variable
Dependent parameter	Velocity of coarsening	$ve{l}_{coarsening}$	Variable
Dependent parameter	Critical radius	$r_p^{*}$	Variable
Dependent parameter	Zeldovich factor	$Z$	Variable
Dependent parameter	Attachment rate	$\beta$	Variable
Dependent parameter	Nucleation rate	$dN/dt$	Variable
Dependent parameter	$\mathrm{Number} \mathrm{density} \mathrm{of} \mathrm{size} \mathrm{class} i$	$ND\left[i\right]$	Variable
Dependent parameter	$\mathrm{Particle} \mathrm{radius} \mathrm{of} \mathrm{size} \mathrm{class} i$	$PR\left[i\right]$	Variable
Dependent parameter	Line tension for strong particles	${{\tau }_c}_{strong}$	Variable
Dependent parameter	Line tension for weak particles	${{\tau }_c}_{weak}$	Variable
Dependent parameter	$\mathrm{Number} \mathrm{density} \mathrm{of} \mathrm{size} \mathrm{class} i$ (only for weak sizes classes)	${ND\left[i\right]}_w$	Variable
Dependent parameter	$\mathrm{Particle} \mathrm{radius} \mathrm{of} \mathrm{size} \mathrm{class} i$ (only for weak sizes classes)	${PR\left[i\right]}_w$	Variable
Dependent parameter	$\mathrm{Number} \mathrm{density} \mathrm{of} \mathrm{size} \mathrm{class} i$ (only for strong sizes classes)	${ND\left[i\right]}_s$	Variable
Dependent parameter	$\mathrm{Particle} \mathrm{radius} \mathrm{of} \mathrm{size} \mathrm{class} i$ (only for weak sizes classes)	${PR\left[i\right]}_s$	Variable
Output (intermediate)	Total volume fraction	$TVF$	Variable
Output (intermediate)	Total number density	$TND$	Variable
Output (intermediate)	Mean particle radius	$MPR$	Variable
Output (final)	Precipitation hardening hardness	${\sigma }_{ppt}$	Variable

in Appendix B includes the names, symbols, nominal values (if not randomly chose), and units of measurement for all the physical parameters. These include independent physical constants, independent experimental parameters, fitting parameters, dependent parameters, and the outputs. Scaling values of $a_1=10$ and $a_2=1$ have been chosen empirically for the sigmoid functions in Equations (2) and (6), respectively.

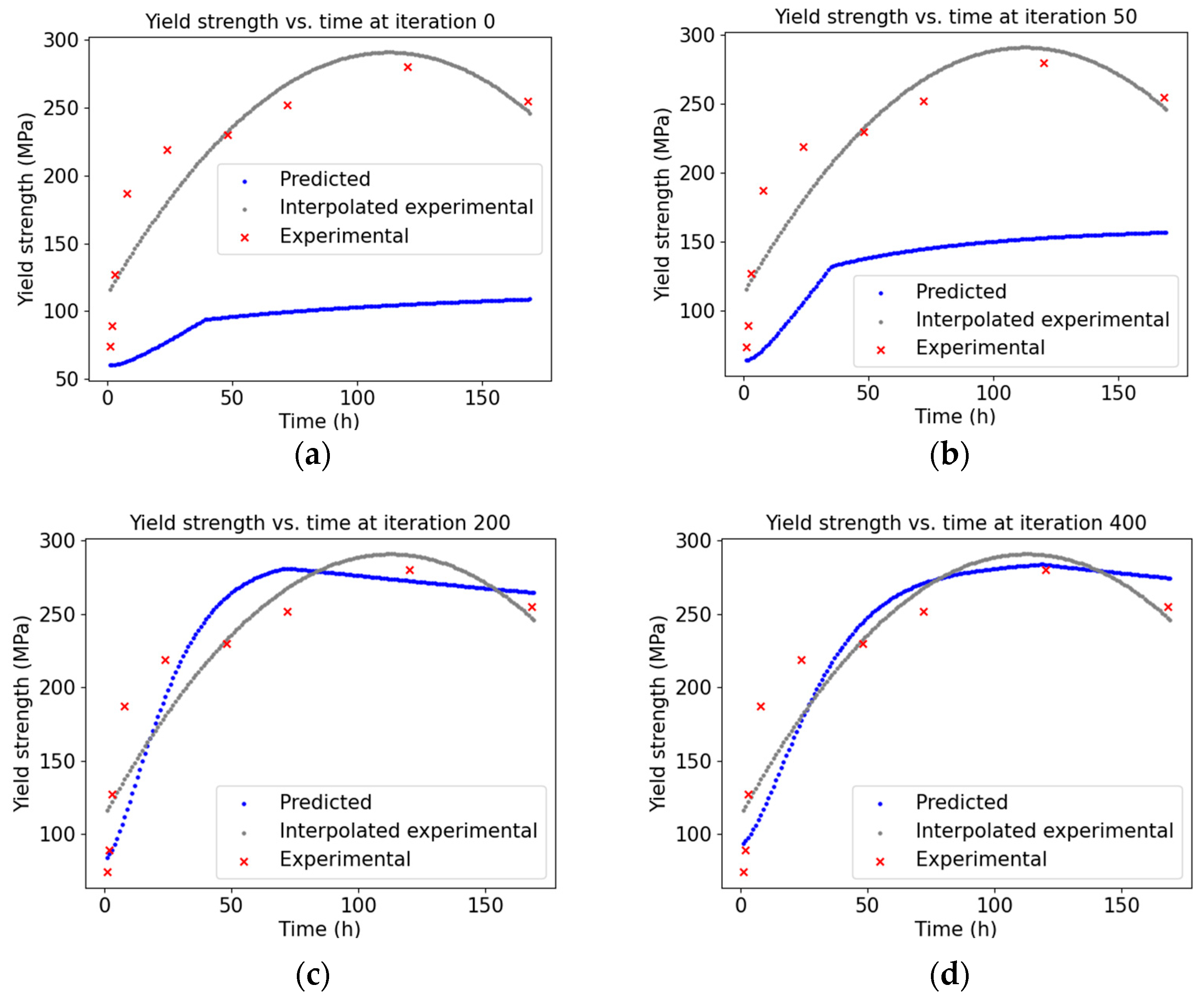
The convergence of the predictions to the experimental data is plotted in Figure 3 for four iterations: namely, iterations of $0$ (upon initialisation), $50, 200,$ and $400$ to reach a function tolerance of $1\times {10}^{-6}$ in the normalised YS predictions and training data. The time step of 0 indicates the YS curve is derived from the initialisation values without any prior optimisation attempts. The interpolated data is generated with the polyfit method of NumPy (version 1.26.0) to fit the scarce experimental data to a polynomial of degree two. The time axis of the interpolated data matches the time axis of the KWN model’s prediction. In our work, a 1-h time resolution has been chosen as a compromise between the computational cost and the required accuracy to cover the domain of the training data. It is worth noting that the interpolation facilitates the model to reach a compromise between the physics-based constraints and the experimental data. The moving breakpoint observed in the predicted YS curves reflects the growth of the precipitate size class over time. As the particles grow and exceed the critical radius, the model transitions from the strong (shearable) to the weak (non-shearable) strengthening mechanisms. The full gradient-based training process is shown in GIF S1 in the Supplementary Material for all the iterations.

The training process of the trainable coefficients $P_i$ is shown in Figure 4. They exhibit convergence and progressively smaller loss gradients in Figure 4a and Figure 4b, respectively. For a clearer visualisation of the changes, a stopping criterion of 300 iterations was used, in this case as iterations $[300-400]$ do not show significant gradients.

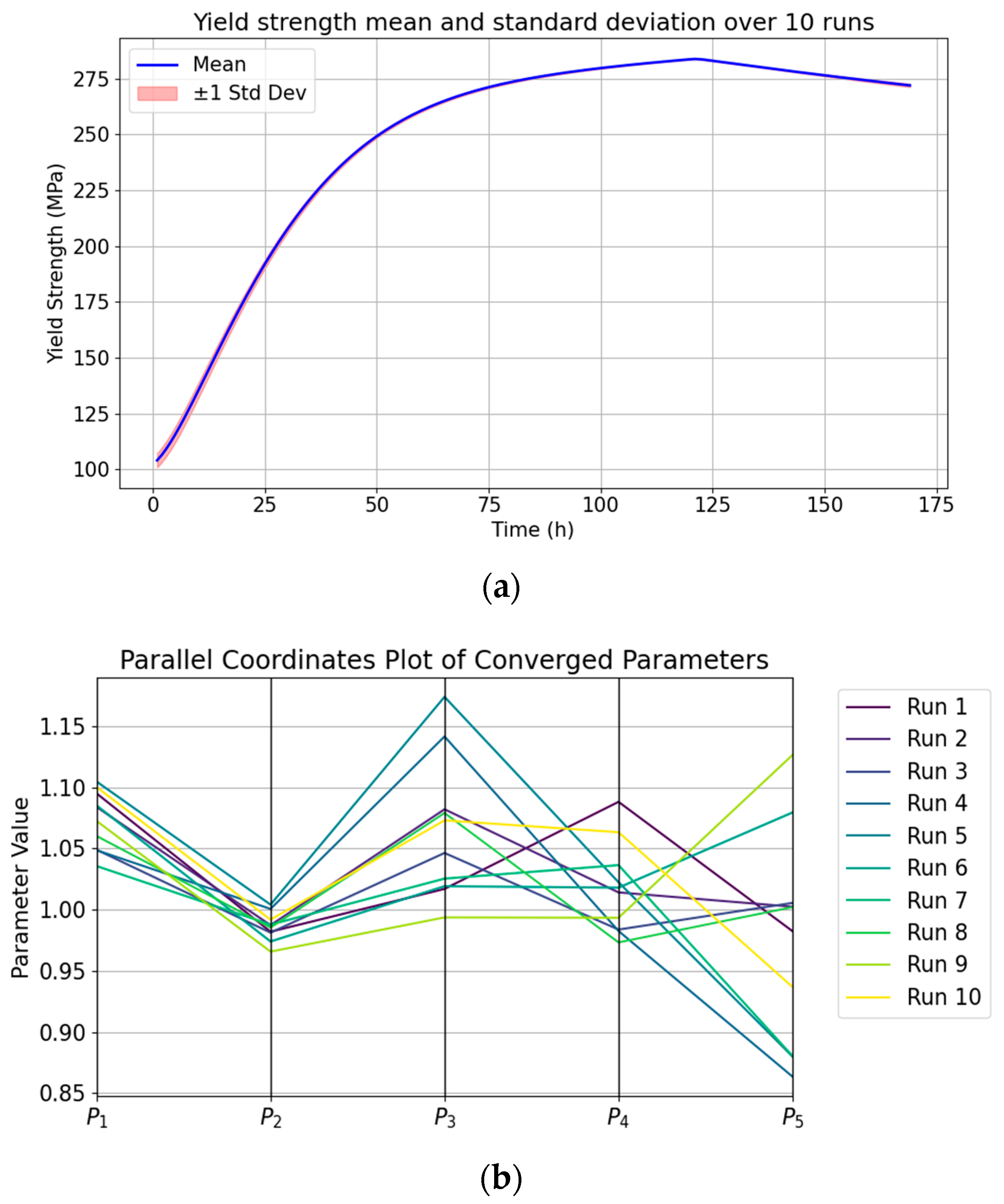
In Figure 5, the collective results of 10 Monter Carlo simulations are plotted. The YS curves in Figure 5a exhibit close agreement across all trials, ranging from 104.0 ± 3.0 MPa in the under-aged to 279.2 ± 0.3 MPa in the peak-aged and to 271.9 ± 0.8 MPa in the over-aged conditions. The relatively larger uncertainty observed in the under-aged regime can be attributed to the fact that the KWN model provides its most accurate description near the peak-aged conditions, where β″ precipitates dominate the microstructure. Although the predicted YS curves show high consistency across the Monte Carlo trials, the corresponding fitted coefficients exhibit substantial variability (Figure 5b). This non-uniqueness reflects the ill-posed nature of the inverse problem in fitting high-dimensional physics-based models: multiple parameter sets can produce similar outcomes. In practice, this means, that although the exact parameter values may not be uniquely identifiable, the model still captures the underlying physical mechanisms governing precipitation hardening. The variance of convergence for the trainable coefficients is $\left\{Var\right(P_1)=5.82 \times {10}^{-4}$, $Var\left(P_2\right)= 1.31 \times {10}^{-4}$, $Var\left(P_3\right)=3.30 \times {10}^{-3}$, $Var\left(P_4\right)=1.38 \times {10}^{-3}$, $Var\left(P_5\right)= 7.59 \times {10}^{-3}\}$.

Finally, we present a comparative benchmark between the ADAM (gradient-based), Powell (gradient-free), and Nelder–Mead (gradient-free) optimisers, using a common function tolerance of 0.001 (

Table 2. Benchmark comparison of the ADAM (gradient-based), Powell (gradient-free), and Nelder–Mead (gradient-free) optimisers applied to the simplified KWN model with a common function tolerance of 0.001. Metrics include convergence time, number of function evaluations, invalid function evaluations per trial, and computational complexity across 10 Monte Carlo runs. The results highlight the computational cost and instability risks associated with the Powell and Nelder–Mead optimisers.

Metric	ADAM	Powell	Nelder–Mead
Time (minutes)	$17.9\pm 2.1$	$57\pm 12$	$45\pm 16$
Number of function evaluations	$139\pm 17$	$886\pm 190$	$620 \pm 170$
Invalid function evaluations per trial	None	$40\pm 38$	$3.2 \pm 1.2$
Computational complexity	$O\left(N\right)$	$O\left(N^2\right)$	$O\left(N\right)$

). As shown in Row 1, the ADAM optimiser demonstrates a faster convergence compared to the gradient-free optimisers thanks to the gradient-informed parameter tuning. Row 2 solidifies this argument further, showing that the number of function evaluations for the ADAM optimiser is significantly smaller than that of the Powell and the Nelder–Mead optimisers. This was expected for gradient-free optimisations due to the internal line searches and simplex operations that take a lot of time and computation. Row 3 highlights another critical drawback in gradient-free optimisation, which is the number of invalid function evaluations. Especially, the Powell optimiser tends to propose more unphysical parameter values. These values cause the KWN model to either produce unrealistic outputs (e.g., negative radius) or fail entirely (e.g., by returning NaN values), which halts the optimisation process and contributes to a high count of invalid function evaluations. It is worth noting that, without imposing bounds on the search space, none of the optimisation trials for the Powell optimiser would achieve meaningful convergence. The invalid evaluations for the Nelder–Mead optimiser are much better but not fully eliminated, highlighting the necessity of expert intervention when using gradient-free calibration methods. Finally, in row 4, the ADAM and Nelder–Mead optimisers have similar orders of computational complexity. However, the latter’s performance degrades with the increasing the number of trainable coefficients N, proving a lack of scalability to a full KWN model.

4. Discussion

In this work, we demonstrated that integrating the gradient-based ADAM optimiser into a simplified KWN model enables more efficient parameter calibration than conventional gradient-free methods. The ADAM algorithm produced a faster convergence of yield strength predictions toward the experimental data, with reduced simulation time, fewer function evaluations, and fewer invalid optimisation attempts. This highlights the potential of gradient-based optimisation for automatic calibration in a full-scale KWN model.

The recent literature on physics-based precipitation-hardening models has increasingly highlighted the challenge of parameter calibration. Traditional approaches often rely on manual tuning, which limits reproducibility and scalability, especially in advanced models with many free parameters. More recently, heuristic optimisation methods, such as the Powell and Nelder–Mead methods, have been applied, but their fundamental limitation is the absence of gradient information. These methods perform a blind search of the parameter space, requiring computationally expensive trial-and-error line searches. By contrast, the gradient-based ADAM optimiser relies on automatic differentiation, ensuring that each optimisation step moves the model closer to experimental data in a more systematic and informed manner.

The present work deliberately employed a simplified KWN framework with one size class, one nucleation event, and one precipitate type. This simplification was necessary because introducing gradient-based optimisation requires the underlying model equations to be made continuous and differentiable. Each conditional branch and if–else logic in the KWN framework had to be carefully examined and modified to avoid discontinuities in the predictions. As such, this study did not attempt detailed physics-based modelling or new experimental measurements. Similarly, microstructural complexities, such as plastic deformation, grain boundaries, heterogeneous microstructures, and thermomechanical histories, were excluded. Incorporating these features would multiply the number of fitting parameters from five to potentially hundreds, which would distract from the core aim of addressing the calibration bottleneck that persists in precipitation models regardless of size or accuracy.

As another simplification, only a single case study was explored, using yield-strength data from a 6xxx series alloy reported in the literature. While this does not reflect the full diversity of alloy compositions and processing routes, it served as a representative example of the calibration challenge in solidification problems.

Overall, the findings suggest that automatic, yet reliable, parameter calibration is crucial for advancing physics-based models of precipitation hardening. By showing that gradient-based optimisation can outperform gradient-free counterparts, this work establishes a framework that may be extended to more complex models and eventually integrated into digital alloy design workflows.

A core part of this framework is making the equations continuous. This was achieved by introducing differentiable approximations, such as a smoothed sigmoid function to handle conditional logic. In addition, instead of directly optimising the free parameters themselves, which often take on extremely large or small values, we introduced trainable coefficients that scale their functional forms. This approach offers two key advantages: (1) it normalises the optimisation landscape by allowing the optimiser to work with coefficients close to unity, thereby improving numerical stability; and (2) it enables the calibration of parameter groups rather than individual parameter instances, since many free parameters appear multiple times across different parts of the model. Optimising their scaling coefficients ensures that the interdependencies among these repeated occurrences are respected. Due to varying sensitivities, the learning rates for each coefficient were empirically chosen to balance convergence speed and model fidelity.

As this is the first step in careful model calibration in the vast world of precipitation hardening, the following provides some ideas for future work:

• Expanding the KWN model: Applying gradient-based calibration to the full KWN model with multiple nucleation events and several size classes, especially in case studies where a finer time resolution on the ageing process is required and all size classes contribute significantly to the ageing dynamics. Additionally, incorporating other precipitate types, extending the applicable temperature range, and including a broader spectrum of alloy compositions would increase the model’s generalisability and industrial relevance. The current framework is restricted to modelling precipitation hardening during ageing heat treatment. Extension to components that undergo prior processing operations will require coupling with additional modules to capture the effects of plastic deformation, heterogeneous microstructures, and thermomechanical histories. This remains an important direction for future work.
• Some key considerations for advancing towards a more detailed physics-based model include (a) a sensitivity analysis to identify which model parameters have the most significant impact on the predictions, so that calibration efforts can prioritise those parameters, (b) dimension reduction techniques to reduce the search space and make the optimisation more tractable when dealing with a very high number of parameters, and (c) studying parameter interdependencies to understand how fitting parameters influence each other and the outputs, which can help in simplifying the model or decoupling certain effects, thereby reducing degrees of freedom without losing predictive power.
• Multi-objective optimisation: in this work, the loss function is based on YS data; however, the intermediate outputs of the precipitation hardening, such as MPR, TVF, and TND, is also experimentally measurable and can be used as training data for the model. This leads to a multi-objective problem which requires a balance between several loss function terms.