Austenite Grain Growth Behavior and Dynamic Model of ADB790E Hydropower Steel

Abstract

The growth behavior of austenite grains in ADB790E hydropower steel under the synergistic effects of heating temperature and holding time was studied using in situ quenching and an in situ high-temperature confocal laser scanning microscope (HT-CLSM) system. The experimental results indicate that the size of the austenite grains exhibits a significant coarsening trend as the heating temperature increases and the holding time extends. Based on the experimental data, the Beck’s model and Sellars’ model for austenite grain growth were constructed and compared and analyzed. The predicted grain size values obtained by the models have a strong correlation with the experimental measured values. To verify the accuracy of the model, the predicted values of the model were compared with the in situ observations of HT-CLSM. The results were highly consistent, effectively revealing the growth law of austenite grains of this steel grade during the thermal cycling process.

1. Introduction

Tremendous changes have taken place in the global energy structure, and fossil fuels are being surpassed by investments in clean energy. Compared with other power generation methods, hydropower has many advantages, such as cleanness and low carbon, environmental sustainability, high conversion rate, low operation cost, and resource localization. Compared with thermal power, hydropower is cleaner, and emissions of waste gas, waste water and waste residue are reduced; compared with wind and solar power, hydropower is more stable [1]; in addition, hydropower is convenient for peak and frequency regulation, and it is difficult to replace at present. With the large-scale development of hydropower resources, the construction of large and even giant hydropower stations has become an inevitable trend [2,3]. The large-scale development of hydropower stations requires higher water heads and greater capacity, which makes the steel used in hydropower stations have to withstand greater pressure. With the trend of enlargement of hydropower station units (high water head/large capacity), steel structures such as penstocks need to bear higher loads, so the materials are required to have high strength, excellent toughness, and good weldability [4,5,6]. Whether for the needs of structural safety design or for reducing steel consumption and engineering costs, an urgent demand has been put forward for the improvement of the strength grade of hydropower steel.

Hydropower steel is classified into three categories according to strength grade: 500 MPa, 600 MPa, and 800 MPa [7]. Among them, the 500 MPa grade mainly includes 16MnR steel and ASTM A547CL1 normalized steel [8]; the 600 MPa grade covers the HT60 series [9] and the HT60CF series [10,11]; the 800 MPa grade includes ASTM, WEL-TEN780, WSD690E, and SG780CFE steels. According to the current development status of hydropower engineering material technology, 800 MPa grade hydropower steel plates have become the standard materials for large hydropower stations. Although 1000 MPa grade hydropower steel with large thickness has not been widely promoted, it has been put into use in ultra-high water head and extra-large capacity power stations [12].

Austenite grain size or austenite grain growth is one of the most important microstructural parameters in iron and steel production and processing. Whether the heating system is reasonable directly affects the austenite grain size, and the austenite grain size determines various properties of the steel, which is a core link in optimizing the mechanical properties of materials, process design, and service reliability. These properties include strength, creep resistance, fatigue behavior, as well as electrical and magnetic properties. Therefore, research on austenite grain size has long been the focus of many research projects [13,14,15]. Grain coarsening temperature is a key thermodynamic parameter in materials science, which refers to the critical temperature at which the second-phase particles in the austenite structure lose their pinning ability, resulting in explosive growth of grain size. It is determined by the thermal stability of the second-phase particles. The key factor affecting the grain coarsening temperature is the pinning effect of second-phase particles on grain boundaries [16,17]. The second-phase particles mainly refer to carbides and nitrides formed by various microalloying elements in the composition of the experimental steel [18]. Trace elements B, Mo, Cr, and Ni are all used to improve the hardenability of the steel; high-temperature hot brittleness may be caused by Cu during rolling. Grain growth is weakly inhibited by these elements. However, N is competed for by Ti, Nb, and Al to form more stable nitrides. Despite higher Als content, Ti nitrides possess stronger binding force, making TiN—not AlN—the actual contributor to pinning. The pinning effect is controlled by TiN. Since the pinning effect of second-phase particles has been verified in multiple studies, it will not be studied in this paper.

Except for the pinning effect of the second-phase particles, parameters such as austenitizing temperature and holding time have a significant impact on the austenite grain size. The austenite structure and precipitation strengthening effect can be balanced by regulating hot working process parameters, and reducing the heating temperature and shortening the holding time are beneficial to obtaining uniform and fine austenite grains. Fine grain strengthening is an important method to improve the strength and toughness of steel [19]. Increasing the temperature and prolonging the holding time can promote the full solid solution of microalloying elements, which lays a foundation for strain-induced precipitation strengthening in subsequent rolling, but higher heating temperature and longer holding time will lead to coarsening of austenite grains, thus reducing the strength and toughness of the steel [20].

The growth behavior of austenite grains is widely applied to various materials. The austenite grain growth behavior of 60Mn3Al3Ni2CrVNb quenched and tempered low-density steel has been studied by Guo et al. [21]. Various characterization methods have been used to discuss the state of a series of precipitated structures such as niobium carbide in the metal at different heating temperatures, and the law of precipitated phases affecting the austenite grain size has been summarized according to different states. The austenite grain growth behavior of Nb-Ti high-strength IF steel has been studied by Zhang et al. [22]. Various characterization methods have been used to discuss the influence law of solid solution second-phase particles on the austenite grain size of the experimental steel under different heating temperatures and holding times. The grain growth behavior of SA508-Ⅲ steel has been studied by Dong et al. [23]. The influence of heating rate on grain growth has been discussed and analyzed, and the phenomena of uniform grain growth and abnormal grain growth have been compared and analyzed, respectively. The grain growth law of AFA steel during normalizing and annealing has been studied by Gao et al. [24], and the isothermal growth kinetic model of grains has been improved. The variation law of austenite grain size of niobium-containing Fe-Mn-Al-C low-density steel with heating temperature and holding time has been studied by Huo et al. [25]. The grain growth behaviors of steels with different Nb contents during heating and holding under different austenitizing and aging conditions are different. At present, many scholars have conducted various studies on the growth behavior of austenite grains through different methods, but relevant research on hydropower steel has not been carried out.

While numerous studies have investigated austenite grain growth behavior using various methodologies, a significant research gap remains regarding the specific hydroelectric steel ADB790E—particularly in combining dynamic in situ observation with the systematic development and validation of multiple grain growth models. The most notable novelty of this study lies in its methodological breakthrough. In contrast to the majority of studies that rely on post-quenching static and ex situ observations, we present—for the first time—an in situ, dynamic, and continuous observation of the austenite grain growth process in ADB790E hydroelectric steel using high-temperature confocal laser scanning microscopy (HT-CLSM). The HT-CLSM system consists of two core components: a laser scanning confocal microscope and a high-temperature chamber with infrared heating [26,27]. This technique offers several key advantages: dynamic real-time capability, high spatial resolution, surface sensitivity, and precise temperature control. These features allow HT-CLSM to effectively compensate for the limitations of conventional room-temperature metallography. It enables direct observation of phase transformations in steel during high-temperature heating, while capturing microstructural evolution—such as grain growth, phase transitions, and dissolution processes—in real time [28].

We selected ADB790E high-strength hydroelectric steel as the research subject due to its outstanding and distinctive features in three key aspects: chemical composition, mechanical properties, and industrial applicability. In terms of chemical characteristics, its carbon content and Nb-Ti complex microalloying design allow it to achieve high strength through quenching and tempering, while simultaneously leveraging highly stable TiN particles to effectively inhibit high-temperature grain coarsement [16,18]. This distinguishes it markedly from many conventional low-alloy steels. Regarding mechanical properties, its core value lies in the combination of ultra-high strength (800 MPa grade) and exceptional low-temperature toughness, along with the ability to maintain performance uniformity across ultra-heavy sections (>100 mm) [5,6]. These attributes meet the rigorous demands for the trend toward larger scale and lighter weight in hydropower equipment. Compared with existing industrial steels, ADB790E demonstrates significant advantages in low-temperature toughness and microstructure uniformity of ultra-thick products while ensuring the same strength. ADB790E is an irreplaceable critical material for manufacturing core load-bearing components in large hydropower stations.

The variation of austenite grain size with heating temperature and holding time in ADB790E hydropower steel has been studied systematically. Heating temperature and holding time will affect the growth of austenite grains. Generally, the size of austenite grains has an exponential relationship with heating temperature and a parabolic relationship with holding time. And based on relevant literature, a simple analysis of the influence of second-phase particles on grains is conducted. The austenite grain growth kinetics model of this material was established through linear regression in order to clarify the growth law of austenite grains of ADB790E hydropower steel during the heating process. By observing the grain size changes of the experimental steel during heating with HT-CLSM and comparing them with the predicted values of the established kinetics model, the accuracy of the model can be verified. In terms of model selection, a phenomenologically based approach was adopted to more effectively establish correlations between processing parameters and microstructural characteristics. It enables precise identification of the critical temperature at which significant grain coarsening begins, thereby defining an optimal processing window and providing a theoretical basis for establishing hot-working parameters and controlling grain size in forgings of this material [29].

2. Materials and Methods

2.1. Experimental Materials and Composition

The experimental material is ADB790E hydropower steel. The chemical composition of the experimental steel was determined using an X-ray fluorescence (XRF) spectrometer (model: Bruker S8 TIGER; manufacturer: Bruker, Karlsruhe, Germany). The detailed results are provided in

Table 1. Chemical composition of ADB790E.

Chemical Composition	Content (%)	Chemical Composition	Content (%)
C	0.0745	Cr	0.4736
Si	0.0493	Cu	0.2628
Mn	1.2865	Mo	0.3709
P	0.00783	Als	0.0359
S	0.00161	N	0.003
Nb	0.0042	B	0.00076
V	0.043	Ceq	0.49319
Ti	0.01	Pcm	0.49319
Ni	0.6722

.

2.2. Experimental Scheme

(1)

The experimental steel is cut into rectangular samples of 5 × 10 × 20 mm (length × width × height) by wire cutting. The surface of the sample is cleaned by an ultrasonic cleaner, and basic treatment is carried out with 400-mesh and 600-mesh sandpaper to eliminate the influence of an oxide layer and stains on the surface of the sample during heat treatment.

(2)

Quenching heat treatment. To explore the influence of different heating temperatures on the growth of austenite grains, the samples are heated to 850 °C, 900 °C, 950 °C, 1000 °C, 1050 °C, 1100 °C, 1150 °C, 1200 °C, and 1250 °C, respectively, in a box-type resistance furnace at 5 °C/min. After the furnace temperature rises back to the heating temperature, timing and holding are started, and the samples are taken out immediately after holding for 20 min and put into cold water for quenching; to explore the influence of different holding times on the growth of austenite grains, the experimental steel is put into a box-type resistance furnace and heated to 1150 °C. After the furnace temperature rises back to 1150 °C, timing and holding are started, and the samples are taken out immediately after holding for 20 min, 40 min, and 60 min to complete austenitization. Subsequently, water quenching was applied to preserve the high-temperature austenite microstructure for metallographic examination. The purpose of selecting water quenching was to accurately characterize the prior austenite grain size after isothermal holding. During cooling, austenite undergoes phase transformation; hence, a sufficiently high cooling rate is essential to suppress any phase transformation and retain the austenite grain boundaries at room temperature. Compared to oil quenching or air cooling, water quenching provides a significantly faster cooling rate, which is critical for obtaining clearly discernible prior austenite grain boundaries and ensuring the accuracy of measurement results. Slower cooling methods may initiate phase transformation, thereby obscuring or obliterating the original austenite boundaries.

It should be noted that the selected holding times (20–60 min) were not intended to simulate the short interpass intervals during hot rolling but were strictly based on the actual industrial heat treatment cycles—such as normalizing or austenitizing prior to quenching and tempering—applied to heavy-gauge hydroelectric steel plates. The objective of hot rolling is to refine the grain structure through deformation and recrystallization, with interpass times typically on the order of seconds to prevent static recrystallization and grain growth. In contrast, the heat treatment processes simulated in this study aim to achieve complete phase transformation, dissolution of alloying elements, and microstructural homogenization throughout the workpiece, which necessitates significantly longer holding times.

(3)

Corrosion of austenite grains. There will be a layer of scale on the surface of the quenched steel, which needs to be treated before the 10 × 20 mm surface of the experimental steel is ground and polished to make metallographic samples. Austenite metallographic etchant is prepared with 1 g picric acid, 50 mL distilled water, and 2.5 g Haier shampoo, and the polished surface of the sample is placed upward. To corrode clear austenite grain boundaries, the sample should be heated in a constant temperature water bath furnace to 60 °C for 4 min of corrosion. During this period, the polished surface is wiped with absorbent cotton or the sample is stirred, and care should be taken not to scratch the surface. After 4 min, the sample is taken out and put into alcohol for soaking and cleaning, then taken out, rinsed with absolute ethanol, and dried on the surface.

(4)

Observation and analysis of metallographic microscope. The microstructure of the experimental steel is observed with a Keyence VHX-5000 ultra-depth 3D digital microscope (Keyence Corporation, Osaka, Japan) to clarify the growth of austenite grains, and the average size of austenite grains is calculated by the intercept method. Beck’s model and Sellars’ model were used to establish the austenite grain variable temperature growth model and the austenite grain isothermal growth model, and the influence laws of heating temperature and holding time on the growth of austenite grains are explored.

3. Results

3.1. Influence of Heating Temperature on Austenite Grain Growth Behavior

When formulating the heating system, two factors, heating temperature and holding time, should be taken into account. When the heating temperature rises and the holding time is extended, the strength of the product can be enhanced. However, if the heating temperature is too high and the holding time is too long, reaching the grain coarsening temperature, it will cause abnormal growth of austenite grains, affecting the strength and toughness of the product. Therefore, reasonable control of temperature and time is the key to formulating the subsequent thermal processing technology.

Figure 1 shows the austenite grain morphology of the experimental steel after being heated at temperatures of 850 °C, 900 °C, 950 °C, 1000 °C, 1050 °C, 1100 °C, 1150 °C, 1200 °C, and 1250 °C for 20 min.

At 850 to 900 °C, it has not yet fully recrystallized and has not formed all austenite. Austenite grains tend to grow at 950 °C to 1100 °C, but slowly. Obvious austenite grains appeared in the experimental steel at 950 °C. When the heating temperature is 950 °C, the average grain size is approximately 24.6 μm. Among them, the grains with a size of approximately 12–22 μm account for 35%, and the grains with a size of approximately 35–48 μm account for 64%. At a heating temperature of 1000 °C, the average grain size is approximately 25.4 μm, among which the grains with a size of about 14 to 27 μm account for 23%, and those with a size of about 38 to 57 μm account for 75%. The size of austenite grains at 950 and 1000 °C varies and is unevenly distributed, which is caused by the uneven distribution of second-phase particles. When the heating temperatures are 1050 °C and 1100 °C, the average grain size is approximately 26.4 μm and 26.8 μm, respectively, and the grain size is relatively uniform at this time. When the heating temperature is between 1150 and 1250 °C, some grains grow abnormally and are unevenly distributed. The average grain size at 1150 °C is approximately 30.2 μm, at 1200 °C it is about 31.1 μm, and at 1250 °C it is approximately 31.9 μm. Therefore, it can be clearly determined that the grain coarsening temperature of the experimental steel is approximately 1150 °C. The determination of grain coarsening temperature can provide a certain reference for subsequent hot working processes and avoid microstructure defects caused by grain coarsening.

It can be seen that, in this experiment, when the holding time is fixed, as the heating temperature rises, the temperature affects the thermal activation of grain boundaries, and the activity rate of metal atoms accelerates, thereby promoting the migration of grain boundaries. As the migration rate of grain boundaries increases, the grain size becomes significantly larger. When the temperature is relatively low, a large amount of TiN remains undissolved and is evenly distributed at the grain boundaries, thus having a strong binding effect. At this time, the austenite grains are fine. However, when the temperature rises above the grain coarsening temperature, the pinning effect is less than the phase transformation driving force, and local grain coarsening, that is, abnormal growth, will occur, as shown in Figure 2.

3.2. Influence of Holding Time on Austenite Grain Growth Behavior

The determination of grain coarsening time can provide a certain reference for subsequent thermal working processes. A reasonable holding time can increase the solid solubility of the second phase particles, give full play to the precipitation strengthening effect of the second phase particles, and improve the final performance of the product.

Figure 3 shows the austenite grain morphology of the experimental steel at a heating temperature of 1150 °C for 20 min, 40 min, and 60 min, respectively. When the heating temperature is the same, it can be found that the grain size of the experimental steel increases significantly with the increase in the holding time. When the holding time is 20 min, the average grain size is approximately 30 μm. The average grain size at 40 min was approximately 32 μm. The grain size was approximately 41 μm at 60 min. The growth rate of grain size is relatively slow within 20 to 40 min, which is due to the pinning effect of the second-phase particles. Within 40 to 60 min, some second-phase particles dissolve, and the grains start to coarsen slightly, with the grain size gradually increasing.

According to the results of this test, the heating temperature should be controlled within 1050–1100 °C, and the holding time should be controlled within 20 to 40 min.

3.3. Comparison of Austenite Grain Growth Models

3.3.1. Beck’s Model for Austenite Grain Growth

The austenite grain growth model is a method to predict the austenite grain size under different temperatures and holding times [30,31]. For the experimental steel, the austenite grain size is critically influenced by the heating temperature and holding time in the processing system. Beck’s model describes the cumulative growth of grain size over time.

• Variable-temperature growth model

The common form of Beck’s equation is as follows:

$${\mathrm{D}}_{\mathrm{A}}=\mathrm{K}{\mathrm{t}}^{\mathrm{n}}$$

(1)

In this equation:

D_A—average austenite grain size, μm;

n—grain growth exponent;

t—holding time, s;

K—grain growth rate constant. This is a parameter strongly dependent on temperature.

The value of K follows the Arrhenius equation and exhibits an exponential relationship with temperature:

$$\mathrm{K}={\mathrm{K}}_0\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\mathrm{Q}}{\mathrm{R}\mathrm{T}}}\right)$$

(2)

In this equation:

K₀—Pre-exponential factor, a material constant;

Q—activation energy for austenite grain growth, J·mol⁻¹;

R—molar gas constant, 8.314 J·(mol·K)⁻¹;

T—heating peak temperature, K.

Substituting Equation (2) into Equation (1), we obtain:

$${\mathrm{D}}_{\mathrm{A}}={\mathrm{K}}_0{\mathrm{t}}^{\mathrm{n}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\mathrm{Q}}{\mathrm{R}\mathrm{T}}}\right)$$

(3)

Furthermore, when the holding time is constant, the term tⁿ in the equation is also a constant. Therefore, Beck’s equation for the variable-temperature growth model can be transformed into:

$${\mathrm{D}}_{\mathrm{A}}=\mathrm{A}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\mathrm{Q}}{\mathrm{R}\mathrm{T}}}\right)$$

(4)

In this equation:

A—constant determined by grain boundary diffusion coefficient and isothermal time factor.

Take the logarithm on both sides of Equation (4):

$$\mathrm{l}\mathrm{n}{\mathrm{D}}_{\mathrm{A}}=\mathrm{l}\mathrm{n}\mathrm{A}-{\displaystyle \frac{\mathrm{Q}}{1000\mathrm{R}}}{\displaystyle \frac{1000}{\mathrm{T}}}$$

(5)

The average size of austenite grains of the experimental steel at the same holding time and different heating temperatures is substituted into Equation (5). According to linear regression analysis, the equation of lnD-1000/T is made, where the slope is −Q/1000 R and the intercept is lnA. Q = 14.421 kJ·mol⁻¹ and A = 99.47 are obtained. The fitting equation is lnD_A = 1734.5/T + 4.5999, and the grain growth equation is D_A = 99.47 exp(−14,421/RT) with a regression accuracy of 0.9255.

The fitting analysis of the variable temperature equation is shown in Figure 4.

2.

Isothermal growth model

At isothermal temperature, the relationship between the average grain size of austenite and holding time can be expressed by Beck’s formula, and it is considered that the grain growth rate remains unchanged during the entire isothermal growth process, as shown in Equation (1).

Take the logarithm on both sides of Equation (1):

$$\mathrm{l}\mathrm{n}{\mathrm{D}}_{\mathrm{A}}=\mathrm{l}\mathrm{n}\mathrm{K}+\mathrm{n}\mathrm{l}\mathrm{n}\mathrm{t}$$

(6)

The average size of austenite grains of the experimental steel at 1150 °C with different holding times is substituted into Equation (6). According to linear analysis, the equation of lnD_A-lnt is made, where the slope is n and the intercept is lnK. n = 0.2552 and K = 4.83 are obtained, the fitting linear equation is lnD_A = 0.2552 lnt + 1.5749, and the fitting Beck’s equation is D_A = 4.83 t^0.2552 with a regression accuracy of 0.9754.

The fitting analysis of the isothermal equation is shown in Figure 5.

The accuracy of the experimental steel grain growth model is analyzed, as shown in Figure 6. In Figure 6, the austenite growth kinetic curves of the experimental steel are shown, affected by heating temperature and holding time. The measured sizes of austenite grains are presented as points, the theoretical sizes calculated by the formula are represented by fitting lines, and the growth rate of austenite grains is reflected in the steepness of the lines. It can be seen from the figure that the calculated values are basically consistent with the measured values. By comparing the two figures, it is found that the heating temperature has a greater influence on the austenite grains of ADB790E hydropower steel than the holding time.

3.3.2. Sellars’ Model for Austenite Grain Growth

The growth size of austenite grains under Sellars’ model must take into account the influence of heating temperature and holding time simultaneously [32]. Its mathematical formulation exhibits a high sensitivity to variations in temperature, as shown in Equation (7).

$${\mathrm{D}}^{\mathrm{n}}-{\mathrm{D}}_0^{\mathrm{n}}=\mathrm{A}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\mathrm{Q}}{\mathrm{R}\mathrm{T}}}\right)$$

(7)

In this equation:

t—insulation time, min;

D₀—initial average grain size, μm;

T—heat treatment temperature, K;

R—gas constant, 8.314 J·(mol·K)⁻¹;

Q—grain growth activation energy, J·mol⁻¹;

n, A—experimental constants.

To determine the model constants, take the logarithm of both sides of Equation (7) and simplify to obtain:

$$\ln \left({\mathrm{D}}^{\mathrm{n}}-{\mathrm{D}}_0^{\mathrm{n}}\right)=\mathrm{l}\mathrm{n}\mathrm{A}+\mathrm{l}\mathrm{n}\mathrm{t}-{\displaystyle \frac{\mathrm{Q}}{\mathrm{R}\mathrm{T}}}$$

(8)

Under high-temperature and prolonged holding conditions, the sensitivity to the initial grain size (D₀) is considerably low. In this study, the value of D₀ is significantly smaller than the average grain size (D) achieved after the designated holding time. Therefore, the influence of D₀ was justifiably neglected in the current model. Thus, we obtain Equation (9):

$$\ln \mathrm{D}={\displaystyle \frac{\mathrm{l}\mathrm{n}\mathrm{A}+\mathrm{l}\mathrm{n}\mathrm{t}}{n}}-{\displaystyle \frac{\mathrm{Q}}{\mathrm{n}\mathrm{R}}}{\displaystyle \frac{1}{\mathrm{T}}}$$

(9)

Based on linear analysis, the linear equation of lnD versus 1/T is derived, where the slope is −Q/nR and the intercept is (lnA + lnt)/n.

Through nonlinear regression analysis, the correlation coefficient obtained when the experimental steel achieves the best fit in the model is: n = 2.5, A = 4.9 × 10³; thus, Q = 36.052 kJ·mol⁻¹. Therefore, the mathematical model for grain growth in ADB790E hydropower steel is:

$${\mathrm{D}}^{2.5}-{\mathrm{D}}_0^{2.5}=4.9\times {10}^3\times \mathrm{t}\times \mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{\mathrm{36,052}}{\mathrm{R}\mathrm{T}}}\right]$$

(10)

An analysis of the accuracy of the experimental steel grain growth model is presented in Figure 7. The points in the figure represent the measured sizes of the austenite grains, while the fitted line represents the theoretical sizes calculated using the formula. As can be seen from the figure, the calculated values and measured values are in good agreement with each other as the heating temperature changes, with a regression accuracy of 0.933. However, as the holding time changes, the calculated values and measured values show significant discrepancies, with a regression accuracy of 0.8358.

3.4. Model Verification

3.4.1. In Situ Observation Experiment with High-Temperature Confocal Laser Scanning Microscope

The samples were heated from room temperature to the melting point by HT-CLSM, and the phase transformation process of the experimental steel was observed in situ at different temperatures to study the influence of heating temperature on the microstructure of ADB790E hydropower steel.

• Sample preparation. Since ordinary metallographic samples cannot meet the requirements of high-temperature in situ observation, special requirements are put forward for sample preparation. The sample is processed into Φ7 × 2.5 mm by wire cutting, and one side of the Φ7 mm experimental steel is ground with 400~1000-mesh sandpaper, then polished to a mirror surface with a polishing machine. But no etching is carried out. Chemical etching is not required for HT-CLSM research.
• High-temperature laser confocal experiment. The ground and polished experimental steel is put into an alumina ceramic crucible, the crucible is placed on a fixed plate connected with a thermocouple and put into the furnace of the high-temperature laser confocal microscope, and the furnace cover is closed. To prevent oxidation of the sample at high temperature which leads to experimental failure, vacuum pumping (3 min) and argon filling (3 min) are carried out, and the program can be input to heat the steel after 3 cycles. The setting logic of the temperature program should cover the research requirements and avoid equipment damage. The heating rate is 200 °C/min, the holding temperature is 1550 °C, the holding time is 5 min, and the cooling rate is 0.5 °C/s. The heating rate was set at 200 °C/min primarily to minimize selective surface evaporation of low-melting-point or high-vapor-pressure elements from the steel sample during extended exposure to high temperatures and high vacuum. Even with an inert gas atmosphere, prolonged experiments cannot fully prevent the release of trace impurity gases from internal furnace components such as the chamber walls and sample stage at elevated temperatures. Minute amounts of oxygen or water vapor are sufficient to cause slight surface oxidation, forming an oxide film that severely interferes with surface energy measurements and obscures genuine grain boundaries, thereby compromising in situ observations. Consequently, an excessively slow heating rate was not feasible in this study.

The surface morphology of the experimental sample at different heating temperatures can be obtained from the continuously taken micrographs, and it is stored as a video file to achieve the best observation effect. However, due to the serious influence of high-temperature radiation on imaging quality, attention should be paid to image processing.

HT-CLSM microstructural images of the experimental steel at 950 °C, 1000 °C, 1050 °C, 1100 °C, 1150 °C, and 1200 °C are presented in Figure 8. With the increase in temperature, the size of austenite grains gradually increases. From 950 °C to 1100 °C, the grains gradually increase, and at 1150 °C, some grains grow abnormally.

3.4.2. Model Verification

The microstructure of the experimental steel observed by HT-CLSM was analyzed, and the grain size was measured using the cross-section method.

Different heating temperatures were substituted into Beck’s model and Sellars’ model to calculate the corresponding average austenite grain sizes predicted by the models. The experimental grain sizes obtained from HT-CLSM observations were compared with the predicted values from the two models, yielding a correlation coefficient of 0.9283 with Beck’s model and 0.9284 with Sellars’ model. This indicates that the model-calculated values are in good agreement with the experimental values, as shown in Figure 9.

As shown in Figure 9, the trend of grain growth is generally consistent, meaning that the experimental values obtained using HT-CLSM are in good agreement with the predicted results from Beck’s model and Sellars’ model. However, there is some error at higher temperatures, primarily due to the abnormal growth of austenite grains, resulting in slight statistical errors in the measurement of austenite grain size. This has significant implications for understanding the grain growth patterns of austenite in ADB790E hydroelectric steel, controlling grain size, and optimizing the performance of the final product.

4. Conclusions

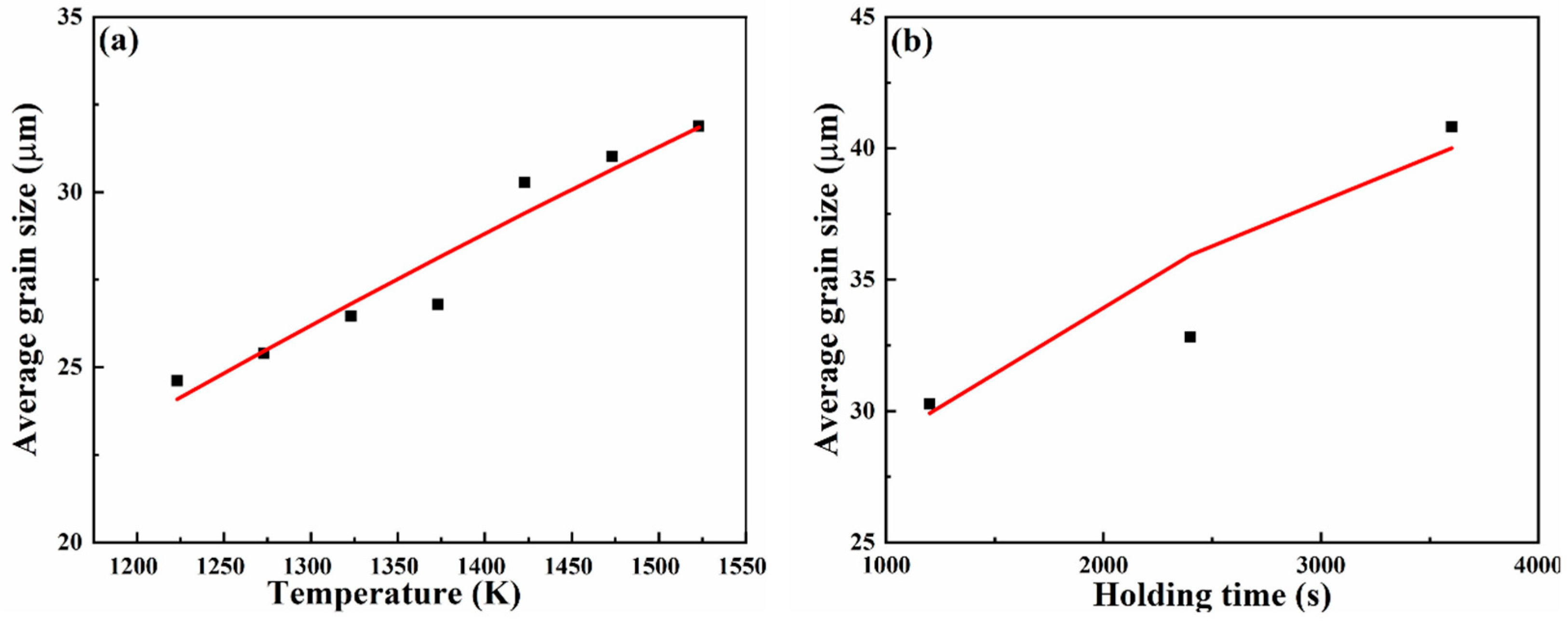
• When the holding time is constant, the average austenite grain size of ADB790E hydropower steel increases with the increase in heating temperature. It can be known from the experimental results that the growth rate of grain size below 1150 °C is less than that above 1150 °C. The grain coarsening temperature should be avoided when formulating hot working processes.
• When the heating temperature is constant, the average austenite grain size of ADB790E hydropower steel increases with the prolongation of holding time. The growth rate of grain size above 40 min of holding is much greater than that below 40 min of holding.
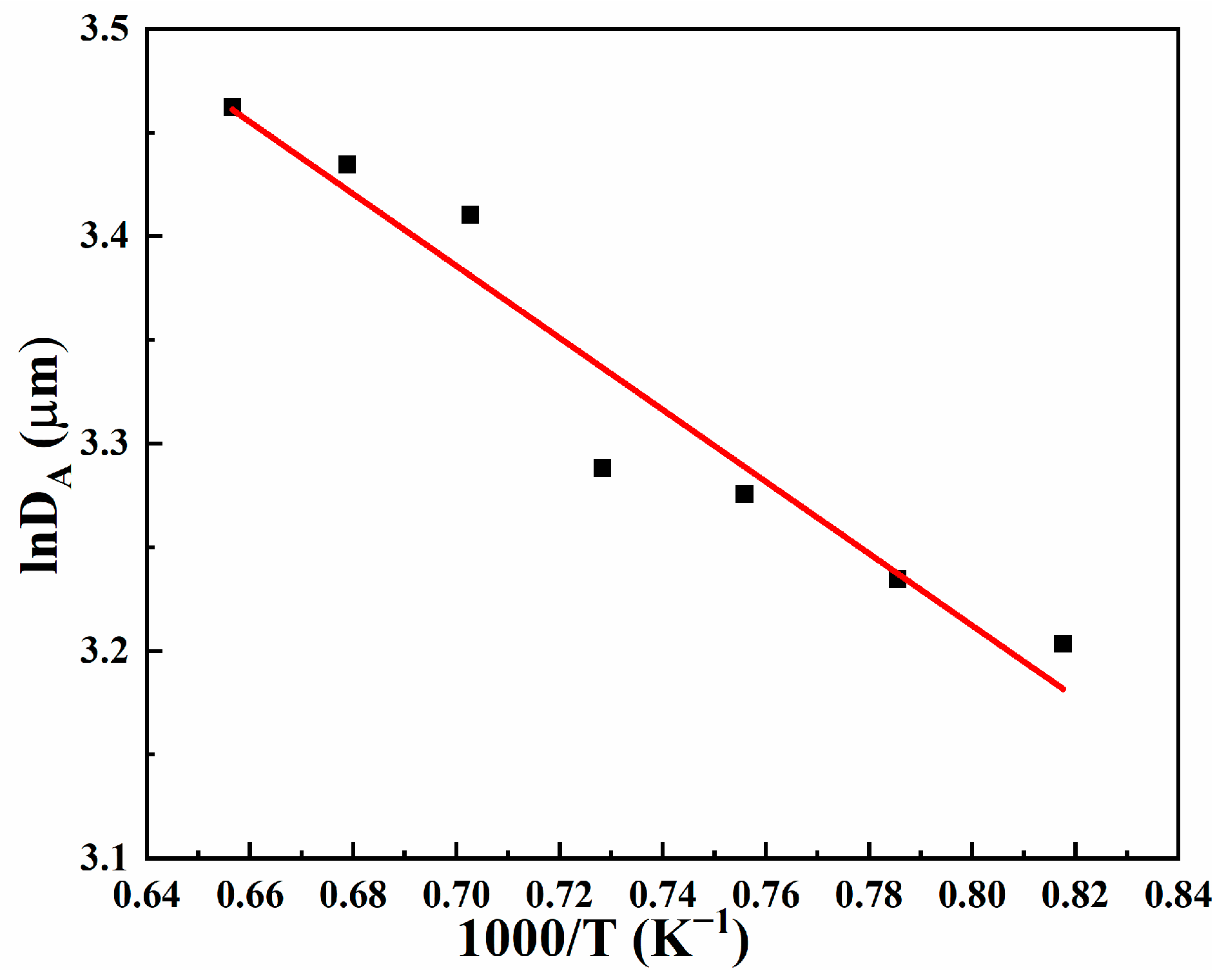
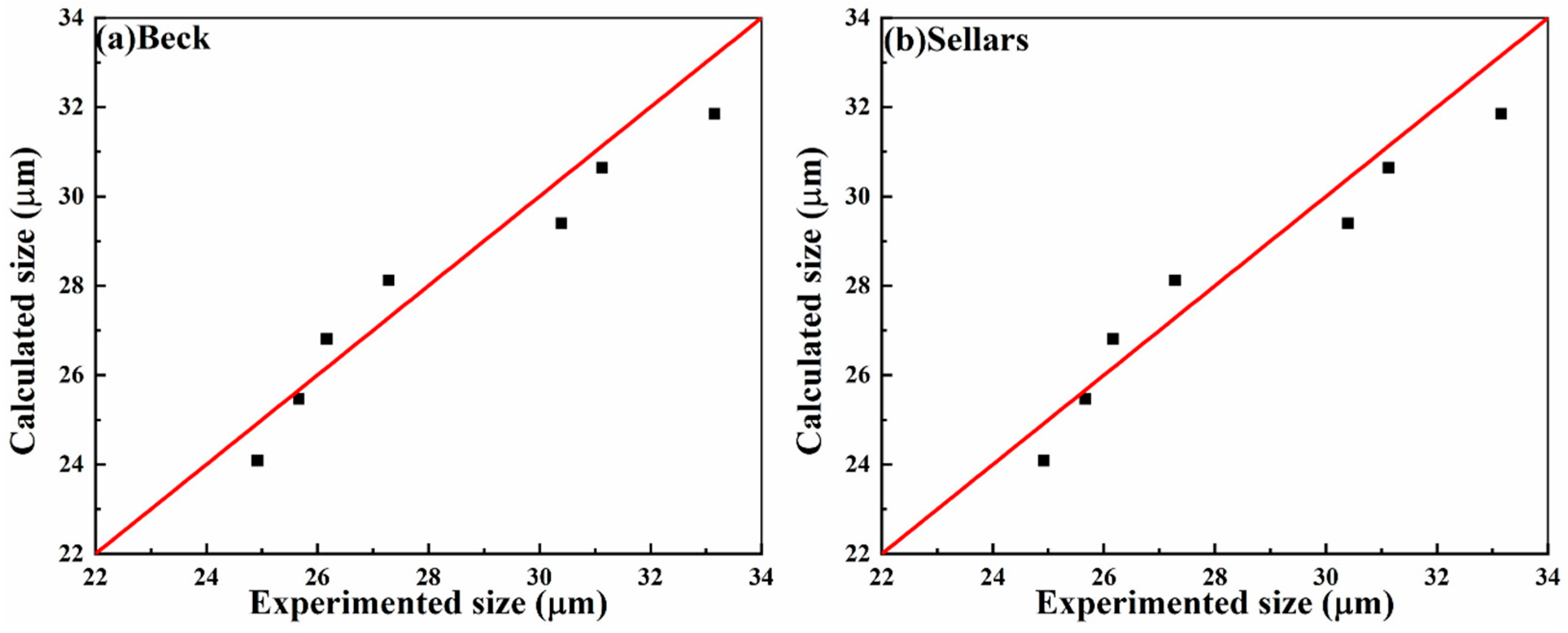
• Based on experimental data, Beck’s and Sellars’ models for ADB790E hydroelectric steel were established. The fitted variable-temperature elongation model is: D_A = 99.47 exp(14,421/RT), with a regression accuracy of 0.9255; the isothermal elongation model is: D_A = 4.83 t^0.2552, with a regression accuracy of 0.9306; Sellars’ model is: D^2.5 − D₀^2.5 = 4.9 × 10³ × t × exp(−36,052/RT), with a regression accuracy of 0.933.
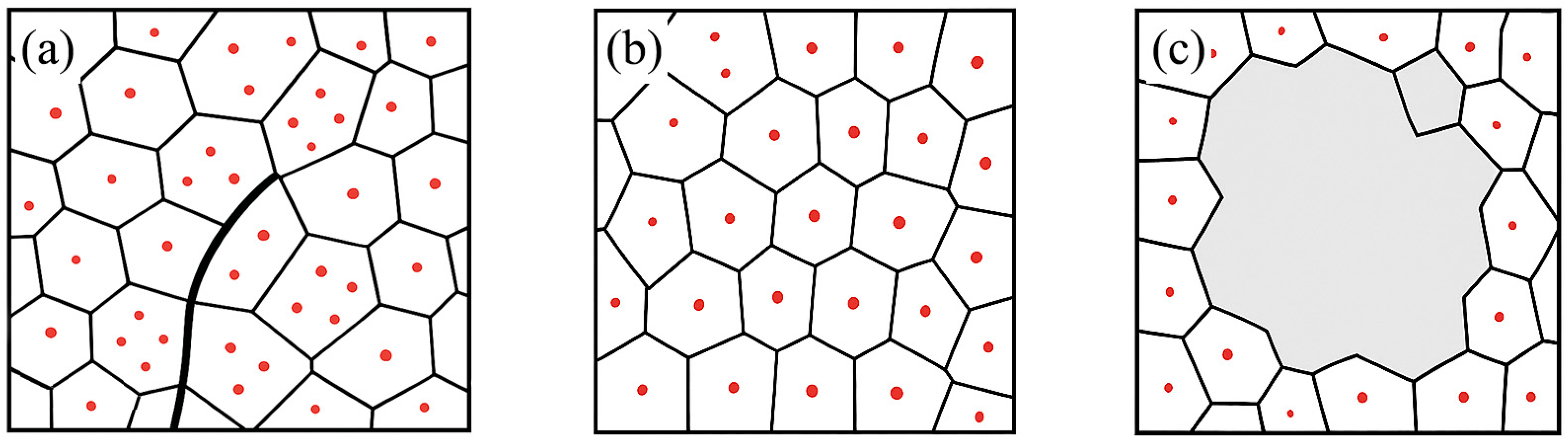
• The calculated apparent activation energy for grain growth in this study was lower than the values commonly reported for simple C-Mn steels. This discrepancy does not stem from experimental error but rather originates from the strong pinning effect of second-phase particles (e.g., TiN) and solute drag effects inherent to ADB790E steel. Furthermore, compared to other steel grades, the abnormal austenite grain growth observed in ADB790E exhibited a limited final grain size. This can be primarily attributed to the unique initial microstructure of ADB790E, characterized by a finer original grain size and a highly dispersed distribution of precipitates. The increased dispersion of carbides and nitrides provides a higher density of pinning sites per unit volume. Consequently, even if local pinning failure occurs and abnormal growth initiates, the ultimate grain size remains significantly constrained.
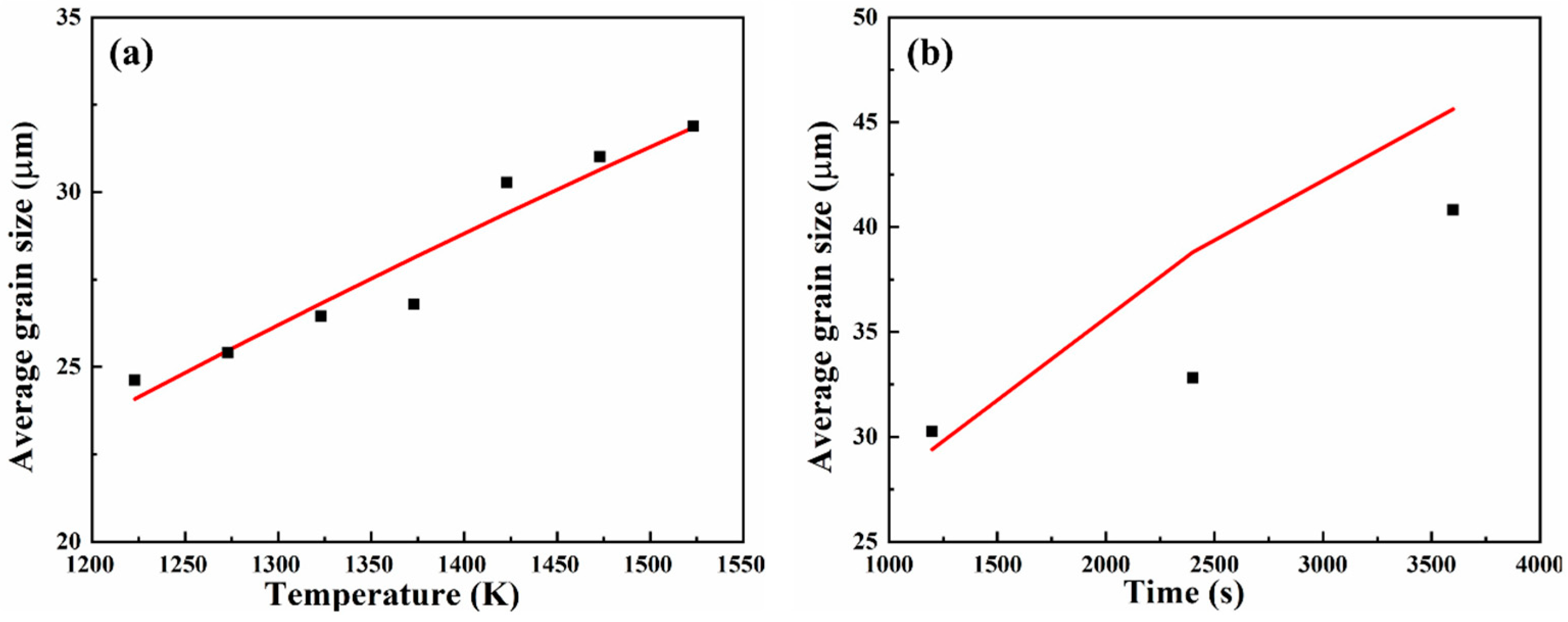
• Using a high-temperature laser confocal microscope to directly observe the changes in austenite grain size during heating, the experimental grain size values measured by the intercept method were found to be consistent with the predicted values from both models. However, Sellars’ model had a higher correlation coefficient. Therefore, during hot processing, the grain refinement temperature can be set based on the Sellars’ model’s predicted values, while the grain refinement holding time can be set based on the Beck’s model’s predicted values.