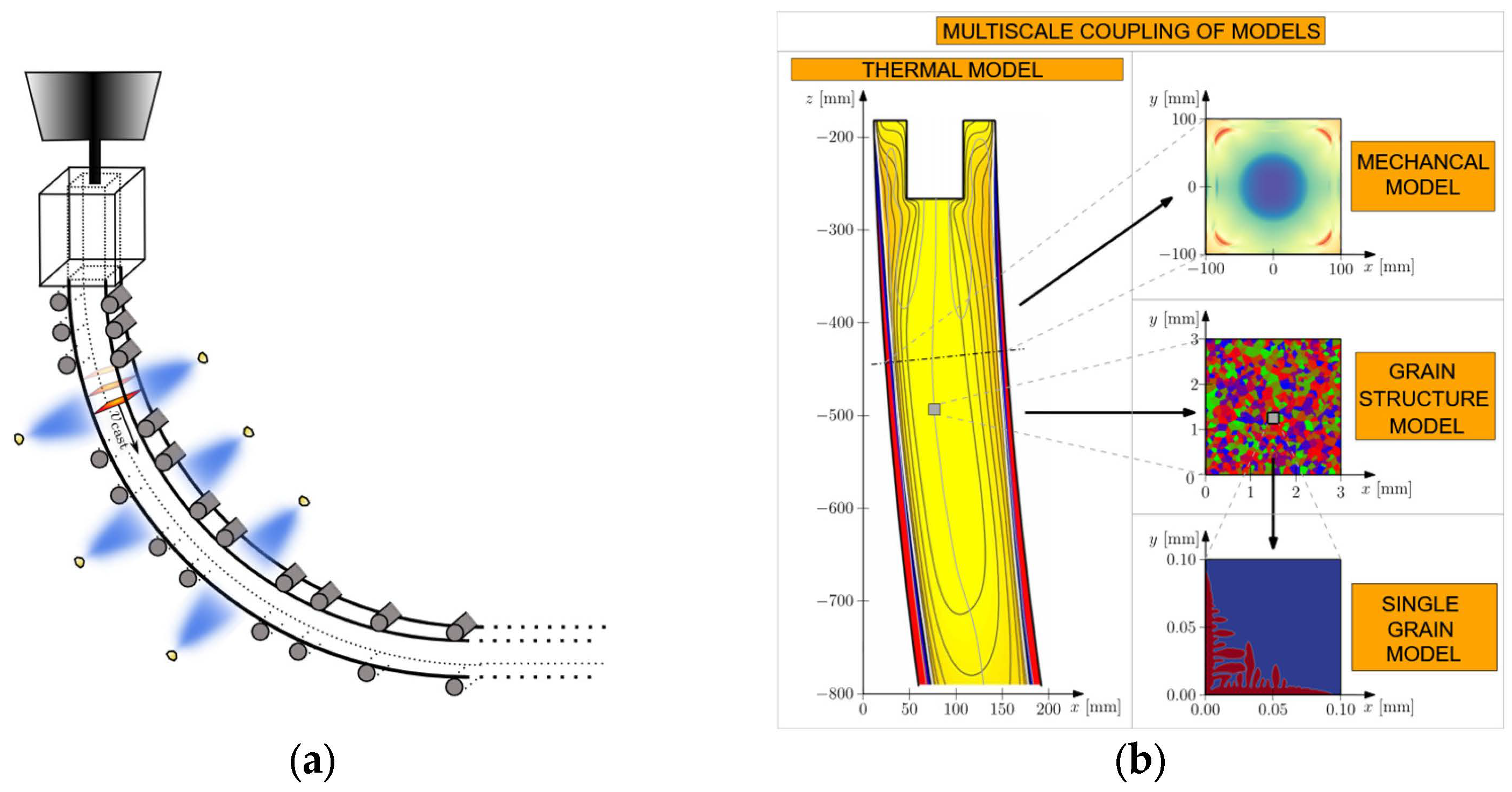
A Meshless Multiscale and Multiphysics Slice Model for Continuous Casting of Steel
Abstract
1. Introduction
2. Materials and Methods
2.1. Thermal Model
2.2. Mechanical Model
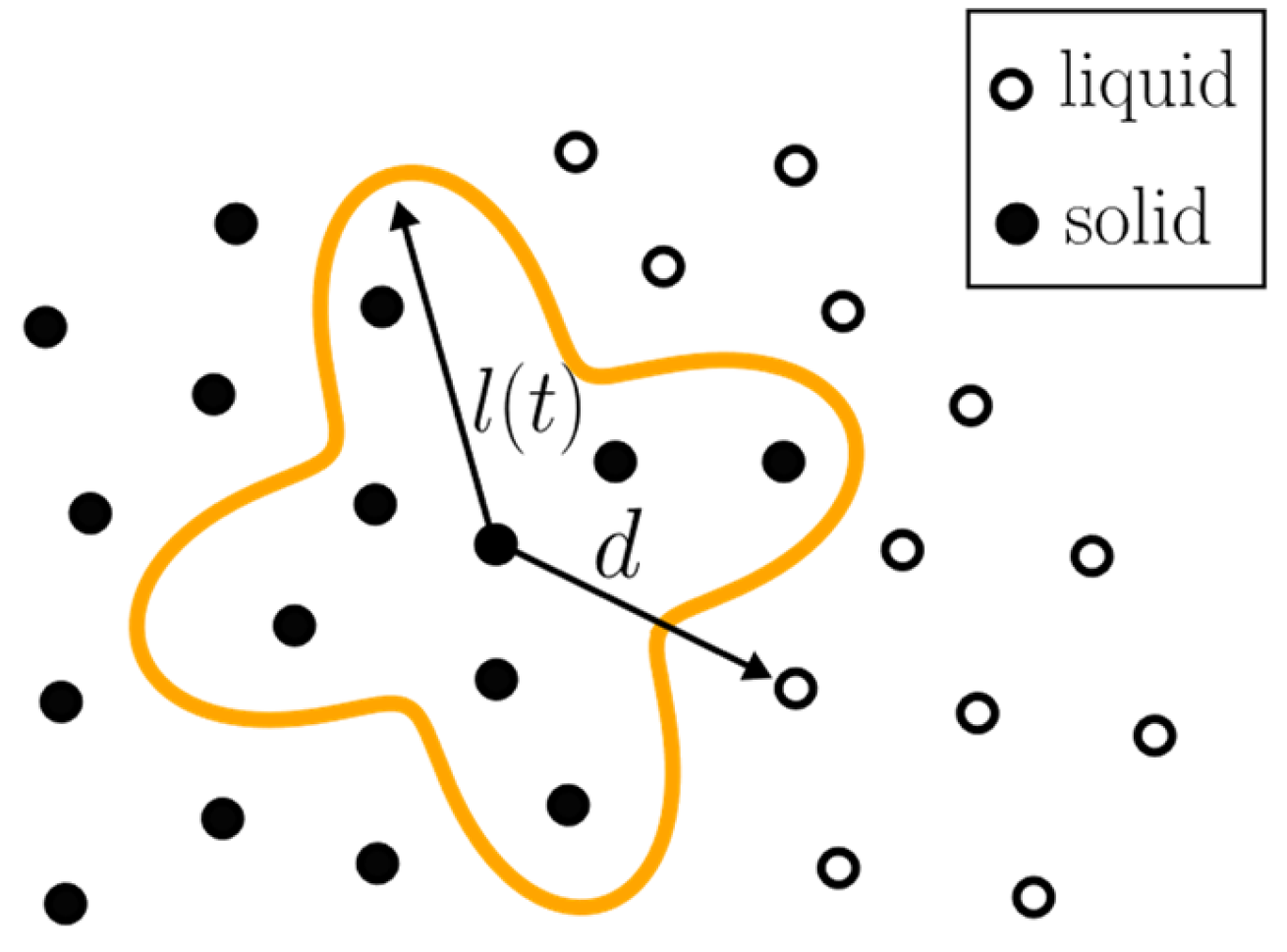
2.3. Grain Structure Model
2.4. Phase-Field Model
2.5. Macrosegregation Model
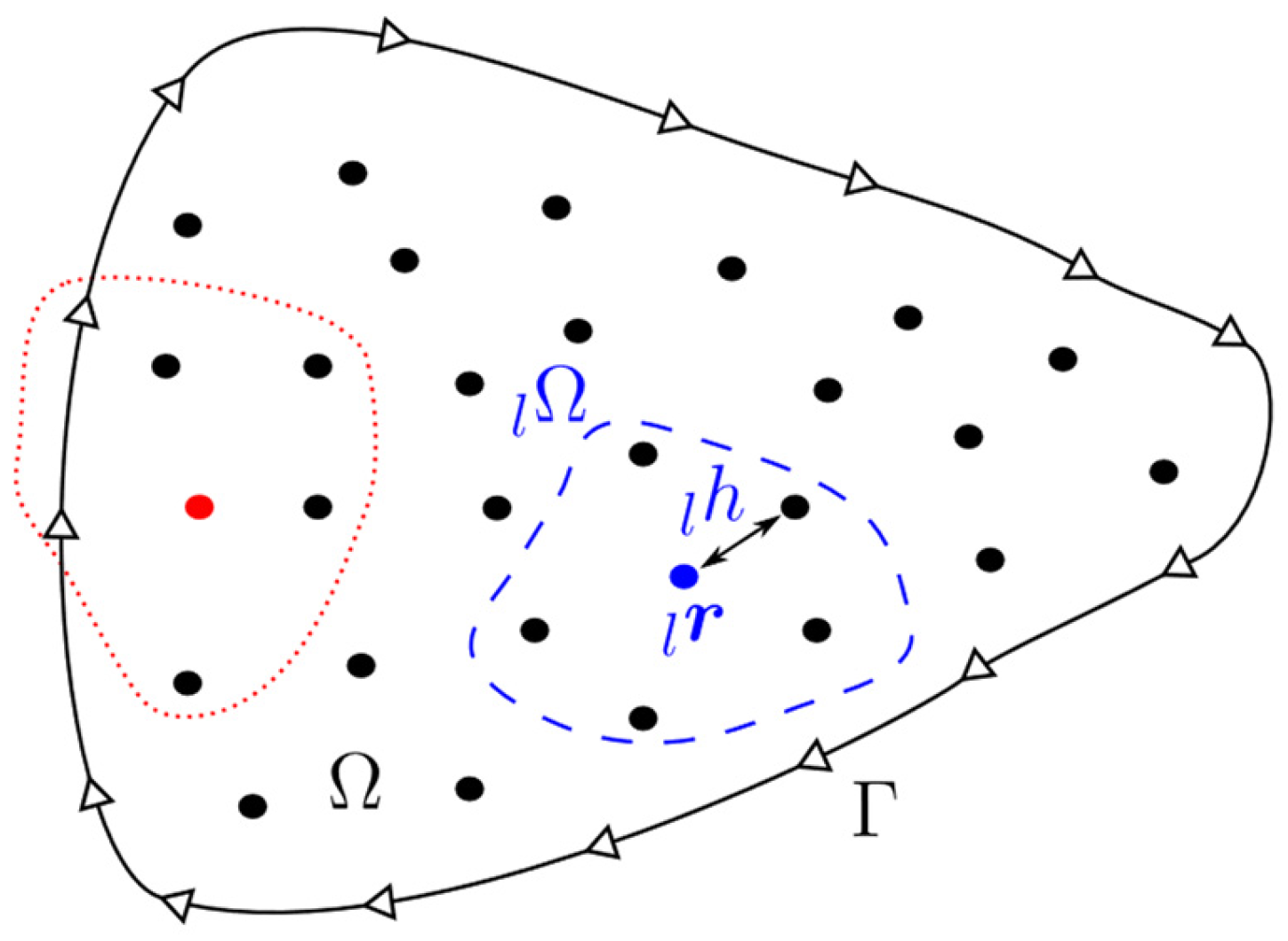
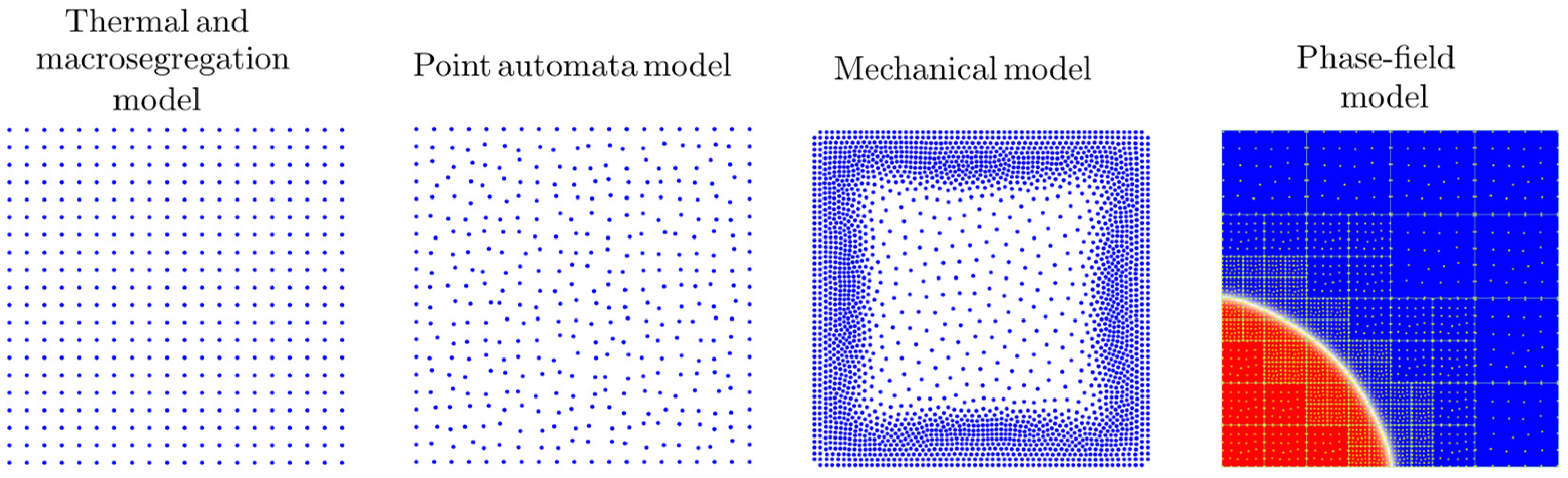
3. Numerical Methods
3.1. RBF-FD Method
3.2. Solution of the Thermal and Macrosegregation Models
3.3. Solution of the Grain Structure Model
3.4. Solution of the PF Model
3.5. Solution of the Mechanical Model
4. Test Problem Definition and Numerical Results
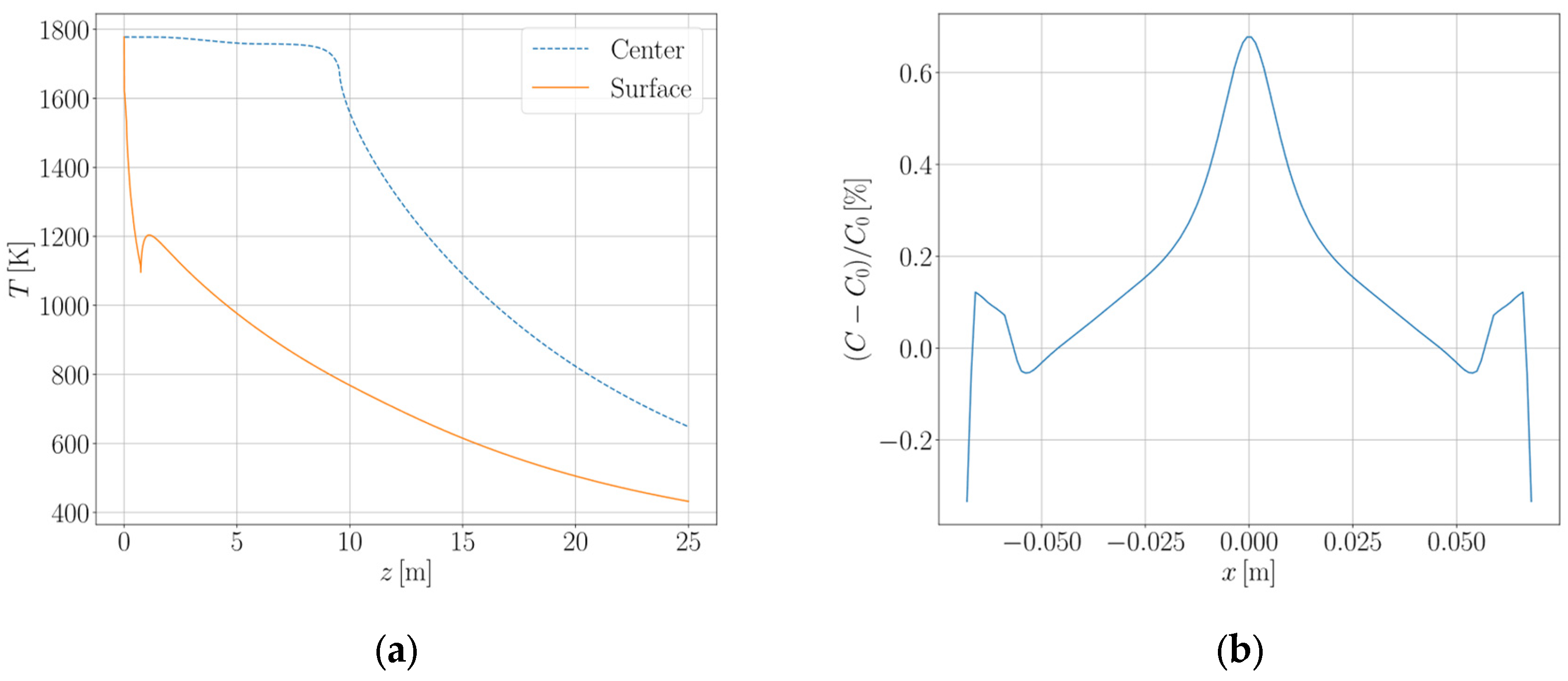
4.1. Thermal and Macrosegregation Model
4.2. Results of the Grain Structure Model
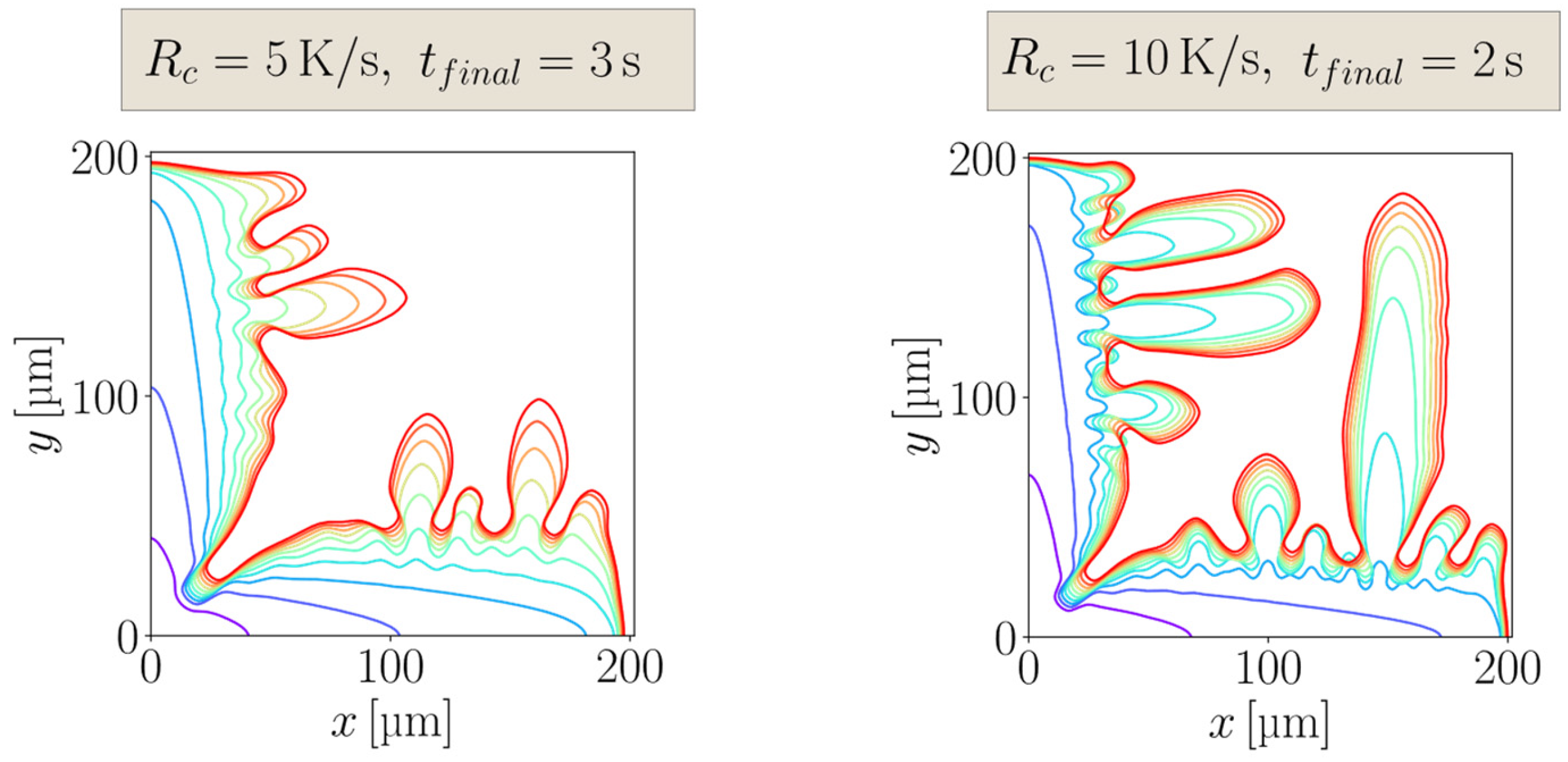
4.3. Results of the PF Model
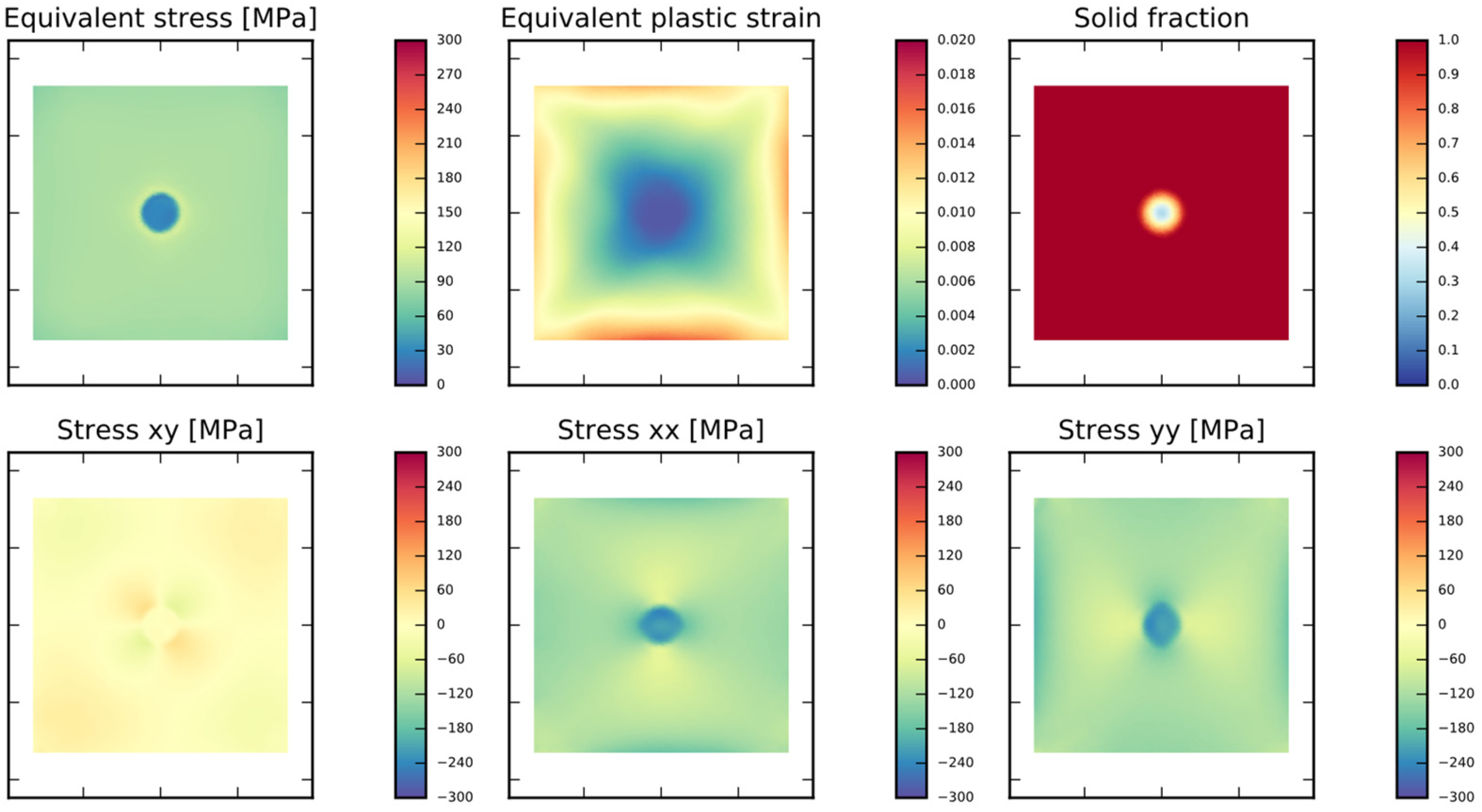
4.4. Results of the Mechanical Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Irving, W.R. Continuous Casting of Steel; Institute of Materials: London, UK, 1993; ISBN 978-0-901716-53-8. [Google Scholar]
- Dong, Q.; Zhang, J.; Yin, Y.; Wang, B. Three-Dimensional Numerical Modeling of Macrosegregation in Continuously Cast Billets. Metals 2017, 7, 209. [Google Scholar] [CrossRef]
- Yang, J.; Ji, Z.; Liu, W.; Xie, Z. Digital-Twin-Based Coordinated Optimal Control for Steel Continuous Casting Process. Metals 2023, 13, 816. [Google Scholar] [CrossRef]
- Kim, H.-S.; Kim, J.-J.; Oh, K.-S. A Simplified Model for Semi-Continuous Casting of Steel. J. Mater. Eng Perform 2023, 32, 4064–4070. [Google Scholar] [CrossRef]
- Klimeš, L.; Štětina, J. A Rapid GPU-Based Heat Transfer and Solidification Model for Dynamic Computer Simulations of Continuous Steel Casting. J. Mater. Process. Technol. 2015, 226, 1–14. [Google Scholar] [CrossRef]
- Li, C.; Thomas, B.G. Thermomechanical Finite-Element Model of Shell Behavior in Continuous Casting of Steel. Met. Mater. Trans. B 2004, 35, 1151–1172. [Google Scholar] [CrossRef]
- Ren, B.; Zhu, L.; Wang, H.; Chen, D. Numerical Simulation of Fluid Flow and Solidification in Round Bloom Continuous Casting with Alternate Final Electromagnetic Stirring. Metals 2025, 15, 605. [Google Scholar] [CrossRef]
- Li, Z.; Lu, Y.; Wang, R.; Li, G.; Cui, H. Numerical Simulation of Effects of Mold Cavity and Submerged Entry Nozzle on Flow, Heat Transfer and Solidification in Funnel-Type Molds for Thin Slab Casting. Metals 2025, 15, 183. [Google Scholar] [CrossRef]
- Li, Y.; He, W.; Zhao, C.; Liu, J.; Yang, Z.; Zhao, Y.; Yang, J. Mathematical Modeling of Transient Submerged Entry Nozzle Clogging and Its Effect on Flow Field, Bubble Distribution and Interface Fluctuation in Slab Continuous Casting Mold. Metals 2024, 14, 742. [Google Scholar] [CrossRef]
- Vušanović, I.; Vertnik, R.; Šarler, B. A Simple Slice Model for Prediction of Macrosegregation in Continuously Cast Billets. IOP Conf. Ser. Mater. Sci. Eng. 2012, 27, 012056. [Google Scholar] [CrossRef]
- Mavrič, B.; Dobravec, T.; Vertnik, R.; Šarler, B. A Meshless Thermomechanical Travelling-Slice Model of Continuous Casting of Steel. IOP Conf. Ser. Mater. Sci. Eng. 2020, 861, 012018. [Google Scholar] [CrossRef]
- Šarler, B.; Vertnik, R.; Lorbiecka, A.Z.; Vušanović, I.; Senčič, B. A Multiscale Slice Model for Continuous Casting of Steel. IOP Conf. Ser. Mater. Sci. Eng. 2012, 33, 012021. [Google Scholar] [CrossRef]
- Bazzaro, G.; De Bona, F. Effectiveness of Travelling Slice Modeling in Representing the Continuous Casting Process of Large Product Sections. Metals 2023, 13, 1505. [Google Scholar] [CrossRef]
- Flyer, N.; Fornberg, B.; Bayona, V.; Barnett, G.A. On the Role of Polynomials in RBF-FD Approximations: I. Interpolation and Accuracy. J. Comput. Phys. 2016, 321, 21–38. [Google Scholar] [CrossRef]
- Bayona, V.; Flyer, N.; Fornberg, B.; Barnett, G.A. On the Role of Polynomials in RBF-FD Approximations: II. Numerical Solution of Elliptic PDEs. J. Comput. Phys. 2017, 332, 257–273. [Google Scholar] [CrossRef]
- Bayona, V.; Flyer, N.; Fornberg, B. On the Role of Polynomials in RBF-FD Approximations: III. Behavior near Domain Boundaries. J. Comput. Phys. 2019, 380, 378–399. [Google Scholar] [CrossRef]
- Kolar-Požun, A.; Jančič, M.; Rot, M.; Kosec, G. Some Observations Regarding the RBF-FD Approximation Accuracy Dependence on Stencil Size. J. Comput. Sci. 2024, 79, 102284. [Google Scholar] [CrossRef]
- Šarler, B.; Vertnik, R. Meshfree Explicit Local Radial Basis Function Collocation Method for Diffusion Problems. Comput. Math. Appl. 2006, 51, 1269–1282. [Google Scholar] [CrossRef]
- Ali, I.; Hanoglu, U.; Vertnik, R.; Šarler, B. Assessment of Local Radial Basis Function Collocation Method for Diffusion Problems Structured with Multiquadrics and Polyharmonic Splines. Math. Comput. Appl. 2024, 29, 23. [Google Scholar] [CrossRef]
- Vertnik, R.; Mramor, K.; Šarler, B. Solution of Three-Dimensional Temperature and Turbulent Velocity Field in Continuously Cast Steel Billets with Electromagnetic Stirring by a Meshless Method. Eng. Anal. Bound. Elem. 2019, 104, 347–363. [Google Scholar] [CrossRef]
- Vuga, G.; Mavrič, B.; Hanoglu, U.; Šarler, B. A Hybrid Radial Basis Function-Finite Difference Method for Modelling Two-Dimensional Thermo-Elasto-Plasticity, Part 2: Application to Cooling of Hot-Rolled Steel Bars on a Cooling Bed. Eng. Anal. Bound. Elem. 2024, 159, 331–341. [Google Scholar] [CrossRef]
- Dobravec, T.; Mavrič, B.; Šarler, B. Reduction of Discretisation-Induced Anisotropy in the Phase-Field Modelling of Dendritic Growth by Meshless Approach. Comput. Mater. Sci. 2020, 172, 109166. [Google Scholar] [CrossRef]
- Dobravec, T.; Mavrič, B.; Šarler, B. Acceleration of RBF-FD Meshless Phase-Field Modelling of Dendritic Solidification by Space-Time Adaptive Approach. Comput. Math. Appl. 2022, 126, 77–99. [Google Scholar] [CrossRef]
- Dobravec, T.; Mavrič, B.; Zahoor, R.; Šarler, B. A Coupled Domain–Boundary Type Meshless Method for Phase-Field Modelling of Dendritic Solidification with the Fluid Flow. Int. J. Numer. Methods Heat Fluid Flow 2023, 33, 2963–2981. [Google Scholar] [CrossRef]
- Dobravec, T.; Mavrič, B.; Šarler, B. A Study on Different Implementations of Neumann Boundary Conditions in the Meshless RBF-FD Method for the Phase-Field Modelling of Dendrite Growth. Eng. Anal. Bound. Elem. 2025, 173, 106154. [Google Scholar] [CrossRef]
- Jiang, P.; Zheng, H.; Xiong, J.; Rabczuk, T. The Localized Radial Basis Function Collocation Method for Dendritic Solidification, Solid Phase Sintering and Wetting Phenomenon Based on Phase Field. J. Comput. Phys. 2025, 520, 113515. [Google Scholar] [CrossRef]
- Zamolo, R.; Bacer, L.; Miotti, D.; Nobile, E.; Munerato, M. RBF-FD Meshless Simulation of 3D Fully Developed Flow and Heat Transfer in Triply Periodic Minimal Surfaces. Int. J. Heat Mass Transf. 2025, 242, 126798. [Google Scholar] [CrossRef]
- Bacer, L.; Zamolo, R.; Miotti, D.; Nobile, E. Adaptive RBF-FD Meshless Solution of 3D Fluid Flow and Heat Transfer Problems. Eng. Anal. Bound. Elem. 2025, 179, 106367. [Google Scholar] [CrossRef]
- Mathews, N.H.; Flyer, N.; Gibson, S.E. Solving 3D Magnetohydrostatics with RBF-FD: Applications to the Solar Corona. J. Comput. Phys. 2022, 462, 111214. [Google Scholar] [CrossRef]
- Lorbiecka, A.Z.; Šarler, B. Simulation of Dendritic Growth with Different Orientation by Using the Point Automata Method. CMC Comput. Mater. Contin. 2010, 18, 69–104. [Google Scholar] [CrossRef]
- Gandin, C.A.; Rappaz, M. A Coupled Finite Element-Cellular Automaton Model for the Prediction of Dendritic Grain Structures in Solidification Processes. Acta Metall. Mater. 1994, 42, 2233–2246. [Google Scholar] [CrossRef]
- Rappaz, M.; Gandin, C.A. Probabilistic Modelling of Microstructure Formation in Solidification Processes. Acta Metall. Mater. 1993, 41, 345–360. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. Perspectives for Cellular Automata for the Simulation of Dendritic Solidification—A Review. Comput. Mater. Sci. 2014, 95, 213–220. [Google Scholar] [CrossRef]
- Asle Zaeem, M.; Yin, H.; Felicelli, S.D. Modeling Dendritic Solidification of Al–3%Cu Using Cellular Automaton and Phase-Field Methods. Appl. Math. Model. 2013, 37, 3495–3503. [Google Scholar] [CrossRef]
- Krane, M.J.M.; Johnson, D.R.; Raghavan, S. The Development of a Cellular Automaton-Finite Volume Model for Dendritic Growth. Appl. Math. Model. 2009, 33, 2234–2247. [Google Scholar] [CrossRef]
- Chen, R.; Xu, Q.; Liu, B. Cellular Automaton Simulation of Three-Dimensional Dendrite Growth in Al–7Si–Mg Ternary Aluminum Alloys. Comput. Mater. Sci. 2015, 105, 90–100. [Google Scholar] [CrossRef]
- Chen, L.-Q. Phase-Field Models for Microstructure Evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Warren, J.A.; Beckermann, C.; Karma, A. Phase-Field Simulation of Solidification. Annu. Rev. Mater. Res. 2002, 32, 163–194. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-Field Models in Materials Science. Model. Simul. Mat. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Nestler, B.; Choudhury, A. Phase-Field Modeling of Multi-Component Systems. Curr. Opin. Solid State Mater. Sci. 2011, 15, 93–105. [Google Scholar] [CrossRef]
- Karma, A.; Tourret, D. Atomistic to Continuum Modeling of Solidification Microstructures. Curr. Opin. Solid State Mater. Sci. 2016, 20, 25–36. [Google Scholar] [CrossRef]
- Liu, Q.; Hanoglu, U.; Rek, Z.; Šarler, B. Simulation of Temperature Field in Steel Billets during Reheating in Pusher-Type Furnace by Meshless Method. Math. Comput. Appl. 2024, 29, 30. [Google Scholar] [CrossRef]
- Hanoglu, U.; Šarler, B. Multi-Pass Hot-Rolling Simulation Using a Meshless Method. Comput. Struct. 2018, 194, 1–14. [Google Scholar] [CrossRef]
- Hanoglu, U.; Šarler, B. Developments towards a Multiscale Meshless Rolling Simulation System. Materials 2021, 14, 4277. [Google Scholar] [CrossRef]
- Ali, I.; Vuga, G.; Mavrič, B.; Šarler, B. Meshless Solution of the Crack Propagation in Brittle Elastic Material under Shear, Compressible and Tensile Loading. Eng. Fract. Mech. 2025, 323, 111207. [Google Scholar] [CrossRef]
- Bennon, W.D.; Incropera, F.P. A Continuum Model for Momentum, Heat and Species Transport in Binary Solid-Liquid Phase Change Systems—I. Model Formulation. Int. J. Heat Mass Transf. 1987, 30, 2161–2170. [Google Scholar] [CrossRef]
- Koric, S.; Thomas, B.G. Thermo-Mechanical Models of Steel Solidification Based on Two Elastic Visco-Plastic Constitutive Laws. J. Mater. Process. Technol. 2008, 197, 408–418. [Google Scholar] [CrossRef]
- Lipton, J.; Glicksman, M.E.; Kurz, W. Equiaxed Dendrite Growth in Alloys at Small Supercooling. Met. Mat Trans. A 1987, 18, 341–345. [Google Scholar] [CrossRef]
- Lipton, J.; Glicksman, M.E.; Kurz, W. Dendritic Growth into Undercooled Alloy Metals. Mater. Sci. Eng. 1984, 65, 57–63. [Google Scholar] [CrossRef]
- Ohno, M. Quantitative Phase-Field Modeling of Nonisothermal Solidification in Dilute Multicomponent Alloys with Arbitrary Diffusivities. Phys. Rev. E 2012, 86, 051603. [Google Scholar] [CrossRef]
- Echebarria, B.; Folch, R.; Karma, A.; Plapp, M. Quantitative Phase-Field Model of Alloy Solidification. Phys. Rev. E 2004, 70, 061604. [Google Scholar] [CrossRef] [PubMed]
- Boukellal, A.K.; Debierre, J.-M.; Reinhart, G.; Nguyen-Thi, H. Scaling Laws Governing the Growth and Interaction of Equiaxed Al-Cu Dendrites: A Study Combining Experiments with Phase-Field Simulations. Materialia 2018, 1, 62–69. [Google Scholar] [CrossRef]
- Tourret, D.; Karma, A. Growth Competition of Columnar Dendritic Grains: A Phase-Field Study. Acta Mater. 2015, 82, 64–83. [Google Scholar] [CrossRef]
- Xie, Y.; Dong, H.; Dantzig, J. Growth of Secondary Dendrite Arms of Fe–C Alloy during Transient Directional Solidification by Phase-Field Method. ISIJ Int. 2014, 54, 430–436. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.-J. Quantitative Phase-Field Modeling of Dendritic Growth in Two and Three Dimensions. Phys. Rev. E 1998, 57, 4323. [Google Scholar] [CrossRef]


| Property | Symbol[Unit] | Value |
|---|---|---|
| Density | 7870.0 | |
| Specific heat in liquid | 1395.8 | |
| Specific heat in solid | 824.9 | |
| Thermal conductivity in liquid | 39.3 | |
| Thermal conductivity in solid | 25.0 | |
| Latent heat of melting | 2.71 × 105 | |
| Solute diffusivity | 1.36 × 10−9 | |
| Melting temperature of Fe | 1811.15 | |
| Eutectic temperature | 1427.15 | |
| Eutectic concentration | 4.3 | |
| Partition coefficient | 0.521 | |
| Gibbs-Thomson coefficient | 3.0 × 10−7 |
| Property | Symbol[Unit] | Value |
|---|---|---|
| Max. nucleation density at the surface | 1.0 × 1010 | |
| Max. nucleation density in bulk | 1.0 × 108 | |
| Mean undercooling at the surface | 0.1 | |
| Mean undercooling in bulk | 0.1 | |
| Scale undercooling at the surface | 0.001 | |
| Scale undercooling in bulk | 0.001 | |
| Envelope ratio | 0.25 |
| Property | Symbol[Unit] | Value |
|---|---|---|
| Young’s modulus | ||
| Poisson’s ratio | 0.3 | |
| Reference stress | 5.0 × 108 | |
| Stress exponent | 6.0 | |
| Reference strain rate | 0.34 | |
| Activation energy | 6.340 × 103 | |
| Thermal expansion coefficient | 0.707 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šarler, B.; Mavrič, B.; Dobravec, T.; Vertnik, R. A Meshless Multiscale and Multiphysics Slice Model for Continuous Casting of Steel. Metals 2025, 15, 1007. https://doi.org/10.3390/met15091007
Šarler B, Mavrič B, Dobravec T, Vertnik R. A Meshless Multiscale and Multiphysics Slice Model for Continuous Casting of Steel. Metals. 2025; 15(9):1007. https://doi.org/10.3390/met15091007
Chicago/Turabian StyleŠarler, Božidar, Boštjan Mavrič, Tadej Dobravec, and Robert Vertnik. 2025. "A Meshless Multiscale and Multiphysics Slice Model for Continuous Casting of Steel" Metals 15, no. 9: 1007. https://doi.org/10.3390/met15091007
APA StyleŠarler, B., Mavrič, B., Dobravec, T., & Vertnik, R. (2025). A Meshless Multiscale and Multiphysics Slice Model for Continuous Casting of Steel. Metals, 15(9), 1007. https://doi.org/10.3390/met15091007







