Investigation on Strain-Forming Limits and Manufacturing Optimization of a Single Deep-Drawing Process Concerning 304 Stainless Steel’s Thin Sheet
Abstract
1. Introduction
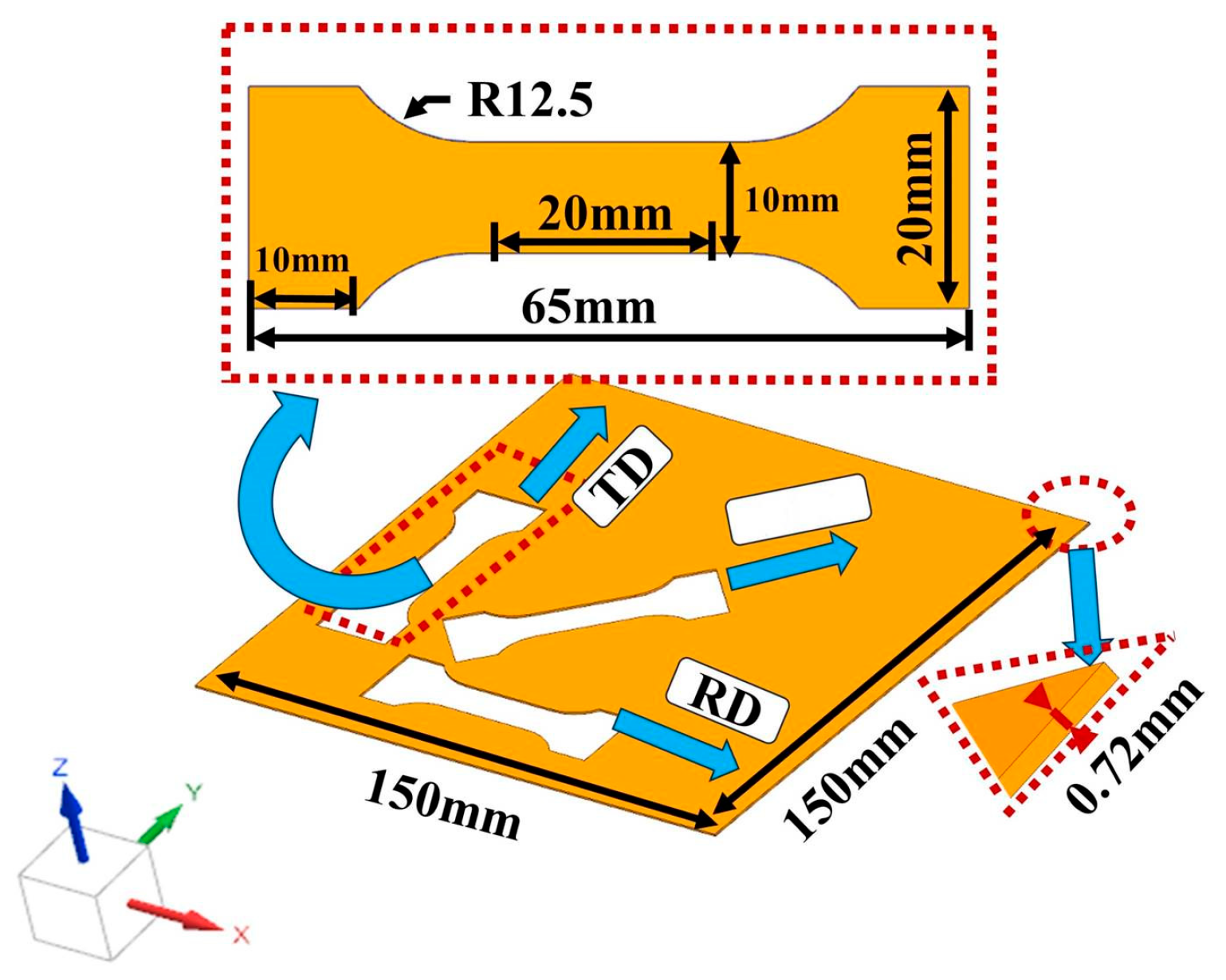
2. Experimental Methods
2.1. Mechanical Properties Experiment
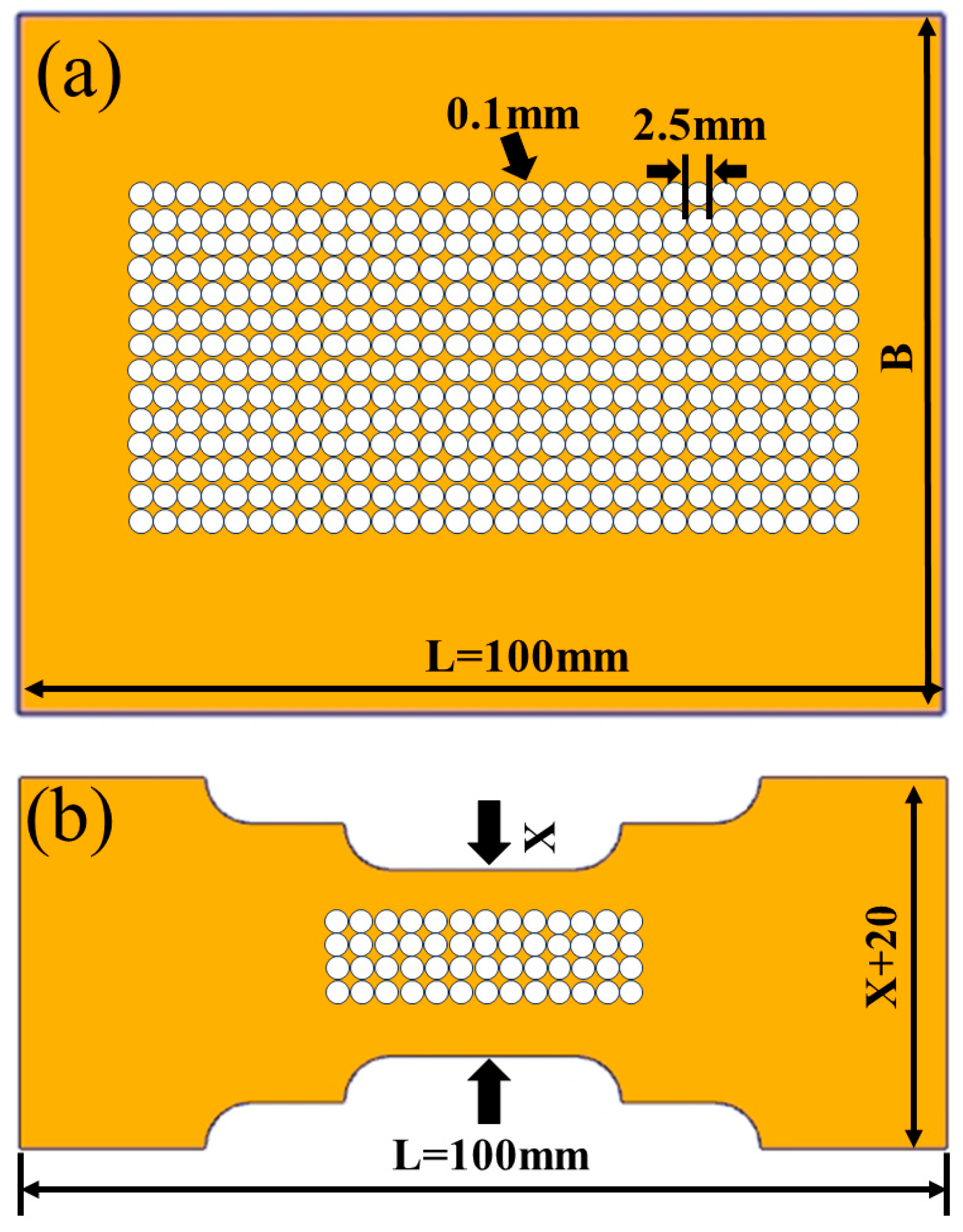
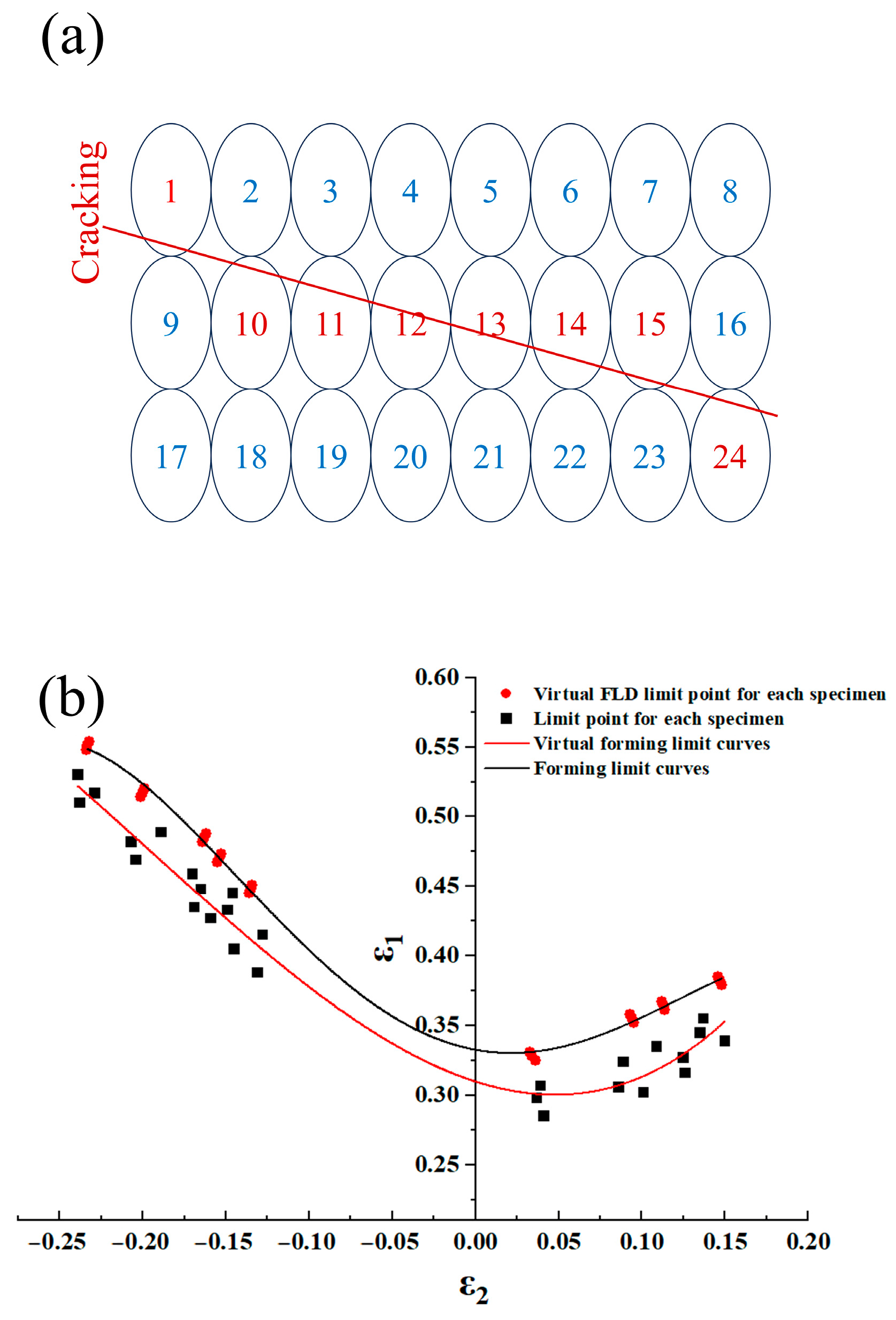
2.2. Simulation of Forming Limit Diagram
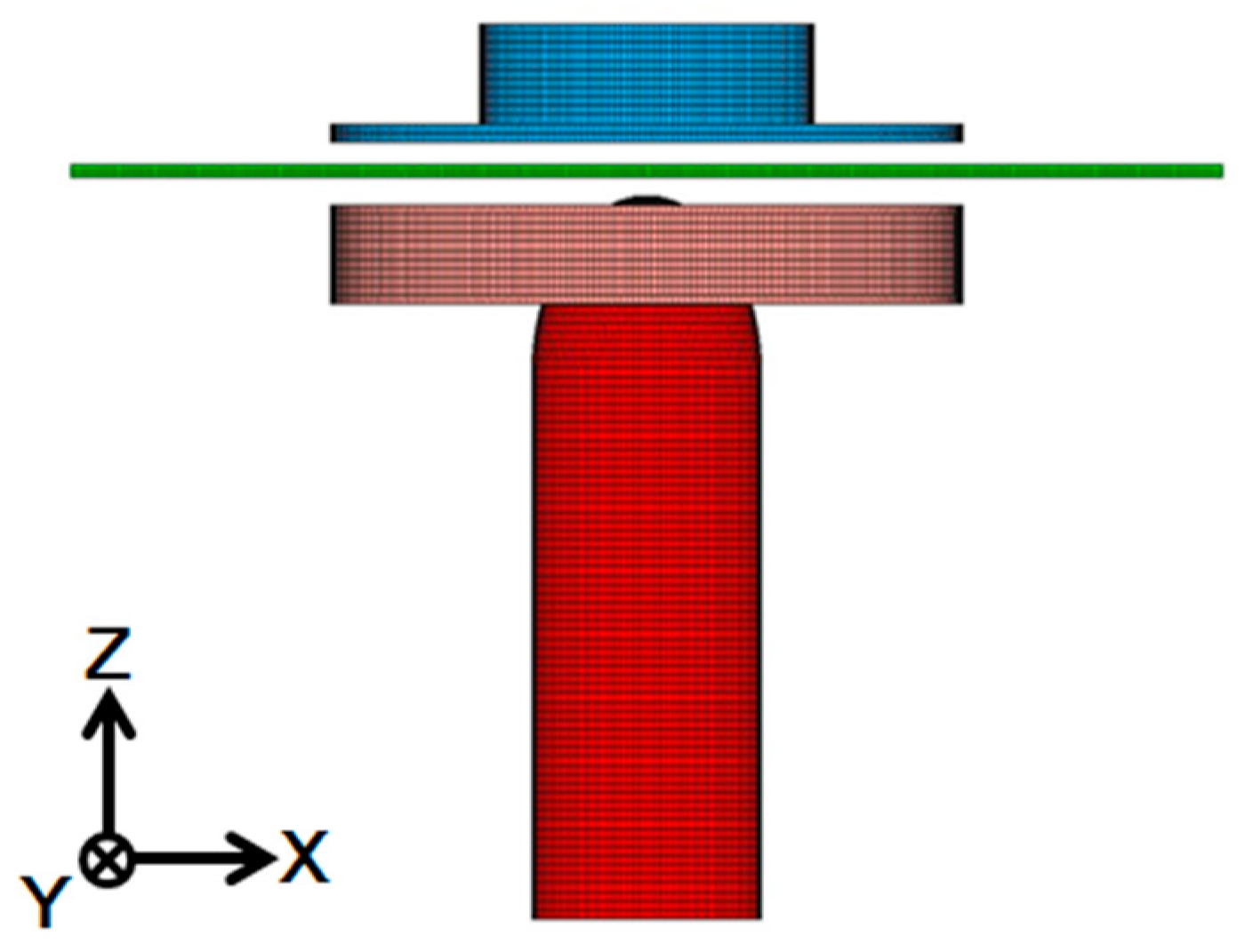
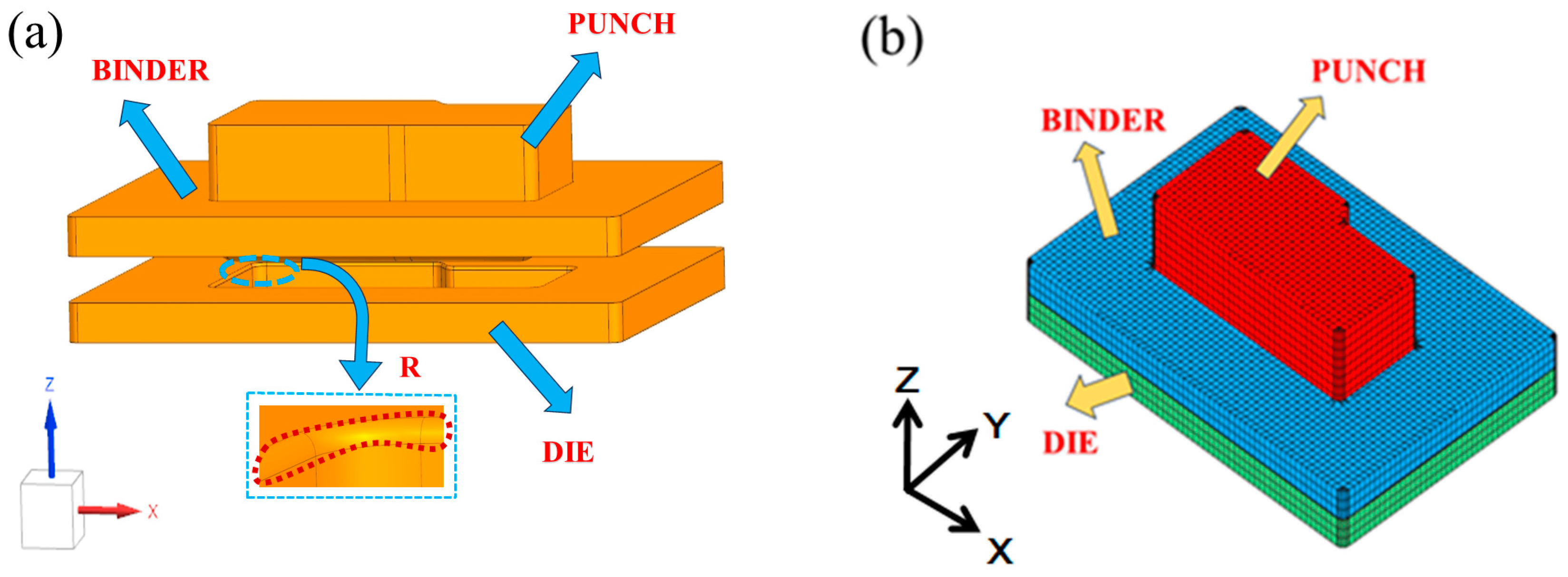
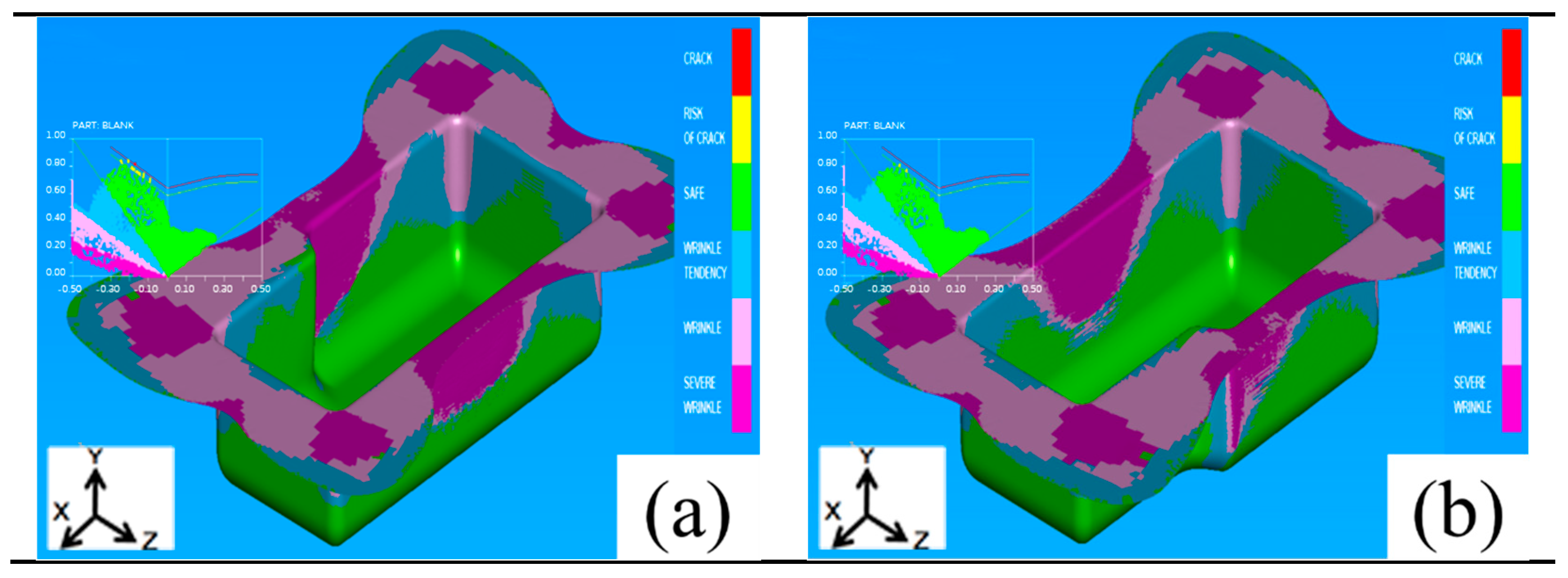
2.3. Finite Element Simulation of Stainless Steel Sink
3. Results and Discussion
3.1. Mechanical Properties Analysis
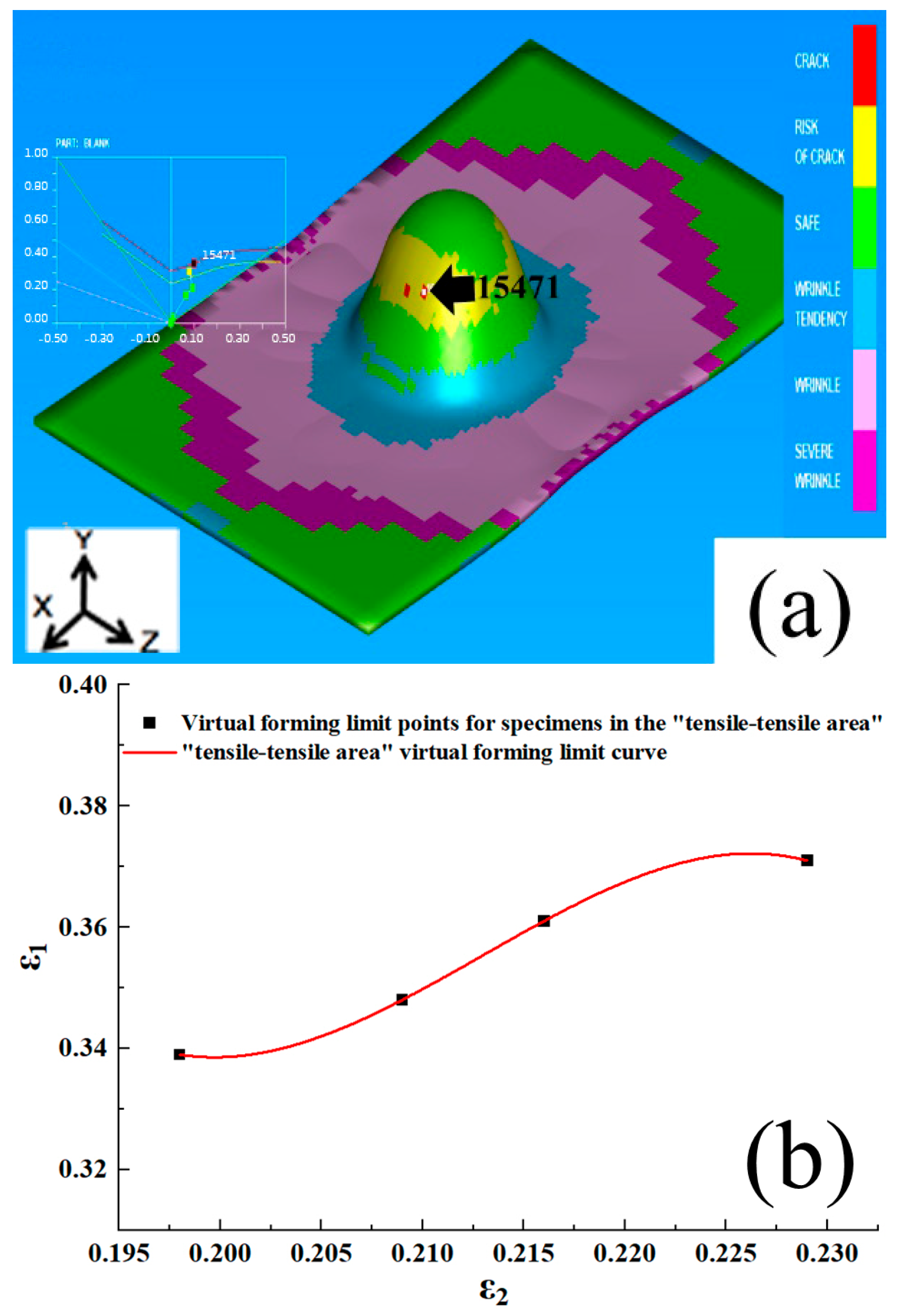
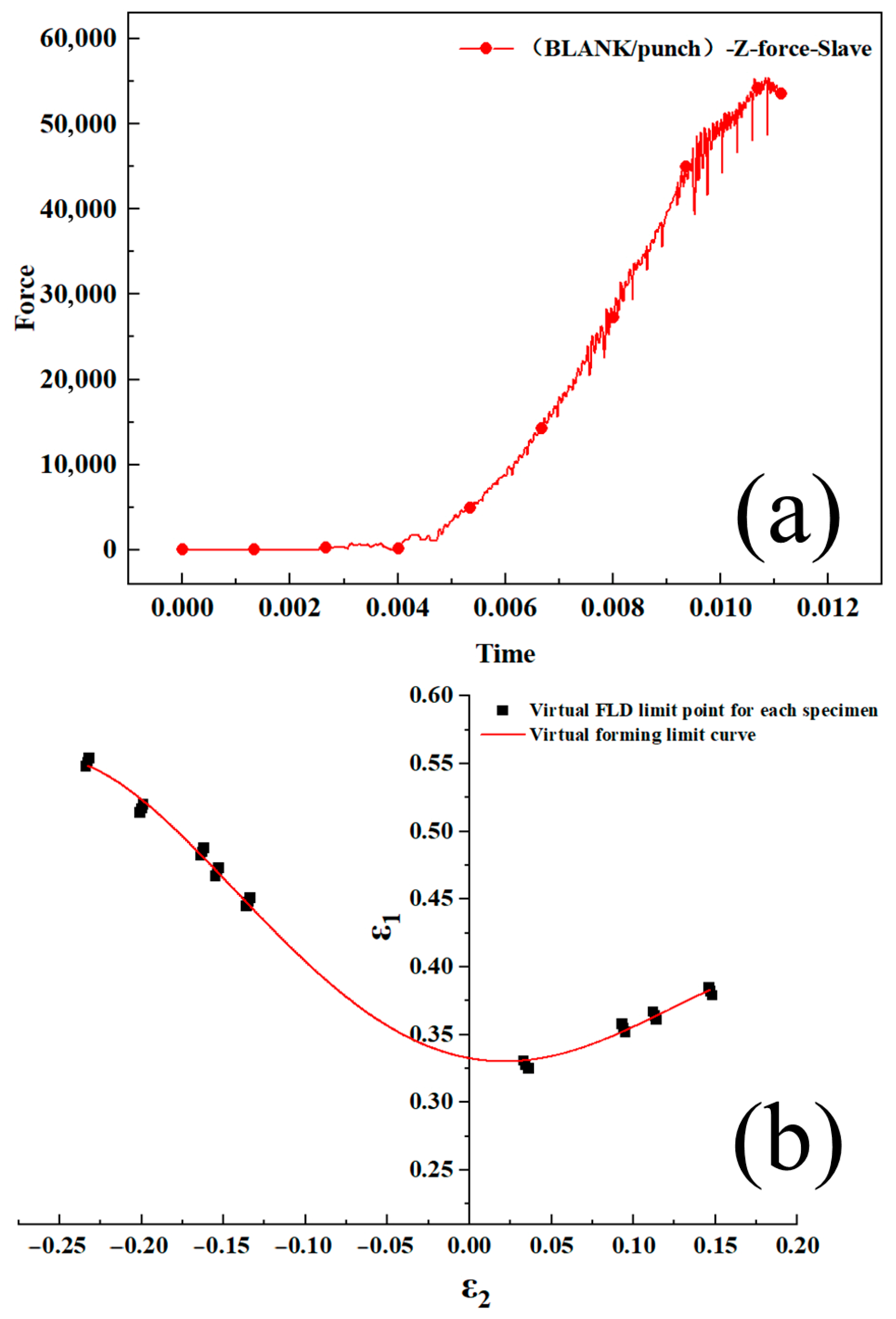
3.2. Simulation and Experiment Analysis of Forming Limit Diagram
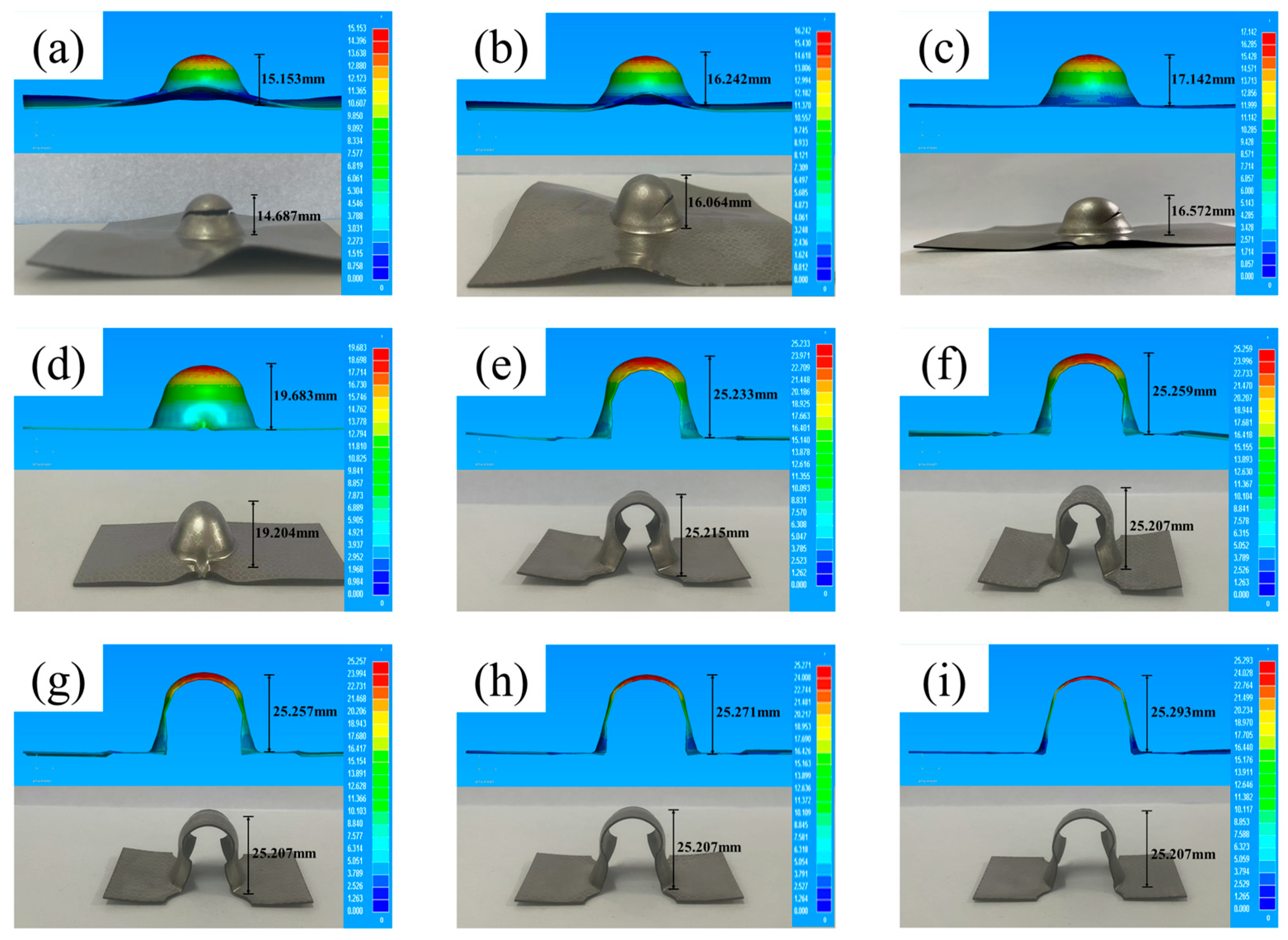
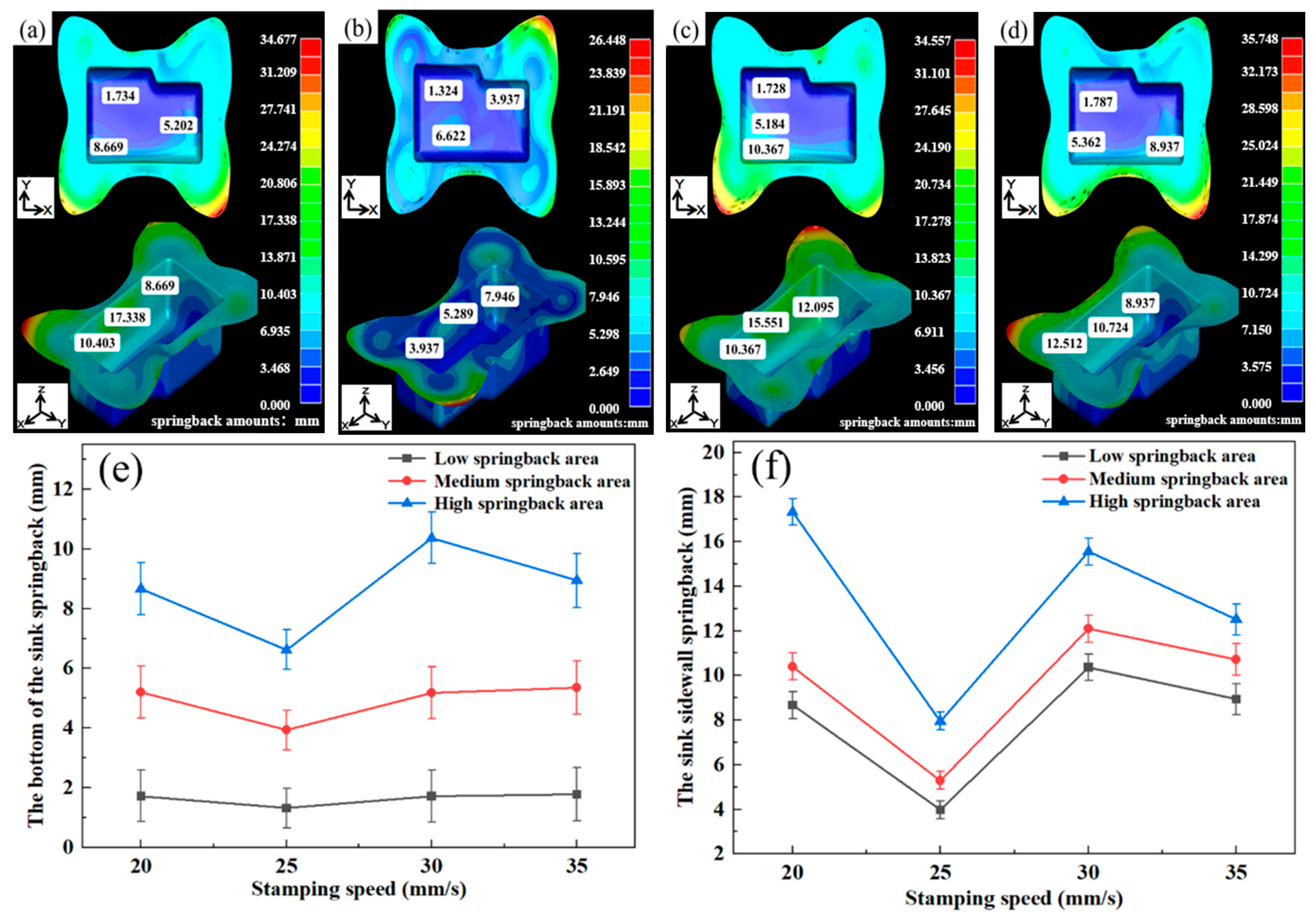
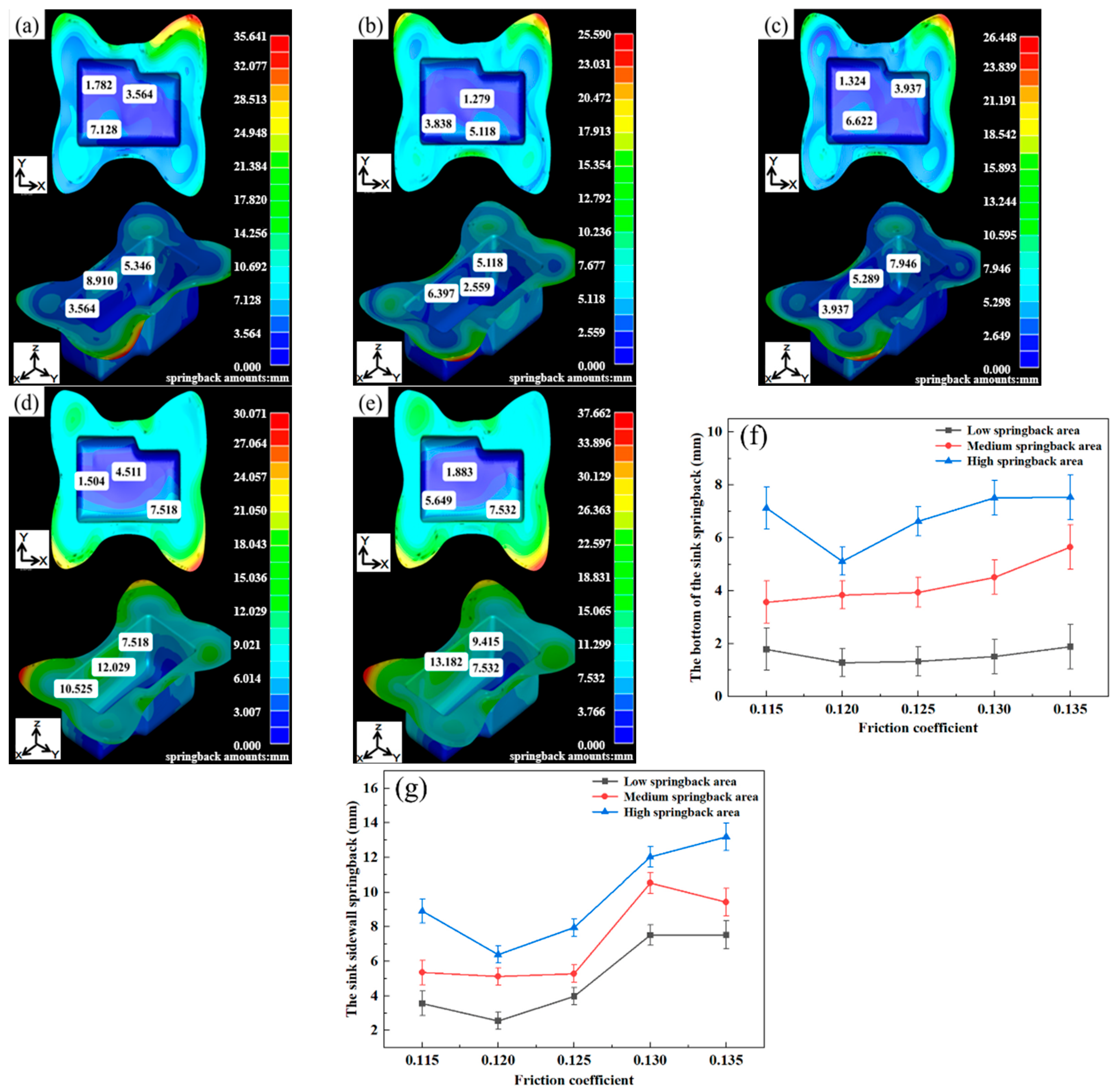
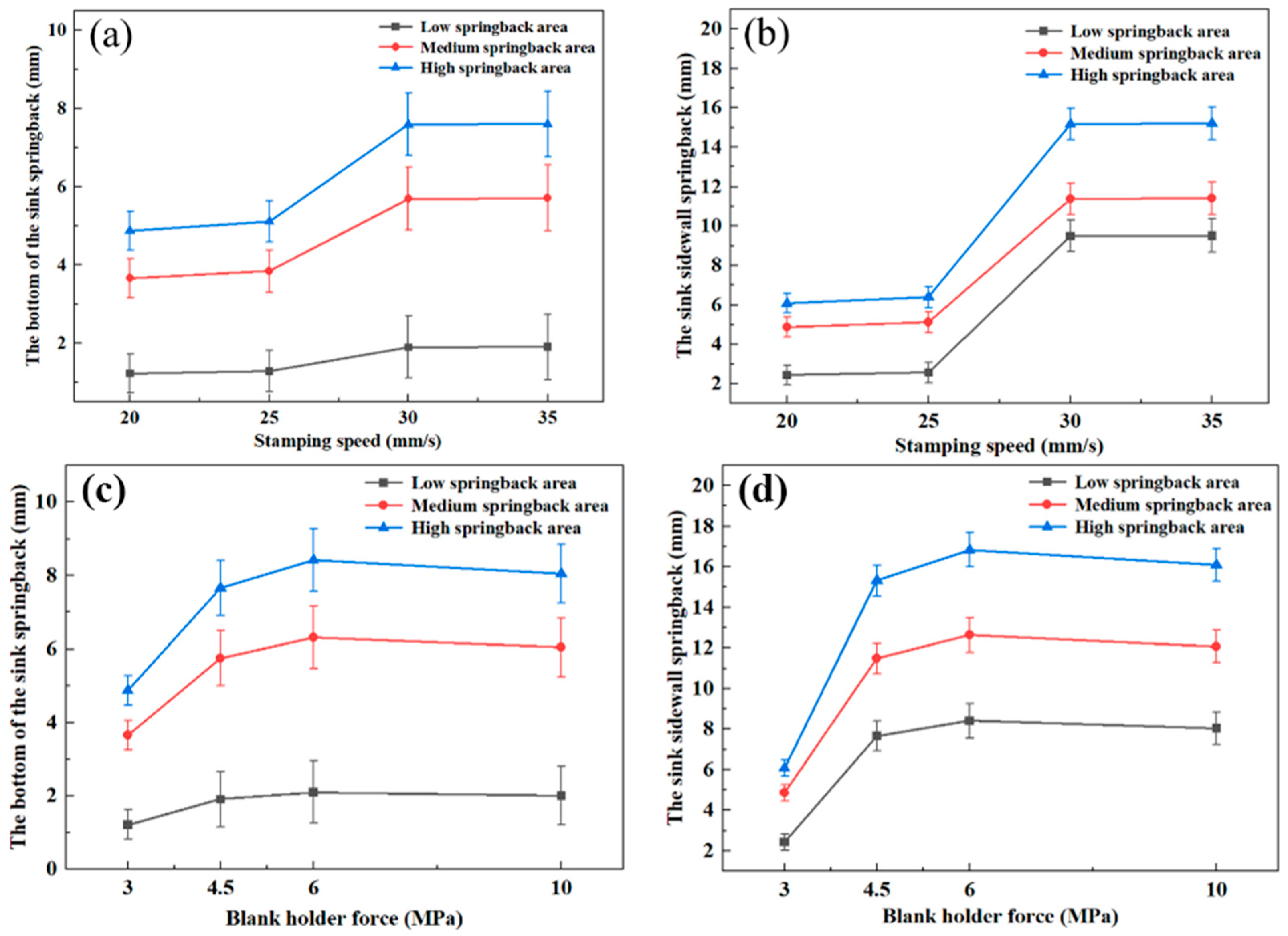
3.3. Finite Element Analysis of Stainless Steel Sink
4. Conclusions
- The mechanical properties of SUS304 stainless steel show obvious anisotropy in TD, R45, and RD directions. The TD direction has the greatest yield strength and tensile strength, while it has the lowest elongation, which is 11.8% lower than that in the rolling direction.
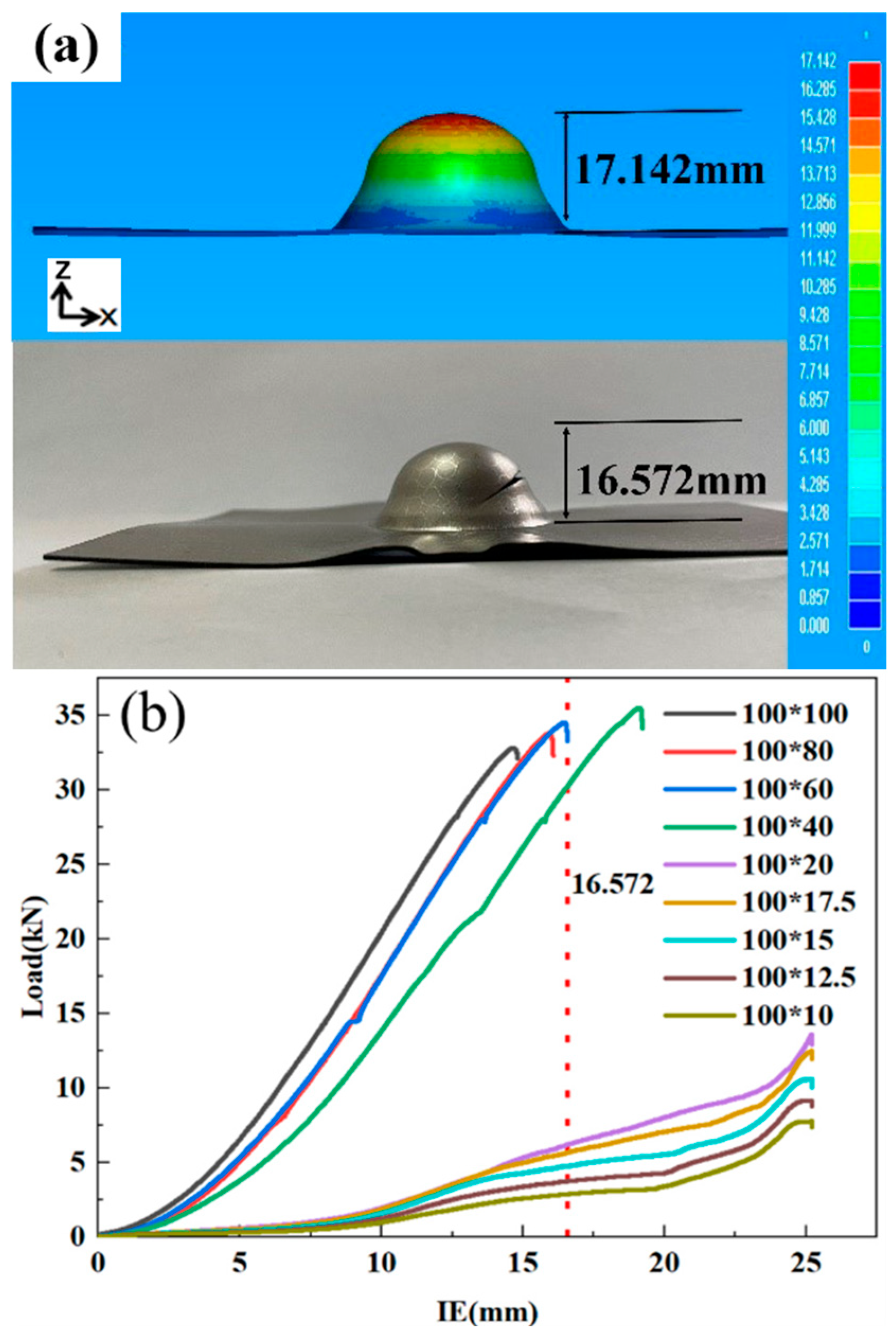
- The cupping test under finite element simulation and experiment shows that under the simulation process parameters of stamping speed of 20 mm/s, blank holder force of 3 MPa, and friction coefficient of 0.120, the IE value of the specimen reaches 17.142 mm, which is slightly larger than that of 16.572 mm obtained by experiment. In terms of forming limits, the forming limit curve obtained by simulation is higher than that obtained by experiment.
- The stamping speed, blank holder force, and friction coefficient have a significant impact on the springback amount. Based on the verification through numerical simulation and on-site experiments in enterprises, the optimum springback was obtained when the fillet radius R was 5 mm, the stamping speed was 20 mm/s, the blank holder force was 3 MPa, and the friction coefficient was 0.120.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alomari, A.S. Serrated yielding in austenitic stainless steels. Mater. High Temp. 2021, 38, 222–236. [Google Scholar] [CrossRef]
- Xie, Y.M.; Feng, K.; Du, M.Y.; Li, L. Robust optimization of stamping process based on Bayesian estimation. J. Manuf. Process. 2023, 101, 245–258. [Google Scholar] [CrossRef]
- Emmens, W.C.; Sebastiani, G.; Van Den Boogaard, A.H. The technology of Incremental Sheet Forming-A brief review of the history. J. Mater. Process. Technol. 2010, 210, 981–997. [Google Scholar] [CrossRef]
- Ieazadeh, A.R.; Shamloofard, M.; Assempour, A. Some improvements on the one-step inverse isogeometric analysis by proposing a multi-step inverse isogeometric methodology in sheet metal stamping processes. Appl. Math. Model. 2021, 91, 476–492. [Google Scholar] [CrossRef]
- Wang, Z.L.; Yuan, Y.J.; Zhang, S.Y.; Lin, Y.C.; Tan, J.R. A multi-state fusion informer integrating transfer learning for metal tube bending early wrinkling prediction. Appl. Soft. Comput. 2024, 151, 110991. [Google Scholar] [CrossRef]
- Wang, G.D.; Cao, J.Y.; Zhou, Y.R.; Tian, N. Effects of Mg content on microstructure, mechanical properties and fracture behavior of wrought Al-8Si-(<0.01–1.32)Mg alloy sheets in T6 temper. J. Alloys Compd. 2023, 960, 170818. [Google Scholar]
- Huang, H.; Yang, W.; Ming, W.Y.; Zhang, G.J.; Xu, Y.J.; Zhang, Z. Mechanism of springback behavior in ultra-thin glass molding process: A molecular dynamics study. J. Non. Cryst. Solids 2022, 596, 121841. [Google Scholar] [CrossRef]
- Kothunde, N.; Krishna, G.; Shenoy, S.K.; Gupta, A.K.; Singh, S.K. Experimental and theoretical investigation of forming limit diagram for Ti-6Al-4V alloy at warm condition. Int. J. Mater. 2017, 10, 255–266. [Google Scholar]
- Adamus, J.; Dyja, K.; Motyka, M. Experimental and Theoretical Determination of Forming Limit Curve. Arch. Metall. Mater. 2015, 60, 1881–1885. [Google Scholar] [CrossRef][Green Version]
- Narayanasamy, R.; Narayanan, C.S. Experimental analysis and evaluation of forming limit diagram for interstitial free steels. Mater. Des. 2007, 28, 1490–1512. [Google Scholar] [CrossRef]
- Narayanasamy, R.; Narayanan, C.S. Forming, fracture and wrinkling limit diagram for if steel sheets of different thickness. Mater. Des. 2007, 29, 1467–1475. [Google Scholar]
- Kuroda, M.; Tvergaard, V. Forming limit diagrams for anisotropic metal sheets with different yield criteria. Int. J. Solids Struct. 2000, 37, 5037–5059. [Google Scholar] [CrossRef]
- Geiger, M.; Merklein, M. Determination of forming limit diagrams—A new analysis method for characterization of materials’ formability. CIRP Ann. Manuf. Technol. 2003, 52, 213–216. [Google Scholar] [CrossRef]
- Nakazima, K.; Kikuma, T.; Hasuka, K. Study on the formability of steel sheets. Yawata Tech. Rep. Sept. 1968, 264, 8414–8442. [Google Scholar]
- Keeler, S.P.; Backhofen, W.A. Plastic Instability and Fracture in Sheet Stretched over Rigid Punches. ASM Sci. J. 1963, 56, 25–48. [Google Scholar]
- Goodwin, G.M. Application of Strain Analysis to Sheet Metal Forming Problems in the Press Shop. SAE Trans. 1968, 77, 380–387. [Google Scholar]
- Wang, L.; Lee, T.C. The effect of yield criteria on the forming limit curve prediction and the deep drawing process simulation. Int. J. Mach. Tool. Manu. 2006, 46, 988–995. [Google Scholar] [CrossRef]
- Takuda, H.; Mori, K.; Hatta, N. The application of some criteria for ductile fracture to the prediction of the forming limit of sheet metals. J. Mater. Process. Technol. 1999, 95, 116–121. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczynski, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Neuhauser, F.M.; Terrazas, O.; Manopulo, N.; Pavel, H.; Chester, V.T. The bending dependency of forming limit diagrams. Int. J. Mater. Form. 2019, 12, 815–825. [Google Scholar] [CrossRef]
- Mohamadnejad, Z.S.; Basti, A.; Ansari, R. Prediction of forming limit diagram for different strain paths in crystalline FCC ideal-orientation material. Mech. Time-Depend. Mater. 2023, 27, 1123–1138. [Google Scholar] [CrossRef]
- Hattalli, V.L.; Srivatsa, S.R. Sheet Metal Forming Processes-Recent Technological Advances. Mater. Today Proc. 2018, 5, 2564–2574. [Google Scholar] [CrossRef]
- Zhang, D.H.; Bai, D.P.; Liu, J.B.; Gou, Z.; Guo, C. Formability behaviors of 2A12 thin-wall part based on DYNAFORM and stamping experiment. Compos. B Eng. 2013, 55, 591–598. [Google Scholar] [CrossRef]
- Hussaini, S.M.; Singh, S.K.; Gupta, A.K. Experimental and numerical investigation of formability for austenitic stainless steel 316 at elevated temperatures. J. Mater. Res. Technol. 2014, 3, 17–24. [Google Scholar] [CrossRef]
- Li, F.Q.; Jiang, J.S.; Wang, J.M.; Wang, J.G.; Chen, X.Y. Experimental study and numerical simulation on springback of Ti-6Al-4V alloy under hot U-bending. J. Mech. Sci. Technol. 2023, 37, 3691–3697. [Google Scholar] [CrossRef]
- Folle, L.F.; Schaeffer, L. Effect of surface roughness and lubrication on the friction coefficient in deep drawing processes of aluminum alloy aa1100 with fem analysis. Materia 2019, 24, e12446. [Google Scholar]
- Tiwari, P.R.; Rathore, A.; Bodkhe, M.G. Factors affecting the deep drawing process—A review. Mater. Today Proc. 2022, 56, 2902–2908. [Google Scholar] [CrossRef]
- Müller, M.; Uhlmann, L.; Herrig, T.; Bergs, T. Numerical analysis of the dependence of damage on friction during deep drawing of asymmetric geometries. Adv. Ind. Manuf. Eng. 2024, 8, 1–10. [Google Scholar] [CrossRef]
- Hou, Z.X.; Liu, Z.G.; Wan, M.; Wu, X.D.; Yang, B.; Lu, X. An Investigation on Anisotropy Behavior and Forming Limit of 5182-H111 Aluminum Alloy. J. Mater. Eng. Perform. 2020, 29, 3745–3756. [Google Scholar] [CrossRef]
- Hussaini, S.M.; Krishna, G.; Gupta, A.K.; Singh, S.K. Development of experimental and theoretical forming limit diagrams for warm forming of austenitic stainless steel 316. J. Manuf. Process. 2015, 18, 151–158. [Google Scholar] [CrossRef]
- Djavanroodi, F.; Derogar, A. Experimental and numerical evaluation of forming limit diagram for Ti6Al4V titanium and Al6061-T6 aluminum alloys sheets. Mater. Des. 2010, 31, 4866–4875. [Google Scholar] [CrossRef]
- Ahmadi, S.; Eivani, A.R.; Akbarzadeh, A. Experimental and analytical studies on the prediction of forming limit diagrams. Comp. Mater. Sci. 2009, 44, 1252–1257. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Zhu, X.H. Review of theoretical models of the strain-based FLD and their relevance to the stress-based FLD. Int. J. Plast. 2004, 20, 1463–1486. [Google Scholar] [CrossRef]
- Ju, L.; Mao, T.T.; Li, H.B. An experimental and numerical study of forming limits of AA5182-O. Int. J. Adv. Manuf. Technol. 2015, 79, 221–228. [Google Scholar] [CrossRef]
- Barlat, F.; Lian, K. Plastic behavior and stretchability of sheet metals. Part I: A yield function for orthotropic sheets under plane stress conditions. Int. J. Plast. 1989, 5, 51–66. [Google Scholar] [CrossRef]
- Sudarsan, C.; Prasad, K.S.; Hazra, S.; Panda, S.K. Forming of serpentine micro-channels on SS304 and AA1050 ultra-thin metallic sheets using stamping technology. J. Manuf. Process. 2020, 56, 1099–1113. [Google Scholar] [CrossRef]
- Xu, Y.W.; Li, W.Z.; Tian, W.; Liang, J.G.; Zhang, G.Q.; Zhao, C.J. Microstructural evolution of external cold extrusion spinning 304 stainless steel with cumulative large deformation in multiple passes. Int. J. Adv. Manuf. Technol. 2022, 123, 1009–1024. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, S.H.; Cheng, M.; Song, H.W. Effect of Loading Modes on Mechanical Property and Strain Induced Martensite Transformation of Austenitic Stainless Steels. Acta Metall. Sin. 2013, 7, 775–782. [Google Scholar] [CrossRef]
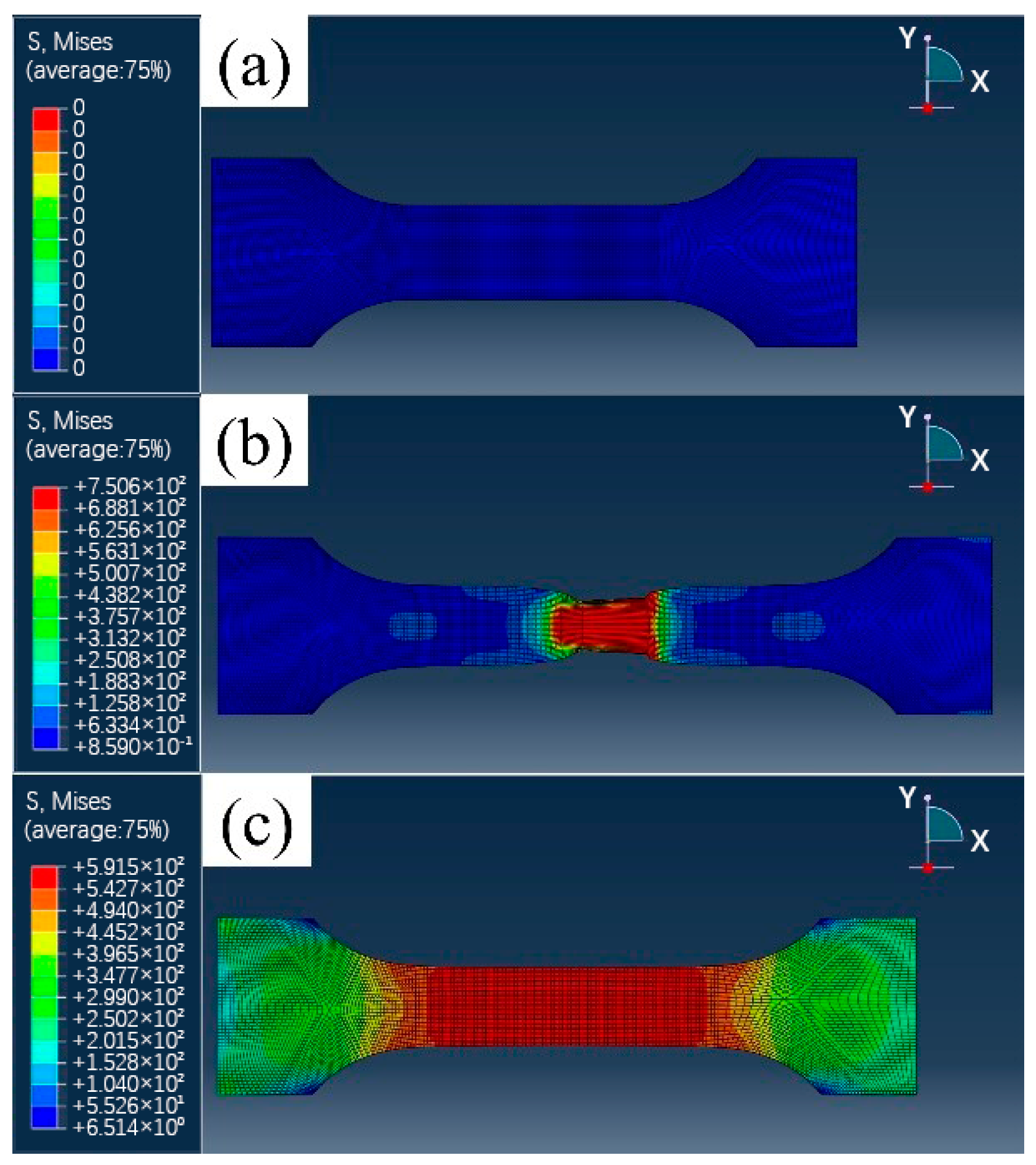
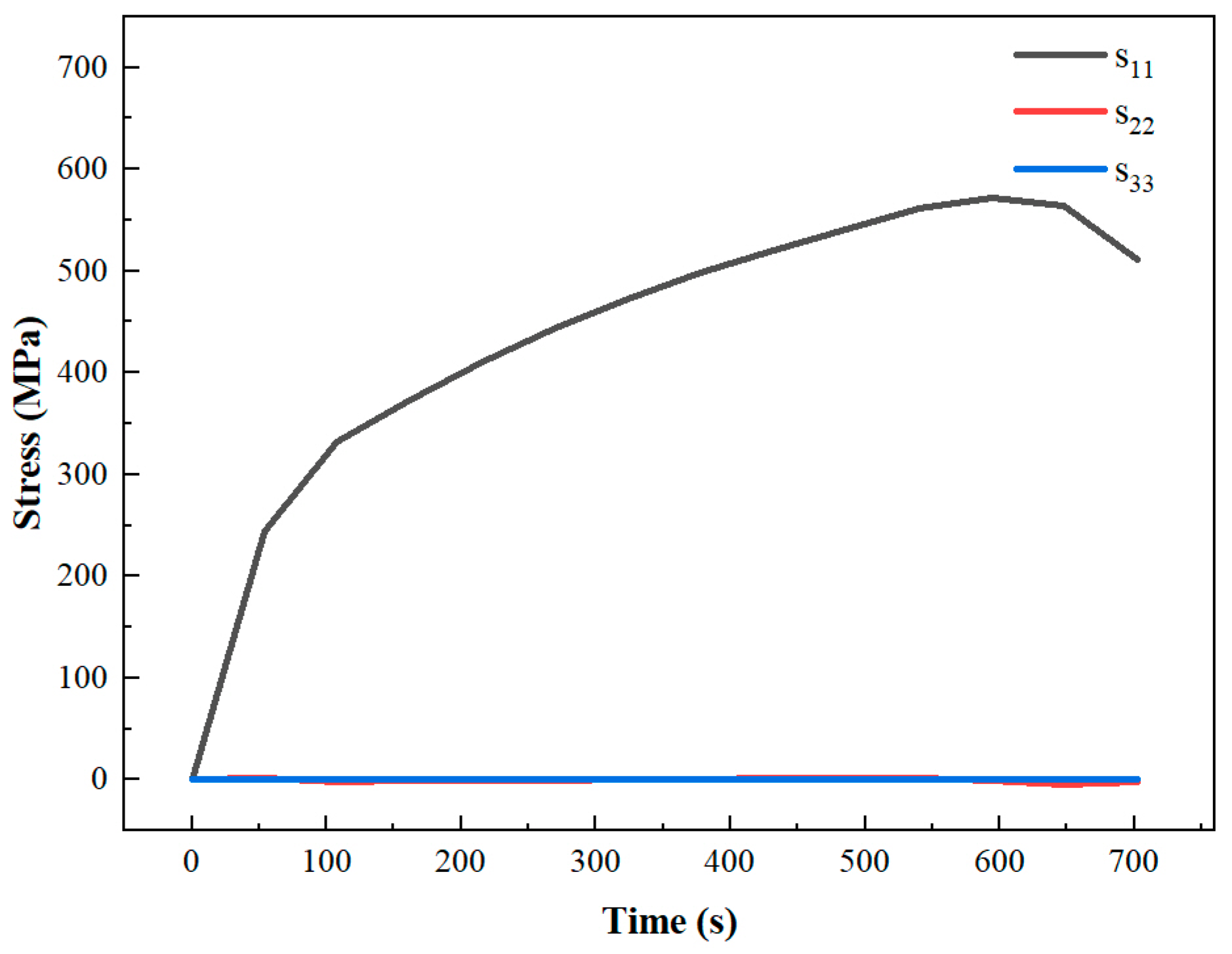
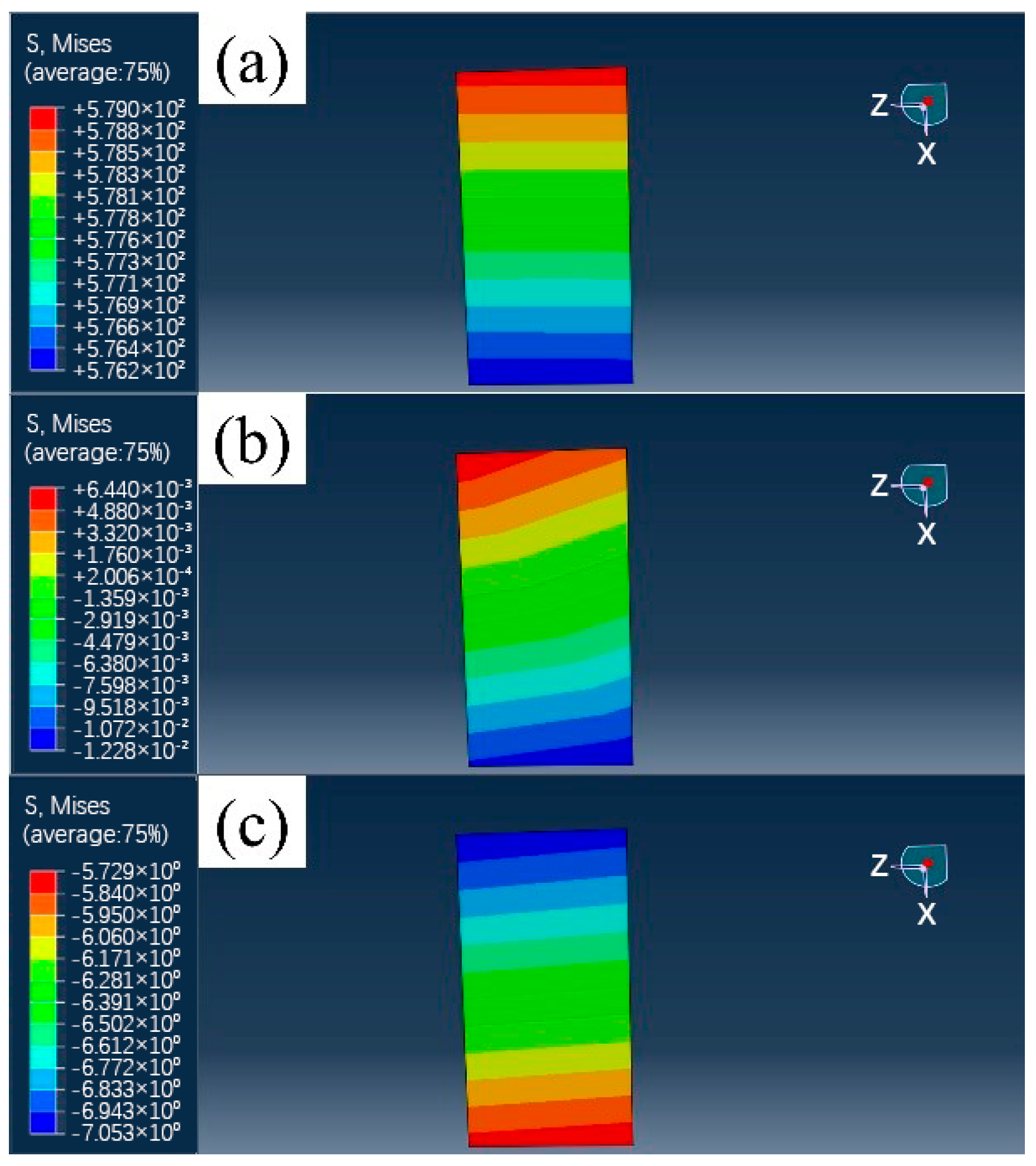
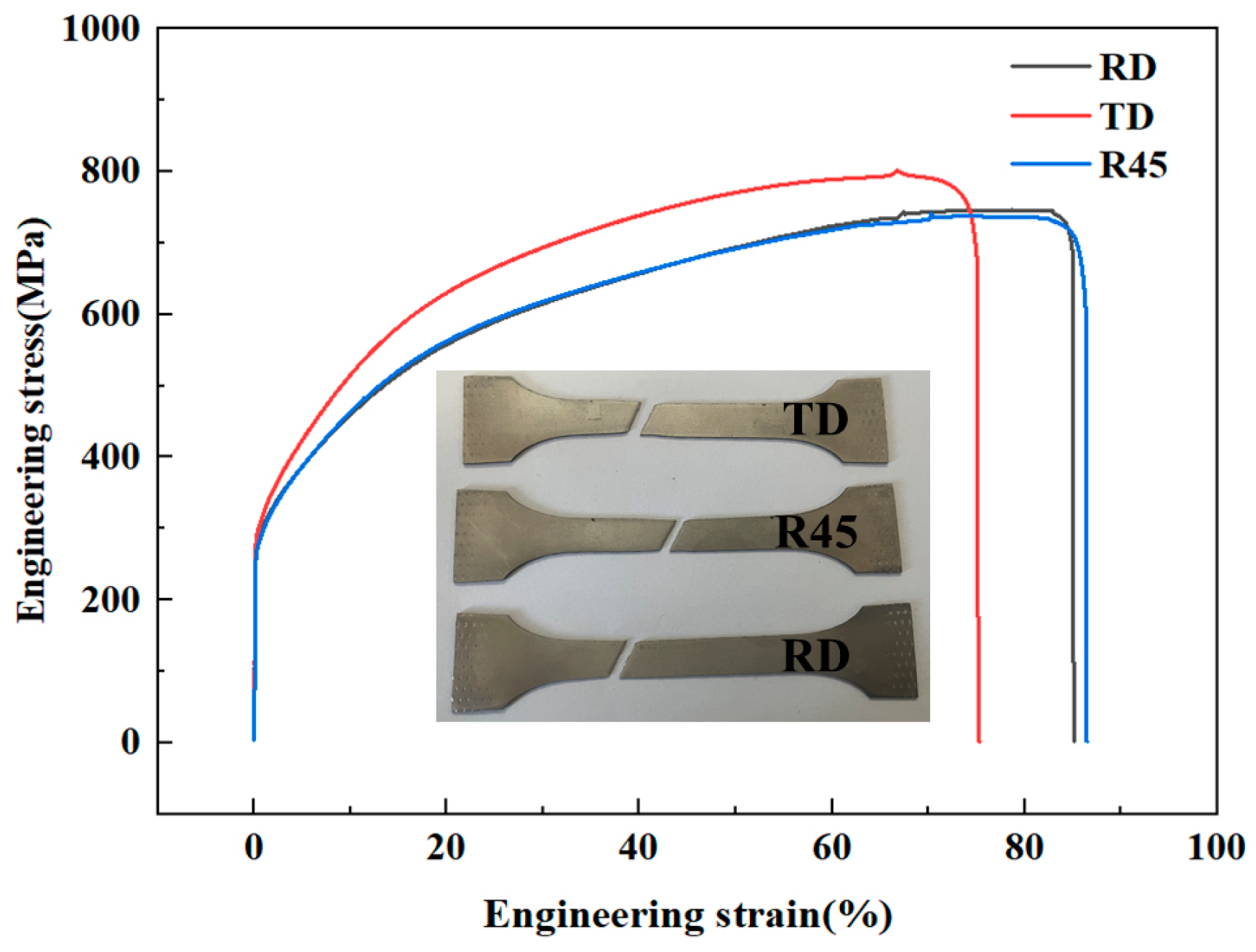



| C | Si | Mn | P | S | Ni | Cr |
|---|---|---|---|---|---|---|
| 0.03–0.08 | ≤1 | ≤2 | ≤0.05 | ≤0.03 | 8–11 | 18–20 |
| Stamping Speed (mm/s) | Closing Speed of Holder Ring (mm/s) | Blank Holder Force (Mpa) | Friction Coefficient |
|---|---|---|---|
| 20 | 10 | 3 | 0.125 |
| Tensile Strain Hardening Exponent (n) | Plastic Strain Ratio (r) | Poisson’s Ratio (v) | m | r0 | r45 | r90 |
|---|---|---|---|---|---|---|
| 0.23 | 1 | 0.28 | 8 | 0.71 | 1.08 | 0.73 |
| Specimen | Yield Strength (Mpa) | Tensile Strength (Mpa) | Elongation (%) | Elastic Modulus (Gpa) | Yield Ratio |
|---|---|---|---|---|---|
| RD | 277.45 ± 3.52 | 746.20 ± 3.90 | 85.04 ± 0.83 | 154.08 ± 2.33 | 0.37 ± 0.02 |
| R45 | 273.37 ± 4.12 | 740.84 ± 2.98 | 85.79 ± 1.01 | 181.70 ± 4.86 | 0.37 ± 0.01 |
| TD | 293.00 ± 8.61 | 800.93 ± 6.72 | 75.06 ± 0.97 | 218.90 ± 9.36 | 0.37 ± 0.01 |
| Die Fillet Radius R | Stamping Speed | Blank Holder Force | Friction Coefficient | Stretching Depth | Die Clearance |
|---|---|---|---|---|---|
| 5 mm | 20 mm/s | 3 MPa | 0.120 | 210 mm | 1.1 t |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xu, J.; Luan, B. Investigation on Strain-Forming Limits and Manufacturing Optimization of a Single Deep-Drawing Process Concerning 304 Stainless Steel’s Thin Sheet. Metals 2025, 15, 1008. https://doi.org/10.3390/met15091008
Li Y, Xu J, Luan B. Investigation on Strain-Forming Limits and Manufacturing Optimization of a Single Deep-Drawing Process Concerning 304 Stainless Steel’s Thin Sheet. Metals. 2025; 15(9):1008. https://doi.org/10.3390/met15091008
Chicago/Turabian StyleLi, Yajie, Jianguang Xu, and Baifeng Luan. 2025. "Investigation on Strain-Forming Limits and Manufacturing Optimization of a Single Deep-Drawing Process Concerning 304 Stainless Steel’s Thin Sheet" Metals 15, no. 9: 1008. https://doi.org/10.3390/met15091008
APA StyleLi, Y., Xu, J., & Luan, B. (2025). Investigation on Strain-Forming Limits and Manufacturing Optimization of a Single Deep-Drawing Process Concerning 304 Stainless Steel’s Thin Sheet. Metals, 15(9), 1008. https://doi.org/10.3390/met15091008





