Numerical and Experimental Investigations on the Compressive Properties of the Graded BCC Lattice Cylindrical Shells Made of 316L Stainless Steel
Abstract
1. Introduction
2. Materials, Experiments, and Methodology
2.1. Design of Structure
2.2. Specimen Preparation
2.3. Microstructure Characterization
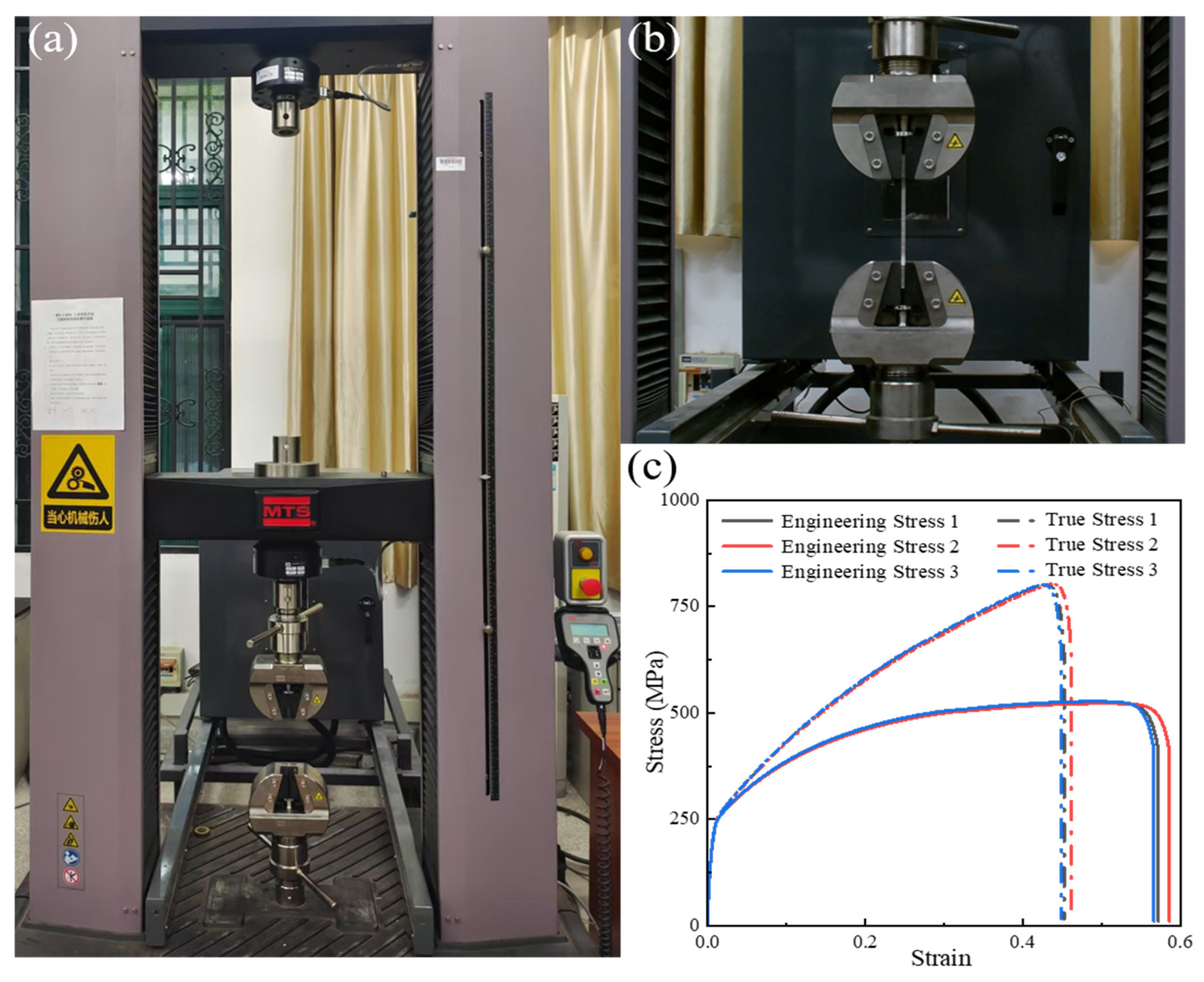
2.4. Quasi-Static Experimental Test
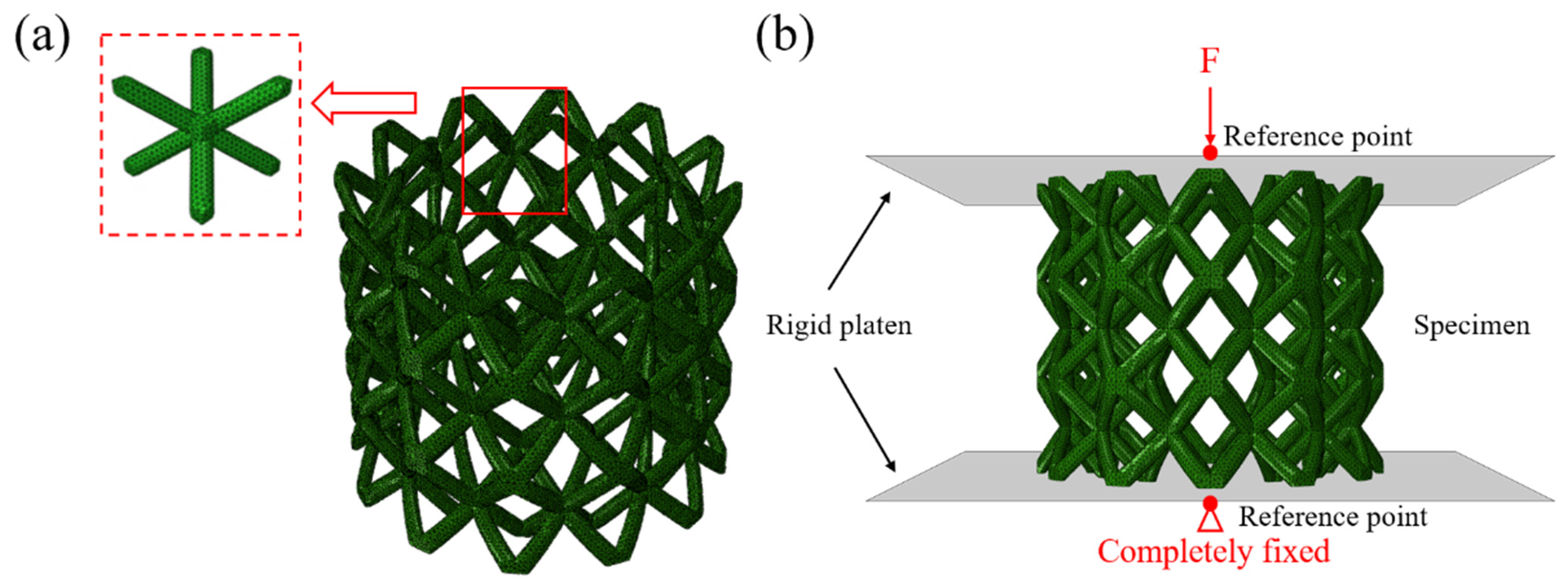
2.5. Computational Model
3. Results and Discussion
3.1. Quasi-Static Compression Mechanical Behavior
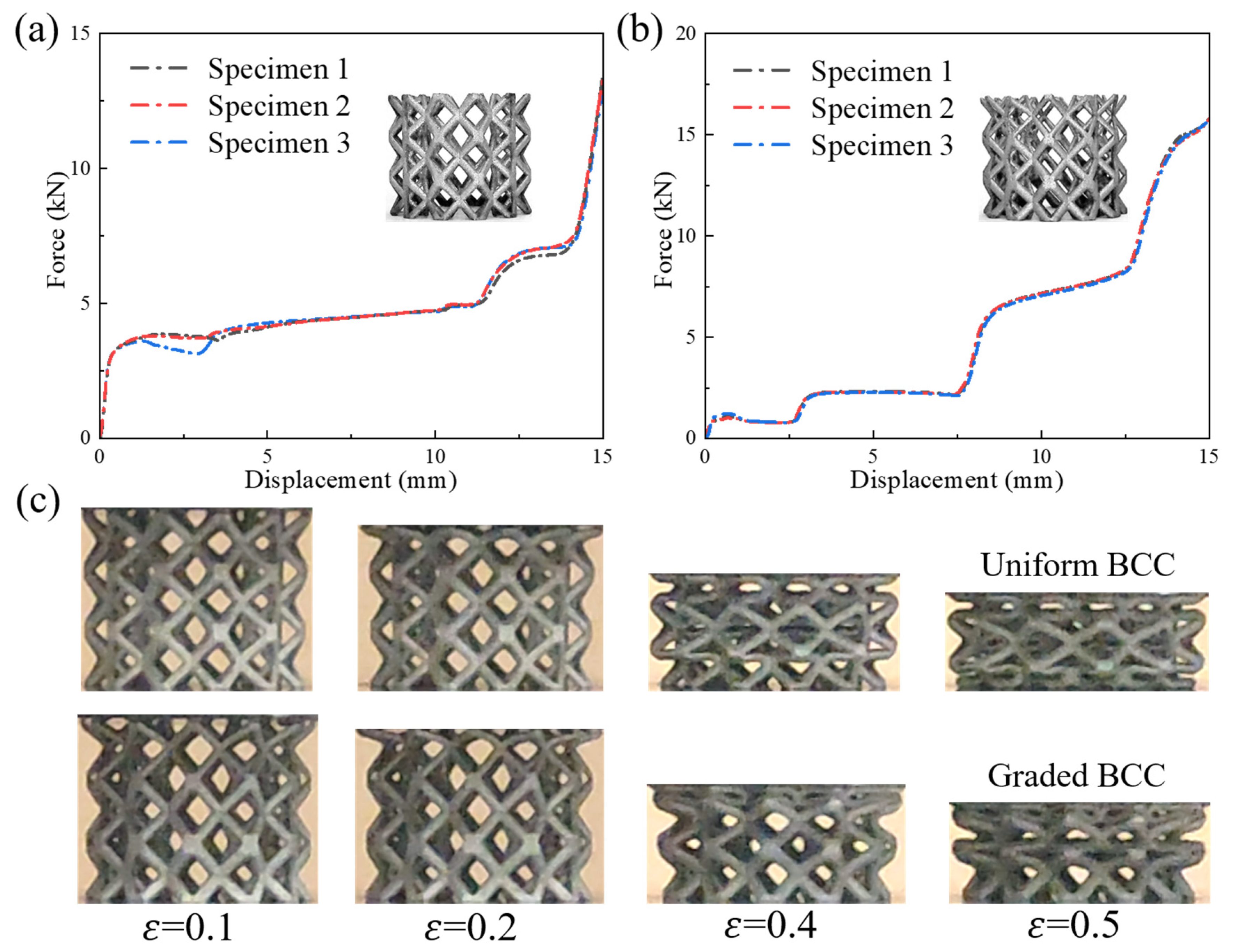
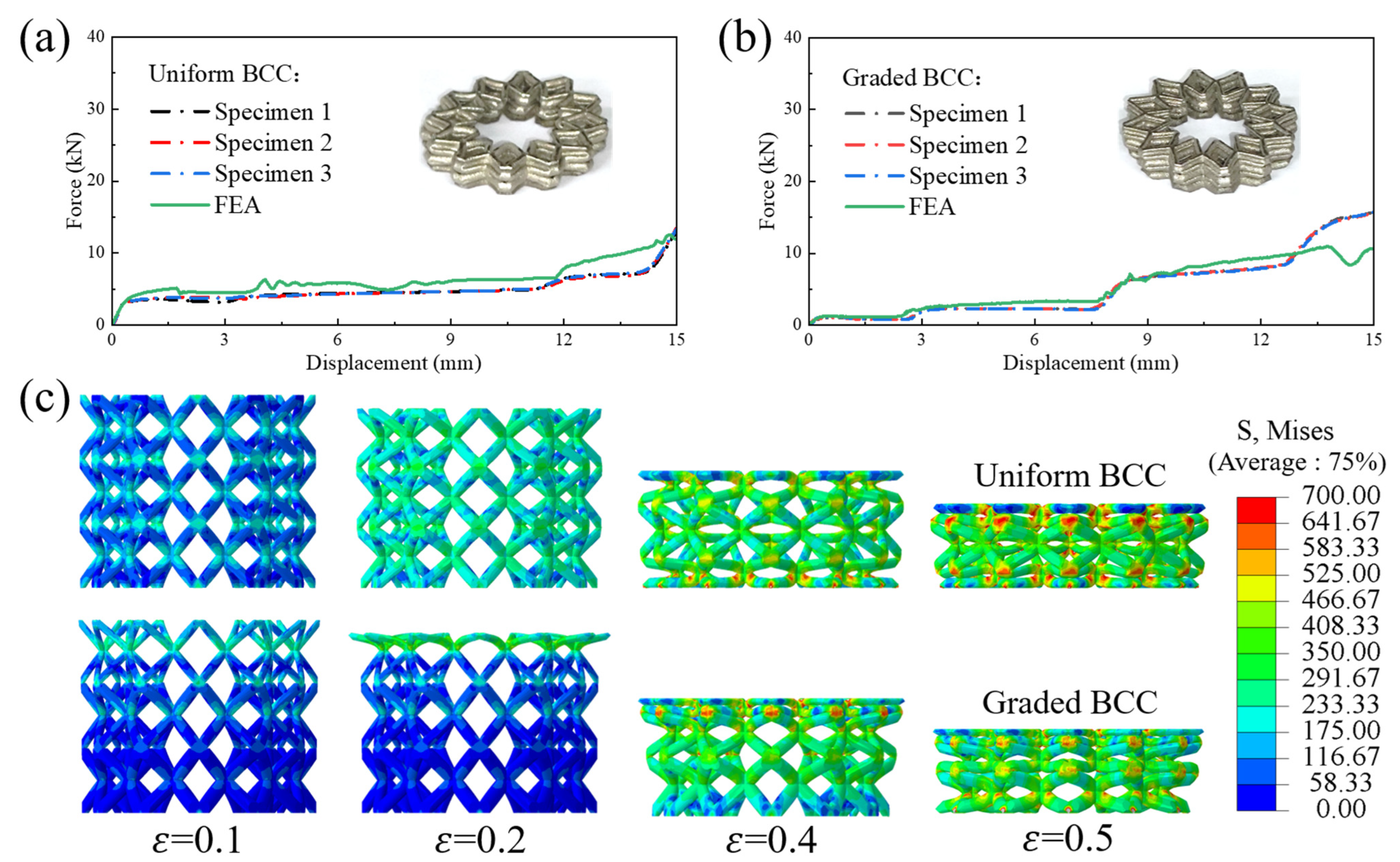
3.1.1. Experimental Results
3.1.2. Validation of Simulation Results
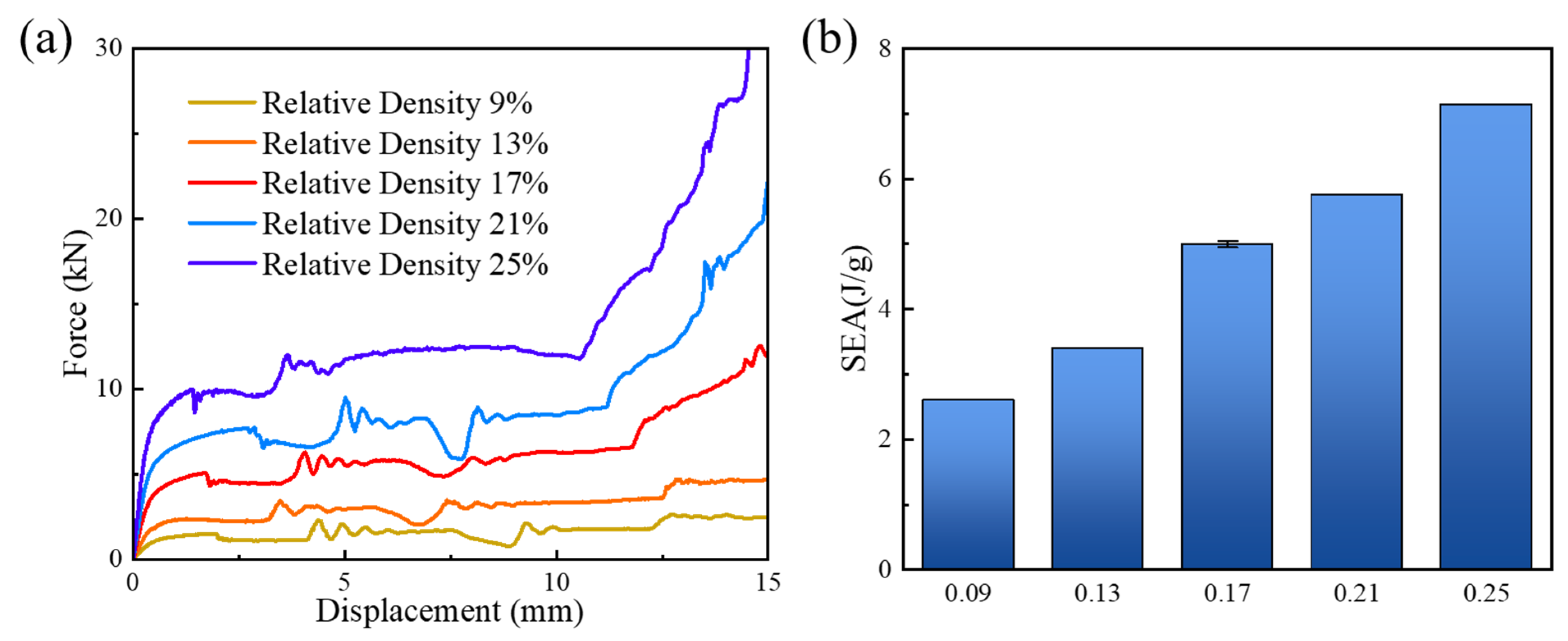
3.1.3. Effect of Relative Density
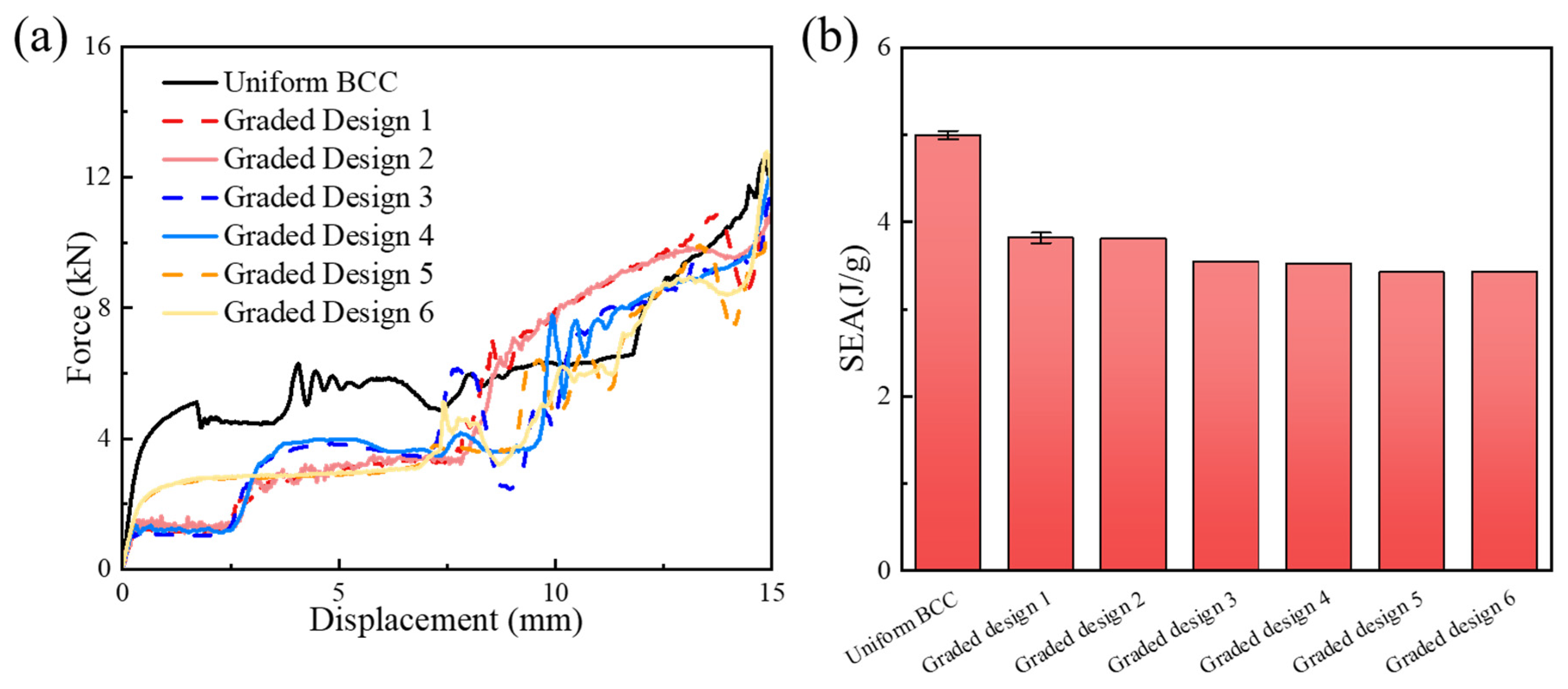
3.1.4. Effect of Gradient Distribution
3.1.5. Deformation Mode
3.2. Dynamic Compression Mechanical Behavior
3.2.1. Low-Speed Compression Behavior (100/s)
3.2.2. Medium-Speed Compression Behavior (500/s)
3.2.3. High-Speed Compression Behavior (1000/s)
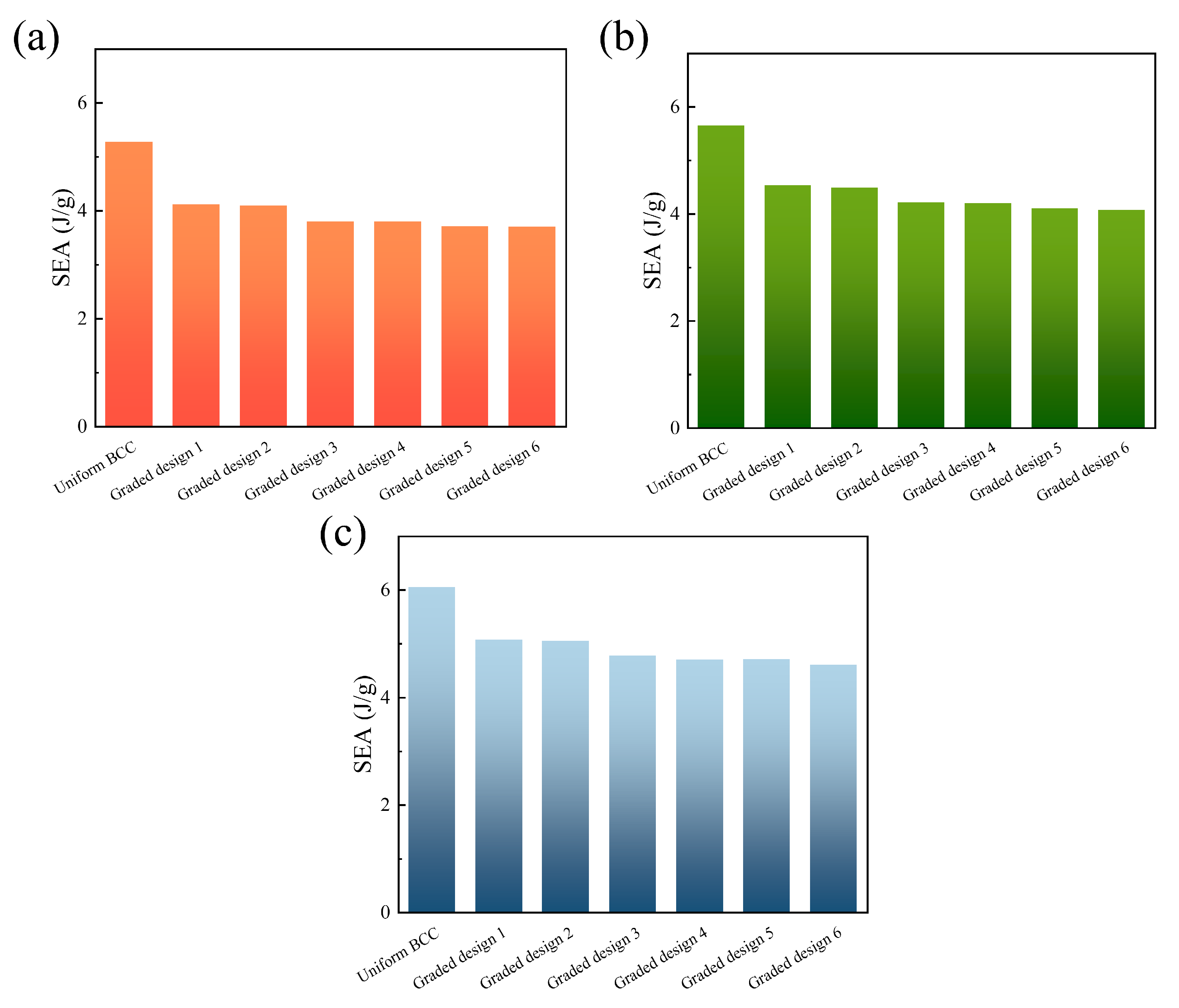
3.2.4. Key Property Parameter
4. Conclusions
- (1)
- Under quasi-static compression loading, when the relative density of the uniform specimen increased from 9% to 25%, a 175% increase in SEA could be witnessed. Three distinct stress plateau stages were observed in the graded specimens, and the quasi-static compression deformation process was closely related to the relative density distribution characteristics of the different layers.
- (2)
- Under dynamic compression loading, a higher performance curve could be seen at a higher loading velocity. There existed a complicated competitive relationship between the deformation law induced by the gradient distribution and the localized deformation induced by high-speed loading.
- (3)
- As for the SEA value, the uniform specimen exhibited higher values than the graded structures across all loading speeds. Among the gradient designs, graded-1 and graded-2 ones demonstrated the highest SEA values. Additionally, a higher SEA value could be obtained under a higher loading velocity. When compared with the SEA value under low-speed loading conditions, a 26.95% maximum increase could be seen in the graded-5 specimen under high-speed loading.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Changdar, A.; Chakraborty, S.S.; Li, Y.; Wen, C. Laser additive manufacturing of aluminum-based stochastic and nonstochastic cellular materials. J. Mater. Sci. Technol. 2024, 183, 89–119. [Google Scholar] [CrossRef]
- Al-Jamal, A.A.; Barsoum, I.; Abu Al-Rub, R.K. Defect-sensitivity of stochastic and periodic minimal surface titanium cellular materials. Int. J. Mech. Sci. 2025, 289, 110063. [Google Scholar] [CrossRef]
- Hong, Y.; Li, X.; Yan, Z.; Liu, Z.; Zhuang, Z. Designing spongy-bone-like cellular materials: Matched topology and anisotropy. Int. J. Mech. Sci. 2025, 285, 109788. [Google Scholar] [CrossRef]
- Ramirez-Chavez, I.E.; Varma, R.; Anderson, D.; Lazar, P.J.L.; Shinde, M.; Goode, Z.; Bhate, D. Strain redistribution in stochastically perturbed single and dual-phase cellular materials under quasistatic compression. Manuf. Lett. 2024, 41, 1034–1045. [Google Scholar] [CrossRef]
- Cao, X.; Jiang, Y.; Zhao, T.; Wang, P.; Wang, Y.; Chen, Z.; Li, Y.; Xiao, D.; Fang, D. Compression experiment and numerical evaluation on mechanical responses of the lattice structures with stochastic geometric defects originated from additive-manufacturing. Compos. B Part Eng. 2020, 194, 108030. [Google Scholar] [CrossRef]
- Ha, N.S.; Lu, G. A review of recent research on bio-inspired structures and materials for energy absorption applications. Compos. Part B Eng. 2020, 181, 107496. [Google Scholar] [CrossRef]
- Bieler, S.; Weinberg, K. Energy absorption in lattice-structured materials under impact loading. Eur. J. Mech. A Solids 2025, 114, 105734. [Google Scholar] [CrossRef]
- Cao, X.; Duan, S.; Liang, J.; Wen, W.; Fang, D. Mechanical properties of an improved 3D-printed rhombic dodecahedron stainless steel lattice structure of variable cross section. Int. J. Mech. Sci. 2018, 145, 53–63. [Google Scholar] [CrossRef]
- Dong, Y.; Yan, F.; Zhang, Z. Three-dimensional annular negative stiffness honeycomb structure design and performance study. Compos. Struct. 2025, 367, 119229. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y. Energy absorption characteristic of auxetic metamaterials honeycombs and lattices with negative thermal expansion. Thin-Walled Struct. 2025, 208, 112824. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, D.; Liao, B.; Fang, S.; Liu, L.; Gao, R.; Li, Y. Numerical analysis of the mechanical behavior and energy absorption of a novel P-lattice. Thin-Walled Struct. 2020, 157, 107147. [Google Scholar] [CrossRef]
- Viswanath, A.; Khalil, M.; Khan, M.K.A.; Cantwell, W.J.; Khan, K.A. Hierarchical cubic lattice structures with bending- and stretching-dominated cellular designs for enhanced buckling resistance. Int. J. Lightweight Mater. Manuf. 2025, 8, 310–320. [Google Scholar] [CrossRef]
- Huang, Z.; Cao, X.; Niu, H.; Ma, B.; Du, X.; Zhou, Z.; Yang, H.; Du, M.K. Numerical and experimental evaluations on the defect sensitivity of the performance of BCC truss-lattice structures. Mech. Mater. 2024, 191, 104937. [Google Scholar] [CrossRef]
- Rahimi, S.; Asghari, M. Design and evaluation of two proposed hybrid FCC-BCC lattice structures for enhanced mechanical performance. Heliyon 2025, 11, e40911. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, X.; Sun, Z.; Guo, Y.; Li, Y.; Chang, H.; Zhou, L. A study on the compressive mechanical properties of 316L diamond lattice structures manufactured by laser powder bed fusion based on actual relative density. J. Manuf. Process. 2022, 84, 414–423. [Google Scholar] [CrossRef]
- Chen, Z.; Mordehai, D. Homogenization of the yield surface of body-centered cubic and octet lattice structures under multiaxial loadings. Int. J. Solids Struct. 2025, 320, 113486. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of compressive properties of SLM-fabricated multi-layer lattice structures by experimental test and μ-CT-based finite element analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Zhang, P.; Yu, P.; Zhang, R.; Chen, X.; Tan, H. Grid octet truss lattice materials for energy absorption. Int. J. Mech. Sci. 2023, 259, 108616. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Latture, R.M.; Rodriguez, R.X.; Holmes, L.R.; Zok, F.W. Effects of nodal fillets and external boundaries on compressive response of an octet truss. Acta Mater. 2018, 149, 78–87. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A. Collapse of truss core sandwich beams in 3-point bending. Int. J. Solids Struct. 2001, 38, 6275–6305. [Google Scholar] [CrossRef]
- Maiti, S.K.; Gibson, L.J.; Ashby, M.F. Deformation and energy absorption diagrams for cellular solids. Acta Metall. 1984, 32, 1963–1975. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, X.; Yang, G.; Song, B.; Sha, H. Design and mechanical performance analysis of T-BCC lattice structures. J. Mater. Res. Technol. 2024, 32, 1538–1551. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, J.; Yang, J.; Hou, J.; Li, J.; Lin, J. Microstructure and mechanical properties of 316L stainless steel manufactured by multi-laser selective laser melting (SLM). Mater. Sci. Eng. A 2024, 913, 147053. [Google Scholar] [CrossRef]
- Siddiqui, N.A.; Muzamil, M.; Jamil, T.; Hussain, G. Heat sources in wire arc additive manufacturing and their impact on macro-microstructural characteristics and mechanical properties—An overview. Smart Mater. Manuf. 2025, 3, 100059. [Google Scholar] [CrossRef]
- Strano, G.; Hao, L.; Everson, R.M.; Evans, K.E. Surface roughness analysis, modelling and prediction in selective laser melting. J. Mater. Process. Technol. 2013, 213, 589–597. [Google Scholar] [CrossRef]
- Zhong, T.; He, K.; Li, H.; Yang, L. Mechanical properties of lightweight 316L stainless steel lattice structures fabricated by selective laser melting. Mater. Des. 2019, 181, 108076. [Google Scholar] [CrossRef]
- McKown, S.; Shen, Y.; Brookes, W.K.; Sutcliffe, C.J.; Cantwell, W.J.; Langdon, G.S.; Nurick, G.N.; Theobald, M.D. The quasi-static and blast loading response of lattice structures. Int. J. Impact Eng. 2008, 35, 795–810. [Google Scholar] [CrossRef]
- Guo, H.; Takezawa, A.; Honda, M.; Kawamura, C.; Kitamura, M. Finite element simulation of the compressive response of additively manufactured lattice structures with large diameters. Comput. Mater. Sci. 2020, 175, 109610. [Google Scholar] [CrossRef]
- Ptochos, E. Elastic modulus and Poisson’s ratio determination of micro-lattice cellular structures by analytical, numerical and homogenisation methods. J. Sandw. Struct. Mater. 2012, 14, 597–626. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.; Mines, R.; Tsopanos, S.; Smith, M. An investigation into the compressive properties of stainless steel micro-lattice structures. J. Sandw. Struct. Mater. 2010, 13, 303–329. [Google Scholar] [CrossRef]
- Babaee, S.; Jahromi, B.H.; Ajdari, A.; Nayeb-Hashemi, H.; Vaziri, A. Mechanical properties of open-cell rhombic dodecahedron cellular structures. Acta Mater. 2012, 60, 2873–2885. [Google Scholar] [CrossRef]
- Cao, X.; Ren, X.; Zhao, T.; Li, Y.; Xiao, D.; Fang, D. Numerical and theoretical analysis of the dynamic mechanical behaviour of a modified rhombic dodecahedron lattice structure. Int. J. Mech. Mater. Des. 2021, 17, 271–283. [Google Scholar] [CrossRef]
- Scalzo, F.; Totis, G.; Vaglio, E.; Sortino, M. Experimental study on the high-damping properties of metallic lattice structures obtained from SLM. Precis. Eng. 2021, 71, 63–77. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, D.; Peng, H.; Yuan, W.; Zhang, Z.; Yang, Z.; Zhang, Z. In-plane crashworthiness study of bio-inspired metallic lattice structure based on deep-sea glass sponge. Thin-Walled Struct. 2024, 205, 112505. [Google Scholar] [CrossRef]
- Collini, F.; Meneghetti, G. Towards a fracture mechanics-based fatigue assessment of lattice structures obtained from additive manufacturing of metallic powders. Mater. Des. 2024, 244, 113077. [Google Scholar] [CrossRef]
- Waqar, S.; Hussain, S.; Ren, C.; Wang, M.; Nazir, A.; Dan, X.; Wang, C.; Chen, Z. Superior strength and energy absorption capability of LPBF metallic functionally graded lattice structures. Thin-Walled Struct. 2024, 205, 112471. [Google Scholar] [CrossRef]
- Eren, O.; Yüksel, N.; Börklü, H.R.; Sezer, H.K.; Canyurt, O.E. Deep learning-enabled design for tailored mechanical properties of SLM-manufactured metallic lattice structures. Eng. Appl. Artif. Intell. 2024, 130, 107685. [Google Scholar] [CrossRef]
- Arslan Bin Riaz, M.; Güden, M. A review of the experimental and numerical studies on the compression behavior of the additively produced metallic lattice structures at high and low strain rates. Def. Technol. 2025, 49, 1–49. [Google Scholar] [CrossRef]
- Wu, F.; Lin, C.; Ge, S.; Xue, X. Energy absorption performance of woven metallic lattices with orthogonal spiral wires under quasi-static compression. Thin-Walled Struct. 2024, 202, 112121. [Google Scholar] [CrossRef]
- Zeng, R.; Xu, M.; Wang, Y.; Guo, J.; Zhang, R.; Yan, B.; Zhao, Z.; Wang, P.; Duan, S.; Lei, H. Three-dimensional bi-metallic lattice with multi-directional zero thermal expansion. Compos. Struct. 2023, 323, 117499. [Google Scholar] [CrossRef]
- Song, W.; Feng, G.; Yu, G.; Shi, G.; Xiao, L. Dynamic mechanical behavior of additively manufactured bio-inspired metallic lattice structure subjected to high strain rate impact loading. Int. J. Impact Eng. 2023, 181, 104752. [Google Scholar] [CrossRef]
- Mazur, M.; Leary, M.; McMillan, M.; Sun, S.; Shidid, D.; Brandt, M. Mechanical properties of Ti6Al4V and AlSi12Mg lattice structures manufactured by Selective Laser Melting (SLM). In Laser Additive Manufacturing: Materials, Design, Technologies, and Applications; Taylor & Francis Inc.: Philadelphia, PA, USA, 2017; pp. 119–161. [Google Scholar]
- Song, X.; Zeng, C.; Hu, J.; Zhao, W.; Liu, L.; Liu, Y.; Leng, J. Compressive behavior and energy absorption of novel body-centered cubic lattice metamaterials incorporating simple cubic truss units. Compos. Struct. 2025, 367, 119230. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, X.; Chen, Z.; Jiang, Y.; Cao, X.; Fang, S.; Zhao, T.; Li, Y.; Fang, D. Numerical and experimental studies on compressive behavior of Gyroid lattice cylindrical shells. Mater. Des. 2020, 186, 108340. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, F.; Chen, J.; Tang, Y.; Zhang, K.; Xie, H.; Xu, T. Dual-graded lattice with mechanical bionics to enhance fatigue performance. Int. J. Mech. Sci. 2024, 279, 109474. [Google Scholar] [CrossRef]
- Laskowska, D.; Szatkiewicz, T.; Bałasz, B.; Mitura, K. Mechanical Properties and Energy Absorption Abilities of Diamond TPMS Cylindrical Structures Fabricated by Selective Laser Melting with 316L Stainless Steel. Materials 2023, 16, 3196. [Google Scholar] [CrossRef]
- Shahriyari, E.; Khiavi, S.G.; Divandari, M.; Ali Boutorabi, S.M. Effect of unit cell topologies on mechanical properties of cylindrical lattice structures fabricated by indirect additive manufacturing. J. Mater. Res. Technol. 2025, 36, 2785–2798. [Google Scholar] [CrossRef]
- Xue, X.; Gao, J.; Zheng, C.; Li, Z.; Liao, J.; Zhang, M. Energy absorption and vibration characteristics of metal/polymer composited pyramidal lattice cylinder structure. Structures 2025, 76, 108878. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, T.; Chen, L.; Guo, Y.; Pan, X.; Zhu, S.; Li, W. Influence of density gradient and hybrid effect on quasi-static axial crushing behavior of lattice cylindrical structures. Thin-Walled Struct. 2023, 186, 110720. [Google Scholar] [CrossRef]
- Kathiresan, M.; Rajamohan, V.; Immanuel R, J.; Gnanasekar, S. Crashworthiness of pomelo-inspired PLA structures with gradient cellular design. Int. J. Mech. Sci. 2025, 299, 110402. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, H.; Huang, W.; Zhang, Y.; Du, G.; Lu, W.; Xiang, X.; Gou, J. Design and crashworthiness analysis of novel gradient hashtag-shaped fractal thin-walled structure. Mater. Des. 2025, 254, 114076. [Google Scholar] [CrossRef]
- Sun, Z.; Gong, Y.; Tian, Y.; Lang, J.; Zhang, J.; Zhao, L.; Hu, N. Design and Mechanical Properties of Layered Gradient Lattice Structures Based on Additive Manufacturing. Addit. Manuf. Front. 2025, 4, 200188. [Google Scholar] [CrossRef]
- Yin, S.; Guo, W.; Wang, H.; Huang, Y.; Yang, R.; Hu, Z.; Chen, D.; Xu, J.; Ritchie, O.R. Strong and Tough Bioinspired Additive-Manufactured Dual-Phase Mechanical Metamaterial Composites. J. Mech. Phys. Solids 2021, 149, 104341. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Tao, C.; Liang, X. Crashworthiness and optimization design of additive manufacturing double gradient lattice enhanced thin-walled tubes under dynamic impact loading. Eng. Fail. Anal. 2024, 166, 108865. [Google Scholar] [CrossRef]
- Lin, H.-B.; Liu, H.-T. Load carrying capacity analysis and gradient design of new 3D zero Poisson’s ratio structures. Mater. Today Commun. 2023, 36, 106915. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, H.; Bi, Y.; Li, Y.; Li, B.; Wang, B. Crashworthiness and gradient optimization of multi-cell thin-walled structures inspired by leaf venation in royal water lily. In Mechanics of Advanced Materials and Structures; Taylor & Francis Inc.: Philadelphia, PA, USA, 2024; pp. 1–17. [Google Scholar]
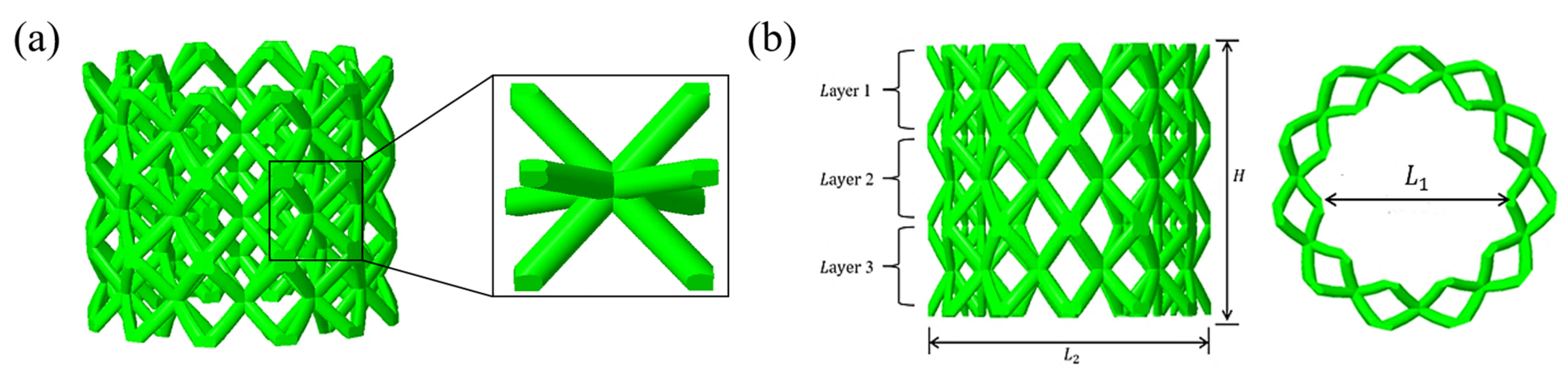




| Sample | ) | (mm) | (mm) | (mm) | (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | |||||||
| Uniform BCC | 0.09 | 0.718 | 20 | 30 | 25 | 0.686 | 0.686 | 0.686 | |
| 0.13 | 1.037 | 0.840 | 0.840 | 0.840 | |||||
| 0.17 | 1.357 | 0.974 | 0.974 | 0.974 | |||||
| 0.21 | 1.676 | 1.096 | 1.096 | 1.096 | |||||
| 0.25 | 1.995 | 1.212 | 1.212 | 1.212 | |||||
| Graded BCC | Graded-1 | 0.17 | 1.357 | 20 | 30 | 25 | 0.686 | 0.974 | 1.212 |
| Graded-2 | 1.212 | 0.974 | 0.686 | ||||||
| Graded-3 | 0.686 | 1.212 | 0.974 | ||||||
| Graded-4 | 0.974 | 1.212 | 0.686 | ||||||
| Graded-5 | 0.974 | 0.686 | 1.212 | ||||||
| Graded-6 | 1.212 | 0.686 | 0.974 | ||||||
| Sample | Designed Mass (g) | Measured Mass (g) | Average (g) | Error | ||
|---|---|---|---|---|---|---|
| Uniform BCC | 0.17 | 1.357 | 13.309 | 12.409 12.887 12.714 | 12.670 | 4.80% |
| Graded BCC | 13.238 | 12.621 13.045 12.736 | 12.801 | 3.30% |
| Density (g/cm3) | Young’s Modulus (GPa) | Poisson’s Ratio | Initial Yield Strength (MP) | Ultimate Strength (MPa) | Ultimate Strain |
|---|---|---|---|---|---|
| 7.89 | 38 | 0.3 | 243 | 800 | 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Ma, W.; Cao, M.; Xu, H.; Luo, W.; Cao, W.; Wang, S.; Qin, Y.; Zhang, X.; Cao, X. Numerical and Experimental Investigations on the Compressive Properties of the Graded BCC Lattice Cylindrical Shells Made of 316L Stainless Steel. Metals 2025, 15, 895. https://doi.org/10.3390/met15080895
Guan Y, Ma W, Cao M, Xu H, Luo W, Cao W, Wang S, Qin Y, Zhang X, Cao X. Numerical and Experimental Investigations on the Compressive Properties of the Graded BCC Lattice Cylindrical Shells Made of 316L Stainless Steel. Metals. 2025; 15(8):895. https://doi.org/10.3390/met15080895
Chicago/Turabian StyleGuan, Yiting, Wenjie Ma, Miao Cao, Hao Xu, Wenchang Luo, Weidong Cao, Siying Wang, Ying Qin, Xiaoyu Zhang, and Xiaofei Cao. 2025. "Numerical and Experimental Investigations on the Compressive Properties of the Graded BCC Lattice Cylindrical Shells Made of 316L Stainless Steel" Metals 15, no. 8: 895. https://doi.org/10.3390/met15080895
APA StyleGuan, Y., Ma, W., Cao, M., Xu, H., Luo, W., Cao, W., Wang, S., Qin, Y., Zhang, X., & Cao, X. (2025). Numerical and Experimental Investigations on the Compressive Properties of the Graded BCC Lattice Cylindrical Shells Made of 316L Stainless Steel. Metals, 15(8), 895. https://doi.org/10.3390/met15080895







