A Review of Heat Transfer and Numerical Modeling for Scrap Melting in Steelmaking Converters
Abstract
1. Introduction
1.1. The BOF Heat Cycle
1.2. Fundamental Transport Phenomena and Dimensionless Numbers
1.3. Challenges in Modeling Heat and Mass Transfer
2. Semi-Empirical Correlations for Predicting Scrap Melting
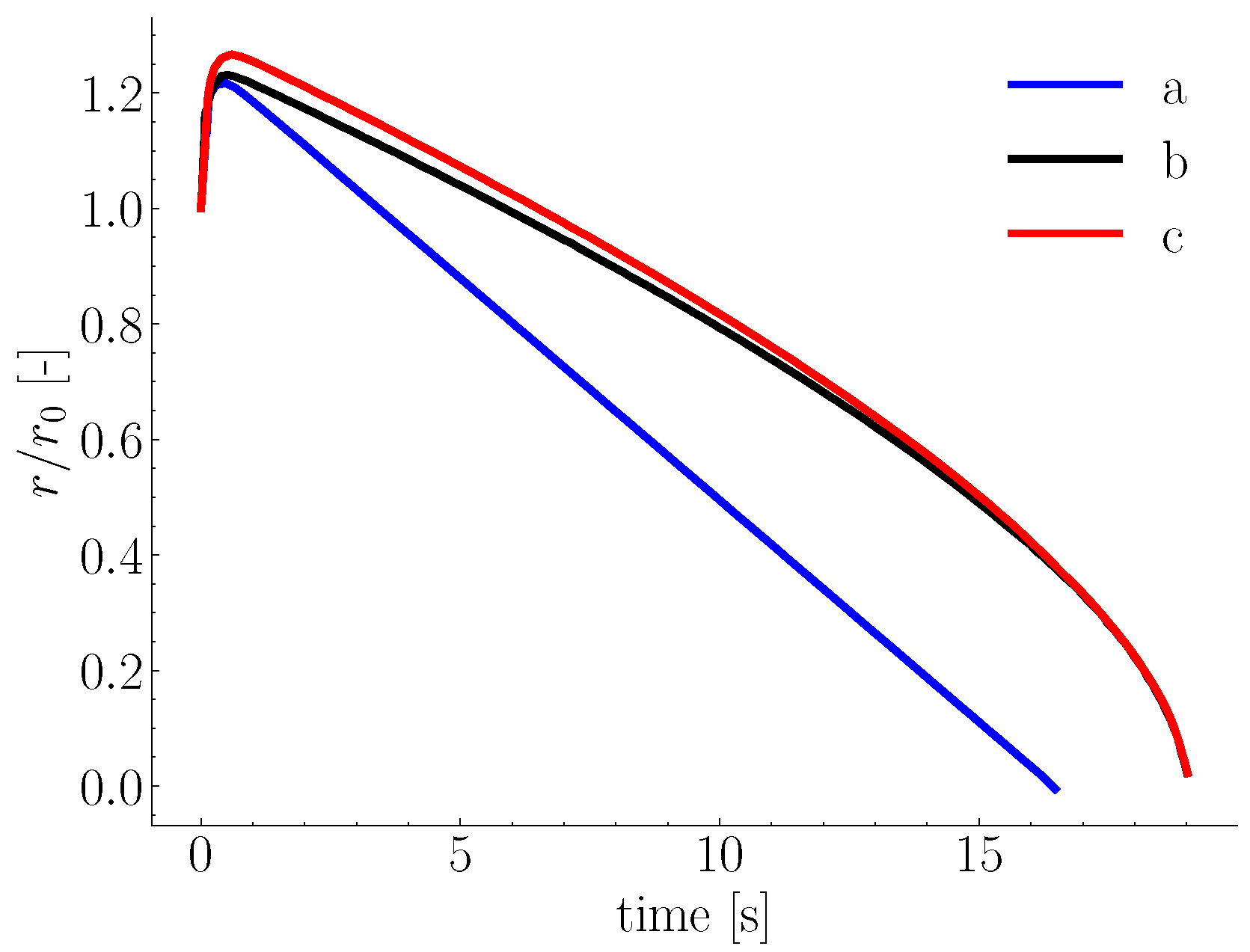
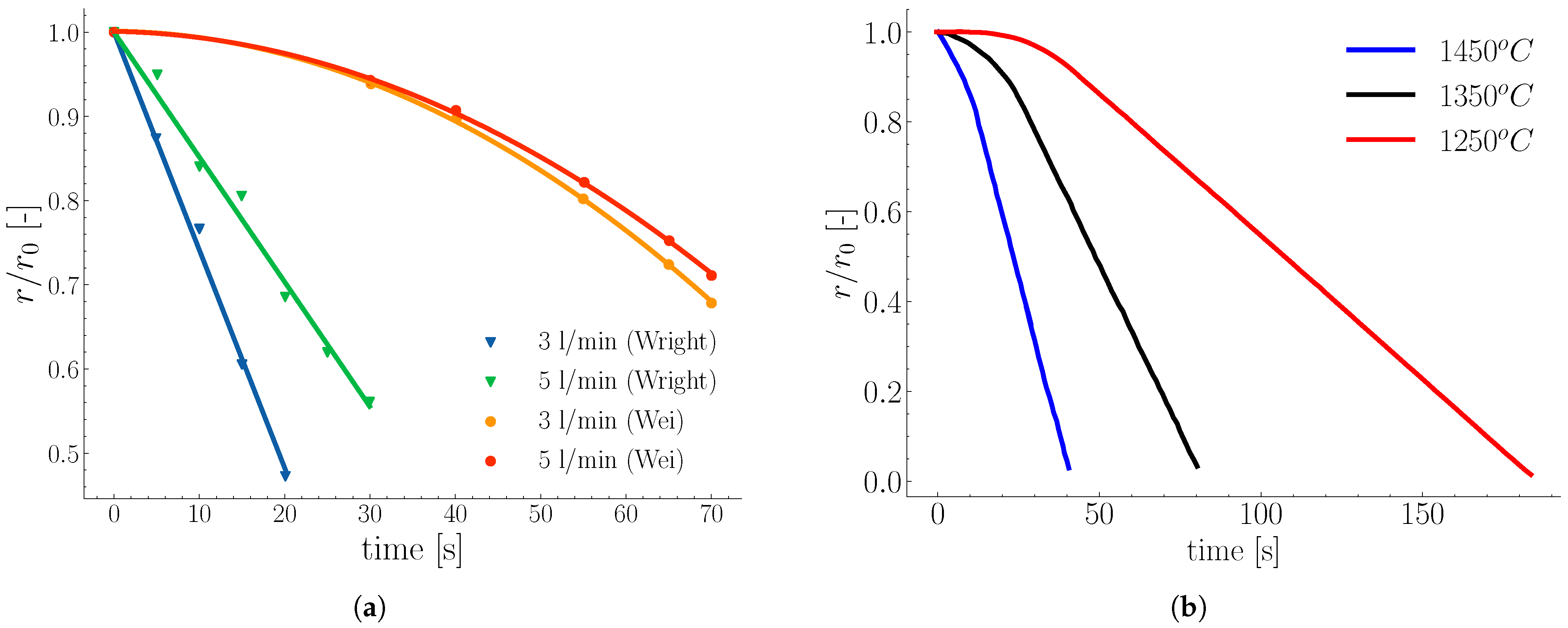
2.1. Melting in Presence of Natural Convection
| Shape | Reference | Range | Correlation | |
|---|---|---|---|---|
| Sphere | [37] | , | (11) | |
| Sphere | [16] | , | (12) | |
| V.P. | [45] | (13) | ||
| V.C. | [54,56] | , | (14) |
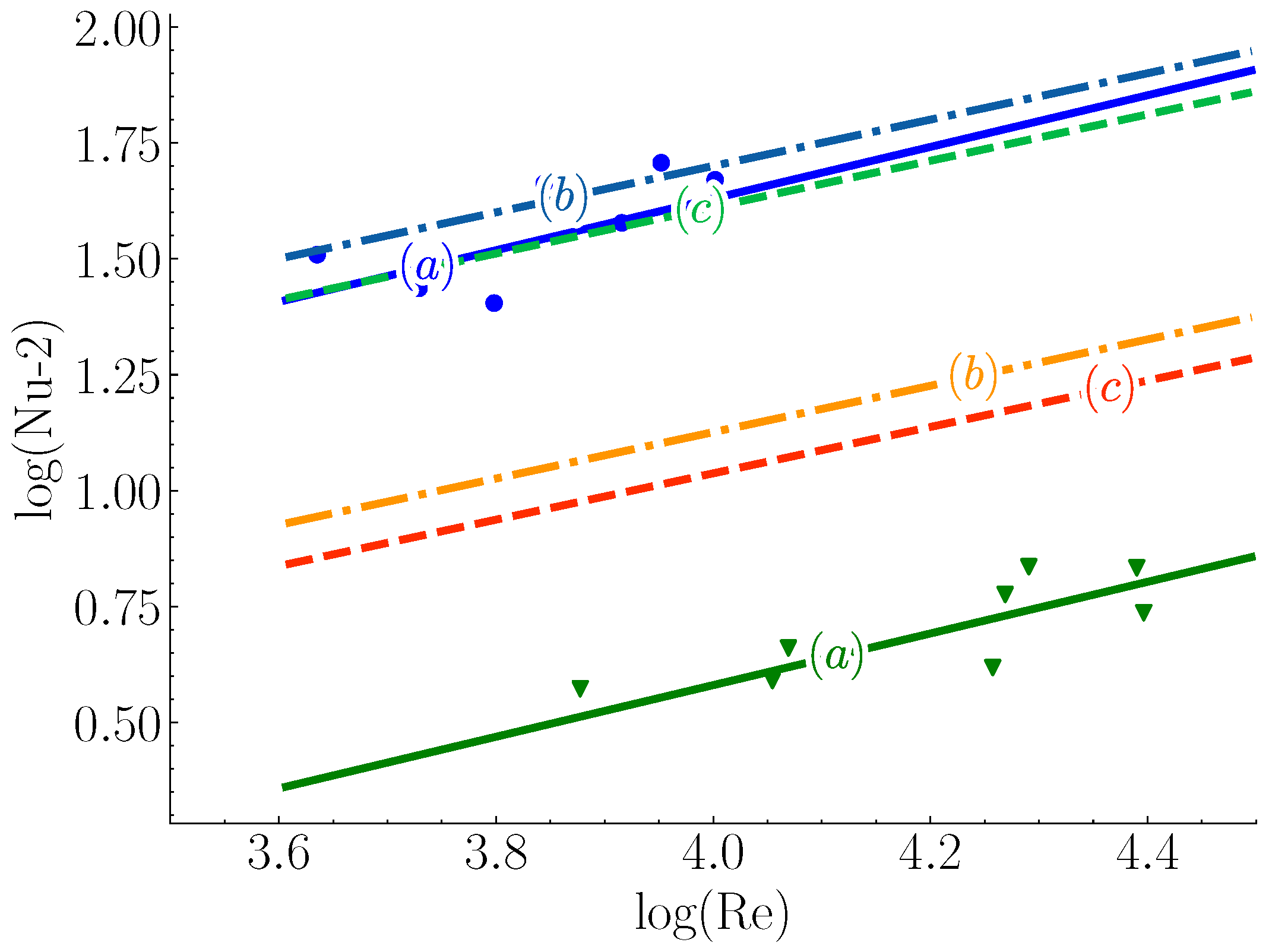
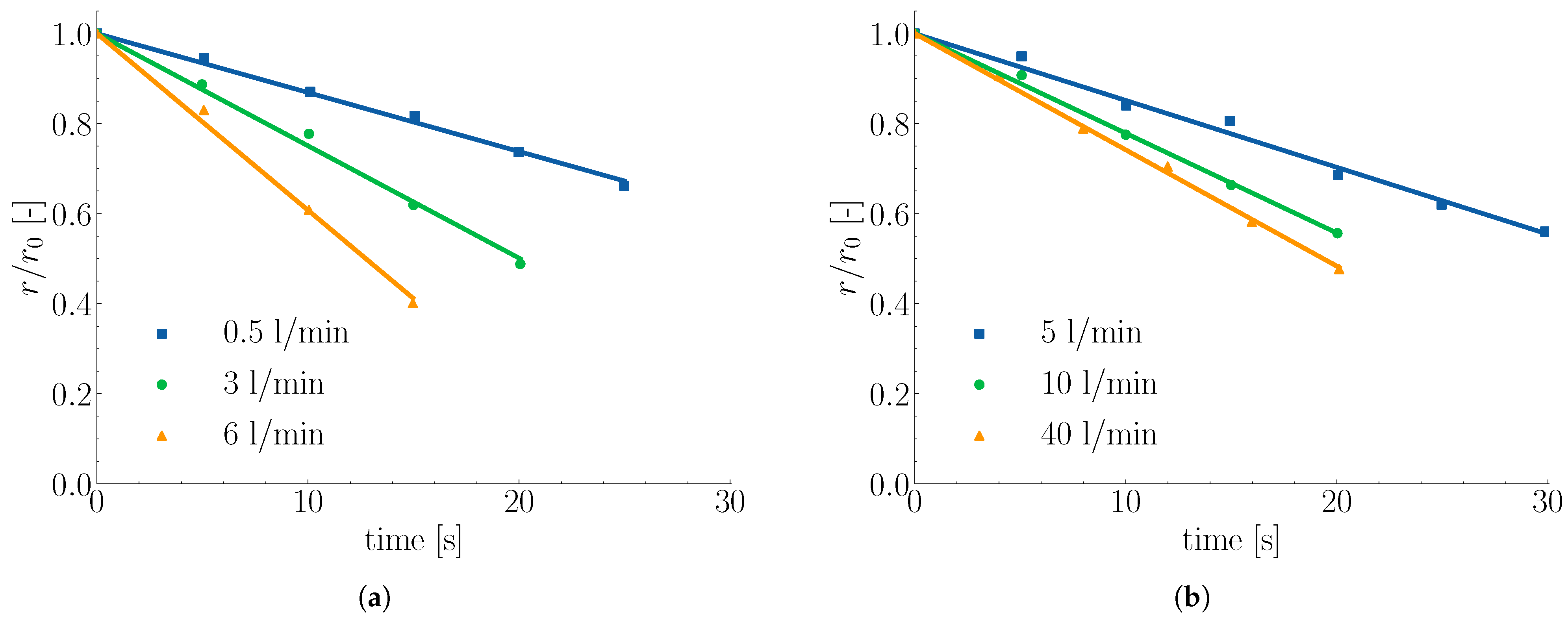
2.2. Melting in Presence of Forced Convection
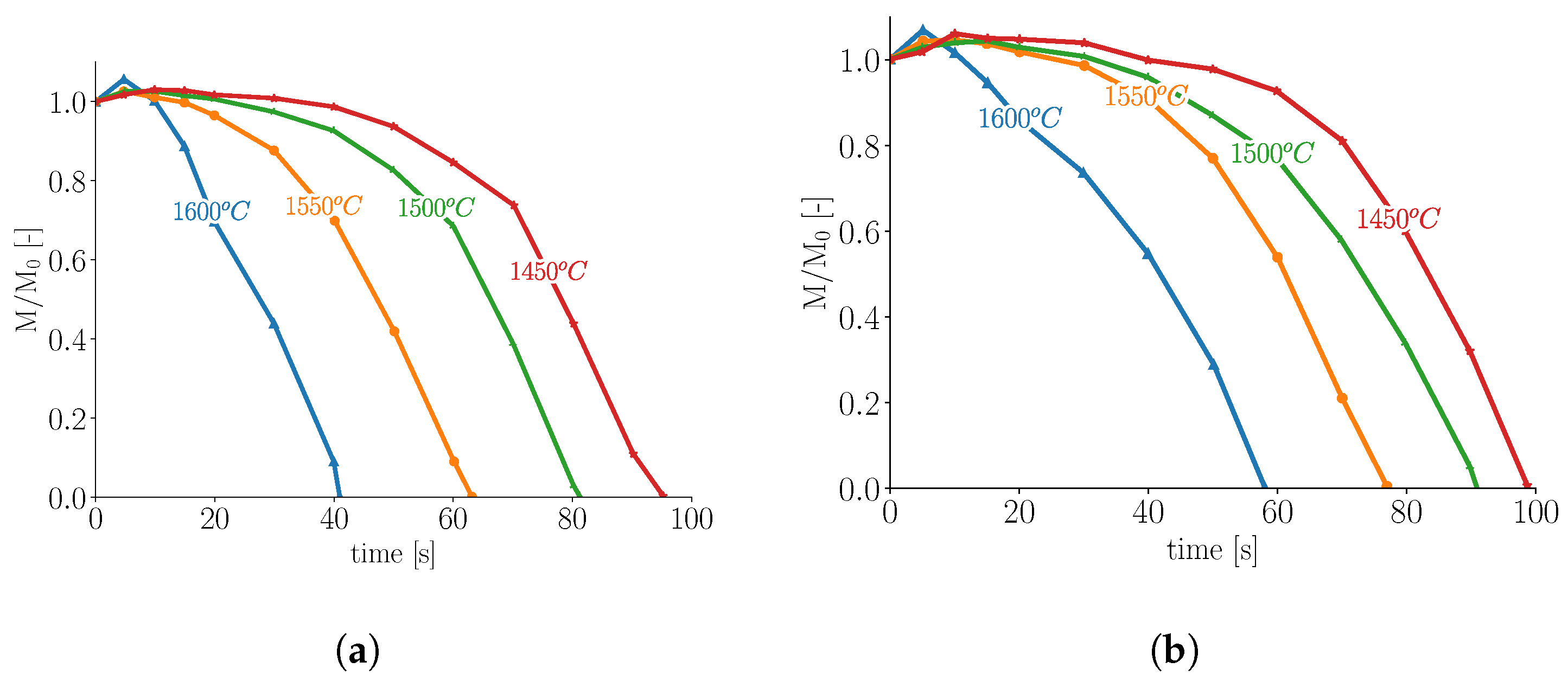
2.3. Influence of Scrap Solid Fraction on Heat Transfer in Liquid Hot Metal
3. Modeling Scrap Melting
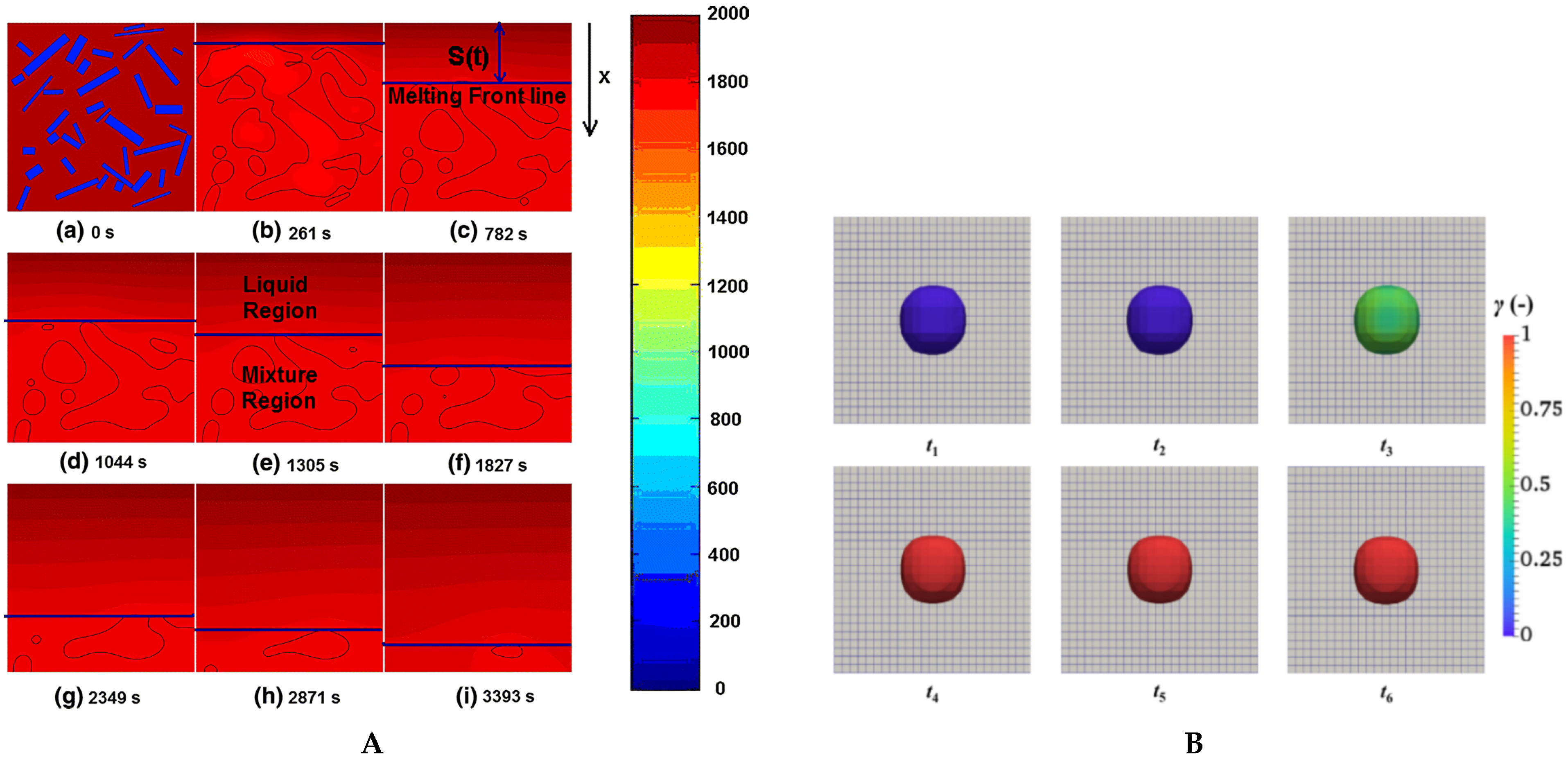
3.1. CFD Simulation of Scrap Melting
3.2. CFD-DEM Simulation
3.3. Particle Resolved Direct Numerical Simulation with Immersed Boundary Method (PR-DNS/IBM)
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BOF | Basic oxygen furnace |
| CFD | Computational fluid dynamics |
| DEM | Discrete element method |
| PR | Particle resolved |
| DNS | Direct numerical simulation |
| BF | Blast furnace |
| TFM | Two-fluid method |
| PIV | Particle image velocimetry |
| IBM | Immersed boundary method |
| REV | Representative element volume |
Appendix A
| Number | Definition | Formula | Physical Meaning |
|---|---|---|---|
| Reynolds () | Ratio of inertial to viscous forces | Describes the flow regime (laminar or turbulent). | |
| Prandtl (Pr) | Ratio of momentum to thermal diffusivity | Indicates the relative thickness of velocity to thermal boundary layer. | |
| Nusselt (Nu) | Ratio of convective to conductive heat transfer | Measures the enhancement of heat transfer by convection over conduction. | |
| Schmidt (Sc) | Ratio of momentum to mass diffusivity | Indicates the relative thickness of the velocity boundary layer to the mass boundary layer. | |
| Sherwood (Sh) | Ratio of convective to diffusive mass transfer | Describes the effectiveness of convective mass transfer compared to diffusion. | |
| Stefan (Ste) | Ratio of sensible to latent heat | Quantifies the available heat to continue the phase change. | |
| Fourier (Fo) | Ratio of time to diffusion scale time | Quantify availability of time for the diffusion to reach steady state. | |
| Biot (Bi) | Ratio of internal to external heat transfer resistance | Quantify the special distribution of the temperature inside the object. |
References
- World Steel in Figures 2024—Worldsteel.Org. Available online: https://worldsteel.org/data/world-steel-in-figures-2024/#world-crude-steel-production-%3Cbr%3E1950-to-2023 (accessed on 11 July 2024).
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Holman, J.P. Heat Transfer; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Stein, R.P. Liquid Metal Heat Transfer. Adv. Heat Transf. 1966, 3, 101–174. [Google Scholar] [CrossRef]
- Li, J.; Provatas, N. Kinetics of Scrap Melting in Liquid Steel: Multipiece Scrap Melting. Metall. Mater. Trans. B 2008, 39, 268–279. [Google Scholar] [CrossRef]
- Xi, X.; Chen, S.; Yang, S.; Ye, M.; Li, J. Melting Characteristics of Multipiece Steel Scrap in Liquid Steel. ISIJ Int. 2021, 61, 190–199. [Google Scholar] [CrossRef]
- Szekely, J.; Chuang, Y.K.; Hlinka, J.W. The Melting and Dissolution of Low-Carbon Steels in Iron-Carbon Melts. Metall. Trans. 1972, 3, 2825–2833. [Google Scholar] [CrossRef]
- Ehrich, O.; Yun-Ken, C.; Schwerdtfeger, K. The Melting of Metal Spheres Involving the Initially Frozen Shells with Different Material Properties. Int. J. Heat Mass. Tran. 1978, 21, 341–349. [Google Scholar] [CrossRef]
- Kurobe, J.; Iguchi, M. Cold Model Experiment on Melting Phenomena of Zn Ingot in Hot Dip Plating Bath. Mater. Trans. 2003, 44, 877–884. [Google Scholar] [CrossRef][Green Version]
- Iguchi, M.; Morita, Z.I.; Tani, J.I.; Uemura, T. Flow Phenomena and Heat Transfer around a Sphere Submerged in Water Jet and Bubbling Jet. ISIJ Int. 1989, 29, 658–665. [Google Scholar] [CrossRef]
- Wright, J.K. Steel Dissolution in Quiescent and Gas Stirred Fe/C Melts. Metall. Trans. B 1989, 20B, 363–374. [Google Scholar] [CrossRef]
- Melissari, B.; Argyropoulos, S.A. Development of a Heat Transfer Dimensionless Correlation for Spheres Immersed in a Wide Range of Prandtl Number Fluids. Int. J. Heat Mass. Tran. 2005, 48, 4333–4341. [Google Scholar] [CrossRef]
- Melissari, B.; Argyropoulos, S.A. Measurement of Magnitude and Direction of Velocity in High-Temperature Liquid Metals. Part II: Experimental Measurements. Metall. Mater. Trans. B 2005, 36B, 639–649. [Google Scholar] [CrossRef]
- Melissari, B.; Argyropoulos, S.A. Measurement of Magnitude and Direction of Velocity in High-Temperature Liquid Metals. Part I: Mathematical Modeling. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2005, 36, 691–700. [Google Scholar] [CrossRef]
- Argyropoulos, S.A.; Mikrovas, A.C. An Experimental Investigation on Natural and Forced Convection in Liquid Metals. Int. J. Heat Mass. Tran. 1996, 39, 547–561. [Google Scholar] [CrossRef]
- Deen, N.G.; Van Sint Annaland, M.; Van der Hoef, M.A.; Kuipers, J.A. Review of Discrete Particle Modeling of Fluidized Beds. Chem. Eng. Sci. 2007, 62, 28–44. [Google Scholar] [CrossRef]
- Deen, N.G.; Peters, E.A.; Padding, J.T.; Kuipers, J.A. Review of Direct Numerical Simulation of Fluid–Particle Mass, Momentum and Heat Transfer in Dense Gas–Solid Flows. Chem. Eng. Sci. 2014, 116, 710–724. [Google Scholar] [CrossRef]
- Noël, E.; Teixeira, D. New Framework for Upscaling Gas-Solid Heat Transfer in Dense Packing. Int. J. Heat Mass Transf. 2022, 189, 122745. [Google Scholar] [CrossRef]
- Kim, J.; Choi, H. An Immersed-Boundary Finite-Volume Method for Simulation of Heat Transfer in Complex Geometries. KSME Int. J. 2004, 18, 1026–1035. [Google Scholar] [CrossRef]
- Tenneti, S.; Sun, B.; Garg, R.; Subramaniam, S. Role of Fluid Heating in Dense Gas–Solid Flow as Revealed by Particle-Resolved Direct Numerical Simulation. Int. J. Heat Mass Transf. 2013, 58, 471–479. [Google Scholar] [CrossRef]
- Deen, N.G.; Kriebitzsch, S.H.; van der Hoef, M.A.; Kuipers, J.A. Direct Numerical Simulation of Flow and Heat Transfer in Dense Fluid–Particle Systems. Chem. Eng. Sci. 2012, 81, 329–344. [Google Scholar] [CrossRef]
- Li, X.; Cai, J.; Xin, F.; Huai, X.; Guo, J. Lattice Boltzmann Simulation of Endothermal Catalytic Reaction in Catalyst Porous Media. Appl. Therm. Eng. 2013, 50, 1194–1200. [Google Scholar] [CrossRef]
- Tavassoli, H.; Kriebitzsch, S.H.; van der Hoef, M.A.; Peters, E.A.; Kuipers, J.A. Direct Numerical Simulation of Particulate Flow with Heat Transfer. Int. J. Multiph. Flow 2013, 57, 29–37. [Google Scholar] [CrossRef]
- Gunn, D.J. Transfer of Heat or Mass to Particles in Fixed and Fluidised Beds. Int. J. Heat Mass Transf. 1978, 21, 467–476. [Google Scholar] [CrossRef]
- Deng, S.; Xu, A.; Yang, G.; Wang, H. Analyses and Calculation of Steel Scrap Melting in a Multifunctional Hot Metal Ladle. Steel Res. Int. 2019, 90, 1800435. [Google Scholar] [CrossRef]
- Li, J.; Brooks, G.; Provatas, N. Kinetics of Scrap Melting in Liquid Steel. Metall. Mater. Trans. B 2005, 36, 293–302. [Google Scholar] [CrossRef]
- Li, J.; Mason, D.J. A Computational Investigation of Transient Heat Transfer in Pneumatic Transport of Granular Particles. Powder Technol. 2000, 112, 273–282. [Google Scholar] [CrossRef]
- Jiang, J.; Hao, Y.; Tao, Y.X. Experimental Investigation of Convective Melting of Granular Packed Bed Under Microgravity. J. Heat Transf. 2002, 124, 516–524. [Google Scholar] [CrossRef]
- Hao, Y.L.; Tao, Y.X. Heat Transfer Characteristics of Melting Ice Spheres Under Forced and Mixed Convection. J. Heat Transf. 2002, 124, 891–903. [Google Scholar] [CrossRef]
- Shukla, A.K.; Dmitry, R.; Volkova, O.; Scheller, P.R.; Deo, B. Cold Model Investigations of Melting of Ice in a Gas-Stirred Vessel. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2011, 42, 224–235. [Google Scholar] [CrossRef]
- Argyropoulos, S.A.; Mazumdar, D.; Mikrovas, A.C.; Doutre, D.A. Dimensionless Correlations for Forced Convection in Liquid Metals: Part II. Two-phase Flow. Metall. Mater. Trans. B 2001, 32B, 247–252. [Google Scholar] [CrossRef]
- Huang, J.; Yuan, Z.; Shi, S.; Wang, B.; Liu, C. Flow Characteristics for Two-Strand Tundish in Continuous Slab Casting Using PIV. Metals 2019, 9, 239. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Y.; Yang, S.; Li, J.; Liu, W.; Song, Z. Flow Behavior and Heat Transfer of Molten Steel in a Two-Strand Tundish Heated by Plasma. J. Mater. Res. Technol. 2021, 13, 561–572. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, S.; Wu, C.; Chen, N.; Li, J.; Liu, Q. Effect of Bottom Stirring on Bath Mixing and Transfer Behavior during Scrap Melting in BOF Steelmaking: A Review. High Temp. Mater. Processes 2024, 43, 20220322. [Google Scholar] [CrossRef]
- Bergman, T.L. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Churchill, S.W. Comprehensive, theoretically based, correlating equations for free convection from isothermal spheres. Chem. Eng. Commun. 1983, 24, 339–352. [Google Scholar] [CrossRef]
- Raithby, G.D.; Hollands, K.G.T. A General Method of Obtaining Approximate Solutions to Laminar and Turbulent Free Convection Problems. Adv. Heat Transf. 1975, 11, 265–315. [Google Scholar]
- Ehrich, O.; Chuang, Y.K.; Schwerdtfeger, K. The Melting of Sponge Iron Spheres in Their Own Melt. Arch. Eisenhüttenwesen 1979, 50, 329–334. [Google Scholar] [CrossRef]
- Jardón-Pérez, L.E.; Ramírez-Argaez, M.A.; Conejo, A.N. Melting Rate of Spherical Metallic Particles in Its Own Melt: Effect of Particle Temperature, Bath Temperature, Particle Size and Stirring Conditions. Trans. Indian Inst. Met. 2019, 72, 2365–2373. [Google Scholar] [CrossRef]
- Boetcher, S.K.S. Natural Convection from Circular Cylinders; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Fujii, T.; Uehara, H. Laminar Natural-Convective Heat Transfer from the Outer Surface of a Vertical Cylinder. Int. J. Heat Mass Transf. 1970, 13, 607–615. [Google Scholar] [CrossRef]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. Handbook of Heat Transfer; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Churchill, S.W.; Chu, H.H. Correlating Equations for Laminar and Turbulent Free Convection from a Horizontal Cylinder. Int. J. Heat Mass Transf. 1975, 18, 1049–1053. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H. Correlating Equations for Laminar and Turbulent Free Convection from a Vertical Plate. Int. J. Heat Mass Tran. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- Churchill, S.W. A Comprehensive Correlating Equation for Laminar, Assisting, Forced and Free Convection. AIChE J. 1977, 23, 10–16. [Google Scholar] [CrossRef]
- Churchill, S.W.; Bernstein, M. A Correlating Equation for Forced Convection from Gases and Liquids to a Circular Cylinder in Crossflow. J. Heat Tran. 1977, 99, 300–306. [Google Scholar] [CrossRef]
- Xi, X.; Yang, S.; Li, J.; Chen, X.; Ye, M. Thermal Simulation Experiments on Scrap Melting in Liquid Steel. Ironmak. Steelmak. 2018, 47, 442–448. [Google Scholar] [CrossRef]
- Isobe, K.; Maede, H.; Ozawa, K.; Umezawa, K.; Saito, C. Analysis of the Scrap Melting Rate in High Carbon Molten Iron. Tetsu-to-Hagane 1990, 76, 2033–2040. [Google Scholar] [CrossRef][Green Version]
- Brabie, L.C.; Kawakami, M. Kinetics of Steel Scrap Melting in Molten Fe-C Bath. High Temp. Mater. Processes 2000, 19, 241–255. [Google Scholar] [CrossRef]
- Penz, F.M.; Schenk, J.; Ammer, R.; Klösch, G.; Pastucha, K.; Reischl, M. Diffusive Steel Scrap Melting in Carbon-Saturated Hot Metal—Phenomenological Investigation at the Solid–Liquid Interface. Materials 2019, 12, 1358. [Google Scholar] [CrossRef] [PubMed]
- Penz, F.M.; Schenk, J.; Ammer, R.; Klösch, G.; Pastucha, K. Dissolution of Scrap in Hot Metal under Linz–Donawitz (LD) Steelmaking Conditions. Metals 2018, 8, 1078. [Google Scholar] [CrossRef]
- Penz, F.M.; Schenk, J.; Ammer, R.; Klösch, G.; Pastucha, K. Evaluation of the Influences of Scrap Melting and Dissolution during Dynamic Linz–Donawitz (LD) Converter Modelling. Processes 2019, 7, 186. [Google Scholar] [CrossRef]
- Penz, F.M.; Tavares, R.P.; Weiss, C.; Schenk, J.; Ammer, R.; Pastucha, K.; Klösch, G. Analytical and Numerical Determination of the Heat Transfer Coefficient between Scrap and Hot Metal Based on Small-Scale Experiments. Int. J. Heat Mass Transf. 2019, 138, 640–646. [Google Scholar] [CrossRef]
- Deng, N.; Zhou, X.; Zhou, M.; Peng, S. Numerical Simulation of the Melting Behavior of Steel Scrap in Hot Metal. Metals 2020, 10, 678. [Google Scholar] [CrossRef]
- Windisch, H. Thermodynamik: Ein Lehrbuch Für ingenieure; Oldenbourg Wissenschaftsverlag Verlag: München, Germany, 2011. [Google Scholar]
- Whitaker, S. Forced Convection Heat Transfer Correlations for Flow in Pipes, Past Flat Plates, Single Cylinders, Single Spheres, and for Flow in Packed Beds and Tube Bundles. AIChE J. 1972, 18, 361–371. [Google Scholar] [CrossRef]
- Ranz, W. Evaporation from Drops. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Aziz, S.A.; Janna, W.; Jakubowski, G.S. A Comparison of Correlations for Forced Convection Heat Transfer from a Submerged Melting Ice Sphere to Flowing Water. In Proceedings of the ASME 1996 International Mechanical Engineering Congress and Exposition, Atlanta, GA, USA, 17–22 November 1996. [Google Scholar]
- Rodriguez, I.; Campo, A. Numerical Investigation of Forced Convection Heat Transfer from a Sphere at Low Prandtl Numbers. Int. J. Therm. Sci. 2023, 184, 107970. [Google Scholar] [CrossRef]
- Argyropoulos, S.A.; Mikrovas, A.C.; Doutre, D.A. Dimensionless Correlations for Forced Convection in Liquid Metals: Part I. Single-phase Flow. Metall. Mater. Trans. B 2001, 32B, 239–246. [Google Scholar] [CrossRef]
- Wei, G.; Zhu, R.; Tang, T.; Dong, K. Study on the Melting Characteristics of Steel Scrap in Molten Steel. Ironmak. Steelmak. 2019, 46, 609–617. [Google Scholar] [CrossRef]
- Mori, K.; Sakuraya, T. Rate of Dissolution of Solid Iron in a Carbon-Saturated Liquid Iron Alloy with Evolution of CO. Trans. Iron Steel Inst. Jpn. 1982, 22, 984–990. [Google Scholar] [CrossRef]
- Cao, L.; Liu, Q.; Wang, Y.; Lin, W.; Sun, J.; Sun, L.; Guo, W. An Attempt to Visualize the Scrap Behavior in the Converter for Steel Manufacturing Process Using Physical and Mathematical Methods. Mater. Trans. 2018, 59, 1829–1836. [Google Scholar] [CrossRef]
- Witte, L.C. An Experimental Study of Forced-Convection Heat Transfer From a Sphere to Liquid Sodium. J. Heat Transf. 1968, 90, 9–12. [Google Scholar] [CrossRef]
- Gaye, H.; Destannes, P.; Roth, J.L.; Guyon, M. Kinetics of Scrap Melting in the Converter and Electric Arc Furnace. In Proceedings of the IISC: The 6th International Iron and Steel Congress, Nagoya, Japan, 21–26 October 1990. [Google Scholar]
- Kravets, B.; Rosemann, T.; Reinecke, S.R.; Kruggel-Emden, H. A New Drag Force and Heat Transfer Correlation Derived from Direct Numerical LBM-simulations of Flown through Particle Packings. Powder Technol. 2019, 345, 438–456. [Google Scholar] [CrossRef]
- Zhu, L.T.; Liu, Y.X.; Luo, Z.H. An Enhanced Correlation for Gas-Particle Heat and Mass Transfer in Packed and Fluidized Bed Reactors. Chem. Eng. J. 2019, 374, 531–544. [Google Scholar] [CrossRef]
- Sethi, G.; Shukla, A.; Chandra, P.; Deo, B. Theoretical Aspects of Scrap Dissolution in Oxygen Steelmaking Converters Thermochemical Study of COREX Process View Project Databased Modeling Approach (ANN) to Control Hot Metal Pretreatment (HMPT) at JSW Steel View Project; Association for Iron & Steel Technology: Warrendale, PA, USA, 2004; Volume 1. [Google Scholar]
- Gol’dfarb, E.M.; Sherstov, B.I. Heat and Mass Transfer When Melting Scrap in an Oxygen Converter. J. Eng. Phys. 1970, 18, 342–347. [Google Scholar] [CrossRef]
- Odenthal, H.J.; Falkenreck, U.; Schlüter, J. CFD Simulation of Multiphase Melt Flows in Steelmaking Converters. In Proceedings of the European Conference on Computational Fluid Dynamics ECCOMAS CFD, Delft, The Netherlands, 5–8 September 2006. [Google Scholar]
- Lv, M.; Zhu, R.; Guo, Y.G.; Wang, Y.W. Simulation of Flow Fluid in the BOF Steelmaking Process. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2013, 44, 1560–1571. [Google Scholar] [CrossRef]
- Odenthal, H.J. An Insight into Steelmaking Processes by Computational Fluid Dynamics. In Proceedings of the XVIII International UIE-Congress—Electrotechnologies for Material Processing, Hannover, Germany, 6–9 June 2017. [Google Scholar]
- Lichtenegger, T.; Pirker, S. Fast Long-Term Simulations of Hot, Reacting, Moving Particle Beds with a Melting Zone. Chem. Eng. Sci. 2023, 283, 119402. [Google Scholar] [CrossRef]
- Climent, M.E.; Jolly, M.M.; Chapelle, M.P.; Denis, M.S.; Fiani, M.E.; Gardin, M.P.; Jardy, M.A.; Pericleous, M.K. Modélisation Multiphysique Du Convertisseur d’aciérie Yannick Nikienta DOH Composition Du Jury. Ph.D. Thesis, Université de Lorraine, Nancy, France, 2012. [Google Scholar]
- Vakhrushev, A.; Ludwig, A.; Wu, M.; Tang, Y.; Hackl, G.; Nitzl, G. Advanced Multiphase Modeling of Solidification with OpenFOAM®. In Proceedings of the Open Source CFD International Conference, London, UK, 29–30 October 2012. [Google Scholar]
- Cao, L.; Wang, Y.; Liu, Q.; Feng, X. Physical and Mathematical Modeling of Multiphase Flows in a Converter. ISIJ Int. 2018, 58, 573–584. [Google Scholar] [CrossRef]
- Salcudean, M.; Abdullah, Z. On the Numerical Modelling of Heat Transfer during Solidification Processes. Int. J. Numer. Methods Eng. 1988, 25, 445–473. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Science and Engineering of Casting Solidification, 3rd ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Kruskopf, A. A Model for Scrap Melting in Steel Converter. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2015, 46, 1195–1206. [Google Scholar] [CrossRef]
- Kruskopf, A.; Holappa, L. Scrap Melting Model for Steel Converter Founded on Interfacial Solid/Liquid Phenomena. Metall. Res. Technol. 2018, 115, 201. [Google Scholar] [CrossRef]
- Arzpeyma, N.; Widlund, O.; Ersson, M.; Jönsson, P. Mathematical Modeling of Scrap Melting in an EAF Using Electromagnetic Stirring. ISIJ Int. 2013, 53, 48–55. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. An Introduction to Phase-Field Modeling of Microstructure Evolution. Calphad 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Wang, S.; Shen, Y. CFD-DEM-VOF-phase Diagram Modelling of Multi-Phase Flow with Phase Changes. Chem. Eng. Sci. 2023, 273, 118651. [Google Scholar] [CrossRef]
- Norouzi, H.R.; Zarghami, R.; Sotudeh-Gharebagh, R.; Mostoufi, N. Coupled CFD-DEM Modeling: Formulation, Implementation and Application to Multiphase Flows; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Zhao, J.; Shan, T. Coupled CFD-DEM Simulation of Fluid-Particle Interaction in Geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A Discrete Numerical Model for Granular Assemblies. Geotechnique 2015, 29, 47–65. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete Particle Simulation of Particulate Systems: Theoretical Developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Kuang, S.B.; Chu, K.W.; Yu, A.B. Discrete Particle Simulation of Particle–Fluid Flow: Model Formulations and Their Applicability. J. Fluid Mech. 2010, 661, 482–510. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, L.; Liu, Z.; Chen, M.; Xia, X.; Zhao, Y. A Review of Recent Development for the CFD-DEM Investigations of Non-Spherical Particles. Powder Technol. 2022, 412, 117972. [Google Scholar] [CrossRef]
- González, O.J.; Guzmán, Y.I.; Ramírez-Argaez, M.A.; Conejo, A.N. Melting Behavior of Simulated DRI in Liquid Steel. Arch. Metall. Mater. 2008, 53, 359–364. [Google Scholar]
- Zheng, C.; Zhang, L.; Govender, N.; Wu, C.Y. DEM Analysis of Residence Time Distribution during Twin Screw Granulation. Powder Technol. 2021, 377, 924–938. [Google Scholar] [CrossRef]
- Vångö, M.; Pirker, S.; Lichtenegger, T. Unresolved CFD–DEM Modeling of Multiphase Flow in Densely Packed Particle Beds. Appl. Math. Model. 2018, 56, 501–516. [Google Scholar] [CrossRef]
- Nijssen, T.M.J.; Kuipers, J.A.M.; Van Der Stel, J.; Adema, A.T.; Buist, K.A. Large-Scale VOF/CFD-DEM Simulation of Blast Furnace Hearth Dynamics. ISIJ Int. 2022, 62, 1146–1158. [Google Scholar] [CrossRef]
- Bansal, H.; Nikrityuk, P. A Submodel for Spherical Particles Undergoing Phase Change under the Influence of Convection. Can. J. Chem. Eng. 2017, 95, 150–156. [Google Scholar] [CrossRef]
- Soleimani, A.; Aigner, A.; Touloupidis, V. Single Particle Growth, Fragmentation and Morphology Modelling: A DEM Approach. React. Eng. 2022, 16, 2200015. [Google Scholar] [CrossRef]
- Braile, D.; Hare, C.; Wu, C.Y. DEM Analysis of Swelling Behaviour in Granular Media. Adv. Powder Technol. 2022, 33, 103806. [Google Scholar] [CrossRef]
- Hassanzadeh Saraei, S.; Peters, B. Immersed Boundary Method for Considering Lubrication Effects in the CFD-DEM Simulations. Powder Technol. 2023, 426, 118603. [Google Scholar] [CrossRef]
- Tavassoli, H.; Peters, E.; Kuipers, J. Direct Numerical Simulation of Fluid–Particle Heat Transfer in Fixed Random Arrays of Non-Spherical Particles. Chem. Eng. Sci. 2015, 129, 42–48. [Google Scholar] [CrossRef]


| Method | Advantages | Limitations |
|---|---|---|
| PR-DNS/IBM | - Resolves local transport (heat and mass) phenomena without requiring closure equations. | - Computationally demanding. |
| - Flexible with varying particle stiffness. | - Explicit treatment of fluid–particle interactions leads to stiffness problems. | |
| - Non-conforming method; therefore, domain remeshing is not required. | - Requires setting particle properties for each particular problem class. | |
| - Useful in obtaining closure relations (e.g., heat or mass coefficients). | ||
| CFD-DEM | - Accurate solid–fluid dynamics for large numbers of solid particles. | - Solution sensitivity to cell size to particle size ratio. |
| - Moderate computational cost compared to DNS-IBM. | - Requires closure correlations for solid–fluid local transport phenomena. | |
| - Applicable to large scales relative to PR-DNS/IBM scale. | - Requires parameter calibration. | |
| CFD | - Low computational cost compared to CFD-DEM and PR-DNS/IBM. | - Packing solids with given porosity is not possible. |
| - Scalability. | - Solid collision and dynamics as results of melting cannot be simulated. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, M.B.A.; Charruault, F.; Rout, B.; Schrama, F.N.H.; Kuipers, J.A.M.; Yang, Y. A Review of Heat Transfer and Numerical Modeling for Scrap Melting in Steelmaking Converters. Metals 2025, 15, 866. https://doi.org/10.3390/met15080866
Hassan MBA, Charruault F, Rout B, Schrama FNH, Kuipers JAM, Yang Y. A Review of Heat Transfer and Numerical Modeling for Scrap Melting in Steelmaking Converters. Metals. 2025; 15(8):866. https://doi.org/10.3390/met15080866
Chicago/Turabian StyleHassan, Mohammed B. A., Florian Charruault, Bapin Rout, Frank N. H. Schrama, Johannes A. M. Kuipers, and Yongxiang Yang. 2025. "A Review of Heat Transfer and Numerical Modeling for Scrap Melting in Steelmaking Converters" Metals 15, no. 8: 866. https://doi.org/10.3390/met15080866
APA StyleHassan, M. B. A., Charruault, F., Rout, B., Schrama, F. N. H., Kuipers, J. A. M., & Yang, Y. (2025). A Review of Heat Transfer and Numerical Modeling for Scrap Melting in Steelmaking Converters. Metals, 15(8), 866. https://doi.org/10.3390/met15080866







