Microstructure Evolution in Homogenization Heat Treatment of Inconel 718 Manufactured by Laser Powder Bed Fusion
Abstract
1. Introduction
2. Material Preparation
3. Results
3.1. Microstructure of L-PBF-Built IN718
3.2. Microstructure of Homogenization-Treated IN718
4. Discussion
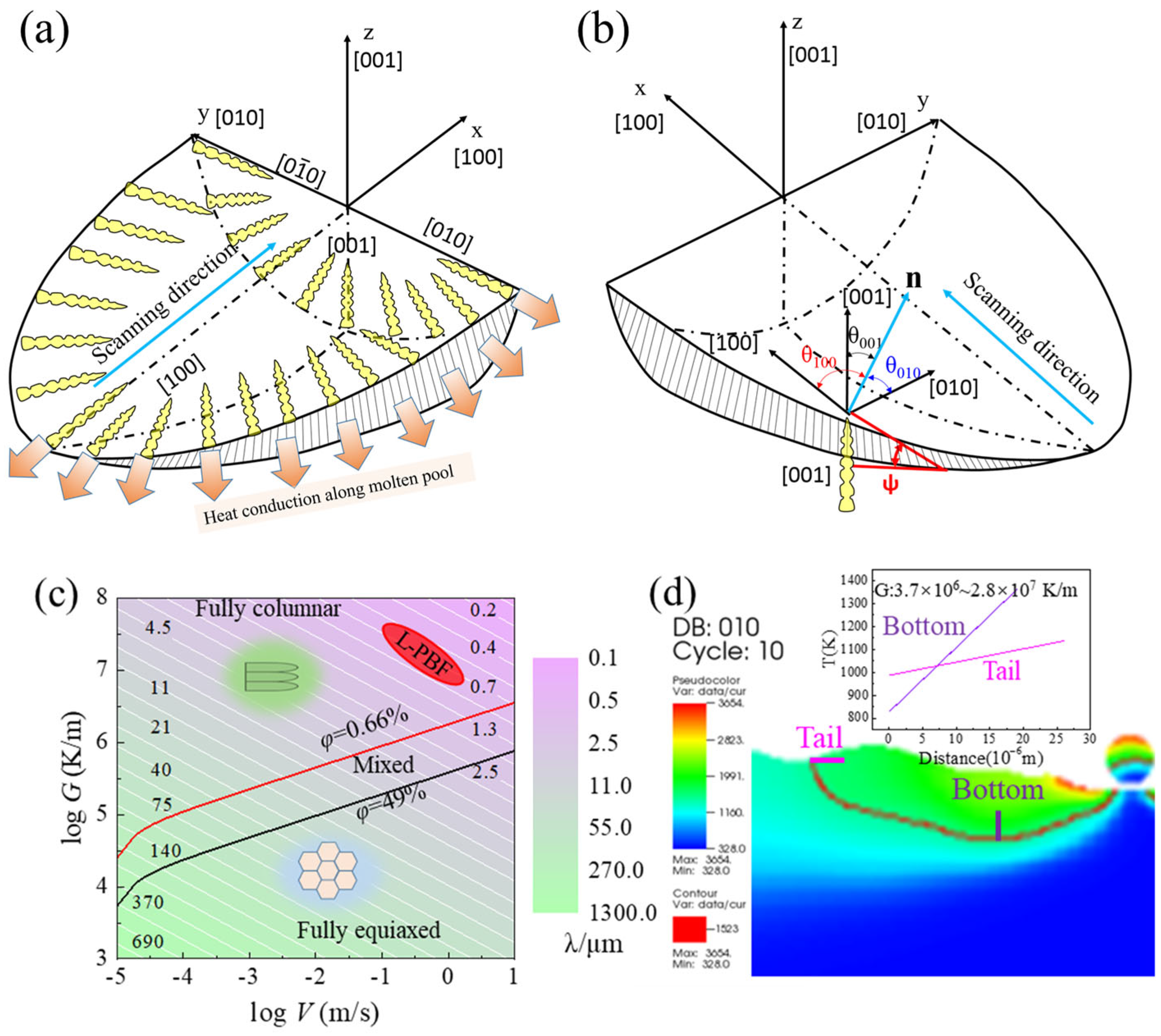
4.1. Microstructure of L-PBF-Built IN718
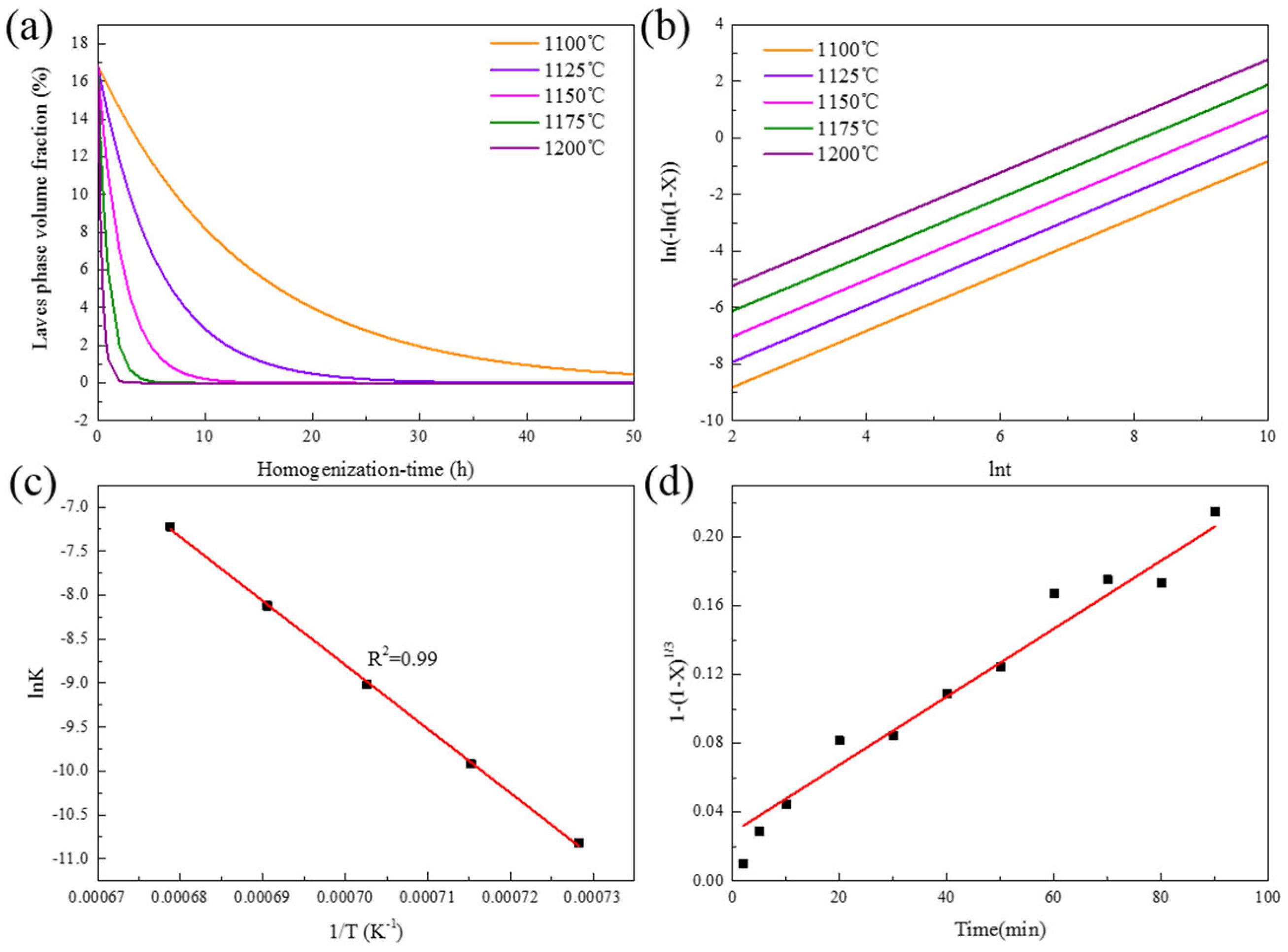
4.2. Dissolution Behavior of the Laves Phase
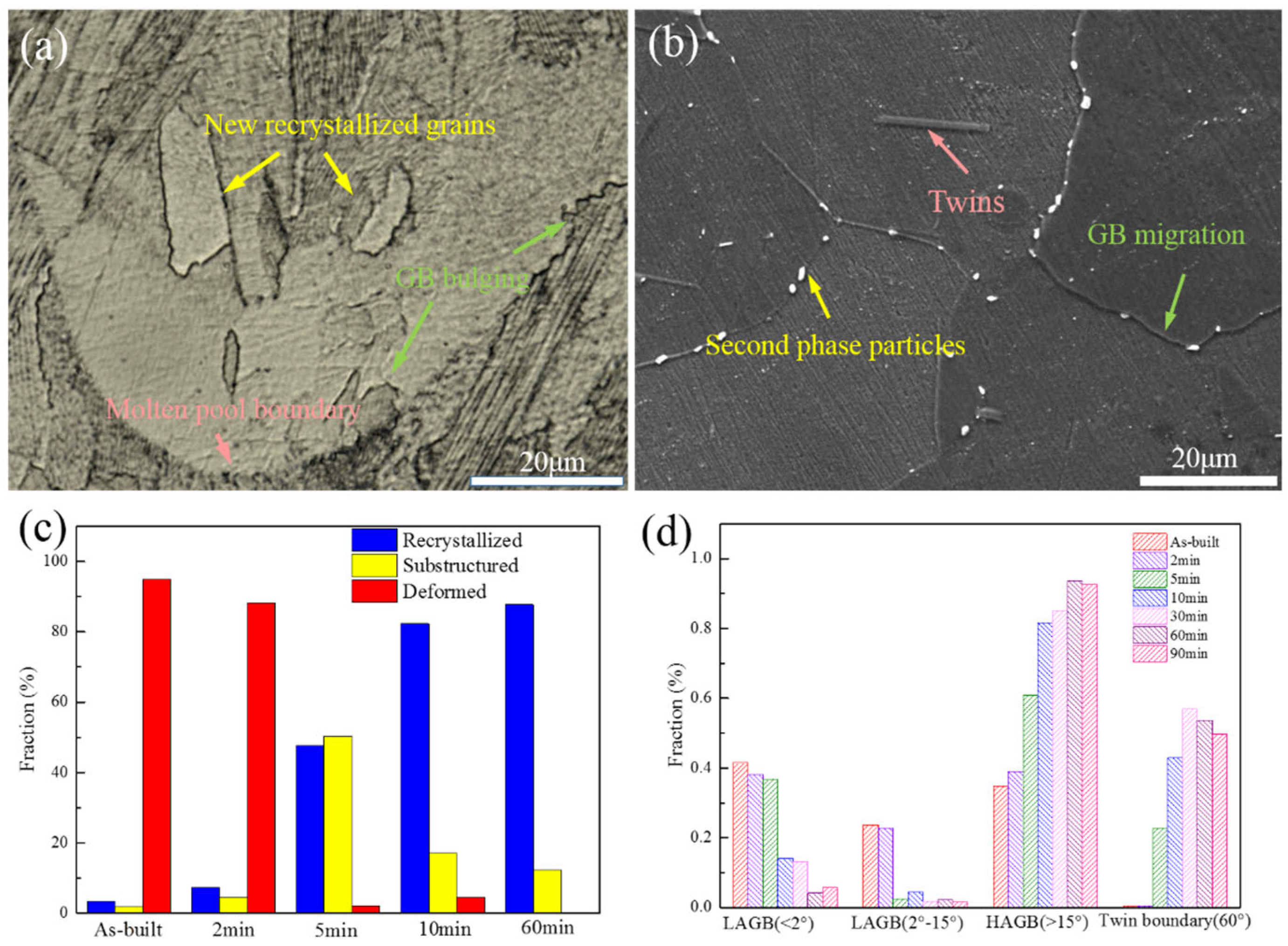
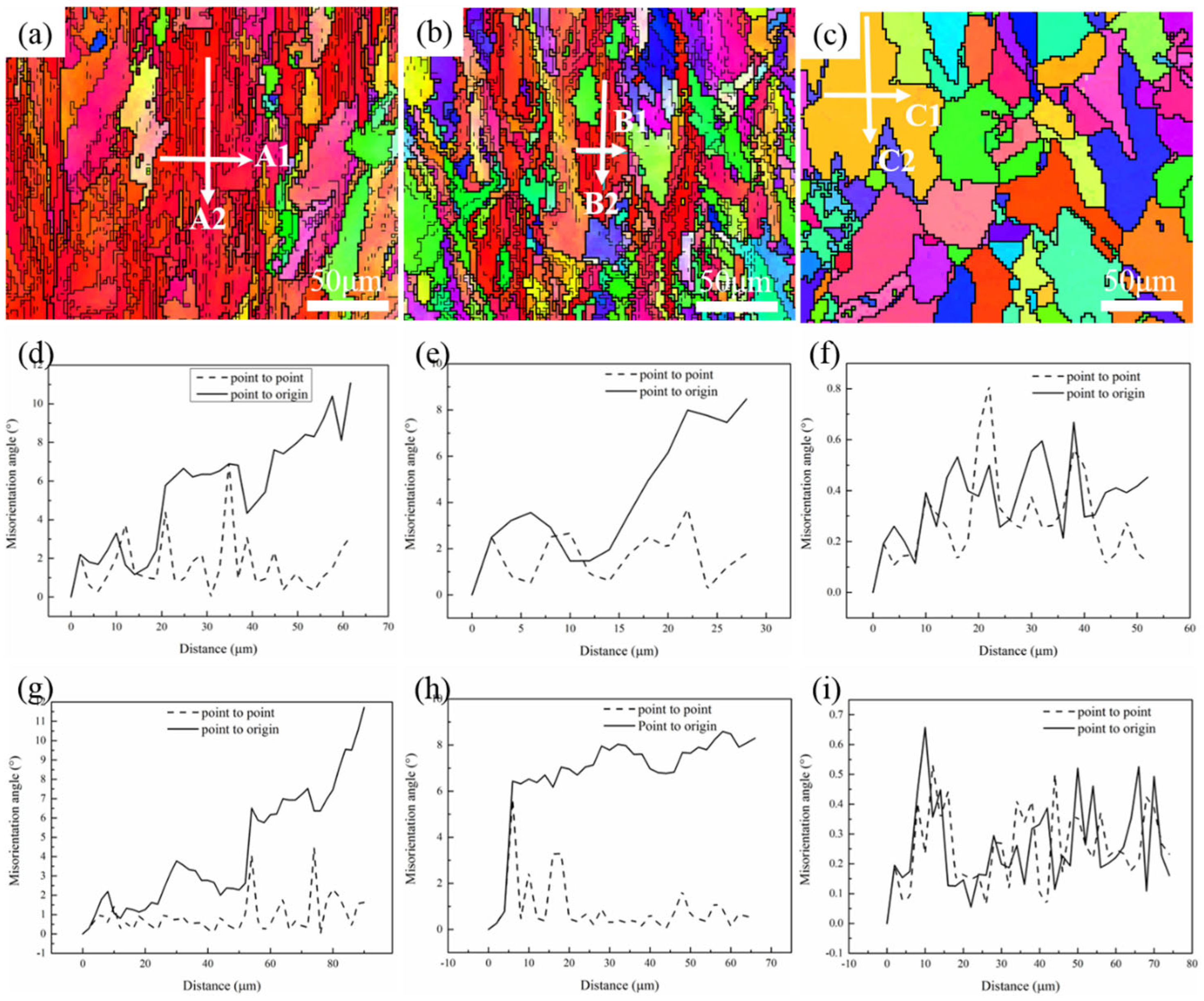
4.3. Recrystallization Behavior
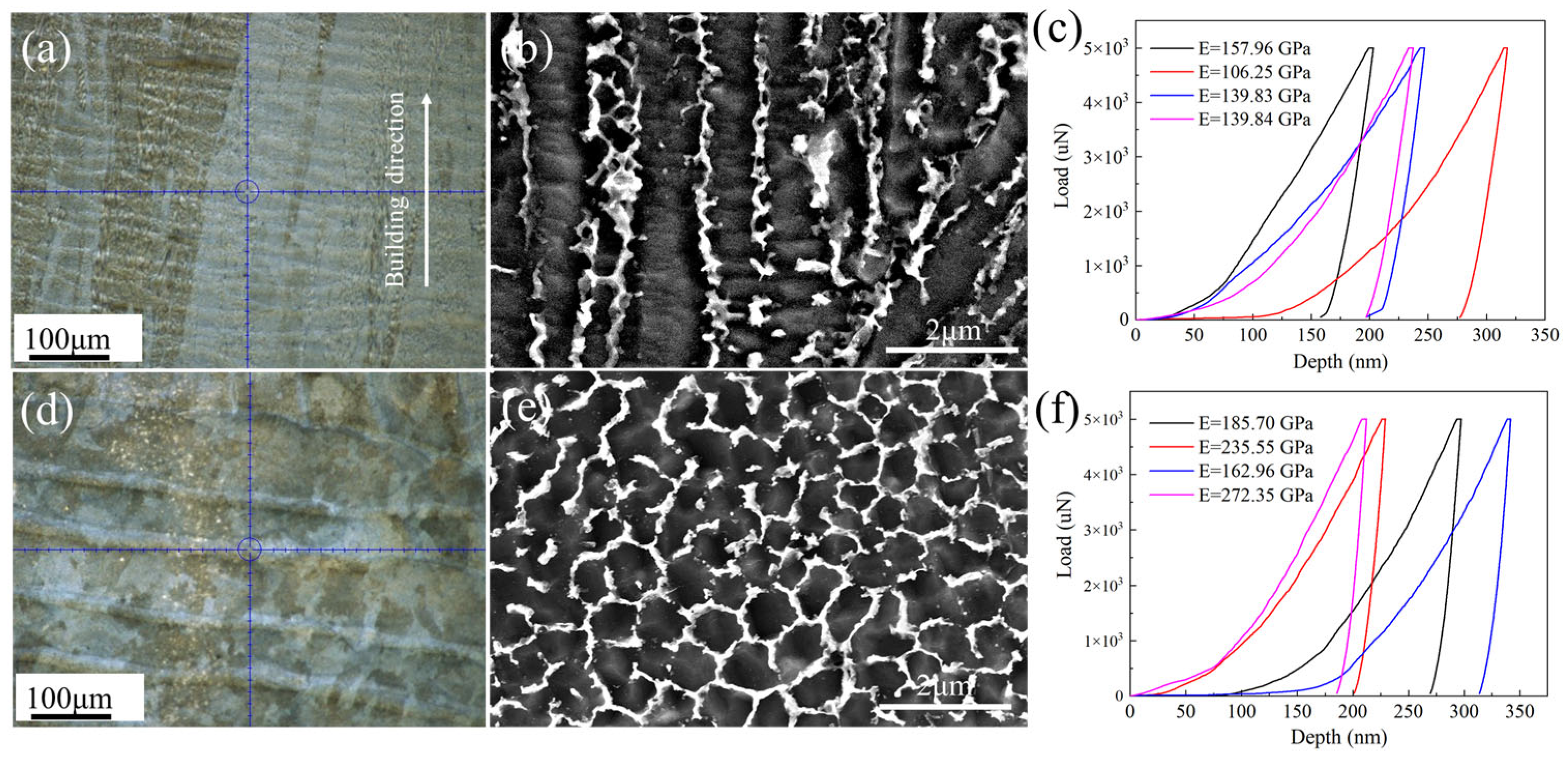
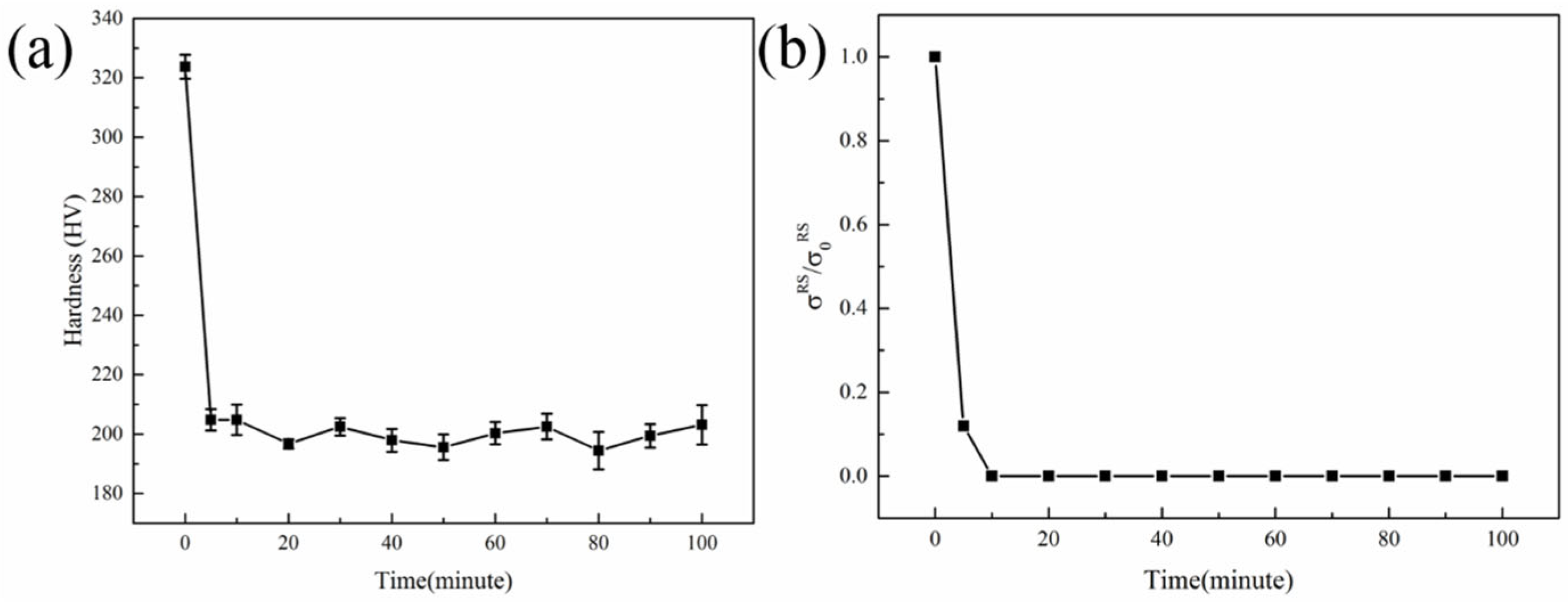
4.4. Vickers Hardness Test
5. Conclusions
- (1)
- The microstructure of L-PBF-built IN718 has a fine dendritic structure, with a large amount of Laves phases precipitating in the inter-dendritic region. The matrix has a high dislocation density, and the sub-grain boundaries have a certain directivity.
- (2)
- The dissolution of the Laves phase is controlled by atomic long-term diffusion in the early stage of homogenization. With the increasing holding time, the interface reaction speed slows down, and the dissolution of the Laves phase is mainly controlled by the interface reaction process. The equation of Laves phase dissolution can be described as .
- (3)
- High dislocation density or local-orientation at the serrated GBs are a large driving force through grain boundary bulging for the recrystallization nucleation. The pinning effect of the Laves phases and carbides makes the mechanism of sub-grain merging nucleation dominant. The growth of newly formed sub-grains along the deposition direction may be related to the directivity of sub-grain boundaries.
- (4)
- Grain growth is mainly controlled by the pinning of the second phase at grain boundaries. The exponent of 4 that determines the mechanism of grain growth explains that the Ostwald ripening of the second phase particles through grain boundary diffusion during homogenization treatment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amato, K.N.; Gaytan, S.M.; Murr, L.E.; Martinez, E.; Shindo, P.; Hernandez, J.; Collins, S.; Medina, F. Microstructures and mechanical behavior of Inconel 718 fabricated by selective laser melting. Acta Mater. 2012, 60, 2229–2239. [Google Scholar] [CrossRef]
- Azadian, S.; Wei, L.; Warren, R. Delta phase precipitation in Inconel 718. Mater. Charact. 2004, 53, 7–16. [Google Scholar] [CrossRef]
- Theska, F.; Stanojevic, A.; Oberwinkler, B.; Ringer, S.; Primig, S. On conventional versus direct ageing of Alloy 718. Acta Mater. 2018, 156, 116–124. [Google Scholar] [CrossRef]
- Hosseini, E.; Popovich, V.A. A review of mechanical properties of additively manufactured Inconel 718. Addit. Manuf. 2019, 30, 100877. [Google Scholar] [CrossRef]
- Cai, D.; Zhang, W.; Nie, P.; Liu, W.; Yao, M. Dissolution kinetics of δ phase and its influence on the notch sensitivity of Inconel 718. Mater. Charact. 2007, 58, 220–225. [Google Scholar] [CrossRef]
- Bahl, S.; Mishra, S.; Yazar, K.U.; Kola, I.R.; Chatterjee, K.; Suwas, S. Non-equilibrium microstructure, crystallographic texture and morphological texture synergistically result in unusual mechanical properties of 3D printed 316L stainless steel. Addit. Manuf. 2019, 28, 65–77. [Google Scholar] [CrossRef]
- Panwisawas, C.; Tang, Y.T.; Reed, R.C. Metal 3D printing as a disruptive technology for superalloys. Nat. Commun. 2020, 11, 2327. [Google Scholar] [CrossRef]
- Sui, S.; Chen, J.; Li, Z.; Li, H.; Zhao, X.; Tan, H. Investigation of dissolution behavior of laves phase in inconel 718 fabricated by laser directed energy deposition. Addit. Manuf. 2020, 32, 101055. [Google Scholar] [CrossRef]
- Sui, S.; Chen, J.; Ma, L.; Fan, W.; Tan, H.; Liu, F.; Lin, X. Microstructures and stress rupture properties of pulse laser repaired Inconel 718 superalloy after different heat treatments. J. Alloys Compd. 2019, 770, 125–135. [Google Scholar] [CrossRef]
- Sui, S.; Tan, H.; Chen, J.; Zhong, C.; Li, Z.; Fan, W.; Gasser, A.; Huang, W. The influence of Laves phases on the room temperature tensile properties of Inconel 718 fabricated by powder feeding laser additive manufacturing. Acta Mater. 2019, 164, 413–427. [Google Scholar] [CrossRef]
- Ono, Y.; Yuri, T.; Nagashima, N.; Sumiyoshi, H.; Ogata, T.; Nagao, N. High-cycle Fatigue Properties of Alloy718 Base Metal and Electron Beam Welded Joint. Phys. Procedia 2015, 67, 1028–1035. [Google Scholar] [CrossRef]
- McClung, R.C. A literature survey on the stability and significance of residual stresses during fatigue. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 173–205. [Google Scholar] [CrossRef]
- Noroozi, A.H.; Glinka, G.; Lambert, S. Prediction of fatigue crack growth under constant amplitude loading and a single overload based on elasto-plastic crack tip stresses and strains. Eng. Fract. Mech. 2008, 75, 188–206. [Google Scholar] [CrossRef]
- Reid, C.N. A method of mapping residual stress in a compact tension specimen. Scr. Metall. 1988, 22, 451–456. [Google Scholar] [CrossRef]
- Li, X.; Shi, J.J.; Wang, C.H.; Cao, G.H.; Russell, A.M.; Zhou, Z.J.; Li, C.P.; Chen, G.F. Effect of heat treatment on microstructure evolution of Inconel 718 alloy fabricated by selective laser melting. J. Alloys Compd. 2018, 764, 639–649. [Google Scholar] [CrossRef]
- Tucho, W.M.; Cuvillier, P.; Sjolyst-Kverneland, A.; Hansen, V. Microstructure and hardness studies of Inconel 718 manufactured by selective laser melting before and after solution heat treatment. Mater. Sci. Eng. A 2017, 689, 220–232. [Google Scholar] [CrossRef]
- Hautfenne, C.; Nardone, S.; De Bruycker, E. Influence of heat treatments and build orientation on the creep strength of additive manufactured IN718. In Proceedings of the 4th International ECCC Conference, Düsseldorf, Germany, 10–14 September 2017. [Google Scholar]
- Zhang, F.; Levine, L.E.; Allen, A.J.; Stoudt, M.R.; Lindwall, G.; Lass, E.A.; Williams, M.E.; Idell, Y.; Campbell, C.E. Effect of heat treatment on the microstructural evolution of a nickel-based superalloy additive-manufactured by laser powder bed fusion. Acta Mater. 2018, 152, 200–214. [Google Scholar] [CrossRef] [PubMed]
- Kirka, M.; Greeley, D.; Hawkins, C.; Dehoff, R. Effect of anisotropy and texture on the low cycle fatigue behavior of Inconel 718 processed via electron beam melting. Int. J. Fatigue 2017, 105, 235–243. [Google Scholar] [CrossRef]
- Javad, S.M.; Hamed, M.; Mohsen, R. Solidification behavior and Laves phase dissolution during homogenization heat treatment of Inconel 718 superalloy. Vacuum 2018, 154, 235–243. [Google Scholar] [CrossRef]
- Miao, Z.J.; Shan, A.D.; Wu, Y.B.; Lu, J.; Xu, W.L.; Song, H.W. Quantitative analysis of homogenization treatment of Inconel 718 superalloy. Trans. Nonferrous Met. Soc. China 2011, 21, 1009–1017. [Google Scholar] [CrossRef]
- Zhang, J.M.; Gao, Z.Y.; Zhuang, J.Y.; Zhong, Z.Y. Grain growth model of IN718 during holding period after hot deformation. J. Mater. Process. Technol. 2000, 101, 25–30. [Google Scholar] [CrossRef]
- Nie, P.; Ojo, O.A.; Li, Z. Numerical modeling of microstructure evolution during laser additive manufacturing of a nickel-based superalloy. Acta Mater. 2014, 77, 85–95. [Google Scholar] [CrossRef]
- Jia, Q.; Gu, D. Selective laser melting additive manufacturing of Inconel 718 superalloy parts: Densification, microstructure and properties. J. Alloys Compd. 2014, 585, 713–721. [Google Scholar] [CrossRef]
- Kunze, K.; Etter, T.; Grässlin, J.; Shklover, V. Texture, anisotropy in microstructure and mechanical properties of IN738LC alloy processed by selective laser melting (SLM). Mater. Sci. Eng. A 2015, 620, 213–222. [Google Scholar] [CrossRef]
- Yamanaka, K.; Saito, W.; Mori, M.; Matsumoto, H.; Chiba, A. Preparation of weak-textured commercially pure titanium by electron beam melting. Addit. Manuf. 2015, 8, 105–109. [Google Scholar] [CrossRef]
- Han, C.S.; Gao, H.; Huang, Y.; Nix, W.D. Mechanism-based strain gradient crystal plasticity—II. Analysis J. Mech. Phys. Solids 2004, 53, 1204–1222. [Google Scholar] [CrossRef]
- Wang, L.; Wang, N. Effect of substrate orientation on the formation of equiaxed stray grains in laser surface remelted single crystal superalloys: Experimental investigation. Acta Mater. 2016, 104, 250–258. [Google Scholar] [CrossRef]
- Raghavan, N.; Simunovic, S.; Dehoff, R.; Plotkowski, A.; Turner, J.; Kirka, M.; Babu, S. Localized melt-scan strategy for site specific control of grain size and primary dendrite arm spacing in electron beam additive manufacturing. Acta Mater. 2017, 140, 375–387. [Google Scholar] [CrossRef]
- Hu, Y.L.; Lin, X.; Zhang, S.Y.; Jiang, Y.M.; Lu, X.F.; Yang, H.O.; Huang, W.D. Effect of solution heat treatment on the microstructure and mechanical properties of Inconel 625 superalloy fabricated by laser solid forming. J. Alloys Compd. 2018, 767, 330–344. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.D.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Sui, S.; Chen, J.; Ming, X.; Zhang, S.; Lin, X.; Huang, W. The failure mechanism of 50% laser additive manufactured Inconel 718 and the deformation behavior of Laves phases during a tensile process. Int. J. Adv. Manuf. Technol. 2017, 91, 2733–2740. [Google Scholar] [CrossRef]
- Aaron, H.B. On the Kinetics of Precipitate Dissolution. Met. Sci. Heat Treat. 1968, 2, 192–193. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, R.; Yang, Y.; Han, Y. An investigation of the homogenization and deformation of alloy718 ingots. In Proceedings of the International Symposium on Superalloys, Pittsburgh, PA, USA, 27–29 June 1994. [Google Scholar]
- Chlebus, E.; Gruber, K.; Kuźnicka, B.; Kurzac, J.; Kurzynowski, T. Effect of heat treatment on the microstructure and mechanical properties of Inconel 718 processed by selective laser melting. Mater. Sci. Eng. A 2015, 639, 647–655. [Google Scholar] [CrossRef]
- Aaron, H.B.; Kotler, G.R. The effects of curvature on the dissolution kinetics of spherical precipitates. Met. Sci. J. 1970, 4, 222–225. [Google Scholar] [CrossRef]
- Rezayat, M.; Mirzadeh, H.; Namdar, M.; Parsa, M.H. Unraveling the Effect of Thermomechanical Treatment on the Dissolution of Delta Ferrite in Austenitic Stainless Steels. Metall. Mater. Trans. A 2016, 47, 641–648. [Google Scholar] [CrossRef]
- Kashyap, B.P.; Chaturvedi, M.C. Activation energy for superplastic deformation of IN718 superalloy. Scr. Mater. 2000, 43, 429–433. [Google Scholar] [CrossRef]
- Vermolen, F.J.; van der Zwaag, S. A numerical model for the dissolution of spherical particles in binary alloys under mixed mode control. Mater. Sci. Eng. A 1996, 220, 140–146. [Google Scholar] [CrossRef]
- Gotor, F.J.; Criado, J.M.; Malek, J.; Koga, N. Kinetic analysis of solid-state reactions: The universality of master plots for analyzing isothermal and nonisothermal experiments. J. Phys. Chem. A 2000, 104, 10777–10782. [Google Scholar] [CrossRef]
- Roucoules, C.; Hodgson, P.D.; Yue, S.; Jonas, J.J. Softening and microstructural change following the dynamic recrystallization of austenite. Metall. Mater. Trans. A 1994, 25, 389–400. [Google Scholar] [CrossRef]
- Atkinson, H.V. Overview no. 65: Theories of normal grain growth in pure single phase systems. Acta Metall. 1988, 36, 469–491. [Google Scholar] [CrossRef]
- Deng, D.; Peng, R.L.; Brodin, H.; Moverare, J. Microstructure and mechanical properties of Inconel 718 produced by selective laser melting: Sample orientation dependence and effects of post heat treatments. Mater. Sci. Eng. A 2018, 713, 294. [Google Scholar] [CrossRef]
- Zhou, Z.; Gill, A.S.; Qian, D.; Mannava, S.; Langer, K.; Wen, Y.; Vasudevan, V.K. A finite element study of thermal relaxation of residual stress in laser shock peened IN718 superalloy. Int. J. Impact Eng. 2011, 38, 590–596. [Google Scholar] [CrossRef]
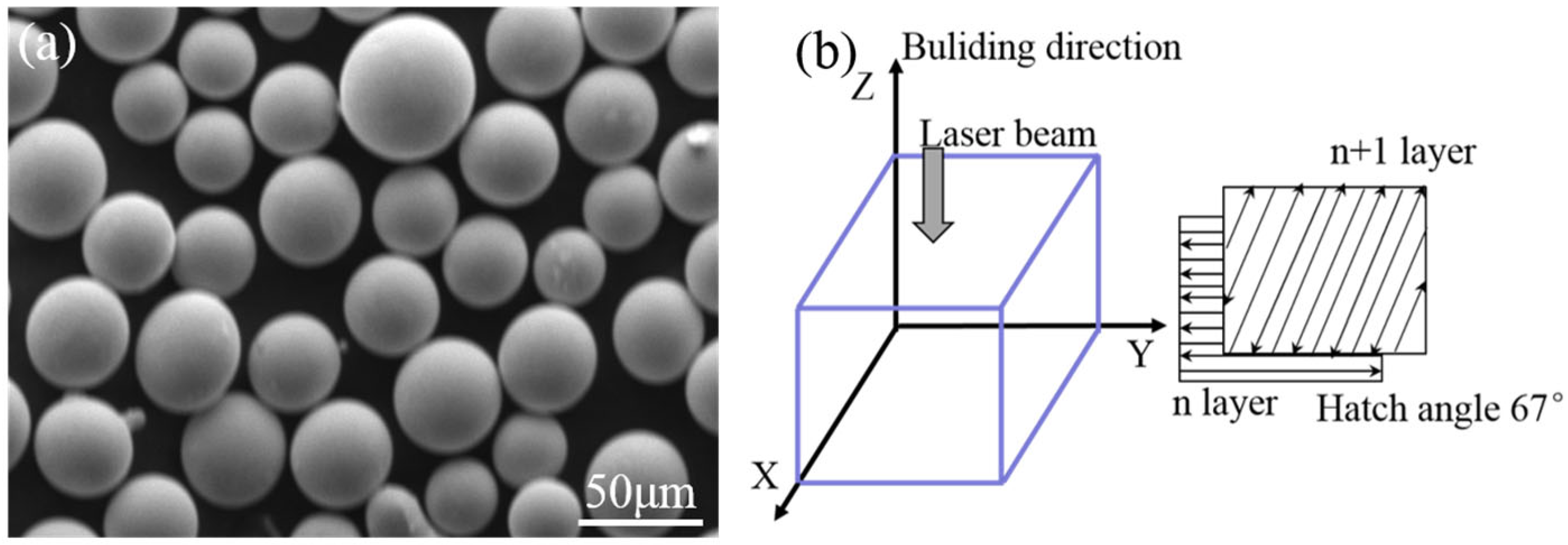



| Laser Power (W) | Point Distance (μm) | Exposure Time (μs) |
|---|---|---|
| 200 | 90 | 100 |
| Layer Thickness(μm) | Hatch Spacing(μm) | Laser Spot Diameter(μm) |
| 30 | 90 | 70 |
| Element | Ni | Cr | Nb | Mo | Ti | Al | C | Fe |
|---|---|---|---|---|---|---|---|---|
| Content (wt.%) | 54.28 | 17.97 | 5.33 | 3 | 0.98 | 0.57 | 0.024 | Bal. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Shen, Y.; Yang, H. Microstructure Evolution in Homogenization Heat Treatment of Inconel 718 Manufactured by Laser Powder Bed Fusion. Metals 2025, 15, 859. https://doi.org/10.3390/met15080859
Zhang F, Shen Y, Yang H. Microstructure Evolution in Homogenization Heat Treatment of Inconel 718 Manufactured by Laser Powder Bed Fusion. Metals. 2025; 15(8):859. https://doi.org/10.3390/met15080859
Chicago/Turabian StyleZhang, Fang, Yifu Shen, and Haiou Yang. 2025. "Microstructure Evolution in Homogenization Heat Treatment of Inconel 718 Manufactured by Laser Powder Bed Fusion" Metals 15, no. 8: 859. https://doi.org/10.3390/met15080859
APA StyleZhang, F., Shen, Y., & Yang, H. (2025). Microstructure Evolution in Homogenization Heat Treatment of Inconel 718 Manufactured by Laser Powder Bed Fusion. Metals, 15(8), 859. https://doi.org/10.3390/met15080859







