Infrared-Guided Thermal Cycles in FEM Simulation of Laser Welding of Thin Aluminium Alloy Sheets
Abstract
1. Introduction
2. Industry Standard Approaches
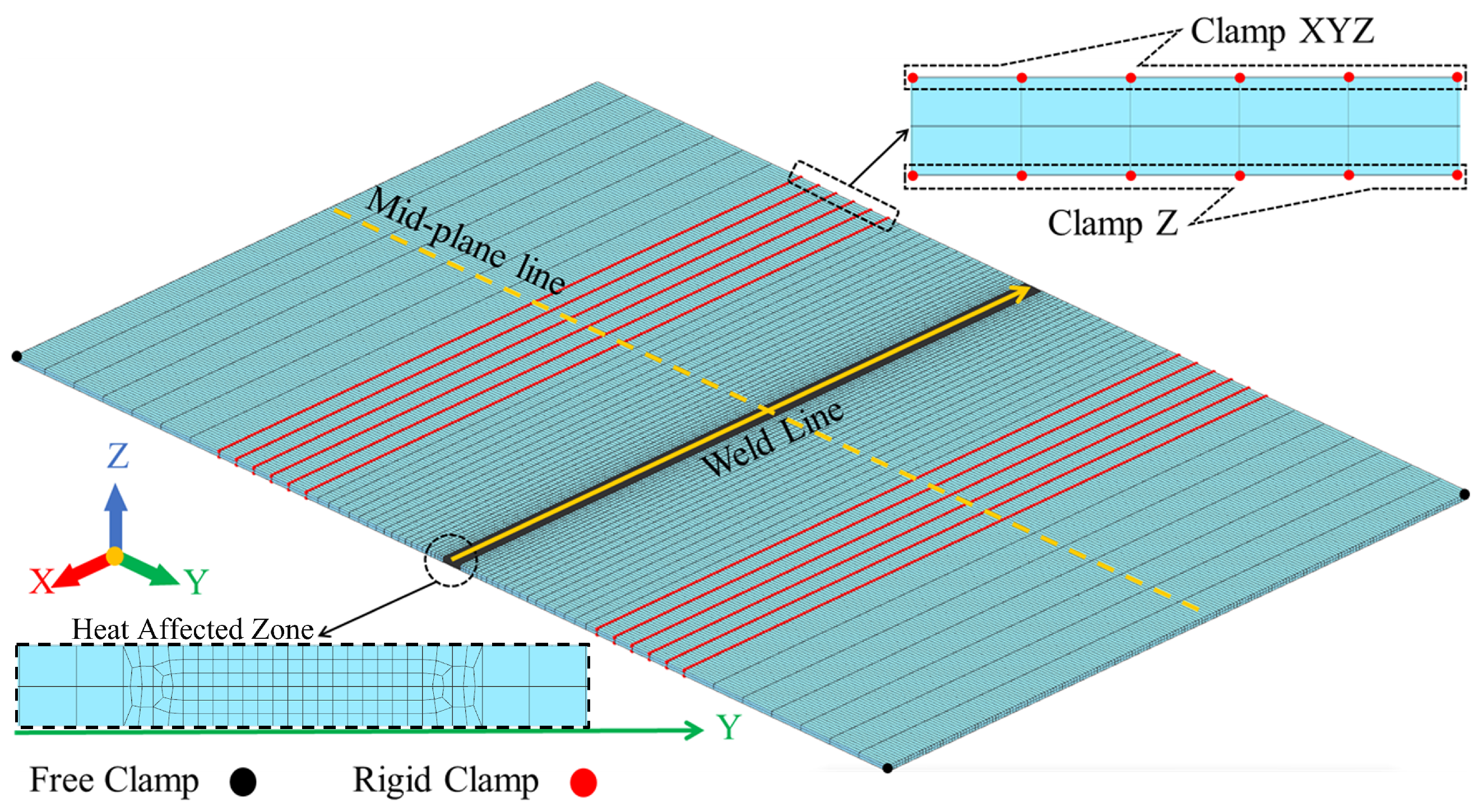
2.1. Numerical Model
2.2. Iterative Calibration via Moving Heat Source
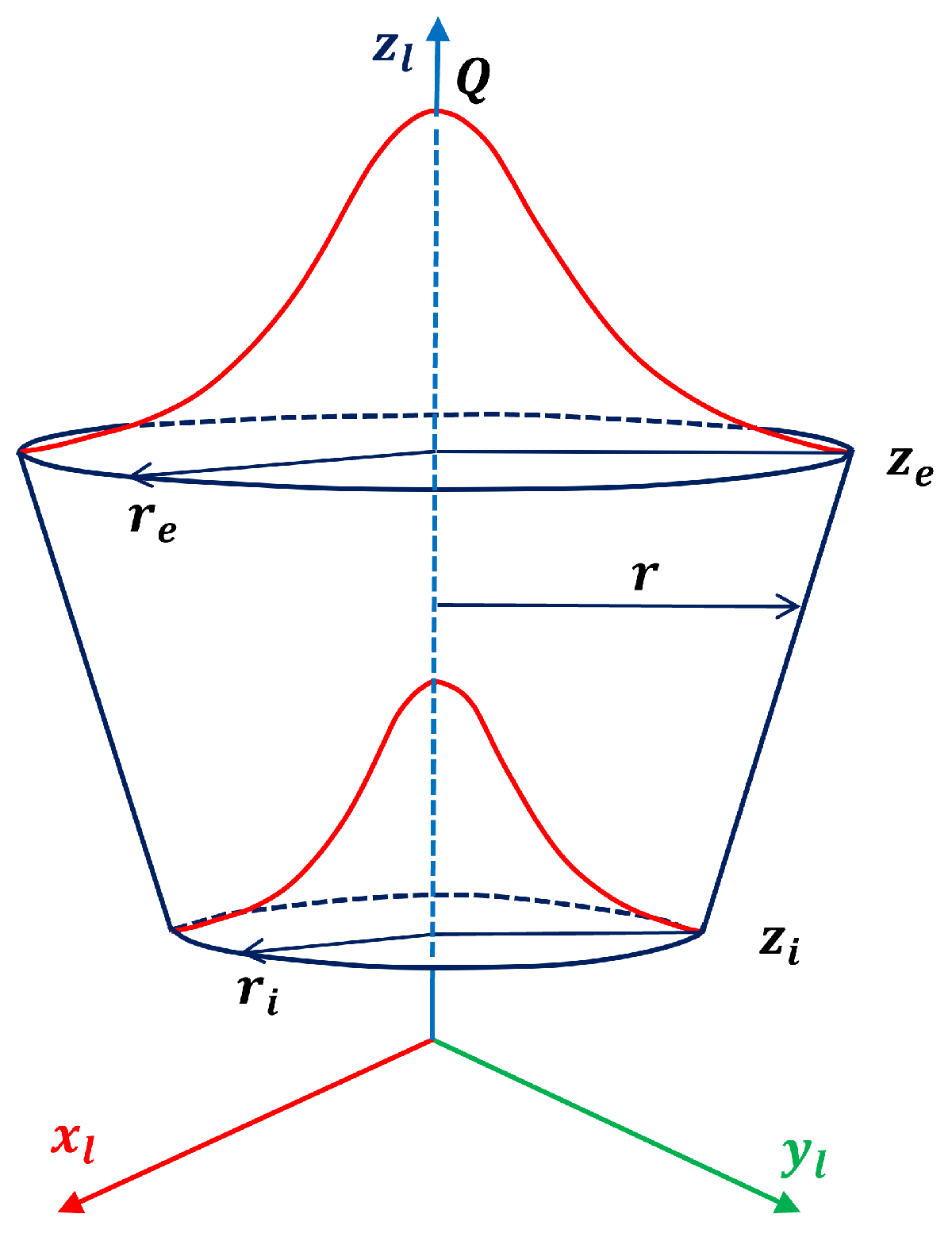
2.3. Imposed Thermal Cycle
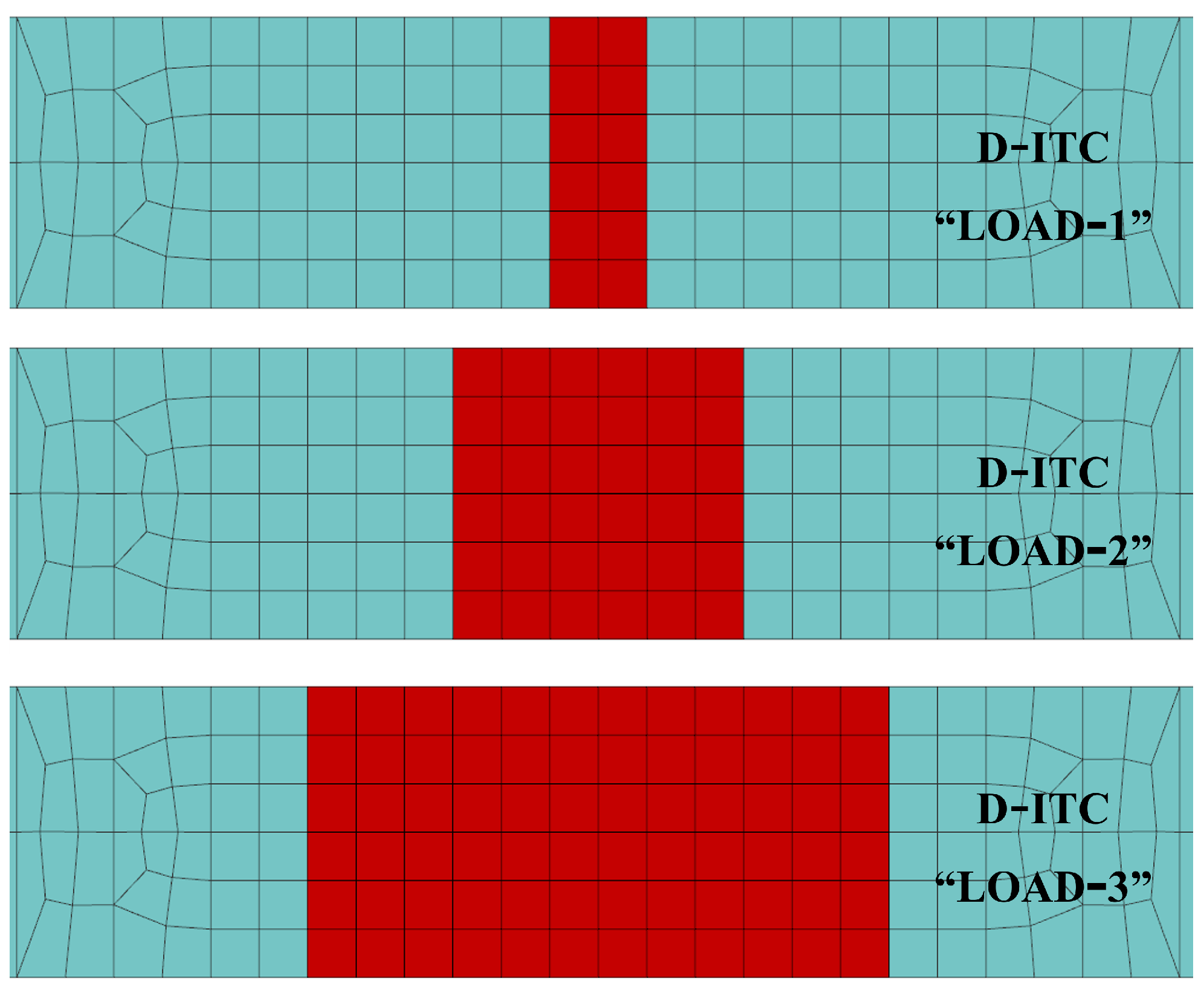
3. Infrared-Guided Imposed Thermal Cycle Method
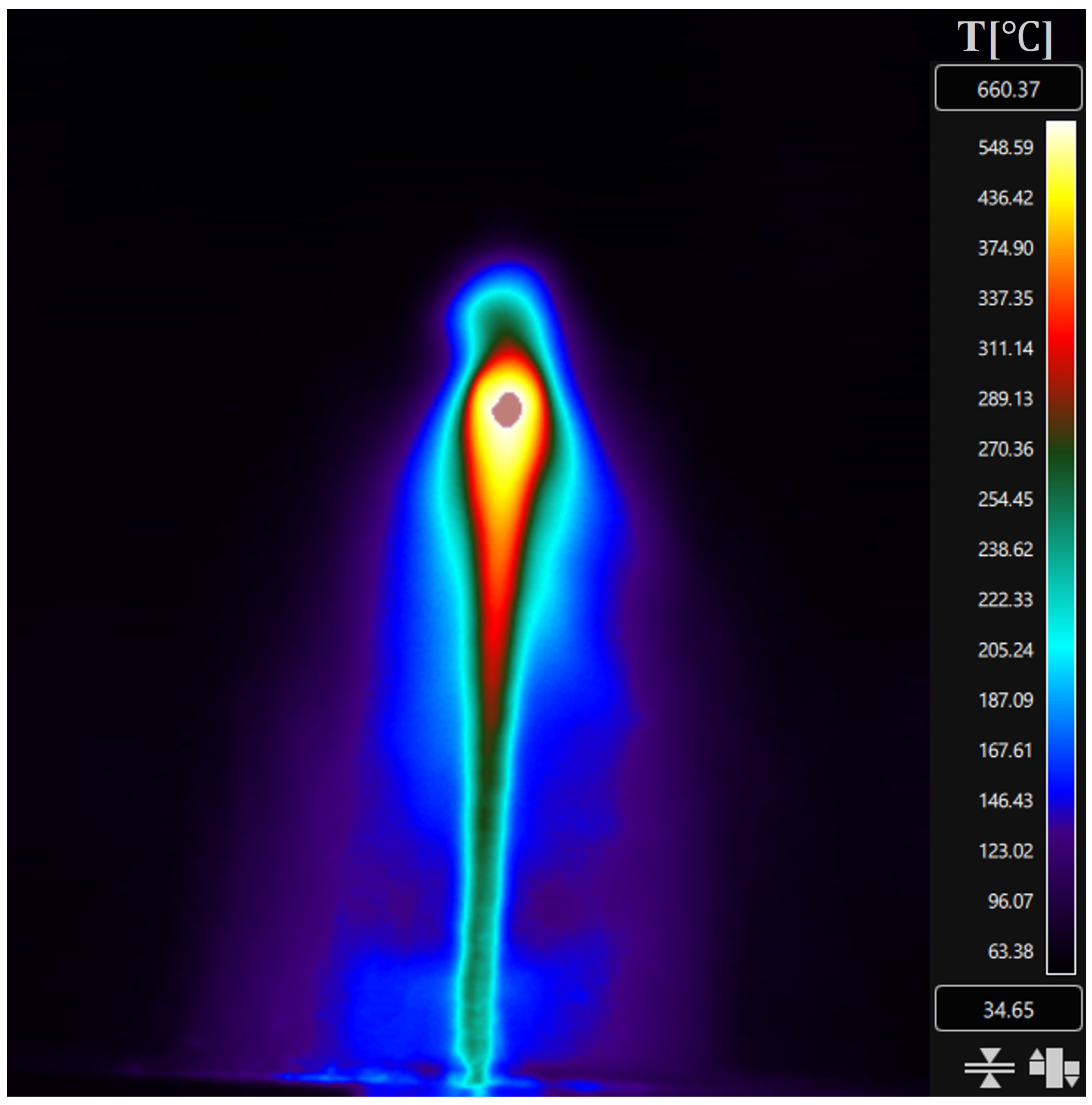
IR Camera Monitoring
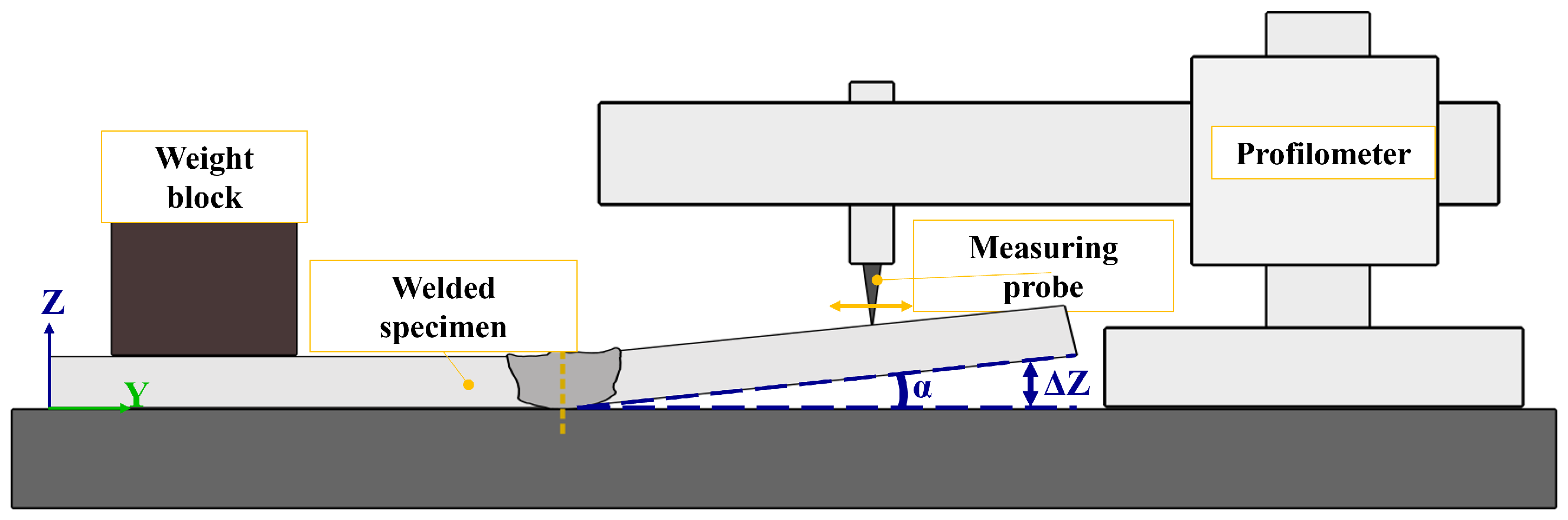
4. Experimental Results
4.1. Materials and Experimental Methodology
4.2. Numerical Solver
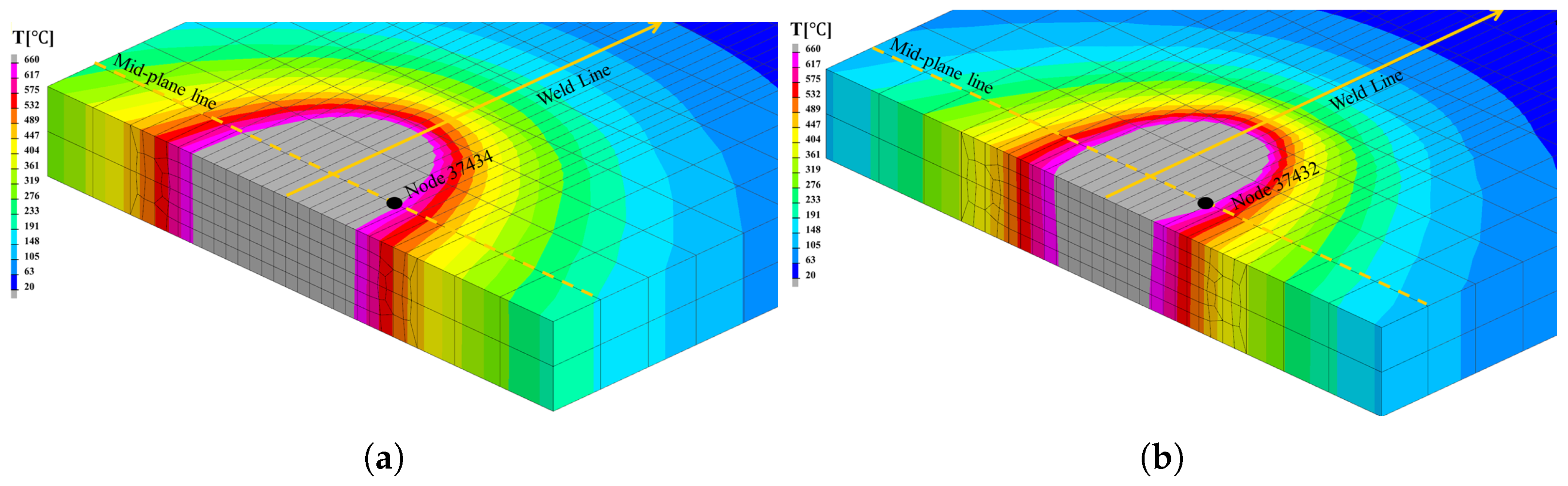
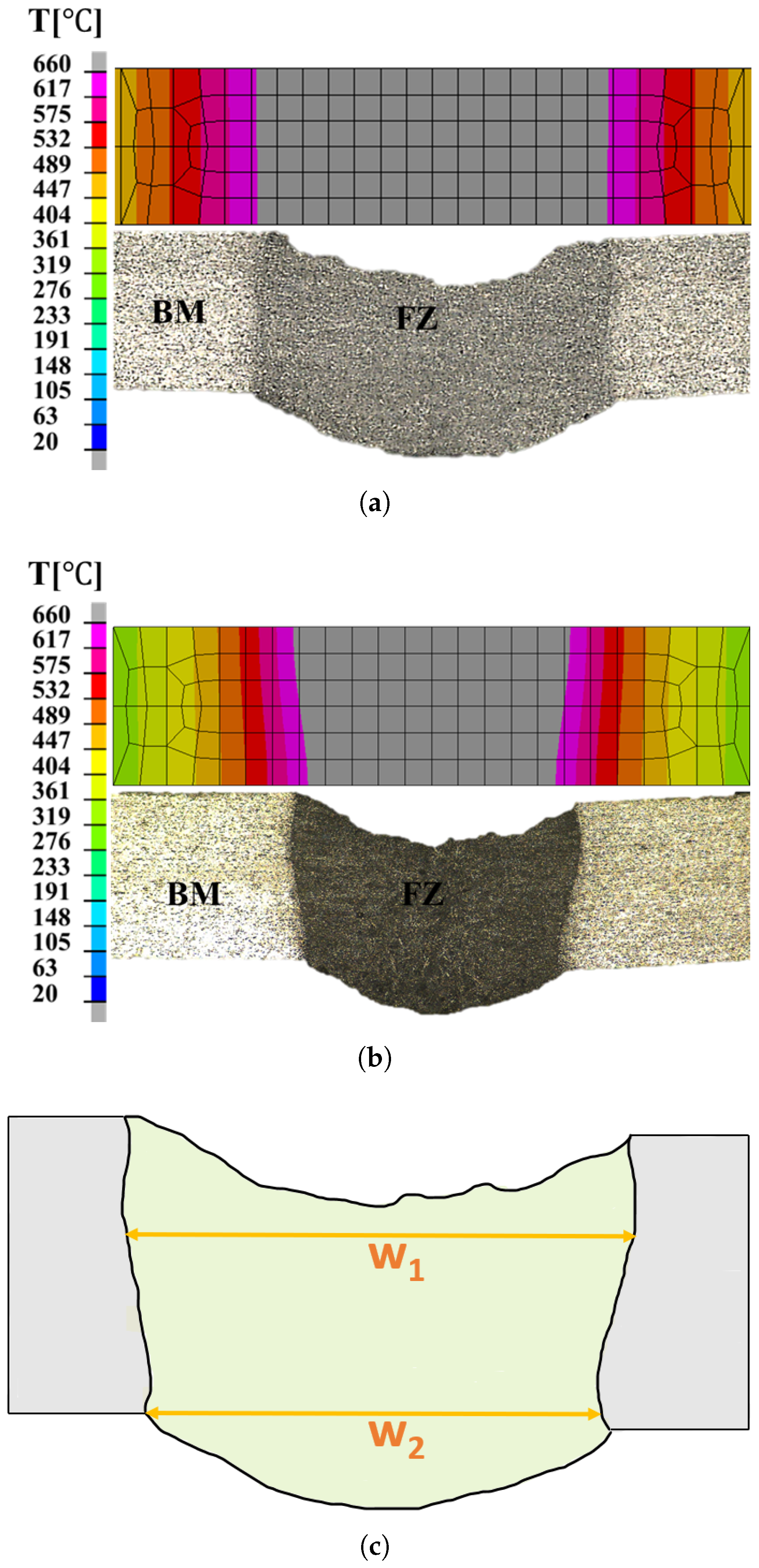
4.3. Cross-Section Comparison and Time Analysis
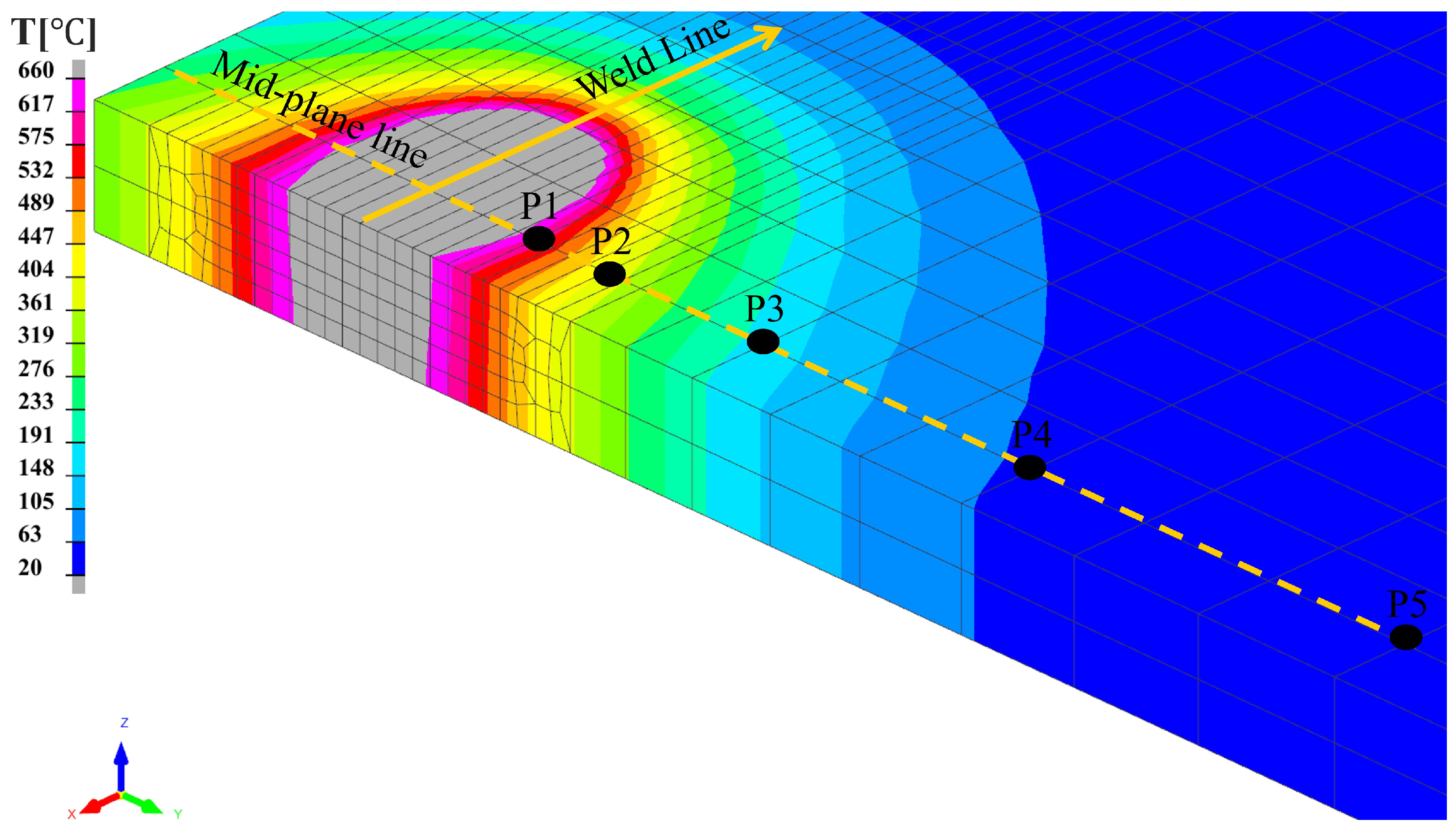
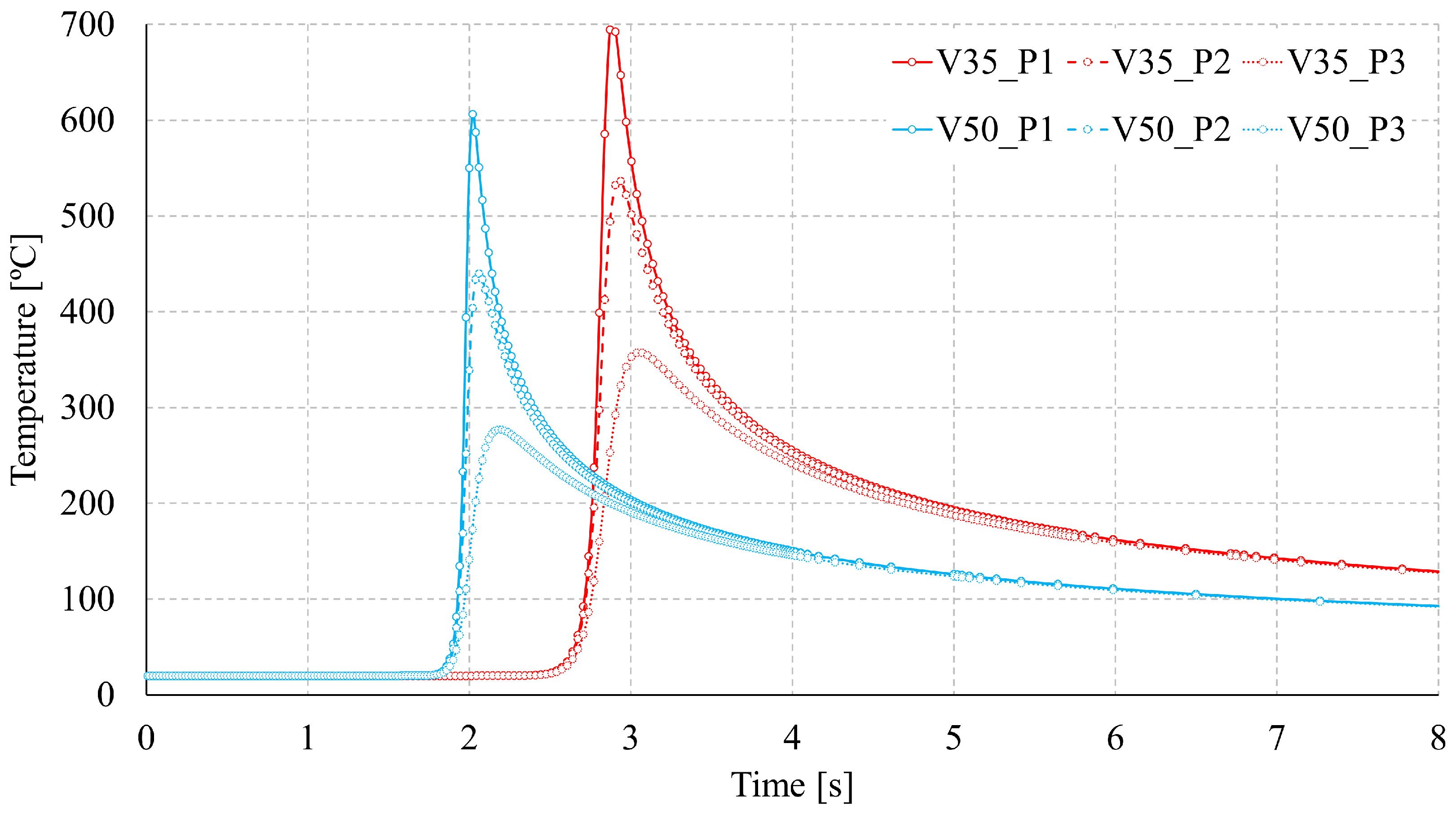
4.4. Thermal Analysis Results
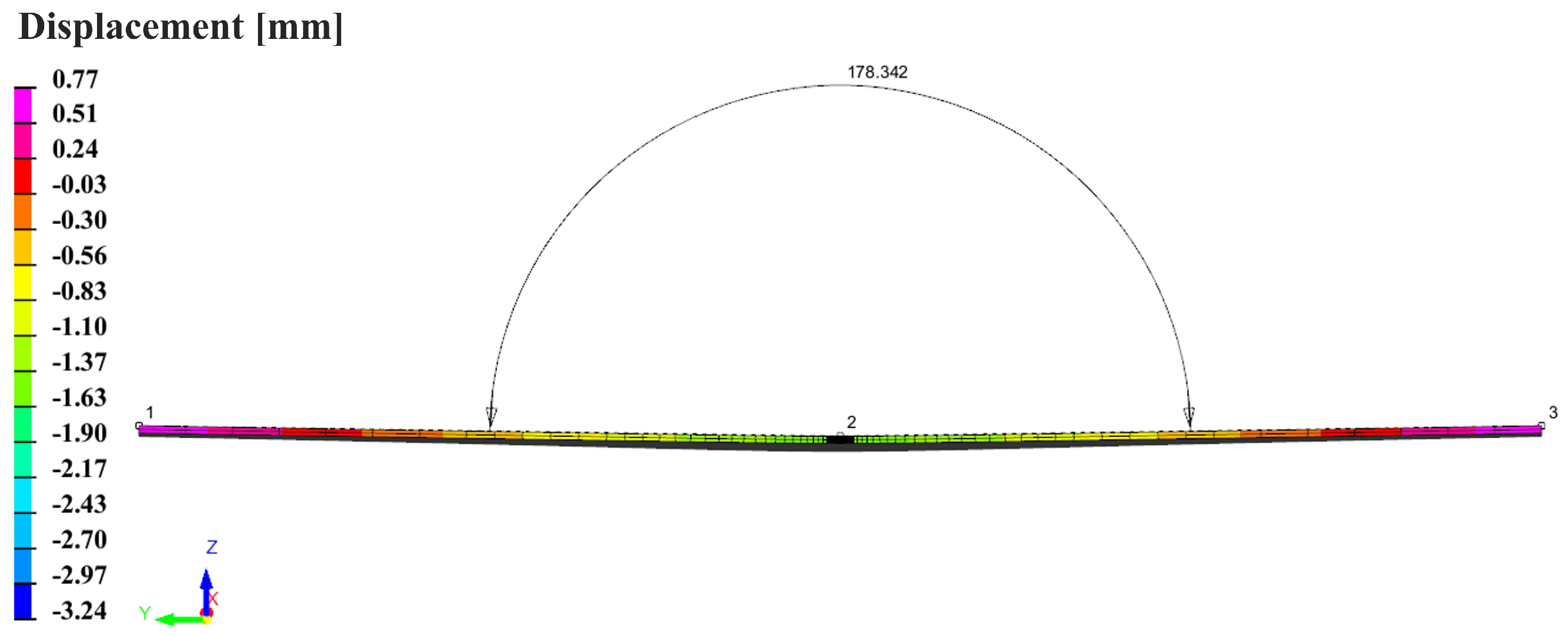
4.5. Mechanical Analysis Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, W.; Xu, J. Advanced lightweight materials for Automobiles: A review. Mater. Des. 2022, 221, 110994. [Google Scholar] [CrossRef]
- Basile, D.; Sesana, R.; De Maddis, M.; Borella, L.; Russo Spena, P. Investigation of Strength and Formability of 6016 Aluminum Tailor Welded Blanks. Metals 2022, 12, 1593. [Google Scholar] [CrossRef]
- Aminzadeh, A.; Silva Rivera, J.; Farhadipour, P.; Ghazi Jerniti, A.; Barka, N.; El Ouafi, A.; Mirakhorli, F.; Nadeau, F.; Gagné, M.O. Toward an intelligent aluminum laser welded blanks (ALWBs) factory based on industry 4.0; A critical review and novel smart model. Opt. Laser Technol. 2023, 167, 109661. [Google Scholar] [CrossRef]
- Bunaziv, I.; Akselsen, O.M.; Ren, X.; Nyhus, B.; Eriksson, M. Laser Beam and Laser-Arc Hybrid Welding of Aluminium Alloys. Metals 2021, 11, 1150. [Google Scholar] [CrossRef]
- Stavridis, J.; Papacharalampopoulos, A.; Stavropoulos, P. Quality assessment in laser welding: A critical review. Int. J. Adv. Manuf. Technol. 2018, 94, 1825–1847. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Yin, X.; Zhang, Z. Laser welding simulation of large-scale assembly module of stainless steel side-wall. Heliyon 2023, 9, e13835. [Google Scholar] [CrossRef] [PubMed]
- Anca, A.; Cardona, A.; Risso, J.; Fachinotti, V.D. Finite element modeling of welding processes. Appl. Math. Model. 2011, 35, 688–707. [Google Scholar] [CrossRef]
- Kik, T. Calibration of Heat Source Models in Numerical Simulations of Welding Processes. Metals 2024, 14, 1213. [Google Scholar] [CrossRef]
- Mohan, A.; Franciosa, P.; Dai, D.; Ceglarek, D. A novel approach to control thermal induced buckling during laser welding of battery housing through a unilateral N-2-1 fixturing principle. J. Adv. Join. Process. 2024, 10, 100256. [Google Scholar] [CrossRef]
- Chuang, T.C.; Lo, Y.L.; Tran, H.C.; Tsai, Y.A.; Chen, C.Y.; Chiu, C.P. Optimization of Butt-joint laser welding parameters for elimination of angular distortion using High-fidelity simulations and Machine learning. Opt. Laser Technol. 2023, 167, 109566. [Google Scholar] [CrossRef]
- Yan, H.; Zeng, X.; Cui, Y.; Zou, D. Numerical and experimental study of residual stress in multi-pass laser welded 5A06 alloy ultra-thick plate. J. Mater. Res. Technol. 2024, 28, 4116–4130. [Google Scholar] [CrossRef]
- Pyo, C.; Kim, J.; Kim, Y.; Kim, M. A study on a representative heat source model for simulating laser welding for liquid hydrogen storage containers. Mar. Struct. 2022, 86, 103260. [Google Scholar] [CrossRef]
- Murua, O.; Arrizubieta, J.; Lamikiz, A.; Schneider, H. Numerical simulation of a laser beam welding process: From a thermomechanical model to the experimental inspection and validation. Therm. Sci. Eng. Prog. 2024, 55, 102901. [Google Scholar] [CrossRef]
- Walker, T.; Bennett, C. An automated inverse method to calibrate thermal finite element models for numerical welding applications. J. Manuf. Process. 2019, 47, 263–283. [Google Scholar] [CrossRef]
- Speka, M.; Matteï, S.; Pilloz, M.; Ilie, M. The infrared thermography control of the laser welding of amorphous polymers. NDT E Int. 2008, 41, 178–183. [Google Scholar] [CrossRef]
- Bagavathiappan, S.; Lahiri, B.; Saravanan, T.; Philip, J.; Jayakumar, T. Infrared thermography for condition monitoring—A review. Infrared Phys. Technol. 2013, 60, 35–55. [Google Scholar] [CrossRef]
- Santoro, L.; Sesana, R.; Molica Nardo, R.; Curá, F. Infrared in-line monitoring of flaws in steel welded joints: A preliminary approach with SMAW and GMAW processes. Int. J. Adv. Manuf. Technol. 2023, 128, 2655–2670. [Google Scholar] [CrossRef]
- Santoro, L.; Sesana, R. A pilot study using flying spot laser thermography and signal reconstruction. Opt. Lasers Eng. 2025, 188, 108901. [Google Scholar] [CrossRef]
- Sesana, R.; Santoro, L.; Curà, F.; Molica Nardo, R.; Pagano, P. Assessing thermal properties of multipass weld beads using active thermography: Microstructural variations and anisotropy analysis. Int. J. Adv. Manuf. Technol. 2023, 128, 2525–2536. [Google Scholar] [CrossRef]
- Vasilev, M.; MacLeod, C.N.; Loukas, C.; Javadi, Y.; Vithanage, R.K.W.; Lines, D.; Mohseni, E.; Pierce, S.G.; Gachagan, A. Sensor-Enabled Multi-Robot System for Automated Welding and In-Process Ultrasonic NDE. Sensors 2021, 21, 5077. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.L.; Van Nguyen, A.; Duy, H.L.; Nguyen, T.H.; Tashiro, S.; Tanaka, M. Relationship among Welding Defects with Convection and Material Flow Dynamic Considering Principal Forces in Plasma Arc Welding. Metals 2021, 11, 1444. [Google Scholar] [CrossRef]
- Zhu, C.; Cheon, J.; Tang, X.; Na, S.J.; Cui, H. Molten pool behaviors and their influences on welding defects in narrow gap GMAW of 5083 Al-alloy. Int. J. Heat Mass Transf. 2018, 126, 1206–1221. [Google Scholar] [CrossRef]
- Filyakov, A.E.; Sholokhov, M.A.; Poloskov, S.I.; Melnikov, A.Y. The study of the influence of deviations of the arc energy parameters on the defects formation during automatic welding of pipelines. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Nizniy Tagil, Russia, 24–29 February 2020; Volume 966. [Google Scholar] [CrossRef]
- Aucott, L.; Huang, D.; Dong, H.B.; Wen, S.W.; Marsden, J.A.; Rack, A.; Cocks, A.C.F. Initiation and growth kinetics of solidification cracking during welding of steel. Sci. Rep. 2017, 7, 40255. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Yang, M.; Chang, B.; Du, D. Filter-PCA-Based Process Monitoring and Defect Identification During Climbing Helium Arc Welding Process Using DE-SVM. IEEE Trans. Ind. Electron. 2023, 70, 7353–7362. [Google Scholar] [CrossRef]
- D’Accardi, E.; Chiappini, F.; Giannasi, A.; Guerrini, M.; Maggiani, G.; Palumbo, D.; Galietti, U. Online monitoring of direct laser metal deposition process by means of infrared thermography. Prog. Addit. Manuf. 2024, 9, 983–1001. [Google Scholar] [CrossRef]
- Razza, V.; Santoro, L.; De Maddis, M. Gradient-based image generation for thermographic material inspection. Appl. Therm. Eng. 2025, 268, 125900. [Google Scholar] [CrossRef]
- Santoro, L.; Razza, V.; De Maddis, M. Frequency-based analysis of active laser thermography for spot weld quality assessment. Int. J. Adv. Manuf. Technol. 2024, 130, 3017–3029. [Google Scholar] [CrossRef]
- Santoro, L.; Razza, V.; De Maddis, M. Nugget and corona bond size measurement through active thermography and transfer learning model. Int. J. Adv. Manuf. Technol. 2024, 133, 5883–5896. [Google Scholar] [CrossRef]
- Zhang, C.; Li, X.; Gao, M. Effects of circular oscillating beam on heat transfer and melt flow of laser melting pool. J. Mater. Res. Technol. 2020, 9, 9271–9282. [Google Scholar] [CrossRef]
- Zhou, Q.; Rong, Y.; Shao, X.; Jiang, P.; Gao, Z.; Cao, L. Optimization of laser brazing onto galvanized steel based on ensemble of metamodels. J. Intell. Manuf. 2018, 29, 1417–1431. [Google Scholar] [CrossRef]
- Mirapeix, J.; García-Allende, P.; Cobo, A.; Conde, O.; López-Higuera, J. Real-time arc-welding defect detection and classification with principal component analysis and artificial neural networks. NDT E Int. 2007, 40, 315–323. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Z.; Zhang, C.; Xi, J.; Le, X. Weld Defect Detection Based on Deep Learning Method. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 1574–1579. [Google Scholar] [CrossRef]
- Sarkar, S.S.; Das, A.; Paul, S.; Mali, K.; Ghosh, A.; Sarkar, R.; Kumar, A. Machine learning method to predict and analyse transient temperature in submerged arc welding. Measurement 2021, 170, 108713. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Kik, T. Computational Techniques in Numerical Simulations of Arc and Laser Welding Processes. Materials 2020, 13, 608. [Google Scholar] [CrossRef] [PubMed]
- Unni, A.K.; Vasudevan, M. Computational fluid dynamics simulation of hybrid laser-MIG welding of 316 LN stainless steel using hybrid heat source. Int. J. Therm. Sci. 2023, 185, 108042. [Google Scholar] [CrossRef]
- Rong, Y.; Huang, Y.; Wang, L. Evolution Mechanism of Transient Strain and Residual Stress Distribution in Al 6061 Laser Welding. Crystals 2021, 11, 205. [Google Scholar] [CrossRef]
- Tian, X.; Liao, J.; Cheng, P.; Ling, Y. Element Simulation of Welding Residual Stresses and Distortion in 5083 Incorporating Metallurgical Phase Transformation. In Proceedings of the 2017 International Conference on Applied Mathematics, Modeling and Simulation (AMMS 2017), Shanghai, China, 26–27 November 2017; Atlantis Press: Dordrecht, The Netherlands, 2017; pp. 164–168. [Google Scholar] [CrossRef]
- Schieck, B.; Stumpf, H. Deformation analysis for finite elastic-plastic strains in a lagrangean-type description. Int. J. Solids Struct. 1993, 30, 2639–2660. [Google Scholar] [CrossRef]
- Lima, T.R.; Tavares, S.M.; de Castro, P.M. Residual stress field and distortions resulting from welding processes: Numerical modelling using Sysweld. Ciência Tecnol. Dos Mater. 2017, 29, e56–e61. [Google Scholar] [CrossRef]
- Kik, T. Heat Source Models in Numerical Simulations of Laser Welding. Materials 2020, 13, 2653. [Google Scholar] [CrossRef] [PubMed]
- Battista, F.R.; Ambrogio, G.; Giorgini, L.; Guerrini, M.; Costantino, S.; Ricciardi, F.; Filice, L. Prediction of the keyhole TIG welding-induced distortions on Inconel 718 industrial gas turbine component by numerical-experimental approach. Int. J. Adv. Manuf. Technol. 2024, 134, 4593–4608. [Google Scholar] [CrossRef]
- Vargas, J.A.; Torres, J.E.; Pacheco, J.A.; Hernandez, R.J. Analysis of heat input effect on the mechanical properties of Al-6061-T6 alloy weld joints. Mater. Des. (1980–2015) 2013, 52, 556–564. [Google Scholar] [CrossRef]
- Marques, E.S.V.; Silva, F.J.G.; Pereira, A.B. Comparison of Finite Element Methods in Fusion Welding Processes—A Review. Metals 2020, 10, 75. [Google Scholar] [CrossRef]
- Long, H.; Gery, D.; Carlier, A.; Maropoulos, P. Prediction of welding distortion in butt joint of thin plates. Mater. Des. 2009, 30, 4126–4135. [Google Scholar] [CrossRef]
- Vinoth, A.; Sivasankari, R. Numerical Simulation Studies in Tungsten Inert Gas Welding of Inconel 718 Alloy Sheet. J. Mater. Eng. Perform. 2024. [Google Scholar] [CrossRef]
- Kožar, I.; Rukavina, T.; Ibrahimbegović, A. Method of Incompatible Modes—Overview and Application. Građevinar 2018, 70, 19–29. [Google Scholar] [CrossRef]




| Sample | FEM (mm) | Experiment (mm) | ||
|---|---|---|---|---|
| 1 | 3.22 | 3.18 | 3.20 | 3.20 |
| 2 | 2.65 | 2.30 | 2.64 | 2.29 |
| Stage | Task | MHS (h) | T-ITC (h) | IR-ITC (h) |
|---|---|---|---|---|
| Calibration MHS | Metallographic sample preparation | 3.75 | 3.75 | 0.00 |
| Macroscopic analysis | 0.25 | 0.25 | 0.00 | |
| LOAD adjustment | 0.90 | 0.90 | 0.00 | |
| Heat Source inner radius adjustment | 0.90 | 0.90 | 0.00 | |
| Heat Source outer radius adjustment | 0.90 | 0.90 | 0.00 | |
| Heat Source height adjustment | 0.90 | 0.90 | 0.00 | |
| Efficiency adjustment | 0.90 | 0.90 | 0.00 | |
| Thermal Cycle Preparation | Thermal cycle extraction and preparation | 0.00 | 0.30 | 0.30 |
| Calibration IR-ITC | LOAD adjustment | 0.00 | 0.00 | 1.20 |
| Computation Time | Thermo-metallurgical–mechanical simulation | 1.50 | 0.40 | 0.00 |
| Total | 10.00 | 9.20 | 1.50 | |
| Sample | Model | P1 | P2 | P3 | P4 | P5 | Avg_Diff (°C) |
|---|---|---|---|---|---|---|---|
| 1 | Experiment | 660 | 532 | 282 | 118 | 71 | – |
| MHS | 695 | 494 | 253 | 97 | 39 | 31 | |
| T-ITC | 695 | 521 | 245 | 69 | 28 | 35 | |
| IR-ITC (LOAD-1) | 470 | 344 | 158 | 49 | 24 | 124 | |
| IR-ITC (LOAD-2) | 540 | 404 | 188 | 55 | 24 | 90 | |
| IR-ITC (LOAD-3) | 655 | 506 | 248 | 70 | 26 | 32 | |
| 2 | Experiment | 628 | 442 | 201 | 86 | 64 | – |
| MHS | 606 | 404 | 173 | 56 | 26 | 31 | |
| T-ITC | 620 | 431 | 159 | 40 | 24 | 29 | |
| IR-ITC (LOAD-1) | 423 | 277 | 102 | 31 | 21 | 113 | |
| IR-ITC (LOAD-2) | 507 | 344 | 127 | 34 | 21 | 77 | |
| IR-ITC (LOAD-3) | 600 | 435 | 168 | 39 | 21 | 31 |
| Sample | Model | Angle (°) | Error (%) |
|---|---|---|---|
| 1 | MHS | 177.98 | 0.15 |
| T-ITC | 177.97 | 0.15 | |
| IR-ITC | 177.92 | 0.18 | |
| Experiment | 178.24 | ||
| 2 | MHS | 178.43 | 0.22 |
| T-ITC | 178.37 | 0.25 | |
| IR-ITC | 178.34 | 0.27 | |
| Experiment | 178.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo Spena, P.; De Maddis, M.; Razza, V.; Santoro, L.; Mamarayimov, H.; Basile, D. Infrared-Guided Thermal Cycles in FEM Simulation of Laser Welding of Thin Aluminium Alloy Sheets. Metals 2025, 15, 830. https://doi.org/10.3390/met15080830
Russo Spena P, De Maddis M, Razza V, Santoro L, Mamarayimov H, Basile D. Infrared-Guided Thermal Cycles in FEM Simulation of Laser Welding of Thin Aluminium Alloy Sheets. Metals. 2025; 15(8):830. https://doi.org/10.3390/met15080830
Chicago/Turabian StyleRusso Spena, Pasquale, Manuela De Maddis, Valentino Razza, Luca Santoro, Husniddin Mamarayimov, and Dario Basile. 2025. "Infrared-Guided Thermal Cycles in FEM Simulation of Laser Welding of Thin Aluminium Alloy Sheets" Metals 15, no. 8: 830. https://doi.org/10.3390/met15080830
APA StyleRusso Spena, P., De Maddis, M., Razza, V., Santoro, L., Mamarayimov, H., & Basile, D. (2025). Infrared-Guided Thermal Cycles in FEM Simulation of Laser Welding of Thin Aluminium Alloy Sheets. Metals, 15(8), 830. https://doi.org/10.3390/met15080830










