Atomic-Scale Mechanisms of Stacking Fault Tetrahedra Formation, Growth, and Transformation in Aluminum via Vacancy Aggregation

Abstract

Stacking fault tetrahedra (SFTs) are typically considered improbable in high stacking fault energy metals like aluminum. Using molecular statics and dynamics simulations, we reveal the formation, growth, and transformation of SFTs in aluminum via vacancy aggregation. Three types—perfect, truncated, and defective SFTs—are characterized by their structure, formation energy, and binding energy across a range of vacancy cluster sizes. Formation energies of perfect and truncated SFTs follow a scaling relation; beyond a critical size, truncated SFTs become thermodynamically favored, indicating a size-dependent transformation pathway. Binding energy and structure evolution exhibit quasi-periodic behavior, where vacancies initially adsorb at the vertices or the midpoints of the edges of a perfect SFT, then aggregate along one facet, triggering fault nucleation and a binding energy jump as the system reconstructs into a new perfect SFT. Molecular dynamics simulations further confirm the SFT nucleation and growth via vacancy aggregation, consistent with thermodynamic predictions. SFTs exhibit notable thermal mobility, enabling coalescence and evolution into vacancy-type dislocation loops. BCC-like $V_5$ clusters are identified as potential nucleation precursors. These findings explain the nanoscale, low-temperature nature of SFTs in aluminum and offer new insights into defect evolution and control in FCC metals.

1. Introduction

Stacking-fault tetrahedra (SFT) are prototypical vacancy-based defect structures frequently observed in face-centered cubic (FCC) metals subjected to plastic deformation, rapid quenching, or irradiation [1,2,3]. However, in aluminum—a metal characterized by a notably high stacking fault energy—the formation of SFTs has long been deemed improbable. This conventional understanding was challenged in 1999, when Kiritani et al. reported the first experimental observation of SFTs in fractured Al thin films [4]. Subsequent work by Satoh et al. confirmed the presence of SFTs in Al under electron, self-ion, and neutron irradiation [5]. Their TEM observations showed that the average size of the SFT is about 2 nm, corresponding to aggregates of a few tens of vacancies, and further demonstrated that for vacancy clusters containing fewer than 100 vacancies, the SFT configuration dominates the defect landscape [5]. Theoretical investigations, including both first-principles and molecular dynamics simulations, have consistently indicated that SFTs are energetically favorable relative to other vacancy cluster morphologies in Al when containing fewer than 50 vacancies [6,7,8].

Despite these advances, the underlying mechanisms governing SFT nucleation and growth in Al remain poorly understood. Among the proposed models, the most widely recognized is the Silcox–Hirsch mechanism, which describes a transformation pathway beginning with the condensation of vacancies into an equilateral triangular plate. This plate subsequently collapses into a Frank dislocation loop, from which Shockley partials emanate to form the SFT. Although MD simulations have shown that such transformations can occur under idealized conditions [9], the spontaneous formation of equilateral vacancy plates in real materials is statistically rare. Recent first-principles calculations further suggest that such planar vacancy clusters are energetically less favorable than isolated vacancies in Al [7,8], undermining the relevance of the Silcox–Hirsch mechanism in this system.

An alternative pathway involves the transformation of a three-dimensional vacancy void into an SFT. Using accelerated MD, Uberuaga et al. demonstrated that such a transformation is feasible in Cu and further explored the size-dependent energetics of void- and SFT-type clusters across multiple FCC metals [10]. Their results suggest that the kinetics of void-to-SFT conversion may be fastest in Pd and comparable in Cu, Ni, and Ag, while voids remain more stable in Pt and Au [10]. However, aluminum was not examined in that study. Recent first-principles results indicate that in Al, small SFT clusters are more stable than voids, implying the possibility of spontaneous void-to-SFT conversion [7,8]. Our recent work further supports this scenario, showing that small voids in Al can spontaneously collapse into SFTs under compressive stress [11]. Nonetheless, such voids are generally thermodynamically unstable under ambient conditions and may require high vacancy supersaturation or chemical facilitation (e.g., by hydrogen) to nucleate [8,12].

A third mechanism—direct SFT formation via vacancy agglomeration—has long been overlooked. First proposed by de Jong and Koehler, this pathway posits that a vacancy-tetrahedron may serve as a nucleation unit for SFT formation [13]. While subsequent theoretical and experimental studies have lent credence to this hypothesis [14,15], direct atomic-scale validation has remained elusive due to experimental limitations. Recently, Aidhy et al. employed MD simulations to capture the formation and growth of SFTs in Ni via vacancy diffusion and agglomeration [16]. Their findings demonstrated that vacancy-tetrahedra act as nucleation sites and that perfect SFTs can grow through successive vacancy capture [16]. Whether this mechanism applies to Al, however, remains unresolved. One of the key questions is that in aluminum, vacancy-tetrahedra are energetically unstable. Instead, a $V_5$ cluster with a BCC-like structure is considered the most stable configuration and is thought to act as the nucleation point for vacancy clusters. Nevertheless, to date, there remains no direct atomic-scale evidence supporting this mechanism.

In this work, we combine molecular statics (MS) and molecular dynamics (MD) simulations to systematically investigate the nucleation and growth mechanisms of SFTs in aluminum. Using MS simulations, we characterize the energetic and structural evolution of SFT as a function of cluster size. We then employ large-scale MD simulations to capture the dynamic formation of SFTs via vacancy diffusion and agglomeration. These findings offer critical atomistic insight into the mechanisms governing SFT evolution in Al.

2. Computational Methodology

2.1. Molecular Statics and Dynamics Simulations

All MS and MD simulations were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS Stable Release 29 August 2024) [17]. To balance computational efficiency with accuracy, simulations were carried out in three distinct FCC supercells of increasing size: 13 × 13 × 13 (8788 lattice sites), 20 × 20 × 20 (32,000 lattice sites), and 40 × 40 × 40 (256,000 lattice sites). The simulation cells were constructed with lattice vectors aligned along the [100], [010], and [001] crystallographic directions, and periodic boundary conditions were imposed along all three spatial dimensions. For MS simulations, full atomic relaxations were performed, including adjustments to both the atomic positions and the shape and volume of the supercell to ensure energy minimization under zero external pressure. For MD simulations, the canonical ensemble was employed with a time integration step of 2 femtoseconds. Structural analysis and post-processing of the simulation data were conducted using the OVITO software package (v 3.11.3) [18]. Defect identification and characterization were performed using Wigner–Seitz cell-based vacancy analysis and the dislocation extraction algorithm (DXA) for identifying extended defect structures such as stacking faults and dislocations.

The fidelity of MS and MD simulations is fundamentally governed by the accuracy of the employed empirical potentials. Despite the widespread use of empirical potentials for simulating aluminum, a systematic evaluation of their reliability in capturing the energetics and dynamical behavior of SFTs has been lacking. To address this gap, we selected ten widely adopted empirical potentials for aluminum—Pot_Pascuet [19], Pot_Lee [20], Pot_Mendelev [21], Pot_Mishin [22], Pot_Winey [23], Pot_Liu [24], Pot_Zope [25], Pot_Sturgeon [26], Pot_Zhakhovskii [27], and Pot_Zhou [28]—and conducted a comprehensive comparative analysis.

To assess their capability in describing SFT energetics and structural stability, we constructed SFT configurations containing up to 36 vacancies in a 5 × 5 × 5 FCC supercell. Structural relaxations were carried out both using first-principles and ten empirical potentials under strictly identical simulation settings, including the same supercell geometry and periodic boundary conditions. Although finite-size effects are inevitable in such small supercells, their uniform presence across all approaches enables a direct and meaningful comparison. The deviation between the first-principles results and those predicted by each potential served as a quantitative benchmark for evaluating accuracy and transferability. Based on their relative agreement with first-principles predictions, a subset of high-performing potentials was identified and selected for in-depth MS and MD simulations throughout this work. The remaining potentials were retained as auxiliary tools for cross-validating energetic trends and capturing qualitative dynamical behavior. This multi-potential strategy not only enhances confidence in our findings but also offers a broader view of potential-dependent uncertainties in the modeling of defect phenomena in aluminum.

2.2. First-Principles Calculations

First-principles calculations were carried out using the Vienna Ab initio Simulation Package (VASP) [29,30] with the projector augmented wave (PAW) method [31]. Exchange–correlation effects were described using the PBEsol functional [32], a revised version of the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) [33] optimized for surface-related systems. A plane-wave energy cutoff of 400 eV was adopted. All simulations were conducted on 5 × 5 × 5 FCC supercells consistent with the empirical-potential-based studies, allowing for a direct comparison. Meanwhile, during relaxation, both atomic positions and the lattice vectors were also allowed to vary to ensure full structural equilibration. The total energy convergence threshold was set to 1 × 10⁻⁶ eV, and ionic relaxations were terminated once the maximum force on any atom dropped below 0.01 eV/Å. Brillouin zone integrations were performed using a Monkhorst-Pack grid of 3 × 3 × 3 k-points.

It should be noted that the use of first-principles calculations in this context is not aimed at producing highly precise absolute energies of SFTs, due to intrinsic limitations in system size and computational cost. Rather, the first-principles results serve as a rigorous reference framework against which the performance of various empirical potentials can be quantitatively assessed. This comparative strategy enables a reliable selection of suitable potentials for subsequent large-scale molecular statics and dynamics simulations of defect formation and evolution in aluminum.

2.3. Formation Energy and Binding Energy of SFTs

The SFT is not simply a vacancy cluster; it comprises a closed three-dimensional network of partial dislocations that enclose intrinsic stacking-faulted planes. Within these planes, atoms are displaced from their ideal FCC lattice sites and occupy energetically metastable positions characteristic of intrinsic stacking faults. To quantify the size of the SFT, we define the associated vacancy number as the difference between the number of atoms in a perfect FCC supercell and that in the defective configuration containing the SFT. This vacancy number provides a consistent metric for characterizing defect magnitude across various configurations.

The formation energy of the SFT with vacancy number $n$ ($V_n$) is given by:

$$E_f^{V_n}=E_{tot}^{V_n}-{\displaystyle \frac{N-n}{N}}{E}_{tot}^{bulk},$$

(1)

where $E_{tot}^{bulk}$ is the total energy of a defect-free FCC supercell containing $N$ aluminum atoms, and $E_{tot}^{V_n}$ is the total energy of the same supercell after introducing and relaxing the SFT $V_n$. To evaluate the energetic driving force for SFT growth, we calculate the binding energy between an existing SFT $V_{n-1}$ and a single isolated monovacancy as:

$$E_b^{V_n}=E_f^{V_1}+E_f^{V_{n-1}}-E_f^{V_n},$$

(2)

where $E_f^{V_1}$ is the formation energy of an isolated monovacancy, and $E_f^{V_{n-1}}$ and $E_f^{V_n}$ are the formation energies of the most stable SFTs with vacancy numbers $n-1$ and $n$, respectively. A positive binding energy indicates an energetically favorable interaction between a monovacancy and the pre-existing SFT $V_{n-1}$, implying a thermodynamic preference for vacancy absorption and subsequent SFT growth. The greater the value, the stronger the tendency of SFT $V_{n-1}$ to incorporate an additional vacancy and the more stable SFT $V_n$ becomes against dissociation. Conversely, a negative binding energy suggests a repulsive interaction, implying that an isolated vacancy and SFT $V_{n-1}$ do not energetically favor aggregation into a larger SFT.

3. Result and Discussion

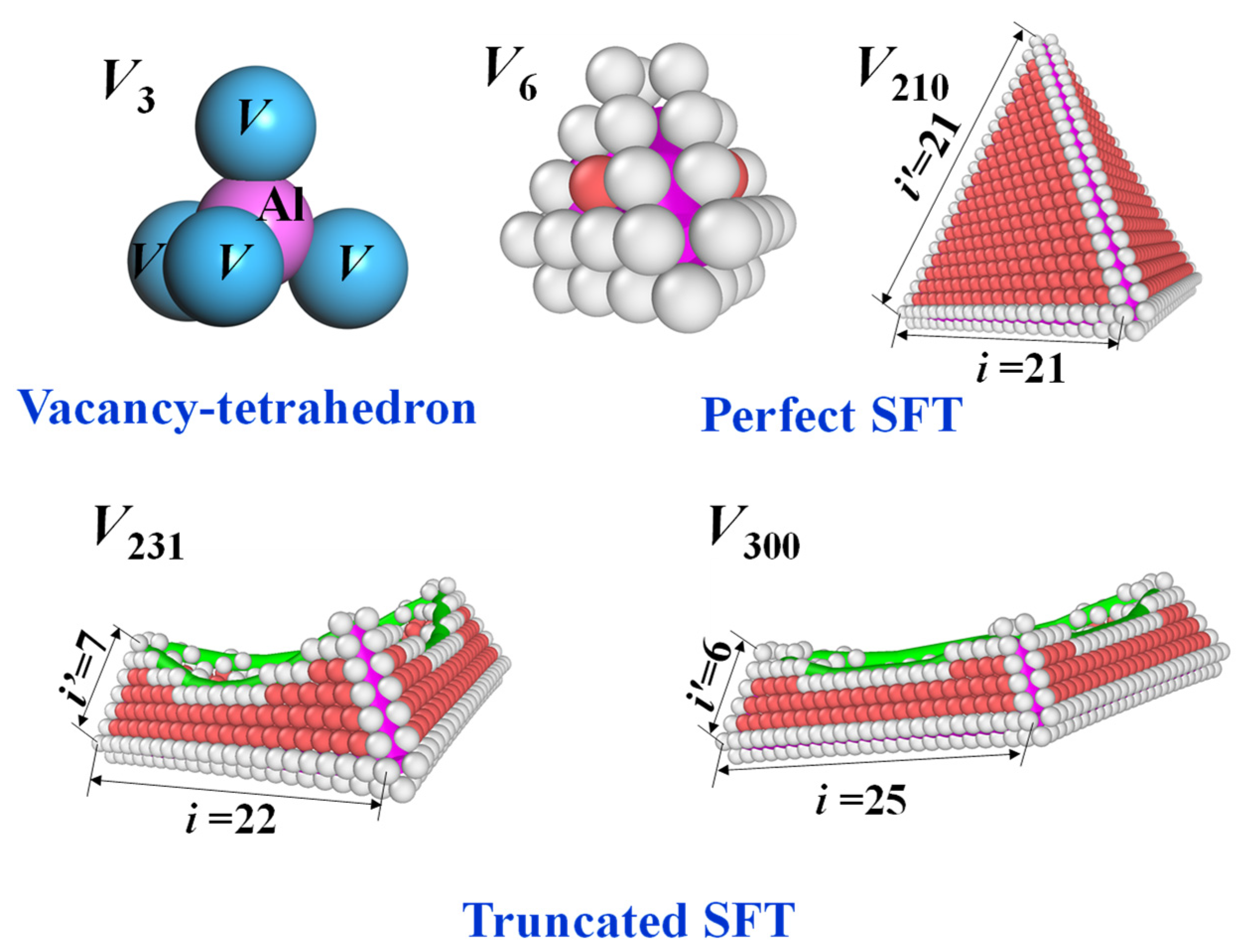
3.1. Structures of SFT

The perfect SFT adopts a highly symmetric tetrahedral morphology, comprising six 1/6<110> stair-rod dislocations along its edges and four intrinsic stacking faults confined to the {111} planes (see Figure 1). The size of such structures is quantized, corresponding to specific “magic numbers” of vacancies defined by $n_i={\displaystyle \frac{i \times \left(i -1\right)}{2}}$, where $i$ is an integer starting from 3. This yields vacancy counts of 3, 6, 10, 15, 21, 28, and so forth. Notably, the case of $i=3$, which nominally corresponds to three vacancies, does not result in a perfect SFT. Instead, it forms a tetrahedron consisting of four nearest-neighbor vacancies enclosing an interstitial aluminum atom. This configuration is usually denoted as a “vacancy-tetrahedron” (see Figure 1). 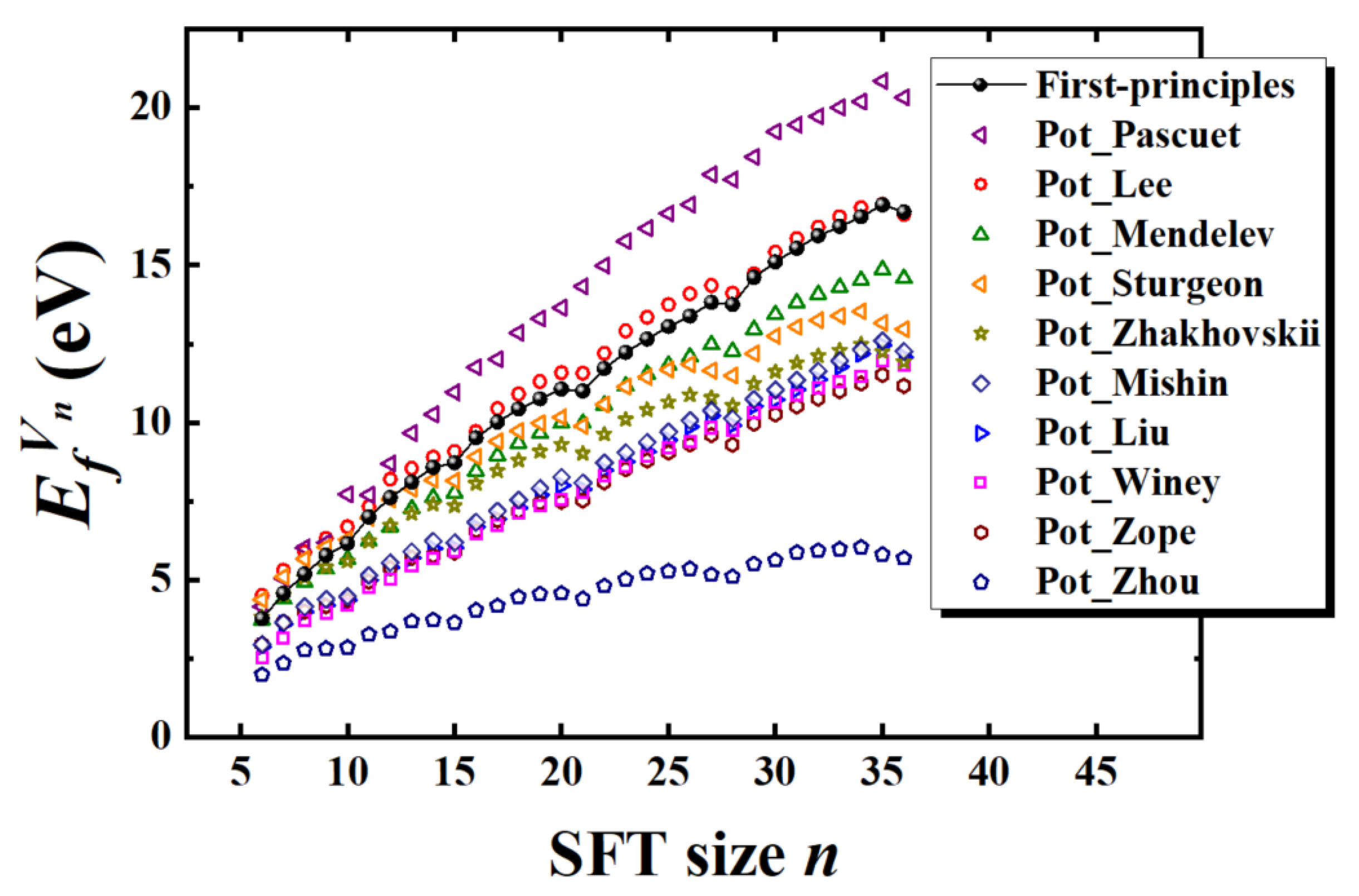The smallest structure that qualifies as a perfect SFT appears at $n=6$, corresponding to $i=4$ (see Figure 1). Perfect SFT configurations can be systematically generated via MS simulations by introducing equilateral triangular vacancy plates into the (111) planes of the FCC matrix and relaxing the structure, following the Silcox–Hirsch mechanism. Among the ten empirical interatomic potentials evaluated, Pot_Zhakhovskii proved most effective in stabilizing perfect SFTs, supporting structures containing up to 780 vacancies. In contrast, other potentials failed to preserve the ideal tetrahedral symmetry at larger sizes—typically beyond 200 to 300 vacancies—resulting instead in truncated configurations, that is, “truncated SFT” (see Figure 1).

The truncated SFT is characterized by the absence of one vertex of the tetrahedron. Specifically, it terminates at the junction of three Shockley partial dislocations, resulting in a geometry where the top facet is re-entrant due to the high intrinsic stacking fault energy of aluminum (see Figure 1). As additional vacancies are incorporated, the structure undergoes further distortion, becoming increasingly compressed and ultimately transforming into a dissociated Frank-type dislocation loop—a transition consistent with prior theoretical predictions. Taking the Pot_Lee potential as a representative example, the formation of truncated SFTs begins at approximately 231 vacancies. The structural height of the truncated SFT, denoted as $i’$ in Figure 1, decreases rapidly with increasing vacancy number. As shown in Figure 2, $i’$ converges to a value of 6 by $i=25$, beyond which it remains invariant despite further increases in vacancy count. These results are in agreement with those reported by Zhang et al. [9].

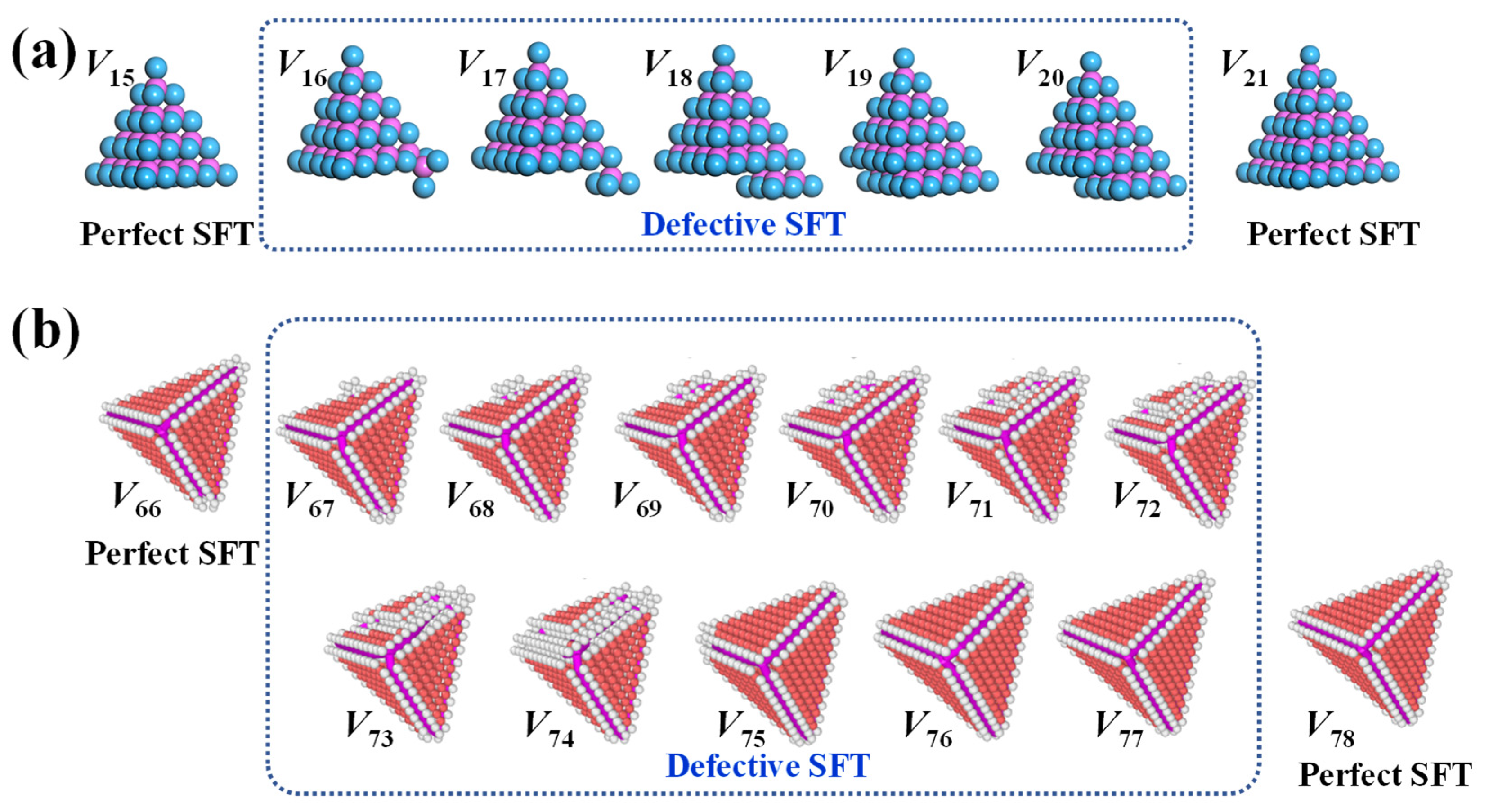
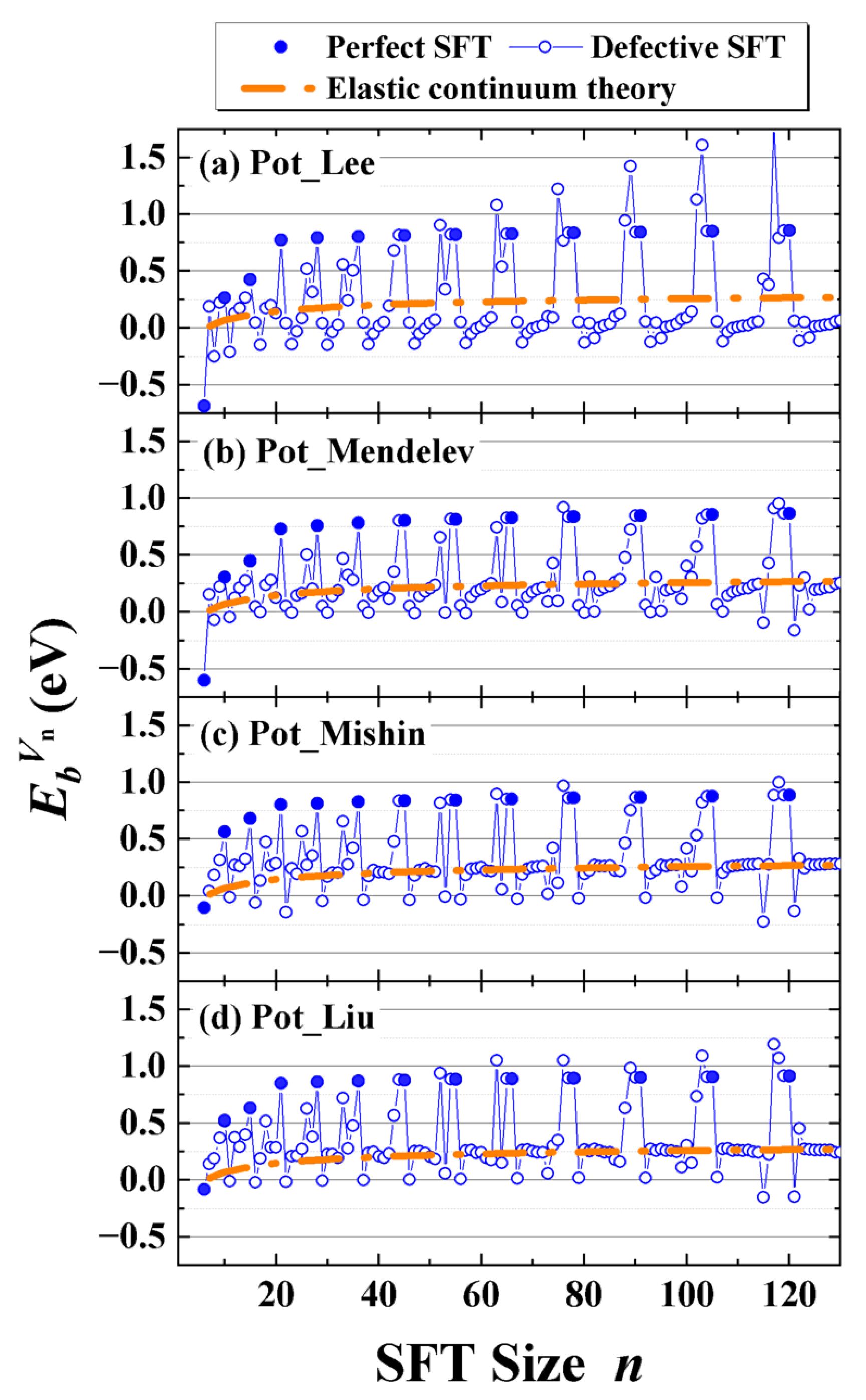
While the structural characteristics of perfect and truncated SFTs have been extensively investigated, our simulations reveal a third, previously underexplored variant: the defective SFT. These configurations emerge between two perfect SFTs. Defective SFTs can also be obtained via the Silcox–Hirsch mechanism, by introducing additional vacancies at lattice sites near the perimeter of an equilateral triangular vacancy plate embedded in the (111) plane. Upon structural relaxation through MS simulations, these perturbed vacancy plates evolve into defective SFTs. To systematically identify energetically favorable defective SFT configurations, we performed short-time MD simulations at representative temperatures (300 K and 600 K), using the aforementioned triangular vacancy plates as initial conditions. A series of intermediate structures was extracted from the MD trajectories and subsequently subjected to energy minimization via MS relaxation. The configuration yielding the lowest energy at each vacancy number was regarded as the most stable defective SFT and selected for detailed analysis. These optimized structures provided the basis for calculating the formation and binding energies, thereby enabling a thermodynamic assessment of the relative stability and growth behavior of defective SFT in aluminum.

Figure 3 presents two representative series of defective SFTs identified in the vacancy ranges between perfect SFTs with magic number counts of $V_{15}$-$V_{21}$ and $V_{66}$-$V_{78}$. These defective configurations consistently preserve the fundamental tetrahedral geometry characteristic of the preceding smaller perfect SFT, yet exhibit incompleteness relative to the next higher-order magic-number structure. Detailed analysis reveals that the formation of these intermediate structures begins with the adsorption of vacancies either at the tetrahedral corners (e.g., $V_{16}$) or at the midpoints along stair-rod dislocation edges (e.g., $V_{67}$). These initial additions give rise to local vacancy-tetrahedron configuration. As more vacancies are incorporated, they preferentially accumulate along one {111} facet of the tetrahedron, initiating the nucleation and growth of an embryonic stacking fault (e.g., $V_{17}$ to $V_{20}$ and $V_{68}$ to $V_{74}$). This evolution continues incrementally until the total vacancy count approaches the next magic number. Strikingly, when the vacancy number falls within three to four of the next perfect SFT configuration, a pronounced structural transition occurs. As shown in configurations such as $V_{75}$ to $V_{77}$, the defective SFT often manifests incomplete vertices at the corners of the tetrahedron, in comparison to the fully enclosed form of the subsequent perfect SFT. These observations illustrate the progressive evolution of defective SFTs as they transition toward the next perfect magic-number configuration.

3.2. Validation of Empirical Potentials for SFT Energetics

Figure 4 and Figure 5 present the formation and binding energies of SFTs, respectively, calculated using first-principles methods and MS simulations based on ten distinct empirical potentials. Noted that, all first-principles and MS calculations were performed using the same 5 × 5 × 5 supercell with identical boundary conditions and relaxation procedures, making the evaluation of the relative accuracy of the ten potentials meaningful. As shown in Figure 4, among all these ten empirical potentials, Pot_Lee exhibits the closest agreement with the first-principles predictions for SFT formation energies, followed by Pot_Mendelev, which slightly underestimates the first-principles values. Pot_Pascuet yields a mild overestimation, while the remaining potentials systematically underestimate the formation energy. All potentials reproduce the expected trend of increasing formation energy with SFT size, in qualitative agreement with first-principles predictions.

Regarding the binding energy, as shown in Figure 5, first-principles calculations reveal a quasi-periodic oscillation in binding energy with increasing SFT size. Within each interval between two perfect SFTs, the binding energy starts from a deep negative minimum, rises sharply, and then increases more gradually until a pronounced jump occurs at the next perfect SFT—marking the start of a new cycle. With the exception of Pot_Pascuet, all empirical potentials qualitatively capture this cyclic pattern, though numerical deviations are observed across specific sizes. In particular, Pot_Lee and Pot_Mendelev continue to exhibit the best agreement with first-principles results. Notably, Pot_Mendelev outperforms Pot_Lee slightly in this regard, as Pot_Lee fails to predict the correct minimum binding energy immediately after the formation of a perfect SFT; instead, it assigns the minimum to the second structure following the perfect SFT. Pot_Mishin and Pot_Liu also perform reasonably well, maintaining qualitative consistency and relatively small deviations. By contrast, the remaining potentials tend to systematically overestimate the binding energy relative to first-principles predictions, indicating limitations in their ability to accurately capture vacancy–SFT interactions during SFT growth.

Based on this comparative analysis, Pot_Lee and Pot_Mendelev were selected for subsequent simulations. Pot_Lee, developed using both first and second nearest-neighbor formulations of the modified embedded atom method, provides high accuracy but is computationally demanding. In contrast, Pot_Mendelev, based on the embedded atom method, offers significantly faster computational performance. Therefore, Pot_Lee and Pot_Mendelev were selected as the primary interatomic potentials in this study, with Pot_Mendelev being preferentially employed for large-scale MD simulations due to its superior performance in capturing binding energetics. In addition, other interatomic potentials were employed to validate the general trends and reinforce the robustness of the observed energetic behaviors of SFTs.

3.3. Formation Energies of Perfect and Truncated SFTs

Figure 6 presents the formation energies of perfect and truncated SFTs as a function of vacancy cluster size, calculated via MS simulations. It can be seen that the formation energies of both perfect and truncated SFTs increase with increasing cluster size across all empirical potentials. Notably, the growth rate is substantially higher for perfect SFTs than truncated SFTs. Consequently, beyond a certain critical size, formation energies of truncated SFTs fall below that of the corresponding perfect SFTs. This crossover marks a stability transition, wherein large perfect SFTs become thermodynamically unfavorable and tend to transform into truncated SFTs. Furthermore, the magnitude of the energy difference between perfect and truncated SFTs continues to grow with increasing cluster size, reinforcing the preference for truncated SFTs at larger scales. The critical vacancy number at which this crossover occurs varies across potentials. For example, Pot_Lee predicts a crossover at $n=231$, while Pot_Mendelev and Pot_Mishin suggest transition points at $n=253$ and $n=210$, respectively.

The formation energy of an SFT can be expressed as the sum of the stacking fault energy and the elastic energy associated with the dislocation loop [34]:

$$E_f^{V_n}=\sqrt{3L^2\gamma }+{\displaystyle \frac{G{b}^{2}L}{6\pi \left(1-\upsilon \right)}}\left\{ln{\displaystyle \frac{4L}{b}}+1.017+0.97\upsilon \right\},$$

(3)

where $\gamma$, $G$, and $\upsilon$ are the stacking fault energy, the shear modulus, and Poisson ratio, respectively. $b$ is the magnitude of the Burgers vector. The parameter $L$ denotes the characteristic edge length of the tetrahedron. For an SFT composed of $n$ vacancies, the edge length scales as $L^2=\sqrt{3}/2\times a_0^2\times n$, where $a_0$ is the lattice constant. Substituting this into the above expression yields a reformulated formation energy:

$$E_f^{V_n}=A\times n+B\times n^{{\displaystyle \frac{1}{2}}},$$

(4)

where $A={\displaystyle \frac{3}{2}}\times a_0^2\times \gamma$ and $B={\displaystyle \frac{G{b}^2}{6\pi (1-\upsilon )}}\left\{ln{\displaystyle \frac{4L}{b}}+1.017+0.97\upsilon \right\}$. The parameter $B$ converges rapidly with increasing cluster size, allowing it to be effectively approximated as a constant. Our previous works have demonstrated that the formation energy of perfect SFTs can be well described by Equation (4) [8]. Here, we find that this scale relation also accurately captures the formation energy behavior of truncated SFTs across a broad range of cluster sizes. As shown in Figure 6, formation energies for both perfect and truncated SFTs can be well fitted by Equation (4), with the main differences arising from the fitted values of the model parameters $A$ and $B$.

For comparison, predictions from elastic continuum theory are also included in the figure, using material parameters from Ref. [34]. As shown in Figure 6, Pot_Lee demonstrates the closest quantitative agreement with elastic continuum theory predictions for perfect SFTs, with Pot_Mendelev performing comparably, albeit slightly underestimating the formation energies. Pot_Pascuet shows a modest tendency to overestimate, whereas the remaining potentials consistently yield lower-than-expected values across the vacancy range. This hierarchy aligns well with trends observed in the first-principles comparisons, reinforcing the credibility of Pot_Lee and Pot_Mendelev in reliably capturing the energetics associated with SFT formation in FCC aluminum.

3.4. Binding Energies of Perfect and Defective SFTs

Figure 7 illustrates the binding energies of both perfect and defective SFTs as a function of vacancy number, as predicted by four interatomic potentials: Pot_Lee, Pot_Mendelev, Pot_Mishin, and Pot_Liu. These potentials have been previously validated for accurately capturing the energetics associated with SFT formation and growth. While quantitative discrepancies exist in the absolute binding energies, all four potentials consistently reproduce a characteristic trend: the sequential binding energy varies cyclically with increasing SFT size. This oscillatory behavior aligns closely with first-principles calculations for small SFTs. It is also worth noting that for larger SFT sizes (typically exceeding about 30 vacancies), the binding energies predicted by Pot_Lee deviate markedly from those obtained using the other three empirical potentials. Specifically, for defective SFTs, Pot_Lee yields values close to 0 eV, whereas Pot_Mendelev, Pot_Mishin, and Pot_Liu consistently predict values in the range of 0.2–0.3 eV. Moreover, as the vacancy count approaches the next magic number configuration, Pot_Lee exhibits a series of anomalously high binding energy spikes, which are not observed in the other three potentials.

To further examine these discrepancies, we compared our results with predictions from elastic continuum theory [34], which—while incapable of capturing the fine-scale fluctuations associated with local atomic rearrangements—provides a reliable baseline for the overall trend of binding energy evolution with increasing defect size. As shown in Figure 7, the elastic theory predicts a rapid rise in binding energy at small sizes, followed by a gradual saturation at approximately 0.25 eV over the vacancy range investigated in this study. This trend aligns closely with the results of Pot_Mendelev, Pot_Mishin, and Pot_Liu, but diverges significantly from those obtained using Pot_Lee. Based on this comparison, subsequent analyses of SFT growth energetics will focus primarily on the Pot_Mendelev, Pot_Mishin, and Pot_Liu potentials.

Building on the structural evolution of defective SFTs presented in Figure 3 and the binding energy profiles shown in Figure 7, the atomistic mechanism by which SFTs grow through the sequential capture of additional vacancies can be elucidated as follows. Starting from a perfect SFT, the initial one additional vacancy prefers to attach to the vertex (e.g., $V_{15}$→$V_{16}$ in Figure 3) or the middle of the stair-rods (e.g., $V_{66}$→$V_{67}$ in Figure 3), forming a vacancy-tetrahedron. In these cases, the binding energy between the perfect SFT and the additional vacancy is either negative or close to zero, indicating that the binding of a single vacancy to the perfect SFT is not energetically favorable (see Figure 7). However, as more vacancies are introduced, they progressively accumulate on one {111} facet of the SFT, initiating the formation of an embryonic stacking fault (see $V_{17}$→$V_{20}$ and $V_{68}$→$V_{74}$ in Figure 3). This growth leads to a rapid increase in binding energy, which eventually saturates in the range of 0.2–0.3 eV. This behavior arises because each additional vacancy induces a similar local structural rearrangement—typically involving partial extension of the faulted plane—leading the binding energies to converge to a nearly constant value. As the vacancy count approaches the next magic-number configuration—typically within four vacancies—the binding energy rises sharply, reaching values between 0.8 and 0.9 eV. This pronounced increase corresponds to the repair of previously underdeveloped vertices. As exemplified by configurations such as $V_{75}$→$V_{77}$ in Figure 3, near-perfect defective SFTs still retain residual corner defects. In this regime, each additional vacancy directly contributes to healing these defects, driving the closure of the SFT structure and ultimately enabling the transition to a fully enclosed tetrahedral geometry.

3.5. Formation and Growth of SFTs via Vacancy Aggregation Mechanism

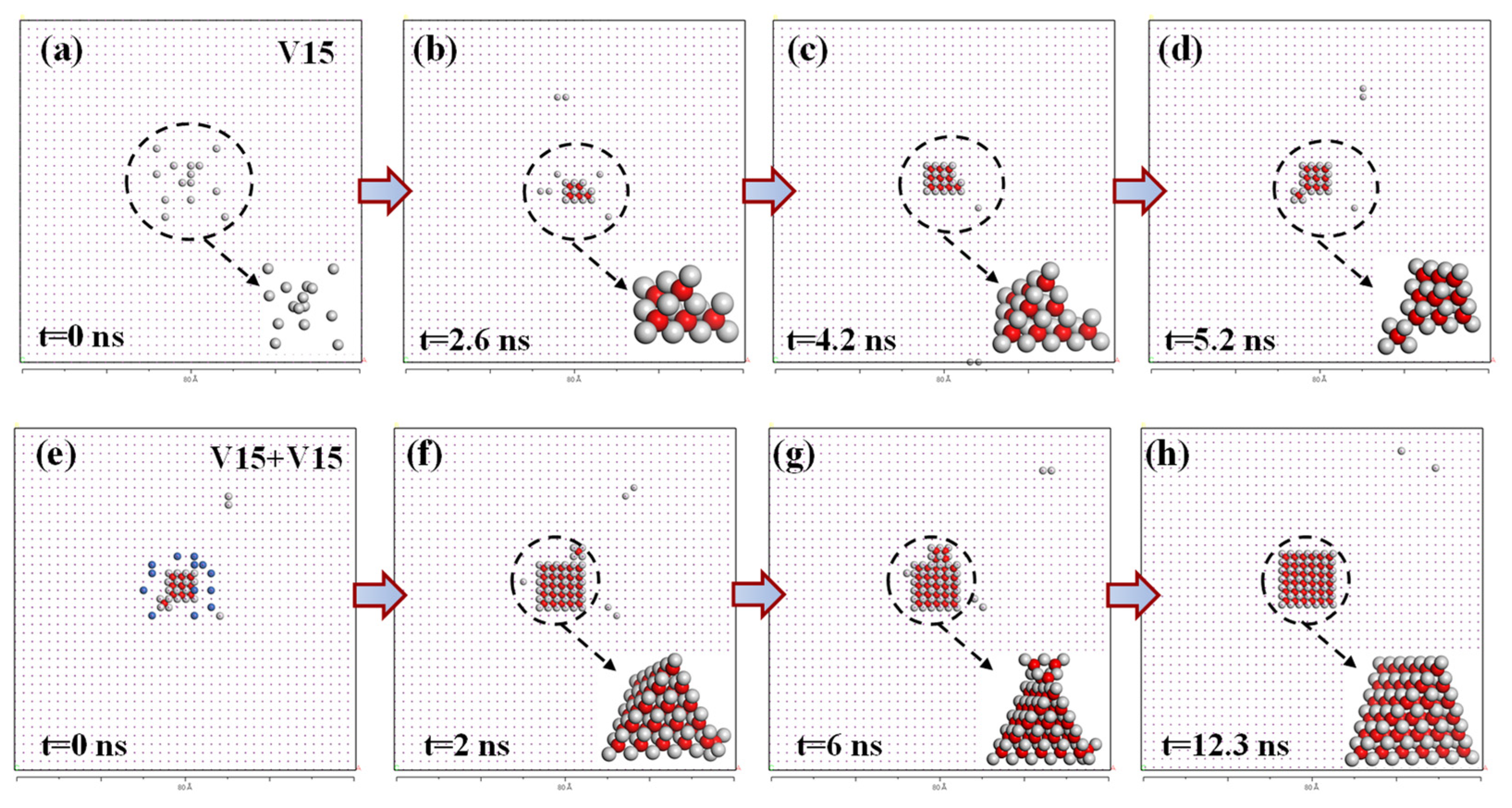
The SFT growth process described above is inferred solely from thermodynamic data—namely, the evolution of stable configurations and binding energies as a function of cluster size—indicating a thermodynamically favorable trend for incremental growth via vacancy capture. To further elucidate the formation and growth of SFTs via vacancy aggregation, we performed MD simulations using the Pot_Mendelev potential. The simulations were conducted at 600 K within a 20 × 20 × 20 supercell. At the onset, 15 vacancies were randomly introduced near the center of the simulation box (see Figure 8a). Over time, these vacancies began to cluster, and at 2.6 ns, a defective SFT comprising eight vacancies emerged (see Figure 8b). This defective SFT structure formed via the attachment of an additional vacancy to the smallest perfect SFT $V_6$ through a vacancy-tetrahedron (see the inset at the lower right of Figure 8b). Prior to the formation of the SFT $V_8$, a transient vacancy-tetrahedron was briefly observed; however, this intermediate configuration proved unstable and rapidly dissociated. The emergence of a stable SFT structure began with the formation of $V_8$, which subsequently grew through the sequential absorption of nearby vacancies. It is important to note that certain stable vacancy cluster configurations (such as $V_5$, which will be discussed later) may exist but were not observed during this sampling. This absence is likely due to the limitations inherent in the sampling process rather than the nonexistence of such structures. By 4.2 ns, the structure evolved into a larger defective SFT $V_{11}$, comprising a perfect SFT $V_{10}$ and an adjacent vacancy-tetrahedron located at one of its vertices (see Figure 8c). Continued vacancy capture led to the development of a defective SFT $V_{12}$ by 5.2 ns, leaving only three isolated vacancies remaining in the system at that time (see Figure 8d).

To investigate further growth behavior, 15 additional vacancies were introduced near the SFT $V_{12}$ structure (see Figure 8e, where the newly added vacancies are marked by small blue spheres), and a new MD simulation was initiated. At 2 ns into this subsequent simulation, a portion of these new vacancies had been captured by pre-existing SFT segments, leading to the formation of a 22-vacancy SFT. Continued evolution resulted in a 25-vacancy SFT by 2.6 ns. Structural comparison between the configurations at 2 ns and 6 ns revealed that, apart from additional apex vacancies, new tetrahedral substructures were observed to nucleate and expand from the midpoint along the edges of the pre-existing SFT. This observation aligns with the static predictions described earlier, which suggest that SFT growth preferentially initiates at the corners or edge midpoints of the existing tetrahedral structure. By 12.3 ns, this defective SFT had further matured into a perfect SFT $V_{28}$ configuration through absorption of nearly all remaining vacancies—only two vacancies remained unincorporated.

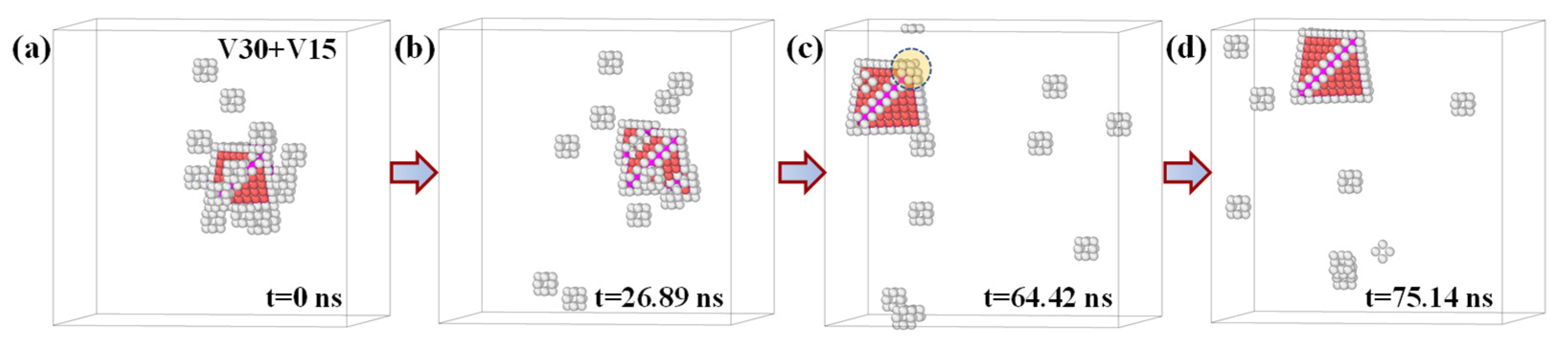
These MD simulations provide direct atomistic evidence that, in aluminum, SFT can indeed nucleate and grow purely via vacancy agglomeration. Importantly, the entire formation and growth process occurred via vacancy diffusion and aggregation. To further investigate the continued evolution of SFTs via vacancy-driven mechanisms, we repeated the aforementioned “vacancy introduction–growth” MD simulation protocol. Specifically, we used the final configuration from the previous MD simulation containing 30 vacancies as the initial structure and introduced an additional 15 vacancies. The subsequent evolution of the SFT structure and surrounding vacancies is illustrated in Figure 9. At t = 26.89 ns, the SFT exhibited growth through vacancy capture at one of its corners, forming an irregular defective region. Concurrently, an embryonic stacking fault emerged on one of the SFT facets, signaling a secondary nucleation site for further structural development. By t = 64.42 ns, a nearly complete SFT comprising 35 vacancies had formed, characterized by a single defect located at one of its vertices. This minor imperfection was resolved by t = 75.14 ns, when the capture of an additional vacancy transformed the structure into a perfect SFT $V_{36}$. These results further strengthen the atomistic evidence that SFTs in aluminum can grow via successive vacancy absorption. Notably, the observed growth pathway involves both vertex- and facet-mediated vacancy capture, consistent with our earlier thermodynamic analysis that predicted preferential growth at corners and along facet edges. In particular, the simultaneous vacancy incorporation at both a vertex and a facet observed at t = 26.89 ns highlights the cooperative and spatially distributed nature of SFT maturation, suggesting that its growth is governed by a more complex and synergistic mechanism than previously assumed.

Figure 9 presents four representative snapshots of the evolving system, all rendered from a consistent viewpoint to clearly illustrate the time-resolved morphological evolution of the SFT and the surrounding vacancy distribution. Notably, beyond the progressive capture and redistribution of vacancies, the spatial position of the SFT itself exhibits significant displacement throughout the simulation. Initially located near the center of the supercell at t = 0 ns, the SFT migrates toward the upper left region of the simulation box by t = 75.14 ns. This substantial relocation offers compelling evidence that, under the present thermal conditions, the SFT possesses notable mobility. This observation stands in stark contrast to the conventional understanding of SFTs as immobile defects. Traditionally, SFTs are considered sessile due to their bounding stair-rod dislocations, whose glide plane is not a compact {111} plane. The finding here directly challenges this long-standing view.

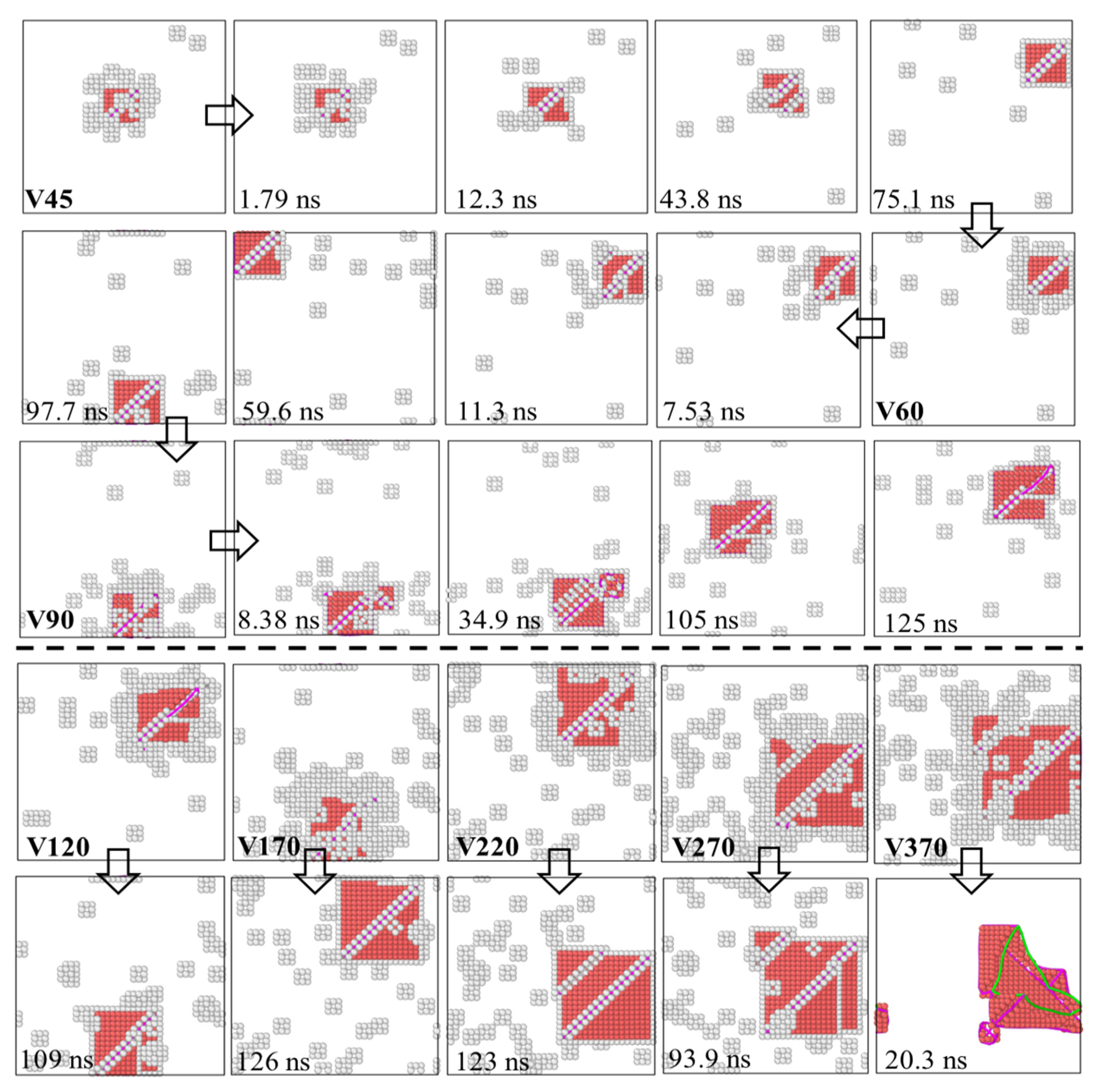
To further investigate the growth dynamics and structural evolution of SFTs driven by vacancy absorption, we systematically extended our MD simulation strategy based on a vacancy-introduction and growth approach. The initial system, denoted as $V_{45}$, consisted of a perfect SFT $V_{36}$ and nine isolated vacancies. Building upon this configuration, additional vacancies were introduced stepwise to construct increasingly complex systems: 15 vacancies were first added to yield the $V_{60}$ system, followed by successive additions of 30 vacancies to form the $V_{90}$ and $V_{120}$ systems. Subsequently, three consecutive batches of 50 vacancies each were introduced, generating the $V_{170}$, $V_{220}$, and $V_{270}$ structures. Finally, an additional 100 vacancies were incorporated into the $V_{270}$ system to produce the $V_{370}$ configuration. Representative structural snapshots along this simulation trajectory are shown in Figure 10, with all structural snapshots visualized from an identical orientation, enabling direct comparison of the evolving SFT geometry and the spatiotemporal distribution of vacancies throughout the simulation. The results reveal that the SFT continuously grow by absorbing vacancies, and exhibit mobility during the process. As the simulations progressed to the $V_{370}$ system, we observed that the conventional SFT architecture became unstable, transforming into a truncated SFT. Further vacancy introduction—up to approximately 700 vacancies—resulted in the destabilization of the truncated SFT itself, which eventually evolved into a dislocation loop structure.

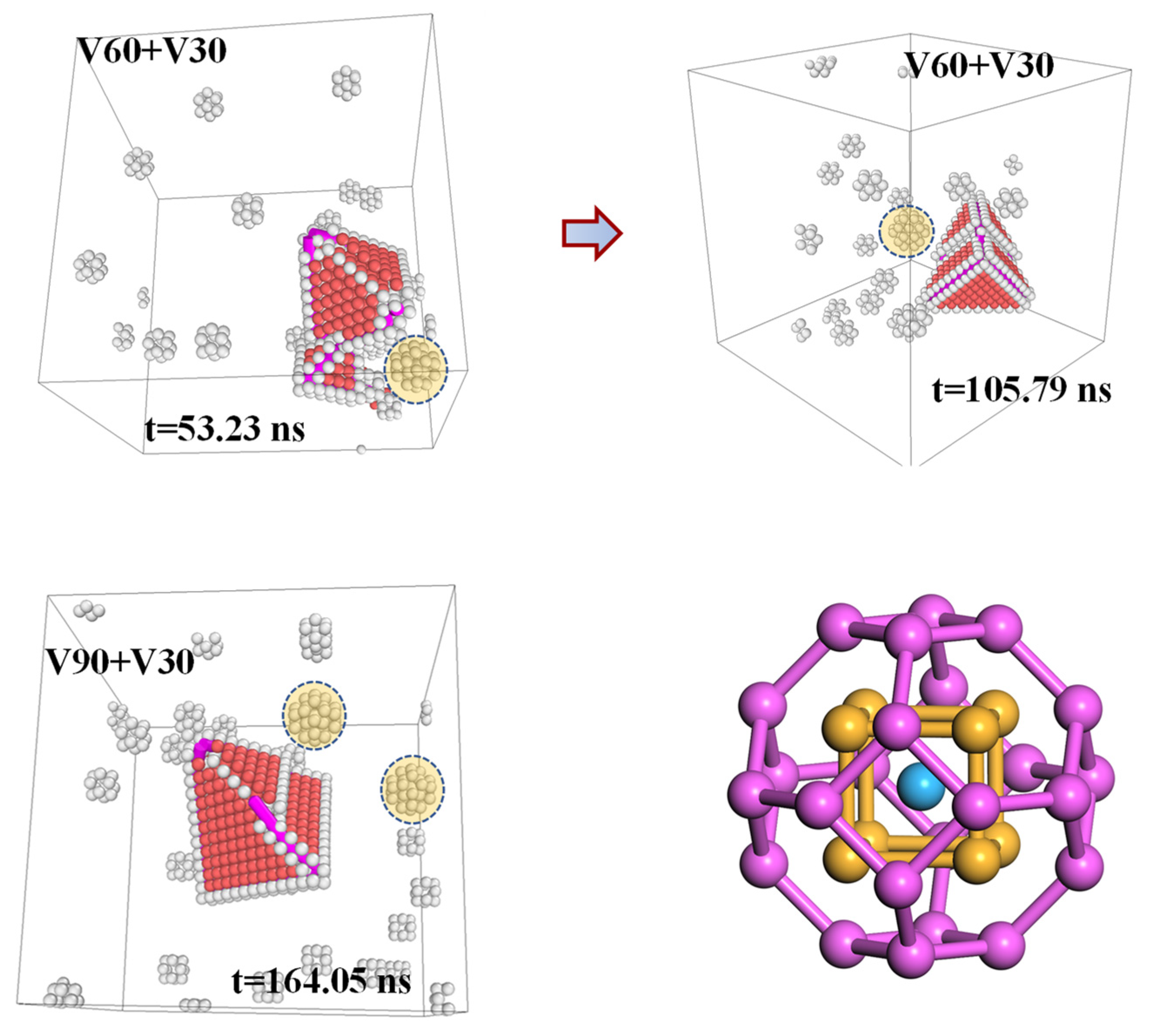
Notably, throughout the simulations, we frequently observed compact vacancy clusters in addition to isolated vacancies. In multiple snapshots—such as those from the $V_{60}+V_{30}$ simulation at t = 53.23 ns and t = 105.79 ns, and the $V_{90}+V_{30}$ simulation at t = 164.05 ns (Figure 11)—truncated octahedral clusters composed of aluminum atoms were identified, featuring a core of nine atoms arranged in a body-centered cubic (BCC) configuration. This structure corresponds to the highly stable vacancy cluster $V_5$ previously confirmed by previous studies and is widely regarded as a key precursor in the nucleation and growth of vacancy aggregates in aluminum [7,35]. Furthermore, an intriguing phenomenon was observed in the $V_{60}+V_{30}$ simulation. Starting from a structure containing a perfect SFT $V_{45}$ and 10 isolated vacancies, the addition of 30 new vacancies followed by MD simulation led to localized vacancy absorption at one corner of the original SFT, triggering the formation of a new, smaller SFT (see Figure 11, t = 53.23 ns). As the simulation progressed, this nascent SFT evolved to display early-stage faulting across two of its facets (Figure 11, t = 105.79 ns), further underscoring the complexity and cooperativity of SFT growth mechanisms.

These MD simulations presented above offer compelling atomistic evidence that SFTs in aluminum can nucleate spontaneously through vacancy agglomeration, without the involvement of dislocation mechanisms. The formation process initiates from the coalescence of small vacancy clusters and proceeds via the progressive absorption of nearby vacancies, ultimately leading to the emergence of a stable SFT. Beyond their ability to grow, the simulations also reveal that SFTs possess notable mobility—an often-overlooked characteristic with profound implications for their structural evolution. The observed mobility of SFTs plays a critical role in their transformation dynamics. On the one hand, mobile SFTs are more effective at capturing surrounding vacancies and can even merge with neighboring SFTs, facilitating cooperative growth. On the other hand, as vacancy accumulation continues, larger SFTs exhibit structural instability and eventually evolve into vacancy-type dislocation loops. This finding redefines SFTs not as terminal defect states but rather as metastable intermediates in a continuous vacancy-driven transformation pathway. This mechanistic insight provides a rational explanation for several long-standing experimental observations regarding SFTs in aluminum [5]. In particular, experimental studies consistently report that SFTs in aluminum are typically very small—on the order of ~2 nm—and are predominantly observed under low-temperature conditions [5]. Such behavior is likely a direct consequence of their intrinsic mobility: mobile SFTs readily coalesce or transform into more complex defect structures, such as dislocation loops, rendering them difficult to detect. In contrast, under cryogenic conditions, vacancy diffusion and SFT migration are suppressed, allowing these structures to persist in an isolated, observable form. Thus, the spontaneous formation and high mobility of SFTs are not only fundamental to their growth and transformation but also directly impact their detectability and morphology in experimental systems.

3.6. Comparison with Literature on SFT Formation Energies and Dynamics in FCC Metals

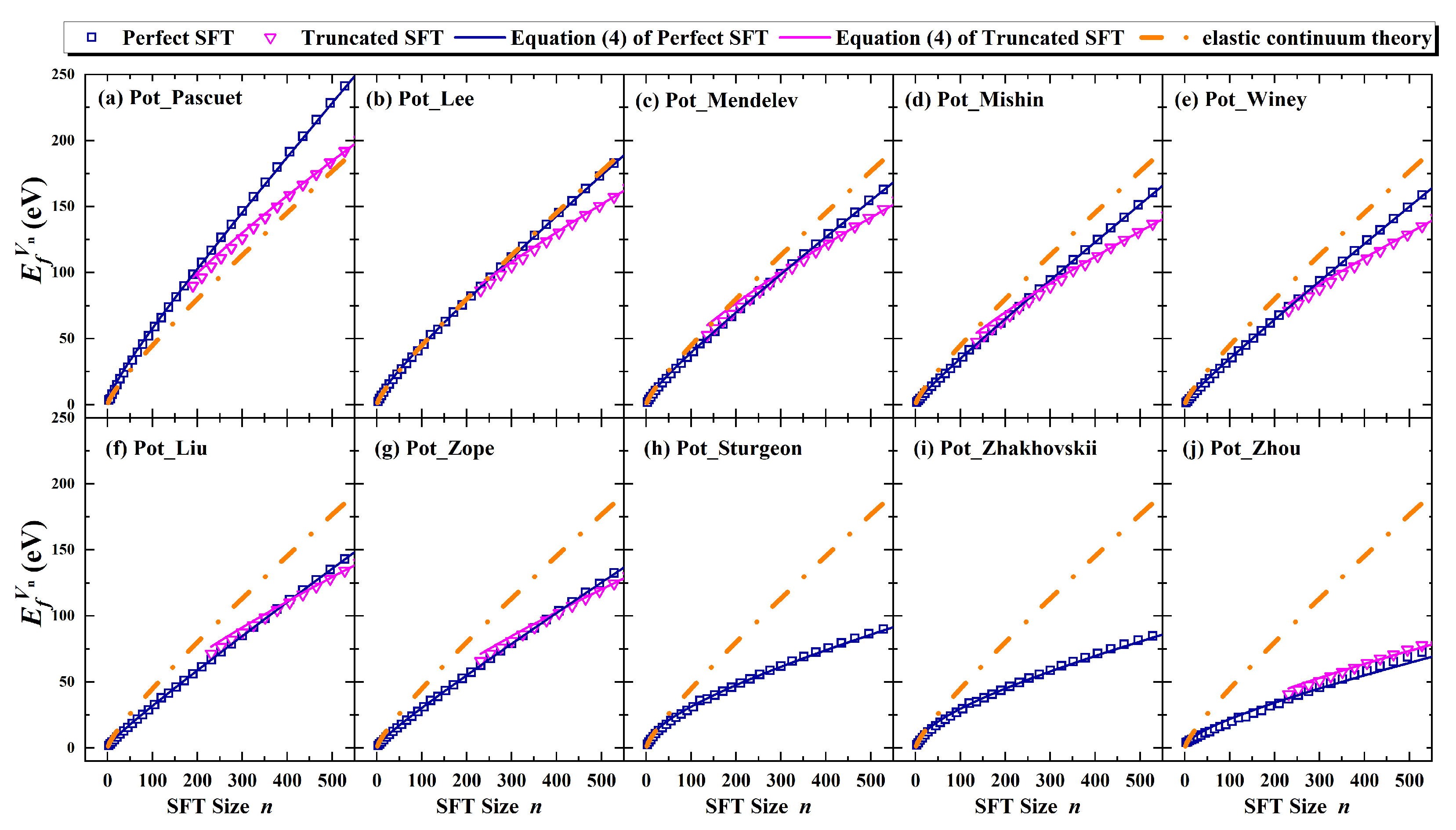
The vacancy formation energies predicted by the ten empirical potentials evaluated in this study range from 0.66 to 0.89 eV, which are in good agreement with both experimental values (0.62–0.72 eV) and DFT calculations (0.5–0.82 eV) reported in the literature [7]. This agreement supports the reliability of these potentials in capturing basic defect energetics. To further assess the validity of our proposed formulation for stacking fault tetrahedron (SFT) formation energy, we applied Equation (4) to data extracted from a recent study by Landeiro Dos Reis et al. 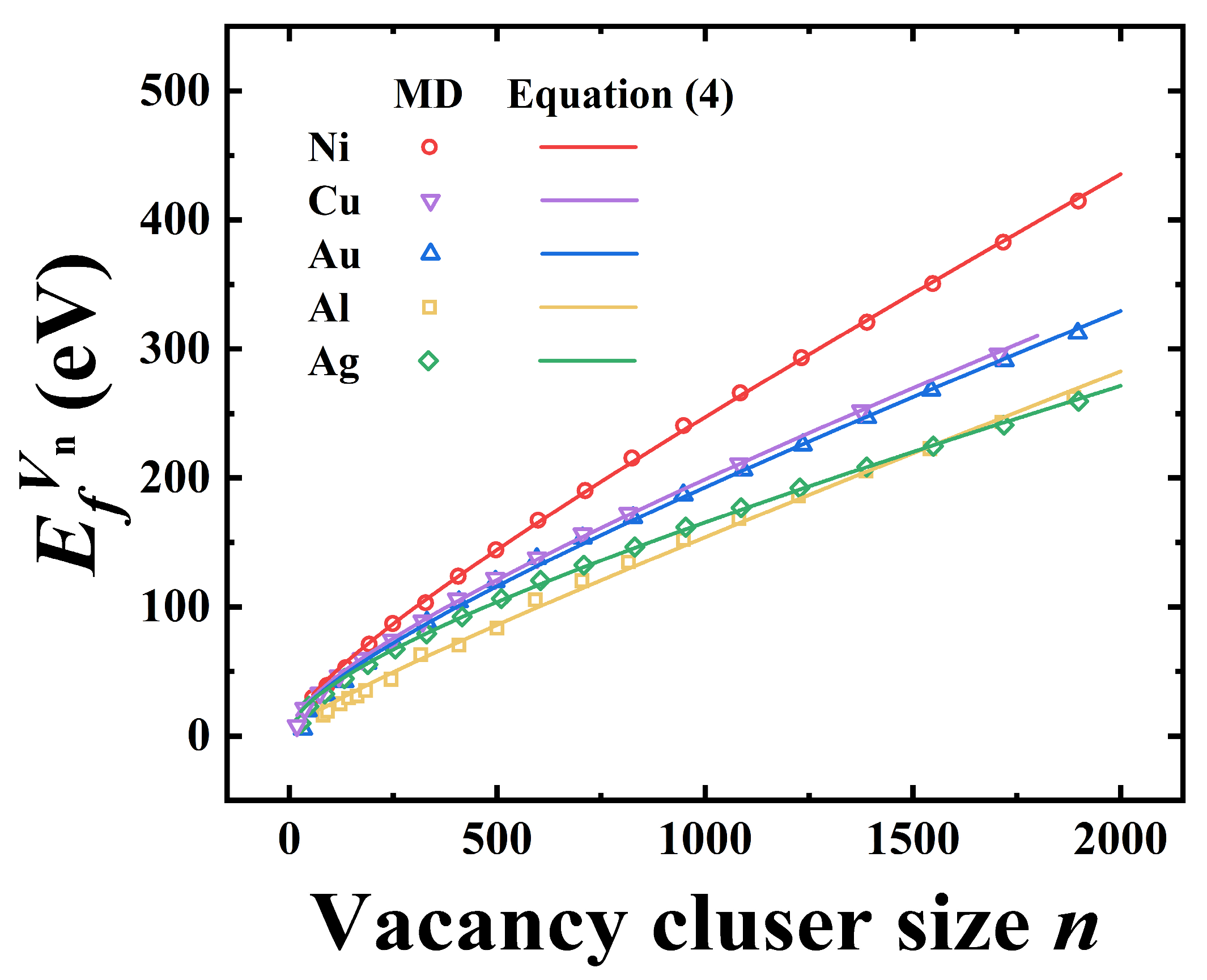on aluminum [12]. Our results show that Equation (4) effectively describes the size dependence of SFT formation energies, indicating the robustness of our model.

Moreover, the general applicability of Equation (4) was tested by extending it to other FCC metals, including Ni, Cu, Au, and Ag, using additional data provided by Landeiro Dos Reis et al. [12]. We found that the equation also captures the SFT formation energy trends in these metals, demonstrating the model’s versatility. These results are summarized in Figure 12 and further strengthen the validity of the proposed formulation across a range of FCC metals.

In terms of the dynamic behavior of SFTs, MD simulations by Martínez and Uberuaga in Cu revealed that small, imperfect SFTs exhibit high mobility, allowing them to migrate and coalesce into larger, more stable structures [36]. This diffusion-assisted growth mechanism suggests that SFT formation can occur through vacancy mobility, rather than being limited to direct cascade effects. Complementary experimental work by Aidhy et al. in Ni supports this view, showing that SFTs can form well beyond the primary damage region, highlighting the role of long-range vacancy and SFT diffusion [16]. Together, these findings provide indirect validation for the mechanisms proposed in our study and affirm the broader relevance and transferability of our results.

It is important to note, however, that while ten empirical potentials were assessed for thermodynamic properties, the long-timescale MD simulations of larger SFT clusters were conducted using the Pot_Mendelev potential alone. This potential was selected due to its strong agreement with ab initio results and elasticity theory, offering superior performance in predicting formation and binding energies of SFTs. Nevertheless, the dynamic evolution of SFTs—especially for larger clusters—may still be sensitive to the choice of interatomic potential. Therefore, further studies employing improved potentials or experimental techniques such as in situ transmission electron microscopy are necessary to validate the generality of these findings.

In addition, although this study primarily focused on the thermodynamic stability and structural evolution of SFTs in aluminum, preliminary long-timescale MD simulations (tens of nanoseconds) have revealed migration events of SFTs. However, quantitative kinetic analysis—such as determining activation barriers and diffusion coefficients—requires significantly longer simulations and extensive statistical sampling (e.g., through mean squared displacement analysis across hundreds of MD runs), which is computationally intensive. To address this challenge, future work will incorporate kinetic modeling approaches, including ab initio-informed atomistic kinetic Monte Carlo and the kinetic Activation–Relaxation Technique. These methods are expected to offer deeper insights into SFT diffusion and transformation mechanisms, and the outcomes will be presented in forthcoming studies. Moreover, in future work, we also plan to extend our investigations to include the effects of impurities, alloying elements, irradiation damage, and microstructural defects. These studies will help validate the current findings under more realistic conditions and broaden their applicability to other FCC metals.

4. Conclusions

In this work, we employ systematic molecular statics and dynamics simulations to reveal the formation, growth, migration, and transformation of SFTs in aluminum via vacancy aggregation. Three types of SFTs—perfect, truncated, and defective—are identified and characterized in terms of their stable configurations, formation energies, and binding energies over a broad range of vacancy cluster sizes. The formation energies of both perfect and truncated SFTs exhibit a clear scaling relationship with cluster size. Importantly, the formation energy of perfect SFTs increases more rapidly with size, making truncated SFTs thermodynamically preferred beyond a critical vacancy cluster size. This observation highlights the thermodynamic driving force for the transformation from perfect to truncated SFTs, and the critical size for this transition is quantitatively determined. The structure and binding energy of SFTs exhibit quasi-periodic oscillations with increasing vacancy number. Vacancies initially adsorb at the vertices or stair-rod dislocation midpoints of existing perfect SFTs, forming unstable vacancy tetrahedra. Subsequent vacancy aggregation along one facet of the SFT initiates fault plane nucleation and leads to a rapid increase in binding energy. As the vacancy count approaches a critical “magic number”, the system undergoes an abrupt structural reconstruction into a new perfect SFT, accompanied by a sharp binding energy jump. This discrete, stepwise growth mechanism reflects self-organized vacancy clustering and geometry-driven transitions between neighboring stable configurations. Further molecular dynamics simulations at 600 K demonstrate that SFTs in aluminum nucleate and grow via spontaneous vacancy aggregation, confirming the thermodynamically predicted SFT growth mechanism. More importantly, SFTs exhibit pronounced thermal mobility, facilitating their coalescence and structural transformation. As the size increases, perfect SFTs become unstable and progressively evolve into truncated forms and eventually into vacancy-type dislocation loops. Additionally, BCC-configured $V_5$ vacancy clusters are observed as key precursors for SFT nucleation. This study elucidates the nanoscale nature and low-temperature stability of SFTs in aluminum and provides new insights into defect evolution and control in FCC metals.