DOE-Based Investigation of Microstructural Factors Influencing Residual Stress in Aluminum Alloys
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Residual Stress Measurement Methods
2.3. Microstructure Characterization
2.4. Design of Experiments (DOE)
3. Results and Discussion
3.1. Analysis of Residual Stress Distribution Through Simulation
3.2. Surface Residual Stress Measurement Results
3.3. Results of the Design of Experiments (DOE)
3.4. Correlation Between Microstructure Factors and Residual Stresses
4. Conclusions
- (1)
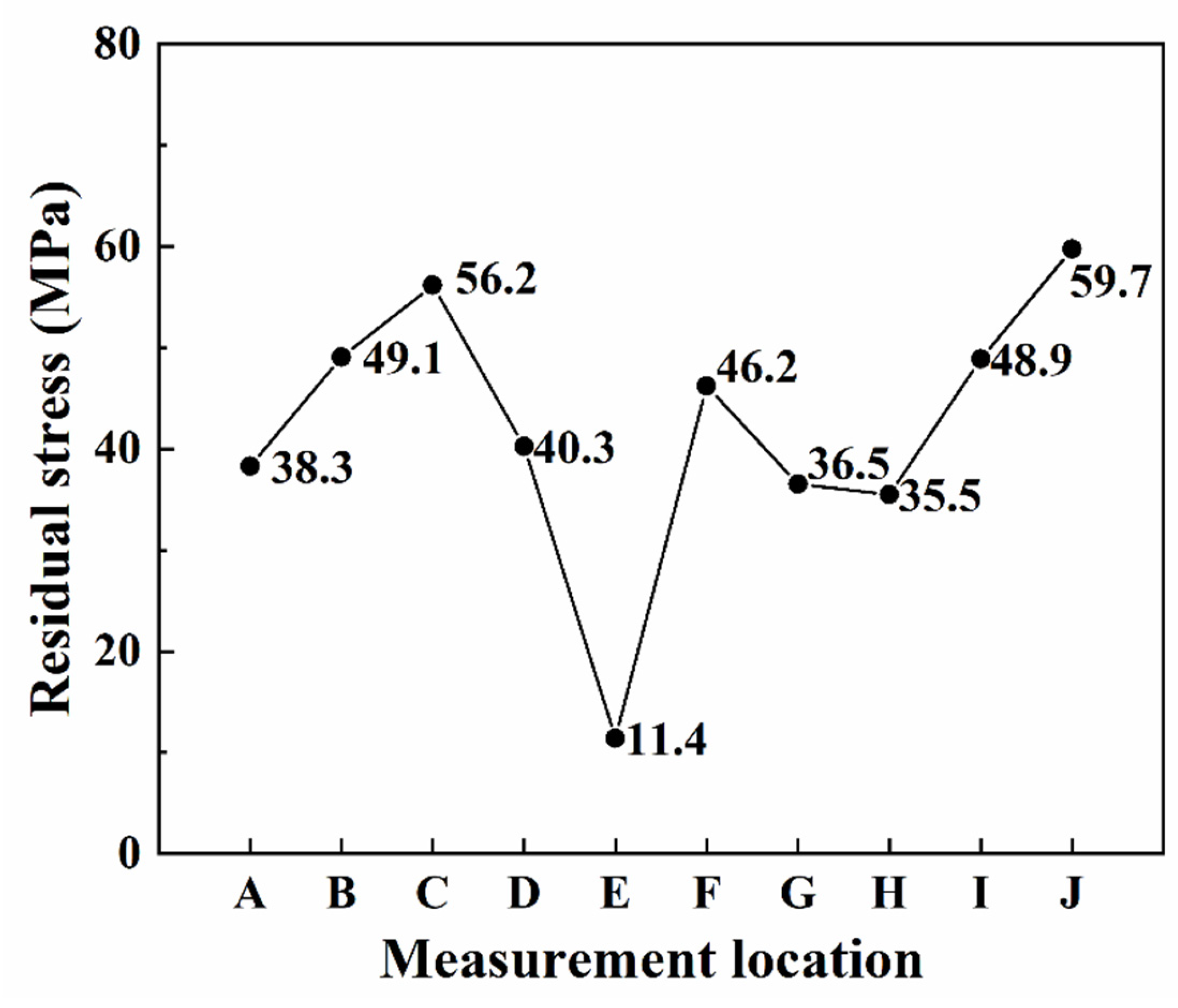
- Based on the simulation, the residual stress measurement zones and locations were selected, with the highest residual stress of 59.7 MPa observed at location J and the lowest residual stress of 11.4 MPa observed at location E.
- (2)
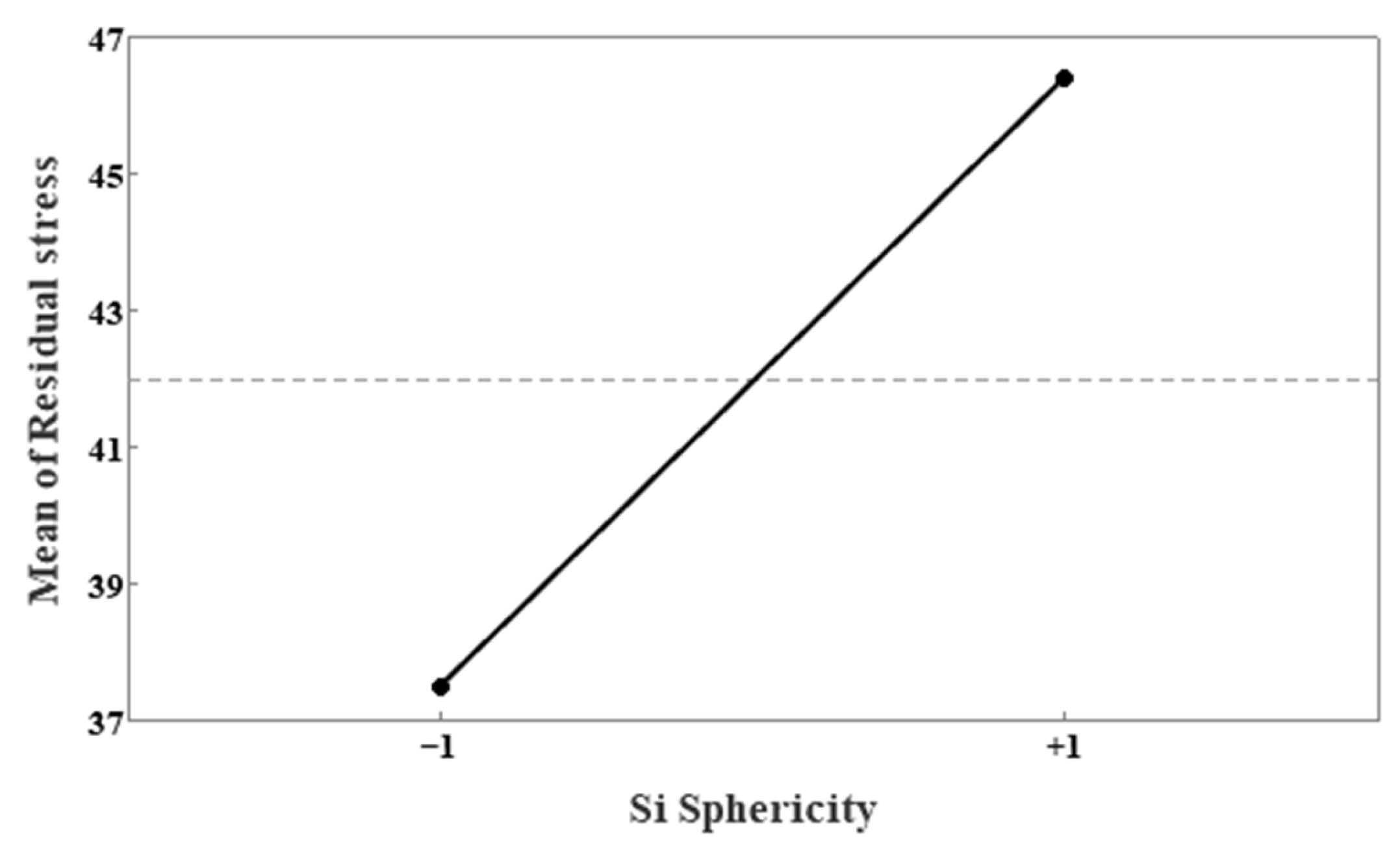
- Through DOE, the microstructural factors affecting the residual stress after surface grinding were statistically analyzed, with Si sphericity (p-value ≤ 0.05) identified as the most significant factor.
- (3)
- The regions where Si particles had insufficient time to grow and thus exhibited higher sphericity showed increased residual stress due to rapid cooling, and DOE allows for the evaluation of the relative significance of variables with strong correlations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, Q.; Chen, T.; Li, D.; Wu, J. Synergistic Optimization of α-Al Grain and Eutectic Si Structures for Al-Si Alloys via a Newly Designed Al-Ce-B Alloy. J. Mater. Sci. Eng. A 2025, 925, 147867. [Google Scholar] [CrossRef]
- Jo, I.; Ahn, C.; Lee, E. High-temperature tensile deformation behavior and failure mechanisms of Al-10Si-Mn-Mg high-pressure die-cast alloy. J. Korean Soc. Mar. Eng. 2019, 43, 788–792. [Google Scholar] [CrossRef]
- Otarawanna, S.; Gourlay, C.M.; Laukli, H.I.; Dahle, A.K. Microstructure Formation in AlSi4MgMn and AlMg5Si2Mn High-Pressure Die Castings. Metall. Mater. Trans. A 2009, 40, 1645–1659. [Google Scholar] [CrossRef]
- Zhang, B.; Cockcroft, S.L.; Maijer, D.M.; Zhu, J.D.; Phillion, A.B. Casting Defects in Low-Pressure Die-Cast Aluminum Alloy Wheels. JOM 2005, 57, 36–43. [Google Scholar] [CrossRef]
- Bang, J.; Lee, E. Enhancing Wear Resistance of A390 Aluminum Alloy: A Comprehensive Evaluation of Thermal Sprayed WC, CrC, and Al2O3 Coatings. Coatings 2024, 14, 853. [Google Scholar] [CrossRef]
- Niklas, A.; Orden, S.; Bakedano, A.; da Silva, M.; Nogués, E.; Fernández-Calvo, A.I. Effect of Solution Heat Treatment on Gas Porosity and Mechanical Properties in a Die Cast Step Test Part Manufactured with a New AlSi10MnMg(Fe) Secondary Alloy. J. Mater. Sci. Eng. A 2016, 667, 376–382. [Google Scholar] [CrossRef]
- Jeon, M.; Lee, E. Effect of Grain Size on Residual Stress in AlSi10MnMg Alloy. J. Adv. Mar. Eng. Technol. 2023, 47, 195–201. [Google Scholar] [CrossRef]
- Nikawa, M.; Sasai, D.; Mizutani, Y.; Yamashita, M. Evaluation of Residual Stress in Die Castings of Al-Si-Cu Alloy Considering Material Composition Change in Thickness Direction. Int. J. Autom. Technol. 2021, 15, 359–365. [Google Scholar] [CrossRef]
- Lei, Y.; Zhao, H.; Bai, W.; Xu, Q.; Han, Z. Microstructure, Mechanical Properties and Residual Stress of High Vacuum Die Casting AlSi10MgMn Alloys with Different Spray Quenching. J. Mater. Process. Technol. 2024, 325, 118284. [Google Scholar] [CrossRef]
- Barsoum, Z.; Barsoum, I. Residual Stress Effects on Fatigue Life of Welded Structures Using LEFM. Eng. Fail. Anal. 2009, 16, 449–467. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Z.; Zhuang, W.; Peng, H. Effects of Pre-Strain on the Surface Residual Stress and Corrosion Behavior of an Al-Zn-Mg-Cu Alloy Plate. Mater. Charact. 2020, 160, 110129. [Google Scholar] [CrossRef]
- Koç, M.; Culp, J.; Altan, T. Prediction of Residual Stresses in Quenched Aluminum Blocks and Their Reduction through Cold Working Processes. J. Mater. Process. Technol. 2006, 174, 342–354. [Google Scholar] [CrossRef]
- Withers, P.J.; Turski, M.; Edwards, L.; Bouchard, P.J.; Buttle, D.J. Recent Advances in Residual Stress Measurement. Int. J. Press. Vessel. Pip. 2008, 85, 118–127. [Google Scholar] [CrossRef]
- Akhtar, W.; Lazoglu, I.; Liang, S.Y. Prediction and Control of Residual Stress-Based Distortions in the Machining of Aerospace Parts: A Review. J. Manuf. Process. 2022, 76, 106–122. [Google Scholar] [CrossRef]
- Lee, J.; Lee, E. Crystallographic Orientation-Dependent Corrosion Behavior of Aluminum under Residual Stress. Mater. Charact. 2023, 205, 113310. [Google Scholar] [CrossRef]
- Rossini, N.S.; Dassisti, M.; Benyounis, K.Y.; Olabi, A.G. Methods of Measuring Residual Stresses in Components. Mater. Des. 2012, 35, 572–588. [Google Scholar] [CrossRef]
- James, M.N. Residual Stress Influences on Structural Reliability. Eng. Fail. Anal. 2011, 18, 1909–1920. [Google Scholar] [CrossRef]
- Grilli, N.; Hu, D.; Yushu, D.; Chen, F.; Yan, W. Crystal Plasticity Model of Residual Stress in Additive Manufacturing Using the Element Elimination and Reactivation Method. Comput. Mech. 2022, 69, 825–845. [Google Scholar] [CrossRef]
- Kianfar, S.; Stroh, J.; Bahramian, N.; Sediako, D.; Lombardi, A.; Byczynski, G.; Mayr, P.; Reid, M.; Paradowska, A. Residual Stress Prediction in the Casting Process of Automotive Powertrain Components. In Light Metals 2021 50th Anniversary Edition; Springer: Berlin/Heidelberg, Germany, 2021; pp. 858–864. [Google Scholar]
- Chen, Z.; Li, Y.; Zhao, F.; Li, S.; Zhang, J. Progress in Numerical Simulation of Casting Process. Meas. Control. 2022, 55, 257–264. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Xu, D.; Yang, R. Recent Progress in the Simulation of Microstructure Evolution in Titanium Alloys. Prog. Nat. Sci. Mater. Int. 2019, 29, 295–304. [Google Scholar] [CrossRef]
- Pei, J.; Wang, S.; Qin, S.; Yu, Z.; Gao, J.; Xiao, J.; Li, Z. Using Iterative Correction to Improve the Accuracy of the Blind-Hole Welding Residual Stress Test. Sensors 2024, 24, 6243. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Men, X.; Liu, Y.; Fu, X. Experiment and Simulation Study on Influence of Ultrasonic Rolling Parameters on Residual Stress of Ti-6Al-4V Alloy. Simul. Model. Pract. Theory 2020, 104, 102121. [Google Scholar] [CrossRef]
- Nycz, A.; Lee, Y.; Noakes, M.; Ankit, D.; Masuo, C.; Simunovic, S.; Bunn, J.; Love, L.; Oancea, V.; Payzant, A.; et al. Effective Residual Stress Prediction Validated with Neutron Diffraction Method for Metal Large-Scale Additive Manufacturing. Mater. Des. 2021, 205, 109751. [Google Scholar] [CrossRef]
- Lee, E.; Mishra, B. Effect of Cooling Rate on the Mechanical Properties of AA365 Aluminum Alloy Heat-Treated Under T4, T5, and T6 Conditions. Int. J. Metalcast. 2018, 12, 449–456. [Google Scholar] [CrossRef]
- Verran, G.O.; Mendes, R.P.K.; Valentina, L.V.O.D. DOE Applied to Optimization of Aluminum Alloy Die Castings. J. Mater. Process. Technol. 2008, 200, 120–125. [Google Scholar] [CrossRef]
- Boonjubut, K.; Wantang, T. Study of Factors Affecting Artificial Aging of 6061 Aluminum Alloy by Factorial Design. Rev. Integr. Bus. Econ. Res. 2014, 3, 62–70. [Google Scholar]
- Jafari, H.; Idris, M.H.; Shayganpour, A. Evaluation of Significant Manufacturing Parameters in Lost Foam Casting of Thin-Wall Al–Si–Cu Alloy Using Full Factorial Design of Experiment. Trans. Nonferrous Met. Soc. China 2013, 23, 2843–2851. [Google Scholar] [CrossRef]
- Visionplus Co., Ltd. Calculation Sheet for Stress, Provided Through Private Communication; Visionplus Co., Ltd.: Seongnam, Republic of Korea, 2025. [Google Scholar]
- Jong, I.; Springer, W. Teaching Von Mises Stress: From Principal Axes To Nonprincipal Axes. In Proceedings of the 2009 Annual Conference & Exposition, Austin, TX, USA, 14 June 2009. [Google Scholar] [CrossRef]
- Abdul-Wahab, S.A.; Abdo, J. Optimization of Multistage Flash Desalination Process by Using a Two-Level Factorial Design. Appl. Therm. Eng. 2007, 27, 413–421. [Google Scholar] [CrossRef]
- Vyas, D.; Balakrishnan, A.; Vyas, A. The Value of the P Value. Am. J. Robot. Surg. 2015, 2, 53–56. [Google Scholar] [CrossRef][Green Version]
- Tenny, S.; Abdelgawad, I. Statistical Significance. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2025. [Google Scholar]
- Faizi, N.; Alvi, Y. Regression and Multivariable Analysis. In Biostatistics Manual for Health Research; Academic Press: Cambridge, MA, USA, 2023; pp. 213–247. [Google Scholar]
- Bašta, M. Properties of Backward Elimination and Forward Selection in Linear Regression. Int. Days Stat. Econ. 2018, 114–124. [Google Scholar] [CrossRef]
- Song, X.Y.; Wang, Y.J.; Zhang, J.X.; Du, D.A.; Yang, H.Y.; Zhao, L.; Peng, F.; Li, X.; Qiu, F. Microstructure and mechanical properties of aluminum alloy composites with endogenous nano-TiCp. Ceram. Int. 2023, 49, 6923–6931. [Google Scholar] [CrossRef]
- Yang, C.; Li, Y.; Dang, B.; Lü, H.; Liu, F. Effects of Cooling Rate on Solution Heat Treatment of As-Cast A356 Alloy. Trans. Nonferrous Met. Soc. China 2015, 25, 3189–3196. [Google Scholar] [CrossRef]
- Gomes, R.; Soares, G.; Madureira, R.; Silva, R.P.; Silva, J.; Neto, R.; Reis, A.; Fernandes, C. Development of Heat Treatments for Structural Parts in Aluminium Alloys Produced by High-Pressure Die Casting (HPDC). Metals 2024, 14, 1059. [Google Scholar] [CrossRef]




| Elements | Si | Mn | Mg | Fe | Cu | Ti | Ni | Sr | Al |
|---|---|---|---|---|---|---|---|---|---|
| wt% | 14.44 | 0.84 | 0.34 | 0.27 | 0.17 | 0.10 | 0.01 | 0.01 | Bal. |
| Casting Parameters | Value |
|---|---|
| Cast material | Silafont-36 |
| Die material | SKD-11 |
| Cast temperature | 700 °C |
| Die temperature | 200 °C |
| Cooling condition | Water Quenching, 20 °C, 60 s |
| Factors | Si Area Fraction | IMC Area Fraction | Si Sphericity |
|---|---|---|---|
| Median | 24.06 | 1.25 | 0.634 |
| Factors | Response | Factors | Response | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Runs | Si Area Fraction (%) | IMC Area Fraction (%) | Si Sphericity | Residual Stress (MPa) | Runs | Si Area Fraction (%) | IMC Area Fraction (%) | Si Sphericity | Residual Stress (MPa) |
| 1 | +1 | +1 | +1 | 38.28 | 29 | +1 | −1 | −1 | 59.73 |
| 2 | −1 | −1 | −1 | 11.39 | 30 | +1 | +1 | +1 | 56.16 |
| 3 | +1 | +1 | −1 | 56.16 | 31 | +1 | −1 | −1 | * 1 |
| 4 | −1 | +1 | −1 | 40.26 | 32 | −1 | +1 | +1 | * 1 |
| 5 | −1 | −1 | −1 | 46.22 | 33 | −1 | −1 | −1 | 46.22 |
| 6 | +1 | +1 | +1 | 38.28 | 34 | +1 | +1 | −1 | * 1 |
| 7 | −1 | −1 | +1 | 48.88 | 35 | −1 | +1 | −1 | 46.22 |
| 8 | +1 | −1 | −1 | 38.28 | 36 | −1 | +1 | −1 | 36.54 |
| 9 | +1 | −1 | +1 | 38.28 | 37 | 1 | −1 | −1 | * 1 |
| 10 | −1 | +1 | −1 | 40.26 | 38 | −1 | −1 | −1 | 35.47 |
| 11 | −1 | +1 | +1 | 36.54 | 39 | −1 | −1 | +1 | * 1 |
| 12 | +1 | +1 | −1 | 36.54 | 40 | −1 | +1 | +1 | * 1 |
| 13 | +1 | −1 | +1 | 49.06 | 41 | −1 | −1 | −1 | 35.47 |
| 14 | −1 | +1 | +1 | 59.73 | 42 | −1 | −1 | 1 | * 1 |
| 15 | +1 | +1 | −1 | 35.47 | 43 | +1 | −1 | −1 | * 1 |
| 16 | +1 | −1 | +1 | 49.06 | 44 | −1 | 1 | +1 | * 1 |
| 17 | −1 | −1 | +1 | 48.88 | 45 | −1 | 1 | +1 | * 1 |
| 18 | +1 | +1 | +1 | 49.06 | 46 | +1 | −1 | +1 | 49.06 |
| 19 | −1 | −1 | +1 | 48.88 | 47 | +1 | +1 | −1 | * 1 |
| 20 | −1 | −1 | −1 | 46.22 | 48 | −1 | −1 | −1 | * 1 |
| 21 | −1 | +1 | −1 | 40.26 | 49 | 1 | −1 | −1 | * 1 |
| 22 | −1 | −1 | +1 | 59.73 | 50 | +1 | −1 | +1 | 11.39 |
| 23 | −1 | +1 | −1 | 40.26 | 51 | +1 | +1 | +1 | 36.54 |
| 24 | −1 | +1 | +1 | 35.47 | 52 | +1 | +1 | −1 | * 1 |
| 25 | −1 | −1 | +1 | * 1 | 53 | +1 | +1 | −1 | * 1 |
| 26 | +1 | +1 | +1 | 56.16 | 54 | +1 | −1 | +1 | 48.88 |
| 27 | −1 | +1 | −1 | 11.39 | 55 | +1 | −1 | +1 | 59.73 |
| 28 | +1 | −1 | −1 | 11.39 | 56 | +1 | +1 | +1 | 56.16 |
| Term | Effect | Coefficients | Standard Error Coefficients | T-Value | p-Value |
|---|---|---|---|---|---|
| Si Area fraction | −0.15 | −0.07 | 2.15 | −0.03 | 0.973 |
| IMC Area fraction | 0.62 | 0.31 | 2.02 | 0.15 | 0.879 |
| Si Sphericity | 8.91 | 4.45 | 2.16 | 2.07 | 0.046 |
| Term | Effect | Coefficients | Standard Error Coefficients | T-Value | p-Value |
|---|---|---|---|---|---|
| Si Sphericity | 8.83 | 4.41 | 1.96 | 2.25 | 0.030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, N.; Lee, E. DOE-Based Investigation of Microstructural Factors Influencing Residual Stress in Aluminum Alloys. Metals 2025, 15, 816. https://doi.org/10.3390/met15070816
Kwak N, Lee E. DOE-Based Investigation of Microstructural Factors Influencing Residual Stress in Aluminum Alloys. Metals. 2025; 15(7):816. https://doi.org/10.3390/met15070816
Chicago/Turabian StyleKwak, Nawon, and Eunkyung Lee. 2025. "DOE-Based Investigation of Microstructural Factors Influencing Residual Stress in Aluminum Alloys" Metals 15, no. 7: 816. https://doi.org/10.3390/met15070816
APA StyleKwak, N., & Lee, E. (2025). DOE-Based Investigation of Microstructural Factors Influencing Residual Stress in Aluminum Alloys. Metals, 15(7), 816. https://doi.org/10.3390/met15070816




