Johnson–Cook Constitutive Model Parameters Estimation of 22MnB5 Hot Stamping Steel for Automotive Application Produced via the TSCR Process
Abstract
1. Introduction
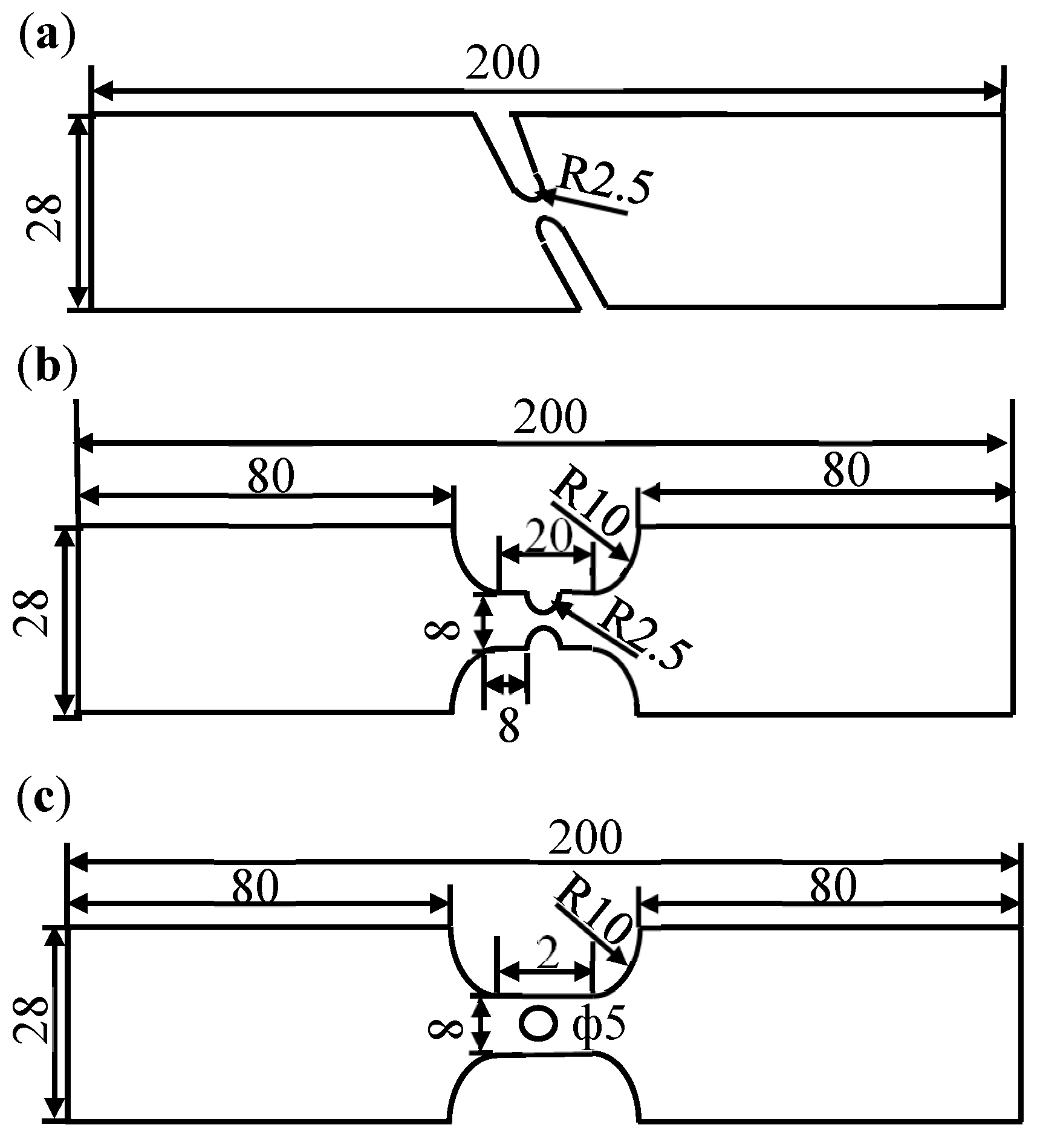
2. Experimental Procedures
3. Tensile Test Results and Discussion
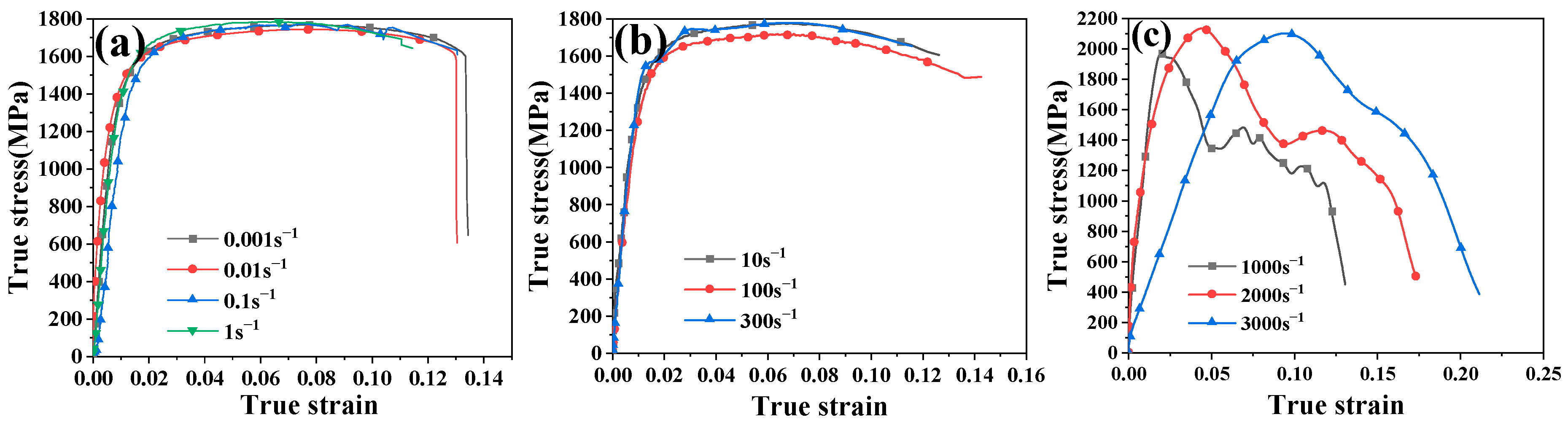
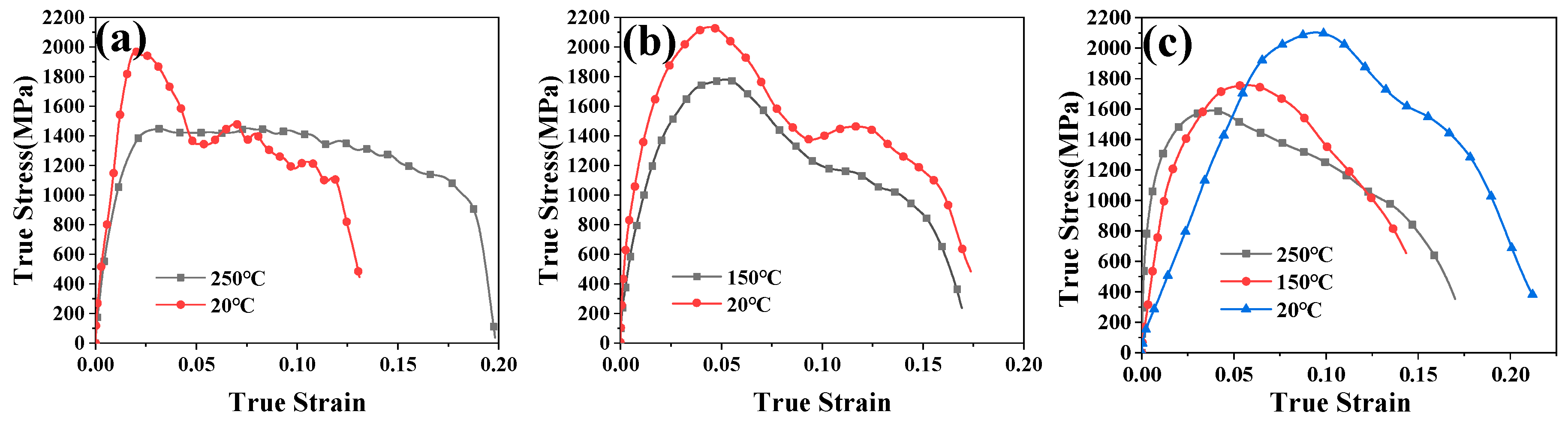
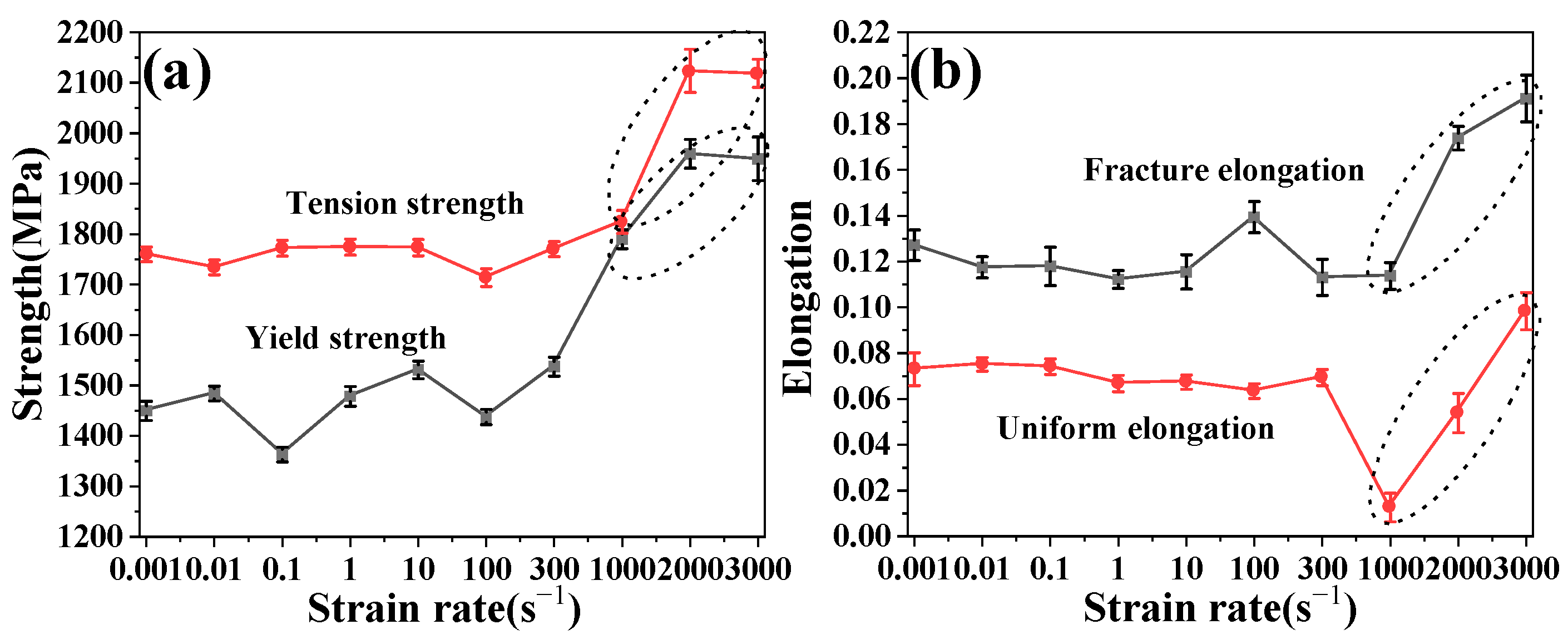
3.1. Tensile Mechanical Properties
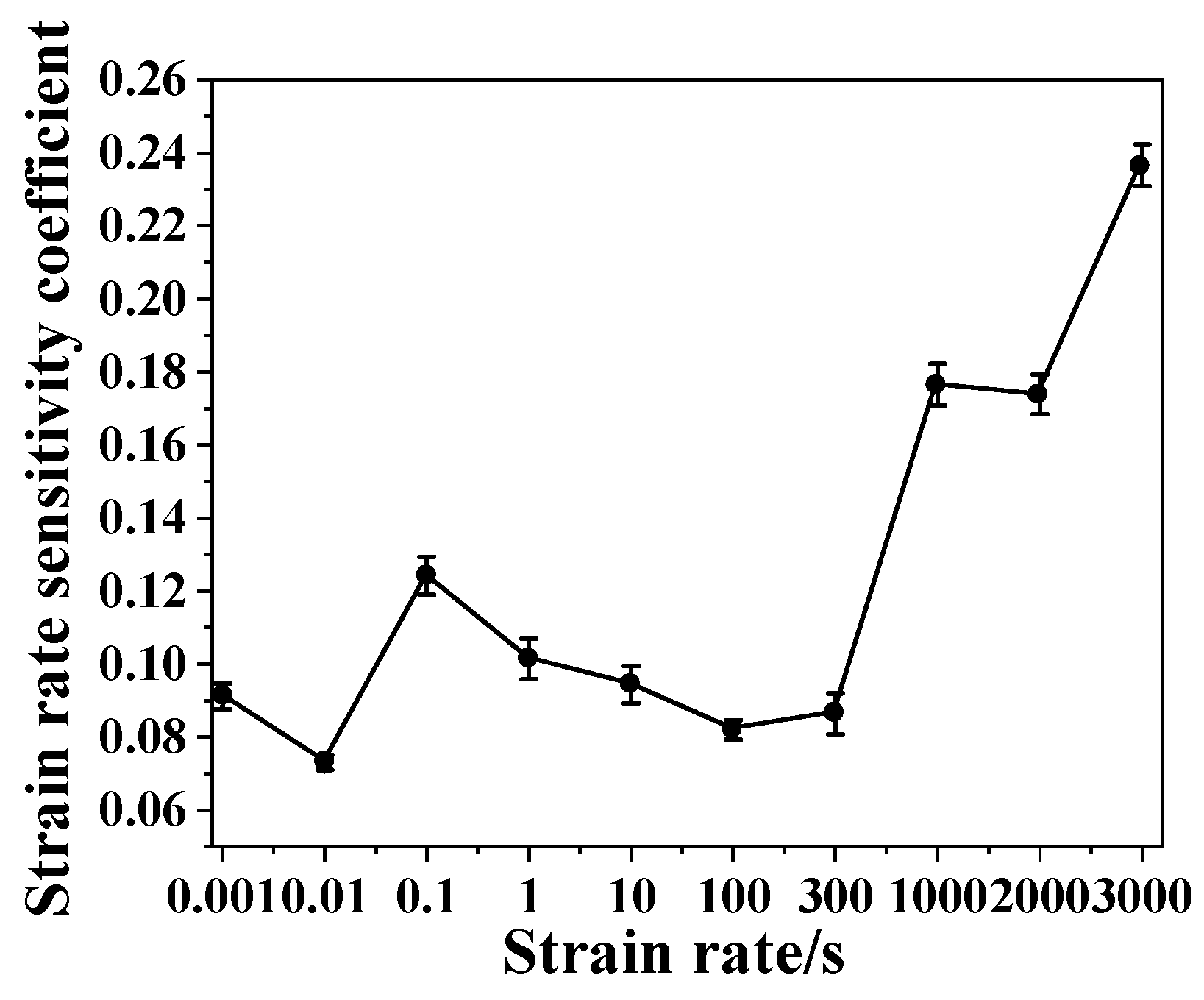
3.2. Sensitivity Coefficient and Strengthening Mechanism
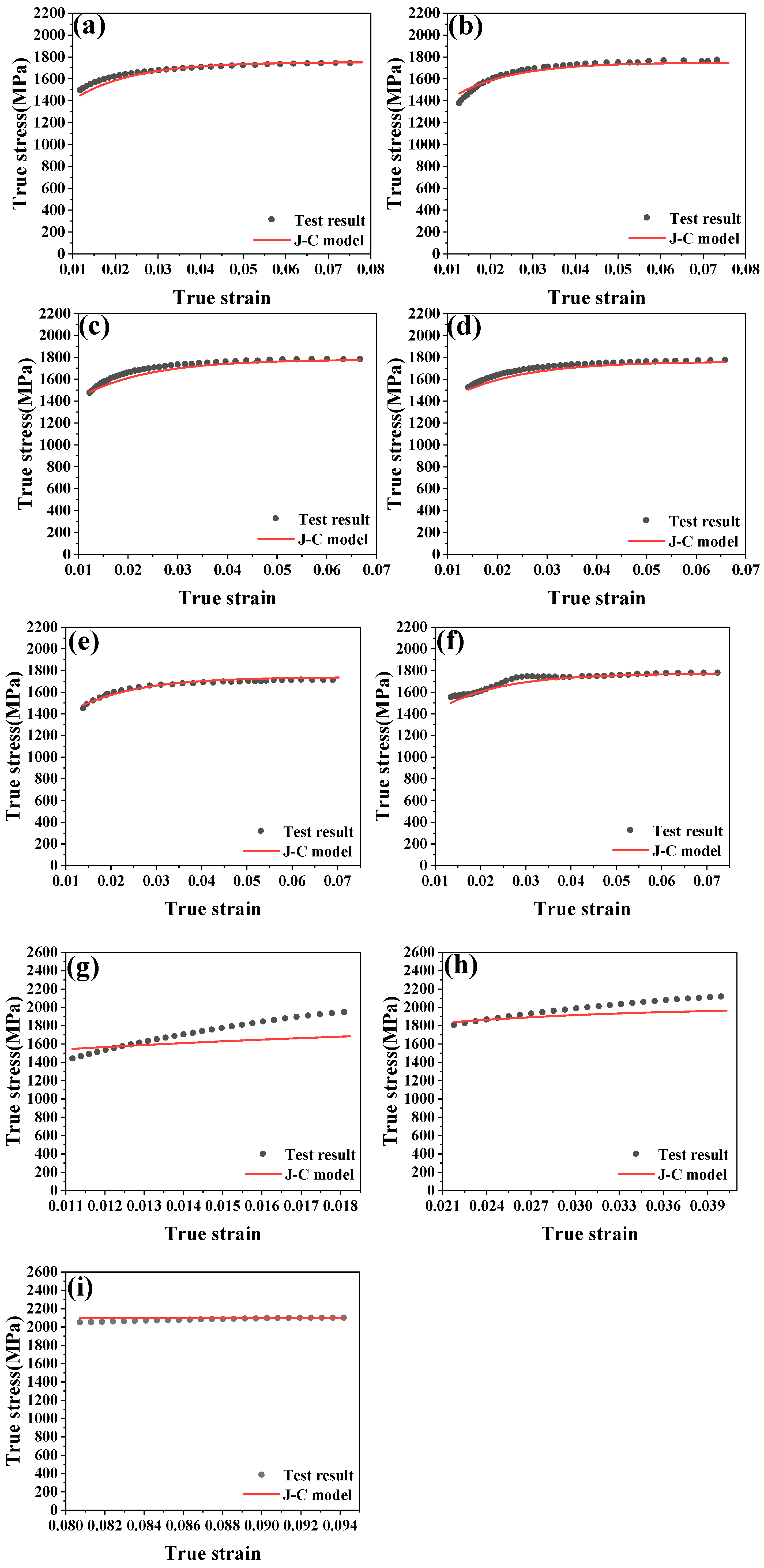
4. Johnson–Cook Constitutive Model
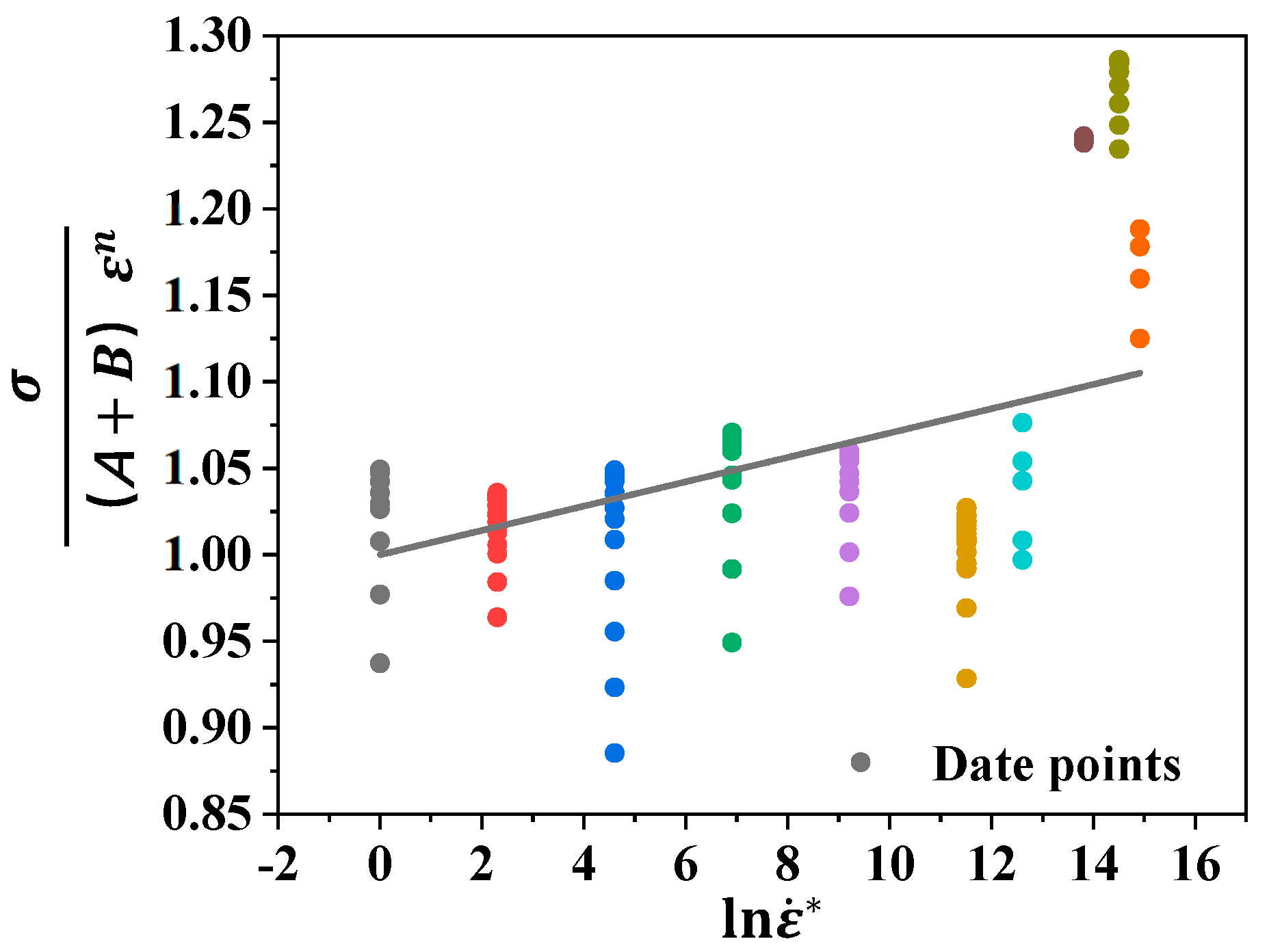
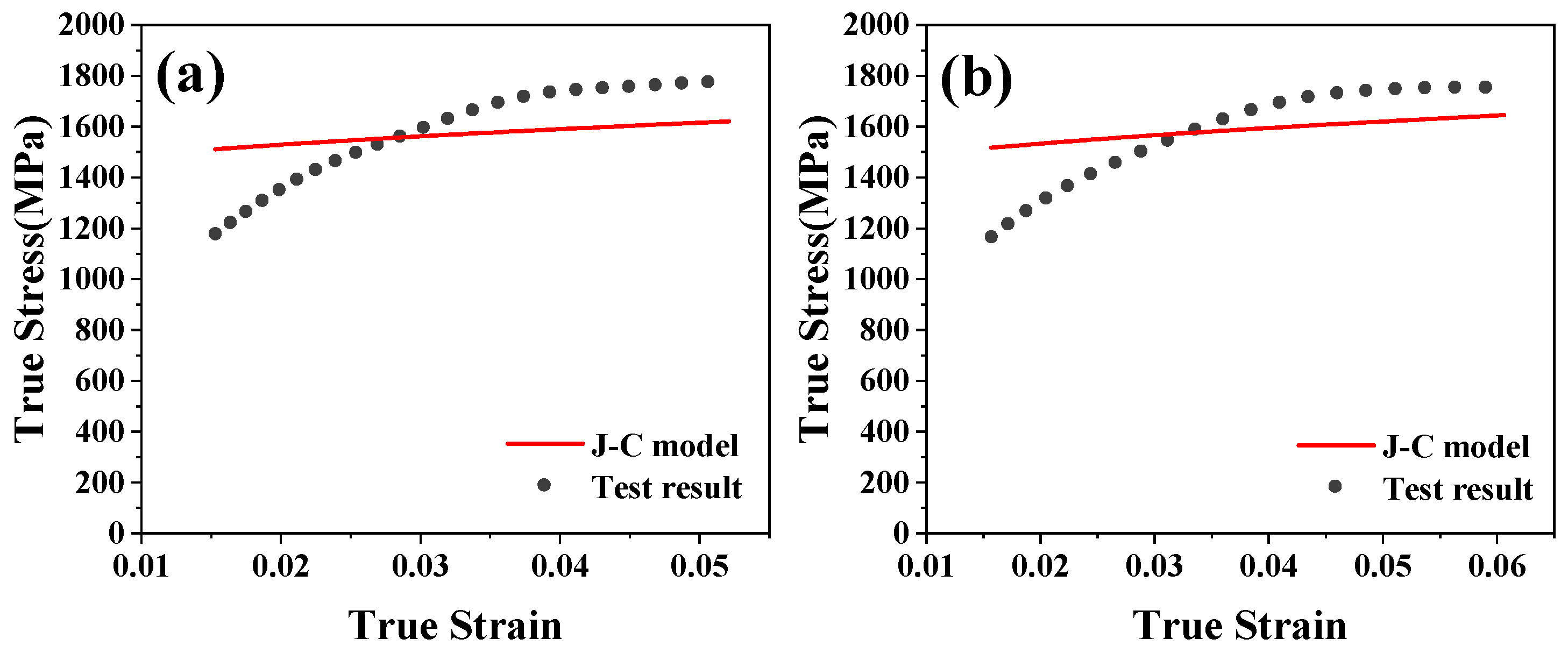
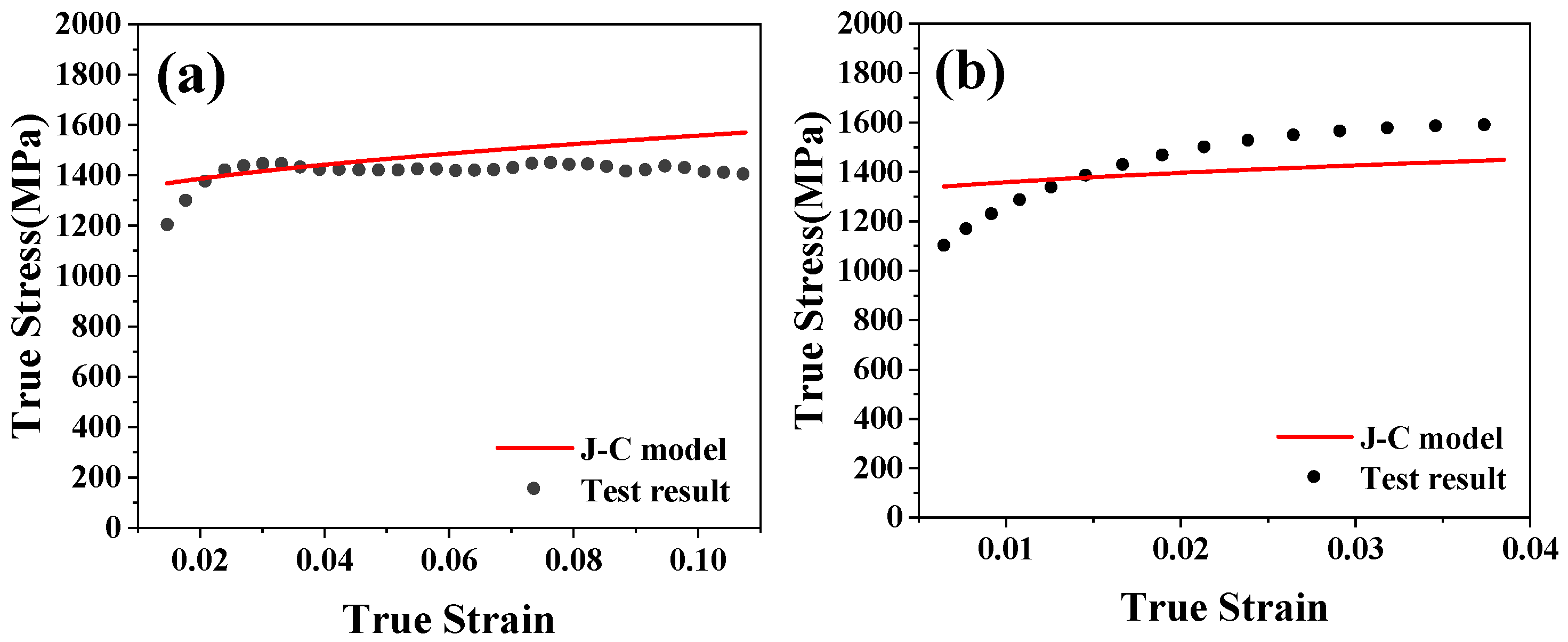
4.1. Establishment of Constitutive Model
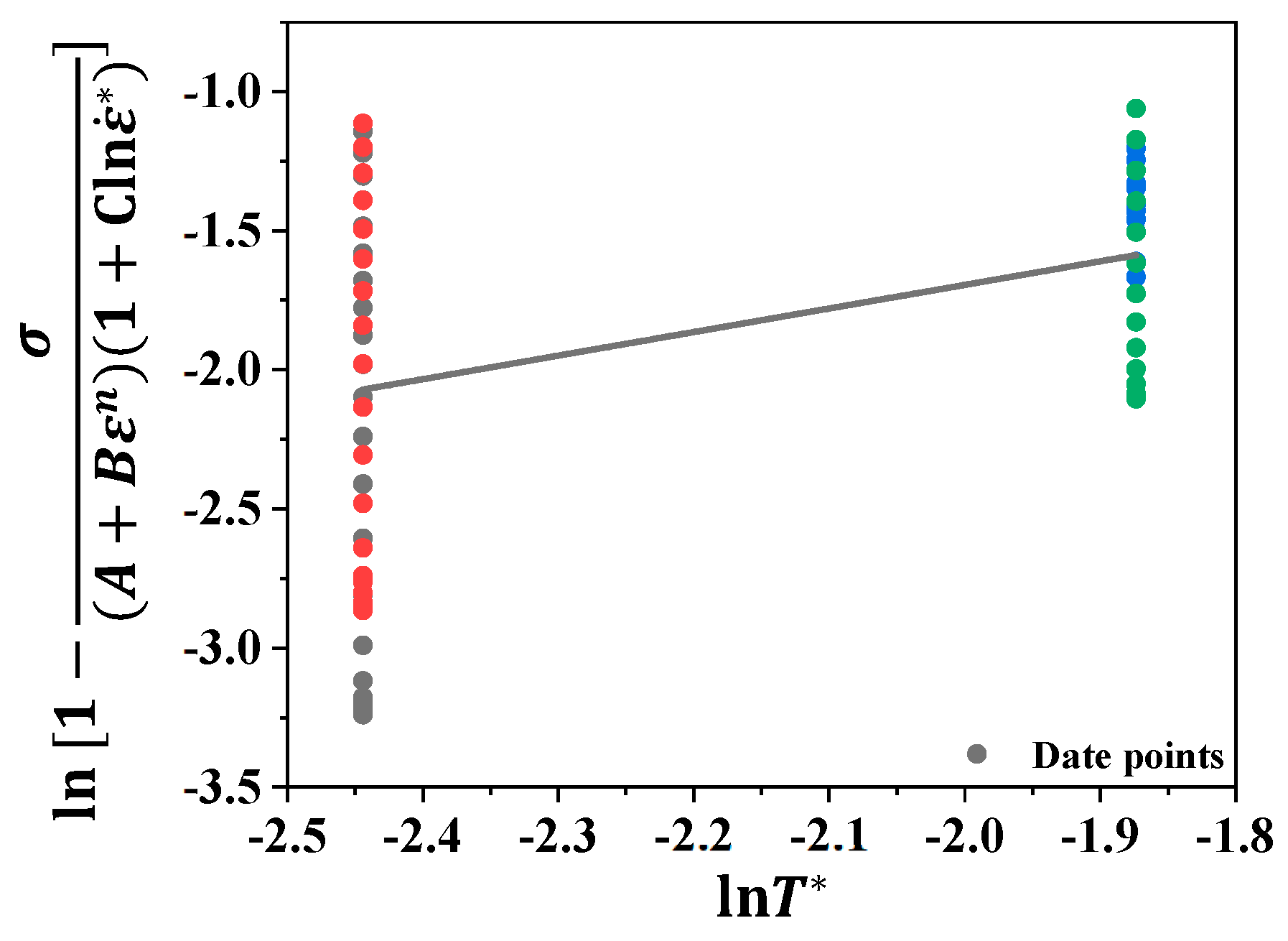
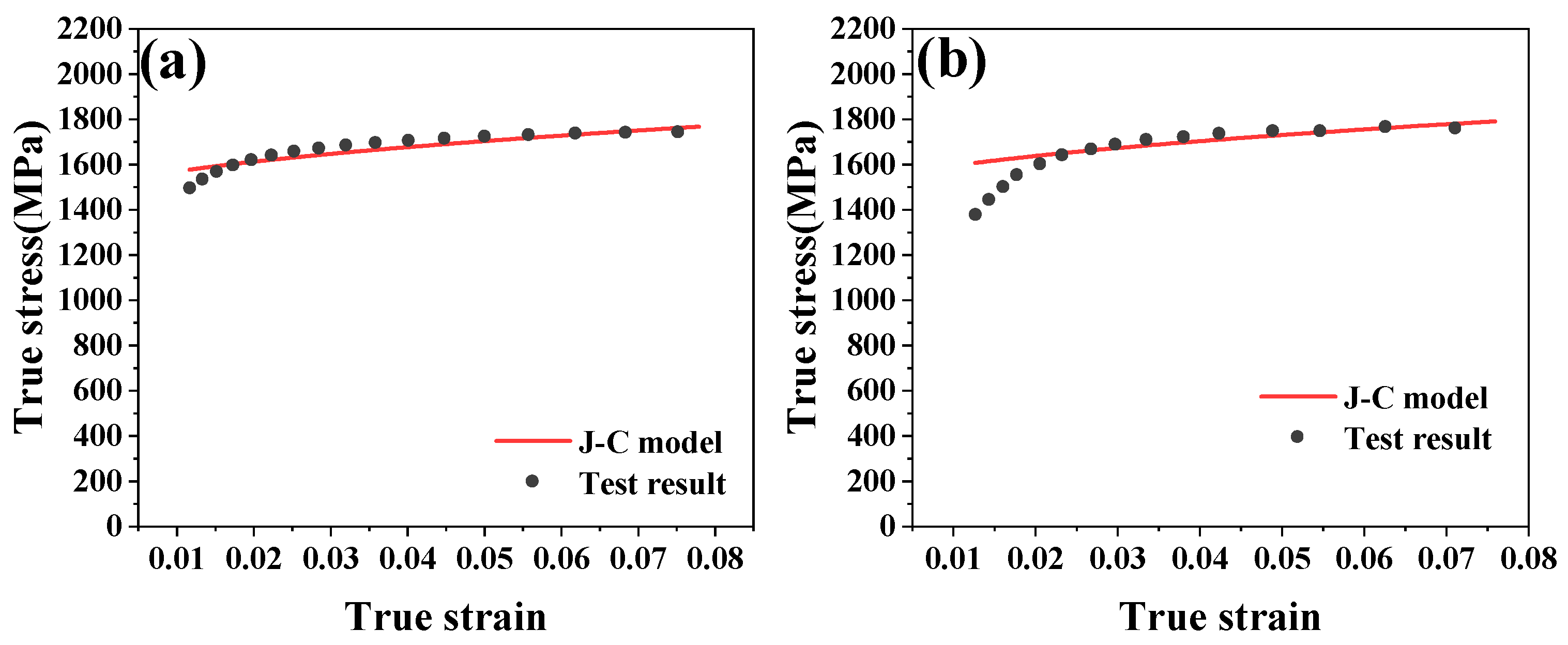
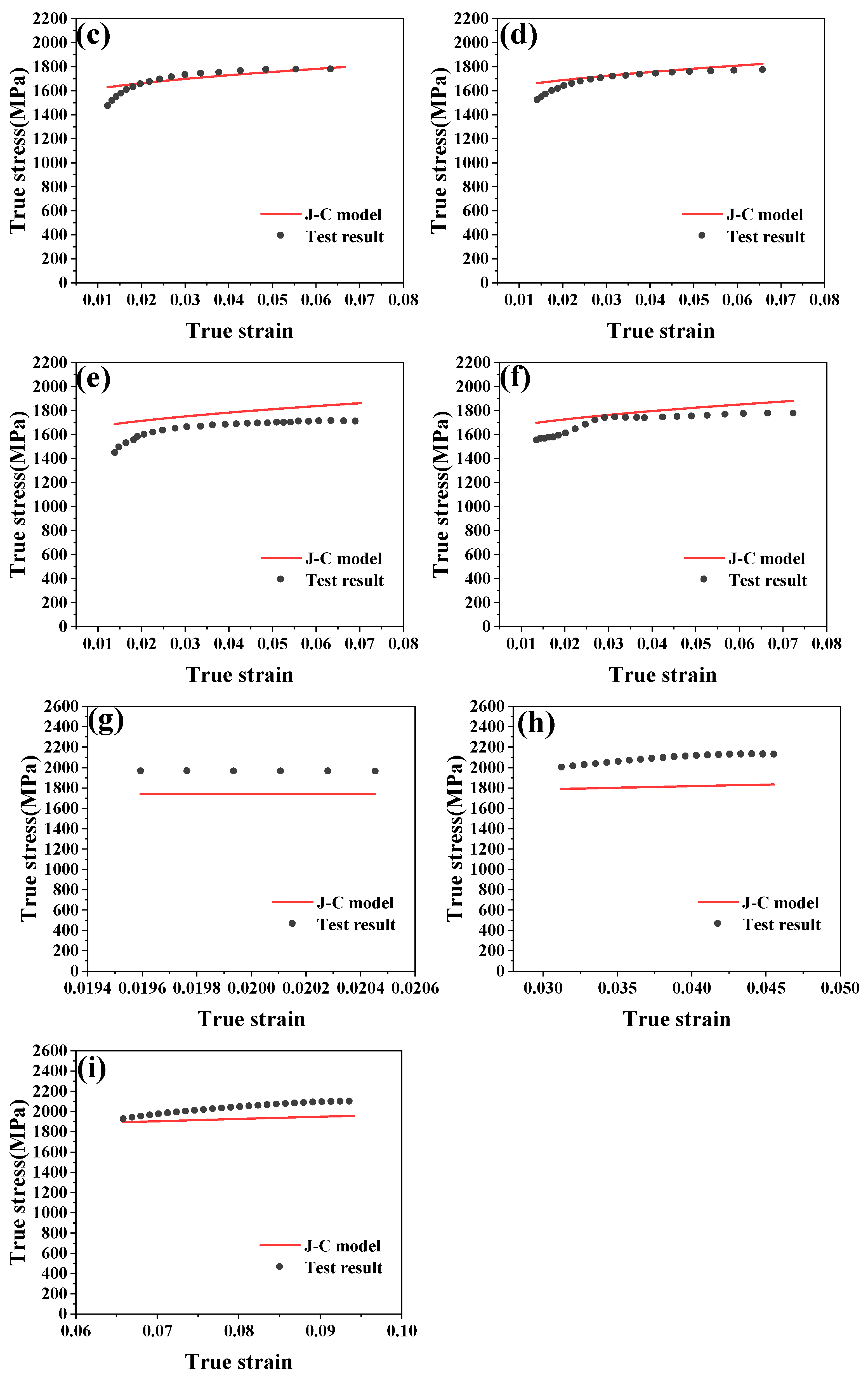
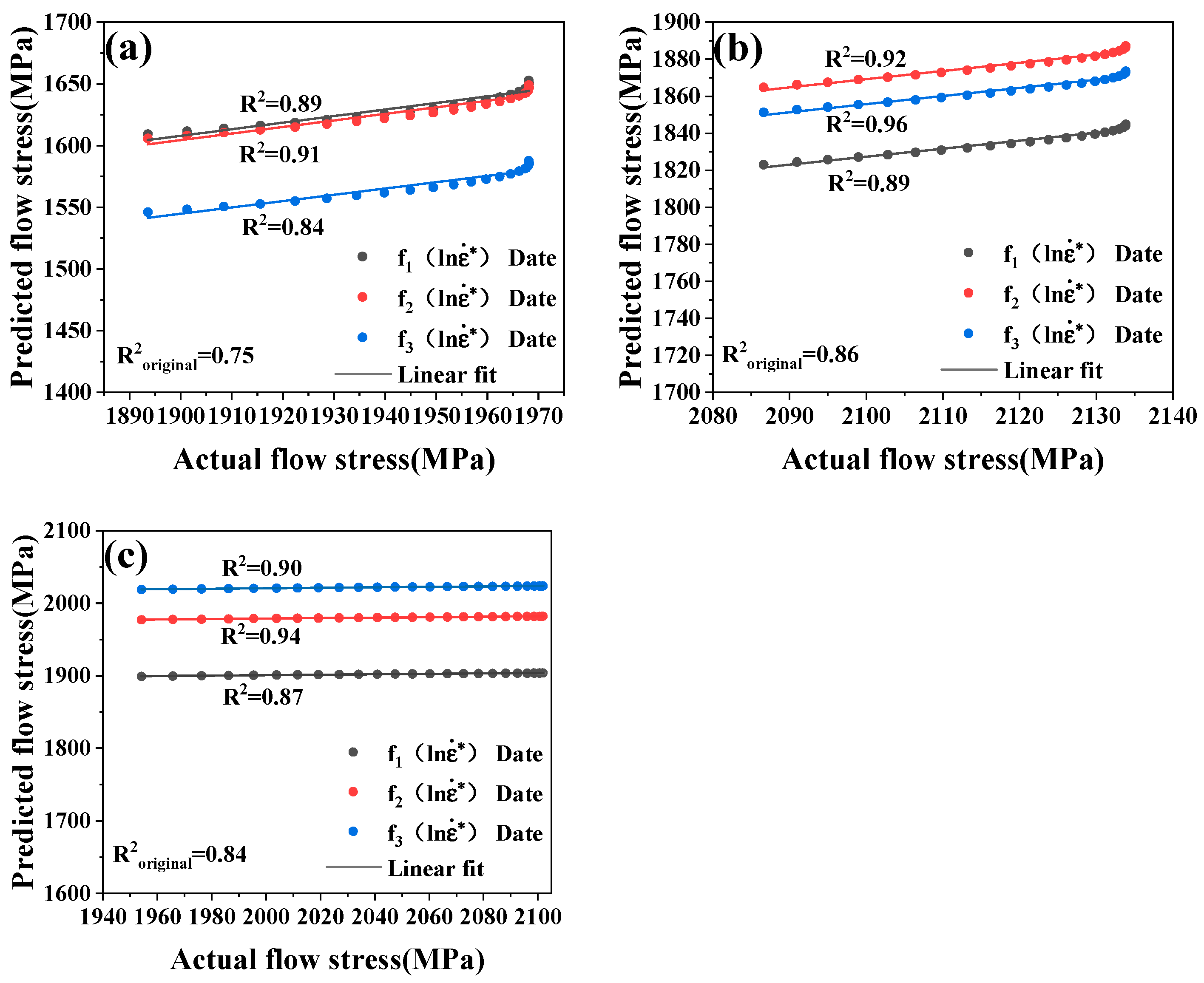
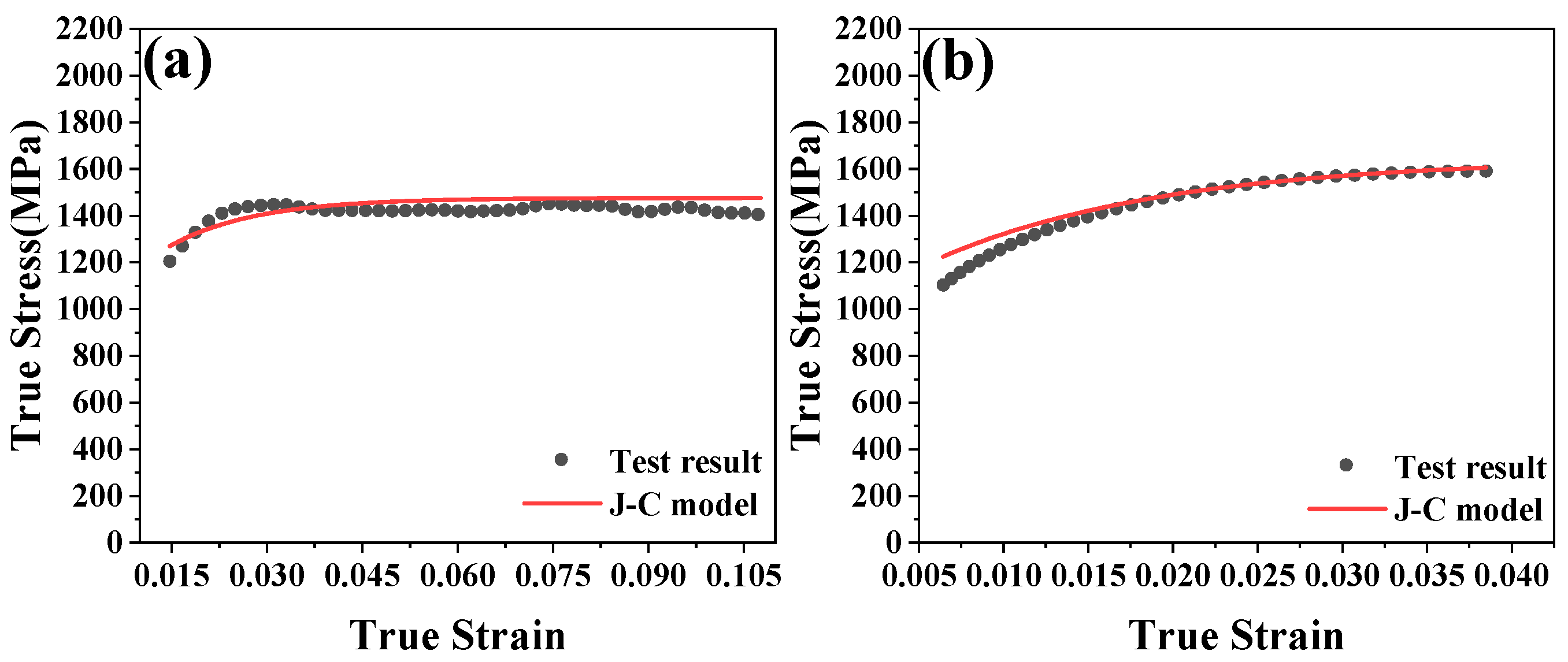
4.2. Modified Johnson–Cook Constitutive Modeling and Validation
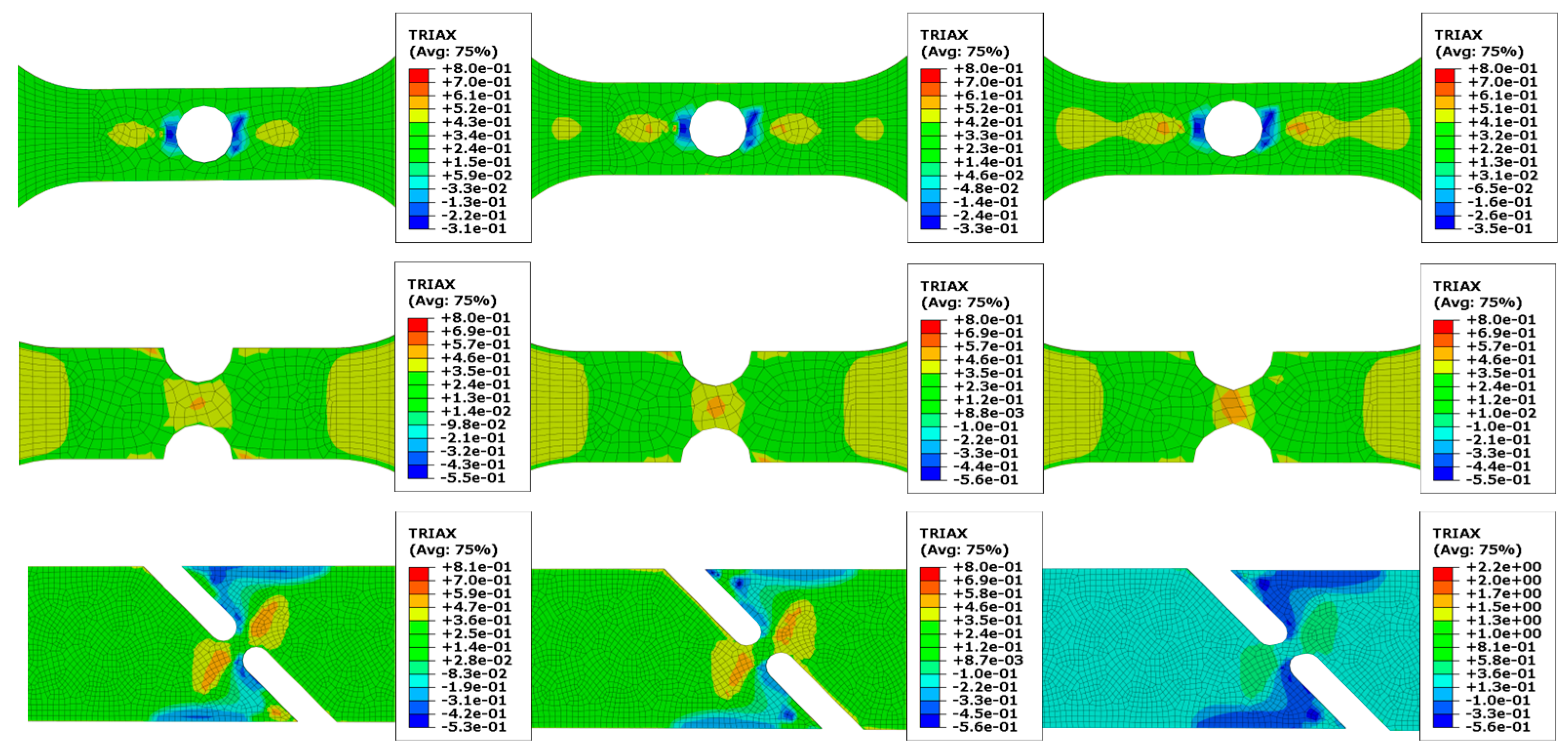
4.3. Johnson–Cook Damage Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, H.; Zhang, R.; Bin, Z. A Review of Automotive Lightweight Technology. In Proceedings of the 2018 International Conference on Mechanical, Electronic, Control and Automation Engineering (MECAE 2018), Qingdao, China, 30–31 March 2018; Atlantis Press: Dordrecht, The Netherlands, 2018. [Google Scholar][Green Version]
- Li, Y.; Lin, Z.; Jiang, A.; Chen, G. Use of High Strength Steel Sheet for Lightweight and Crashworthy Car Body. Mater. Des. 2003, 24, 177–182. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, S.; Hong, Y.; Li, X.; Zhang, J.; Xiao, Y.; Luo, G.; Yu, Y.; Hu, J. Multi-Scale Damage Mechanism of Hierarchically Structured High-Strength Martensitic Steels under Shock Loading. Int. J. Plast. 2024, 175, 103945. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.; Wan, X.; Zhang, X.; Shen, Y.; Wu, K. Toughness Improvement by Zr Addition in the Simulated Coarse-Grained Heat-Affected Zone of High-Strength Low-Alloy Steels. Ironmak. Steelmak. 2019, 46, 113–123. [Google Scholar] [CrossRef]
- Kumar, A.; Paul, S.K. Local Strain Evolution and Microstructural Characterisation of Hydrogen-Induced Damage at Different Strain Rates in Dual Phase (DP 780) Steel. Forces Mech. 2023, 13, 100237. [Google Scholar] [CrossRef]
- Li, Y.; Wang, E.; Zhang, L.; Ma, B.; Du, J.; Zhang, S. High Strength and High Ductility of 60Si2CrVAT Spring Steel through a Novel Quenching and Partitioning (Q-P) Process. Mater. Sci. Eng. A 2024, 899, 146444. [Google Scholar] [CrossRef]
- Li, D.-F.; Cheng, J.-H.; Bai, C.-G.; Zhang, Z.-Q.; Du, F.-F.; Wang, R.; Zhao, J.; Li, N.; Yang, R. Multi-Scale α-Phase Heterostructure Induced Transformation-Induced Plasticity (TRIP) Effect in Metastable A+β Titanium Alloy Showing Excellent Strength and Work-Hardening Combination. J. Mater. Process. Technol. 2025, 341, 118880. [Google Scholar] [CrossRef]
- Li, B.; Zhu, H.; Sun, J.; Song, M.; Zhao, J. Effect of Ti Addition on Non-Metallic Inclusion Characteristics in TRIP Steel. Steel Res. Int. 2022, 93, 2200064. [Google Scholar] [CrossRef]
- Braga, D.P.; Palhares, I.C.; Moreira Afonso, C.R.; Camilo Magalhães, D.C.; Della Rovere, C.A.; Kliauga, A.M. Effects of Temperature, Strain Rate and Grain Size on the Twin Induced Plasticity (TWIP) Effect of an AISI 316 LV Austenitic Stainless Steel. Mater. Sci. Eng. A 2025, 931, 148234. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, L.; Lin, Y.; Wang, J.; Wang, K.; Guo, Z.; Cao, R.; Zhu, L.; Wang, B.; Zhang, D.; et al. Effect of Compound Addition of Ti–B on Hardenability and Hot Ductility of 22MnB5 Hot Stamped Steel. J. Mater. Res. Technol. 2025, 36, 1173–1193. [Google Scholar] [CrossRef]
- Kubota, K.; Ohba, T.; Morito, S. Frictional Properties of New Developed Cold Work Tool Steel for High Tensile Strength Steel Forming Die. Wear 2011, 271, 2884–2889. [Google Scholar] [CrossRef]
- Xu, Y.; Ji, Q.; Yang, G.; Bao, S.; Zhao, G.; Miao, X.; Mao, X. Effect of Cooling Path on Microstructures and Hardness of Hot-Stamped Steel. Metals 2020, 10, 1692. [Google Scholar] [CrossRef]
- Jiang, C.; Shan, Z.; Zhuang, B.; Zhang, M.; Xu, Y. Hot Stamping Die Design for Vehicle Door Beams Using Ultra-High Strength Steel. Int. J. Precis. Eng. Manuf. 2012, 13, 1101–1106. [Google Scholar] [CrossRef]
- Karbasian, H. A Review on Hot Stamping. J. Mater. Process. Technol. 2010, 210, 2103–2118. [Google Scholar] [CrossRef]
- Merklein, M.; Wieland, M.; Lechner, M.; Bruschi, S.; Ghiotti, A. Hot Stamping of Boron Steel Sheets with Tailored Properties: A Review. J. Mater. Process. Technol. 2016, 228, 11–24. [Google Scholar] [CrossRef]
- Mori, K. Hot Stamping of Ultra-High Strength Steel Parts. CIRP Ann. 2017, 66, 755–777. [Google Scholar] [CrossRef]
- Liu, C.; Xiong, F.; Wang, Y.; Cao, Y.; Liu, X.; Xue, Z.; Peng, Q.; Peng, L. Strengthening Mechanism and Carbide Precipitation Behavior of Nb-Mo Microalloy Medium Mn Steel. Materials 2021, 14, 7461. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, G.; Wan, X.; Wang, H.; Wu, K.; Misra, R.D.K. The Role of Cu and Al Addition on the Microstructure and Fracture Characteristics in the Simulated Coarse-Grained Heat-Affected Zone of High-Strength Low-Alloy Steels with Superior Toughness. Mater. Sci. Technol. 2017, 33, 1750–1764. [Google Scholar] [CrossRef]
- Mao, X.; Huo, X.; Sun, X.; Chai, Y. Strengthening Mechanisms of a New 700MPa Hot Rolled Ti-Microalloyed Steel Produced by Compact Strip Production. J. Mater. Process. Technol. 2010, 210, 1660–1666. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–548. [Google Scholar]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of Constitutive Laws, Kinematics, Homogenization and Multiscale Methods in Crystal Plasticity FInite-Element Modeling: Theory, Experiments, Applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Zerilli, F.J. Dislocation Mechanics-Based Constitutive Equations. Metall. Mater. Trans. A 2004, 35, 2547–2555. [Google Scholar] [CrossRef]
- Rusinek, A.; Klepaczko, J.R. Shear Testing of a Sheet Steel at Wide Range of Strain Rates and a Constitutive Relation with Strain-Rate and Temperature Dependence of the Flow Stress. Int. J. Plast. 2001, 17, 87–115. [Google Scholar] [CrossRef]
- Steinberg, D.S. Vibration Analysis for Electronic Equipment; Wiley: Hoboken, NJ, USA, 2000; ISBN 978-0-471-37685-9. [Google Scholar]
- Non-Linear Analysis of Composite Structure Subjected to Impact Load Based on Johnson-Cook Constitutive Model. Int. J. Non-Linear Mech. 2025, 178, 105176. [CrossRef]
- Research on the Expansion and Failure of Solid Expandable Tubular Based on the Johnson-Cook Failure Model. Int. J. Press. Vessel. Pip. 2025, 218, 105567. [CrossRef]
- GB/T 228.1-2010; Metallic Materials Tensile Testing-Part 1: Method of Test at Room Temperature. China Standard Publishing House: Beijing, China, 2011.
- ISO 26203-2:2011; Metallic Materials—Tensile Testing at High Strain Rates—Part 2: Servo-Hydraulic and Other Test Systems. German Version DIN EN ISO 26203-2:2011. International Organization for Standardization: Geneva, Switzerland, 2011.
- Liu, X.; He, Z.; Ye, J.; Yan, L.; Li, S.; Tang, Y. Study on Dynamic Mechanical Behavior of Q460JSC and HQ600 High Strength Steel. J. Constr. Steel Res. 2020, 173, 106232. [Google Scholar] [CrossRef]
- GB/T 30069–2013; Metallic Material Tensile Testing at High Strain Rates-Part 1: Elastic Rod Type System. China Standard Publishing House: Beijing, China, 2013.
- Bardelcik, A. A Strain Rate Sensitive Constitutive Model for Quenched Boron Steel with Tailored Properties. Int. J. Impact Eng. 2012, 50, 49–62. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, F.; Liu, H.; Könemann, M.; Münstermann, S. Temperature-Dependent Deformation and Fracture Properties of Low-Carbon Martensitic Steel in Different Stress States. J. Mater. Res. Technol. 2023, 25, 1931–1943. [Google Scholar] [CrossRef]
- Woo, W.; Em, V.T. Stress–Strain Relationship between Ferrite and Martensite in a Dual-Phase Steel Studied by in Situ Neutron Diffraction and Crystal Plasticity Theories. Acta Mater. 2012, 60, 6972–6981. [Google Scholar] [CrossRef]
- Hu, C.; Huang, C.P.; Liu, Y.X.; Perlade, A.; Zhu, K.Y.; Huang, M.X. The Dual Role of TRIP Effect on Ductility and Toughness of a Medium Mn Steel. Acta Mater. 2023, 245, 118629. [Google Scholar] [CrossRef]
- Çavuşoğlu, O.; Çavuşoğlu, O.; Yılmazoğlu, A.G.; Üzel, U.; Aydın, H.; Güral, A. Microstructural Features and Mechanical Properties of 22MnB5 Hot Stamping Steel in Different Heat Treatment Conditions. J. Mater. Res. Technol. 2020, 9, 10901–10908. [Google Scholar] [CrossRef]
- Guan, J.; Yuan, Q.; Zhang, Q.; Qiao, W.; Xu, G. Simultaneous Enhancement of Strength and Toughness in a Medium-Carbon Martensitic Steel by Ti-Mo Addition. J. Mater. Eng. Perform. 2022, 31, 4273–4281. [Google Scholar] [CrossRef]
- Li, C.; Li, X.; Yu, W.; Shi, J.; Wang, M.; Wu, R. Microstructure Characteristics and Strengthening Mechanism of Martensitic Steel at Two Quenching Rates. J. Mater. Eng. Perform. 2022, 31, 8711–8720. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, F.; Münstermann, S. Crystal Plasticity Modeling of Prior Austenite Orientation Effects on Deformation Behaviors of Martensitic Steels under Different Strain Paths. Mater. Des. 2024, 245, 113280. [Google Scholar] [CrossRef]
- Krauss, G. Martensite in Steel: Strength and Structure. Mater. Sci. Eng. A 1999, 273–275, 40–57. [Google Scholar] [CrossRef]
- Dannoshita, H.; Hasegawa, H.; Matsuda, H.; Gong, W.; Kawasaki, T.; Harjo, S.; Umezawa, O. Evolution of Dislocation Structure Determined by Neutron Diffraction Line Profile Analysis during Tensile Deformation in Quenched and Tempered Martensitic Steels. Mater. Sci. Eng. A 2022, 854, 143795. [Google Scholar] [CrossRef]
- Li, N.; Xu, Y.; Yang, G.; Fu, Z. Dynamic Mechanical Properties and Constitutive Model Establishment of QSTE420 Steel. J. Constr. Steel Res. 2024, 213, 108342. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.-M.; Liu, G. A Modified Johnson–Cook Model for Tensile Behaviors of Typical High-Strength Alloy Steel. Mater. Sci. Eng. A 2010, 527, 6980–6986. [Google Scholar] [CrossRef]
- Murugesan, M.; Jung, D. Johnson Cook Material and Failure Model Parameters Estimation of AISI-1045 Medium Carbon Steel for Metal Forming Applications. Materials 2019, 12, 609. [Google Scholar] [CrossRef] [PubMed]
- Bian, Y. Mechanical Properties and JC Constitutive Modification of Tungsten Alloys under High Strain Rates and High/Low Temperatures. Mater. Today Commun. 2024, 41, 110542. [Google Scholar] [CrossRef]
- He, J.; Chen, F.; Wang, B.; Zhu, L.B. A Modified Johnson-Cook Model for 10%Cr Steel at Elevated Temperatures and a Wide Range of Strain Rates. Mater. Sci. Eng. A 2018, 715, 1–9. [Google Scholar] [CrossRef]
- Liu, Y. Unbiased Estimate of Generalization Error and Model Selection in Neural Network. Neural Netw. 1995, 8, 215–219. [Google Scholar] [CrossRef]
- Murugesan, M.; Kang, B.-S.; Lee, K. Multi-Objective Design Optimization of Composite Stiffened Panel Using Response Surface Methodology. Compos. Res. 2015, 28, 297–310. [Google Scholar] [CrossRef]
- Lee, K.; Murugesan, M.; Lee, S.-M.; Kang, B.-S. A Comparative Study on Arrhenius-Type Constitutive Models with Regression Methods. Trans. Mater. Process. 2017, 26, 18–27. [Google Scholar] [CrossRef]
- Di Bucchianico, A. Coefficient of Determination (R2). In Encyclopedia of Statistics in Quality and Reliability; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; ISBN 978-0-470-06157-2. [Google Scholar]
- Murugesan, M.; Lee, S.; Kim, D.; Kang, Y.-H.; Kim, N. A Comparative Study of Ductile Damage Models Approaches for Joint Strength Prediction in Hot Shear Joining Process. Procedia Eng. 2017, 207, 1689–1694. [Google Scholar] [CrossRef]
- Banerjee, A.; Dhar, S.; Acharyya, S.; Datta, D.; Nayak, N. Determination of Johnson Cook Material and Failure Model Constants and Numerical Modelling of Charpy Impact Test of Armour Steel. Mater. Sci. Eng. A 2015, 640, 200–209. [Google Scholar] [CrossRef]
- Buzyurkin, A.E.; Gladky, I.L.; Kraus, E.I. Determination and Verification of Johnson–Cook Model Parameters at High-Speed Deformation of Titanium Alloys. Aerosp. Sci. Technol. 2015, 45, 121–127. [Google Scholar] [CrossRef]
- Owen, D.R.J.; Hinton, E. Finite Elements in Plasticity: Theory and Practice; Pineridge Press: Swansea, UK, 1980; ISBN 978-0-906674-05-5. [Google Scholar]

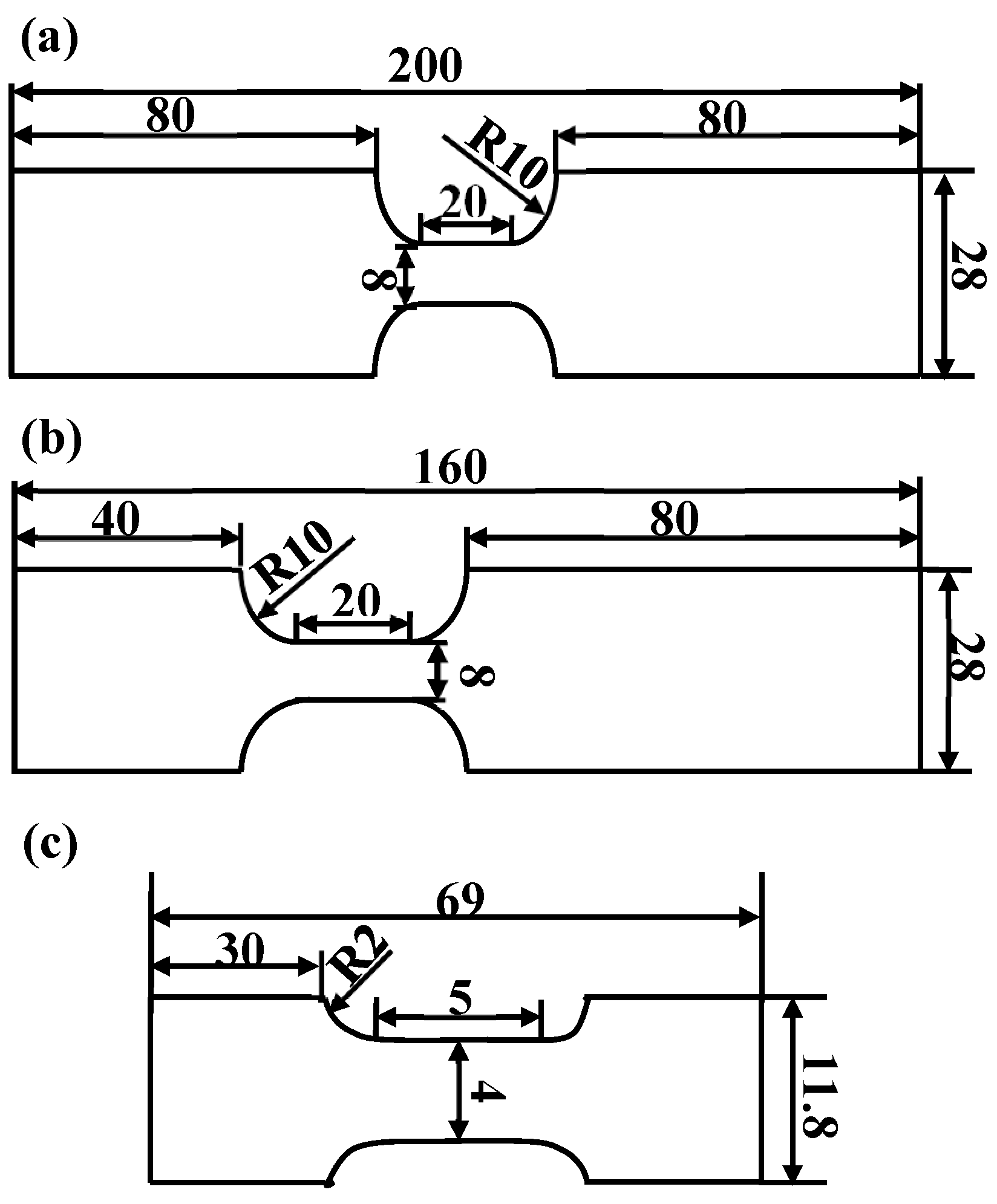


| C | Si | Mn | P | S | B | N | Fe |
|---|---|---|---|---|---|---|---|
| 0.214 | 0.228 | 1.297 | 0.011 | 0.0042 | 0.0028 | 0.0057 | Bal. |
| A | B | n | C | m |
|---|---|---|---|---|
| 1452.03 | 1201.14 | 0.56 | 0.00704 | 0.84736 |
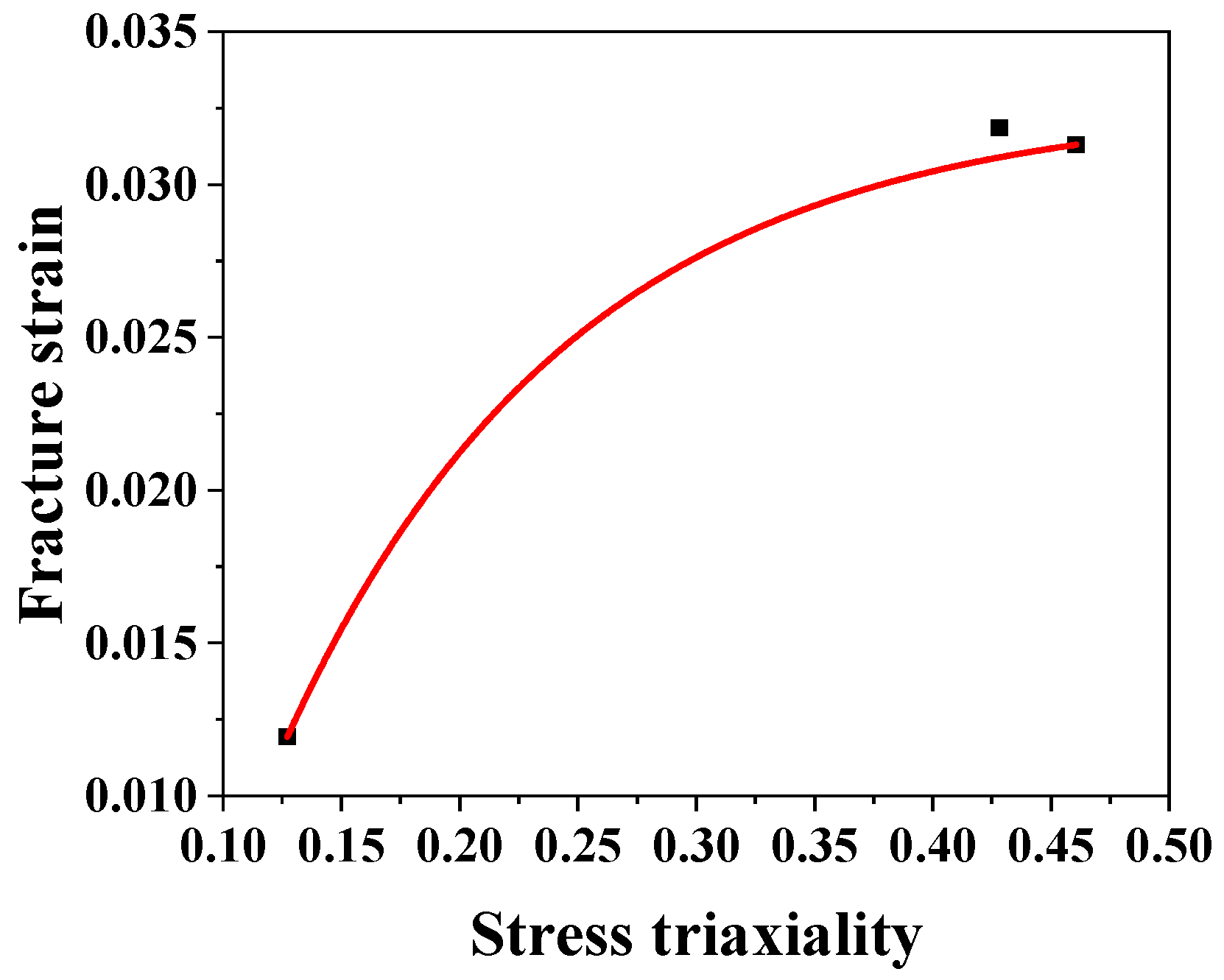
| Position | Stress Triaxiality | Fracture Strain |
|---|---|---|
| 45° Shear | 0.1272 | 0.01193 |
| Notch | 0.4606 | 0.0313 |
| Hole | 0.4281 | 0.03185 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Xu, Y.; Yang, G. Johnson–Cook Constitutive Model Parameters Estimation of 22MnB5 Hot Stamping Steel for Automotive Application Produced via the TSCR Process. Metals 2025, 15, 811. https://doi.org/10.3390/met15070811
Song Y, Xu Y, Yang G. Johnson–Cook Constitutive Model Parameters Estimation of 22MnB5 Hot Stamping Steel for Automotive Application Produced via the TSCR Process. Metals. 2025; 15(7):811. https://doi.org/10.3390/met15070811
Chicago/Turabian StyleSong, Yuxin, Yaowen Xu, and Gengwei Yang. 2025. "Johnson–Cook Constitutive Model Parameters Estimation of 22MnB5 Hot Stamping Steel for Automotive Application Produced via the TSCR Process" Metals 15, no. 7: 811. https://doi.org/10.3390/met15070811
APA StyleSong, Y., Xu, Y., & Yang, G. (2025). Johnson–Cook Constitutive Model Parameters Estimation of 22MnB5 Hot Stamping Steel for Automotive Application Produced via the TSCR Process. Metals, 15(7), 811. https://doi.org/10.3390/met15070811






