Fracture Initiation in Aluminum Alloys Under Multiaxial Loading at Various Low Strain Rates
Abstract
1. Introduction
2. Stress Triaxiality Locus
3. Experiment and Simulation Methods
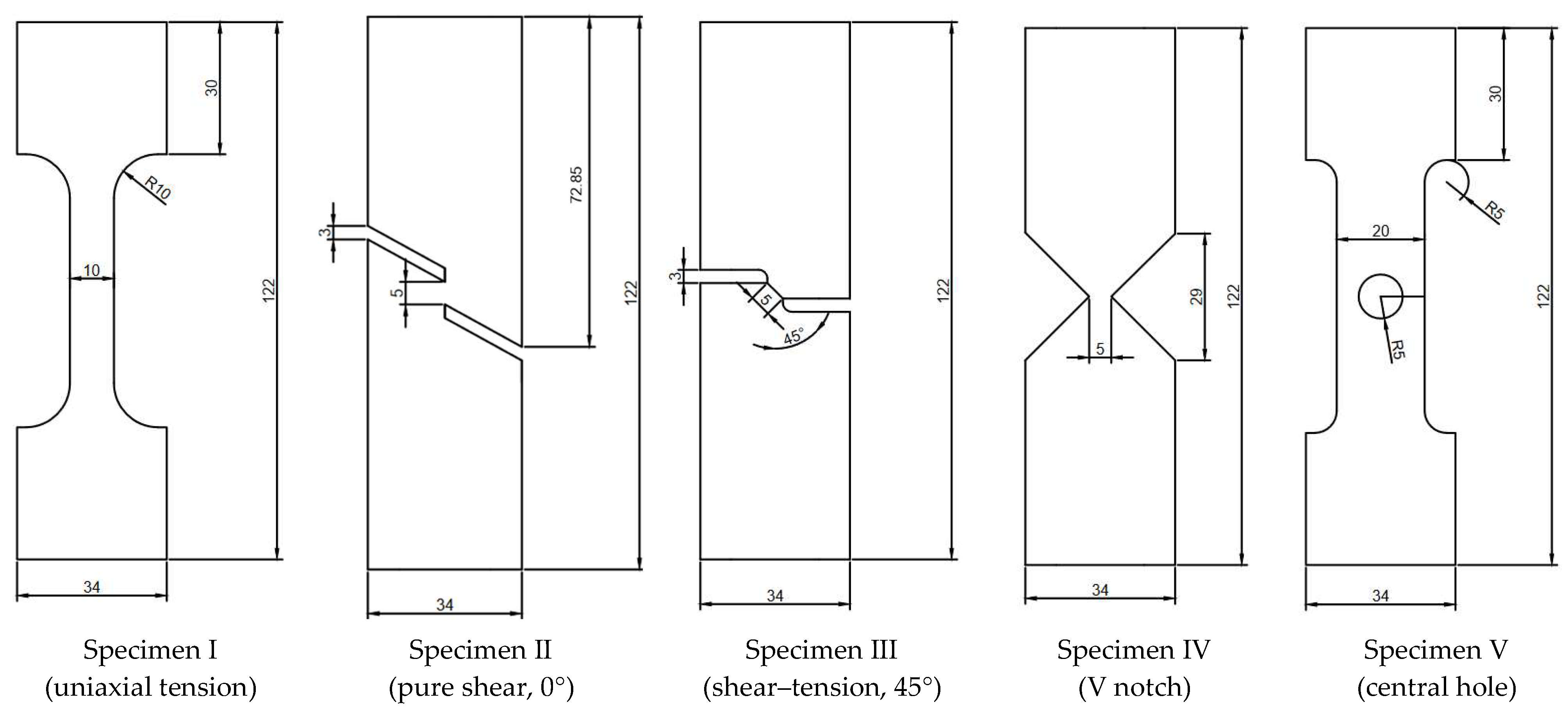
3.1. Experiment
3.2. Fractographic Analysis
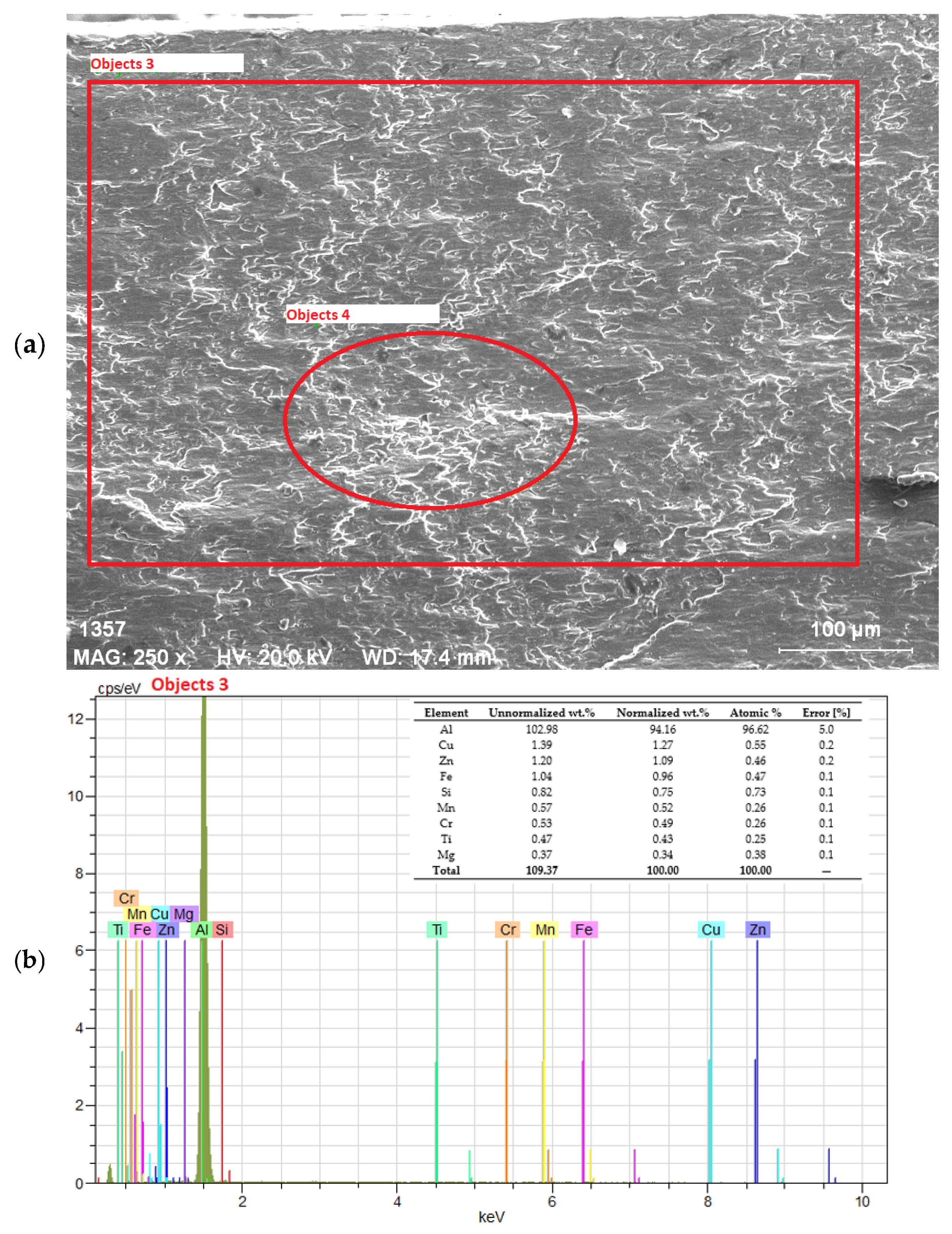
3.3. SEM-EDS Analysis and Elemental Characterization
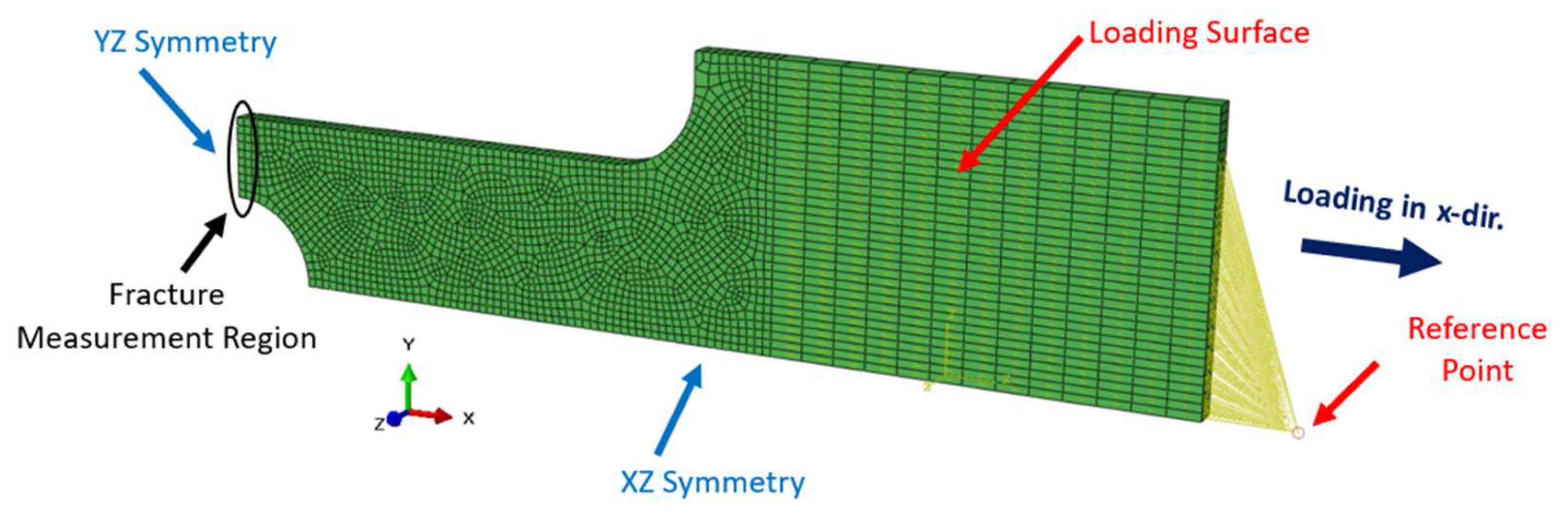
3.4. Finite Element Models
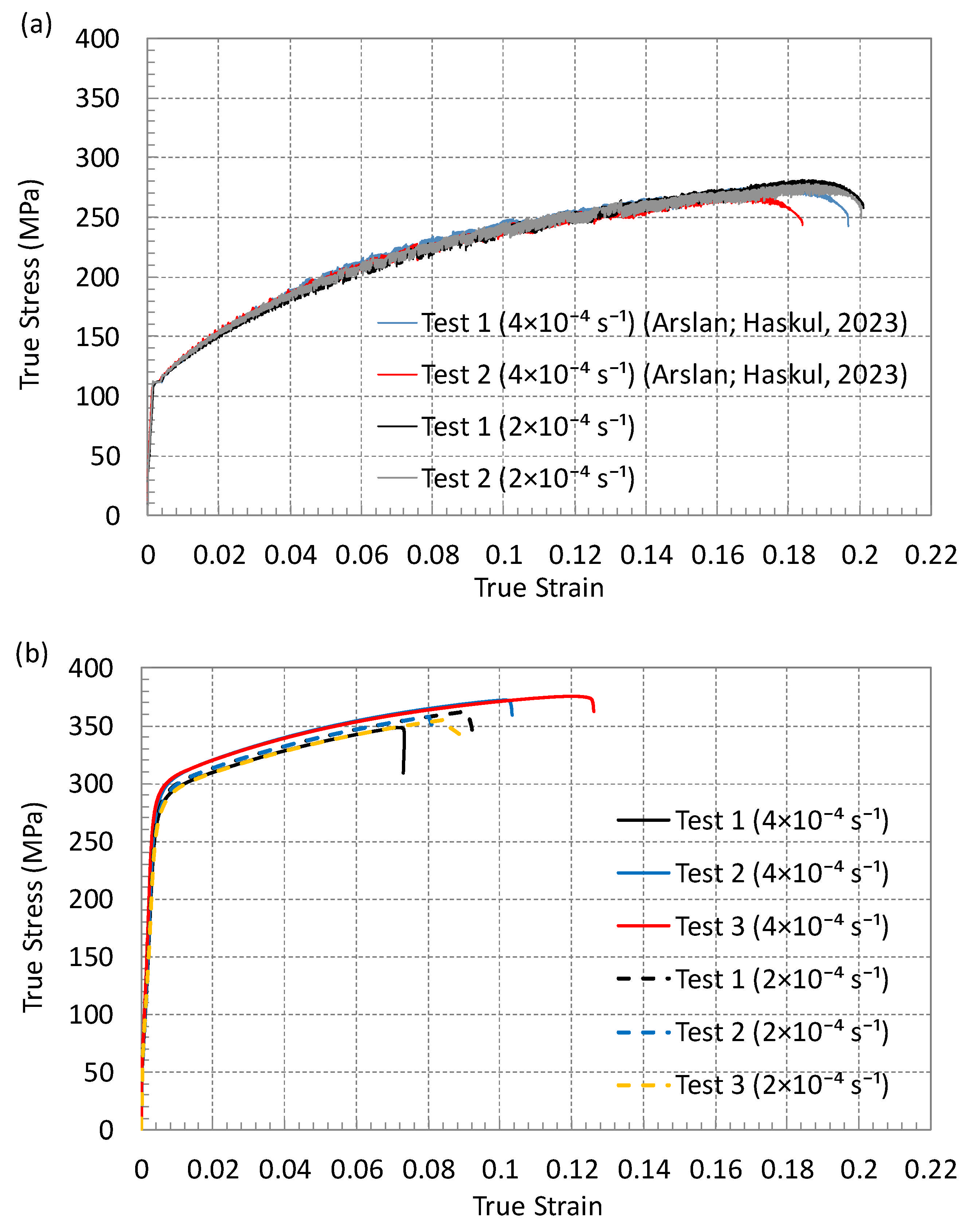
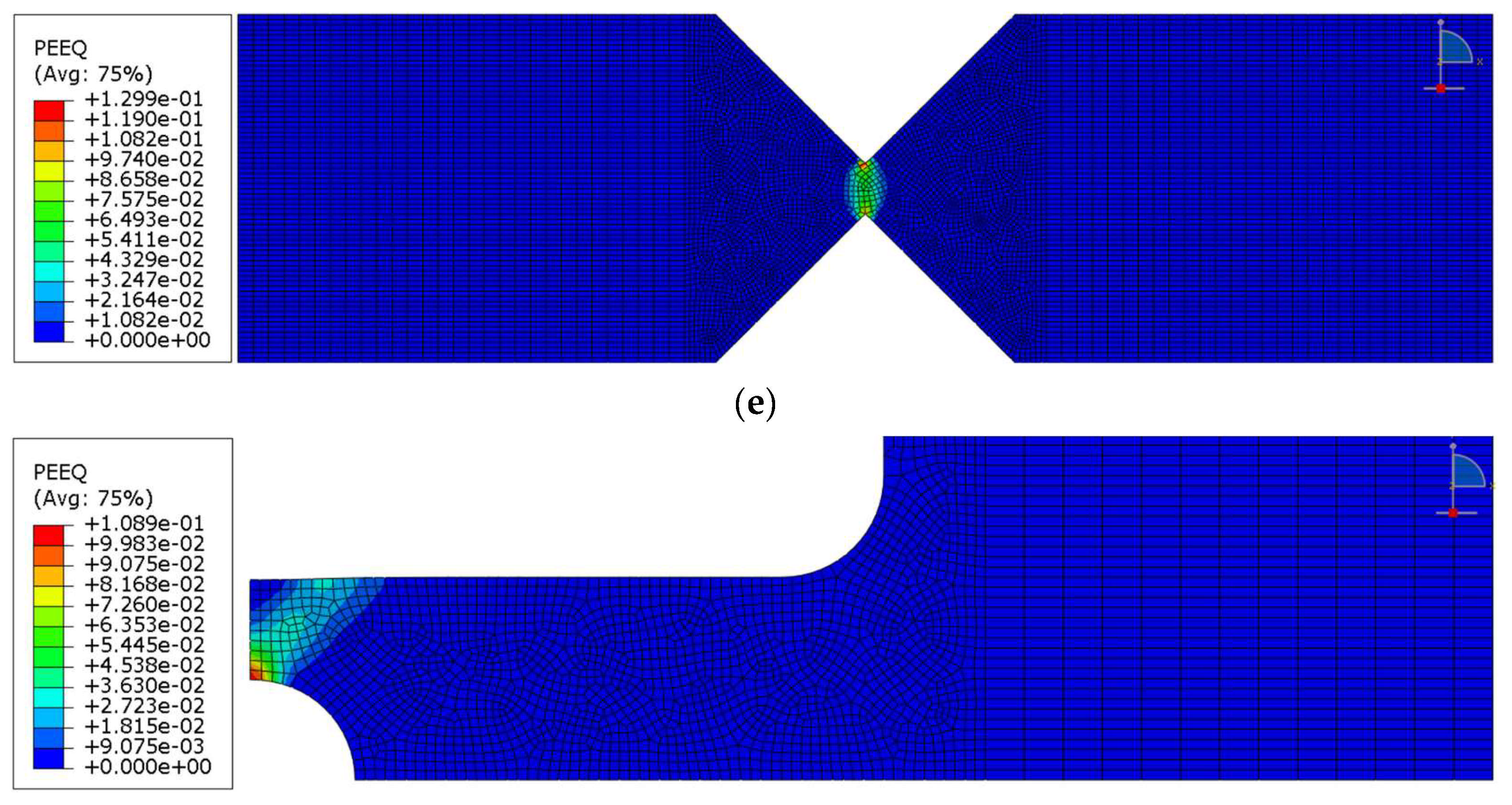
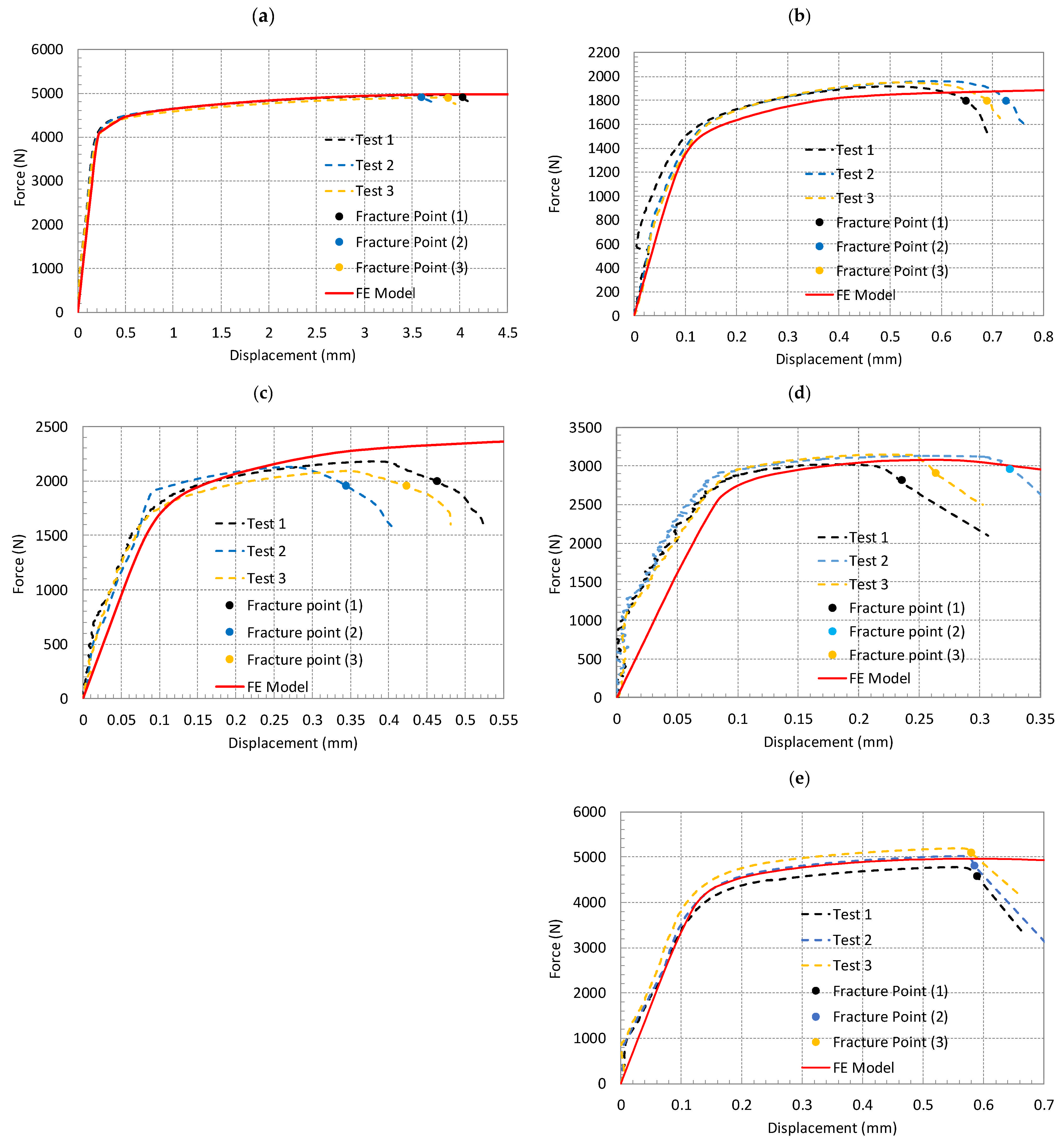
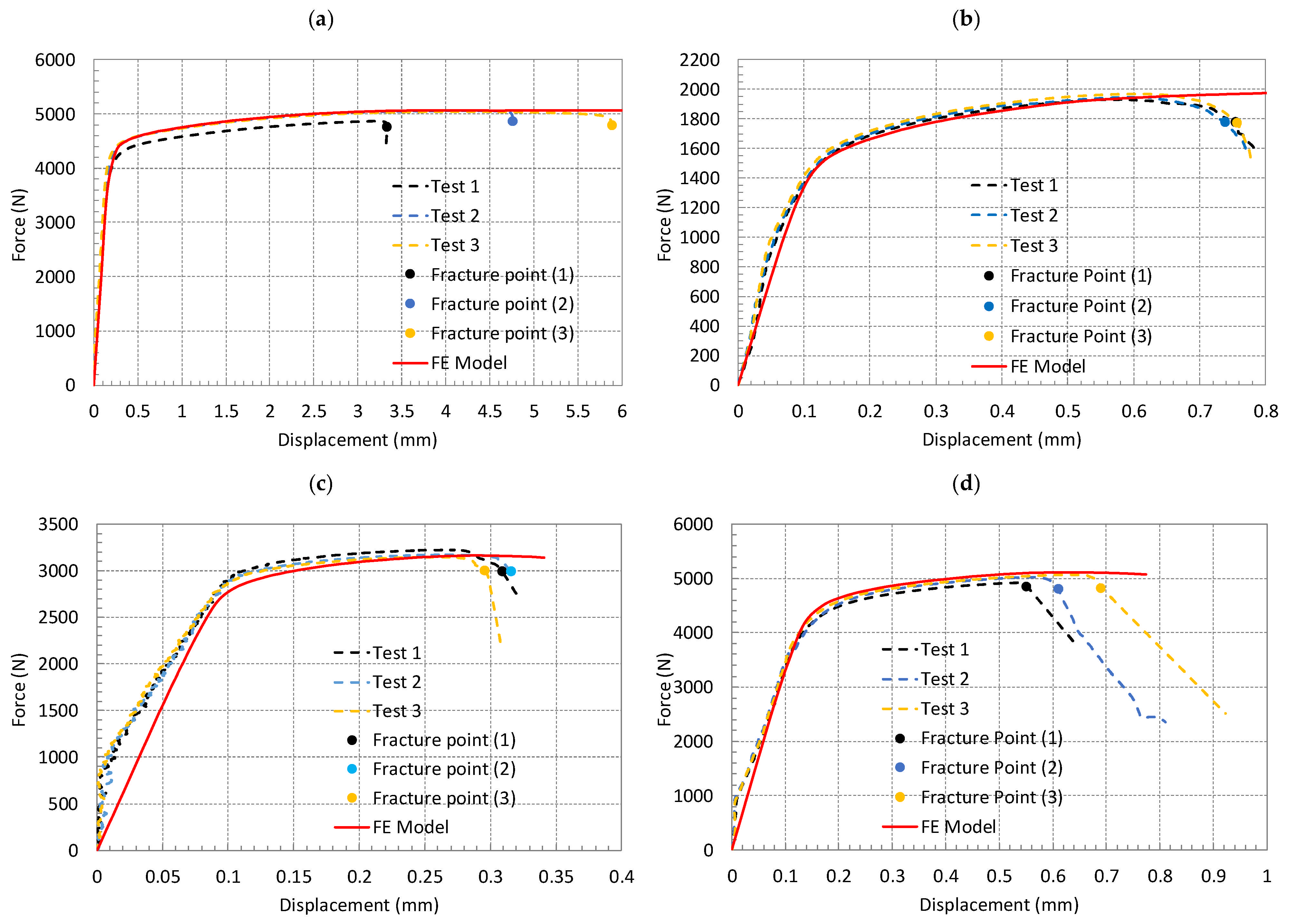
3.5. FE Simulation Validation and Fracture Initiation
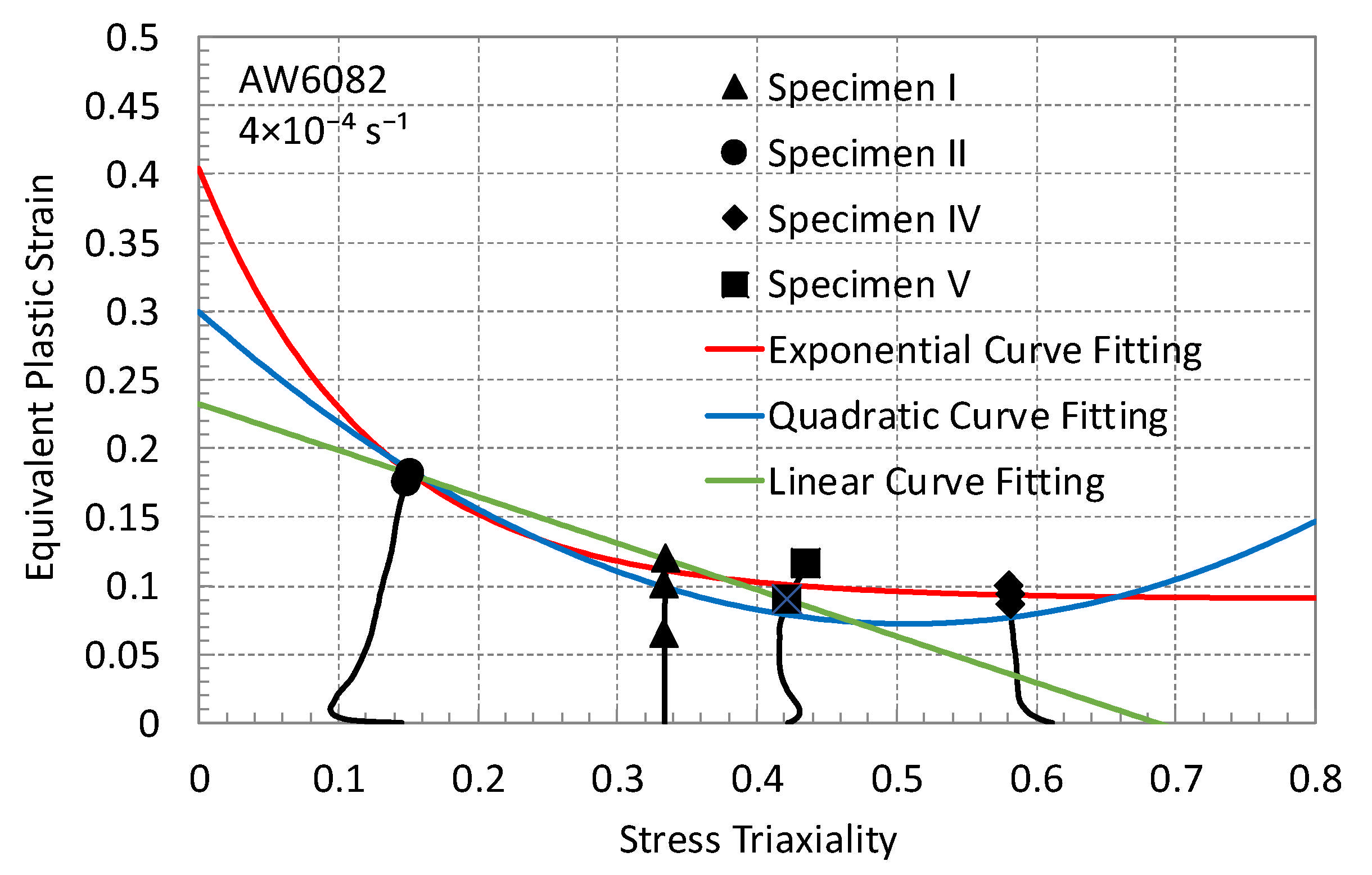
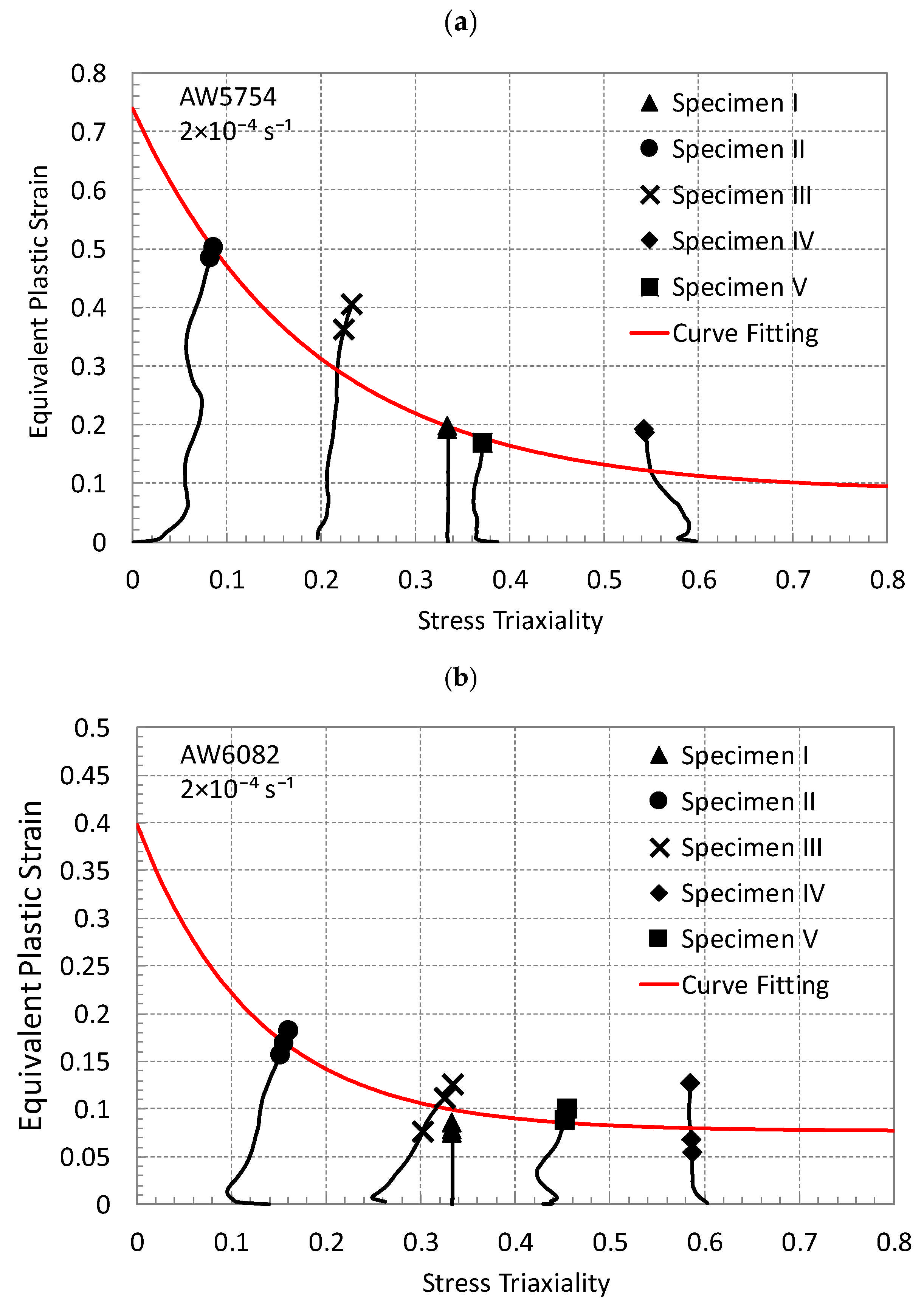
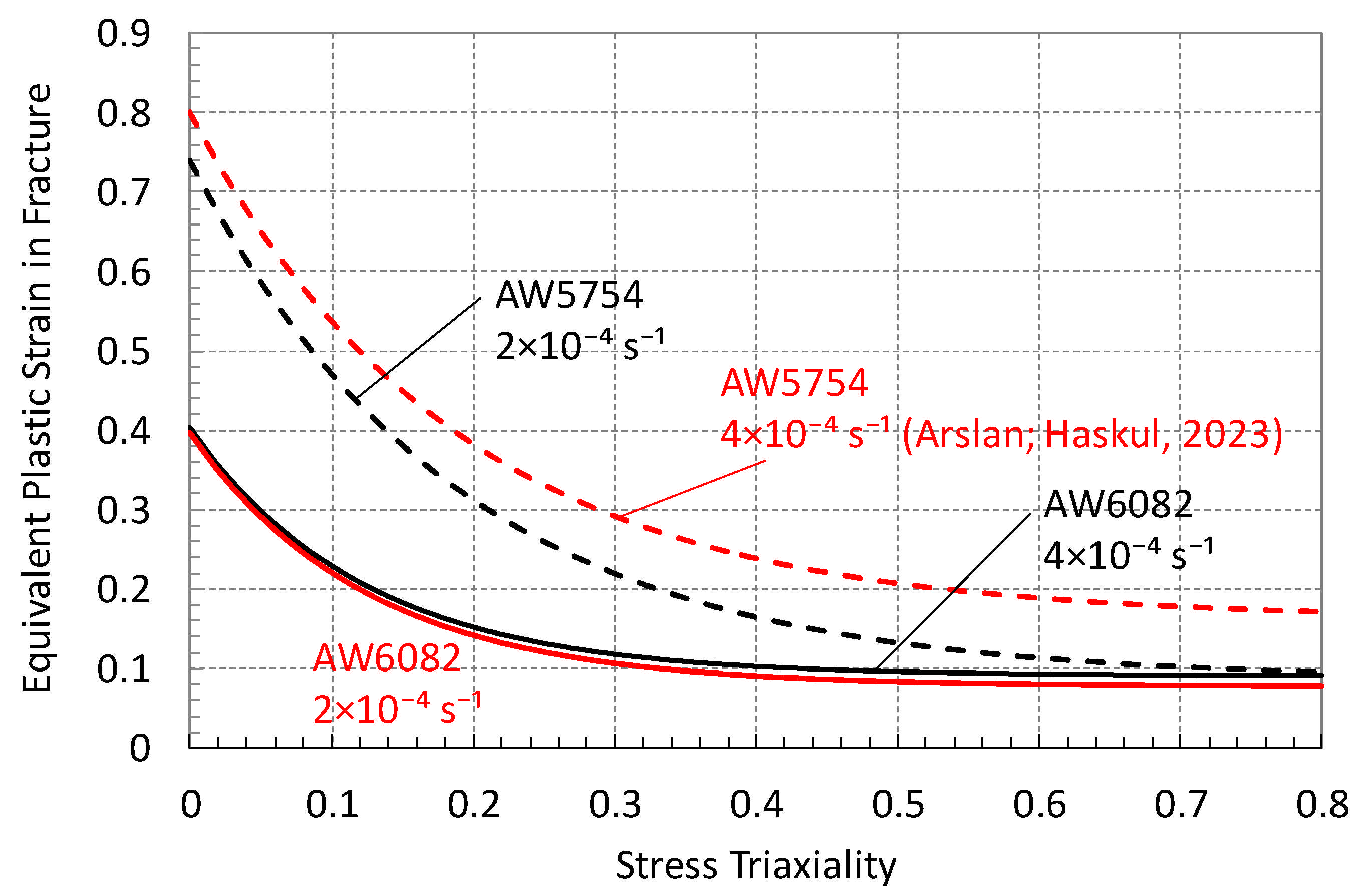
4. Determination of Triaxiality Loci
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foti, P.; Razavi, N.; Fatemi, A.; Berto, F. Multiaxial fatigue of additively manufactured metallic components: A review of the failure mechanisms and fatigue life prediction methodologies. Prog. Mater. Sci. 2023, 137, 101126. [Google Scholar] [CrossRef]
- Rolfe, S.T.; Barsom, J.M. Fracture and Fatigue Control in Structures: Applications of Fracture Mechanics; ASTM International: West Conshohocken, PA, USA, 1977. [Google Scholar]
- Jones, D.R.; Ashby, M.F. Engineering Materials 2: An Introduction to Microstructures and Processing, 4th ed.; Butterworth-Heinemann: Oxford, UK; Waltham, MA, USA, 2012. [Google Scholar]
- Trzepieciński, T.; Najm, S.M.; Oleksik, V.; Vasilca, D.; Paniti, I.; Szpunar, M. Recent developments and future challenges in incremental sheet forming of aluminium and aluminium alloy sheets. Metals 2022, 12, 124. [Google Scholar] [CrossRef]
- Baral, M.; Korkolis, Y.P. Ductile fracture under proportional and non-proportional multiaxial loading. Int. J. Solids Struct. 2021, 210, 88–108. [Google Scholar] [CrossRef]
- Lian, Y.; Wu, F.; Zhao, Q.; Han, Y.; Wang, B. Multiaxial failure behavior and fatigue life prediction of unidirectional composit laminates. Compos. Sci. Technol. 2024, 247, 110430. [Google Scholar] [CrossRef]
- Cui, J.; Wang, S.; Wang, S.; Li, G.; Wang, P.; Liang, C. The effects of strain rates on mechanical properties and failure behavior of long glass fiber reinforced thermoplastic composites. Polym. 2019, 11, 2019. [Google Scholar] [CrossRef]
- Oosterkamp, L.D.; Ivankovic, A.; Venizelos, G. High strain rate properties of selected aluminium alloys. Mater. Sci. Eng. A 2000, 278, 225–235. [Google Scholar] [CrossRef]
- Ma, H.; Huang, L.; Tian, Y.; Li, J. Effects of strain rate on dynamic mechanical behavior and microstructure evolution of 5A02-O aluminum alloy. Mater. Sci. Eng. A 2014, 606, 233–239. [Google Scholar] [CrossRef]
- Chen, X.; Peng, Y.; Peng, S.; Yao, S.; Chen, C.; Xu, P. Flow and fracture behavior of aluminum alloy 6082-T6 at different tensile strain rates and triaxialities. PLoS ONE 2017, 12, e0181983. [Google Scholar] [CrossRef]
- Sharma, S.M.; Mishra, K.; Rodriguez, O.; Whittington, W.R.; Allison, P.; Bhat, S.P.; Gokhale, A.M.; Thadhani, N.N. Effects of Strain Rate on Mechanical Properties and Fracture Mechanisms in a Dual Phase Steel. In Dynamic Behavior of Materials, Volume 1: Proceedings of the 2017 Annual Conference on Experimental and Applied Mechanics, Indianapolis, IN, USA, 12–15 June 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 209–216. [Google Scholar]
- Zhou, J.; Hayden, M.; Gao, X. An investigation of the strain rate and temperature effects on the plastic flow stress and ductile failure strain of aluminum alloys 5083-H116, 6082-T6 and a 5183 weld metal. Proc. Inst. Mech. Eng. C 2013, 227, 883–895. [Google Scholar] [CrossRef]
- Li, P.; Siviour, C.R.; Petrinic, N. The effect of strain rate, specimen geometry and lubrication on responses of aluminium AA2024 in uniaxial compression experiments. Exp. Mech. 2009, 49, 587–593. [Google Scholar] [CrossRef]
- Brünig, M.; Brenner, D.; Gerke, S. Stress state dependence of ductile damage and fracture behavior: Experiments and numerical simulations. Eng. Fract. Mech. 2015, 141, 152–169. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Kõrgesaar, M. The effect of low stress triaxialities and deformation paths on ductile fracture simulations of large shell structures. Mar. Struct. 2019, 63, 45–64. [Google Scholar] [CrossRef]
- Mehari, Z.A.; Han, J. Numerical prediction of ductile fracture during the partial heating roll forming process of DP980. Int. J. Fract. 2022, 234, 97–112. [Google Scholar] [CrossRef]
- Asadi, M.; Haji Aboutalebi, F.; Poursina, M. A comparative study of six fracture loci for DIN1623 St12 steel to predict strip tearing in a tandem cold rolling mill. Arch. Appl. Mech. 2021, 91, 1859–1878. [Google Scholar] [CrossRef]
- Kõrgesaar, M.; Romanoff, J.; Remes, H.; Palokangas, P. Experimental and numerical penetration response of laser-welded stiffened panels. Int. J. Impact Eng. 2018, 114, 78–92. [Google Scholar] [CrossRef]
- Zhou, L.; Wen, H. A new dynamic plasticity and failure model for metals. Metals 2019, 9, 905. [Google Scholar] [CrossRef]
- Mae, H.; Teng, X.; Bai, Y.; Wierzbicki, T. Comparison of ductile fracture properties of aluminum castings: Sand mold vs. metal mold. Int. J. Solids Struct. 2008, 45, 1430–1444. [Google Scholar] [CrossRef]
- Fraccaroli, L.; Mastrone, M.N.; Concli, F. Calibration of the fracture locus of an AlSi10 aluminum alloy. In High Performance and Optimum Design of Structures and Materials IV; Hernandez, S., De Wilde, W.P., Sejnoha, M., Eds.; WIT Press: Southampton, UK, 2020; pp. 3–10. [Google Scholar]
- Mae, H.; Teng, X.; Bai, Y.; Wierzbicki, T. Ductile fracture locus of AC4CH-T6 cast aluminium alloy. Arch. Comput. Mater. Sci. Surf. Eng. 2009, 1, 100–105. [Google Scholar]
- Peng, Y.; Chen, X.; Peng, S.; Chen, C.; Li, J.; Liu, G. Strain Rate-Dependent Constitutive and Low Stress Triaxiality Fracture Behavior Investigation of 6005 Al Alloy. Adv. Mater. Sci. Eng. 2018, 1, 2712937. [Google Scholar] [CrossRef]
- Arslan, E.; Haskul, M. Fracture behavior prediction of a high-strength aluminum alloy under multiaxial loading. In Proceedings of the 9th World Congress on Mechanical, Chemical, and Material Engineering, London, UK, 6–8 August 2023; pp. 143–151. [Google Scholar]
- Hong, T.; Ding, F.; Chen, F.; Zhang, H.; Zeng, Q.; Wang, J. Study on the fracture behaviour of 6061 aluminum alloy extruded tube during different stress conditions. Crystals 2023, 13, 489. [Google Scholar] [CrossRef]
- Mucha, J.; Kaščák, Ľ.; Witkowski, W. Research on the influence of the AW 5754 aluminum alloy state condition and sheet arrangements with AW 6082 aluminum alloy on the forming process and strength of the Clinch Rivet joints. Materials 2021, 14, 2980. [Google Scholar] [CrossRef] [PubMed]
- Amer, M.; Shazly, M.; Mohamed, M.; Hegazy, A.A. Ductile damage prediction of AA 5754 sheet during cold forming condition. J. Mech. Sci. Technol. 2020, 34, 4219–4228. [Google Scholar] [CrossRef]
- Chen, Y.; Clausen, A.H.; Hopperstad, O.S.; Langseth, M. Stress–strain behaviour of aluminium alloys at a wide range of strain rates. Int. J. Solids Struct. 2009, 46, 3825–3835. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, T.; Hayden, M.; Roe, C. Effects of the stress state on plasticity and ductile failure of an aluminum 5083 alloy. Int. J. Plast. 2009, 25, 2366–2382. [Google Scholar] [CrossRef]
- Kang, J.; Wilkinson, D.S.; Wu, P.D.; Bruhis, M.; Jain, M.; Embury, J.D.; Mishra, R.K. Constitutive behavior of AA5754 sheet materials at large strains. J. Eng. Mater. Technol. 2008, 130, 031004. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zheng, L.H.; Wang, Z. Characterization of Forming Limits at Fracture for Aluminum Alloy 6K21-T4 Sheets in Non-Linear Strain Paths Using a Biaxial Tension/Shear Loading Test. Int. J. Mech. Sci. 2020, 184, 105672. [Google Scholar] [CrossRef]
- Ganjiani, M.; Homayounfard, M. Development of a Ductile Failure Model Sensitive to Stress Triaxiality and Lode Angle. Int. J. Solids Struct. 2021, 225, 111066. [Google Scholar] [CrossRef]
- Zong, S.; Chen, Q.; Guo, X.; Liu, W.; Zhang, J. Micromechanics-Based Modified Ductile Fracture Criterion for Extruded Aluminum Alloys under Multi-Axial Loading. Adv. Struct. Eng. 2025, 27, 13694332251340727. [Google Scholar] [CrossRef]
- Algarni, M.; Ghazali, S.; Zwawi, M. The Emerging of Stress Triaxiality and Lode Angle in Both Solid and Damage Mechanics: A Review. Mech. Solids 2021, 56, 787–806. [Google Scholar] [CrossRef]
- Lee, J.; Bong, H.J.; Park, H.; Kim, D. Micromechanics-Based Modeling of Plastic and Ductile Fracture of Aluminum Alloy 2024-O. Eng. Fract. Mech. 2022, 261, 108213. [Google Scholar] [CrossRef]
- Nouira, M.; Oliveira, M.C.; Khalfallah, A.; Alves, J.L.; Menezes, L.F. Comparative fracture prediction study for two materials under a wide range of stress states using seven uncoupled models. Eng. Frac. Mech. 2023, 279, 108952. [Google Scholar] [CrossRef]
- Sagar, S.; Singh, N.K.; Maurya, N.S. Strain rate behaviour and notch sensitivity of Aluminium 6082-T6 alloy under tensile loads. UPB Sci. Bull. Series B 2023, 85, 202–212. [Google Scholar]
- Park, S.J.; Heogh, W.; Yang, J.; Kang, S.; Jeong, W.; Lee, H.; Jang, T.S.; Jung, H.D.; Jahazi, M.; Han, S.C.; et al. Meta-structure of amorphous-inspired 65.1 Co28. 2Cr5. 3Mo lattices augmented by artificial intelligence. Adv. Compos. Hybrid Mater. 2024, 7, 224. [Google Scholar] [CrossRef]
- Andrade, F.; Conde, S.; Feucht, M.; Helbig, M.; Haufe, A. Estimation of stress triaxiality from optically measured strain fields. In Proceedings of the 12th European LS-DYNA Conference, Koblenz, Germany, 14–16 May 2019. [Google Scholar]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture: With Special Emphasis on the Effects of Hydrostatic Pressure; Harvard University Press: Cambridge, MA, USA, 1964. [Google Scholar]
- ASTM International. Committee E-28 on Mechanical Testing. In Standard Test Methods for Tension Testing of Metallic Materials; ASTM international: West Conshohocken, PA, USA, 2021. [Google Scholar]
- Dassault Systèmes. ABAQUS 2022 Documentation; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2022. [Google Scholar]
- Lapidus, L.; Pinder, G.F. Numerical Solution of Partial Differential Equations in Science and Engineering; John Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Abushawashi, Y.; Xiao, X.; Astakhov, V. A novel approach for determining material constitutive parameters for a wide range of triaxiality under plane strain loading conditions. Int. J. Mech. Sci. 2013, 74, 133–142. [Google Scholar] [CrossRef]







| Element Size (mm) | Node | Stress Triaxiality | Relative Error (%) | Equivalent Plastic Strain | Relative Error (%) | Computation Time (s) |
|---|---|---|---|---|---|---|
| 0.25 | 194,921 | 0.367898 | - | 0.237044 | - | 14,444 |
| 0.35 | 77,017 | 0.371302 | 0.93 | 0.247407 | 4.37 | 2473.4 |
| 0.5 | 25,134 | 0.374208 | 1.72 | 0.251759 | 6.21 | 386.90 |
| 0.75 | 7744 | 0.388926 | 5.72 | 0.26948 | 13.68 | 71.8 |
| 1.0 | 3408 | 0.396468 | 7.77 | 0.305871 | 29.04 | 26.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haskul, M.; Arslan, E. Fracture Initiation in Aluminum Alloys Under Multiaxial Loading at Various Low Strain Rates. Metals 2025, 15, 785. https://doi.org/10.3390/met15070785
Haskul M, Arslan E. Fracture Initiation in Aluminum Alloys Under Multiaxial Loading at Various Low Strain Rates. Metals. 2025; 15(7):785. https://doi.org/10.3390/met15070785
Chicago/Turabian StyleHaskul, Mehmet, and Eray Arslan. 2025. "Fracture Initiation in Aluminum Alloys Under Multiaxial Loading at Various Low Strain Rates" Metals 15, no. 7: 785. https://doi.org/10.3390/met15070785
APA StyleHaskul, M., & Arslan, E. (2025). Fracture Initiation in Aluminum Alloys Under Multiaxial Loading at Various Low Strain Rates. Metals, 15(7), 785. https://doi.org/10.3390/met15070785






