Numerical Analysis of Aspect Ratio Effects on the Mechanical Behavior of Perforated Steel Plates
Abstract
1. Introduction
2. Materials and Methods
2.1. Buckling and Post-Buckling of Plates
2.2. Computational Model
2.3. Constructal Design Method
2.4. AH-36 and AISI 4130 Steel
2.5. Case Study
3. Results and Discussion
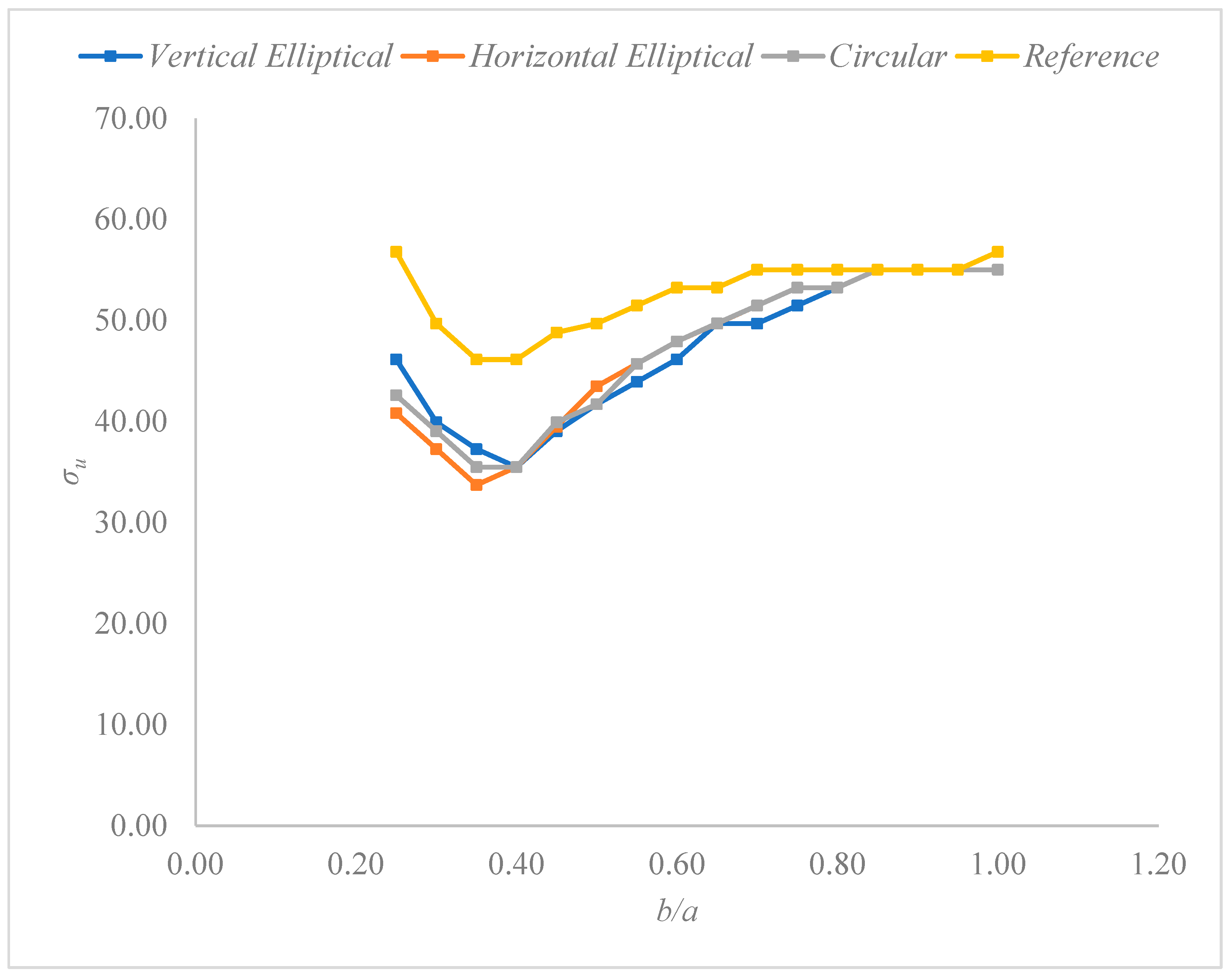
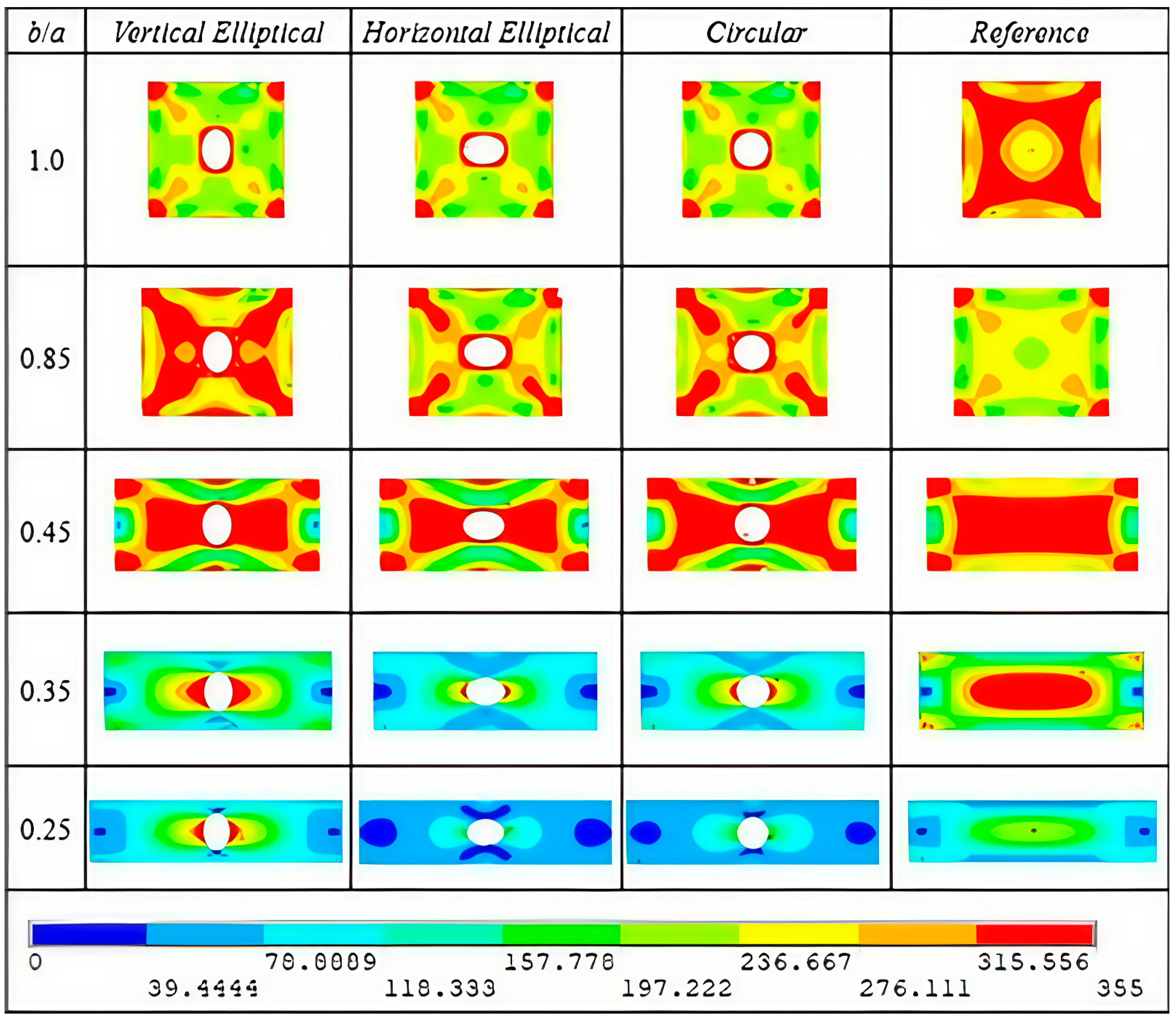
3.1. Ultimate Stress Analysis for AH-36 Steel
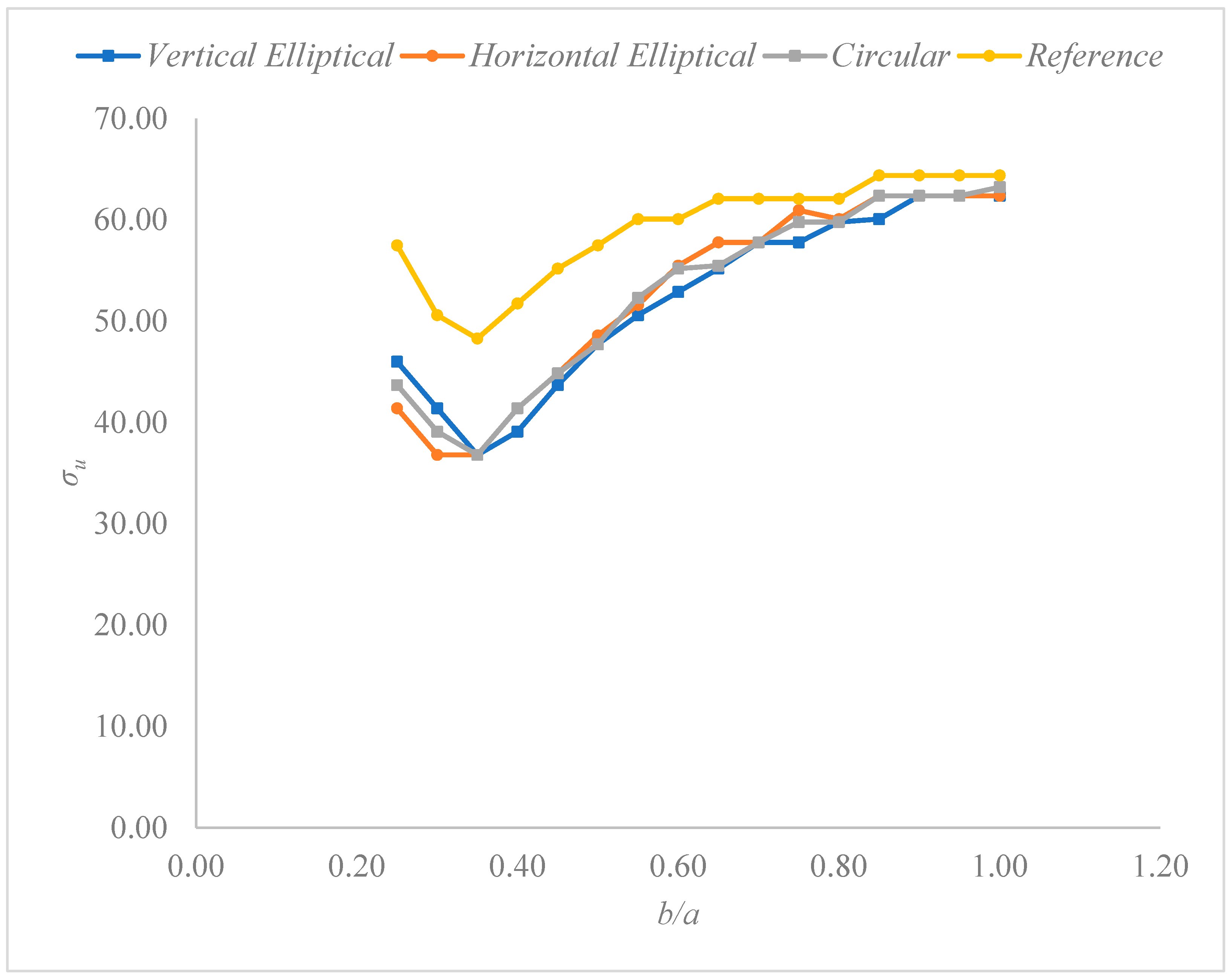
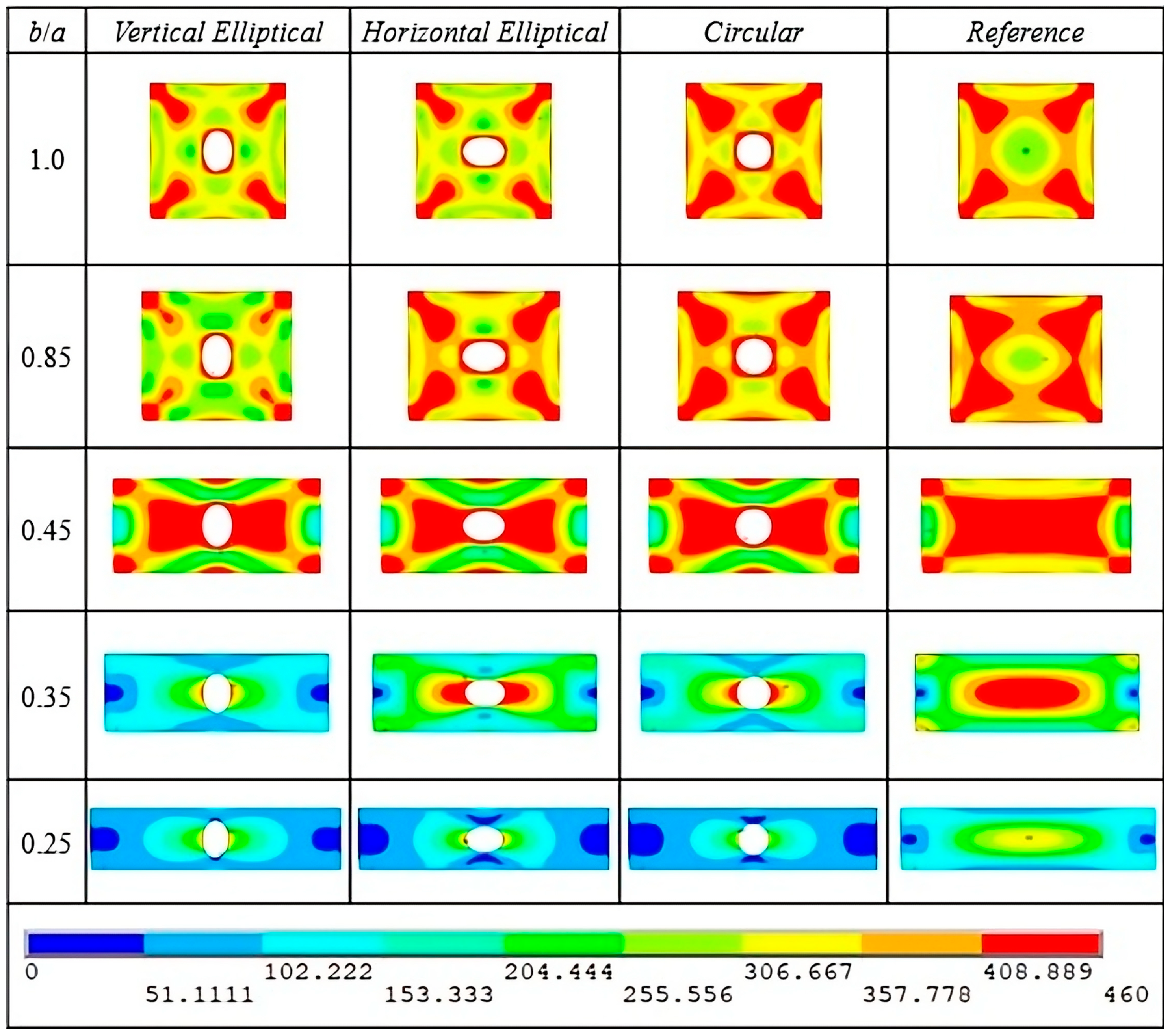
3.2. Ultimate Stress Analysis for AISI 4130 Steel
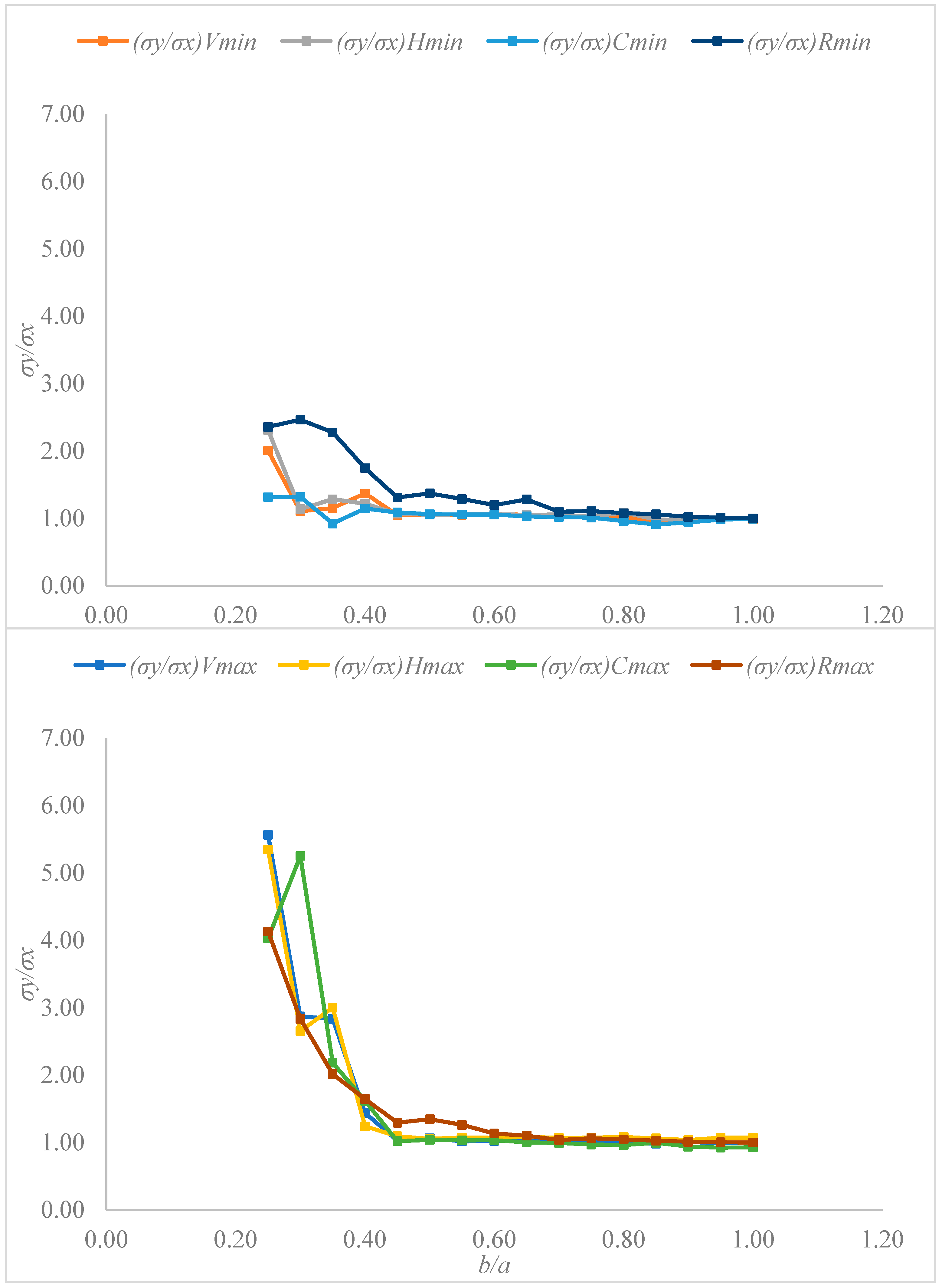
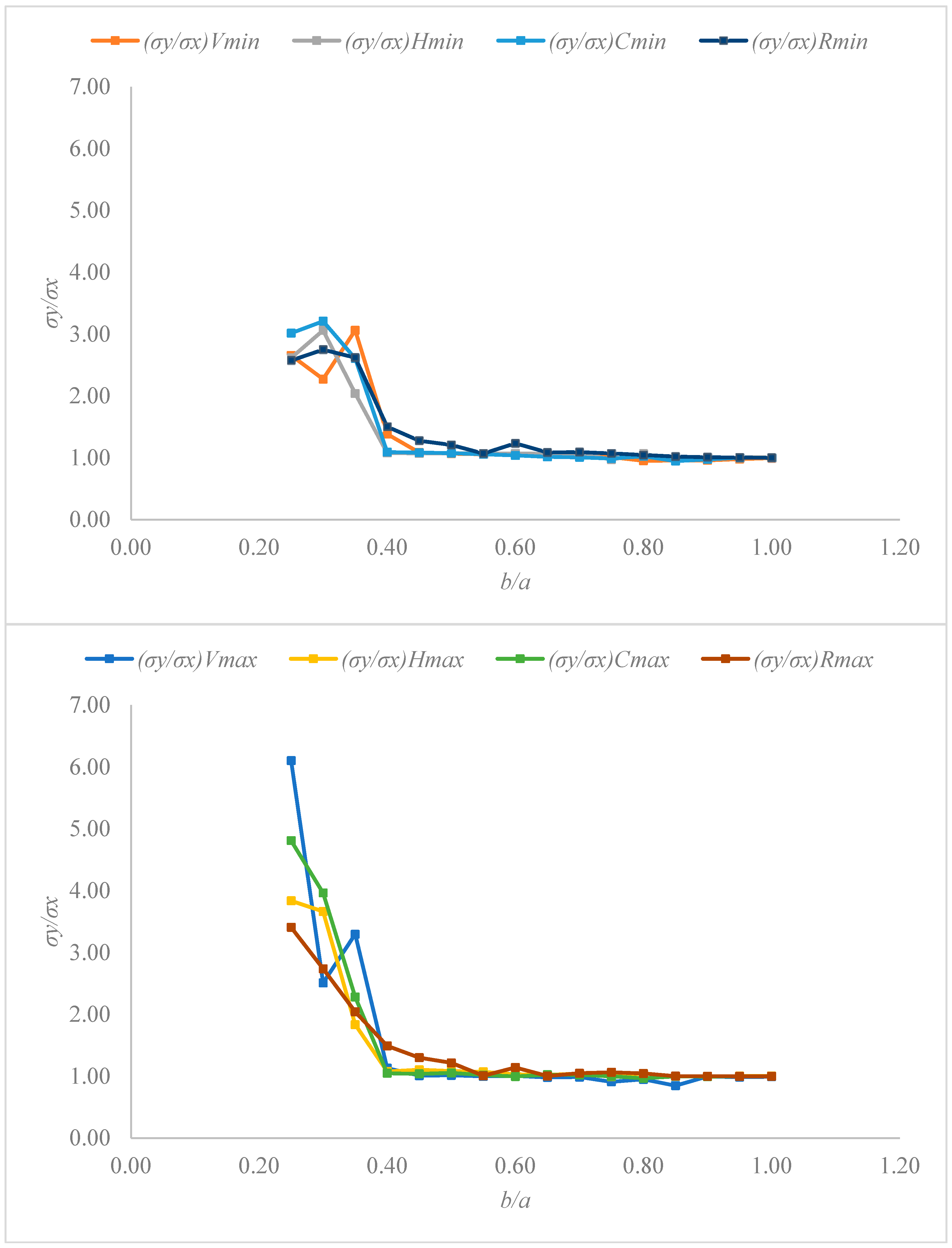
3.3. Stress Component Analysis Through the Ratio σy/σx
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| b/a | Vertical Elliptical (MPa) | Horizontal Elliptical (MPa) | Circular (MPa) | Reference (MPa) |
|---|---|---|---|---|
| 1.00 | 55.03 | 55.03 | 55.03 | 56.80 |
| 0.95 | 55.03 | 55.03 | 55.03 | 55.03 |
| 0.90 | 55.03 | 55.03 | 55.03 | 55.03 |
| 0.85 | 55.03 | 55.03 | 55.03 | 55.03 |
| 0.80 | 53.25 | 53.25 | 53.25 | 55.03 |
| 0.75 | 51.48 | 53.25 | 53.25 | 55.03 |
| 0.70 | 49.70 | 51.48 | 51.48 | 55.03 |
| 0.65 | 49.70 | 49.70 | 49.72 | 53.25 |
| 0.60 | 46.15 | 47.93 | 47.93 | 53.25 |
| 0.55 | 43.93 | 45.71 | 45.71 | 51.48 |
| 0.50 | 41.71 | 43.49 | 41.71 | 49.70 |
| 0.45 | 39.05 | 39.49 | 39.94 | 48.81 |
| 0.40 | 35.50 | 35.50 | 35.50 | 46.15 |
| 0.35 | 37.28 | 33.73 | 35.50 | 46.15 |
| 0.30 | 39.94 | 37.28 | 39.05 | 49.70 |
| 0.25 | 46.15 | 40.83 | 42.60 | 56.80 |
| b/a | Vertical Elliptical (MPa) | Horizontal Elliptical (MPa) | Circular (MPa) | Reference (MPa) |
|---|---|---|---|---|
| 1.00 | 62.39 | 62.39 | 63.25 | 64.40 |
| 0.95 | 62.39 | 62.39 | 62.39 | 64.40 |
| 0.90 | 62.39 | 62.39 | 62.39 | 64.40 |
| 0.85 | 60.09 | 62.39 | 62.39 | 64.40 |
| 0.80 | 59.80 | 60.09 | 59.80 | 62.10 |
| 0.75 | 57.79 | 60.95 | 59.80 | 62.10 |
| 0.70 | 57.79 | 57.79 | 57.79 | 62.10 |
| 0.65 | 55.20 | 57.79 | 55.49 | 62.10 |
| 0.60 | 52.90 | 55.49 | 55.20 | 60.09 |
| 0.55 | 50.60 | 51.61 | 52.33 | 60.09 |
| 0.50 | 47.73 | 48.59 | 47.73 | 57.50 |
| 0.45 | 43.70 | 44.85 | 44.85 | 55.20 |
| 0.40 | 39.10 | 41.40 | 41.40 | 51.75 |
| 0.35 | 36.80 | 36.80 | 36.80 | 48.30 |
| 0.30 | 41.40 | 36.80 | 39.10 | 50.60 |
| 0.25 | 46.00 | 41.40 | 43.70 | 57.50 |
| b/a | (σy/σx)Vmin | (σy/σx)Vmax | (σy/σx)Hmin | (σy/σx)Hmax | (σy/σx)Cmin | (σy/σx)Cmax | (σy/σx)Rmin | (σy/σx)Rmax |
|---|---|---|---|---|---|---|---|---|
| 1.00 | 0.99 | 1.01 | 1.00 | 1.07 | 0.99 | 0.93 | 1.00 | 1.00 |
| 0.95 | 1.00 | 0.99 | 0.99 | 1.07 | 0.98 | 0.93 | 1.01 | 1.01 |
| 0.90 | 0.98 | 1.01 | 0.98 | 1.04 | 0.94 | 0.94 | 1.02 | 1.01 |
| 0.85 | 0.94 | 0.98 | 0.98 | 1.06 | 0.91 | 1.00 | 1.06 | 1.03 |
| 0.80 | 1.02 | 1.01 | 1.09 | 1.08 | 0.96 | 0.96 | 1.08 | 1.05 |
| 0.75 | 1.02 | 1.03 | 1.02 | 1.07 | 1.01 | 0.97 | 1.11 | 1.06 |
| 0.70 | 1.03 | 1.03 | 1.06 | 1.07 | 1.02 | 0.99 | 1.10 | 1.04 |
| 0.65 | 1.05 | 1.05 | 1.05 | 1.09 | 1.03 | 1.00 | 1.28 | 1.10 |
| 0.60 | 1.06 | 1.02 | 1.06 | 1.07 | 1.05 | 1.04 | 1.20 | 1.13 |
| 0.55 | 1.05 | 1.02 | 1.06 | 1.07 | 1.06 | 1.03 | 1.29 | 1.26 |
| 0.50 | 1.06 | 1.07 | 1.05 | 1.05 | 1.06 | 1.04 | 1.37 | 1.35 |
| 0.45 | 1.05 | 1.03 | 1.07 | 1.09 | 1.09 | 1.02 | 1.31 | 1.30 |
| 0.40 | 1.37 | 1.44 | 1.22 | 1.24 | 1.15 | 1.62 | 1.74 | 1.65 |
| 0.35 | 1.15 | 2.83 | 1.28 | 3.00 | 0.92 | 2.19 | 2.28 | 2.02 |
| 0.30 | 1.10 | 2.87 | 1.14 | 2.65 | 1.32 | 5.26 | 2.46 | 2.84 |
| 0.25 | 2.01 | 5.57 | 2.31 | 5.35 | 1.31 | 4.03 | 2.36 | 4.13 |
| b/a | (σy/σx)Vmin | (σy/σx)Vmax | (σy/σx)Hmin | (σy/σx)Hmax | (σy/σx)Cmin | (σy/σx)Cmax | (σy/σx)Rmin | (σy/σx)Rmax |
|---|---|---|---|---|---|---|---|---|
| 1.00 | 1.00 | 0.99 | 1.01 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 |
| 0.95 | 0.98 | 0.99 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 0.90 | 0.96 | 1.00 | 0.99 | 0.99 | 0.97 | 0.99 | 1.01 | 1.00 |
| 0.85 | 0.96 | 0.85 | 0.97 | 1.00 | 0.95 | 1.00 | 1.02 | 1.00 |
| 0.80 | 0.95 | 0.95 | 1.07 | 1.05 | 1.02 | 0.97 | 1.04 | 1.04 |
| 0.75 | 1.01 | 0.91 | 0.97 | 0.99 | 0.99 | 1.00 | 1.07 | 1.06 |
| 0.70 | 1.03 | 0.99 | 1.07 | 1.04 | 1.01 | 1.02 | 1.09 | 1.05 |
| 0.65 | 1.04 | 0.98 | 1.06 | 1.02 | 1.02 | 1.03 | 1.09 | 1.00 |
| 0.60 | 1.06 | 1.01 | 1.07 | 1.03 | 1.04 | 1.00 | 1.23 | 1.14 |
| 0.55 | 1.06 | 1.00 | 1.07 | 1.07 | 1.06 | 1.02 | 1.07 | 1.01 |
| 0.50 | 1.07 | 1.02 | 1.07 | 1.08 | 1.08 | 1.05 | 1.21 | 1.22 |
| 0.45 | 1.08 | 1.01 | 1.07 | 1.10 | 1.08 | 1.04 | 1.28 | 1.30 |
| 0.40 | 1.38 | 1.13 | 1.08 | 1.08 | 1.09 | 1.05 | 1.50 | 1.49 |
| 0.35 | 3.06 | 3.30 | 2.04 | 1.83 | 2.61 | 2.28 | 2.62 | 2.04 |
| 0.30 | 2.27 | 2.51 | 3.06 | 3.66 | 3.21 | 3.96 | 2.75 | 2.74 |
| 0.25 | 2.65 | 6.10 | 2.62 | 3.84 | 3.02 | 4.81 | 2.57 | 3.41 |
References
- Jones, R.M. Buckling of Bars, Plates and Shells; Bull Ridge Publishing: Blacksburg, VA, USA, 2006. [Google Scholar]
- Chajes, A. Principles of Structural Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1974. [Google Scholar]
- Szilard, R. Theories and Applications of Plate Analysis: Classical Numerical and Engineering Methods; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Åkesson, B. Plate Buckling in Bridges and Other Structures; Taylor & Francis Group: London, UK, 2007. [Google Scholar]
- Shojaee, T.; Mohammadi, B.; Madoliat, R.; Salimi-Majd, D. Development of a finite strip method for efficient prediction of buckling and post-buckling in composite laminates containing a cutout with/without stiffener. Compos. Struct. 2019, 210, 538–552. [Google Scholar] [CrossRef]
- Da Silveira, T.; Fragasssa, C.; Rocha, L.A.O.; Dos Santos, E.D.; Isoldi, L.A. Geometric Investigation of Thin Perforated Steel Plates Under Biaxial Elasto-Plastic Buckling by using Constructal Design. Rep. Mech. Eng. 2024, 5, 43–67. [Google Scholar]
- Asemi, K.; Ashrafi, H.; Shariyat, M. Three-dimensional stress and free vibration analyses of functionally graded plates with circular holes by the use of the graded finite element method. J. Appl. Mech. Tech. Phys. 2016, 57, 690–700. [Google Scholar] [CrossRef]
- Liang, K.; Yin, Z. Investigation on nonlinear buckling performance of the optimized wing structure under the realistic flight cases. Aerosp. Sci. Technol. 2023, 139, 108416. [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, Y.; Tian, S.; Takagi, J.; Li, Z.; Fang, D.; Fang, X. Performance of novel perforated double-core steel-plate assembled buckling-restrained braces. J. Build. Eng. 2024, 82, 108326. [Google Scholar] [CrossRef]
- Figueiredo, J.; Simões, F.; da Costa, A.P. Unilateral buckling of thin plates by complementarity eigenvalue analyses. Thin-Walled Struct. 2024, 205, 112387. [Google Scholar] [CrossRef]
- Ghorbanhosseini, S.; Yaghoubi, S.; Bahrambeigi, M.R. A Comprehensive Study on the Effects of the Boundary Conditions on the Elastic Buckling Capacity of a Perforated Plate. Int. J. Adv. Des. Manuf. Technol. 2021, 14, 45–53. [Google Scholar] [CrossRef]
- Gore, R.; Lokavarapu, B.R. Effect of Elliptical Cutout on Buckling Load for Isotropic Thin Plate. In Innovations in Mechanical Engineering: Select Proceedings of ICIME 2021; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Rocha, L.A.; Lorente, S.; Bejan, A. Constructal theory in heat transfer. In Handbook of Thermal Science and Engineering; Springer: Cham, Switzerland, 2018; pp. 329–360. [Google Scholar] [CrossRef]
- dos Santos, E.D.; Isoldi, L.A.; Gomes, M.d.N.; Rocha, L.A. The constructal design applied to renewable energy systems. In Sustainable Energy Technologies; CRC Press: Boca Raton, FL, USA, 2017; pp. 45–62. [Google Scholar] [CrossRef]
- Da Silveira, T.; Pinto, V.T.; Neufeld, J.P.S.; Pavlovic, A.; Rocha, L.A.O.; Dos Santos, E.D.; Isoldi, L.A. Applicability evidence of constructal design in structural engineering: Case study of biaxial elasto-plastic buckling of square steel plates with elliptical cutout. J. Appl. Comput. Mech. 2021, 7, 922–934. [Google Scholar]
- Trahair, N.S.; Bradford, M.; Nethercot, D.; Gardner, L. The Behavior and Design of Steel Structures to EC3; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y. Experimental and Numerical Analysis of Structural Capacity of Perforated Stiffened Plates. J. Mar. Sci. Eng. 2023, 11, 842. [Google Scholar] [CrossRef]
- Dong, J.; Ma, X.; Zhuge, Y.; Mills, J.E. Local buckling of thin plate on tensionless elastic foundations under interactive uniaxial compression and shear. Theor. Appl. Mech. Lett. 2018, 8, 75–82. [Google Scholar] [CrossRef]
- Baumgardt, G.R.; Fragassa, C.; Rocha, L.A.O.; Dos Santos, E.D.; Da Silveira, T.; Isoldi, L.A. Computational model verification and validation of elastoplastic buckling due to combined loads of thin plates. Metals 2023, 13, 731. [Google Scholar] [CrossRef]
- Milazzo, A.; Benedetti, I.; Gulizzi, V. An extended Ritz formulation for buckling and post-buckling analysis of cracked multilayered plates. Compos. Struct. 2018, 201, 980–994. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B. A novel one-variable first-order shear deformation theory for biaxial buckling of a size-dependent plate based on Eringen’s nonlocal differential law. World J. Eng. 2018, 15, 633–645. [Google Scholar] [CrossRef]
- da Silveira, T.; Baumgardt, G.; Rocha, L.; dos Santos, E.; Isoldi, L. Numerical simulation and constructal design applied to biaxial elastic buckling of plates of composite material used in naval structures. Compos. Struct. 2022, 290, 115503. [Google Scholar] [CrossRef]
- Farajpour, M.; Shahidi, A.; Farajpour, A. A nonlocal continuum model for the biaxial buckling analysis of composite nanoplates with shape memory alloy nanowires. Mater. Res. Express 2018, 5, 035026. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A.; Malek, N.G. Optimum stacking sequence design of composite laminates for maximum buckling load capacity using parameter-less optimization algorithms. Eng. Comput. 2019, 35, 813–832. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A.; Malek, N.G. Buckling load of laminated composite plates using three variants of the biogeography-based optimization algorithm. Acta Mech. 2018, 229, 1551–1566. [Google Scholar] [CrossRef]
- Moita, J.S.; Araújo, A.L.; Correia, V.F.; Soares, C.M.M.; Herskovits, J. Material distribution and sizing optimization of functionally graded plate-shell structures. Compos. Part B Eng. 2018, 142, 263–272. [Google Scholar] [CrossRef]
- Ehsani, A.; Dalir, H. Multi-objective optimization of composite angle grid plates for maximum buckling load and minimum weight using genetic algorithms and neural networks. Compos. Struct. 2019, 229, 111450. [Google Scholar] [CrossRef]
- da Silva, C.C.C.; Helbig, D.; Cunha, M.L.; dos Santos, E.D.; Rocha, L.A.O.; Real, M.d.V.; Isoldi, L.A. Numerical buckling analysis of thin steel plates with centered hexagonal perforation through constructal design method. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 309. [Google Scholar] [CrossRef]
- Hu, H.-S.; Fang, P.-P.; Liu, Y.; Guo, Z.-X.; Shahrooz, B.M. Local buckling of steel plates in composite members with tie bars under axial compression. Eng. Struct. 2020, 205, 110097. [Google Scholar] [CrossRef]
- Zureick, A.-H. On the buckling of an isotropic rectangular plate uniformly compressed on two simply supported edges and with two free unloaded edges. Thin-Walled Struct. 2018, 124, 180–183. [Google Scholar] [CrossRef]
- Lima, J.P.S.; Cunha, M.L.; dos Santos, E.D.; Rocha, L.A.O.; de Vasconcellos Real, M.; Isoldi, L.A. Constructal Design for the ultimate buckling stress improvement of stiffened plates submitted to uniaxial compressive load. Eng. Struct. 2020, 203, 109883. [Google Scholar] [CrossRef]
- Yuan, T.; Yang, Y.; Kong, X.; Wu, W. Similarity criteria for the buckling process of stiffened plates subjected to compressive load. Thin-Walled Struct. 2021, 158, 107183. [Google Scholar] [CrossRef]
- Falkowicz, K.; Debski, H. Stability analysis of thin-walled composite plate in unsymmetrical configuration subjected to axial load. Thin-Walled Struct. 2021, 158, 107203. [Google Scholar] [CrossRef]
- Hou, J.; Guo, L.; Yan, J. Steel plate–restraining panel interaction behavior in buckling-restrained steel plate shear walls. Thin-Walled Struct. 2021, 169, 108348. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y. Statics, vibration, and buckling of sandwich plates with metamaterial cores characterized by negative thermal expansion and negative Poisson’s ratio. Appl. Math. Mech. 2023, 44, 1457–1486. [Google Scholar] [CrossRef]
- Jin, Q.; Leng, L.; Yang, S. Buckling analysis of composite plates surface bonded with graphene-reinforced piezoelectric actuators. Polym. Compos. 2024, 45, 1793–1809. [Google Scholar] [CrossRef]
- Park, J.-S.; Yi, M.-S. Root Causes of Thin-Plate Buckling Damage at the Aft-End in Crude Oil Tanker and Verification through Buckling Analysis. Metals 2024, 14, 158. [Google Scholar] [CrossRef]
- Cheng, B.; Zhao, J. Strengthening of perforated plates under uniaxial compression: Buckling analysis. Thin-Walled Struct. 2010, 48, 905–914. [Google Scholar] [CrossRef]
- Mohammadzadeh, B.; Choi, E.; Kim, W.J. Comprehensive investigation of buckling behavior of plates considering effects of holes. Struct. Eng. Mech. 2018, 68, 261–275. [Google Scholar] [CrossRef]
- El-Sawy, K.M.; Martini, M.I. Stability of biaxially loaded square plates with single central holes. Ships Offshore Struct. 2010, 5, 283–293. [Google Scholar] [CrossRef]
- Wysmulski, P. Analysis of the Effect of an Open Hole on the Buckling of a Compressed Composite Plate. Materials 2024, 17, 1081. [Google Scholar] [CrossRef] [PubMed]
- Deng, C.; Qi, X.; Liu, Y. Numerical study on equilibrium stability of objects in fluid flow—A case study on constructal law. Case Stud. Therm. Eng. 2019, 15, 100539. [Google Scholar] [CrossRef]
- Vaghefi, R. Elastoplastic buckling analysis of FG skew plates using a 3D meshfree Tchebychev-radial point interpolation approach. Eng. Struct. 2024, 311, 118162. [Google Scholar] [CrossRef]
- Vaghefi, R. Three-dimensional elastoplastic post-buckling analysis of functionally graded plates using a novel meshfree Tchebychev-radial point interpolation approach. Mech. Based Des. Struct. Mach. 2024, 53, 1120–1143. [Google Scholar] [CrossRef]
- Amor, M.B.H.; Bettaieb, M.B.; Mezlini, S.; Abed-Meraim, F. Development and implementation of a new computational strategy for the prediction of elastoplastic buckling. Int. J. Appl. Mech. 2024, 16, 2450091. [Google Scholar]
- Shanmugam, N.; Narayanan, R. Ultimate Strength of Biaxially Loaded Plates. In Stability and Ductility of Steel Structures (SDSS’97); Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar] [CrossRef]
- Pavlovic, A.; Fragassa, C.; Minak, G. Analiza izvijanja teleskopske dizalice: Teorijska i numerička procjena kliznih oslonaca. Teh. Vjesn. 2017, 24, 729–735. [Google Scholar] [CrossRef]
- Fragassa, C.; Minak, G.; Pavlovic, A. Measuring deformations in the telescopic boom under static and dynamic load conditions. Facta Univ. Ser. Mech. Eng. 2020, 18, 315–328. [Google Scholar] [CrossRef]
- ANSYS. Mechanical APDL 2024R2; ANSYS Inc.: Canonsburg, PA, USA, 2024. [Google Scholar]
- Ota, N.S.N. O Elemento Finito T6-3i na Análise de Placas e Dinâmica de Cascas. Master’s Thesis, Escola Politécnica da Universidade de São Paulo, São Paulo, Brazil, 2016. [Google Scholar][Green Version]
- Vieira, R.L.; Baumgardt, G.R.; Dos Santos, E.D.; Rocha, L.A.O.; Da Silveira, T.; Lima, J.P.S.; Isoldi, L.A. Computational Model and Constructal Design Applied to Thin Stiffened Plates Subjected to Elastoplastic Buckling Due to Combined Loading Conditions. Appl. Sci. 2025, 15, 3354. [Google Scholar] [CrossRef]
- Musmar, M.A. A Parametric Study on the Buckling Behavior of Square Steel Plates under Uniaxial Compression. Civ. Eng. Arch. 2021, 9, 2292–2302. [Google Scholar] [CrossRef]
- Han, H.; Dong, C. Buckling Analysis for Carbon and Glass Fiber Reinforced Hybrid Composite Stiffened Panels. J. Compos. Sci. 2024, 8, 34. [Google Scholar] [CrossRef]
- Pavlovic, A.; Fragassa, C. Geometry optimization by fem simulation of the automatic changing gear. Rep. Mech. Eng. 2020, 1, 199–205. [Google Scholar] [CrossRef]
- Skripnyak, V.A.; Iokhim, K.; Skripnyak, E.; Skripnyak, V.V. Modeling of titanium alloys plastic flow in linear friction welding. Facta Univ. Ser. Mech. Eng. 2021, 19, 91–104. [Google Scholar] [CrossRef]
- Bhadra, R.; Jana, T.; Mitra, A.; Sahoo, P. Effect of CNT radius on flattening contact behaviour of CNT-Al nanocomposite: A numerical approch. Rep. Mech. Eng. 2023, 4, 121–130. [Google Scholar] [CrossRef]
- El-Sawy, K.M.; Nazmy, A.S.; Martini, M.I. Elasto-plastic buckling of perforated plates under uniaxial compression. Thin-Walled Struct. 2004, 42, 1083–1101. [Google Scholar] [CrossRef]
- Shanmugam, N.; Thevendran, V.; Tan, Y. Design formula for axially compressed perforated plates. Thin-Walled Struct. 1999, 34, 1–20. [Google Scholar] [CrossRef]
- Narayanan, R.; Chow, F.-Y. Strength of Biaxially Compressed Perforated Plates. 1984. Available online: https://scholarsmine.mst.edu/cgi/viewcontent.cgi?article=1168&context=isccss (accessed on 15 January 2025).
- Bejan, A.; Peder Zane, J. Design in nature. Mech. Eng. 2012, 134, 42–47. [Google Scholar] [CrossRef]
- Rocha, L.; Santos, E.D.; Cunha, D.; Garcia, F.; Lorenzini, G.; Biserni, C.; Letzow, M.; Costa, J.; Souza, J.; Isoldi, L. Constructal Design of Thermal Systems. In Constructal Law and the Unifying Principle of Design; Springer: New York, NY, USA, 2013; pp. 295–321. [Google Scholar] [CrossRef]
- Bejan, A. Constructal theory of pattern formation. Hydrol. Earth Syst. Sci. 2007, 11, 753–768. [Google Scholar] [CrossRef]
- Chen, L.; Feng, H.; Zhang, F.; Ge, Y. Constructal design for composite heat dissipating structure composed of an “arrow”-shaped high conductivity channel and an externally connected “T”-shaped fin. Int. Commun. Heat Mass Transf. 2024, 153, 107341. [Google Scholar] [CrossRef]
- Cunegatto, E.H.T.; Gotardo, M.; Zinani, F.S.F. Numerical analysis of tube arrangements with one, two, and four degrees of freedom for heat transfer with pseudoplastic fluids. Int. J. Heat Mass Transf. 2023, 208, 124080. [Google Scholar] [CrossRef]
- Dan, Z.; Feng, H.; Chen, L.; Liao, N.; Ge, Y. Constructal design of printed circuit recuperator for S-CO2 cycle via multi-objective optimization algorithm. Sci. China Technol. Sci. 2024, 67, 285–294. [Google Scholar] [CrossRef]
- Feijó, B.C.; Pavlovic, A.; Rocha, L.A.O.; Isoldi, L.A.; Lorente, S.; dos Santos, E.D. Geometrical investigation of microchannel with two trapezoidal blocks subjected to laminar convective flows with and without boiling. Rep. Mech. Eng. 2022, 3, 20–36. [Google Scholar] [CrossRef]
- Feng, H.; Sun, K.; Chen, L.; Ge, Y. Constructal design of a nanofluid cooling channel with sidewall ribs and cavities in a rectangular heat generation body. Case Stud. Therm. Eng. 2023, 41, 102640. [Google Scholar] [CrossRef]
- Feng, H.; Zhang, Z.; Chen, L.; Ge, Y. Constructal design for H-shaped compound heat transfer path in a rectangular heat generation body. Int. J. Heat Mass Transf. 2024, 225, 125442. [Google Scholar] [CrossRef]
- Liu, H.; Xi, K.; Xie, Z.; Lu, Z.; Chen, H.; Zhang, J.; Ge, Y. Constructal design of double-layer asymmetric flower baffles. Energy 2023, 280, 128254. [Google Scholar] [CrossRef]
- Lu, Z.; Xie, Z.; Xi, K.; Lin, D.; Liu, H.; Ge, Y.; Wu, F. Constructal evolutionary design of liquid cooling heat sink embedded in 3D-IC based on deep neural network prediction. Int. Commun. Heat Mass Transf. 2024, 152, 107273. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S. Design with Constructal Theory; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Bejan, A.; Lorente, S. The constructal law of design and evolution in nature. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 1335–1347. [Google Scholar] [CrossRef]
- Troina, G.; Cunha, M.; Pinto, V.; Rocha, L.; dos Santos, E.; Fragassa, C.; Isoldi, L. Computational Modeling and Constructal Design Theory Applied to the Geometric Optimization of Thin Steel Plates with Stiffeners Subjected to Uniform Transverse Load. Metals 2020, 10, 220. [Google Scholar] [CrossRef]
- Cunha, M.L.; Troina, G.S.; Santos, E.D.; Rocha, L.A.O.; Isoldi, L.A. Computational modeling and Constructal Design method applied to the geometric optimization of stiffened steel plates subjected to uniform transverse load. Res. Eng. Struct. Mat. 2018, 4, 139–149. [Google Scholar] [CrossRef]
- Callister, W.D. Materials Science and Engineering: An Introduction, 6th ed.; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction, 9th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Adak, M.; Soares, C.G. Effects of different restraints on the weld induced residual deformations and stresses in a steel plate. Int. J. Adv. Manuf. Technol. 2014, 71, 699–710. [Google Scholar] [CrossRef]
- ASTM A131/A131M–19; Standard Specification for Structural Steel for Ships. ASTM International: West Conshohocken, PA, USA, 2019.
- Purnama, D.; Winarto, W.; Sofyan, N.; Prihastomo, A.; Ito, K. Microstructure and Mechanical Properties of Ah-36 Steel Weldment Welded using Magnesium Modified E6013 Electrode. Int. J. Technol. 2020, 11, 48–59. [Google Scholar] [CrossRef]

| Steel | E (GPa) | ν | σy (MPa) |
|---|---|---|---|
| AH-36 | 210 | 0.3 | 355 |
| AISI 4130 | 210 | 0.3 | 460 |
| b/a | a (mm) | b (mm) |
|---|---|---|
| 1.00 | 1414.214 | 1414.214 |
| 0.95 | 1450.953 | 1378.405 |
| 0.90 | 1490.712 | 1341.641 |
| 0.85 | 1533.930 | 1303.840 |
| 0.80 | 1581.139 | 1264.911 |
| 0.75 | 1632.993 | 1224.745 |
| 0.70 | 1690.309 | 1183.216 |
| 0.65 | 1754.116 | 1140.175 |
| 0.60 | 1825.742 | 1095.445 |
| 0.55 | 1906.925 | 1048.809 |
| 0.50 | 2000.000 | 1000.000 |
| 0.45 | 2108.185 | 948.683 |
| 0.40 | 2236.068 | 894.427 |
| 0.35 | 2390.457 | 836.660 |
| 0.30 | 2581.989 | 774.597 |
| 0.25 | 2828.427 | 707.107 |
| Perforation | b0/a0 | b0 (mm) | a0 (mm) |
|---|---|---|---|
| Circular | 1.000 | 356.830 | 356.830 |
| Horizontal Elliptical | 0.707 | 300.000 | 424.426 |
| Vertical Elliptical | 1.415 | 424.426 | 300.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silveira, T.; Crestani, E.A.; dos Santos, E.D.; Isoldi, L.A. Numerical Analysis of Aspect Ratio Effects on the Mechanical Behavior of Perforated Steel Plates. Metals 2025, 15, 786. https://doi.org/10.3390/met15070786
da Silveira T, Crestani EA, dos Santos ED, Isoldi LA. Numerical Analysis of Aspect Ratio Effects on the Mechanical Behavior of Perforated Steel Plates. Metals. 2025; 15(7):786. https://doi.org/10.3390/met15070786
Chicago/Turabian Styleda Silveira, Thiago, Eduardo Araujo Crestani, Elizaldo Domingues dos Santos, and Liércio André Isoldi. 2025. "Numerical Analysis of Aspect Ratio Effects on the Mechanical Behavior of Perforated Steel Plates" Metals 15, no. 7: 786. https://doi.org/10.3390/met15070786
APA Styleda Silveira, T., Crestani, E. A., dos Santos, E. D., & Isoldi, L. A. (2025). Numerical Analysis of Aspect Ratio Effects on the Mechanical Behavior of Perforated Steel Plates. Metals, 15(7), 786. https://doi.org/10.3390/met15070786








