Precipitation Dynamics and Mechanical Properties Analysis of a Nickel-Based Superalloy Cooled Under Different Rates

Abstract

The solid solution cooling heat treatment of powder, high-temperature alloys is a crucial part of the process for ensuring the strength of materials during the forging processing. The influence of the γ′ phase and other microstructures in high-temperature alloy forgings on their macroscopic mechanical properties has been confirmed in numerous studies. Among them, the performance of the γ′ phase during the solid solution cooling process varies significantly depending on the cooling rate. This study uses the FGH99 nickel-based high-temperature alloy as the research material. It examines the precipitation and microstructure evolution law of the material under different cooling rates and its impact on the macroscopic mechanical properties of the material. Additionally, a prediction model of the organizational properties based on the cooling rate is constructed. The research findings indicate that there is a distinct positive correlation between the yield strength of the material and the cooling rate. As the cooling rate increases, the yield strength rises from 910.8 MPa to 1025.4 MPa, showing an increase of 12.6%. Moreover, an increase in the cooling rate has an evident promoting effect on the refinement of the precipitation phase. When the cooling rate is elevated from 50 °C/min to 250 °C/min, the average size of the γ′ phase decreases from 106 nm to 82.1 nm, and its morphology transforms from an irregular state to a spherical shape. For the microstructure of the material, such as the size of the precipitated phase and dislocation density, the maximum prediction error of the heat treatment organization performance prediction model established in this study is 2.97%. Moreover, the prediction error of the yield strength is 1.76%.

1. Introduction

Nickel-based high-temperature alloys are extensively employed in the manufacturing of aero-engines and gas turbines due to their high strength at elevated temperatures and excellent corrosion and oxidation resistance [1,2,3]. Among these alloys, FGH99 is a high-strength, damage-tolerant powder metallurgy alloy developed for use at temperatures up to 800 °C and has been successfully utilized in the turbine discs of advanced aero-engines [4,5]. Heat treatment, a crucial process for regulating the microstructure and mechanical properties of high-temperature alloys, is directly related to enhancing the mechanical properties of the alloys [6,7]. For critical components such as advanced turbine disks and turbine blades, the heat treatment process is one of the core processes for ensuring the service performance of the material [8].

As one of the primary strengthening mechanisms for the mechanical properties of nickel-based high-temperature alloys, the ordered arrangement of the γ′ phase establishes a co-lattice relationship with the γ phase in the matrix. This relationship plays a crucial role in enhancing the material’s mechanical properties [9,10,11]. During the cooling process of solid solution heat treatment, the cooling rate significantly influences the size, shape, and distribution of the γ′ phase. Yang et al. [12] investigated the evolution of γ′ phase morphology in a K5 high-temperature alloy through directional solidification under vacuum conditions. Their findings indicated that as the cooling rate increased, both size reduction and morphological transformation from cubic to spherical particles occurred within the γ′ phase. Additionally, Ding et al. [13] employed oil quenching and air quenching methods to examine how cooling rate affects γ′ phase characteristics; they demonstrated that after water quenching—characterized by a faster cooling rate—the volume fraction of γ′ phase was smaller compared to that observed following oil quenching. However, traditional heat treatment processes often rely on empirical trial-and-error approaches, which complicate efforts to accurately quantify relationships among cooling rate, γ′ phase characteristics, and mechanical properties. Therefore, developing a predictive model for heat treatment organization performance is essential for optimizing process parameters and ultimately enhancing parts’ mechanical properties.

Most existing models for predicting organizational properties utilize a set of differential equations to describe microkinetic processes, such as the precipitation of reinforced phases and dislocation evolution at constant temperatures. However, there is currently no established correlation between cooling rates and microstructural features—such as precipitated phases—and the macroscopic mechanical properties of materials. For instance, Lan et al. [14] investigated the phase transformation and grain growth behavior of IN718 within a temperature range of 920 °C to 1080 °C, developing a model that accurately predicts variations in initial phase volume fractions and grain growth concerning δ, γ′, and γ′’ phase volume fraction and size evolution. Similarly, Aoki et al. [15] created a predictive model for microstructure and strength based on data from the heat treatment process involving 720 Li’s microstructure.

In order to investigate the influence of cooling rate on the microstructural evolution and mechanical properties of nickel-based high-temperature alloys and subsequently optimize the heat treatment process for large-sized components, this study systematically conducted heat treatment experiments under varying cooling rates. The γ′-strengthened phase was quantitatively characterized using Electron Backscattering Diffraction (EBSD) and Transmission Electron Microscopy (TEM) to elucidate the effects of cooling rate on the size/volume fraction of the precipitated phase, dislocation density, and substructure evolution. Drawing upon theories related to γ′ phase shear resistance, dislocation bypass mechanisms, and dislocation strengthening, a predictive model for heat treatment performance has been developed. This model integrates organizational evolution with mechanical response to quantitatively describe the relationship between cooling rate, microstructure, and room temperature mechanical properties (specifically yield strength). The findings from this research provide a theoretical foundation as well as an optimization framework for designing heat treatment process parameters applicable to large-sized high-temperature alloy components.

2. Materials and Methods

2.1. Experimental Material

In this study, an independently developed heat treatment cooling device, as illustrated in Figure 1, was employed to perform heat treatment tests at various cooling rates. The closed-loop control system, which utilizes thermocouple temperature sensing and infrared heating technology, enabled the device to maintain precise temperature fluctuations within ±1 °C. This ensured the reliability of the test data. Additionally, stable airflow from the cooling vents, in conjunction with the heating apparatus, facilitated a consistent and accurate cooling rate throughout the testing process.

The material investigated in this study is FGH99, a powder metallurgy nickel-based superalloy. It was prepared as a disc billet through vacuum induction melting followed by atomization and hot isostatic pressing. The chemical composition of this superalloy is presented in

Table 1. Chemical composition of nickel-based powder superalloys (wt.%).

Cr	Co	Mo	Ta	Nb	Al	Ti	C	Zr	B	Ni
11.0–13.0	19.0–22.0	3.5–6.0	2.4–4.0	0.5–1.0	3.0–5.0	0.0–4.5	0.05	0.05	0.03	Bal.

. A rectangular thin-plate specimen measuring 50 × 24 × 1 mm was cut from the disk blank using wire cutting techniques. The thickness of the specimen was limited to 1 mm to ensure that it reached a uniform temperature state rapidly during heat treatment; this approach mitigated any potential effects of uneven temperatures on the γ′-phase formation. The dimensions of the sample are depicted in Figure 1c.

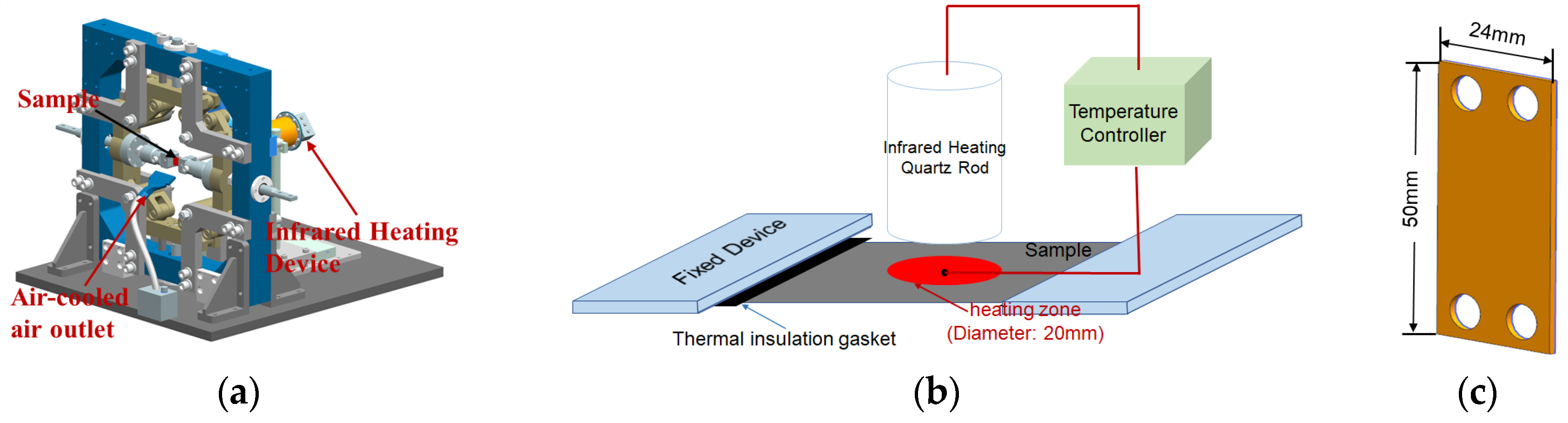
2.2. Heat Treatment Tests with Different Cooling Rates

The surface of the sample was polished using 800-mesh fine sandpaper to eliminate any visible defects. Subsequently, the sample was positioned in the clamping apparatus, with a heat insulation plate placed between the sample and the fixture to minimize heat transfer. The servo system was calibrated to apply a preload of 200 N at both ends of the sample, ensuring that the heating area remained stable and did not shift due to relaxation of the fixture. The experimental flow chart is illustrated in Figure 2a. During the experiment, samples were heated at a constant rate of 5 °C/s until reaching 1150 °C, where they were held for 5 min to achieve a saturated single-phase solid solution. Following this phase, samples were cooled down to 600 °C at rates of 50, 100, 150, 200, and 250 °C/min [16]. As depicted in Figure 2b, the closed-loop control system facilitated a nearly linear cooling profile at these target rates. Minor deviations observed at higher cooling rates (>150 °C/min) are attributed to thermal lag within the control response. Subsequent room-temperature tensile tests were conducted to assess the mechanical properties of the cooled samples.

The microstructure of the heat-treated specimens was thoroughly analyzed. Sections were prepared from the red area highlighted in Figure 2a to facilitate observation of the specimens’ microstructure. The specimen slices were embedded in epoxy resin and sequentially sanded using progressively finer mesh sandpaper (400–2000) to achieve a flat surface; subsequently, the sanded surfaces were mechanically polished to ensure an optimal finish for the specimens. Grain morphology and orientation were assessed using EBSD. For TEM specimen preparation, it is essential to obtain as large a thin zone as possible. During manual grinding and polishing, the specimen must be reduced to a thickness of 0.05 mm sheets, followed by employing an electrolytic double spray method for final thinning of the specimens. In comparison with EBSD analysis, TEMs selected for examination utilize higher magnification, which facilitates detailed analysis of fine precipitation phases within the material.

3. Results and Discussion

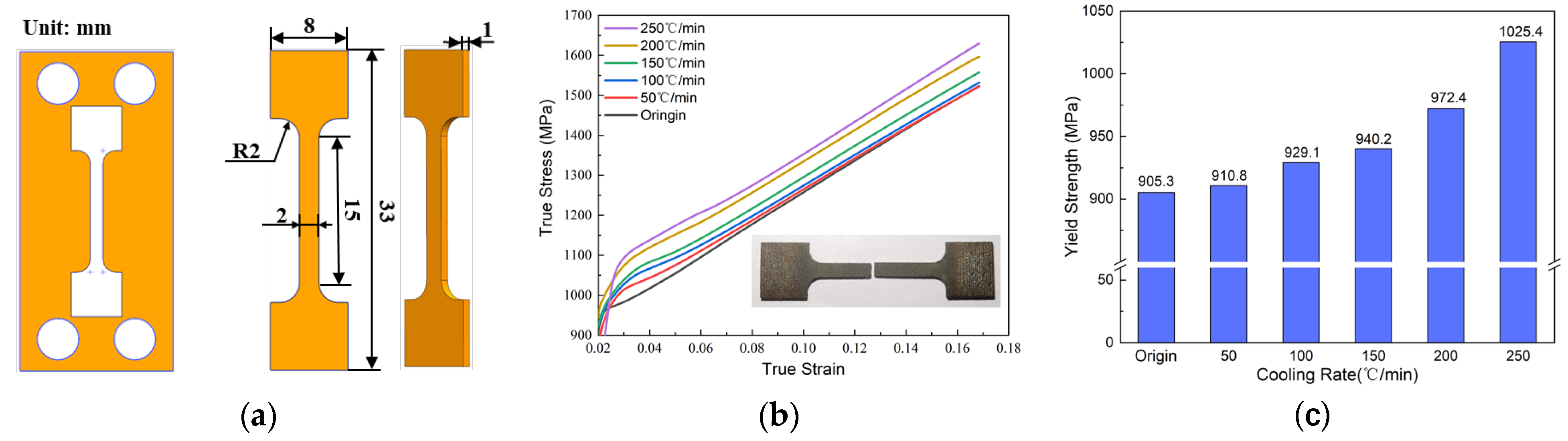
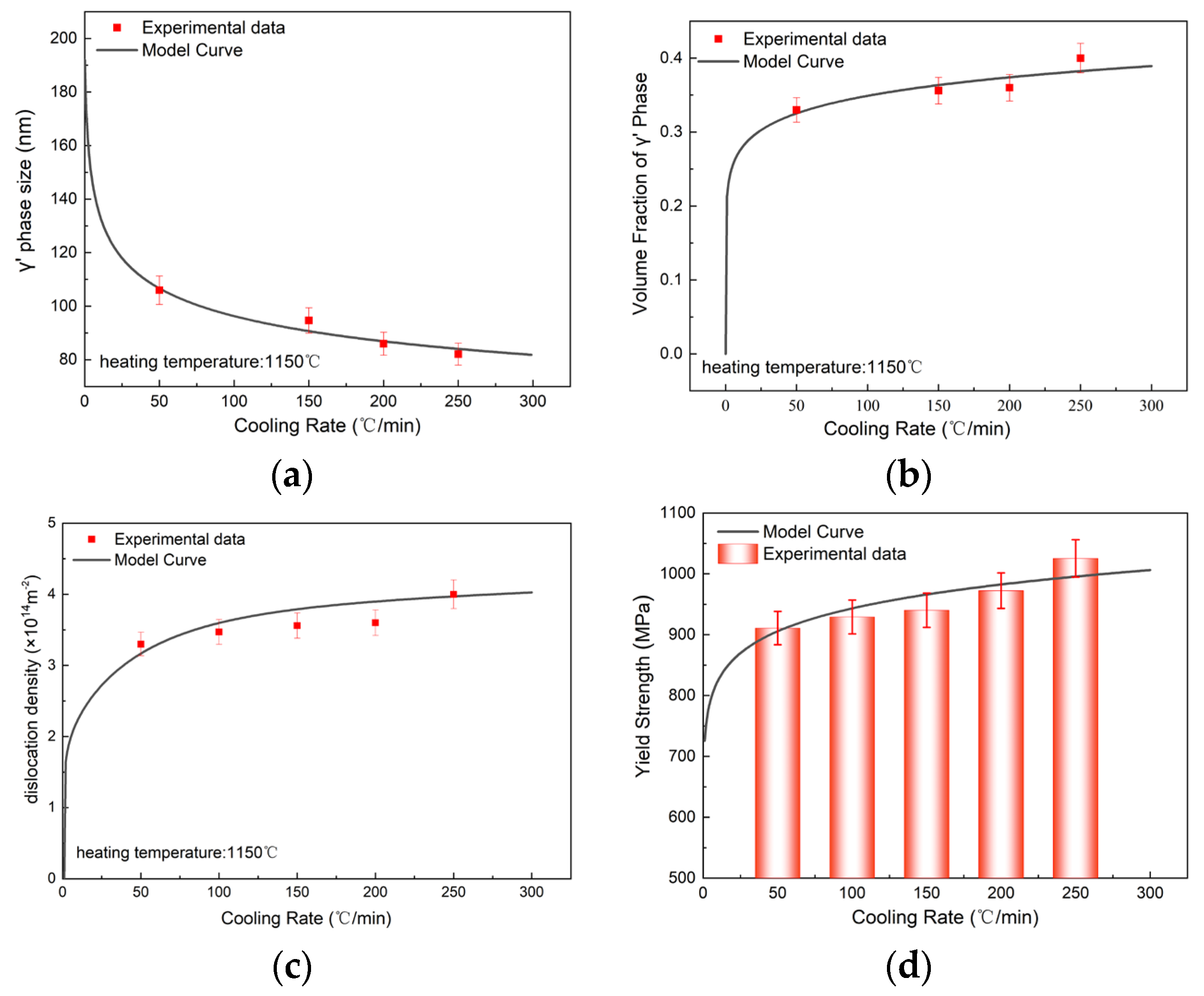
3.1. The Influence of Cooling Rate on the Mechanical Properties of Superalloy

To investigate the effects of varying cooling rates during heat treatment on nickel-based superalloys, room-temperature tensile samples were prepared with a strain rate of 0.001/s. The sampling position and dimensions of the tensile samples are illustrated in Figure 3a. The stress–strain curves and yield strength of the tensile samples following room-temperature tests at different cooling rates are presented in Figure 3b,c, respectively. As depicted in Figure 3b, the stress–strain curves for all samples tested under different cooling rates exhibit a consistent trend; throughout the tensile process, the material demonstrates significant work hardening. Additionally, due to lower dynamic recovery driving forces at room temperature, no softening behavior is observed in the material. Notably, the fracture surfaces of the tensile samples did not display necking phenomena but instead exhibited a brittle fracture morphology. From Figure 3c, it can be seen that yield strength increases progressively with higher cooling rates. At a cooling rate of 50 °C/min, the yield strength measures 910.8 MPa; conversely, at a rate of 250 °C/min, it reaches up to 1025.4 MPa—an increase of approximately 12.58%. This finding confirms that elevated cooling rates significantly enhance the room-temperature strength of FGH99.

3.2. Microstructure Characterization

As illustrated in Figure 4, EBSD observation diagrams for both the original sheet sample and high-temperature alloy samples subjected to varying cooling rates are presented. The microscopic images reveal that following heat treatment at different cooling rates, the grain structure predominantly consists of equiaxed grains. Notably, the average grain size across samples with differing cooling rates is comparable to that of the original grain size. This phenomenon can be attributed to the brief cooling duration experienced by the material, which does not allow sufficient time for grain growth. Furthermore, since the material has not undergone significant microstructural deformation, the driving force for recrystallization remains weak; consequently, there is no evident refinement of grains within the samples. Therefore, in subsequent predictions regarding heat treatment models, it can be concluded that the impact of grain refinement on material strength may be considered negligible [17].

As illustrated in Figure 5, the geometric dislocation density of nickel-based superalloys subjected to various heat treatment cooling rates is compared. From Figure 5a, it can be observed that smaller grains effectively restrict dislocation slip and proliferation; consequently, dislocations tend to accumulate along the grain boundaries of fine grains. Following heat treatment and cooling, a pronounced phenomenon of dislocation accumulation is evident within larger grains. Notably, in Figure 5d, there exists a clustered accumulation of dislocations between grain boundaries, which contrasts with the linear dislocations traversing through the grains. In this region, larger dislocation cells are formed.

The TEM images obtained under various heat treatment cooling rates are presented in Figure 6. To quantitatively analyze the influence of heat treatment cooling rate on the precipitation of the γ′ phase, we measured the size and area of the γ′ particles in specimens subjected to different conditions using ImageJ software (1.54p, 17 February 2025). The specific measurement procedure is outlined as follows:

(1)

The resulting TEM image is a black-and-white representation where color brightness corresponds to gray scale values. The overall dimensions of the image were established by aligning the ImageJ scale with that of the TEM.

(2)

During the selection process, it was not feasible to completely isolate the γ′ phase solely by adjusting the overall grayscale threshold value. Therefore, boundary curves were employed to assist in delineating and defining the boundaries of the γ′ phase.

(3)

Selected regions corresponding to γ′-phase particles were filled with red color, allowing for subsequent calculations of equivalent diameter and area for each individual γ′ phase particle using ImageJ software. The results obtained were further processed using Origin 2021 to determine both the grain size and volume fraction of the γ′ phase across varying heat treatment cooling rates. In considering grain sizes within this analysis, grains exceeding 500 nm in diameter observed in images were classified as part of a γ/γ′-phase eutectic structure and thus excluded from statistical evaluation.

TEM images of the specimens subjected to heat treatment at various cooling rates are presented in Figure 6. As illustrated in Figure 6, the morphology of the γ′ phase evolves as its size diminishes with increasing cooling rate. This phenomenon can be attributed to the elevated degree of subcooling experienced by the material under high cooling rate conditions, which enhances the nucleation driving force for the γ′ phase and promotes its nucleation. Concurrently, excessive subcooling inhibits element diffusion rates, preventing sufficient growth of the precipitated phase and resulting in a granular morphology. As the cooling rate decreases, both the degree of subcooling and the nucleation driving force for the γ′ phase diminish, leading to a reduction in the number of nucleated sites. Additionally, lower cooling rates provide ample time for elemental diffusion, facilitating the formation of larger cubic γ′ phases [18]. Furthermore, as depicted in Figure 2b, during heat treatment tests where specimens were cooled down to 600 °C at a specified rate, it was observed that subsequent cooling from this temperature to room temperature occurred at a significantly higher rate than during initial cooling to 600 °C. This resulted in a multi-stage cooling process for each specimen and consequently led to a bimodal distribution regarding the precipitation phase dimensions post-test [19].

During deformation, coarse γ′ phases become pinned at grain boundaries, which inhibits recrystallization processes. Nevertheless, with continued deformation, the high hardness associated with γ′ leads to dislocation entanglement. Influenced by a unidirectional valve mechanism, dislocations within γ′ can enter into the γ phase matrix; conversely, dislocations present within the matrix do not penetrate into the γ′ phase—this interaction promotes recovery and recrystallization within the matrix. Simultaneously, large-sized γ′ phases exhibit hetero-epitaxial growth that forms recrystallization cores. Under room temperature tensile testing conditions, dislocation annihilation provides a driving force for recrystallization; however, this mechanism is less pronounced due to its subtle manifestation under these circumstances. In contrast to this behavior observed with coarse particles, the dispersed fine γ′ phases inhibit subgrain boundary movement and restrict dislocation slip mechanisms, thereby further suppressing recrystallization processes. The enhancement resulting from processing hardening is clearly demonstrated in Figure 3.

4. Heat Treatment Model

4.1. Prediction Model for Microstructure and Properties of Heat Treatment

We primarily focus on elucidating the relationship between γ′ precipitate evolution and cooling rate during solution treatment. Based on McLean’s classical theory of precipitate coarsening and thermodynamic principles, a power-law relationship can be derived to describe the dependence of precipitate size on cooling rate [20]. This formulation, while simple, demonstrates a high degree of correlation with the experimental results. Accordingly, the average γ′ precipitate diameter r as a function of cooling rate $\dot{T}$ can be expressed as follows:

$$r=b{\dot{T}}^{-n_1}$$

(1)

where b is a material-dependent constant, and $n_1$ is the power-law exponent which is equal to 1/2 for interface-controlled growth and 1/3 for diffusion-dominated growth.

In addition to the size distribution of the precipitated phase, the volume distribution of γ′ is also regarded as a strength consideration factor during the solid solution cooling process of nickel-based powder superalloys. The volume fraction of γ′ precipitate f can be calculated by the Johnson–Mehl–Avrami (JMA) model, which is applicable to both isothermal and non-isothermal conditions [21]. The influence of the cooling rate on the γ′ precipitate volume fraction f can be described as follows:

$$f=1-\mathit{exp}\left(-{\left({\displaystyle \frac{T_0}{\tau \dot{T}}}\right)}^{n_2}\right)$$

(2)

where $T_0$ is the solvus temperature, $n_2$ is the Avrami exponent, and τ is a time-related material constant. This relation captures the kinetic nature of γ′ precipitation during non-isothermal cooling, where faster cooling rates promote higher subcooling and accelerate nucleation, resulting in greater volume fractions of fine precipitates within a limited time frame.

During the high-temperature deformation process of the material, a large number of dislocations will accumulate. When the material undergoes solid solution treatment at a higher temperature, the higher activation energy can enhance the material’s dynamic recovery ability, and the accumulated dislocations within the material will decrease. When the material is cooled from the solid solution temperature, a large number of supersaturated vacancies are generated inside. Affected by the temperature gradient changes, the contraction of different parts of the crystal is not uniform, resulting in the generation of new dislocations.

The effect of both cooling rate and precipitate evolution on dislocation density $\rho$ can be expressed as follows:

$$\rho =A{\rho }_0\left(1-exp \left(-k_1\dot{T}\right)\right)+k_{2}f$$

(3)

where ${\rho }_0$ is the initial dislocation density, $A$ and $k_1$ are material constants characterizing thermal activation and cooling sensitivity, and $k_2$ is a strengthening coefficient associated with the γ′ precipitate volume fraction. The first term reflects the suppression of dislocation recovery at higher cooling rates, while the second term captures the increase in dislocation density due to precipitate–dislocation interactions.

For nickel-based superalloys, the main contributions to their yield strength include nickel-based superalloy matrix hardening, solid solution strengthening, precipitation strengthening, and dislocation strengthening [22]. Equation (4) is the yield strength model of nickel-based superalloys:

$$\sigma ={\sigma }_0+{\sigma }_{ss}+\sqrt{{\sigma }_p^2+{\sigma }_{\rho }^2}$$

(4)

where ${\sigma }_0$ is the matrix hardening term for nickel-based superalloys, ${\sigma }_{ss}$ is the solid solution strengthening, ${\sigma }_p$ precipitation strengthening, and ${\sigma }_{\rho }$ is dislocation strengthening.

Solid solution strengthening of nickel-based high-temperature alloys refers to the addition of alloying elements such as Cr, Co, and Mo to the γ matrix to improve the interatomic bonding and hinder the dislocation motion, thereby increasing the strength and hardness of the material [22]. In this study, solid solution strengthening during heat treatment is evaluated by introducing Labusch’s theory [23,24], which is calculated as follows:

$${\sigma }_{ss}=(1-f){\left({\sum }_i{k_i}^{{\displaystyle \frac{3}{2}}}{c}_i\right)}^{{\displaystyle \frac{2}{3}}}$$

(5)

The coefficient term $(1-f)$ is introduced since solid solution strengthening is mainly considered as the hindering effect of solid solution elements in the γ matrix on dislocations [11]. $c_i$ is the concentration of solute i, and $k_i$ is the strengthening constant of solute I; the values are shown in

Table 2. Solid solution strengthening coefficient ($k_i$) and atomic fraction for solute in FGH99. Values for k taken adapted from Ref. [27].

Alloy	Cr	Co	Mo	Ta	Nb	Al
wt.%	11.0–13.0	19.0–22.0	3.5–6.0	2.4–4.0	0.5–1.0	3.0–5.0
k (MPa.%−1)	337	39.4	1015	1191	1183	225
atomic fraction, %	12.2–14.19	18.55–21.19	2.10–3.55	0.76–1.26	0.31–0.61	6.40–10.52
Alloy	Ti	C	Zr	B	Ni
wt.%	0.0–4.5	0.05	0.05	0.03	44.37–60.47
k (MPa.%−1)	775	1061	2359	-	-
atomic fraction, %	0.00–5.33	0.24	0.03	0.16	42.92–59.28

.

For nickel-based superalloys, the strengthening of the γ′ phase makes an important contribution to their high strength, especially the shear resistance and dislocation bypass mechanism of the γ′ precipitates [25], and the precipitated phase strengthening of the material is expressed as follows:

$${\sigma }_p=k_{4}f{r}^{n_3}$$

(6)

where $k_4$ is the material constant.

During plastic deformation, as dislocations proliferate, a large number of accumulated dislocations impede deformation, which is manifested as work hardening in the stress–strain curve [26].

$${\sigma }_{\rho }=M\alpha \mu b\sqrt{\rho }$$

(7)

where α = 0.2 is a constant dependent on crystal structure, μ is the shear modulus, and B is the Burgers vector modulus.

4.2. Model Verification

The parameters utilized in the microstructure-property prediction model are presented in

Table 3. Parameters used in the prediction model of FGH99 heat treatment.

${\mathit{T}}_0$(°C)	b	${\mathit{n}}_1$	$\mathit{\tau }$(min)	${\mathit{n}}_2$
1150	192	−0.126	71.56	0.1495
${\rho }_0$ (m−2)	A	$k_1$ (min/K)	$k_2$ (m−2)	${\sigma }_0$ (MPa)
3.62 × 1012	0.3	10.34	−3.086 × 1011	268.9
${\mathit{k}}_4$	${\mathit{n}}_3$	M	$\mathit{\mu }$(MPa)	B (m)
1047	0.1	0.4	25,800	7.5 × 10−8
$\alpha$	${\sigma }_{ss}$ (MPa)
0.2	221.38

. The model-predicted γ′ precipitate size, volume fraction, and yield strength—accounting for the influence of microstructural features—are illustrated in Figure 7. As observed, the prediction errors for the precipitate size and volume fraction are 2.07% and 2.97%, respectively, while the error for yield strength is only 1.76%. These results indicate that the cooling-rate-based model, which incorporates γ′ evolution and dislocation strengthening, demonstrates high predictive accuracy. Consequently, it is well suited for quantitatively evaluating the microstructural characteristics and mechanical performance of FGH99 subjected to varying cooling rates.

5. Conclusions

This paper establishes a performance model for heat treatment organization based on the cooling rate during heat treatment, which can accurately predict the macroscopic mechanical properties of materials subjected to different cooling rates. This is achieved by characterizing the evolution of size and volume fraction of the precipitated phase and elucidating the mapping mechanism between microstructure and macroscopic properties as influenced by this precipitated phase. The main findings of this study are as follows:

(1)

Within the solid solution cooling rate range of 50–250 °C/min, it was observed that the yield strength of tensile specimens made from high-temperature alloys increases with an increase in the solid solution cooling rate, achieving a maximum enhancement of 12.58%. The stress–strain curves exhibit pronounced work-hardening behavior, while tensile specimens display characteristics indicative of brittle fracture.

(2)

Observations from EBSD microstructural analysis revealed that within this range of cooling rates, no significant recrystallization phenomena were detected. Compared to the original grain structure, the maximum difference in grain size for cooled specimens was found to be 2.78%. Dislocation structures remained relatively unchanged post heat treatment; thus, strengthening due to dislocations primarily arises from their accumulation during deformation at room temperature.

(3)

The γ′ phase of high-temperature alloys has been observed using TEM, revealing a significant negative correlation between the size of the γ′ phase and the cooling rate. The coarse γ′ phase, which is pinned at grain boundaries during deformation, inhibits recrystallization. However, the high hardness of the γ′ phase also contributes to dislocation entanglement, thereby promoting recrystallization. Additionally, the fine dispersed γ′ phase further serves to inhibit recrystallization.

(4)

A predictive model for organizational performance based on heat treatment cooling rate has been established. The prediction error concerning microstructural features such as precipitation phase and dislocation density does not exceed 2.97%, while the prediction error for yield strength is limited to 1.76%, demonstrating good agreement with experimental results.