Optimizing Al7072 Grooved Joints After Gas Tungsten Arc Welding

Abstract

Aluminum alloy, due to its low melting point and high thermal conductivity, deforms and contracts significantly during welding. To mitigate this and achieve full penetration in a single pass, this study uses GTAW (Gas Tungsten Arc Welding) additive manufacturing and optimizes welding groove parameters via the Box-Behnken Response Surface Methodology. The focus is on improving tensile strength and penetration depth by analyzing the effects of groove angle, root face width, and root gap. The results show that groove angle most significantly affects tensile strength and penetration depth. Hardness profiles exhibit a W-shape, with base material hardness decreasing and weld zone hardness increasing as groove angle rises. Root face width reduces hardness fluctuation in the weld zone, and an appropriate root gap compensates for thermal expansion, enhancing joint performance. The interaction between root face width and root gap most impacts tensile strength, while groove angle and root face width interaction most affects penetration depth. The optimal welding parameters for 7xxx aluminum alloy GTAW are a groove angle of 70.8°, root face width of 1.38 mm, and root gap of 0 mm. This results in a tensile strength of 297.95 MPa and penetration depth of 5 mm, a 90.38% increase in tensile strength compared to the RSM experimental worst group. Microstructural analysis reveals the presence of β-Mg₂Si and η-MgZn₂ strengthening phases, which contribute to the material’s enhanced mechanical properties. Fracture surface examination exhibits characteristic ductile fracture features, including dimples and shear lips, confirming the material’s high ductility. The coexistence of these strengthening phases and ductile fracture behavior indicates excellent overall mechanical performance, balancing strength and plasticity.

1. Introduction

Al7072 stands out for its exceptional strength, excellent ductility, and superior corrosion resistance, enabling broad industrial applications—particularly as the material of choice for high-stress structural components and precision functional parts in specialized vehicle bodies, chassis suspension systems, and high-end electronic components. This alloy achieves an optimal balance of lightweight design with high strength and hardness through advanced alloying techniques [1]. Its performance remains remarkably stable under extreme operating conditions, retaining robust mechanical properties even at elevated temperatures, thereby meeting the stringent requirements of aerospace, rail transportation, precision instrumentation, and other high-end sectors [2,3]. As an important industrial material, the performance of Al7072 largely depends on its microstructure. Essentially, Al7072 is an alloy with aluminum as the matrix and an appropriate amount of zinc added. Its typical microstructure features a face-centered cubic aluminum matrix with fine second-phase particles uniformly dispersed throughout. These particles are primarily compounds formed through the interaction between zinc and aluminum elements or metastable phases precipitated from supersaturated solid solutions. These fine second-phase particles not only influence the mechanical properties of the material—such as strengthening the matrix by impeding dislocation movement—but their specific composition and distribution are also key factors determining the alloy’s excellent corrosion resistance. It is suitable for welding fabrication in various environments due to its excellent material properties. However, due to the high zinc content in this alloy, it is highly prone to grain boundary liquefaction cracks during welding repair. Moreover, the sensitivity of thin-walled components (with a wall thickness of 3–5 mm) to heat input is 2.3 times that of conventional structural components. This leads to a series of common challenges in traditional Gas Tungsten Arc Welding (GTAW) for repairing welds, such as an excessively high burn-off rate of zinc elements and the presence of various welding defects.

Gas Tungsten Arc Welding (GTAW), owing to its characteristics of low heat input, stable arc, and inert gas shielding, can effectively suppress microstructural defects in the heat-affected zone (HAZ) of high-strength steels (e.g., ASTM CA6NM martensitic stainless steel), such as grain coarsening, uneven phase transformation, and embrittlement, thereby enhancing the toughness and fatigue resistance of the weld. Studies indicate that by optimizing GTAW process parameters (e.g., current, welding speed), the thermal cycle in the HAZ can be precisely controlled to minimize excessive formation of hard and brittle martensitic phases while avoiding the development of softened zones. This makes GTAW particularly suitable for engineering applications with stringent HAZ performance requirements, such as hydraulic turbine runners and pressure vessels [4]. As a critical process parameter affecting the quality of welded joints, the groove plays a vital role in achieving full penetration welding joints for thicker or complexly shaped base materials. To achieve a rational distribution of heat within the joint, minimize thermal deformation of the welded components to the greatest extent, and ensure the strength of the weld zone, it is generally necessary to design and machine a groove at the welding joint [5]. The three pivotal parameters of the groove process encompass the groove shape, angle, and dimension. By adjusting these parameters, particularly the groove angle and dimension, one can exercise greater control over the weld seam’s appearance and the heat distribution at the joint. This refinement leads to an enhancement in the weld zone’s microhardness and an improvement in the joint’s mechanical properties [6]. Within narrow-gap grooves, a spatial constraint effect arises during welding, and this effect fortifies the stability of the welding arc, attributed to the configuration of the narrow gap itself. Compared to traditional grooves, narrow-gap grooves exhibit reduced volumetric expansion and contraction during welding, significantly decreasing the generation of residual stresses. Selecting an appropriate reserved gap offers notable benefits in terms of arc stability, full penetration morphology, mitigation of welding residual stresses, and enhancement of joint plasticity and toughness [7]. In the heating connection process of carbon fiber materials and titanium alloys, the incorporation of a groove serves to cushion the energy input, elevate the inter-facial contact thermal resistance, and reinforce the mechanical interlocking effect at the joint interface [8]. The welding process has a profound impact on the temperature distribution, bonding condition, and joint strength of the welded components. During the process of composite surface modification on high-strength, low-density alloys, the application of laser-fabricated microstructure grooves serves to augment mechanical interlocking, chemical bonding, and functional group interactions, ultimately enhancing the mechanical properties of the alloy’s surface [9]. A well-designed groove ensures the stability of the weld pool during the welding process, facilitating the melting of metals and the growth and transformation of grain structures within the weld pool. This, in turn, enhances the quality of the welded joint [10].

Currently, most of the research on GTAW welding of high-strength and high-hardness alloys focuses on microstructures and mechanical properties. However, there are few systematic studies on the effects of GTAW grooving process parameters on the structure and performance of welded joints. Considering the critical role of groove parameters, this study innovatively focuses on optimizing the groove parameters (groove angle, root face, and reserved gap) of Al7072 instead of merely adjusting the welding heat input parameters (such as current and speed). By employing the Response Surface Method (RSM), a mathematical model was constructed. This approach ingeniously utilizes multivariate quadratic regression equations to accurately depict the intricate functional relationships between multiple influencing factors and response values. It enables an in-depth analysis of how these parameters affect the tensile strength and penetration depth of welded joints, followed by performance optimization and prediction. Finally, the optimization results were effectively verified, aiming to fill the research gap and provide theoretical support and practical guidance for the optimization of the aluminum alloy GTAW welding process.

2. Experimental

Welded Joint Preparation Methods

Welding Al7072 often uses ER5356, ER2319, ER4043 and other wires. In this paper, the choice of ER 5356 wire for welding Al7072 is to ensure the welding strength and toughness, at the same time, to improve the corrosion resistance of the weld, and to ensure the stability of the welding process and weld quality, by adjusting the groove process parameters of the Al7072 plate welding test, 7072 plate, and ER5356 wire; its composition is shown in

Table 1. Al7072 matrix and ER5356 welding wire composition (wt%).

Elements	Si	Fe	Cu	Mn	Mg	Zn	Ti	Al
7072	0.7	1	0.1	0.1	0.1	0.8~1.3	/	Bal
ER5356	≤0.25	≤0.4	≤0.1	0.05–0.2	4.5–5.5	/	0.06	Bal

. The tensile strength of ER5356 welding wire is 255 MPa (meeting the requirement of ≥240 MPa specified in AWS A5.10 standard [11]), and the tensile strength of the 7072 aluminum alloy base material is 520 MPa. The microhardness of the joint was measured by FM-800 Vickers hardness tester with a load of 200 g and a dwell time of 15 s; the measurement interval for the specimen is 0.5 mm. Tensile specimens are shown in Figure 1a,b. The tensile test was performed by MTS Criterion Universal Testing Machine with constant tensile test speed of 2 mm/min for elongation measurement. The tensile strength test method for welded joints was adopted from the ISO 9692-3 standard [12]. The size of the base material is 200 × 100 × 5 mm³. Welding was performed using a Panasonic YC-350WX5 system; the welding process is argon arc welding (shown in Figure 1c); the welding method is butt welding of two plates, and 15 different parameters of grooves are prefabricated on the substrate by a wire cutting machine before the test (the welding process parameters are shown in Figure 2 and

Table 2. Welding process parameters.

Sample	Coding Matrix			Groove Angle (°)	Root Face (mm)	Reserved Gap (mm)
1	−1	−1	0	45	1	0.75
2	1	−1	0	75	1	0.75
3	−1	1	0	45	2	0.75
4	1	1	0	75	2	0.75
5	−1	0	−1	45	1.5	0
6	1	0	−1	75	1.5	0
7	−1	0	1	45	1.5	1.5
8	1	0	1	75	1.5	1.5
9	0	−1	−1	60	1	0
10	0	1	−1	60	2	0
11	0	−1	1	60	1	1.5
12	0	1	1	60	2	1.5
13	0	0	0	60	1.5	0.75
14	0	0	0	60	1.5	0.75
15	0	0	0	60	1.5	0.75

). The groove pre-treatment method is wire electrical discharge machining (wire cutting for short). Subsequently, the groove is polished using 500# and 800# sandpapers, followed by ultrasonic cleaning. After that, it is rinsed with alcohol and then dried with a hairdryer to ensure the cleanliness of the weld groove. In Table 2, the coding matrix corresponds one-to-one with the three process parameters listed on the right side. The tack welding specifications are as follows: three tack welds at the head, middle, and tail of the weld seam, and 30% of final current. In this paper, the wire feed speed is selected to be a constant 250 mm/min. Following the premise of the previous research basis [11], the welding current of 190 A and welding speed of 2.5 mm/s were originally used to carefully analyze the I-shape groove, single-side V-shape groove, and V-shape groove. In order to achieve this welding specimen to achieve full penetration morphology (single-sided welding, double-sided forming) for a 5 mm plate thickness Al7072 plate, this paper expected to reduce the welding current to 165 A; the welding speed is still 2.5 mm/s. In the case of reducing the heat input parameter, the optimization of groove process parameters is to achieve the full penetration of the plate as well as high-performance goals. Except for the groove machining process parameters, the control variable method was applied to keep the remaining parameters constant. In this research, the current polarity was set to direct current electrode negative (DCEN) (for breaking down the oxide film on the surface of the aluminum alloy). The shielding gas was argon with a purity of 99%, the shielding gas flow rate was regulated at 15 L/min, the welding method was butt welding, the welding current was 165 A, the voltage was 15 V, and the welding speed was set at 2.5 mm/s.

3. Results and Discussion

3.1. The Influence of Groove Angle on Welding Quality

Groove parameters (groove angle, root face, and reserved gap) affect the dissolution, diffusion, and precipitation behavior of gases by regulating the temperature distribution, fluidity, and cooling rate of the molten pool. At the molecular and atomic level, an unreasonable design of the groove leads to gas oversaturation in the molten pool, intensified crystal interface segregation, and gas atom precipitation to form pores. At the crystal level, the porosity defects combine with microcracks at the grain boundary to become the weak region of the weld. Therefore, a reasonable design of the groove angle to improve the molten pool fluidity and optimization of the passivated root face and the reserved gap to provide an escape gas channel are the key strategies to inhibit weld porosity defects and enhance the overall performance of the weld. As shown in Figure 3, when controlling the size of the root face, and the reserved gap is unchanged, the groove angle has a significant effect on the weld depth and porosity distribution. When the groove angle is 45°, the cooling rate is faster, the local heat dissipation is intensified, and the gas cannot be diffused to the surface of the molten pool in time to escape and ultimately is captured by the crystal, leading to the formation of micro-scale porosity defects, resulting in the emergence of a larger number of larger porosities near the fusion line, the growth of an equiaxial crystal area downward, the weld depth of melting being only 3 mm, and the organization not being uniform. When the groove angle is increased to 60°, the molten pool mobility is improved; the weld depth reaches 5 mm and shows smooth, consistent bead morphology. The cross-section defects are significantly reduced, and only in the heat-affected zone and the center of the weld are a few porosities found. With the groove angle further increased to 75°, the minimum height of the front of the weld is 0.9 mm, the cooling rate is moderate, the gas escape is more adequate to achieve single-sided welding and double-sided molding, the cross-section did not see obvious defects, and the metallographic organization of the pores is small in size and in a uniform distribution.

It can be concluded that, when the groove angle is too small (45°), the arc heat input is concentrated on the upper surface of the plate, and part of the arc fails to penetrate deep into the interior of the groove, which results in the molten pool not completely melting through the plate, forming localized unfused defects. At the same time, the groove volume is small; the molten pool is subject to both sides of the groove inclined surface and the geometry of the V-shaped groove compression and extrusion effect, so that the molten pool mobility is reduced, the gas escape channel is blocked, and the gas dissolved in the molten pool cannot diffuse to the surface to escape. During the rapid cooling process, the gas solubility decreases dramatically, leading to the precipitation of gas at the grain boundaries and within the grain, forming more and larger porosity defects. At the crystal structure level, these porosities are mostly distributed near the fusion line, and the angle between the fusion line and the horizontal plane is the smallest (37°), which further limits the metallurgical bonding effect of the weld.

With the groove angle increased to 60°, the fusion line and the horizontal plane angle are increased to 55°, the melt pool geometric space increases, the arc goes more easily deeper into the inside of the groove, the heat distribution is more uniform, and the fluidity of the melt pool is significantly improved. At this time, the downward convection of the molten pool enhances the gas diffusion and escape more fully, there is the formation of a smooth fish-scale pattern of full penetration morphology, and the porosity defects are significantly reduced. When the groove angle was further increased to 75°, the fusion line angle (52°) was slightly reduced, but the welded joints realized one-side welding and two-side forming, and no obvious defects were found in the cross-section. The moderate fusion angle improves the heat transfer between the molten pool and the base material and promotes the metallurgical bonding of the crystalline structure, which improves the densification and mechanical properties of the weld [13].

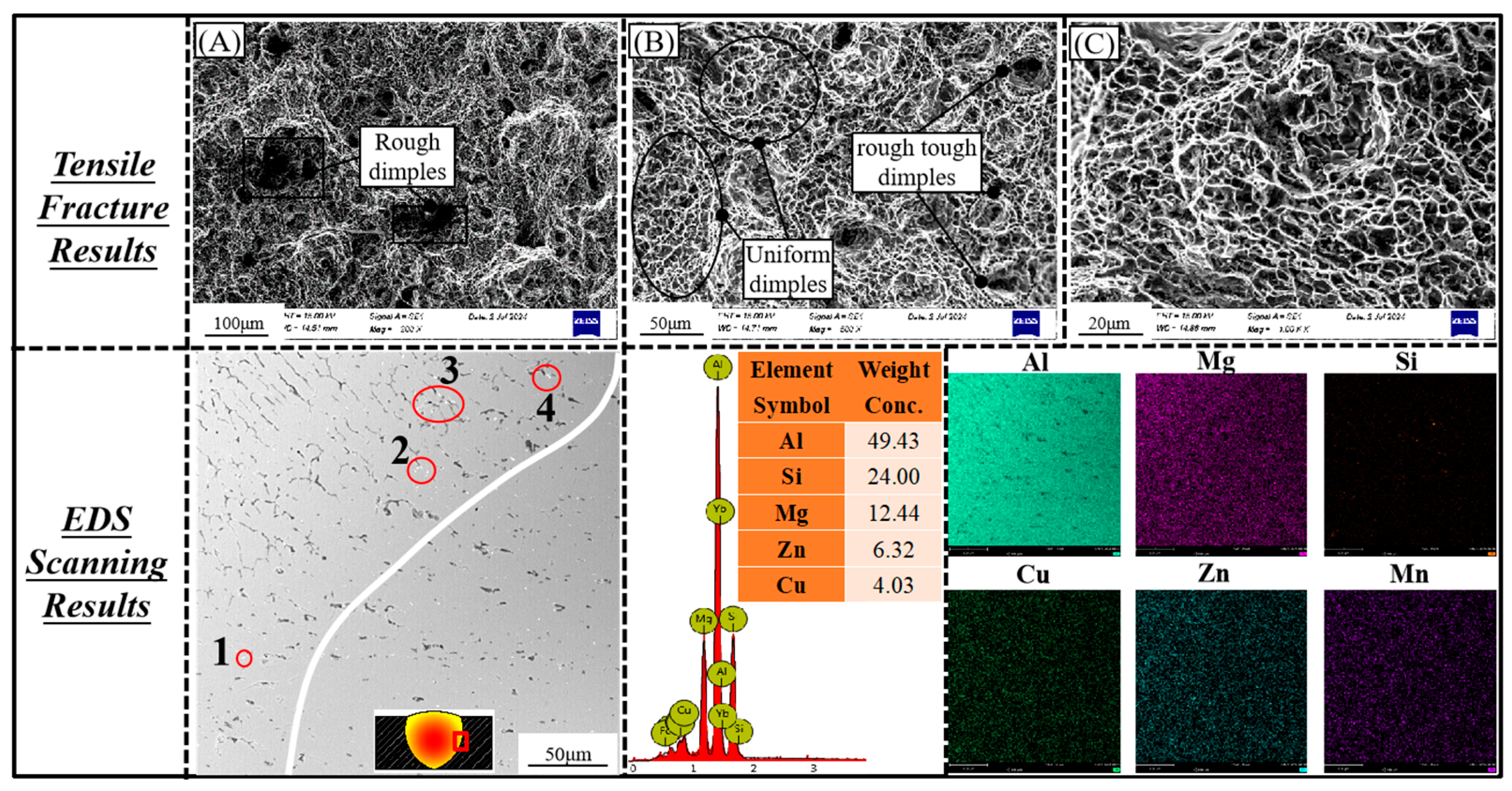
As a high-strength aluminum alloy, the main alloying element of Al7072 is zinc (Zn), which has a complex phase transition and microstructure evolution mechanism during the welding process. During the GTAW welding process, the precipitation phases in the weld seam of ER5356 wire are distributed in granular and chain form (as shown in Figure 4), and the main phases include α-Al, β-AlFeMg, θ-Al₂Cu, β-Mg₂Si, and η-MgZn₂, etc. These precipitated phases significantly enhance the weld strength through solid-solution hardening and age hardening mechanisms, but they are also accompanied by the formation of brittle phases [14]. During the welding process, the Mg element is susceptible to burnout due to high evaporation, and the supplementation of the Mg content in the ER5356 wire promotes the generation of β-Mg₂Si-strengthened phases, whereas η-MgZn₂ mainly originates from the base material Al7072. The increase in weld heat input at increasing groove angle exacerbated the vaporization of Zn and its redeposition in the cooled region, thus elevating the Zn content in the weld (as shown in the SEM surface scan in Figure 4). The increase in Zn content in the weld promoted the generation of a MgZn₂-reinforced phase, which significantly increased the tensile strength and elongation at break of the weld by hindering the dislocation motion and optimizing the weld microstructure, which was highly consistent with the experimental results. This process reflects the coupled mechanism of heat input–matter transport-–tissue strengthening [15].

In the metallographic organization, the grain size in the heat-affected zone (HAZ) increases compared to that of the base material, mainly due to grain re-growth caused by welding heat input and the formation of low melting point eutectics (e.g., AlFeSi) at the grain boundaries. These eutectics partially “self-heal” during cooling; however, the presence of brittle phases (e.g., AlFeSi and β-AlFeMg) reduces the fracture toughness and hardness of the alloy, resulting in the lowest microhardness of the HAZ [16]. In addition, the θ(Al₂Cu)-strengthened phases together with grain boundary precipitation-strengthened phases (e.g., β-Mg₂Si and η-MgZn₂) enhance the strength of the weld through the solid-solution hardening mechanism but reduce the plasticity and toughness (as shown in Figure 4, points 1–3) [17].

Taken together, a reasonable groove angle (e.g., 60° or 75°) and appropriate root face design can balance the mobility of the molten pool and the metallurgical reaction rate, inhibit the formation of porosity defects, optimize the crystal structure and the distribution of reinforcing phases, and thus enhance the comprehensive performance of the weld. At the same time, through the regulation of heat input and groove geometry parameters, the heat-affected zone grain growth and brittle phase precipitation of Al7072 welded joints can be effectively controlled to ensure the strength, toughness, and stability of the joint [18].

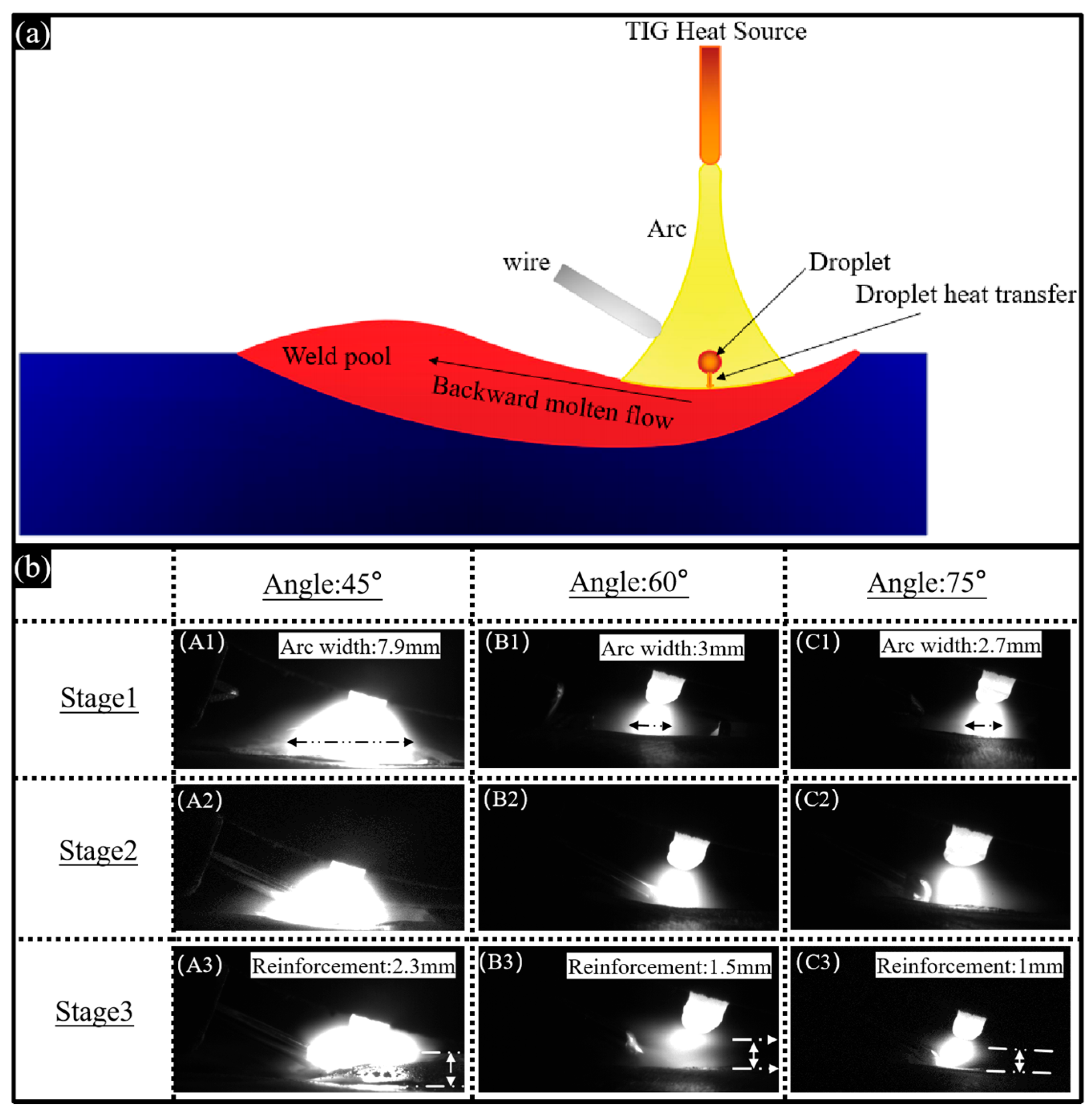
The welding molten pool undergoes three critical stages, the formation stage (stage 1), the stabilization stage (stage 2), and the solidification stage (stage 3), as shown in Figure 5b. As can be seen from Figure 5b, the groove angle has a significant impact on the arc distribution, melt pool flow, and weld forming quality. When the groove angle is small (45°), the arc is attracted by the top of the plate, and, according to the minimum voltage theorem, the arc tends to the shortest path and cannot penetrate deep into the groove, and the heat is distributed on the surface, and the arc width is the largest (7.9 mm). At this time, the volume of the melt pool is limited, and the geometric extrusion effect of the grooves on both sides further reduces the fluidity of the melt pool, and the gas escape channel is blocked, resulting in the dissolved gas in the melt pool not being able to diffuse to the surface in time to escape. In the process of rapid cooling, the solubility of the gas drops sharply, and the precipitated gas aggregates in the grain boundary and the grain, forming more and larger porosity defects, with the largest residual height (2.3 mm), insufficient weld penetration, and easy-to-produce defects such as non-fusion. As the groove angle increases to 60°, the arc gradually penetrates into the groove, the arc width shrinks to 3 mm, the heat distribution is more concentrated, the fluidity and downward convection of the molten pool are significantly enhanced, the molten droplets fill the root of the groove more evenly, and the residual height is significantly reduced to 1.5 mm. When the groove angle is further increased to 75°, the arc concentration is the largest, the melting position at the top of the groove side surface is reduced, the molten pool is enhanced by downward convection under the action of gravity, the penetration effect is better, the residual height is the smallest (1 mm), and the welded joint is single-sided welding and double-sided forming. In this case, the root face plays a critical role in controlling the penetration depth, preventing excessive heat input from causing burn-through of the plate, while maintaining the integrity and quality of the weld [19].

With appropriate addition of the reserved gap, under the synergistic effect of the surface tension of the molten droplets and gravity, the metal liquid can flow freely and penetrate, further improving the effect of filling the molten pool. At the same time, the reserved gap can compensate for the dimensional changes caused by thermal expansion and cooling contraction during the welding process, reduce residual stress and microcracks, and improve the denseness and metallurgical bonding quality of the weld.

Taken together, the increase in groove angle optimizes arc heat distribution, improves molten pool fluidity and downward convection, and significantly reduces defects such as residual height and porosity. The synergistic regulation of the root face size and the reserved gap further balances the depth of penetration and heat input, suppressing the problems of burn-through and thermal deformation of the sheet. At the mechanism level, the groove parameter significantly improves the densification, strength, and stability of the weld by regulating the thermodynamic behavior of the molten pool, solid–liquid phase transition, and gas precipitation process, which provides a theoretical basis and practical guidance for the optimization of the welding process.

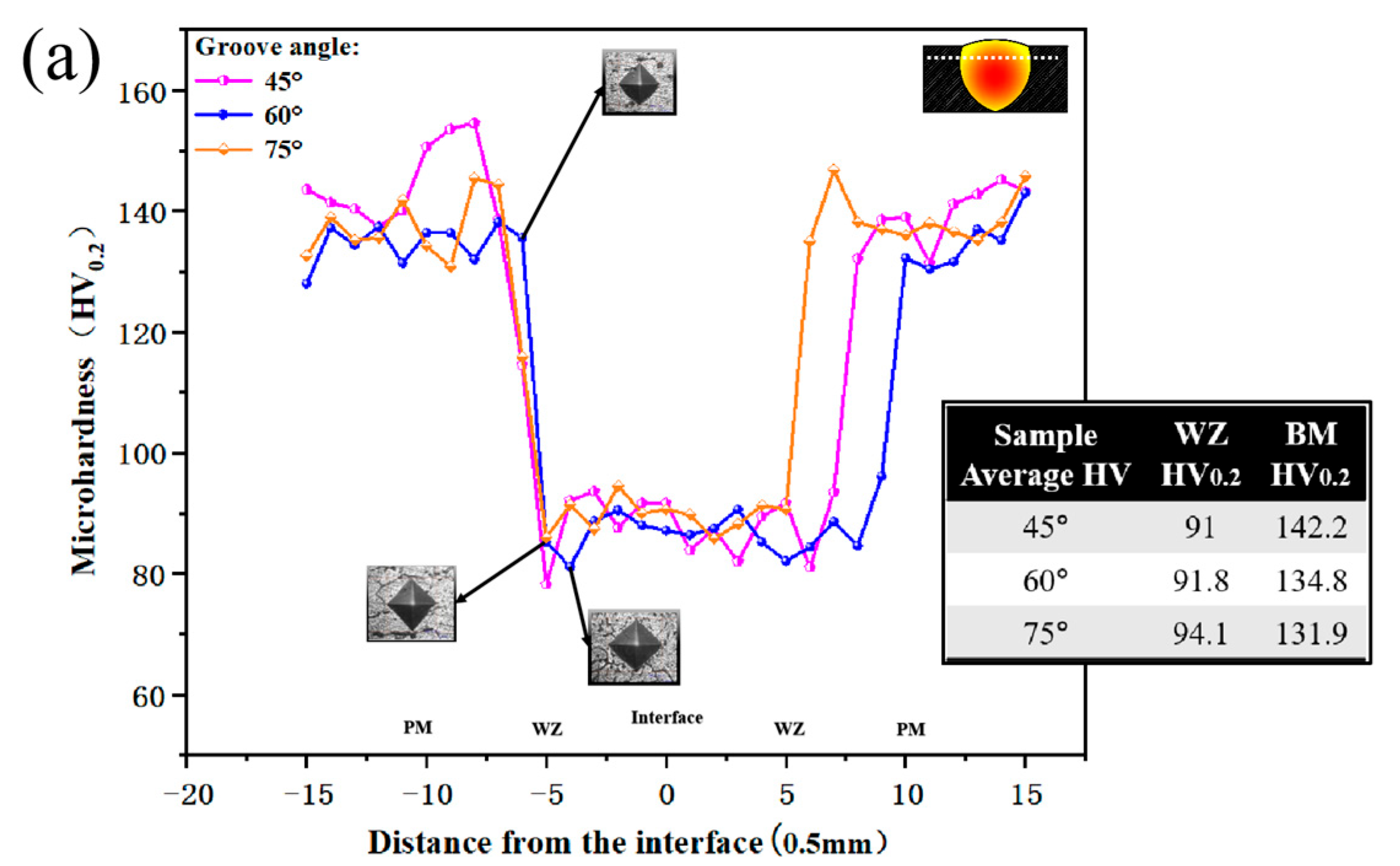
Figure 6a illustrates the hardness gradient across the cross-sections of welds with different groove angles, exhibiting a W-shaped hardness curve. For the joint with a 45° groove angle, the base metal exhibits the highest hardness, while the weld metal demonstrates the lowest. Conversely, for the 75° groove angle, due to the significant influence of arc heat, the hardness of the base metal decreases, but the hardness of the weld metal increases. The weld metal hardness distribution in joints with 60° and 75° groove angles is uniform, with minimal fluctuations. The 45° groove angle, due to its smaller groove inclination, significantly enhances the compressive effect on the molten pool, restricting its fluidity and leading to uneven heat distribution [20].

Figure 6b presents the tensile fracture morphologies. The fracture specimen from the 45° groove angle contains numerous large pores and quasi-cleavage planes, suggesting the possibility of brittle fracture (as shown in Figure 6(bA1–bA3)). In contrast, the 60° groove angle fracture specimen exhibits fewer and smaller pores, along with large bands of equiaxed dimples, indicating good plasticity and toughness (as shown in Figure 6(bB1–bB3)). The 75° groove angle fracture specimen has the fewest pores (as shown in Figure 6(bC1–bC3)), featuring rough and deep dimples as well as fine and uniform dimple bands, primarily indicating ductile fracture. The tensile strengths are 170 MPa, 263.8 MPa, and 293.5 MPa, respectively, which align with the observed fracture morphologies. All tensile fractures occurred in the heat-affected zone (HAZ), as the tensile strength of the ER5356 welding wire is significantly lower than that of the 7072 base material. Additionally, the welding thermal cycling in this zone leads to microstructural coarsening, phase transformation embrittlement, residual stress concentration, and reduced toughness, resulting in a locally weakened area that becomes the preferred initiation site for fracture.

3.2. Influence of Root Face Height on Weld Quality

In welding, the purpose of the root face is to prevent the molten pool from melting through the base material while providing a smooth transition area. A root face height parameter that is either too large or too small can compromise the stability of the molten pool, particularly at the root. An unstable molten pool can hinder the ability of gas bubbles to break up and escape, leading to the formation of pores, cracks, and unfused defects within the joint [21].

When the groove angle is set to 45°, with a 0.75 mm reserved gap and a 2 mm root face, the penetration depth is 2 mm. At the start of the root face, incomplete fusion is observed, and there are large pores at the top of the weld. The fusion angle is measured at 33°. When the root face is reduced to 1 mm, the penetration depth increases to 3.4 mm, with incomplete fusion still present at the top. The fusion angle remains at 32°, indicating that the root face has a minor impact on the fusion angle with a smaller groove angle.

For a groove angle of 60°, a 0.75 mm reserved gap, and a 1.5 mm root face, the number of pores decreases but their size remains large, with a penetration depth of 3.75 mm. This is due to the shortened existence time of the molten pool when the root face is too large, limiting the escape of gases, which then form pores during solidification. When the root face is reduced to 1 mm (Figure 7d), the penetration depth increases to 4 mm, and the pores are significantly reduced. The fusion angle decreases to 32° (compared to 46° with a 1.5 mm root face). A smaller fusion angle can reduce welding deformation and heat input but may also increase the risk of defects. An appropriate fusion angle is crucial for achieving high-quality joints.

In summary, achieving an optimal root face is paramount for ensuring high-quality joints. When considering weld shaping, melting depth, and defect control, the parameter of a 1 mm root face, as depicted in Figure 7d, emerges as the best choice. This configuration enhances melting depth, effectively minimizes porosity defects, optimizes molten pool stability, and elevates the overall quality of the welded joint.

As shown by the FM-800 measurements and subsequent analysis, the PM hardness rises in tandem with the increasing size of the root face, whereas the WZ hardness exhibits an inverse trend. An enlargement of the root face leads to a reduction in the groove area, which in turn decreases the cooling rate of the weld. This deceleration hinders the refinement of equiaxial crystals, ultimately causing a decline in WZ hardness. Simultaneously, as the root face increases, the initial distance between the heat source and the base material expands, reducing heat transfer efficiency. This helps preserve the hardness of the base material, resulting in a gradual increase followed by a decrease in hardness from the WZ through the HAZ. This variation is influenced by the inhomogeneous structure of the weld. Consequently, the hardness curve typically assumes a W-shape. Notably, an increase in the root face significantly diminishes the WZ hardness amplitude while enhancing the WZ width and hardness uniformity (as illustrated in Figure 8(aA,aB)).

Figure 8b displays the tensile fracture morphologies for different root faces. In Group 1 (as shown in Figure 8(bA1,bB1)), when the root face is 1 mm, the fractures are characterized by multiple porosity defects, with a small number of ductile dimple areas visible at the bottom (see Figure 8(bA2) for details). All the welded joints in this group exhibit incomplete fusion issues. However, when the root face increases to 2 mm, welding slag inclusion occurs (as shown in Figure 8(bB1)), a defect that significantly weakens the tensile strength, plasticity, and toughness of the weld. Upon further examination of the fracture at 500× magnification (Figure 8(bB2)), rough and large ductile dimples are visible, indicating an adverse effect on the ductility and toughness of the joint.

In Group 2, the tensile fractures of both sets of specimens occurred in the HAZ; the tensile fracture observed at a 1.5 mm root face exhibited large and deep porosity defects, with rough and prominent dimples in the center (as shown in Figure 8(bC1–bC3)). Across all the joints, unfused issues were prevalent. However, when the root face was 1 mm, a fine dimple bands strip was present at the junction of the weld and base metal. Under 500× magnification, small and uniform dimple bands were visible, potentially resulting from uneven plastic deformation during the tensile process. The size of the root face had a significant impact on tensile strength, with the experimental groups recording tensile strengths of 166.5 MPa and 156.5 MPa (Group 1) and 247.65 MPa and 251.11 MPa (Group 2), respectively. A properly blunted root face prevents fusion penetration and ensures weld stability, while an excessively large root face leads to unfused (defective) welds. The tensile strength and tensile fracture morphology characteristics of the experimental groups were highly consistent, confirming the crucial influence of root face on weld quality.

3.3. Influence of Reserved Gap on Weld Quality

A reasonable reserved gap helps minimize thermal stresses and deformations during the welding process, allowing the weld pool to expand more freely into the reserved gap without exerting excessive thermal influence on the workpiece. Reserving an appropriate reserved gap compensates for the dimensional changes in the base material due to thermal expansion, thereby ensuring welding quality [22].

When comparing the joints in Figure 9a,b, which feature a groove angle of 60° and a root face of 2 mm, the welded joints exhibit satisfactory forming quality. However, they do possess unfused defects, suggesting inadequate melt pool fluidity and filling. Upon increasing the reserved gap to 1.5 mm, the depth of fusion increased from 3.59 mm to 3.9 mm, the fusion angle expanded from 31° to 53°, the stability of the molten pool significantly improved, and porosity defects were greatly diminished. In the scenario featuring a groove angle of 60° and a root face of 1 mm, achieving full penetration is observed when the reserved gap is set to 0 mm. This results in a fusion depth of 5 mm, an optimized fusion angle of 55°, minimal porosity content, and exceptional weld density and forming effects. Conversely, increasing the reserved gap to 0.75 mm leads to a decrease in fusion depth to 3.4 mm, a narrowing of the fusion angle to 32°, and an increase in porosity. This suggests that an excessively wide reserved gap causes heat dispersion and impedes melt pool flow, compromising penetration and defect control.

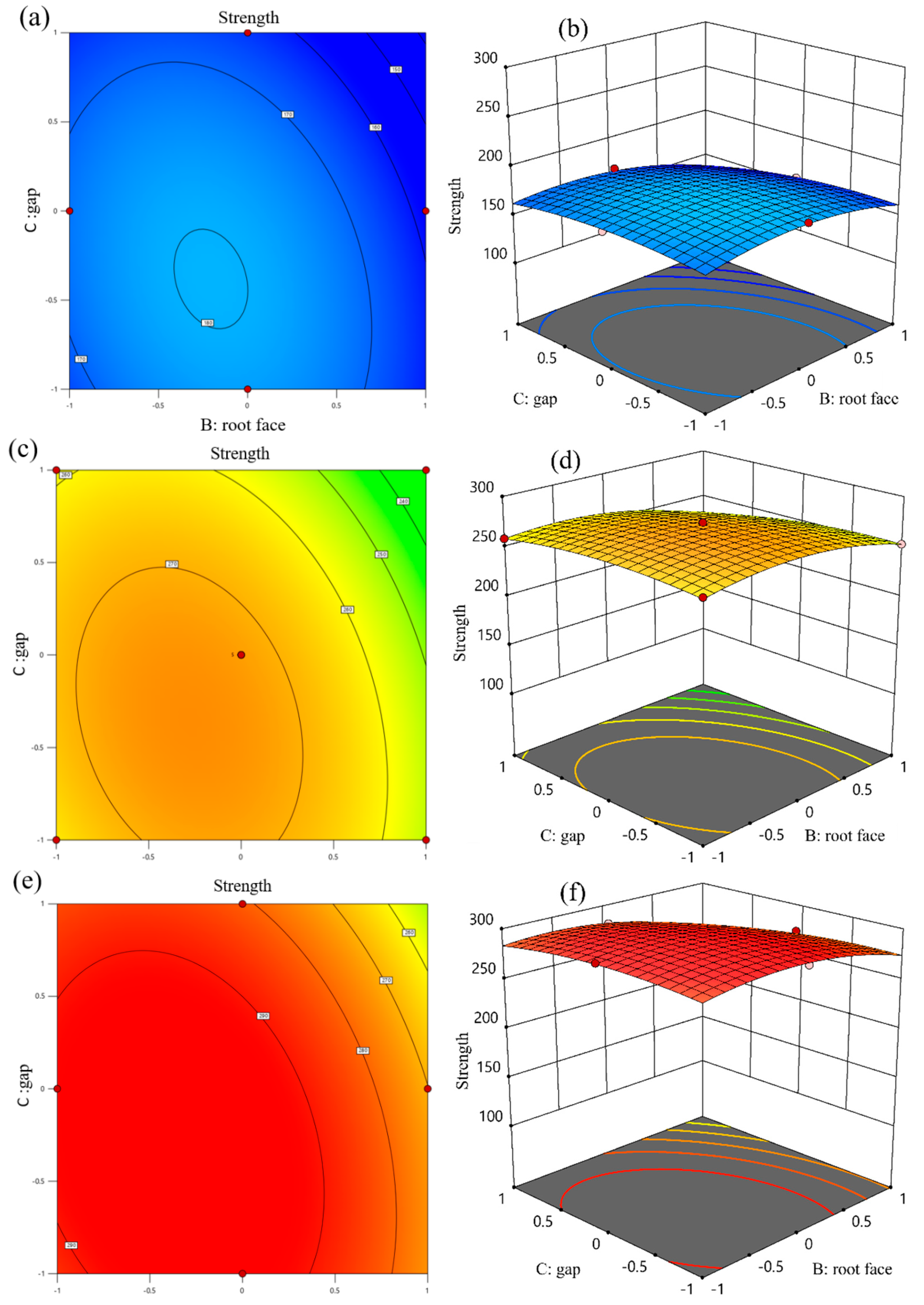
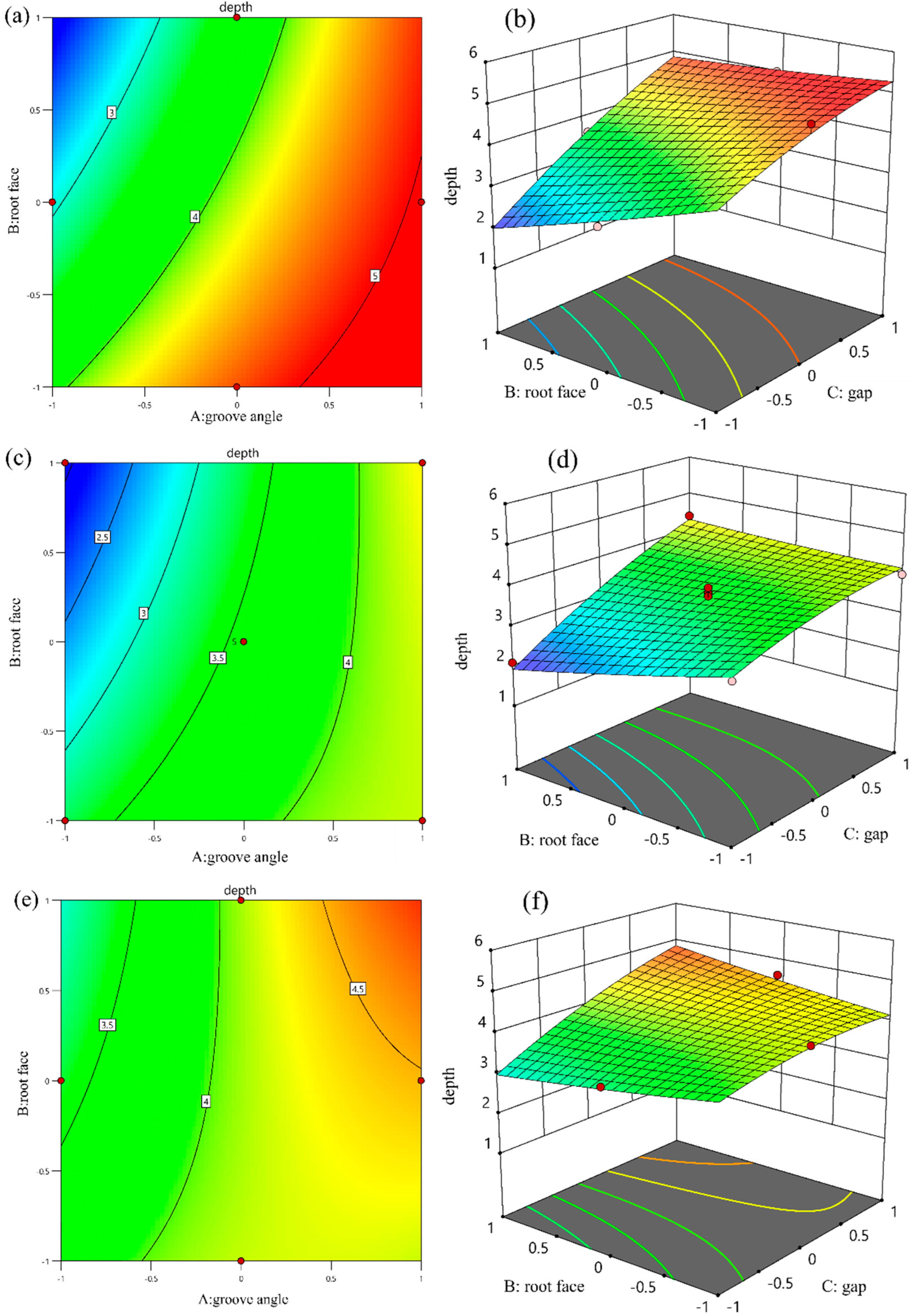
Hence, widening the reserved gap when dealing with a large root face promotes stable flow of the molten pool, boosts penetration, minimizes porosity, and enhances joint quality. Conversely, in the case of a small root face, an excessively large or mismatched reserved gap leads to heat loss from the molten pool, compromising fusion quality. Therefore, in this paper, the BBD method is used to optimize the groove parameters in order to enhance the depth of fusion and tensile strength.

Figure 10a illustrates that the relationship between the reserved gap and microhardness is nonlinear. Specifically, the highest average hardness of 94.1 HV_0.2 was recorded for the weld zone (WZ), with a reserved gap of 0.75 mm, while the average hardness for the parent metal (PM) was 136 HV_0.2. A moderate increase in the reserved gap to 0.75 mm enhanced the microhardness of the WZ. However, an excessive enlargement of the reserved gap to 1.5 mm resulted in a decrease in microhardness. As previously discussed, a moderate reserved gap can effectively compensate for the dimensional changes due to thermal expansion during welding, thereby enhancing the overall performance of the welded joint. Conversely, an excessively large reserved gap can lead to welding omission, manifesting as unfused defects in parts of the weld, which ultimately compromises weld quality.

Figure 10b displays the morphology of tensile fractures observed with varying the reserved gap. In Group 1, fine dimples bands and large air holes are evident when the reserved gap is 0 mm (as shown in Figure 10(bA1–bA3)). As the reserved gap increases to 1.5 mm (as shown in Figure 10(bB1–bB3)), the number of air holes rises, and the dimples becomes rough. In Group 2, with a 0 mm gap (as shown in Figure 10(bC1–bC3)), numerous small air holes are present, and SEM images at 500× magnification reveal microvoids, indicative of good plasticity and toughness. When the gap is 0.75 mm (as shown in Figure 10(bD1–bD3)), fine dimples strips are visible in the center, accompanied by unfused defects. The large dimples in the lower left end are densely populated with smaller dimples, potentially resulting from the unique role of uneven plastic deformation during aluminum alloy stretching. The tensile strength data for the reserved gap parameter groups (Group 1 and Group 2) are 253.2 MPa and 263.8 MPa (Group 1) and 229.05 MPa and 251.11 MPa (Group 2), respectively. These results suggest that selecting an appropriate reserved gap can significantly reduce porosity defects and their sizes, thereby enhancing the depth of fusion to a certain extent. Conversely, an excessively large reserved gap leads to poor fusion of the joint, which aligns with the morphological characteristics of the tensile fracture, further confirming the crucial impact of the reserved gap on weld quality.

4. Response Equation Development and Significance Analysis

4.1. (Box-Behnken) BBD Response Equation Establishment

By scientifically and rationally designing the grooving parameters, the quality of welded joints can be significantly improved, the efficiency of the welding process optimized, and the reliability of the results enhanced. In the pursuit of optimizing the quality of aluminum alloy GTAW welded joints, several common optimization design methods are employed, including the orthogonal experiment method, Taguchi method, artificial neural network method, and response surface methodology. Response surface methodology is a Design of Experiments (DOE) technique that aims to establish a functional relationship between a response and multiple input variables, while also identifying the control factors that exert a significant influence on the response. In RSM, Central Composite Design (CCD) and BBD are the most widely used techniques for developing second-order models [23,24]. CCD, or Central Composite Design, is a fractional factorial design that typically employs five levels per factor. It has been extensively studied for the purpose of investigating welding processes.

In the realm of welding, the BBD strategically avoids the extreme corners and starting points of the model space, instead centering its design matrix around the midpoint of the operational range. In this particular study, the DOE approach involves a combination of three factors, each evaluated at three distinct levels. Notably, BBD, being inherently a three-level design that assigns three specific values to each input parameter, necessitates a more compact sample size compared to the CCD. Despite its reduced sample requirement, BBD maintains a robust level of prediction accuracy, ranging from medium to high. Considering that the objective of this paper does not extend to predicting complex, higher-order interactions, the BBD design was deemed the most suitable choice for our experimental setup.

In this paper, three key parameters of the groove were selected for investigation: groove angle, root face height, and reserved gap. A three-factor, three-level BBD response surface model was subsequently developed, and a schematic representation of this model is depicted in Figure 11. Among these parameters, the groove angle has a significant impact on the fusion ratio (defined as the area of weld metal melted divided by the total area of the weld joint) and the weld heat input. Specifically, smaller groove angles generally necessitate more weld layers but can help minimize heat input and reduce distortion. Conversely, larger groove angles decrease the number of weld layers required but may lead to increased heat input and greater distortion [25].

The root face refers to the portion of the groove’s bottom that is not fully cut away. This feature serves to decrease the depth of the weld pool and aids in controlling both the heat input and the shape of the pool. A root face that is excessively large can pose welding challenges, while one that is too small may result in inadequate fusion of the joint.

The reserved gap, on the other hand, pertains to the space present between the plates prior to welding. Properly sized gaps contribute positively to the formation of the weld pool and the flow of filler material into the joint. However, excessively large gaps can lead to poor weld formation and the occurrence of welding defects [26].

Consequently, in this paper, the BBD response surface model is employed to identify the optimal combination of groove parameters. The aim is to achieve superior welding outcomes, enhance the performance of welded joints, minimize defects, and boost productivity.

Table 3. Test factors and levels.

Factor	Coded Values and Levels
	−1	0	1
Groove angle (A)	45	60	75
Root face height (B)	1	1.5	2
Reserved GAP (C)	0	0.75	1.5

below presents the experimental factors and their respective levels utilized in the BBD design.

Tensile strength and melting depth are the two primary indicators used to assess the performance of welded joints. Consequently, we have established tensile strength (T) and melting depth (M) as functions of the groove angle (A), root face height (S), and reserved gap (G). Mathematically, this relationship can be expressed as follows:

Tensile strength/Melting depth (TS/MD) = F (A, S, G)

(1)

The second order polynomial (regression) equation used to represent the response surface for tensile strength, melt depth is given in the following Equation:

$$\gamma ={\beta }_0+\sum _{i=1}^k{\beta }_i X_i+\sum _{i=1}^k\sum _{i=1}^k{\beta }_{ij} X_{i }{X}_i+\sum _{i=1}^k{\beta }_{ii} {X^2}_i+\epsilon$$

(2)

where y is the response variable for tensile strength and melt depth; ε is various errors; β is the coefficient estimate. Table 3 shows the factor codes (

Table 4. The tensile strength and elongation properties of the response surface experimental group after welding and after breaking.

Sample	Coding Matrix			Strength (MPa)	Elongation (%)	Depth (mm)
1	−1	−1	0	170	8.29	3.2
2	1	−1	0	293.5	13.63	4
3	−1	1	0	156.5	7.27	2.1
4	1	1	0	272.5	12.46	4.4
5	−1	0	−1	178.55	7.8	2.8
6	1	0	−1	291.88	13.55	5
7	−1	0	1	166.5	7.73	3.4
8	1	0	1	280.2	13.01	4.6
9	0	−1	−1	263.8	12.25	5
10	0	1	−1	253.2	11.75	3.59
11	0	−1	1	258.6	12.1	4.2
12	0	1	1	229.05	10.64	3.9
13	0	0	0	269.8	11.5	3.69
14	0	0	0	273.8	11.66	3.38
15	0	0	0	272.1	11.56	3.61

shows the tensile strength and elongation at break of welded joints in the experimental group).

4.2. BBD Response Equation Analysis

Design-Expert software was utilized to carry out the center combination experiment. Table 4 outlines the factorial coding and the measured response values for GTAW welding in this experiment. Within the specified range of grooving process parameters, the tensile strength varied between 156.5 MPa and 291.88 MPa, while the depth of fusion ranged from 2.1 mm to 5 mm. The R² values for the quadratic equation models for tensile strength and penetration depth were 0.9988 and 0.9609, respectively, indicating a good fit of the model. The F-value and probability p-value (>F) of the model were significant, suggesting a small model misfit. The final fitted quadratic polynomials for the response variables, tensile strength (S) and depth of fusion (P), are as follows:

Strength = 272.40 + 58.32A − 9.33B − 6.64C − 1.88A ∗ B + 0.0925A ∗ C − 4.74B ∗ C − 35.58A² − 13.70B² − 7.54C²

Penetration = 3.576 + 0.8125 ∗ A − 0.30125 ∗ B − 0.03625 ∗ C + 0.375 ∗ AB − 0.25 ∗ AC + 0.2775 ∗ BC − 0.18675 ∗ A²+ 0.03575 ∗ B² + 0.56075 ∗ C²

In response surface analysis, Analysis of Variance (ANOVA) is frequently employed to verify the accuracy of the established models. The F-values for the models corresponding to tensile strength and depth of fusion are 9 and 8.59, respectively(as shown in

Table 5. ANOVA results of tensile strength regression models.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	35,159.36	9	3906.60	667.70	<0.0001	significant
A-groove	27,206.28	1	27,206.28	4649.97	<0.0001
B-root face	696.58	1	696.58	119.06	<0.0001
C-gap	352.19	1	352.19	60.19	0.0001
AB	14.06	1	14.06	2.40	0.1650
AC	0.0342	1	0.0342	0.0058	0.9412
BC	89.78	1	89.78	15.34	0.0058
A2	5329.51	1	5329.51	910.89	<0.0001
B2	789.99	1	789.99	135.02	<0.0001
C2	239.38	1	239.38	40.91	0.0004
Residual	40.96	7	5.85
Lack of Fit	27.38	3	9.13	2.69	0.1817	not significant
Pure Error	13.58	4	3.39
Cor Total	35,200.31	16

and

Table 6. ANOVA results of the melt depth regression model.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	8.58	9	0.9534	19.13	0.0004	significant
A-groove	5.28	1	5.28	105.99	<0.0001
B-root face	0.7260	1	0.7260	14.57	0.0066
C-gap	0.0105	1	0.0105	0.2110	0.6599
AB	0.5625	1	0.5625	11.29	0.0121
AC	0.2500	1	0.2500	5.02	0.0601
BC	0.3080	1	0.3080	6.18	0.0418
A2	0.1468	1	0.1468	2.95	0.1297
B2	0.0054	1	0.0054	0.1080	0.7520
C2	1.32	1	1.32	26.57	0.0013
Residual	0.3488	7	0.0498
Lack of Fit	0.1983	3	0.0661	1.76	0.2940	not significant
Pure Error	0.1505	4	0.0376
Cor Total	8.93	16

). The probability values p > F are both less than 0.05, and, specifically, for tensile strength, the p > F value is less than 0.0001, indicating that the models are significant and statistically reliable. These models can accurately reflect the relationship between the groove angle, root face dimensions, and reserved gap, and the regression models are suitable for predicting the outcomes. The Lack of Fit (LF) values for the tensile strength and depth of fusion models are 27.38 and 0.1983, respectively, which are non-significant, further confirming the reliability of the models and the goodness of fit of the regression models. The p-values for both models are 0.1817 and 0.294, respectively, both exceeding 0.05, which underscores the high accuracy of the regression equations. Ideally, a signal-to-noise ratio greater than 4 is desired, and both corresponding ratios exceed this threshold, indicating sufficient signal. Therefore, the experimentally developed model can analyze and predict the tensile strength and depth of fusion of Al7072 welded joints with relatively high accuracy.

The p-values for the effects of groove angle, root face height, and reserved gap on tensile strength in the quadratic model are <0.0001, <0.0001, and 0.0001, respectively. This suggests that the groove angle and root face height have a highly significant impact on tensile strength, followed by the reserved gap. For the interaction effects, the p-value of the coefficient for the interaction between root face height and reserved gap is 0.0058, which is less than 0.05 and therefore considered to have the most significant effect among the interaction terms.

Regarding the penetration depth in the quadratic model, the p-values for groove angle, root face height, and reserved gap are <0.0001, 0.0066, and 0.6599, respectively. This indicates that the groove angle has a very significant effect on melt depth, followed by a moderate effect from the root face height. The reserved gap has a negligible effect. For the interaction effects, the p-value of the coefficient for the interaction between groove angle and root face height is 0.0121, which is less than 0.05 and therefore considered to be the most significant interaction term.

4.3. Optimization and Selection of Groove Parameters

Figure 12a illustrates the normal probability distribution of the residuals for the tensile strength model. It is evident that the residuals of the model are approximately aligned along a straight line, suggesting that the regression model exhibits a good fit. The distribution of errors is relatively uniform, with no significant large deviations or singularities. This indicates that the model can predict the values of the response quantities with high accuracy [27]. By understanding the influence of each input variable (A, B, C) and their interaction terms (such as AB, AC, BC, etc.) on the nature of the response quantity, one can more accurately predict the trends in the variation of the GTAW welding groove process parameters. Furthermore, analyzing these variables can provide theoretical insights and references for fine-tuning the process parameters.

The quadratic fitting equation and ANOVA results reveal that the groove angle exerts the most profound influence on the tensile strength of welded joints, demonstrating a consistent trend in its variations. As the groove angle progressively increases (such as from 45°, 60°, to 75°), the tensile strength of the welded joints exhibits a linear upward trend(as shown in Figure 13). This is primarily attributed to the larger melt pool space afforded by the increased groove angle, facilitating uniform flow and expansion of the molten metal, thereby achieving excellent penetration and effectively minimizing weld defects like unfused areas, which significantly enhances the mechanical properties of the joint.

Conversely, when the groove angle is narrow, the arc struggles to effectively penetrate the groove’s bottom. Consequently, the molten pool experiences geometric constraints, and the arc’s heat becomes highly concentrated, making it challenging for the molten pool to adequately fill the groove’s bottom, leading to the formation of unfused defects. Moreover, uneven local heating at the groove’s root causes a sharp increase in the solubility of hydrogen in the metal at high temperatures. During the rapid cooling process post-welding, hydrogen diffusion is hindered, leading to the formation of pores, which severely impacts the weld’s density and tensile strength(as shown in Figure 13a,b).

Additionally, the appropriate combination of root face and reserved gap is pivotal to the quality of the welded joint. An excessively large root face restricts penetration depth, necessitates higher heat input during the welding process, and complicates single-sided welding, potentially causing insufficient penetration at the root and compromising weld performance. A moderately root face size, however, can balance penetration depth and weld formation quality even with lower heat input, optimizing weld performance.

The purpose of the reserved gap is to provide filling space and a cushioning effect. A properly sized gap enhances the fluidity of molten droplets, improving the molten pool’s filling effect at the groove’s root and ensuring complete metal fusion. Simultaneously, the gap accommodates thermal expansion and contraction during welding, reducing the incidence of microcracks and porosity defects. Furthermore, when complemented by the root face, the reserved gap facilitates consistent penetration depth and a stable weld seam shape.

Taken together, there is a significant coupling effect between the groove angle, root face, and reserved gap:

Groove angle determines the fluidity and penetration effect of the molten pool, which is the core factor affecting the quality of the weld. Root face size controls the depth of penetration; too large or too small will affect the formation of the molten pool and uniform filling. The reserved gap helps to minimize the generation of cracks and porosity defects by improving the fluidity of the molten droplet and buffering the thermal stress.

Figure 14a displays the normal probability distribution of the residuals from the tensile strength model. It is evident that the residuals are approximately aligned along a straight line, suggesting a good fit of the regression model and a more uniform error distribution.

Figure 14b presents the perturbation diagram for the welding joint’s depth of fusion. It is clear that the groove angle has the most significant impact, with a direct proportional relationship to the depth of fusion. As the groove angle increases, the arc can penetrate deeper into the groove, achieving a fused state within. Since the total volume of the molten pool remains constant, the center surface of the molten pool lowers, causing the melting position of the droplets to descend. This enhances convection downwards from the molten pool, consequently increasing the depth of the weld (as previously shown in Figure 4b).

When using a groove angle of 75° and a root face height of 1 mm (as depicted in Figure 15a,b), the butt plate can be welded directly with full penetration, ensuring that the depth of penetration matches the plate’s thickness without the need for a gap. However, when the groove angle is decreased to 45° and the height of the root face is increased to 2 mm (as shown in Figure 15b,d,f), the depth of melt can be significantly increased by appropriately adjusting the reserved gap. It is further noted that as the height of the root face passively increases, the melt depth of the welded joints decreases, as the passive root face effectively hinders the penetration of the melt pool. If the height of the root face becomes too large, it will make back-forming of the welded joint challenging. Therefore, by precisely adjusting the parameters of the reserved gap and enhancing the downward mobility of the molten droplets during welding, it is feasible to ensure complete fusion of the weld seam, thereby increasing the depth of fusion.

Obviously, when the groove angle remains constant, there exists an optimal combination of interaction parameters between the root face height and the reserved gap. This optimal parameter combination ensures a harmonious match between the two, facilitating the achievement of a greater depth of fusion in the welded joint.

4.4. Selection and Analysis of Optimal Parameters

After analyzing and validating the model’s reliability, the welding parameters were optimized. In the Optimization module of the Design-Expert 10.0.7 software (version 13.0.1), the “Criteria” tab allows for setting desired values for each welding parameter, as illustrated in Figure 16. Based on experimental conditions or the practical requirements of the welding process, welding parameters can be set to a fixed value (target, maximize, minimize) or optimized within a certain range (in range). Since the groove angle has the most significant impact on tensile strength, it was set to minimize in the “Criteria” tab to reduce the amount of weld filler material and overall heat accumulation [28]. The size of the root face has a relatively minor influence on tensile strength and was therefore set to “in range”. Similarly, to ensure adequate fusion of the weld, the reserved gap was also set to “in range”. The combination of parameters under these conditions is shown in Figure 16, with the optimal parameters found near the center of the gray area in the figure (A/B correspond respectively to X1/X2 in the input parameters of the figure box). After optimization under these conditions, the results obtained were a groove angle of 70.8°, a root face of 1.38 mm, a reserved gap of 0 mm, and predicted tensile strength and penetration values of 295.997 MPa and 4.991177 mm, respectively.

4.5. Characterization and Verification of Welded Joint Performance with Optimized Parameters

When selecting a groove angle of 70.8°, a root face of 1.38 mm, and a reserved gap of 0 mm (as depicted in Figure 17), the depth of fusion reached 5 mm, with a low frontal residual height of 1.2 mm. The base material achieved one-time weld forming. Upon examination of the optimized parameter joint sections (WZ, HAZ, BM) in the metallographic diagram, no obvious defects were observed. The welded joint surface exhibited overall good formation.

As illustrated in Figure 18A–C, the morphology of the tensile fracture obtained under the optimized groove parameters is displayed. The tensile fracture features a shallower appearance on the left side and a deeper one on the right side, exhibiting a tear-like toughness fracture with evident tear marks and fibrous characteristics on its surface (as depicted in Figure 18A). The depth of the dimples varies, with longitudinal and transverse small dense ligament nest strips staggered throughout. This observation suggests that the wire is securely bonded to the plate.

This observation suggests that the 5356 wire is thoroughly integrated with the base material. The tensile strength was accurately determined to be 297.95 MPa using the MTS Criterion universal testing machine. Meanwhile, under the optimized parameters, the BBD model predicted a tensile strength of 295.997 MPa and an elongation at break of 4.99117 mm, demonstrating an exceptional level of agreement between the modeled predictions and the experimentally obtained results.

The EDS surface scan reveals that the fusion zone comprises elements such as Al, Mg, Si, Cu, Zn, and Mn. Notably, a significant presence of white material phases, identified as β-Mg₂Si and η-MgZn₂, is observed near the fusion line of the welded joints, as indicated by the EDS point scans 1, 2, 3, and 4. The solid-solution hardening and precipitation strengthening effects of these β and η phases substantially contribute to the enhanced tensile strength of the welded joints, in line with the experimental findings. This confirms the validity and innovation of the three process parameters employed in this study to optimize the bevel using the BBD model, with the objective of achieving high-performance joints.

5. Conclusions

In this paper, based on previous research (where higher heat input parameters were employed in the initial stage to achieve full-penetration morphologies of welded joints with various groove types for 5 mm thick Al7072 aluminum alloy plates), after determining the groove type, subsequently, the welding current was reduced from the original 190 A—used for full-penetration welding of I-groove, single-bevel V-groove, and V-groove joints—to 165 A, while maintaining the welding speed at 2.5 mm/s. By optimizing the groove process parameters, I successfully achieved the objectives of full penetration and high-performance welding for the plates while reducing the heat input.

In this paper, the response surface method is used to optimize the grooving process parameters of 5 mm Al7072 base material GTAW welded joints, and the welded joints prepared under different grooving process parameters are analyzed by detailed microstructural characterization, surface morphology, and arc influence shooting. The influence mechanism of the grooving process parameters on the microstructure evolution and mechanical properties of welded joints was explored.

According to the BBD response surface method, with high tensile strength and high melt depth of welded joints as the response quantities, the optimized parameters are a groove angle of 70.8°, root face of 1.38 mm, and 0 mm of reserved gap. It was found that among the grooving process parameters, the groove angle had the most critical influence on the tensile strength and penetration depth of the welded joints. The interaction between the groove angle and the root face size dominated the change in penetration depth. Increasing the groove angle could lower the melting position at the top of the side surface of the molten pool under constant heat input, enhancing downward convection by gravity. At the same time, a larger root face size required more cumulative heat input for penetration, and the combination of the two significantly affected the penetration depth. The interaction between the root face size and the reserved gap had the most significant impact on the tensile strength. When the root face size was large, the introduction of the reserved gap could promote the free flow and penetration of molten droplets under the action of surface tension, thereby optimizing the tensile strength. Through these comprehensive optimization measures, the overall performance and reliability of the welded joints were effectively improved.

Future research could leverage advanced characterization techniques, such as TEM, AFM, and synchrotron X-ray imaging, to gain deeper insights into the microstructural evolution and defect formation in welded joints. The integration of multi-scale simulations with machine learning could further optimize welding parameters, enhancing both efficiency and precision while reducing defects. Additionally, exploring the thermodynamic and mechanical behaviors of materials, combined with data-driven approaches, will offer robust theoretical and practical support for the continued advancement of aluminum alloy welding technologies.