Abstract
Thin steel plates with stiffeners are widely used in shipbuilding, aeronautics, and civil construction due to their lightness and structural strength. This study presents a numerical model developed using ANSYS Mechanical APDL with SHELL281 finite elements to evaluate the deflection of thin steel plates with trapezoidal-shaped box-beam stiffeners, known as hat-stiffened plates. The structure is analyzed under a uniformly distributed load perpendicular to the plate, with simply supported boundary conditions. The constructal design method combined with the exhaustive search technique is employed to optimize the geometry. A volume fraction of 30% is used, transferring material from the reference plate (without stiffeners) to the stiffeners, defining parameters such as number, height, and thickness—considered degrees of freedom. The stiffener angle is fixed at 120°. The results show that increasing stiffener height and reducing thickness generally improve structural performance by reducing deflections. The best configuration with transverse stiffeners reduced deflection by 97.15% compared to the reference plate, and by 79.27% compared to the best longitudinal configuration from previous studies. Therefore, transverse stiffeners were more effective than longitudinal ones. This study highlights the importance of stiffener orientation and geometry in the structural optimization of thin steel plates.
1. Introduction
Steel plates with stiffeners are widely used in naval, automotive, aerospace industries, and in civil engineering structures [1,2]. The stiffeners make the steel plates act simultaneously as both finishing and structural elements that combine good load-bearing capacity and low weight [3]. The shape of the stiffener is critical, as it influences the mechanical behavior of the structural component composed by the plate and stiffeners. Figure 1 shows some types of stiffeners, including the hat-stiffener type illustrated in Figure 1d and investigated in the present work. The flat or I-shaped stiffener (Figure 1a) is well known as the most commonly used in structural engineering; however, the other types (Figure 1b–d) are also adopted in specific applications (Figure 1e,f).

Figure 1.
Main types of stiffeners: (a) I-shaped; (b) L-shaped; (c) T-shaped; (d) hat-stiffener; (e) application of steel hat-stiffeners in aeronautical panels, adapted from [2]; and (f) application of steel hat-stiffeners in civil construction (bridge structures), adapted from [4].
Stiffened plates have been investigated by means of computational modeling due to their great potential to develop and study different combinations of plates and stiffeners. The finite element method (FEM) plays a key role in this context, and is widely implemented in commercial software, such as ANSYS and ABAQUS. Several assessments are made during the study and development of plates with stiffeners, including geometric evaluations. For instance, the constructal design method, based on the constructal theory proposed by Adrian Bejan in 1996 [5,6,7,8,9], has proven to be an efficient tool for the geometric analysis of structural engineering problems [10]. The method is based on the constructal law as follows: “For a system with finite dimensions to remain in operation, its geometric configuration must constantly evolve always to allow the best flow of currents that flow within the system” [6,7,8,9,11]. This theory affirms that the shapes found in nature are the result of continuous evolution to allow the best flow within them. In the field of structural engineering, a structural system can be analyzed several times, adopting criteria, to find the geometry that provides the best flow of stress within it. Therefore, the application of the constructal design method requires that restrictions, degrees of freedom, and performance indicators be defined so that, in addition to finding the best geometries, it is possible to evaluate the influence of the variation of the degrees of freedom on the performance indicators and better understand the problem [6,7,8,9,11,12].
The geometric evaluation with the constructal design of stiffened plates subject to bending has already been carried out through studies that use numerical simulation. Troina et al. [13] studied plates with longitudinal and transverse I-shaped stiffeners having the same height, aiming to minimize the central deflection of these structures. Nogueira et al. [14] also investigated plates with I-shaped stiffeners, but considered different heights for the longitudinal and transverse ones, in order to minimize the maximum and central deflections of the plate.
In turn, according to Tharian and Nandakumar [15], hat-stiffeners (see Figure 1d–e) have greater torsional stiffness and a higher strength/weight ratio when compared to open section stiffeners (see Figure 1a–c). Therefore, concerning hat-stiffened plates that are the focus of the present work, some previous studies can be highlighted: Tharian and Nandakumar [16] performed a FEM numerical analysis comparing open-section stiffeners with hat-stiffeners, and highlighted the advantages of closed box beam stiffeners over open section stiffeners. Pal et al. [17] analyzed the stresses and deflections of plates with trapezoidal box beam stiffeners, keeping constant the plate volume while its geometries and boundary conditions were varied. Virág and Szirbik [18] conducted a study whose objective was to identify potentially dangerous vibration frequencies and eliminate the possibilities of failure in plates with hat-stiffeners, by means of modal analysis. Tharian and Nandakumar [15] performed a structural analysis of bunkers and developed a super element used in the numerical analysis of plates with hat-stiffeners. Filippatos et al. [19] improved the efficiency of components made of composite materials in the aeronautical industry using hat-stiffeners. Aneja et al. [20] investigated the variation of the inclination angle of the sidewalls of hat-stiffeners, indicating that an inclination angle of 120° allows for an increase in mechanical resistance. Recently, Alves et al. [21] applied the constructal design method to perform a geometric evaluation of plates with longitudinal hat-stiffeners, aiming to minimize its maximum and central deflections.
In this context, this work proposes the geometric evaluation and optimization of steel plates with transverse hat-stiffeners, simply supported and under the incidence of a uniformly distributed load. The constructal design method and the exhaustive search technique are employed in association with a FEM numerical model to reduce the maximum and central deflection of plates having transverse hat-stiffeners. For this purpose, a reference plate without stiffeners is considered, and 30% of its volume is redistributed to form hat-stiffeners; i.e., the stiffeners are generated by reducing the reference plate’s thickness while maintaining constant its width and length. The angle of the hat-stiffener sidewalls is 120°, as recommended by Aneja et al. [20]. Based on these definitions, it is possible to build hat-stiffened plates with one to nine transverse stiffeners, with heights between 175 mm and 400 mm, and thicknesses from 4.75 mm to 12.7 mm. The FEM computational model is developed in ANSYS Mechanical APDL 2024 R2 software, with the SHELL281 finite element. The obtained results are analyzed and discussed, and then compared with those reported by Alves et al. [21], who adopted a similar approach to study the maximum and central deflections of plates reinforced with longitudinal hat-stiffeners.
In addition, the relevance of the present study also lies in its focus on thin steel plates reinforced with steel hat-stiffeners, a topic that remains relatively underexplored in the current literature. While a considerable number of the published works investigate hat-stiffened plates made of composite materials [22,23,24,25,26,27,28,29,30,31,32,33], there is a clear gap when it comes to similar studies involving steel, particularly under bending loads. Given the widespread use of steel structures in civil, naval, and offshore engineering, a deeper understanding of the structural behavior of steel hat-stiffened plates is essential. This article contributes to filling this gap by offering detailed numerical analyses and insights that are directly applicable to practical engineering design with conventional construction materials.
2. Materials and Methods
To carry out the evaluation and optimization of the geometric configurations of the simply supported A36 steel plates with transverse hat-stiffeners, the constructal design method was employed in conjunction with the exhaustive search technique. It is important to note that constructal design is a geometric evaluation method and not an optimization method. Therefore, for optimization to take place, the process must be combined with an optimization method, such as the exhaustive search technique. In this way, the constructal design method is responsible for generating the search space (possible geometric configurations) while the exhaustive search technique identifies the geometry that leads to the best system performance. For the constructal design application, it is also necessary to define global and/or local constraints, degrees of freedom (which vary within the defined constraints to generate the geometric configurations), and performance indicators (which can be minimized or maximized to improve the system performance) [12].
In addition, the simply supported boundary conditions were adopted for all numerical simulations. This choice reflects practical situations frequently encountered in structural applications, where stiffened plates are supported along their edges without full rotational restraint. Examples include steel floors, bridge panels, and ship deck structures, where the plate is allowed to rotate at the supports while its vertical displacement is constrained.
In turn, the choice of A36 steel for the present study is justified by its widespread use in civil construction and naval/offshore engineering, where stiffened steel plates are commonly employed to enhance structural performance under various loading conditions. A36 steel offers a balanced combination of mechanical strength, weldability, availability, and cost-effectiveness, making it a practical and widely adopted material for structural components. In civil construction, it is frequently used in floor systems, bridge components, and industrial buildings, where stiffeners improve load-bearing capacity and control deflection. In the naval and offshore sectors, A36 steel stiffened plates are found in ship hulls, decks, bulkheads, and offshore platform modules, where they provide mechanical resistance to bending and buckling. These applications reinforce the relevance of selecting A36 steel as a representative material for investigating the structural behavior of thin plates with hat-stiffeners.
To numerically simulate the mechanical behavior of all the geometries investigated in this work, the finite element method (FEM) was used through the ANSYS Mechanical APDL software (version 2024 R2, ANSYS Inc., Canonsburg, PA, USA). The SHELL281 finite element, illustrated in Figure 2 and suitable for modeling thin to moderately thick plates, was adopted for both the plate and the stiffeners in the present work, following its application in previous studies on plated structures [10,14,21]. SHELL281 is a finite element with 8 nodes and 6 degrees of freedom per node, consisting of 3 rotations (θx, θy, and θz) and 3 translations (Ux, Uy, and Uz) [34]. In the FEM, the unknown displacements are obtained through the matrix manipulation of a system of algebraic equations [1,35,36], represented as follows:
where [K] is the global stiffness matrix, {U} represents the vector of nodal displacements to be obtained, and {F} represents the vector of nodal forces, equivalent to the forces applied to the system. To ensure that the computational model is correctly defined, validations and verifications were carried out, comparing its results with those presented in the references found in the literature.
[K]{U} = {F},
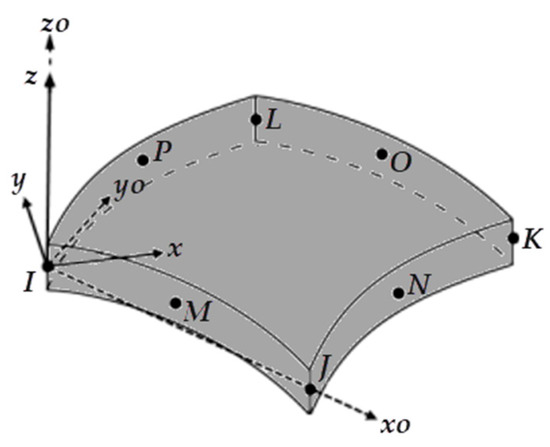
Figure 2.
Geometry of the SHELL281 element, adapted from [34].
Regarding the case study, as previously mentioned, this work aims to analyze simply supported rectangular steel plates subjected to uniformly distributed loads, reinforced with trapezoidal hat-stiffeners positioned transversely to the plate’s longest dimension. The main objective is to use the constructal design method, combined with the exhaustive search technique, to minimize both the maximum and central displacements of the hat-stiffened plates by varying the height and thickness of the stiffeners. To establish the initial dimensions of the stiffeners, a reference plate (without stiffeners) was considered, with a width of a = 2000 mm, length of b = 1000 mm, and a thickness of trp = 20 mm. A volumetric fraction corresponding to 30% of the total volume of the plate [13,14,21] was removed and transformed into stiffeners. Since a and b were considered constraints, the reduction was made in the plate’s thickness. Thus, the plates with hat-stiffeners had their thickness reduced to t = 14 mm. It is important to mention that the total material volume of the plates with stiffeners remained equal to the reference plate, since there was only a material redistribution, with the removed volume being transformed into hat-stiffeners. The material used was A36 steel, which has an elastic modulus of E = 200 GPa and a Poisson’s ratio of ν = 0.3, such as in [13,14,21]. All four edges of the hat-stiffened plates are considered to be simply supported, and a distributed load of 10 kPa is applied [13,14,21]. This load level was chosen to ensure that the structural response remains within the elastic regime. In addition, the sidewalls of the hat-stiffeners have an inclination angle of 120°, as indicated by Aneja et al. [20]. Figure 3 shows a schematic representation of a plate with two transverse hat-stiffeners. The thickness of the hat-stiffeners was based on commercially available plate thicknesses: ts = 4.75 mm; ts = 6.35 mm; ts = 8.00 mm; ts = 9.53 mm, and ts = 12.7 mm. The height of the stiffeners, hs, is related to the number of stiffeners, and the following maximum values were adopted: hs = 400 mm (one stiffener); hs = 250 mm (two and three stiffeners), and hs = 175 mm (four or more stiffeners). The application of the constructal design method allowed for the generation of 224 distinct geometries of plates with transverse hat-stiffeners. Appendix A presents the dimensions of the stiffeners used in each geometric configuration, as well as the numerical results obtained in terms of the maximum and central deflection for each proposed geometric configuration, through the Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8 and Table A9.
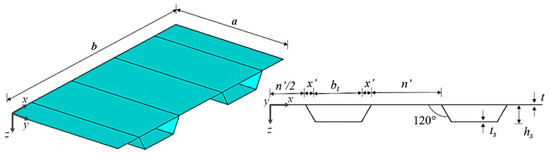
Figure 3.
Schematic representation of a plate with two transverse hat-stiffeners.
As can be seen in the example with two stiffeners, as shown in Figure 3, in order to allow multiple plates to be joined together, the distance from the transverse stiffeners to the edge of the plate will always be half the distance between the stiffeners. An exception occurs when only one transverse stiffener is used—in this case, it will be centered along the longest dimension of the plate. Also in Figure 3, bt represents the base width of the hat-stiffener, and n’ represents the distance between two stiffeners.
3. Results and Discussions
3.1. Computational Model Validation and Verification
Although the validation and verification procedures were previously presented by Alves et al. [21], they are reproduced here to clearly show the accuracy of the proposed computational model.
Regarding the model validation, an experimental study developed by Carrijo et al. [37] was numerically simulated. Figure 4a presents the geometry of the plate with I-shaped stiffeners, which has its four corners simply supported. A uniformly distributed load of 0.96 kPa is applied to the stiffened plate. The material of the plate and stiffeners has the following mechanical properties: E = 2.5 GPa and ν = 0.36. For this analysis, a converged regular mesh generated by square SHELL281 finite elements was adopted, each with a side length of 2.436 mm. Figure 4b shows the numerical result for the out-of-plane displacement distribution. The experimental test performed by Carrijo et al. [37] found a central deflection of Uz = 6.2200 mm, whereas the proposed computational model found a central deflection of Uz = 6.5075 mm. Therefore, a relative error of 4.58% between the numerical and experimental results was reached. However, it is worth explaining that the comparison with the experiment presented by Carrijo et al. [37] serves as a representative validation that supports the general reliability of the proposed FEM strategy. Although there are some differences (such as the type of stiffeners, dimensions, material, and boundary conditions), the numerical simulation of this case allows for the assessment of whether the computational model can accurately capture the fundamental physical behavior of the stiffened plates under bending. That said, one can consider the computational model validated through a proof-of-concept strategy, which is commonly adopted when an exact experimental counterpart is not available.
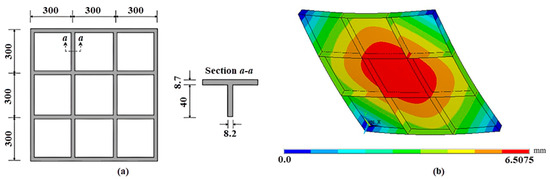
Figure 4.
Validation of the computational model: (a) dimensions (in mm) of the stiffened plate experimentally tested, adapted from [37]; (b) deflection distribution obtained numerically with the proposed computational model (adapted from [21]).
After that, when considering simply supported hat-stiffened steel plates, two computational model verifications were carried out. The first consisted of comparing the results obtained in this study with those of Tharian and Nandakumar [16], who modeled a plate with two stiffeners (Figure 5) using the finite elements SHELL63 and SHELL93. The hat-stiffened plate is subjected to a uniform distributed loading of 10 kPa, and it is made of steel with E = 210 GPa and ν = 0.3.
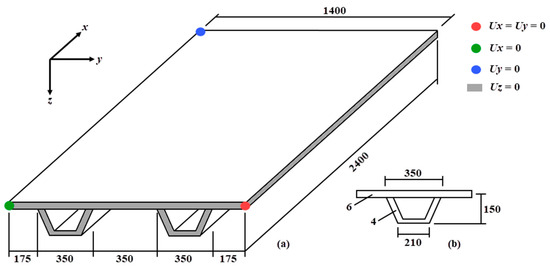
Figure 5.
First verification of the computational model, adapted from [16]: (a) dimensions (in mm) of the plate with stiffeners, and (b) details of the hat-stiffeners.
The results can be seen in Figure 6. Employing a converged mesh of square SHELL281 finite elements with a size of 10 mm, a maximum displacement of 0.7295 mm was found with the proposed numerical model, while Tharian and Nandakumar [16] obtained values of 0.7198 mm (SHELL63) and 0.7214 mm (SHELL93), resulting in relative differences of 1.35% and 1.12%, respectively, thus verifying the proposed numerical model.
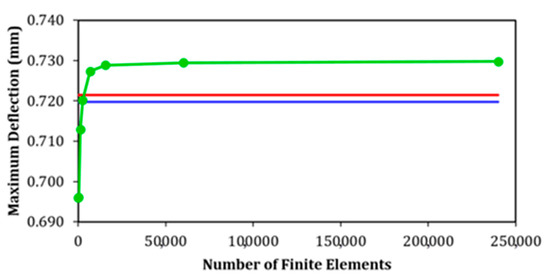
Figure 6.
Mesh convergence and results of the first verification: SHELL63 (the blue line, adapted from [16]), SHELL93 (the red line, adapted from [16]) and SHELL 281 (the green line, the present study).
The second verification was carried out considering a simply supported steel plate with a centered hat-stiffener, as shown in Figure 7. A total of 25 hat-stiffener configurations were analyzed, which were simulated using the finite elements SHELL181 for the plate and BEAM3 for the hat-stiffener in the study conducted by Pal et al. [17]. It is worth mentioning that, despite the hat-stiffener having different dimensions (as presented in Table 1), its total volume is kept constant and equal to 320,000 mm3 in the 25 configurations.
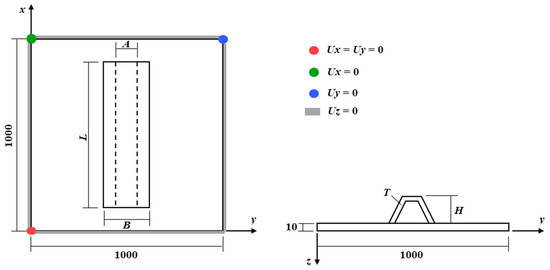
Figure 7.
Second verification of the computational model. The plate analyzed with a centered hat-stiffener (in mm), adapted from [17].

Table 1.
Dimensions (in mm, see Figure 7) of the hat-stiffener for the second verification [17].
Moreover, both the plate and the hat-stiffener are made of steel with E = 200 GPa and ν = 0.3, being subjected to a uniform distributed load of 1 kPa. A mesh convergence test was carried out, considering Case 1 of Table 1, and defining a mesh generated with square SHELL281 finite elements with a size of 10 mm for the 25 cases.
Figure 8 presents the results obtained with the proposed model in comparison with those of Pal et al. [17]. Among all cases, the average relative difference was 3.3%, and the maximum relative difference was 5%, which verifies the developed computational model.
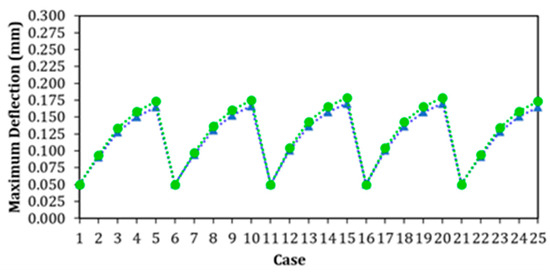
Figure 8.
Results of the second verification for the 25 cases: the blue dot line shows the SHELL181 and BEAM3 adapted from [17], and the green dot line shows the SHELL181 and BEAM3 in the present study.
3.2. Case Study
As previously explained, a reference plate without stiffeners was adopted, and all geometric configurations of plates with stiffeners were derived from this plate, maintaining the two conditions: (i) the total material volume of the reference plate and the plates with hat-stiffeners is the same, by transforming 30% of the reference plate’s volume into stiffeners; and (ii) the angle of the stiffener’s side wall must be 120°, as shown in Figure 3. Based on this approach, it was possible to generate, through the constructal design method, the geometric configurations of plates with transverse stiffeners, varying between one and nine stiffeners, and considering five different thicknesses for the stiffeners.
A mesh convergence test was performed using the hat-stiffened plate with the highest level of complexity, that is, the plate with nine stiffeners. In this test, the SHELL281 element was used, with square shapes forming regular meshes with sizes ranging from 5 to 40 mm. The maximum deflection of the hat-stiffened plate was evaluated for each tested mesh. Observing Figure 9, one can infer that the results stabilized at mesh M5 (10 mm), which was adopted for the spatial discretization of all 224 numerically simulated cases.
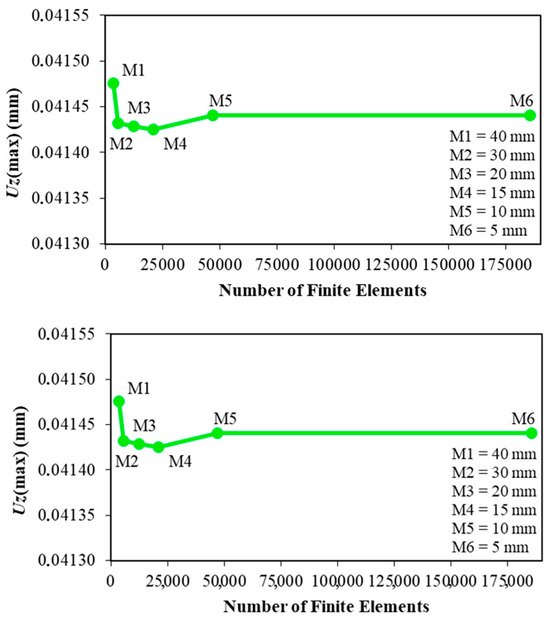
Figure 9.
Convergence test for the present study.
As the main purpose of applying the constructal design method is to increase its structural efficiency by understanding how the variation of the geometric configuration leads to superior mechanical performance, the numerical results obtained in terms of the maximum and central out-of-plane displacement were recorded, and can be seen in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 for the plates with one to nine transverse hat-stiffeners, respectively. In addition, the maximum deflection of the reference plate (with no stiffeners) is also plotted in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18.
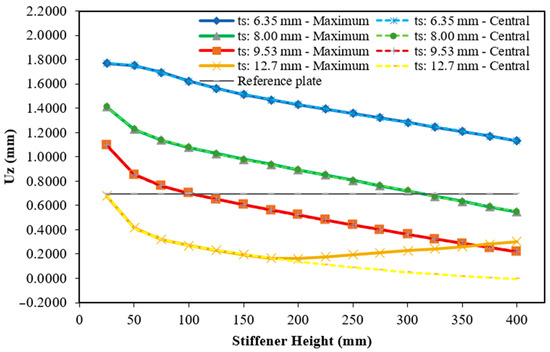
Figure 10.
Maximum and central deflection for the plate with one hat-stiffener.
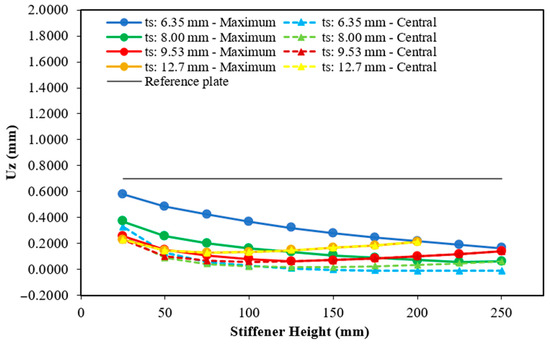
Figure 11.
Maximum and central deflection for the plate with two hat-stiffeners.
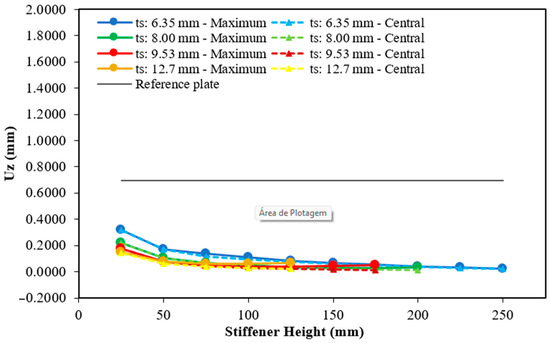
Figure 12.
Maximum and central deflection for the plate with three hat-stiffeners.
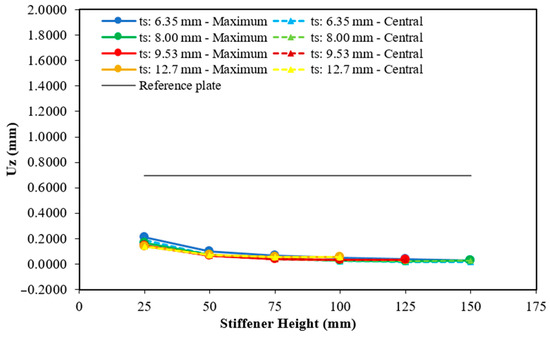
Figure 13.
Maximum and central deflection for the plate with four hat-stiffeners.
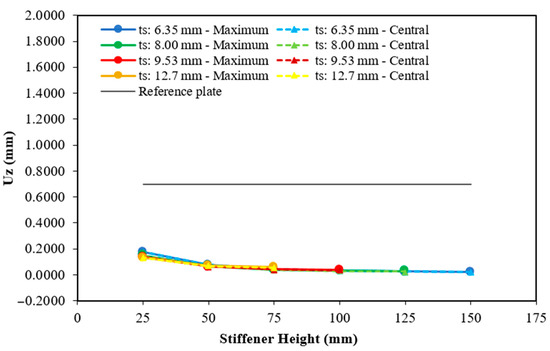
Figure 14.
Maximum and central deflection for the plate with five hat-stiffeners.
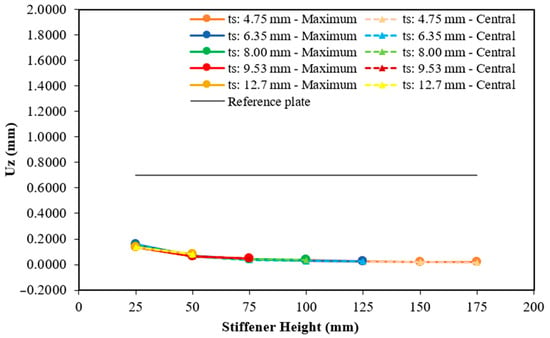
Figure 15.
Maximum and central deflection for the plate with six hat-stiffeners.
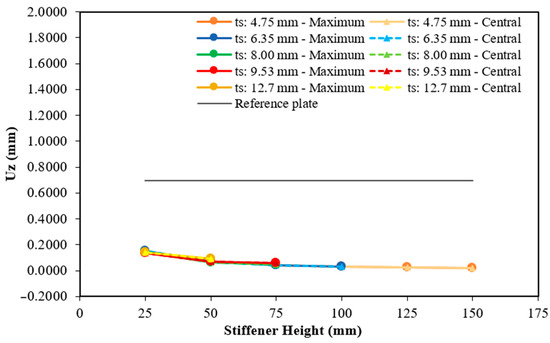
Figure 16.
Maximum and central deflection for the plate with seven hat-stiffeners.
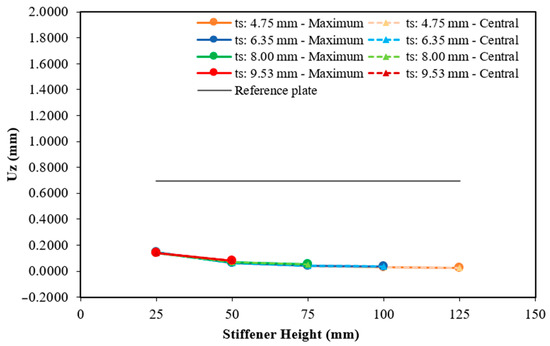
Figure 17.
Maximum and central deflection for the plate with eight hat-stiffeners.
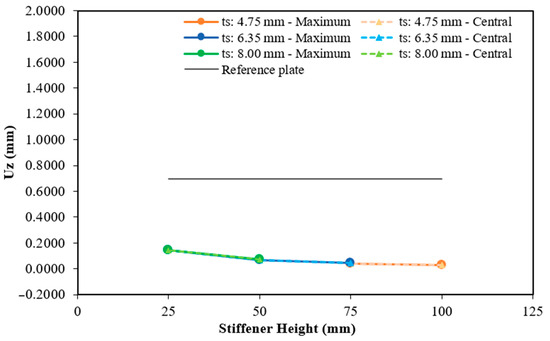
Figure 18.
Maximum and central deflection for the plate with nine hat-stiffeners.
As can be seen, except for a few cases with one stiffener (see Figure 10), all maximum and central deflections were less than those of the reference plate. In other words, for the vast majority of cases, transforming 30% of the reference plate material into hat-stiffeners improved the structural mechanical performance. Furthermore, as illustrated in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, there is a very small difference between the maximum and central deflections, except for specific cases, such as the plate with one stiffener (see Figure 10), with a thickness of 12.70 mm and heights greater than 200 mm, and the plate with two stiffeners, with thicknesses of 6.35 mm and 8.00 mm (see Figure 11). In general, it can also be observed that, as the hat-stiffener height increases, the hat-stiffened plate displacements decrease.
Regarding the case with one stiffener (see Figure 10), 66 geometries were evaluated considering four commercial thicknesses. In general, one can observe that the largest deflections occur with the smallest stiffener thickness, while the smallest deflections occur with the largest thickness. The best result is achieved when the stiffener has a height of 200 mm and a thickness of 12.70 mm, showing an improvement of 76.39% in the maximum deflection and 80.04% in the central deflection compared to the reference plate. Unlike other configurations, for the 12.70 mm thickness, only the central deflection of the plate follows the pattern in which the greater stiffener heights result in smaller deflections—even generating a negative central deflection at the maximum height (400 mm). Meanwhile, the results for the maximum deflection initially decrease up to the intermediate height considered, and then increase as the hat-stiffener height increases. This behavior occurs due to two factors: (i) the transverse stiffener is located in the central region of the plate, leaving large areas of the plate “unstiffened”; and (ii) at greater heights, the hat-stiffener takes on a geometric shape that increases the stiffness of this region, causing the largest displacements to occur in the “unstiffened” regions of the plate, as can be seen in Figure 19.
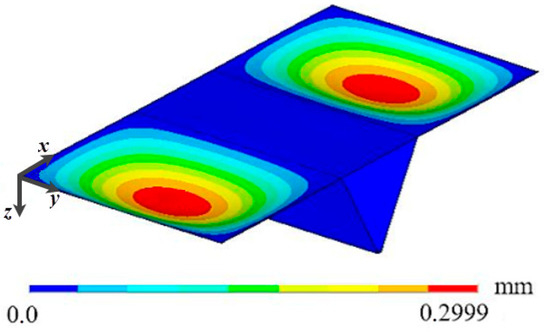
Figure 19.
Displacement distribution of the plate having one transverse hat-stiffener, with hs = 400 mm and ts = 12.70 mm.
In turn, when two hat-stiffeners are considered (see Figure 11) it is possible to identify that the maximum and central deflections coincide only for the cases having thickness of 12.70 mm and heights greater than 100 mm for the 9.53 mm thickness. Unlike the other cases presented, in which the deflections decrease as the height increases, in these thicknesses, the deflections decrease up to an intermediate height (75 mm for the 12.70 mm thickness) and then increase, because, as in the plate with one stiffener, the geometry of the stiffeners and their location influence the distribution of displacements along the structure, as can be seen in Figure 20. For the other thicknesses (6.35 mm and 8.00 mm), although the maximum and central deflections do not coincide, their values decrease with the increasing height, with the central deflection always being smaller than the maximum. When adopting the 6.35 mm thickness, the central deflection above a height of 150 mm assumed negative values, because the central region of the plate has greater stiffness due to the geometry of the transverse hat-stiffener. The maximum height adopted for the stiffeners in this case was 250 mm, making it possible to carry out 38 geometric analyses. The smallest maximum deflection occurs at a height of 225 mm when using a stiffener with a thickness of 8.00 mm. Thus, the maximum and central deflections were 0.0545 mm and 0.0466 mm, respectively. These results show a reduction of 92.19% and 93.32% in relation to the maximum and central deflections of the reference plate. On the other hand, the worst result occurs at a height of 25 mm and a thickness of 6.35 mm, with values of 0.5790 mm and 0.3262 mm for the maximum and central deflection, with a reduction of 17.00% and 53.24%, respectively.
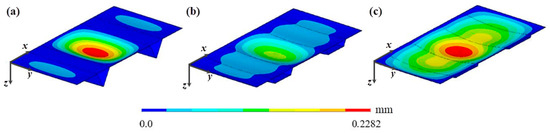
Figure 20.
Displacement distribution of the plate having two transverse hat-stiffeners for a ts = 12.70 mm: (a) hs = 200 mm; (b) hs = 75 mm; and (c) hs = 25 mm.
For the plates with three transverse hat-stiffeners, Figure 12 presents the results of the 30 geometric configurations investigated, indicating a reduction in the maximum and central deflections as the height of the stiffeners increases. For the thicknesses of 6.35 mm and 8.00 mm, small differences between the maximum and central deflections were observed. However, for the thickness of 9.53 mm, the difference between the maximum and central deflection values starts to increase at heights above 75 mm. When adopting the thickness of 12.70 mm, there is also a difference between the maximum and central deflection, with the central deflection being smaller than the maximum. These differences between the maximum and central deflections are associated with the presence of a stiffener at the center of the plate, leading to a phenomenon similar to the plates with one or two stiffeners, where changes in the geometry cause displacements to concentrate in regions with lower structural stiffness. Unlike the previous geometric configurations, where the lowest deflection occurs either in the largest thickness or in an intermediate thickness, for the plates with three hat-stiffeners, the lowest deflection was achieved in the smallest thickness of 6.35 mm and at a height of 250 mm—the largest among those analyzed—with values of 0.0252 mm for the maximum deflection and 0.0227 mm for the central deflection. This result shows a reduction of 96.38% and 96.74% in relation to the maximum and central deflections of the reference plate. On the other hand, the worst result also occurs in the 6.35 mm thickness, but at the smallest height of 25 mm, 2.2 times smaller than the result of the reference plate, with the maximum and central deflection being 0.3169 mm.
From Figure 13 the results for the plate with four transverse hat-stiffeners can be viewed. There is no variation between the maximum and central deflections for stiffener thicknesses greater than 8 mm. The 6.35 mm thickness showed both the highest and lowest deflection values, showing variations of up to 49%. Still, for the 6.35 mm thickness, greater displacements were observed in the outermost stiffeners compared to the central stiffeners, as depicted in Figure 21, which are probable causes of the significant variations recorded for this hat-stiffeners thickness. The maximum height for this stiffeners arrangement was 150 mm, resulting in 21 geometric configurations analyzed. The lowest maximum deflection occurs when stiffeners with a thickness of 8.00 mm and a height of 125 mm are used, resulting in a maximum and central deflection of 0.0253 mm—a reduction of 96.38%. The worst result corresponds to 0.2115 mm and 0.1882 mm for the maximum and central deflection, respectively, with stiffeners of 25 mm in height and 6.35 mm in thickness. However, even in this case, there is still an improvement of 69.68% and 73.03% over the maximum and central deflections of the reference plate.
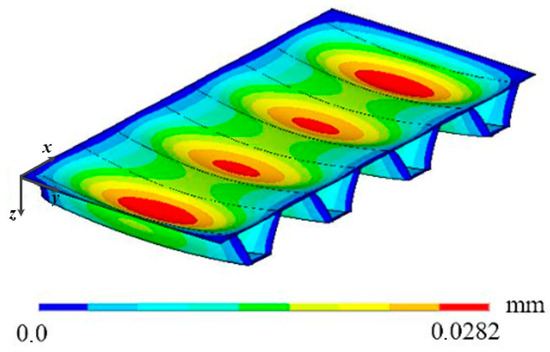
Figure 21.
Displacement distribution in the plate with four transverse stiffeners with ts = 6.35 mm and hs = 150 mm.
When using five transverse hat-stiffeners in the plate (see Figure 14), the stiffeners’ height restrictions become more severe as its thickness increases. Thus, 18 geometric analyses were carried out, with the maximum height being 150 mm for a thickness of 6.35 mm and 75 mm of the maximum height for a thickness of 12.70 mm. The smallest and largest maximum deflection results occur when the stiffeners have a thickness of 6.35 mm. The best result happens at the greatest height of 150 mm, with the maximum and central deflections of 0.0211 mm, about 33 times smaller than the deflections of the reference plate. On the other hand, the worst result, which occurs at the smallest height (25 mm), presents the maximum and central deflections of 0.1771 mm, a relative difference of 74.61% compared to the reference plate.
Using six hat-stiffeners, it was also possible to numerically investigate 18 geometric configurations of stiffened plates (see Figure 15), varying the stiffener thickness between 4.75 mm and 12.70 mm. The geometry that achieved the lowest deflection result used transverse stiffeners with a thickness of 4.75 mm and a height of 175 mm (a combination of the smallest thickness and the greatest height), resulting in a maximum deflection of 0.0199 mm and a central deflection of 0.0166 mm. These values represent reductions of 97.15% and 97.62%, respectively, compared to the deflections of the reference plate. The highest deflection result occurs with stiffeners of 25 mm in height and 6.35 mm in thickness, with values of 0.1594 mm for the maximum deflection and 0.1562 mm for the central deflection. These values are approximately 4.4 times smaller than those of the reference plate.
For the plates with seven transverse hat-stiffeners (see Figure 16), it was possible to perform 16 geometric analyses, from which the lowest deflection result was obtained with a height of 150 mm and a thickness of 4.75 mm. Both the maximum and central deflections were 0.0220 mm, representing a 96.84% improvement over the reference plate. As in the previous case, the worst result occurs in the plate with stiffeners of 25 mm in height and 6.35 mm in thickness, with the maximum and central deflections of 0.1525 mm, corresponding to a reduction of 78.14%.
By adding eight transverse hat-stiffeners to the plate (see Figure 17), the number of analyses was reduced to 12 due to the problem’s constraints. There was little variation between the maximum and central deflection and, in general, the best results were found with the smallest stiffener thicknesses. The smallest deflection occurred for the plate with hat-stiffeners having 125 mm in height and 4.75 mm in thickness. The maximum and central deflections achieved reached a reduction of approximately 96% in the plate’s displacements, with values of 0.0257 mm and 0.0255 mm, respectively. On the other hand, the highest deflection was 0.1478 mm for the maximum deflection and 0.1473 mm for the central deflection, approximately 78.80% lower than the displacements of the reference plate.
Finally, from Figure 18, only seven geometric configurations were possible for the plates with nine transverse hat-stiffeners. The lowest deflection result was 0.0315 mm for both the maximum and central deflections, achieved by adopting a stiffener height of 75 mm and a thickness of 4.75 mm, representing a 95.34% reduction compared to the reference plate. The highest values for the maximum and central deflections were 0.1466 mm, obtained with a height of 25 mm and a thickness of 6.35 mm, corresponding to a 4.76-fold reduction in plate deflections compared to the reference plate.
Based on the results presented in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, Table 2 compiles the best and worst cases according to the number of transverse hat-stiffeners in the plate, as well as the relative difference (RD) between the maximum and central deflections of the hat-stiffened plates and the reference plate.

Table 2.
Best and worst results of the maximum and central deflections according to the number of hat-stiffeners in the transverse direction of the plate.
From Table 2, one can infer that the configurations with 3 and from 5 to 9 transverse hat-stiffeners, the lowest displacements occur in the configurations with greater heights and smaller thickness. On the other hand, with a single transverse stiffener, the maximum displacement occurred at an intermediate height with the greatest thickness. Table 2 reinforces the observation that displacements decrease with the increase in the height of the transverse hat-stiffeners.
Figure 22 shows the displacement distribution of the best case for each of the nine proposed groups of transverse hat-stiffened plate geometries. It is worth noting that the same color scale was used for all geometric configurations, allowing a visual identification of how the variation in geometry influences the magnitude of out-of-plane displacements.
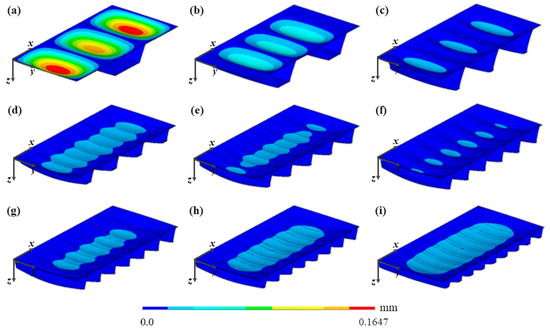
Figure 22.
Deflection distribution of the best geometric configurations among the studied plates, with: (a) one hat-stiffener; (b) two hat-stiffeners; (c) three hat-stiffeners; (d) four hat-stiffeners; (e) five hat-stiffeners; (f) six hat-stiffeners; (g) seven hat-stiffeners; (h) eight hat-stiffeners; and (i) nine hat-stiffeners.
The observation of Figure 22 indicates that reducing the number of transverse stiffeners leads to a concentration of the displacement field in specific regions, accentuating the maximum displacements. On the other hand, increasing the number of transverse stiffeners leads to a more uniform displacement distribution, with a tendency to concentrate along the longitudinal central axis (perpendicular to the transverse stiffeners). This behavior is in agreement with the constructal principle of the optimal distribution of imperfections [9,10], allowing to identify the case having six hat-stiffeners (Figure 22f) as the optimized geometric configuration that conducted to the superior structural performance, corroborating the data presented in Table 2.
It was also observed among the obtained results and illustrated in Figure 22 that, mainly in the cases of plates with one (Figure 22a) and three (Figure 22c) transverse hat-stiffeners, the maximum deflection is different from the central deflection of the stiffened plate. The existence of a transverse hat-stiffener aligned with the transverse central axis of the plate increased the stiffness in this region and directed the displacement field toward the ‘non-stiffened’ regions, located laterally to the stiffener in the case of the plate with one hat-stiffener, and between stiffeners, in the case of the plate with three hat-stiffeners. The size of the ‘non-stiffened’ regions in these two cases may also have influenced this behavior.
3.3. Comparison Between Plates Reinforced with Transverse or Longitudinal Hat-Stiffeners
As previously mentioned, Alves et al. [21] studied a structural component with the same characteristics considered in this work, but with hat-stiffeners oriented longitudinally on the plate. Both works adopted the same approach, i.e., the constructal design method combined with the exhaustive search technique, and the constraint that a maximum of 30% of the reference plate volume could be transformed into longitudinal or transverse hat-stiffeners. In addition, the dimensions of the reference plate, boundary conditions, and applied loading are the same in both works, thus allowing a fair comparison between the hat-stiffened plates with transverse or longitudinal stiffeners.
Considering the constraints and degrees of freedom, five groups of geometries were generated, with plates containing from one to five longitudinal hat-stiffeners in Alves et al. [21]. The hat-stiffeners height ranged from 25 mm to 300 mm. The plate thickness and the lateral wall angle of the stiffeners are the same as those adopted in the present work (120°). In total, 100 different geometric configurations were generated, numerically simulated, and analyzed by Alves et al. [21]. Table 3 presents the best and worst results in terms of the central and maximum deflection for each number of longitudinal hat-stiffeners.

Table 3.
Best and worst results of the maximum and central deflections according to the number of hat-stiffeners in the longitudinal direction of the plate.
When comparing the results related to transverse hat-stiffeners (presented in Table 2) with those related to longitudinal stiffeners (presented in Table 3) for analogous plates under the same boundary and loading conditions, it is observed that the transverse hat-stiffeners demonstrated greater structural efficiency. This statement is supported by the fact that the results obtained using the hat-stiffeners in the transverse direction of the plates showed a noticeable reduction in both the maximum and central displacements when compared to those achieved in the configuration with the hat-stiffened plates in the longitudinal direction.
In Figure 23, the out-of-plane displacement distributions of the cases that achieved the best performance with the longitudinal hat-stiffeners (Figure 23a) and the transverse hat-stiffeners (Figure 23b) are depicted. It is observed that the use of a single longitudinal hat-stiffener in the plate, with a height of hs = 250 mm and a thickness of ts = 9.53 mm, resulted in a reduction of 86.26% in both the maximum and central deflections when compared to the values obtained for the reference plate. On the other hand, when employing six hat-stiffeners in the transverse direction of the plate, with a height of hs = 175 mm and a thickness of ts = 4.75 mm, there was a reduction of 97.62% in the central deflection and 97.15% in the maximum deflection, when compared to the reference plate. The direct comparison between the best case with the longitudinal hat-stiffeners and the best case with the transverse hat-stiffeners shows that the maximum deflections obtained using the transverse stiffeners are 79.27% smaller. The greater efficiency of the transverse stiffeners in reducing deflections can be explained by the fact that their walls are parallel to the shortest span. According to Araújo [38] and Nogueira et al. [14], the bending moment demand is higher in the direction of the shortest span. Therefore, using a geometric configuration that increases the stiffness in the direction of the shortest span leads to a reduction in deflections.
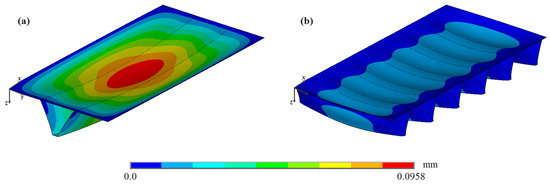
Figure 23.
Best cases obtained using hat-stiffeners: (a) longitudinal direction and (b) transverse direction.
4. Conclusions
This study investigated the structural efficiency, in terms of deflection, of a steel plate with hat-stiffeners installed in the transverse direction of the plate. The constructal design method was employed together with the exhaustive search technique to convert 30% of the volume of an unstiffened reference plate into transverse stiffeners. Considering the imposed constraints and degrees of freedom, a total of 224 geometries were generated. The numerical simulation of these geometries was carried out using a computational model developed in the FEM, which was verified and validated.
As one of the main purposes of using stiffeners is to reduce plate deflection, the primary objective of this work was to minimize the displacements occurring in the hat-stiffened plates. The results obtained showed that the vast majority of the tested configurations reduced the displacements when compared to the reference plate. The best result was achieved by using six transverse hat-stiffeners with a height of 175 mm and a thickness of 4.75 mm, leading to a reduction of approximately 97% in both the maximum and central deflections of the plate compared to the unstiffened reference plate. This demonstrates that the strategic development of hat-stiffeners can significantly improve the efficiency of steel plates in terms of deflection reduction.
Comparing the present study with that conducted by Alves et al. [21], which applied the same approach but with longitudinal hat-stiffeners, it is evident that the best-performing plate with one longitudinal hat-stiffener (see Figure 23a) showed inferior performance compared to the best plate with six transverse hat-stiffeners (see Figure 23b). Although the plates with longitudinal stiffeners demonstrated a significant ability to reduce out-of-plane displacements—by approximately 86% relative to the reference plate—this value was about 11% lower than the reduction achieved using transverse stiffeners.
In general, considering the results of Alves et al. [21] and those obtained in the present study, it is observed that, while maintaining a constant material volume, the addition of stiffeners does not necessarily lead to a reduction in the displacements of the plate. This behavior was observed both with the use of longitudinal hat-stiffeners [21] and with transverse hat-stiffeners (present study). It was also noted that the height of the hat-stiffeners has a significant influence on the deflection obtained. As expected, increasing the stiffener height usually results in a reduction of the deflection.
Finally, it is worth noting that constructal theory states that a system can undergo continuous evolution over time in order to improve its internal flow patterns. In the case of the constructal design method, this evolution can be understood as the variation of degrees of freedom to improve the performance indicators, always maintaining the total volume constant [9,21]. In the present study, the material redistributes itself due to the variation of these degrees of freedom, generating new geometries that adapt to achieve a better performance, while respecting the imposed constraints and the search space. Therefore, it can be considered that the constructal principle of the optimal distribution of imperfections [7,9] has been achieved, generating the geometry that best adapts to the investigated situation within the proposed constraints. In the case of structural systems, the internal flow referred to by constructal theory can be understood as a stress flow [7], which changes as the geometry assumes different shapes. According to constructal theory and as stated by da Silveira et al. [10], the geometry that best meets the situation is the one that best distributes imperfections, facilitating the stress flow and resulting in lower displacements.
Future research may continue this study by considering different aspect ratios for the plate dimensions, different boundary conditions, and other volumetric ratios between the reference plate and the volume converted into the stiffeners. Additionally, including von Mises stresses as a performance indicator could provide a deeper understanding of the structural behavior.
Author Contributions
Conceptualization, M.A.A., W.R.A. and L.A.I.; methodology, M.A.A. and L.A.I.; software, M.A.A. and E.M.R.; validation, M.A.A. and E.M.R.; formal analysis, L.A.O.R., E.D.d.S., W.R.A. and L.A.I.; investigation, M.A.A., E.M.R. and L.A.I.; resources, L.A.O.R., E.D.d.S. and L.A.I.; data curation, M.A.A. and W.R.A.; writing—original draft preparation, W.R.A. and L.A.I.; writing—review and editing, M.A.A., L.A.O.R., E.D.d.S., W.R.A. and L.A.I.; visualization, L.A.O.R., E.D.d.S., W.R.A. and L.A.I.; supervision, W.R.A. and L.A.I.; project administration, L.A.I.; funding acquisition, L.A.O.R., E.D.d.S. and L.A.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Coordination for the Improvement of Higher Education Personnel—CAPES, funding code 001 and National Council for Scientific and Technological Development—CNPq, grant numbers: 307791/2019-0, 308396/2021-9, and 309648/2021-1.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors acknowledge the financial support for conducting this research provided by CAPES (funding code 001) and CNPq (processes: 307791/2019-0, 308396/2021-9, and 309648/2021-1).
Conflicts of Interest
The authors declare no conflicts of interest and the funders had no role in the design of this study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
Here, all the geometric configurations numerically simulated, generated through the application of the constructal design method, and evaluated in this study are presented. Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8 and Table A9 show the hat-stiffener height, hs, and the respective thicknesses, ts, adopted for each case. Subsequently, the maximum deflection, Uzmax, and the central deflection, Uzcentral, are presented. Finally, the percentage difference between these two deflections is shown.

Table A1.
Plate with one transverse hat-stiffener.
Table A1.
Plate with one transverse hat-stiffener.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 400 | 6.35 | 1.1309 | 1.1310 | 0.005 |
| 375 | 6.35 | 1.1700 | 1.1700 | −0.003 |
| 350 | 6.35 | 1.2083 | 1.2084 | 0.007 |
| 325 | 6.35 | 1.2462 | 1.2461 | −0.004 |
| 300 | 6.35 | 1.2833 | 1.2834 | 0.006 |
| 275 | 6.35 | 1.3202 | 1.3202 | −0.003 |
| 250 | 6.35 | 1.3569 | 1.3569 | 0.003 |
| 225 | 6.35 | 1.3938 | 1.3939 | 0.007 |
| 200 | 6.35 | 1.4316 | 1.4316 | −0.003 |
| 175 | 6.35 | 1.4713 | 1.4713 | 0.003 |
| 150 | 6.35 | 1.5146 | 1.5146 | −0.002 |
| 125 | 6.35 | 1.5644 | 1.5645 | 0.004 |
| 100 | 6.35 | 1.6248 | 1.6248 | 0.002 |
| 75 | 6.35 | 1.6953 | 1.6954 | 0.005 |
| 50 | 6.35 | 1.7542 | 1.7542 | 0.002 |
| 25 | 6.35 | 1.7712 | 1.7712 | 0.002 |
| 400 | 8.00 | 0.5481 | 0.5481 | 0.000 |
| 375 | 8.00 | 0.5906 | 0.5907 | 0.014 |
| 350 | 8.00 | 0.6337 | 0.6337 | 0.000 |
| 325 | 8.00 | 0.6767 | 0.6768 | 0.012 |
| 300 | 8.00 | 0.7201 | 0.7201 | 0.000 |
| 275 | 8.00 | 0.7634 | 0.7635 | 0.010 |
| 250 | 8.00 | 0.8067 | 0.8067 | 0.000 |
| 225 | 8.00 | 0.8500 | 0.8501 | 0.009 |
| 200 | 8.00 | 0.8933 | 0.8934 | 0.009 |
| 175 | 8.00 | 0.9370 | 0.9370 | 0.000 |
| 150 | 8.00 | 0.9812 | 0.9813 | 0.008 |
| 125 | 8.00 | 1.0274 | 1.0274 | −0.001 |
| 100 | 8.00 | 1.0776 | 1.0777 | 0.006 |
| 75 | 8.00 | 1.1383 | 1.1383 | 0.000 |
| 50 | 8.00 | 1.2264 | 1.2265 | 0.007 |
| 25 | 8.00 | 1.4100 | 1.4100 | 0.001 |
| 400 | 9.53 | 0.2203 | 0.2203 | 0.000 |
| 375 | 9.53 | 0.2537 | 0.2538 | 0.024 |
| 350 | 9.53 | 0.2887 | 0.2887 | 0.000 |
| 325 | 9.53 | 0.3248 | 0.3249 | 0.018 |
| 300 | 9.53 | 0.3623 | 0.3623 | 0.000 |
| 275 | 9.53 | 0.4007 | 0.4008 | 0.017 |
| 250 | 9.53 | 0.4401 | 0.4401 | 0.000 |
| 225 | 9.53 | 0.4803 | 0.4803 | 0.000 |
| 200 | 9.53 | 0.5212 | 0.5213 | 0.015 |
| 175 | 9.53 | 0.5630 | 0.5630 | 0.000 |
| 150 | 9.53 | 0.6059 | 0.6060 | 0.012 |
| 125 | 9.53 | 0.6508 | 0.6508 | 0.000 |
| 100 | 9.53 | 0.6998 | 0.6999 | 0.011 |
| 75 | 9.53 | 0.7599 | 0.7599 | 0.000 |
| 50 | 9.53 | 0.8545 | 0.8546 | 0.008 |
| 25 | 9.53 | 1.0965 | 1.0965 | −0.002 |
| 400 | 12.7 | 0.2999 | −0.0049 | −101.644 |
| 375 | 12.7 | 0.2810 | 0.0057 | −97.989 |
| 350 | 12.7 | 0.2625 | 0.0185 | −92.967 |
| 325 | 12.7 | 0.2445 | 0.0334 | −86.337 |
| 300 | 12.7 | 0.2269 | 0.0505 | −77.756 |
| 275 | 12.7 | 0.2100 | 0.0696 | −66.856 |
| 250 | 12.7 | 0.1939 | 0.0908 | −53.192 |
| 225 | 12.7 | 0.1787 | 0.1140 | −36.233 |
| 200 | 12.7 | 0.1647 | 0.1392 | −15.461 |
| 175 | 12.7 | 0.1666 | 0.1666 | 0.030 |
| 150 | 12.7 | 0.1966 | 0.1966 | 0.000 |
| 125 | 12.7 | 0.2299 | 0.2300 | 0.026 |
| 100 | 12.7 | 0.2692 | 0.2693 | 0.022 |
| 75 | 12.7 | 0.3218 | 0.3218 | 0.000 |
| 50 | 12.7 | 0.4138 | 0.4139 | 0.014 |
| 25 | 12.7 | 0.6799 | 0.6799 | 0.000 |

Table A2.
Plate with two transverse hat-stiffeners.
Table A2.
Plate with two transverse hat-stiffeners.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 250 | 6.35 | 0.1646 | −0.0107 | −106.521 |
| 225 | 6.35 | 0.1894 | −0.0125 | −106.616 |
| 200 | 6.35 | 0.2163 | −0.0119 | −105.515 |
| 175 | 6.35 | 0.2458 | −0.0088 | −103.560 |
| 150 | 6.35 | 0.2793 | −0.0025 | −100.899 |
| 125 | 6.35 | 0.3188 | 0.0079 | −97.515 |
| 100 | 6.35 | 0.3670 | 0.0255 | −93.060 |
| 75 | 6.35 | 0.4245 | 0.0578 | −86.382 |
| 50 | 6.35 | 0.4853 | 0.1277 | −73.678 |
| 25 | 6.35 | 0.5790 | 0.3262 | −43.656 |
| 250 | 8.00 | 0.0612 | 0.0612 | 0.000 |
| 225 | 8.00 | 0.0545 | 0.0466 | −14.532 |
| 200 | 8.00 | 0.0702 | 0.0345 | −50.940 |
| 175 | 8.00 | 0.0882 | 0.0252 | −71.435 |
| 150 | 8.00 | 0.1086 | 0.0193 | −82.190 |
| 125 | 8.00 | 0.1323 | 0.0180 | −86.411 |
| 100 | 8.00 | 0.1611 | 0.0234 | −85.485 |
| 75 | 8.00 | 0.1989 | 0.0415 | −79.146 |
| 50 | 8.00 | 0.2556 | 0.0911 | −64.347 |
| 25 | 8.00 | 0.3690 | 0.2500 | −32.246 |
| 250 | 9.53 | 0.1404 | 0.1404 | 0.000 |
| 225 | 9.53 | 0.1192 | 0.1192 | 0.000 |
| 200 | 9.53 | 0.1003 | 0.1003 | 0.040 |
| 175 | 9.53 | 0.0839 | 0.0839 | 0.000 |
| 150 | 9.53 | 0.0705 | 0.0705 | 0.043 |
| 125 | 9.53 | 0.0612 | 0.0612 | 0.000 |
| 100 | 9.53 | 0.0793 | 0.0581 | −26.796 |
| 75 | 9.53 | 0.1066 | 0.0662 | −37.923 |
| 50 | 9.53 | 0.1515 | 0.1009 | −33.415 |
| 25 | 9.53 | 0.2566 | 0.2269 | −11.580 |
| 200 | 12.7 | 0.2107 | 0.2107 | 0.000 |
| 175 | 12.7 | 0.1864 | 0.1864 | 0.027 |
| 150 | 12.7 | 0.1645 | 0.1646 | 0.030 |
| 125 | 12.7 | 0.1462 | 0.1462 | 0.000 |
| 100 | 12.7 | 0.1326 | 0.1327 | 0.038 |
| 75 | 12.7 | 0.1280 | 0.1280 | 0.000 |
| 50 | 12.7 | 0.1436 | 0.1437 | 0.028 |
| 25 | 12.7 | 0.2282 | 0.2282 | 0.000 |

Table A3.
Plate with three transverse hat-stiffeners.
Table A3.
Plate with three transverse hat-stiffeners.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 250 | 6.35 | 0.0252 | 0.0227 | −9.905 |
| 225 | 6.35 | 0.0326 | 0.0303 | −6.882 |
| 200 | 6.35 | 0.0416 | 0.0394 | −5.405 |
| 175 | 6.35 | 0.0528 | 0.0499 | −5.527 |
| 150 | 6.35 | 0.0668 | 0.0620 | −7.203 |
| 125 | 6.35 | 0.0847 | 0.0759 | −10.436 |
| 100 | 6.35 | 0.1080 | 0.0928 | −14.077 |
| 75 | 6.35 | 0.1369 | 0.1176 | −14.100 |
| 50 | 6.35 | 0.1710 | 0.1692 | −1.093 |
| 25 | 6.35 | 0.3169 | 0.3170 | 0.009 |
| 200 | 8.00 | 0.0336 | 0.0130 | −61.399 |
| 175 | 8.00 | 0.0277 | 0.0177 | −35.960 |
| 150 | 8.00 | 0.0268 | 0.0246 | −8.427 |
| 125 | 8.00 | 0.0362 | 0.0339 | −6.272 |
| 100 | 8.00 | 0.0494 | 0.0469 | −5.022 |
| 75 | 8.00 | 0.0689 | 0.0668 | −3.063 |
| 50 | 8.00 | 0.1055 | 0.1055 | 0.019 |
| 25 | 8.00 | 0.2184 | 0.2184 | 0.000 |
| 175 | 9.53 | 0.0497 | 0.0128 | −74.139 |
| 150 | 9.53 | 0.0422 | 0.0156 | −62.989 |
| 125 | 9.53 | 0.0379 | 0.0212 | −44.093 |
| 100 | 9.53 | 0.0380 | 0.0305 | −19.700 |
| 75 | 9.53 | 0.0463 | 0.0463 | 0.000 |
| 50 | 9.53 | 0.0788 | 0.0788 | 0.013 |
| 25 | 9.53 | 0.1750 | 0.1750 | −0.006 |
| 125 | 12.7 | 0.0678 | 0.0226 | −66.603 |
| 100 | 12.7 | 0.0616 | 0.0266 | −56.913 |
| 75 | 12.7 | 0.0630 | 0.0374 | −40.638 |
| 50 | 12.7 | 0.0799 | 0.0629 | −21.252 |
| 25 | 12.7 | 0.1497 | 0.1410 | −5.851 |

Table A4.
Plate with four transverse hat-stiffeners.
Table A4.
Plate with four transverse hat-stiffeners.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 150 | 6.35 | 0.0283 | 0.0162 | −42.640 |
| 125 | 6.35 | 0.0369 | 0.0190 | −48.563 |
| 100 | 6.35 | 0.0488 | 0.0254 | −47.961 |
| 75 | 6.35 | 0.0648 | 0.0391 | −39.698 |
| 50 | 6.35 | 0.0992 | 0.0729 | −26.592 |
| 25 | 6.35 | 0.2115 | 0.1882 | −11.049 |
| 150 | 8.00 | 0.0263 | 0.0263 | 0.000 |
| 125 | 8.00 | 0.0253 | 0.0253 | 0.040 |
| 100 | 8.00 | 0.0306 | 0.0283 | −7.800 |
| 75 | 8.00 | 0.0445 | 0.0381 | −14.398 |
| 50 | 8.00 | 0.0743 | 0.0650 | −12.604 |
| 25 | 8.00 | 0.1642 | 0.1578 | −3.886 |
| 125 | 9.53 | 0.0350 | 0.0350 | 0.057 |
| 100 | 9.53 | 0.0349 | 0.0349 | 0.000 |
| 75 | 9.53 | 0.0420 | 0.0420 | 0.000 |
| 50 | 9.53 | 0.0651 | 0.0649 | −0.384 |
| 25 | 9.53 | 0.1464 | 0.1464 | 0.000 |
| 100 | 12.7 | 0.0539 | 0.0539 | −0.019 |
| 75 | 12.7 | 0.0539 | 0.0539 | 0.000 |
| 50 | 12.7 | 0.0707 | 0.0707 | 0.014 |
| 25 | 12.7 | 0.1383 | 0.1383 | 0.000 |

Table A5.
Plate with five transverse hat-stiffeners.
Table A5.
Plate with five transverse hat-stiffeners.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 150 | 6.35 | 0.0211 | 0.0212 | 0.047 |
| 125 | 6.35 | 0.0251 | 0.0251 | −0.040 |
| 100 | 6.35 | 0.0324 | 0.0325 | 0.031 |
| 75 | 6.35 | 0.0462 | 0.0462 | −0.022 |
| 50 | 6.35 | 0.0768 | 0.0768 | 0.013 |
| 25 | 6.35 | 0.1771 | 0.1771 | 0.006 |
| 125 | 8.00 | 0.0295 | 0.0263 | −10.885 |
| 100 | 8.00 | 0.0306 | 0.0299 | −2.290 |
| 75 | 8.00 | 0.0404 | 0.0404 | −0.025 |
| 50 | 8.00 | 0.0663 | 0.0663 | 0.000 |
| 25 | 8.00 | 0.1499 | 0.1499 | −0.007 |
| 100 | 9.53 | 0.0386 | 0.0341 | −11.580 |
| 75 | 9.53 | 0.0433 | 0.0411 | −4.948 |
| 50 | 9.53 | 0.0638 | 0.0637 | −0.266 |
| 25 | 9.53 | 0.1390 | 0.1390 | −0.007 |
| 75 | 12.7 | 0.0598 | 0.0537 | −10.224 |
| 50 | 12.7 | 0.0713 | 0.0674 | −5.445 |
| 25 | 12.7 | 0.1334 | 0.1312 | −1.634 |

Table A6.
Plate with six transverse hat-stiffeners.
Table A6.
Plate with six transverse hat-stiffeners.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 175 | 4.75 | 0.0199 | 0.0166 | −16.566 |
| 150 | 4.75 | 0.0224 | 0.0178 | −20.651 |
| 125 | 4.75 | 0.0269 | 0.0212 | −21.176 |
| 100 | 4.75 | 0.0346 | 0.0277 | −19.763 |
| 125 | 6.35 | 0.0256 | 0.0250 | −2.265 |
| 100 | 6.35 | 0.0303 | 0.0283 | −6.796 |
| 75 | 6.35 | 0.0417 | 0.0383 | −8.017 |
| 50 | 6.35 | 0.0690 | 0.0648 | −6.118 |
| 25 | 6.35 | 0.1594 | 0.1562 | −1.989 |
| 100 | 8.00 | 0.0360 | 0.0360 | 0.000 |
| 75 | 8.00 | 0.0417 | 0.0417 | 0.000 |
| 50 | 8.00 | 0.0645 | 0.0637 | −1.318 |
| 25 | 8.00 | 0.1422 | 0.1422 | −0.007 |
| 75 | 9.53 | 0.0487 | 0.0487 | −0.021 |
| 50 | 9.53 | 0.0664 | 0.0664 | 0.000 |
| 25 | 9.53 | 0.1376 | 0.1376 | 0.000 |
| 50 | 12.7 | 0.0785 | 0.0785 | −0.013 |
| 25 | 12.7 | 0.1361 | 0.1361 | 0.000 |

Table A7.
Plate with seven transverse hat-stiffeners.
Table A7.
Plate with seven transverse hat-stiffeners.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 150 | 4.75 | 0.0220 | 0.0220 | 0.000 |
| 125 | 4.75 | 0.0248 | 0.0248 | 0.000 |
| 100 | 4.75 | 0.0309 | 0.0309 | 0.032 |
| 75 | 4.75 | 0.0432 | 0.0432 | −0.023 |
| 100 | 6.35 | 0.0324 | 0.0324 | 0.000 |
| 75 | 6.35 | 0.0414 | 0.0414 | 0.000 |
| 50 | 6.35 | 0.0665 | 0.0665 | −0.015 |
| 25 | 6.35 | 0.1525 | 0.1525 | −0.007 |
| 75 | 8.00 | 0.0464 | 0.0462 | −0.539 |
| 50 | 8.00 | 0.0661 | 0.0661 | −0.015 |
| 25 | 8.00 | 0.1408 | 0.1408 | 0.000 |
| 75 | 9.53 | 0.0589 | 0.0576 | −2.224 |
| 50 | 9.53 | 0.0706 | 0.0701 | −0.581 |
| 25 | 9.53 | 0.1376 | 0.1375 | −0.065 |
| 50 | 12.7 | 0.0910 | 0.0895 | −1.714 |
| 25 | 12.7 | 0.1395 | 0.1386 | −0.667 |

Table A8.
Plate with eight transverse hat-stiffeners.
Table A8.
Plate with eight transverse hat-stiffeners.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 125 | 4.75 | 0.0257 | 0.0245 | −4.779 |
| 100 | 4.75 | 0.0303 | 0.0286 | −5.638 |
| 75 | 4.75 | 0.0415 | 0.0395 | −4.816 |
| 100 | 6.35 | 0.0377 | 0.0377 | −0.053 |
| 75 | 6.35 | 0.0433 | 0.0427 | −1.410 |
| 50 | 6.35 | 0.0661 | 0.0651 | −1.468 |
| 25 | 6.35 | 0.1478 | 0.1473 | −0.318 |
| 75 | 8.00 | 0.0543 | 0.0543 | 0.000 |
| 50 | 8.00 | 0.0692 | 0.0692 | −0.014 |
| 25 | 8.00 | 0.1409 | 0.1409 | −0.007 |
| 50 | 9.53 | 0.0774 | 0.0774 | 0.000 |
| 25 | 9.53 | 0.1406 | 0.1406 | −0.007 |

Table A9.
Plate with nine transverse hat-stiffeners.
Table A9.
Plate with nine transverse hat-stiffeners.
| hs (mm) | ts (mm) | (mm) | (mm) | RD (%) |
|---|---|---|---|---|
| 100 | 4.75 | 0.0315 | 0.0315 | 0.000 |
| 75 | 4.75 | 0.0415 | 0.0414 | −0.024 |
| 75 | 6.35 | 0.0472 | 0.0472 | 0.000 |
| 50 | 6.35 | 0.0675 | 0.0675 | 0.000 |
| 25 | 6.35 | 0.1466 | 0.1466 | −0.007 |
| 50 | 8.00 | 0.0708 | 0.0708 | 0.000 |
| 25 | 8.00 | 0.1422 | 0.1422 | −0.007 |
References
- Szilard, R. Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Li, B.; Gong, Y.; Gao, Y.; Hou, M.; Li, L. Failure Analysis of Hat-Stringer-Stiffened Aircraft Composite Panels under Four-Point Bending Loading. Materials 2022, 15, 2430. [Google Scholar] [CrossRef] [PubMed]
- Ventsel, E.; Krauthammer, T. Thin Plates and Shells: Theory: Analysis, and Applications; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Michigan DOT Selects Steel for 19-Bridge Bundling Project. Available online: https://www.shortspansteelbridges.org/mdot-bridge-bundling-project/ (accessed on 26 May 2025).
- Bejan, A. Constructal-Theory Network of Conducting Paths for Cooling a Heat Generating Volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Bejan, A.; Lorente, S. Design with Constructal Theory; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Bejan, A.; Zane, J.P. Design in Nature: How the Constructal Law Governs Evolution in Biology, Physics, Technology, and Social Organization; Anchor Books: New York, NY, USA, 2013. [Google Scholar]
- Bejan, A. The Physics of Life: The Evolution of Everything; St. Martin’s Press: New York, NY, USA, 2024. [Google Scholar]
- da Silveira, T.; Pinto, V.; Neufeld, J.P.; Pavlovic, A.; Rocha, L.; dos Santos, E.; Isoldi, L.A. Applicability Evidence of Constructal Design in Structural Engineering: Case Study of Biaxial Elasto-Plastic Buckling of Square Steel Plates with Elliptical Cutout. J. Appl. Comput. Mech. 2021, 7, 922–934. [Google Scholar] [CrossRef]
- Reis, A.H. Constructal Theory: From Engineering to Physics, and How Flow Systems Develop Shape and Structure. Appl. Mech. Rev. 2006, 59, 269–282. [Google Scholar] [CrossRef]
- Dos Santos, E.D.; Isoldi, L.A.; Gomes, M.N.; Rocha, L.A.O. The Constructal Design Applied to Renewable Energy Systems. In Sustainable Energy Technologies; Rincón-Mejía, E., Heras, A., Eds.; CRC Press–Taylor and Francis: Boca Raton, FL, USA, 2017; pp. 63–87. [Google Scholar]
- Troina, G.; Cunha, M.; Pinto, V.; Rocha, L.; dos Santos, E.; Fragassa, C.; Isoldi, L. Computational Modeling and Constructal Design Theory Applied to the Geometric Optimization of Thin Steel Plates with Stiffeners Subjected to Uniform Transverse Load. Metals 2020, 10, 220. [Google Scholar] [CrossRef]
- Nogueira, C.M.; Pinto, V.T.; Rocha, L.A.O.; dos Santos, E.D.; Isoldi, L.A. Numerical Simulation and Constructal Design Applied to Plates with Different Heights of Traverse and Longitudinal Stiffeners. Eng. Solid Mech. 2021, 9, 221–238. [Google Scholar] [CrossRef]
- Tharian, M.; Nandakumar, C.G. Superelement for Structural Analysis of Steel Bunkers. SSRN J. 2023. [Google Scholar] [CrossRef]
- Tharian, M.; Nandakumar, C.G. Hat stiffened plates for ship building. Int. J. Agric. Econ. Rural. Dev. 2014, 4, 43–52. [Google Scholar]
- Pal, A.K.; Harry, N.N.; Upadhyay, R.; Kushwaha, Y.K. Static Analysis of hat stiffened plate: A parametric study. Int. J. Res. Eng. Sci. Manag (IJRESM) 2018, 1, 128–131. [Google Scholar]
- Virág, Z.; Szirbik, S. Modal Analysis of Optimized Trapezoidal Stiffened Plates under Lateral Pressure and Uniaxial Compression. Appl. Mech. 2021, 2, 681–693. [Google Scholar] [CrossRef]
- Filippatos, A.; Markatos, D.; Tzortzinis, G.; Abhyankar, K.; Malefaki, S.; Gude, M.; Pantelakis, S. Sustainability-Driven Design of Aircraft Composite Components. Aerospace 2024, 11, 86. [Google Scholar] [CrossRef]
- Aneja, R.; Choudharry, A.; Jain, K.K.; Dave, R.K. Design and Optimization of Hat Stiffened Plate using Finite Element Method. Int. Res. J. Eng. Technol. 2018, 5, 578–584. [Google Scholar]
- Alves, M.A.; Rodrigues, E.M.; Pinto, V.T.; Rocha, L.A.O.; dos Santos, E.D.; Isoldi, L.A. Numerical Simulation, Constructal Design, and Systematic Search Applied to the Geometrical Evaluation of Hat-Stiffened Plates under Bending. Res. Eng. Struct. Mater. 2025. [Google Scholar] [CrossRef]
- Kim, G.-H.; Choi, J.-H.; Kweon, J.-H. Manufacture and performance evaluation of the composite hat-stiffened panel. Compos. Struct. 2010, 92, 2276–2284. [Google Scholar] [CrossRef]
- Jin, B.C.; Li, X.; Mier, R.; Pun, A.; Joshi, S.; Nutt, S. Parametric modeling, higher order FEA and experimental investigation of hat-stiffened composite panels. Compos. Struct. 2015, 128, 207–220. [Google Scholar] [CrossRef]
- Yetman, J.E.; Sobey, A.J.; Blake, J.I.R.; Shenoi, R.A. Investigation into skin stiffener debonding of top-hat stiffened composite structures. Compos. Struct. 2015, 132, 1168–1181. [Google Scholar] [CrossRef]
- El Samrout, A.; Braydi, O.; Younes, R.; Trouchu, F.; Lafon, P. A New Hybrid Method to Solve the Multi-objective Optimization Problem for a Composite Hat-Stiffened Panel. In Bioinspired Heuristics for Optimization. Studies in Computational Intelligence; Talbi, E.G., Nakib, A., Eds.; Springer: Cham, Switzerland, 2019; Volume 774. [Google Scholar] [CrossRef]
- Murthy, V.R.; Annamalai, K.; Elango, M. Numerical analysis of hat stiffened composite panels for pre and post buckling conditions. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1128, 012021. [Google Scholar] [CrossRef]
- Shi, M.; Chen, P. Simulation of manufacture of the hat-stiffened composite plate based on multidisciplinary coupling. Acta Mater. Compos. Sin. 2021, 38, 4150–4160. [Google Scholar] [CrossRef]
- Wang, T.; Bai, R.; Wei, C.; Huang, X.; Bai, H. Interface damage analysis of composite hat-stiffened panels. J. Phys. Conf. Ser. 2021, 1948, 012139. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, K.; Yu, T.; Zong, S.; Wang, X. Structural deformation mechanism of the hat-stiffened plate used in marine structures under impact load. Ocean. Eng. 2022, 266, 112736. [Google Scholar] [CrossRef]
- Hochster, H.; Ranatunga, V.; Shemesh, N.N.; Haj-Ali, R. Surrogate PHFGMC micromechanical models for multiscale analysis: AI-enhanced low-velocity impact analysis of hat-stiffened composite panels. J. Compos. Mater. 2024, 59, 305–320. [Google Scholar] [CrossRef]
- Shi, G.-J.; Ji, Y.-H.; Xu, J.-B.; Wang, D.-Y.; Xu, Z.-T. Experimental study of structural failure and ultimate strength of GFRP girder with hat stiffeners and foams under bending load. Mar. Struct. 2024, 96, 103607. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.; Liu, A.; Guedes Soares, C. Integrated design method of marine C/GFRP hat-stiffened panels towards ultimate strength optimization. Ocean. Eng. 2025, 317, 120052. [Google Scholar] [CrossRef]
- Yang, X.; Li, G.; Sun, C.; Niu, S.; Yang, Y.; Liu, X.; Shao, C. The influence of high toughness resin region on the pull-off failure process of hat-stiffened composite structures. Eng. Fail. Anal. 2025, 169, 109214. [Google Scholar] [CrossRef]
- ANSYS. Release 2021 R2 Engineering What’s Ahead–Element Reference; ANSYS: Canonsburg, PA, USA, 2021. [Google Scholar]
- Zienkiewicz, O.C. The Finite Element Method; McGraw-Hill: London, UK, 1986. [Google Scholar]
- Moaveni, S. Finite Element Analysis: Theory and Application with ANSYS, 3rd ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 2008. [Google Scholar]
- Carrijo, E.C.; Paiva, J.B.; Giogo, J.S. A numerical and experimental study of stiffened plates in bending. Trans. Model. Simul. 1999, 21, 12–18. [Google Scholar]
- Araújo, J.M. Curso de Concreto Armado, 4th ed.; Dunas: Rio Grande, RS, Brazil, 2014; Volume 2. (In Portuguese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).