The Dual Influence of Silicon Content and Mechanical Stress on Magnetic Barkhausen Noise in Non-Oriented Electrical Steel
Abstract
1. Introduction
2. Experimental
2.1. Materials
2.2. Microstructure and Texture Characterization
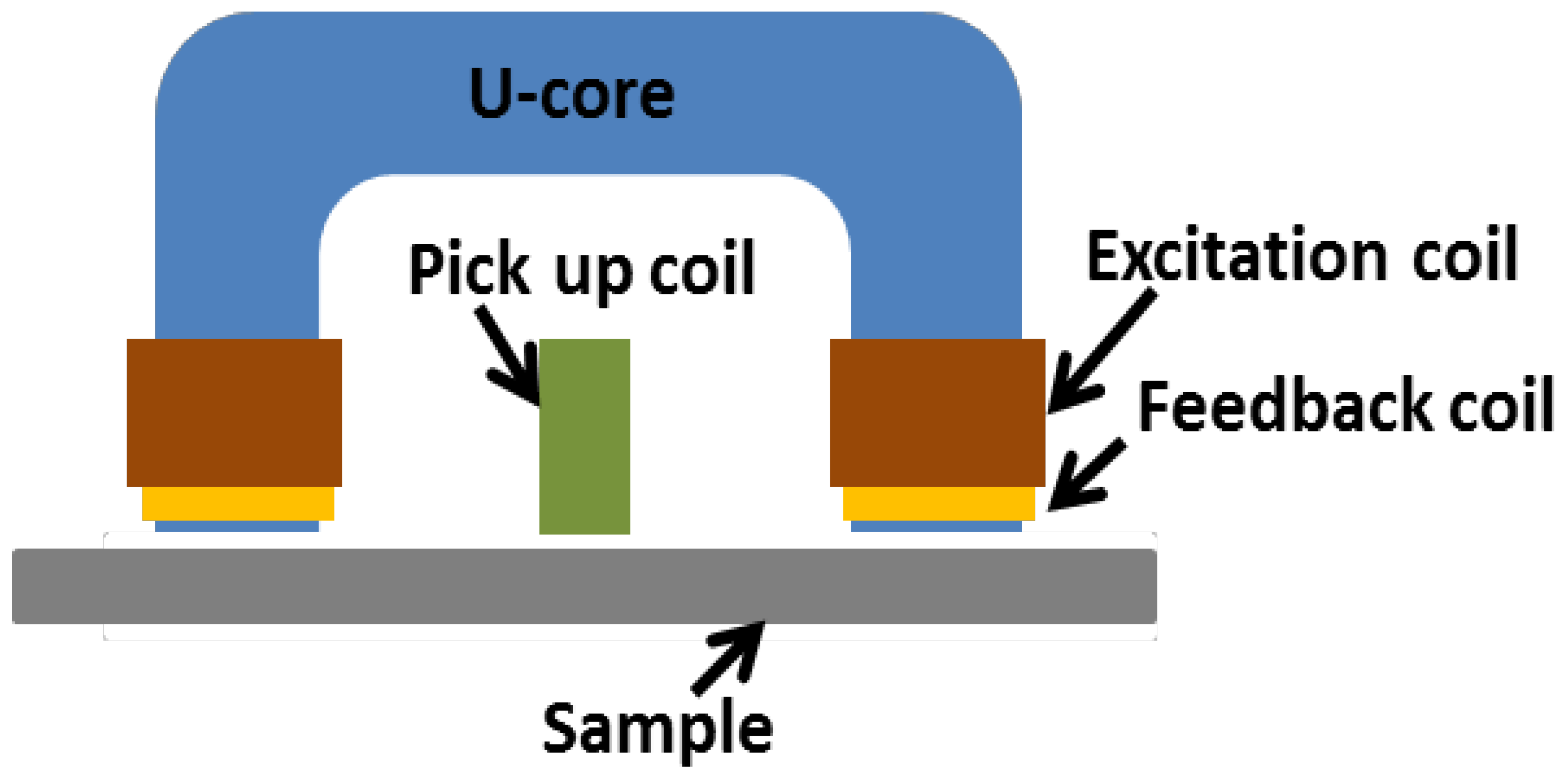
2.3. MBN Measurements
3. Results and Discussion
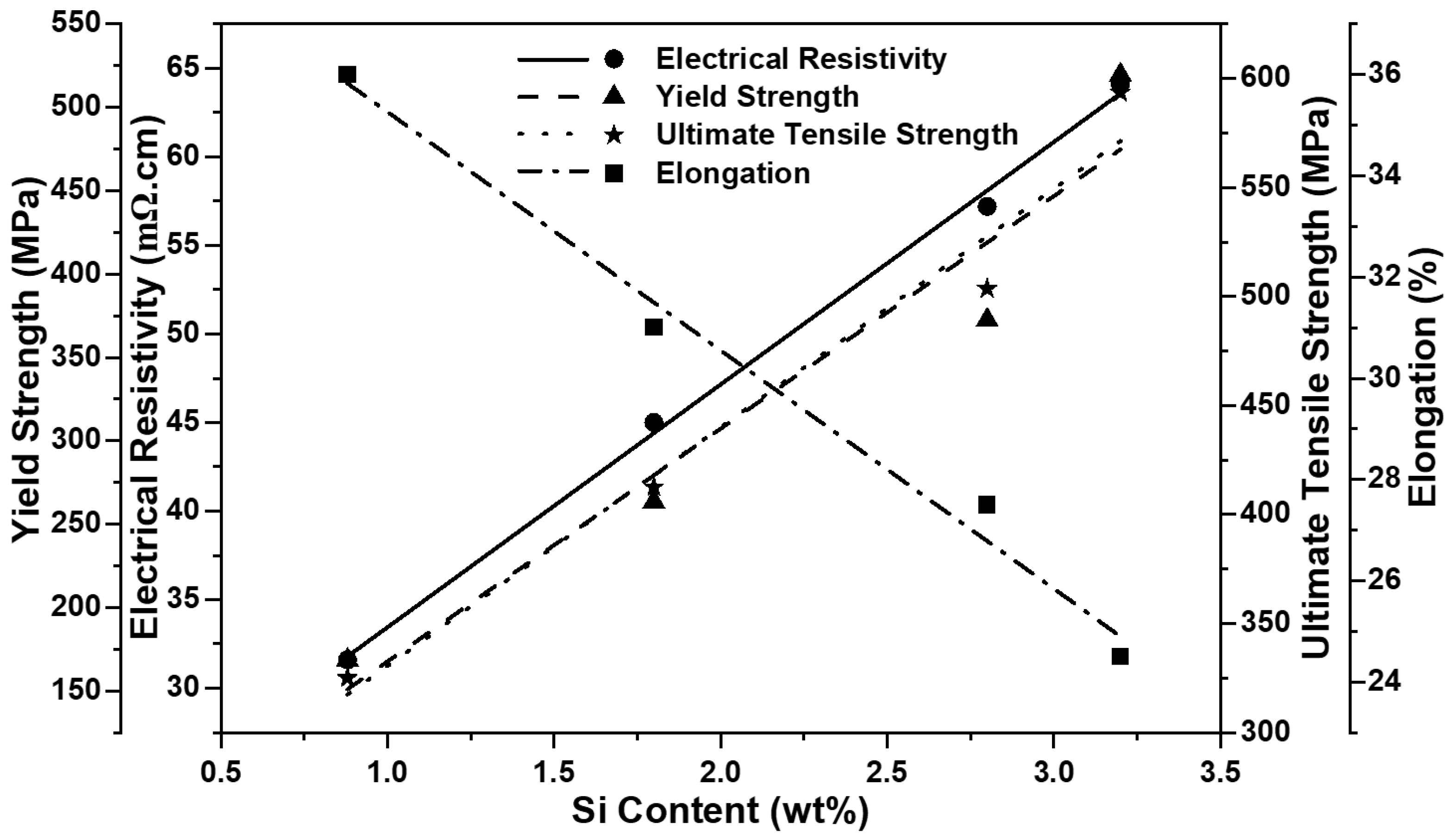
3.1. Material Properties
3.2. Microstructure and Texture
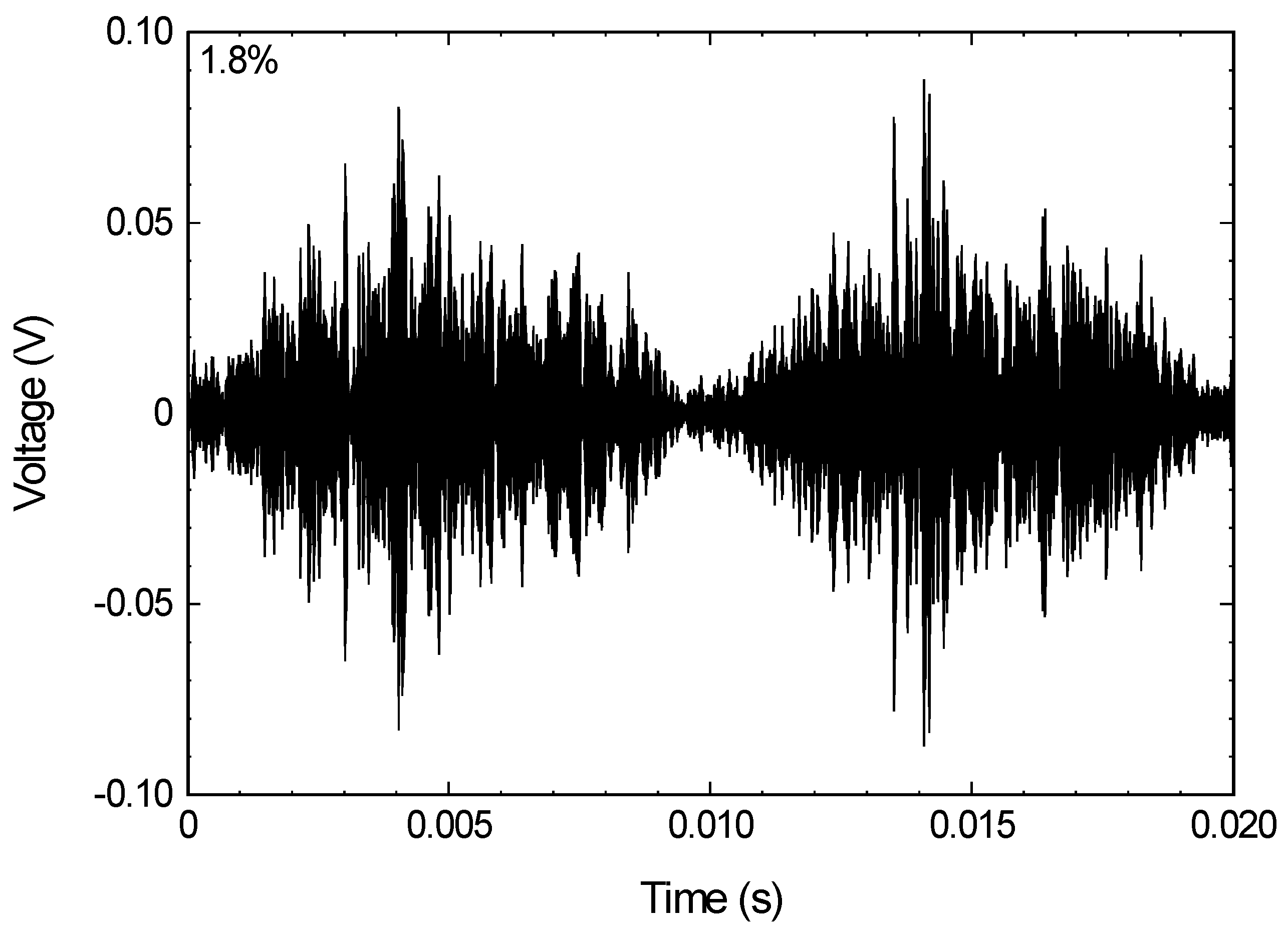
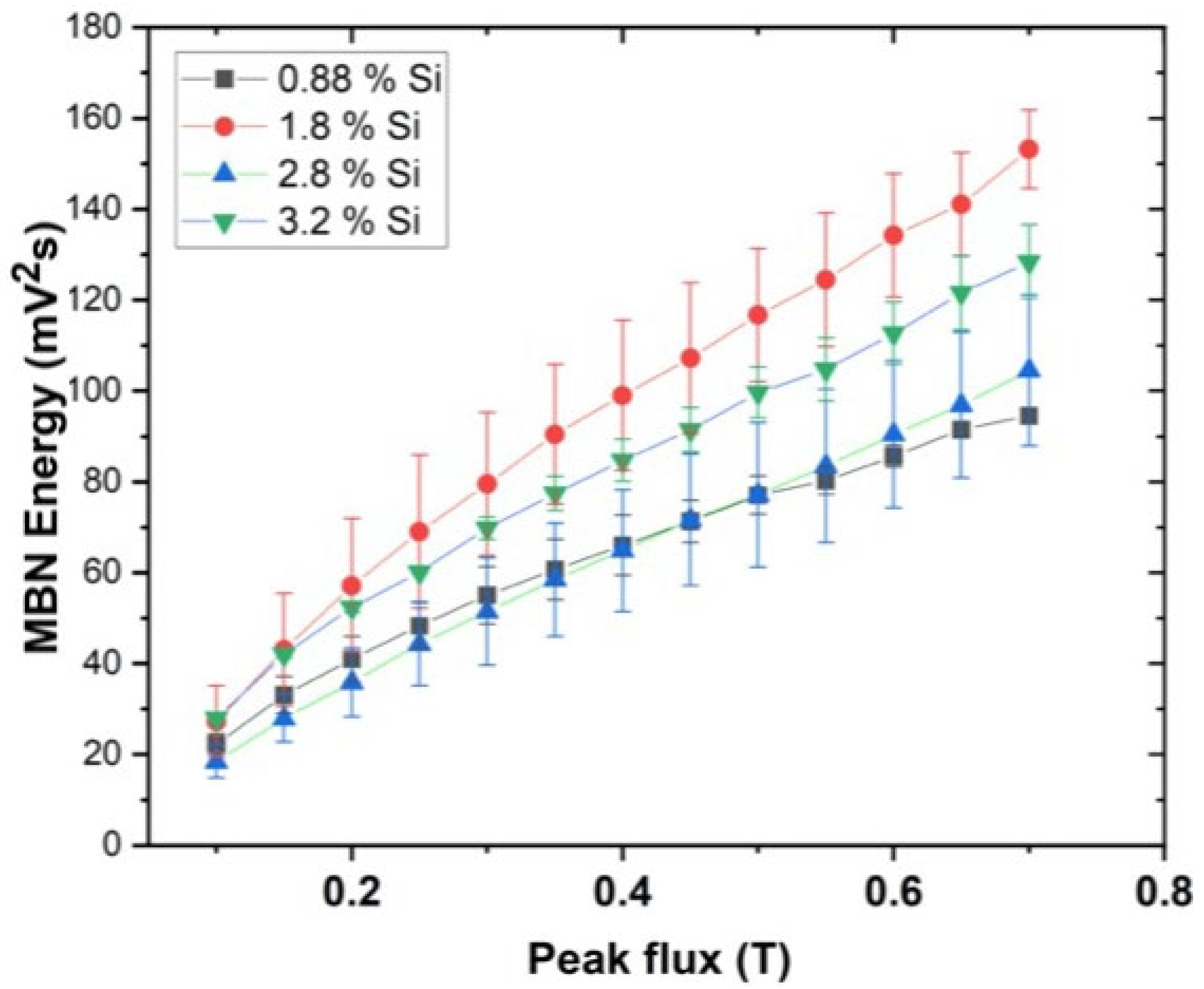
3.3. MBN Without Elastic Stress
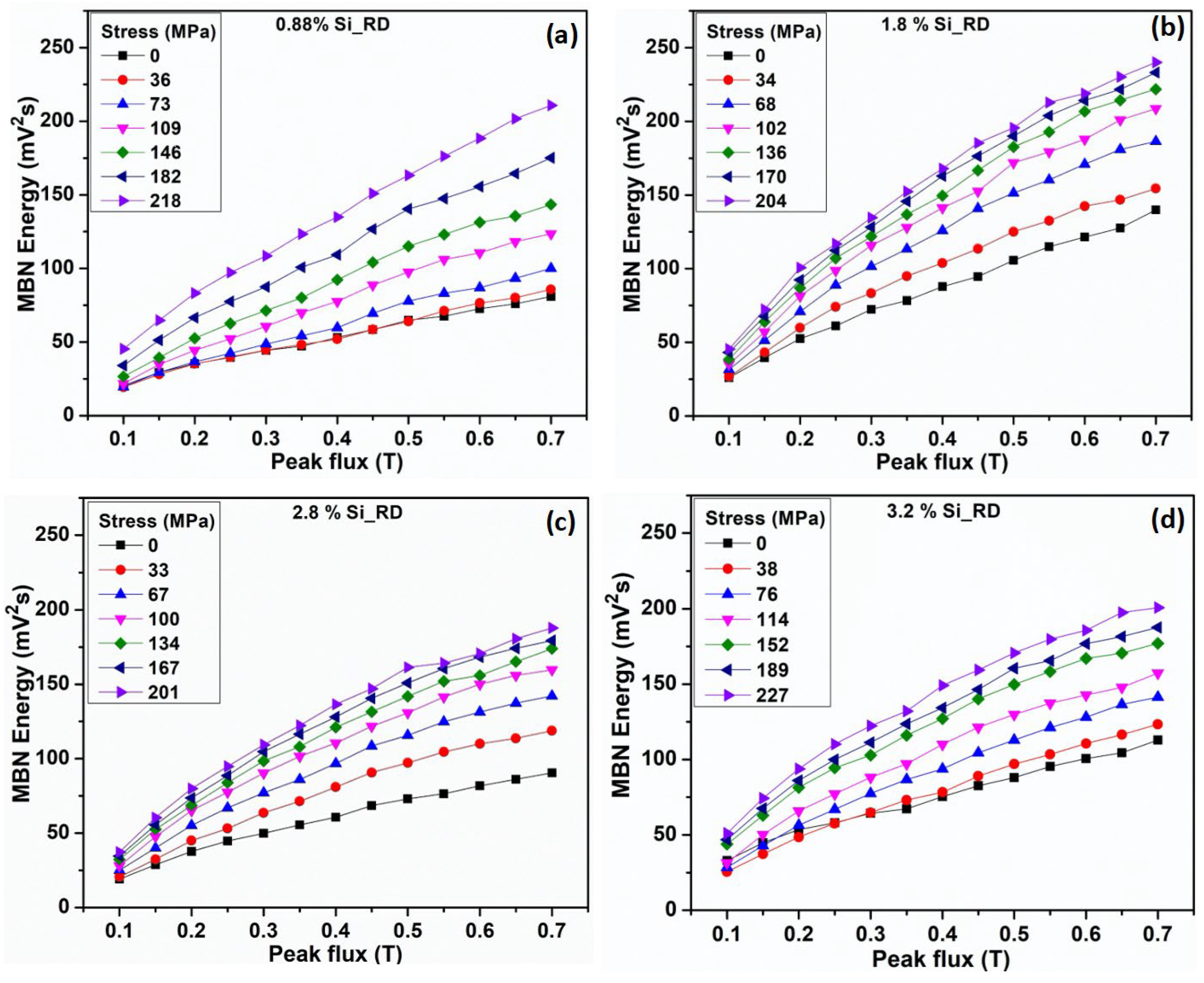
3.4. Elastic Stress Dependence of MBN
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karami, R.; Butler, D.; Tamimi, S. Manufacturing of non-grain-oriented electrical steels. Int. J. Adv. Manuf. Tech. 2024, 133, 1083–1109. [Google Scholar] [CrossRef]
- Paltanea, G.; Manescu, V.; Antoniac, A.; Nemoianu, I.V.; Gavrila, H. Mechanical and magnetic properties variation in non-oriented electrical steels with different cutting technology: A review. Materials 2024, 17, 1345. [Google Scholar] [CrossRef] [PubMed]
- Matsumura, K.; Fukuda, B. Recent developments of non-oriented electrical steel sheets. IEEE Trans. Magn. 1984, 20, 1533–1538. [Google Scholar] [CrossRef]
- Petrovic, D.S. Non-oriented electrical steel sheets. Mater. Technol. 2010, 44, 317–325. [Google Scholar]
- Bohn, F.; Gündel, A.; Landgraf, F.J.G.; Severino, A.M.; Sommer, R.L. Magnetostriction, Barkhausen noise and magnetization processes in E110 grade non-oriented electrical steels. J. Magn. Magn. Mater. 2007, 317, 20–28. [Google Scholar] [CrossRef]
- Kestens, L.; Jacobs, S. Texture Control During theManufacturing of Nonoriented Electrical Steels, Texture, Stress, and Microstructure; Wiley: Hoboken, NJ, USA, 2008; Article ID 173083; pp. 1–9. [Google Scholar]
- Xia, Z.; Kang, Y.; Wang, Q. Developments in the production of grain-oriented electrical steel. J. Magn. Magn. Mater. 2008, 320, 3229–3233. [Google Scholar] [CrossRef]
- Sundaria, R.; Lehikoinen, A.; Arkkio, A.; Belahcen, A. Effects of Manufacturing Processes on Core Losses of Electrical Machine. IEEE Trans. Energy Convers. 2021, 36, 197–206. [Google Scholar] [CrossRef]
- Füzer, J.; Dobák, S.; Petryshynets, I.; Kollár, P.; Kovác, F.; Slota, J. Correlation between Cutting Clearance, Deformation Texture, and Magnetic Loss Prediction in Non-Oriented Electrical Steels. Materials 2021, 14, 6893. [Google Scholar] [CrossRef]
- Ouyang, G.; Chen, X.; Liang, Y.; Macziewski, C.; Cui, J. Review of Fe-6.5 wt%Si high silicon steel—A promising soft magnetic material for sub-kHz application. J. Magn. Magn. Mater. 2019, 481, 234–250. [Google Scholar] [CrossRef]
- Bozorth, R.M. Ferromagnetism, 3rd ed.; D. Van Nostrand Company, Inc.: Toronto, ON, Canada, 1951. [Google Scholar]
- Hawezy, D. The influence of silicon content on physical properties of non-oriented silicon steel. Mater. Sci. Technol. 2017, 33, 1560–1569. [Google Scholar] [CrossRef]
- Perevertov, O.; Schäfer, R. Influence of applied tensile stress on the hysteresis curve and magnetic domain structure of grain-oriented Fe–3% Si steel. J. Phys. D Appl. Phys. 2014, 47, 185001. [Google Scholar] [CrossRef]
- Dijkstra, L.J.; Martius, U.M. Domain pattern in silicon-iron under stress. Rev. Mod. Phys. 1953, 25, 146. [Google Scholar] [CrossRef]
- Saleem, A.; Goldbaum, D.; Brodusch, N.; Gauvin, R.; Chromik, R.R. Microstructure and mechanical property connections for a punched non-oriented electrical steel lamination. Mater. Sci. Eng. A 2018, 725, 456–465. [Google Scholar] [CrossRef]
- Samimi, A.A. Magnetic Barkhausen Noise Testing: Steel Grades and Stress Response. Ph.D. Dissertation, Queen’s University, Kingston, ON, Canada, 2015. [Google Scholar]
- Liu, J.; Tian, G.Y.; Gao, B.; Zeng, K.; Liu QHZheng, Y. Magnetic Barkhausen Noise Transient Analysis for Microstructure Evolution Characterization with Tensile Stress in Elastic and Plastic Status. Sensors 2021, 21, 8310. [Google Scholar] [CrossRef]
- Yamaura, S.; Furuya, Y.; Watanabe, T. The effect of grain boundary microstructure on Barkhausen noise in ferromagnetic materials. Acta. Mater. 2001, 49, 3019–3027. [Google Scholar] [CrossRef]
- Maciusowicz, M.; Psuj, G. Use of time-dependent multispectral representation of magnetic Barkhausen noise signals for the needs of non-destructive evaluation of steel materials. Sensors 2019, 19, 1443. [Google Scholar] [CrossRef]
- Bahleda, F.; Neslušan, M.; Pastorek, F.; Koňár, R.; Kubjatko, T. Barkhausen Noise Emission as a Function of Tensile Stress in Low-Alloyed Steels: Influence of Corrosion and Steel Strength. Appl. Sci. 2023, 13, 6574. [Google Scholar] [CrossRef]
- Yelbay, H.İ.; Gür, C.H. Non-Destructive Determination of Surface Residual Stresses in Electron Beam Welded AISI 410 Martensitic Stainless Steel Using the Magnetic Barkhausen Noise Technique. Metals 2025, 15, 305. [Google Scholar] [CrossRef]
- Vourna, P.; Ktena, A.; Tsakiridis, P.E.; Hristoforou, E. An accurate evaluation of the residual stress of welded electrical steels with magnetic Barkhausen noise. Measurement 2015, 71, 31–45. [Google Scholar] [CrossRef]
- Wang, L.; Xu, C.; Feng, L.; Wang, W. A Survey of the Magnetic Anisotropy Detection Technology of Ferromagnetic Materials Based on Magnetic Barkhausen Noise. Sensors 2024, 24, 7587. [Google Scholar] [CrossRef]
- Tam, P.L.; Hammersberg, P.; Persson, G.; Olavison, J. Case depth evaluation of induction-hardened camshaft by using magnetic Barkhausen noise (MBN) method. Nondestruct. Test. Eval. 2020, 36, 494–514. [Google Scholar] [CrossRef]
- Lasaosa, A.; Gurruchaga, K.; Arizti, F.; Martinez-de-Guerenu, A. Induction Hardened Layer Characterization and Grinding Burn Detection by Magnetic Barkhausen Noise Analysis. J. Nondestruct. Eval. 2017, 36, 27. [Google Scholar] [CrossRef]
- Samimi, A.A.; Krause, T.W.; Clapham, L.; Gallaugher, M.; Ding, Y.; Ghosh, P.; Chromik, R.; Knight, A.M. Correlation between ac core loss and surface magnetic Barkhausen noise in electric motor steel. J. Nondestruct. Eval. 2014, 33, 663–669. [Google Scholar] [CrossRef]
- de Campos, M.F.; Campos, M.A.; Landgraf, F.J.G.; Padovese, L.R. Anisotropy study of grain oriented steels with magnetic Barkhausen Noise. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2011; Volume 303, p. 012020. [Google Scholar]
- Krause, T.W.; Samimi, A.A. Micromagnetic Techniques. In ASM Handbook Volume17: Nondestructive Evaluation and Quality Control, 10th ed.; ASM International: Almere, The Netherlands, 2018. [Google Scholar]
- Krause, T.W.; Clapham, L.; Pattantyus, A.; Atherton, D.L. Investigation of the stress-dependent magnetic easy axis in steel using magnetic Barkhausen noise. J. Appl. Phys. 1996, 79, 4242–4252. [Google Scholar] [CrossRef]
- Lemke, J.N.; Simonelli, M.; Garibaldi, M.; Ashcroft, I.; Hague, R.; Vedani, M.; Wildman, R.; Tuck, C. Calorimetric study and microstructure analysis of the order-disorder phase transformation in silicon steel built by SLM. J. Alloys Compd. 2017, 722, 293–301. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Chikazumi, S.; Charap, S.H. Physics of Magnetism; Krieger: Malaba, FL, USA, 1964. [Google Scholar]
- He, Y.; Hilinski, E.J. Skew rolling and its effect on the deformation textures of non-oriented electrical steels. J. Mater. Process. Technol. 2017, 242, 182–195. [Google Scholar] [CrossRef]
- Singh, Y. Electrical resistivity measurements: A review. In International Journal of Modern Physics: Conference Series; World Scientific Publishing Company: Singapore, 2013; Volume 22, pp. 745–756. [Google Scholar]
- White, S.A. A Barkhausen Noise Testing SYSTEM for CANDU Feeder Pipes. Ph.D. Thesis, Department of Physics, Queen’s University, Kingston, ON, Canada, 2009. [Google Scholar]
- Böhm, T.; Schneider, J.; Telger, K.; Wuppermann, C.-D.; Kawalla, R.; Friedrich, K.E. Method of Producing Non-Grain-Oriented Electrical Sheet. U.S. Patent US6582528B1, 24 June 2003. [Google Scholar]
- Tomida, T.; Uenoya, S.; Sano, N. Fine-grained doubly oriented silicon steel sheets and mechanism of cube texture development. Mater. Trans. 2023, 44, 1106–1115. [Google Scholar] [CrossRef]
- Ahn, Y.-K.; Jeong, Y.-K.; Kim, T.-Y.; Cho, J.-U.; Hwang, N.-M. Texture evolution of non-oriented electrical steel analyzed by EBSD and in-situ XRD during the phase transformation from γ to α. Mater. Today Commun. 2020, 25, 101307. [Google Scholar] [CrossRef]
- Sahoo, G.; Singh, C.D.; Deepa, M.; Dhua, S.K.; Saxena, A. Recrystallization behaviour and texture of non-oriented electrical steels. Mater. Sci. Eng. A 2018, 734, 229–243. [Google Scholar] [CrossRef]
- Ahn, Y.K.; Kwon, S.B.; Jeong, Y.K.; Cho, J.U.; Kim, T.Y.; Hwang, N.M. Fabrication of cube-on-face textured Fe-1wt% Si and Fe-2wt% Si-1wt% Ni electrical steel using surface nucleation during γ→α phase transformation. Mater. Charact. 2020, 170, 110724. [Google Scholar] [CrossRef]
- Sha, Y.H.; Sun, C.; Zhang, F.; Patel, D.; Chen, X.; Kalidindi, S.R.; Zuo, L. Strong cube recrystallization texture in silicon steel by twin-roll casting process. Acta. Mater. 2014, 76, 106–117. [Google Scholar] [CrossRef]
- Wang, L.; He, C.; Liu, X. Evaluation of the Magnetocrystalline Anisotropy of Typical Materials Using MBN Technology. Sensors 2021, 21, 3330. [Google Scholar] [CrossRef] [PubMed]
- Stefanita, C.G.; Atherton, D.L.; Clapham, L. Plastic versus elastic deformation effects on magnetic Barkhausen noise in steel. Acta Mater. 2000, 48, 3545–3551. [Google Scholar] [CrossRef]
- Di, J.; He, C.; Lee, Y.C.; Liu, X. Evaluation of the stress gradient of the superficial layer in ferromagnetic components based on sub-band energy of magnetic Barkhausen noise. Nondestruct. Test. Eval. 2021, 37, 41–55. [Google Scholar] [CrossRef]
- Chen, C.-W. Magnetism and Metallurgy of Soft Magnetic Materials; Dover Publications, Inc.: Garden City, NY, USA, 1986; p. 130. [Google Scholar]
- Corner, W.D.; Mason, J.J. The Effect of Stress on the Domain Structure of Cube-textured Silicon Iron. Proc. Phys. Soc. 1963, 81, 925. [Google Scholar] [CrossRef]
- Lee, K.; Park, S.; Huh, M.; Kim, J.; Engler, O. Effect of texture and grain size on magnetic flux density and core loss in non-oriented electrical steel containing 3.15% Si. J. Magn. Magn. Mater. 2014, 354, 324–332. [Google Scholar] [CrossRef]




| Steel | Si | C | Mn | Al | Fe | Thickness (mm) |
|---|---|---|---|---|---|---|
| A | 0.88 | 0.0021 | 0.307 | 0.461 | Bal. | 0.56 |
| B | 1.8 | 0.0023 | 0.299 | 0.515 | Bal. | 0.59 |
| C | 2.8 | 0.0033 | 0.303 | 0.516 | Bal. | 0.60 |
| D | 3.2 | 0.0029 | 0.400 | 0.580 | Bal. | 0.61 |
| Steel | Average Grain Size (μm) | Yield Strength (MPa) |
|---|---|---|
| A | 178 ± 31 | 168.5 |
| B | 172 ± 25 | 263.5 |
| C | 160 ± 22 | 372.5 |
| D | 124 ± 15 | 519.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleem, A.; Mehdi, M.; Underhill, P.R.; He, Y.; Krause, T.W. The Dual Influence of Silicon Content and Mechanical Stress on Magnetic Barkhausen Noise in Non-Oriented Electrical Steel. Metals 2025, 15, 600. https://doi.org/10.3390/met15060600
Saleem A, Mehdi M, Underhill PR, He Y, Krause TW. The Dual Influence of Silicon Content and Mechanical Stress on Magnetic Barkhausen Noise in Non-Oriented Electrical Steel. Metals. 2025; 15(6):600. https://doi.org/10.3390/met15060600
Chicago/Turabian StyleSaleem, Aroba, Mehdi Mehdi, P. Ross Underhill, Youliang He, and Thomas W. Krause. 2025. "The Dual Influence of Silicon Content and Mechanical Stress on Magnetic Barkhausen Noise in Non-Oriented Electrical Steel" Metals 15, no. 6: 600. https://doi.org/10.3390/met15060600
APA StyleSaleem, A., Mehdi, M., Underhill, P. R., He, Y., & Krause, T. W. (2025). The Dual Influence of Silicon Content and Mechanical Stress on Magnetic Barkhausen Noise in Non-Oriented Electrical Steel. Metals, 15(6), 600. https://doi.org/10.3390/met15060600







