Machinability Assessment and Multi-Objective Optimization of Graphene Nanoplatelets-Reinforced Aluminum Matrix Composite in Dry CNC Turning
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Workpiece Material Fabrication
- Placing a ceramic container with aluminum in the laboratory furnace,
- Heating the laboratory furnace to 750 °C,
- Liquefying aluminum and removal of oxides from the melt surface,
- Aluminum casting into a preheated cylindrical mold at 100 °C using an electronic thermometer/heat-gun,
- Adding graphene nanostructures (GNPs) and stirring,
- Removing the split cylindrical mold after 3 min,
- Cooling in free air at room temperature of 20 °C.
2.3. CNC Turning Set-Up and Measuring Equipment
3. Non-Dominated Sorting Genetic Algorithm II (NSGA-II)
4. Results and Discussion
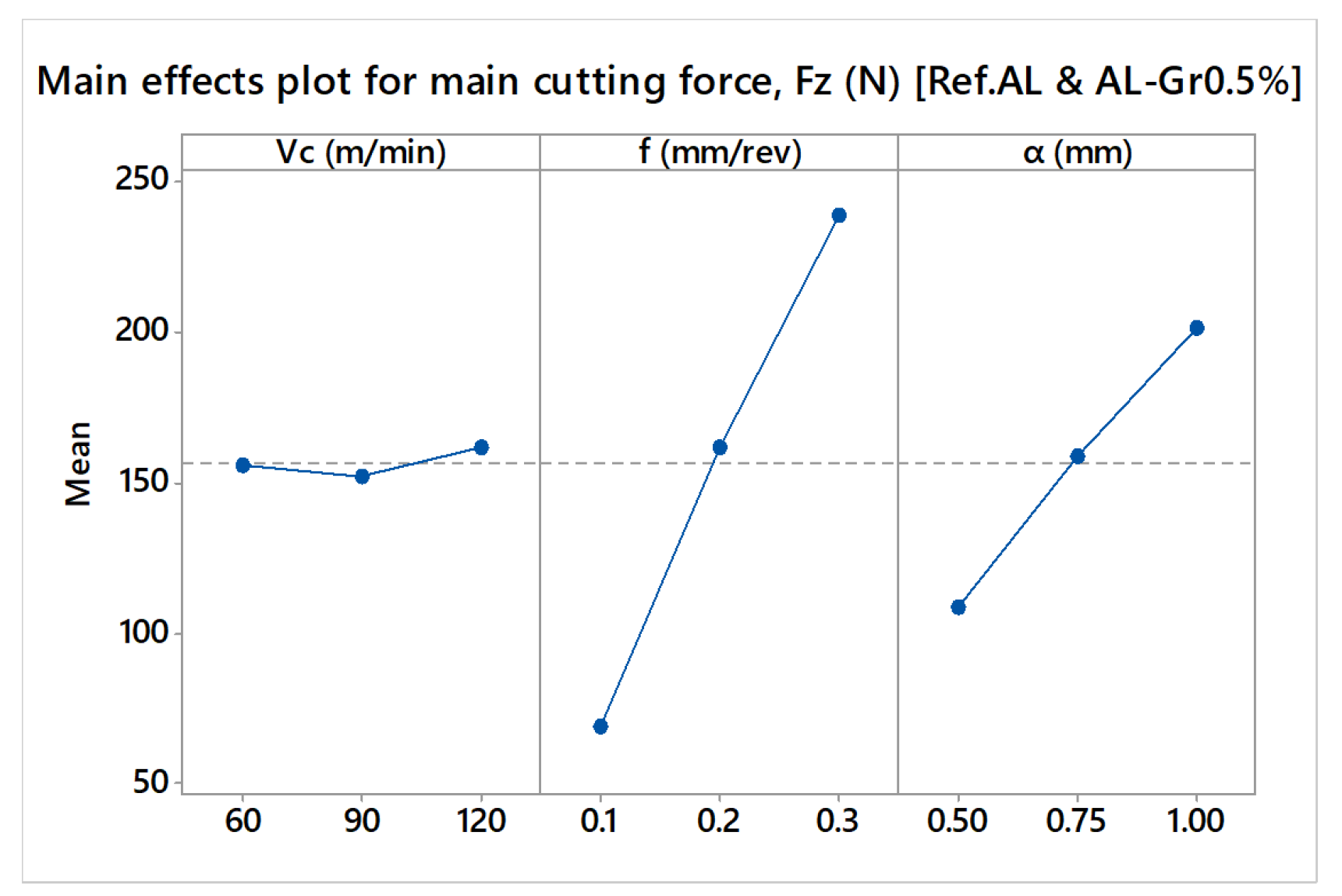
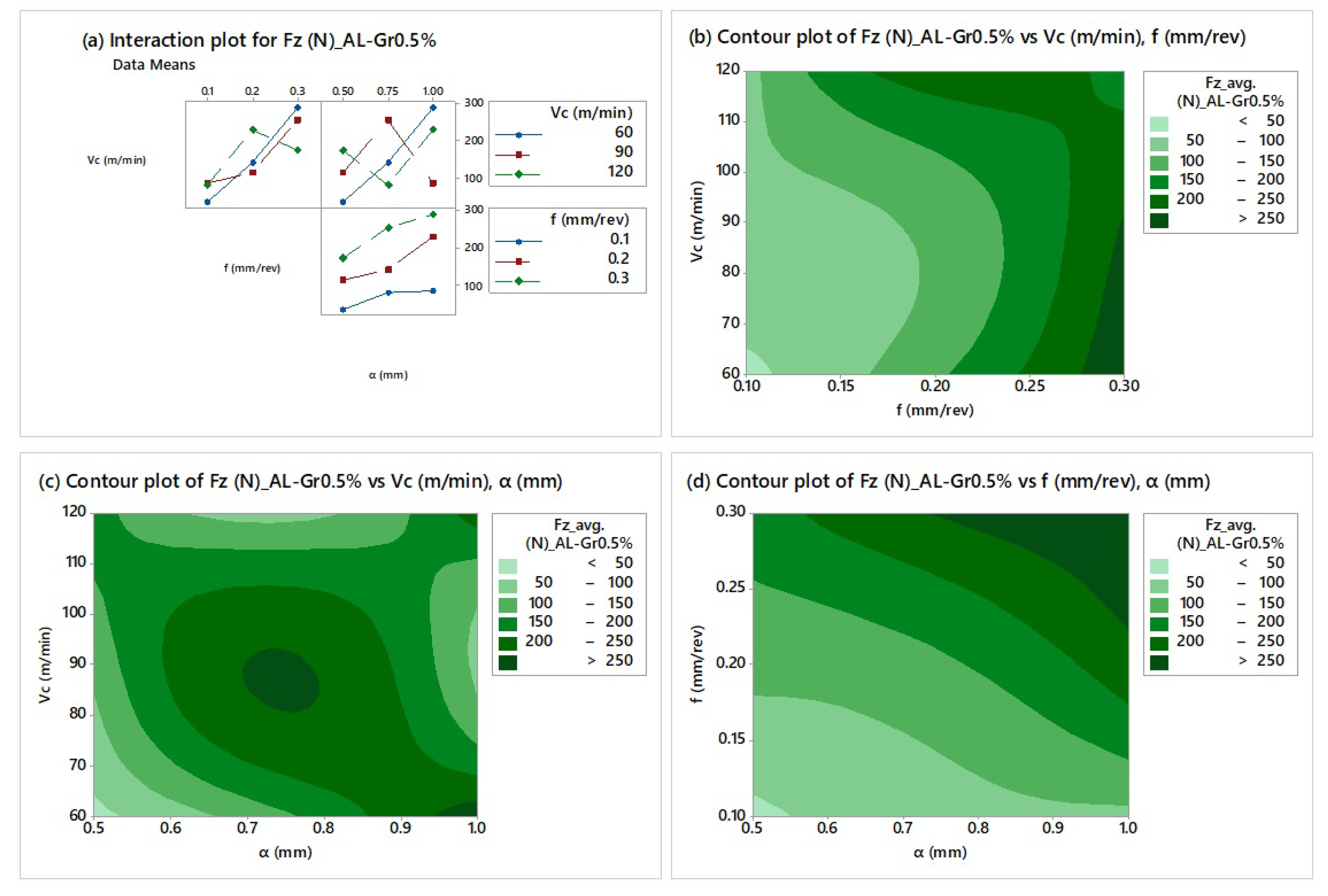
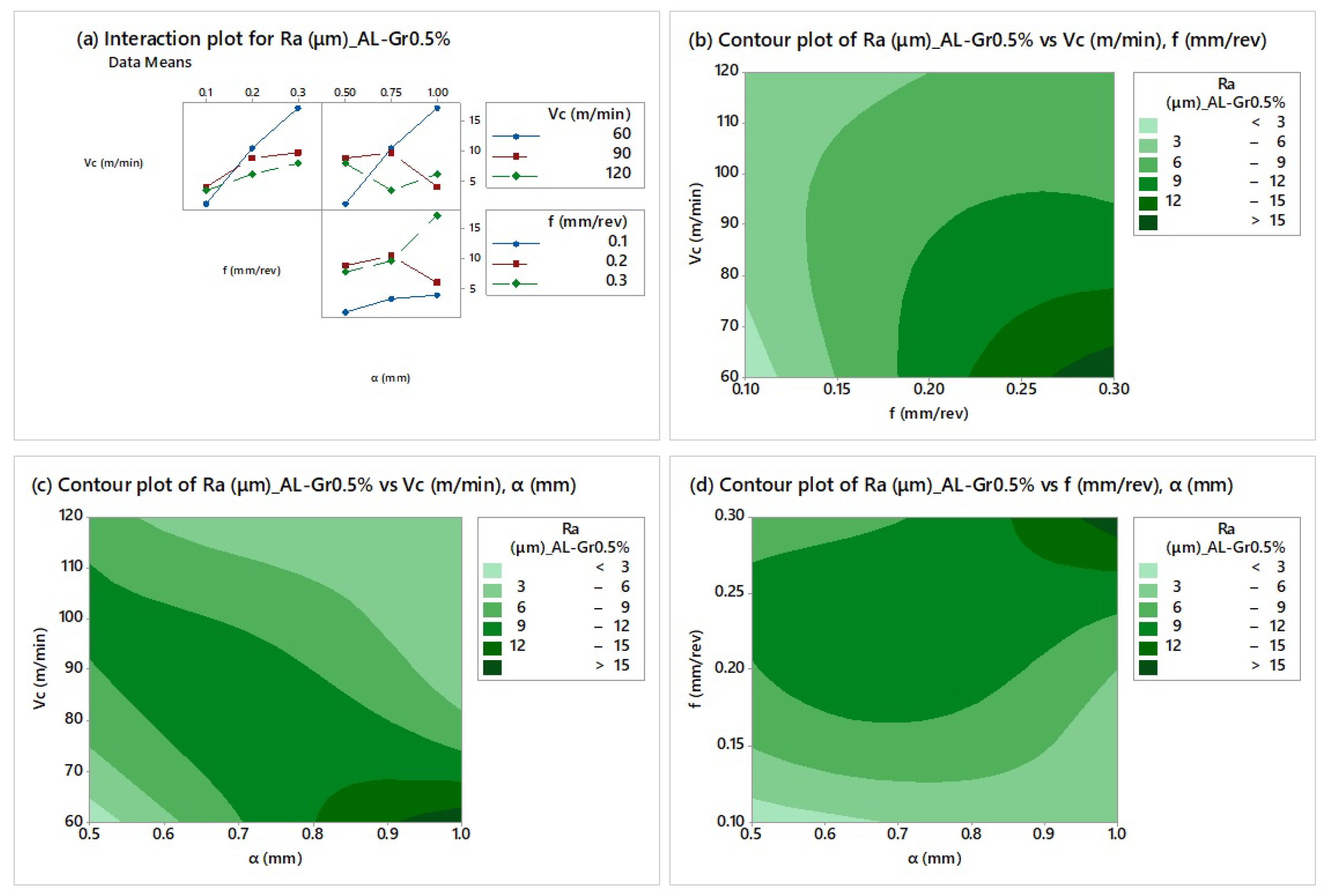
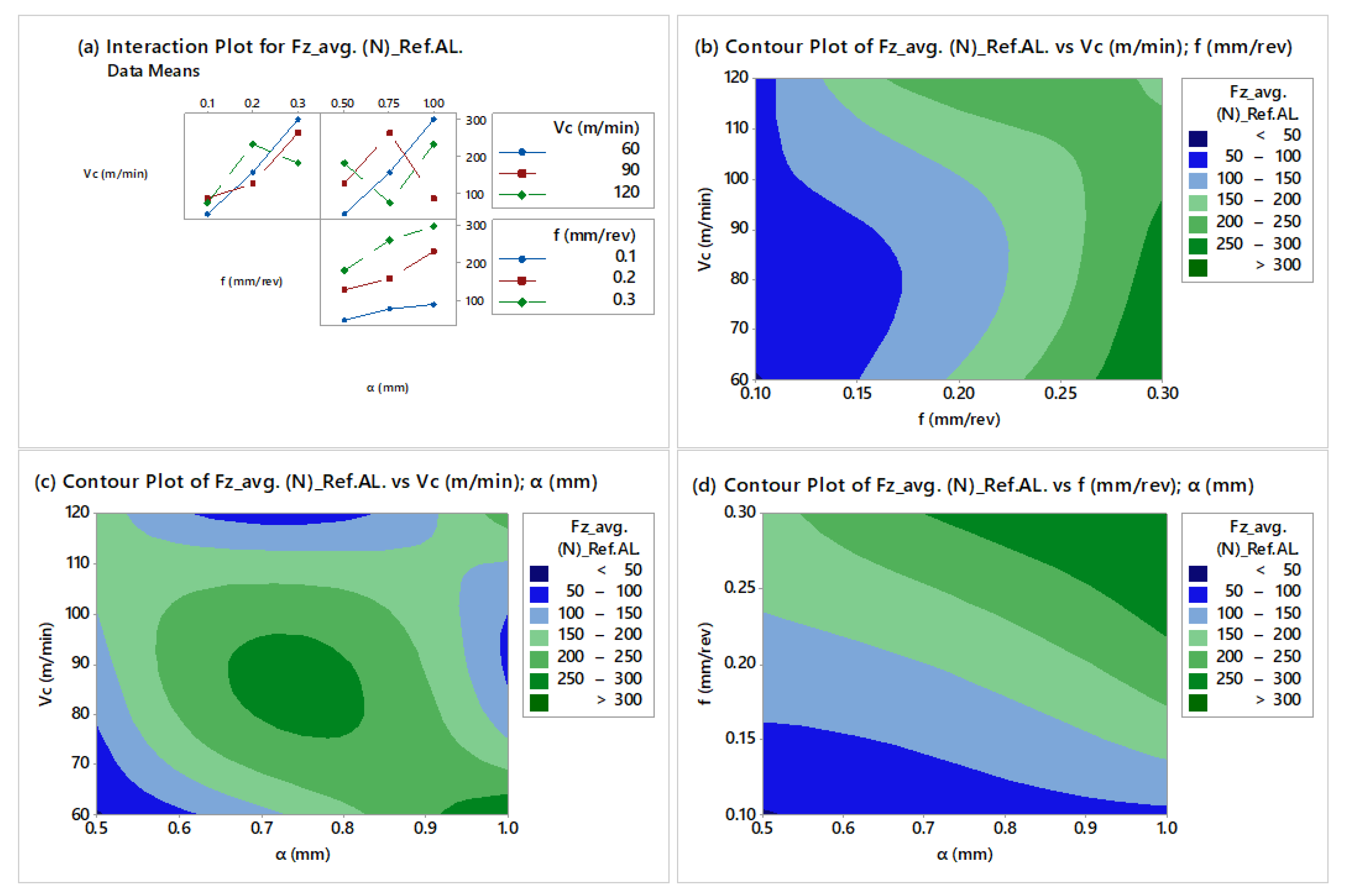
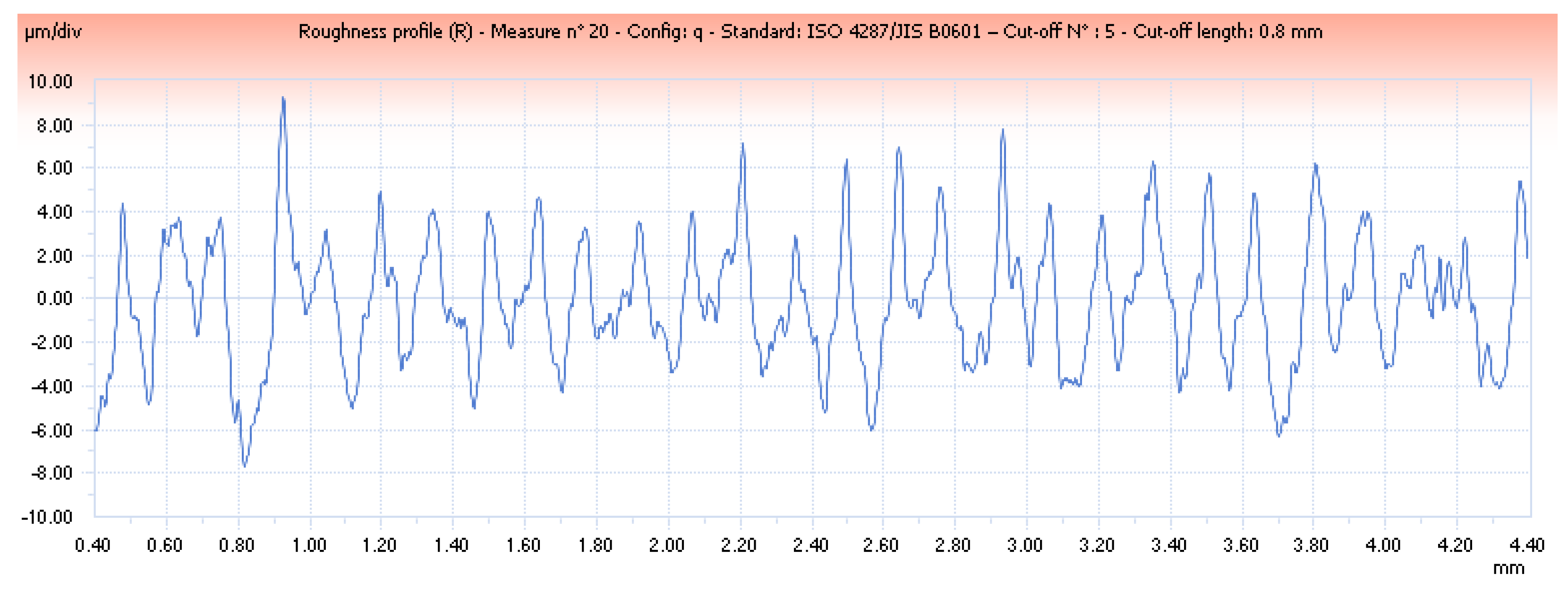
4.1. Experimental Results and Major Observations
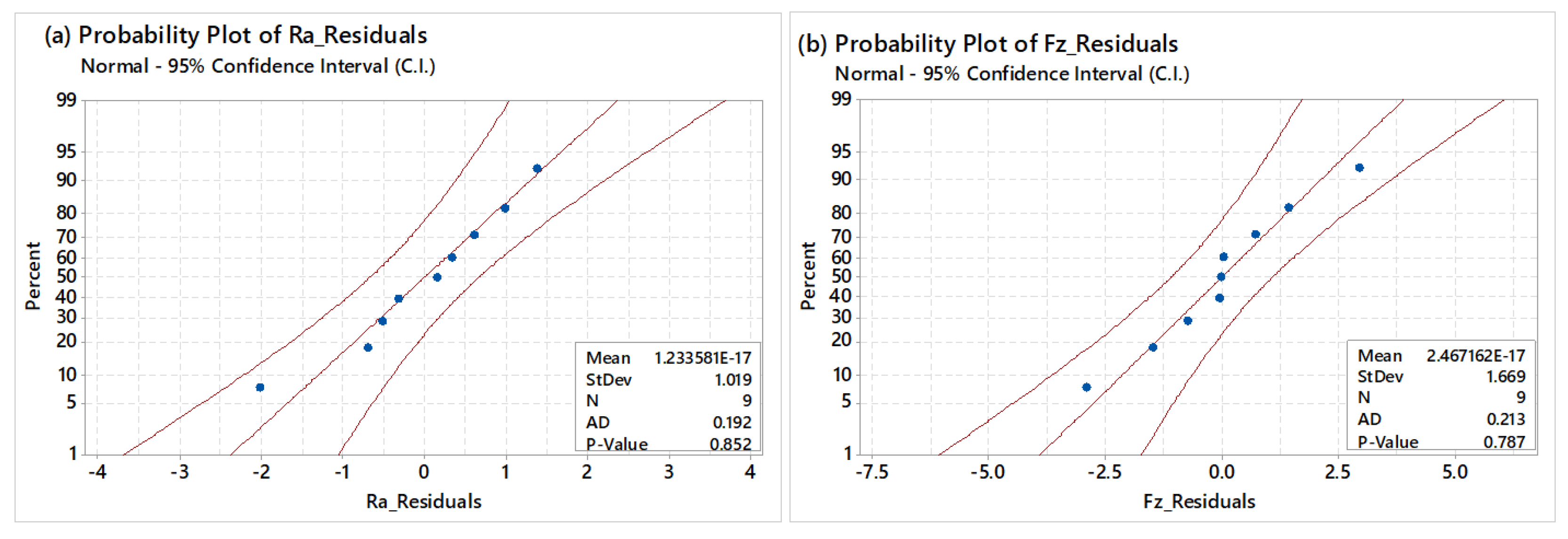
4.2. Analysis of Variance and Response Surface Regression
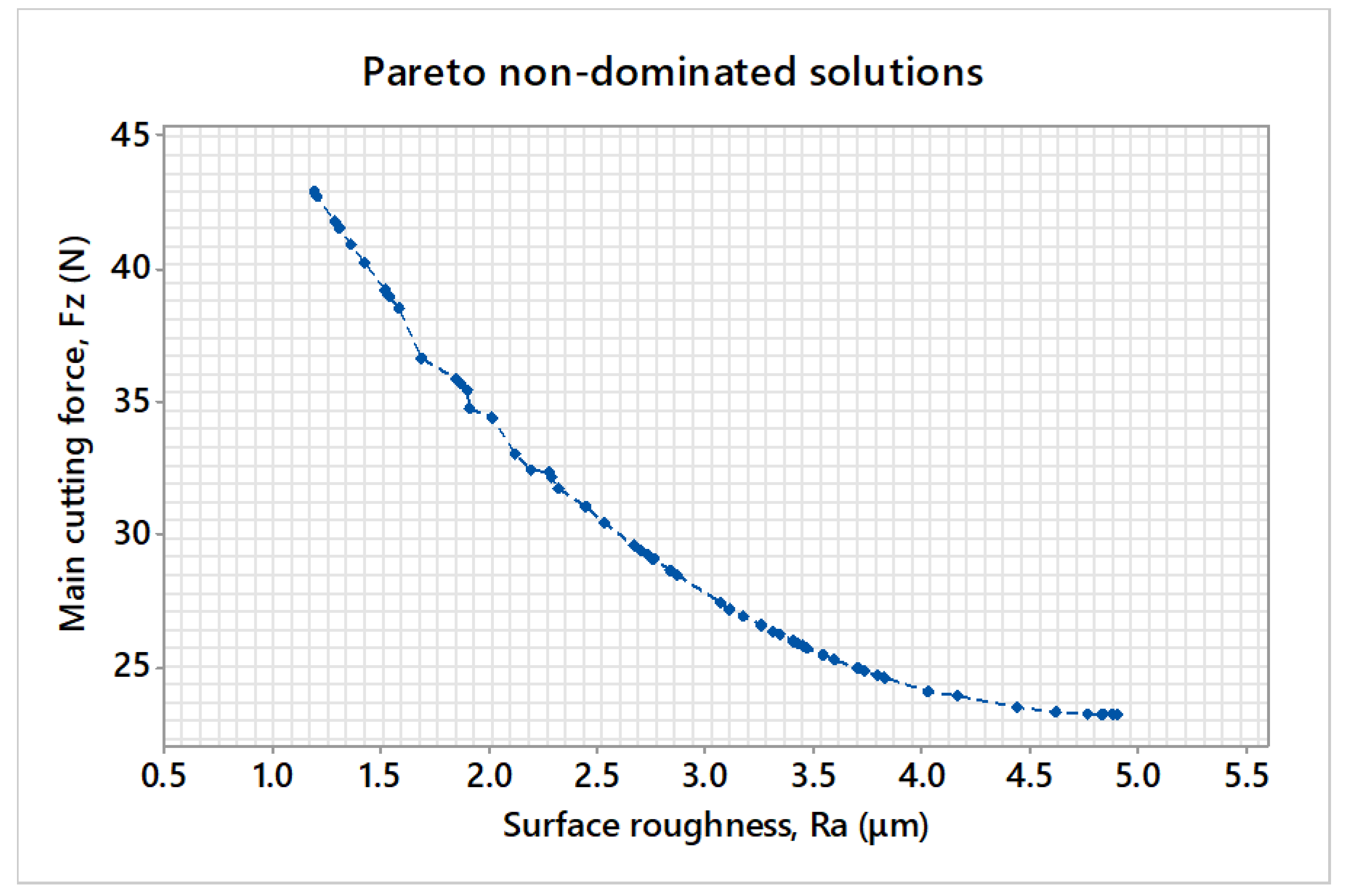
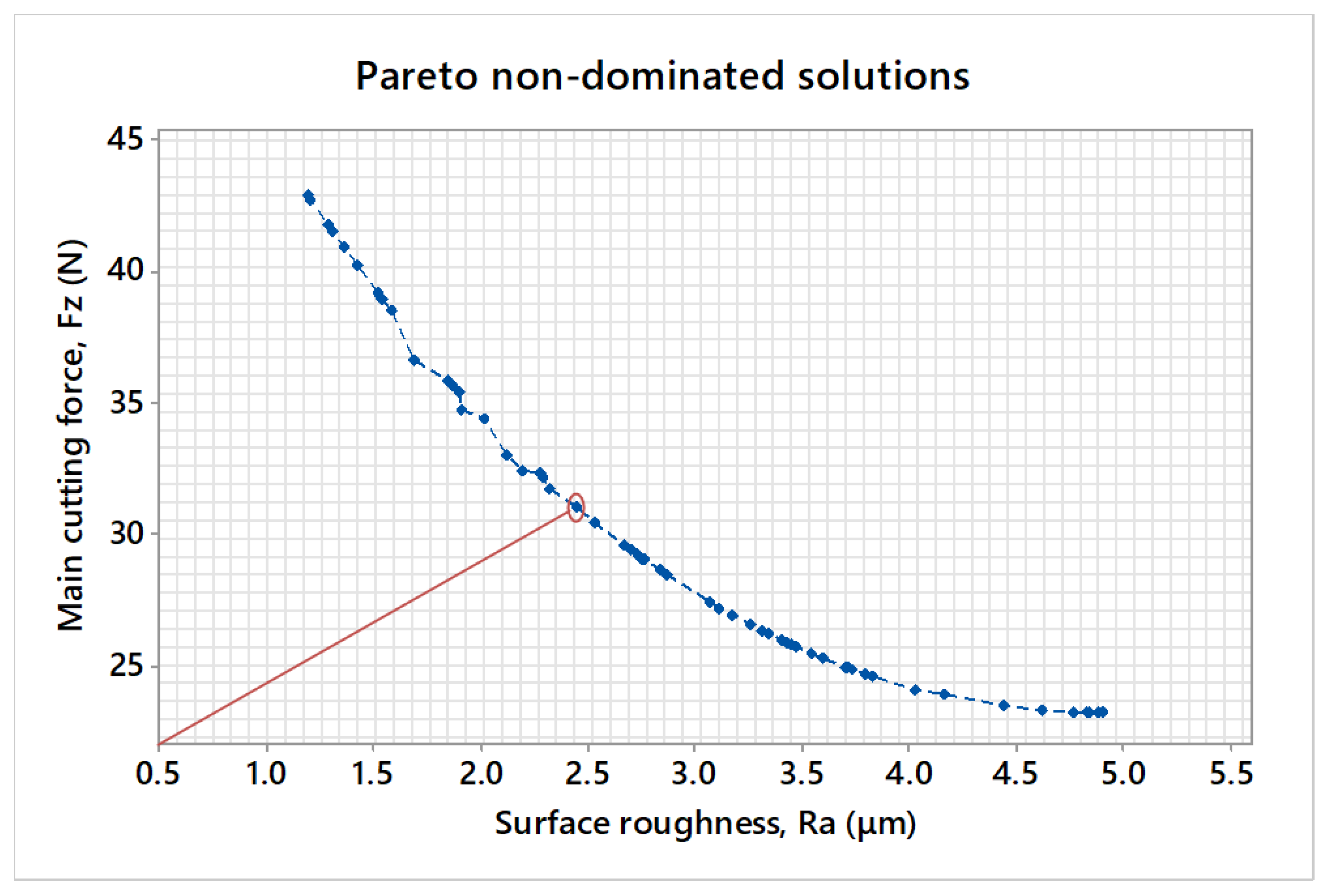
4.3. Implementation of NSGA-II for Multi-Objective Optimization
4.4. Confirmatory CNC Dry-Turning Experiment
5. Conclusions
- The machining process of the Al-Gr0.5% composite aluminum material introduced a highly non-linear problem that warrants further research in regard to the optimization of crucial metrics related to productivity and surface finish.
- Significant variations among the cutting parameters were observed during dry CNC turning of Al-Gr0.5% composite Al. However, it clearly appeared that the feed rate holds a dominant effect on the main cutting force and surface roughness, followed by the depth of cut and cutting speed.
- Chip formation was influenced by the content of the graphene nanoplatelets when compared to high-purity Al, thus introducing a significant change in terms of the material properties referring to both machinability criteria.
- The NSGA-II algorithm obtained beneficial non-dominated solutions for process planners to select from, with reference to the production requirements. Both machinability criteria, Fz and Ra, revealed a complex experimental search domain. This observation justifies the need for implementing intelligent algorithms for multi-criteria optimization problems related to machining processes.
- Confirmatory experimental results were in very good percentage agreement with those proposed by the NSGA-II algorithm. This encourages its application to examine and optimize the machinability aspects of a wide range of engineering materials for conventional and non-conventional material removal processes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCD | Central Composite Design |
| RSM | Response Surface Methodology |
| GNPs | Graphene Nanoplatelets |
| BUE | Built-up edge |
| ANOVA | Analysis of Variance |
| C.I. | Confidence Interval |
References
- Rawat, P.; Singh, K.K. An impact behavior analysis of CNT based fiber reinforced composites validated by LS-DYNA: A review. Polym. Compos. 2015, 38, 175–184. [Google Scholar] [CrossRef]
- Shrivastava, R.; Singh, K.K. Interlaminar fracture toughness characterization of laminated composites: A review. Polym. Rev. 2019, 60, 542–593. [Google Scholar] [CrossRef]
- Boostani, A.F.; Tahamtan, S.; Jiang, Z.Y.; Wei, D.; Yazdani, S.; Azari Khosroshahi, R.; Taherzadeh Mousavian, R.; Xu, J.; Zhang, X.M.; Gong, D. Enhanced tensile properties of aluminium matrix composites reinforced with graphene encapsulated SiC nanoparticles. Compos. Part A Appl. Sci. Manuf. 2015, 68, 155–163. [Google Scholar] [CrossRef]
- Gao, M.; Chen, T.; Ma, S.; Wang, H. Endowing a superior synergy of strength and ductility to aluminum matrix composite by dual-structured reinforcement and matrix. Mater. Sci. Eng A 2025, 924, 147820. [Google Scholar] [CrossRef]
- Guo, B.; Ni, S.; Shen, R.; Song, M. Fabrication of Ti–Al3Ti core–shell structured particle reinforced Al based composite with promising mechanical properties. Mater. Sci. Eng. A 2015, 639, 269–273. [Google Scholar] [CrossRef]
- Gupta, R.; Chaudhari, G.P.; Daniel, B.S.S. Strengthening mechanisms in ultrasonically processed aluminium matrix composite with in-situ Al3Ti by salt addition. Compos. B Eng. 2018, 140, 27–34. [Google Scholar] [CrossRef]
- Khosroshahi, N.B.; Mousavian, T.R.; Khosroshahi, R.A.; Brabazon, D. Mechanical properties of rolled A356 based composites reinforced by Cu-coated bimodal ceramic particles. Mater. Des. 2015, 83, 678–688. [Google Scholar] [CrossRef]
- Hong, S.-J.; Kim, H.-M.; Huh, D.; Suryanarayana, C.; Chun, B.S. Effect of clustering on the mechanical properties of SiC particulate-reinforced aluminum alloy 2024 metal matrix composites. Mater. Sci. Eng. A 2003, 347, 198–204. [Google Scholar] [CrossRef]
- Valibeygloo, N.; Khosroshahi, R.A.; Mousavian, R.T. Microstructural and mechanical properties of Al–4.5 wt% Cu reinforced with alumina nanoparticles by stir casting method. Int. J. Miner. Metall. Mater. 2013, 20, 978–985. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Khosroshahi, R.A.; Taherzadeh, R.M.; Brabazon, D. Effect of interfacial-active elements addition on the incorporation of micron-sized SiC particles in molten pure aluminum. Ceram. Int. 2014, 40, 8323–8332. [Google Scholar] [CrossRef]
- Huang, Z.; Yan, H. Improved mechanical properties of GNPs/Al composites by eliminating alumina and obtaining a strong bonded GNPs-Al direct contact interface and Mg-rich phases. J. Alloys Compd. 2024, 984, 173982. [Google Scholar] [CrossRef]
- Moheimani, S.K.; Dadkhah, M.; Saboori, A. Development of Novel AlSi10Mg Based Nanocomposites: Microstructure, Thermal and Mechanical Properties. Metals 2019, 9, 1000. [Google Scholar] [CrossRef]
- Azizi, Z.; Rahmani, K.; Taheri-Behrooz, F. The Influence of Graphene Nanoplatelets Addition on the Electrical and Mechanical Properties of Pure Aluminum Used in High-Capacity Conductors. Metals 2022, 12, 1883. [Google Scholar] [CrossRef]
- Na, H.-B.; Xu, L.-H.; Han, G.-C.; Liu, S.-K.; Lu, L.-H. Machinability Research on the Micro-Milling for Graphene Nano-Flakes Reinforced Aluminum Alloy. Metals 2019, 9, 1102. [Google Scholar] [CrossRef]
- Ju, B.; Yang, W.; Sun, J.; Han, Z.; Zhang, Q.; Xiu, Z.; Wu, G. Effect of vacancy defects of graphene on the interfacial bonding and strengthening mechanism of graphene/Al composite. Surf. Interfaces 2023, 41, 103272. [Google Scholar] [CrossRef]
- Lava Kumar, P.; Lombardi, A.; Byczynski, G.; Narayana Murty, S.V.S.; Murty, B.S.; Bichler, L. Recent advances in aluminium matrix composites reinforced with graphene-based nanomaterial: A critical review. Prog. Mater. Sci. 2022, 128, 100948. [Google Scholar] [CrossRef]
- El-Ghaoui, K.; Chatelain, J.-F.; Ouellet-Plamondon, C. Effect of Graphene on Machinability of Glass Fiber Reinforced Polymer (GFRP). J. Manuf. Mater. Process. 2019, 3, 78. [Google Scholar] [CrossRef]
- Nasr, M.M.; Anwar, S.; Al-Samhan, A.M.; Ghaleb, M.; Dabwan, A. Milling of Graphene Reinforced Ti6Al4V Nanocomposites: An Artificial Intelligence Based Industry 4.0 Approach. Materials 2020, 13, 5707. [Google Scholar] [CrossRef]
- Yu, H.; He, Z.; Li, J.; Li, B.; Xin, J.; Yao, L.; Yan, F. Finite element modeling on micro-machining of graphene-reinforced aluminum matrix composites. Int. J. Adv. Manuf. Technol. 2023, 124, 97–110. [Google Scholar] [CrossRef]
- Porwal, H.; Tatarko, P.; Grasso, S.; Khaliq, J.; Dlouhý, I.; Reece, M.J. Graphene reinforced alumina nano-composites. Carbon 2013, 64, 359–369. [Google Scholar] [CrossRef]
- Muduli, S.; Mahapatra, T.R.; Murty, A.V.K.; Parimanik, S.R.; Mishra, D.; Padhi, P.C. Supervised Machine Learning Algorithms for Machinability Assessment of Graphene Reinforced Aluminium Metal Matrix Composites. In Smart Technologies for Improved Performance of Manufacturing Systems and Services, 1st ed.; Behera, B.K., Moharana, B.R., Muduli, K., Islam, S.M.N., Eds.; CRC Press: Abingdon, UK, 2023; p. 18. [Google Scholar] [CrossRef]
- Ajithkumar, J.P.; Anthony, X.M. Machinability Analysis and Optimization of A17075 based B4C, Graphene and CNT Hybrid Composites. In Emerging Technologies for Sustainability, 1st ed.; Thomas, P.C., Mathai, V.J., Geevarghese, T., Eds.; CRC Press: Boca Raton, FL, USA, 2020; p. 10. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 7th ed.; John Wiley & Sons: New York, NY, USA, 2009; ISBN 978-0-470-12866-4. [Google Scholar]
- Bhushan, R.K. Optimization of cutting parameters for minimizing power consumption and maximizing tool life during machining of Al alloy SiC particle composites. J. Clean. Prod. 2013, 39, 242–254. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evolut. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evolut. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- ISO 4287:1997/JIS B0601; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters. Japanese Standards Association: Tokyo, Japan, 1998.













| Central Composite Design of Experiments | |||||
|---|---|---|---|---|---|
| Parameter | Symbol | Level | |||
| Low (−1) | Center (0) | High (1) | Unit | ||
| Cutting speed | Vc | 60 | 90 | 120 | m/min |
| Feed rate | f | 0.10 | 0.20 | 0.30 | mm/rev |
| Depth of cut | α | 0.50 | 0.75 | 1.00 | mm |
| Al | Si | Fe | Cu | Mg | Hf | Mn | Hg |
|---|---|---|---|---|---|---|---|
| 96.83 | 0.18 | 0.46 | 0.22 | 1.06 | 0.05 | 1.07 | 0.00 |
| CrMn | Zn | Ti | Cr | Ga | FeMn | FeSi | MgMn |
| 1.08 | 0.03 | 0.02 | 0.01 | 0.01 | 1.528 | 0.643 | 2.14 |
| No. | Vc (m/min) | f (mm/rev) | a (mm) | Fz (N) Al | Ra (μm) Al | Fz (N) Al-Gr0.5% | Ra (μm) Al-Gr0.5% |
|---|---|---|---|---|---|---|---|
| 1 | 60 | 0.10 | 0.50 | 46.30 | 1.80 | 37.90 | 1.20 |
| 2 | 60 | 0.20 | 0.75 | 159.10 | 5.80 | 141.70 | 10.40 |
| 3 | 60 | 0.30 | 1.00 | 300.40 | 11.80 | 287.80 | 17.00 |
| 4 | 90 | 0.20 | 0.50 | 128.20 | 10.60 | 114.30 | 8.80 |
| 5 | 90 | 0.30 | 0.75 | 263.00 | 4.60 | 254.30 | 9.60 |
| 6 | 90 | 0.10 | 1.00 | 89.10 | 3.00 | 87.20 | 4.00 |
| 7 | 120 | 0.30 | 0.50 | 181.90 | 4.00 | 174.50 | 7.80 |
| 8 | 120 | 0.10 | 0.75 | 75.50 | 1.00 | 81.60 | 3.40 |
| 9 | 120 | 0.20 | 1.00 | 232.70 | 4.20 | 228.80 | 6.00 |
| Source | DF | Seq.SS | Contribution% | Adj.SS | Adj.MS | F-Val. | p-Val. |
|---|---|---|---|---|---|---|---|
| Model | 6 | 58,811.8 | 99.96 | 58,811.80 | 09802.00 | 0879.13 | 0.001 |
| Linear | 3 | 56,181.4 | 95.49 | 44,358.30 | 14,786.10 | 1326.15 | 0.001 |
| Vc (m/min) | 1 | 51.0 | 00.09 | 00369.60 | 00369.60 | 0033.15 | 0.029 |
| f (mm/rev) | 1 | 43,333.0 | 73.65 | 23,643.10 | 23,643.10 | 2120.52 | 0.001 |
| a (mm) | 1 | 12,797.4 | 21.75 | 04653.60 | 04653.60 | 0417.38 | 0.002 |
| Two-way int. | 3 | 2630.4 | 04.47 | 02630.40 | 00876.80 | 0078.64 | 0.013 |
| Vc × f | 1 | 136.2 | 00.23 | 00077.60 | 00077.60 | 0006.96 | 0.119 |
| Vc × a | 1 | 2120.4 | 03.60 | 00459.40 | 00459.40 | 0041.20 | 0.023 |
| f × a | 1 | 373.8 | 00.64 | 00373.80 | 00373.80 | 0033.53 | 0.029 |
| Error | 2 | 22.3 | 00.04 | 00022.30 | 00011.10 | ||
| Total | 8 | 58,834.1 | 100.00 | ||||
| R2 | 99.96% |
| Source | DF | Seq.SS | Contribution% | Adj.SS | Adj.MS | F-Val. | p-Val. |
|---|---|---|---|---|---|---|---|
| Model | 6 | 167.490 | 95.28 | 167.490 | 27.9149 | 06.72 | 0.013 |
| Linear | 3 | 146.707 | 83.45 | 055.478 | 18.4925 | 04.45 | 0.019 |
| Vc (m/min) | 1 | 021.660 | 12.32 | 012.705 | 12.7050 | 03.06 | 0.022 |
| f (mm/rev) | 1 | 110.940 | 63.11 | 042.602 | 42.6021 | 10.26 | 0.085 |
| a (mm) | 1 | 014.107 | 08.02 | 000.069 | 00.0688 | 00.02 | 0.091 |
| Two-way int. | 3 | 020.783 | 11.82 | 020.783 | 06.9276 | 01.67 | 0.040 |
| Vc × f | 1 | 018.496 | 10.52 | 008.777 | 08.7771 | 02.11 | 0.028 |
| Vc × a | 1 | 001.867 | 01.06 | 000.344 | 00.3438 | 00.08 | 0.081 |
| f × a | 1 | 000.420 | 00.24 | 000.420 | 00.4200 | 00.10 | 0.078 |
| Error | 2 | 008.306 | 04.72 | 008.306 | 04.1530 | ||
| Total | 100.00 | ||||||
| R2 | 95.28% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fountas, N.A.; Manolakos, D.E.; Vaxevanidis, N.M. Machinability Assessment and Multi-Objective Optimization of Graphene Nanoplatelets-Reinforced Aluminum Matrix Composite in Dry CNC Turning. Metals 2025, 15, 584. https://doi.org/10.3390/met15060584
Fountas NA, Manolakos DE, Vaxevanidis NM. Machinability Assessment and Multi-Objective Optimization of Graphene Nanoplatelets-Reinforced Aluminum Matrix Composite in Dry CNC Turning. Metals. 2025; 15(6):584. https://doi.org/10.3390/met15060584
Chicago/Turabian StyleFountas, Nikolaos A., Dimitrios E. Manolakos, and Nikolaos M. Vaxevanidis. 2025. "Machinability Assessment and Multi-Objective Optimization of Graphene Nanoplatelets-Reinforced Aluminum Matrix Composite in Dry CNC Turning" Metals 15, no. 6: 584. https://doi.org/10.3390/met15060584
APA StyleFountas, N. A., Manolakos, D. E., & Vaxevanidis, N. M. (2025). Machinability Assessment and Multi-Objective Optimization of Graphene Nanoplatelets-Reinforced Aluminum Matrix Composite in Dry CNC Turning. Metals, 15(6), 584. https://doi.org/10.3390/met15060584








