Theoretical Predictions for the Equation of State of Metal Nickel at Extreme Conditions
Abstract
1. Introduction
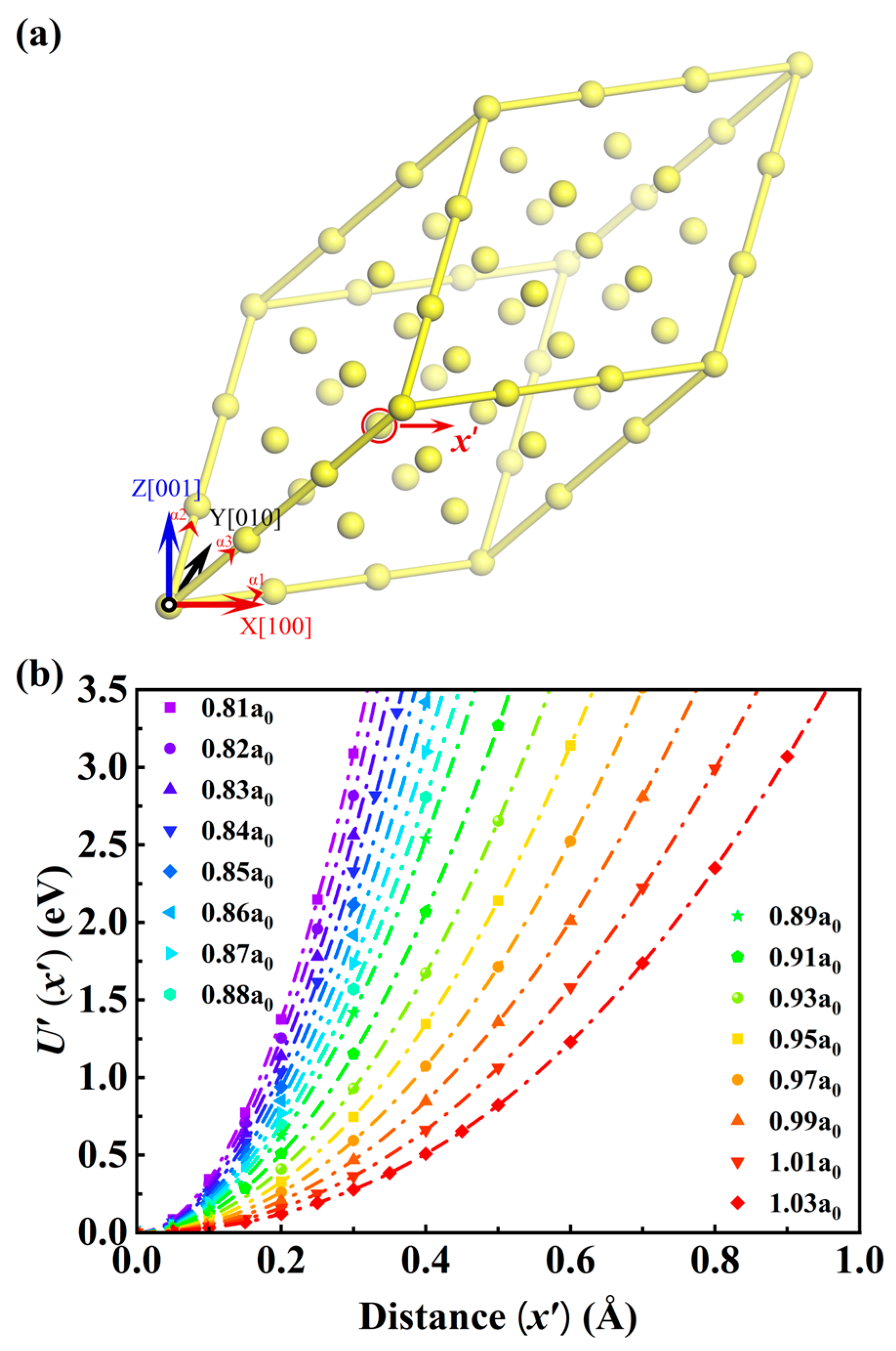
2. Calculation Method
3. Results and Discussion
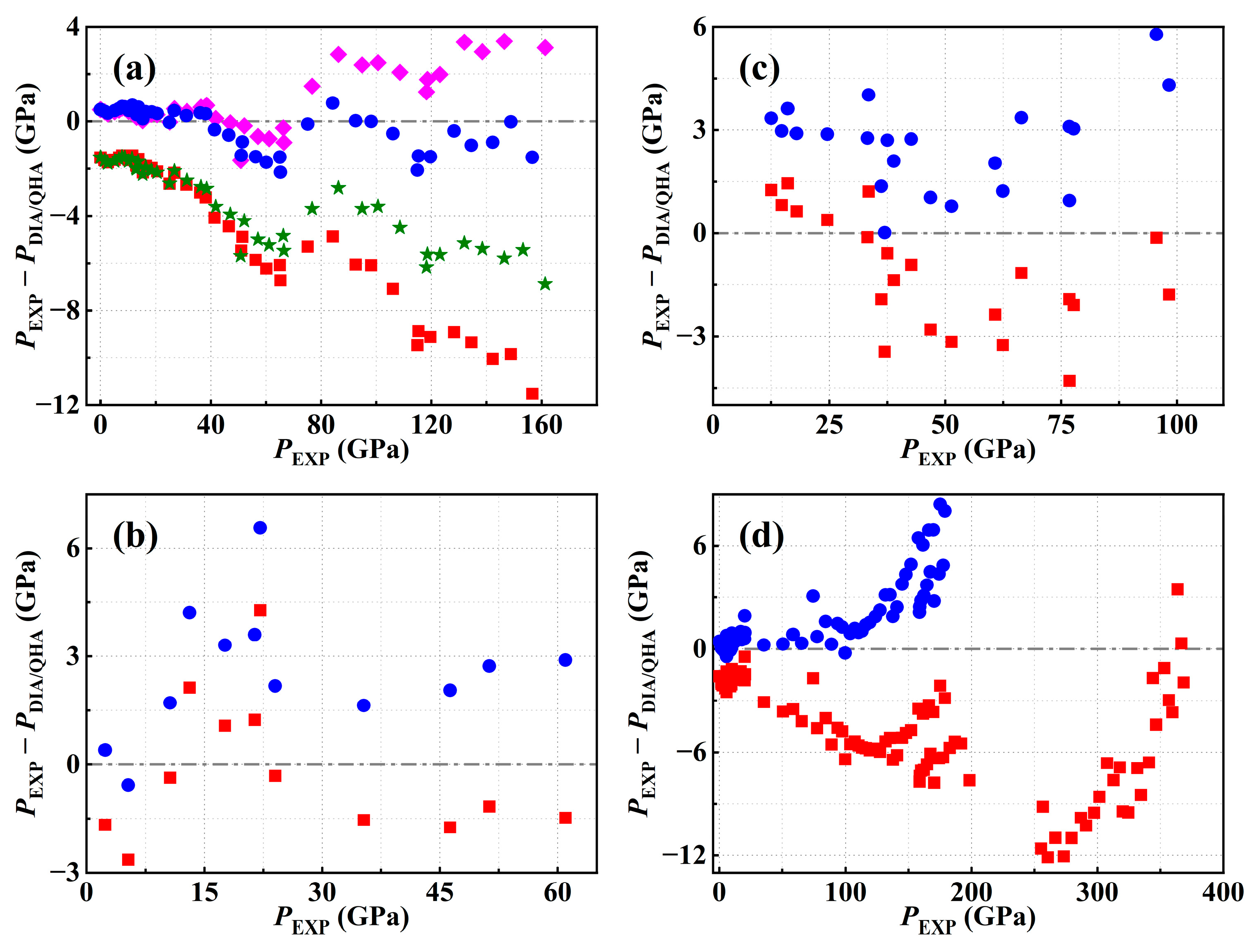
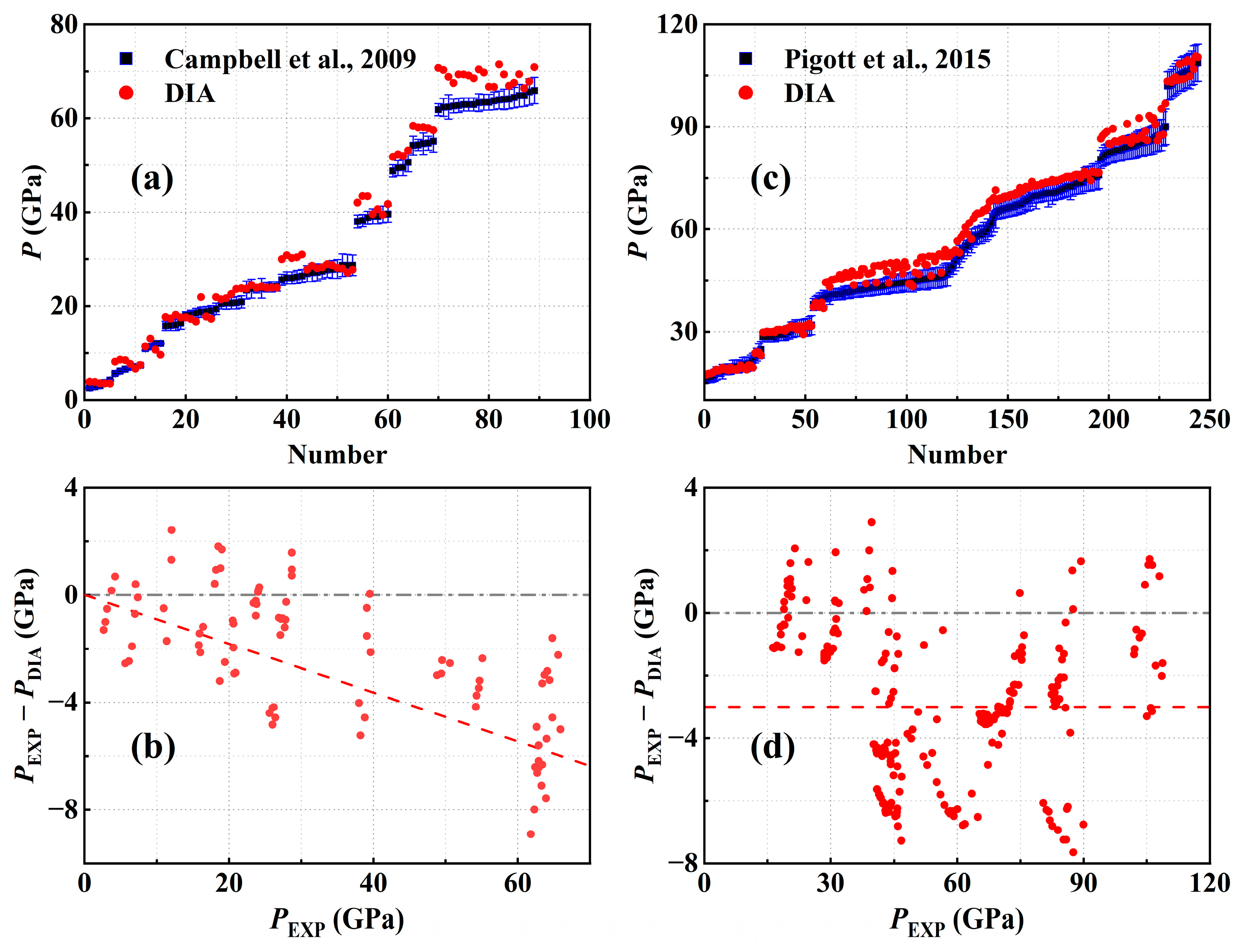
3.1. The Room Temperature Isotherm
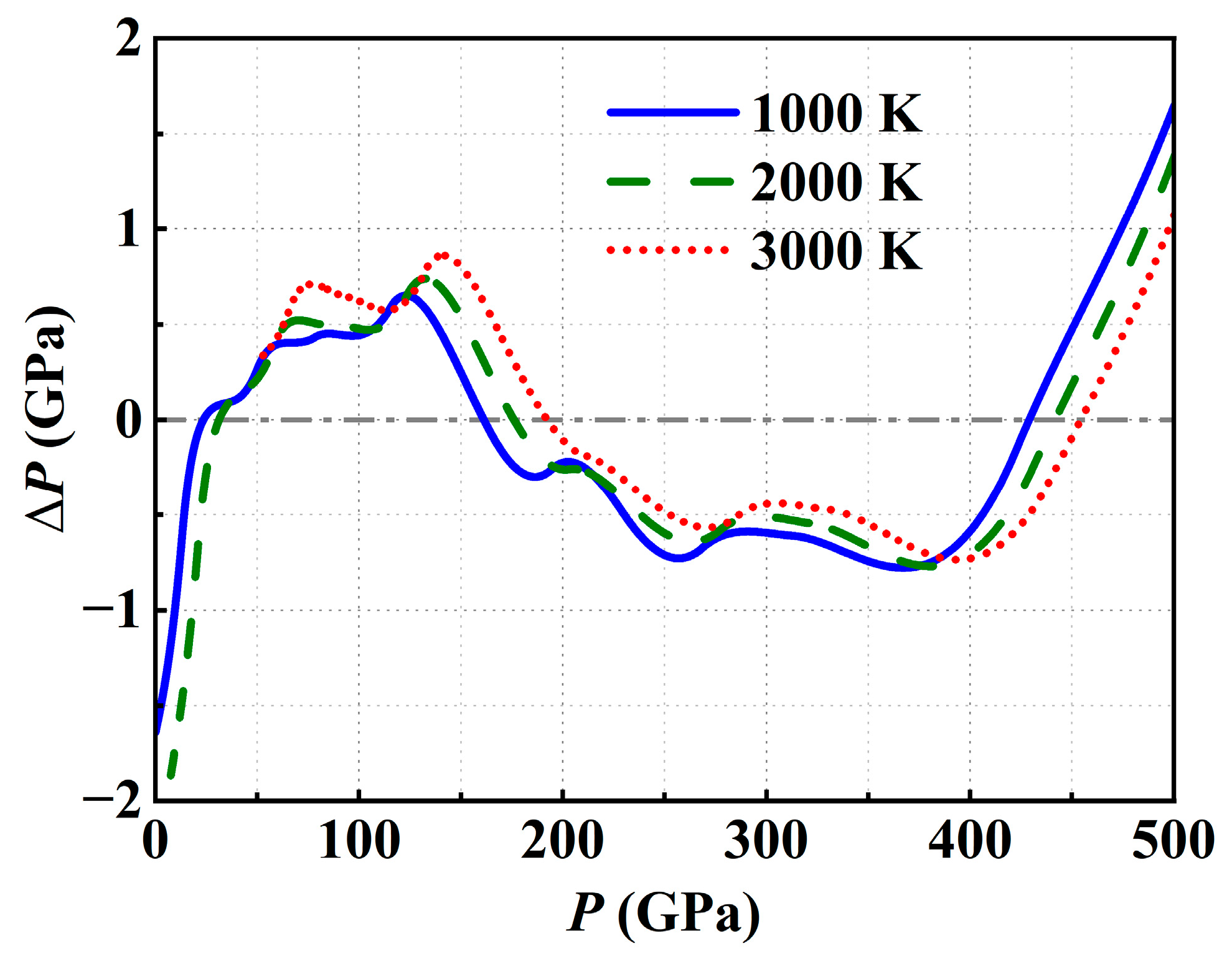
3.2. The High-Temperature Isotherms
3.3. The Analytical EOS
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holland, H.D.; Turekian, K.K. Treatise on Geochemistry; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3, pp. 559–577. [Google Scholar]
- Dewaele, A.; Torrent, M.; Loubeyre, P.; Mezouar, M. Compression curves of transition metals in the Mbar range: Experiments and projector augmented-wave calculations. Phys. Rev. B 2008, 78, 104102. [Google Scholar] [CrossRef]
- Campbell, A.J.; Danielson, L.; Righter, K.; Seagle, C.T.; Wang, Y.; Prakapenka, V.B. High pressure effects on the iron–iron oxide and nickel–nickel oxide oxygen fugacity buffers. Earth Planet. Sci. Lett. 2009, 286, 556. [Google Scholar] [CrossRef]
- Pigott, J.S.; Ditmer, D.A.; Fischer, R.A.; Reaman, D.M.; Hrubiak, R.; Meng, Y.; Davis, R.J.; Panero, W.R. High-pressure, high-temperature equations of state using nanofabricated controlled-geometry Ni/SiO2/Ni double hot-plate samples. Geophys. Res. Lett. 2015, 42, 10. [Google Scholar] [CrossRef]
- Hirao, N.; Akahama, Y.; Ohishi, Y. Equations of state of iron and nickel to the pressure at the center of the Earth. Matter Radiat. Extremes 2022, 7, 038403. [Google Scholar] [CrossRef]
- Karki, B.B.; Wentzcovitch, R.M.; de Gironcoli, S.; Baroni, S. High-pressure lattice dynamics and thermoelasticity of MgO. Phys. Rev. B 2000, 61, 8793. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Hoja, J.; Reilly, A.M.; Tkatchenko, A. First-principles modeling of molecular crystals: Structures and stabilities, temperature and pressure. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 7, e1294. [Google Scholar] [CrossRef]
- Gong, L.-C.; Ning, B.-Y.; Ming, C.; Weng, T.-C.; Ning, X.-J. How accurate for phonon models to predict the thermodynamics properties of crystals. J. Phys. Condens. Matter 2020, 33, 085901. [Google Scholar] [CrossRef]
- Wasserman, E.; Stixrude, L.; Cohen, R.E. Thermal properties of iron at high pressures and temperatures. Phys. Rev. B 1996, 53, 8296. [Google Scholar] [CrossRef]
- Cohen, R.E.; Gülseren, O. Thermal equation of state of tantalum. Phys. Rev. B 2001, 63, 224101. [Google Scholar] [CrossRef]
- Gannarelli, C.M.S.; Alfe, D.; Gillan, M.J. The particle-in-cell model for ab initio thermodynamics: Implications for the elastic anisotropy of the Earth’s inner core. Phys. Earth Planet. Inter. 2003, 139, 243. [Google Scholar] [CrossRef]
- Xiang, S.; Xi, F.; Bi, Y.; Xu, J.A.; Geng, H.; Cai, L.; Liu, J. Ab initio thermodynamics beyond the quasiharmonic approximation: W as a prototype. Phys. Rev. B 2010, 81, 014301. [Google Scholar] [CrossRef]
- Wang, Y. Classical mean-field approach for thermodynamics: Ab initio thermophysical properties of cerium. Phys. Rev. B 2000, 61, R11863. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, D.; Zhang, X. Calculated equation of state of Al, Cu, Ta, Mo, and W to 1000 GPa. Phys. Rev. Lett. 2000, 84, 3220. [Google Scholar] [CrossRef]
- Wang, Y.; Ahuja, R.; Johansson, B. Reduction of shock-wave data with mean-field potential approach. J. Appl. Phys. 2002, 92, 6616. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.K.; Chen, L.Q.; Burakovsky, L.; Preston, D.L.; Luo, W.; Ahuja, R. Mean-field potential calculations of shock-compressed porous carbon. Phys. Rev. B 2005, 71, 054110. [Google Scholar] [CrossRef]
- Ning, B.-Y.; Gong, L.-C.; Weng, T.-C.; Ning, X.-J. Efficient approaches to solutions of partition function for condensed matters. J. Phys. Condens. Matter 2020, 33, 115901. [Google Scholar] [CrossRef]
- Fei, Y.; Mao, H.K.; Shu, J.; Hu, J. P-V-T equation of state of magnesiowüstite (Mg0.6Fe0.4)O. Phys. Chem. Miner. 1992, 18, 416. [Google Scholar] [CrossRef]
- Jackson, I.; Rigden, S.M. Analysis of P-V-T data: constraints on the thermoelastic properties of high-pressure minerals. Phys. Earth Planet. Inter. 1996, 96, 85. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Occelli, F.; Mezouar, M.; Dorogokupets, P.I.; Torrent, M. Quasihydrostatic equation of state of iron above 2 Mbar. Phys. Rev. Lett. 2006, 97, 215504. [Google Scholar] [CrossRef]
- Dierckx, P. An algorithm for smoothing, differentiation and integration of experimental data using spline functions. J. Comput. Appl. Math. 1975, 1, 165. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci 1996, 6, 15. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; John Wiley and Sons: Hoboken, NJ, USA, 1986. [Google Scholar]
- Zeng, Z.-Y.; Hu, C.-E.; Cai, L.-C.; Jing, F.-Q. Ab initio study of lattice dynamics and thermal equation of state of Ni. Physica B 2012, 407, 330. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. Solid Earth 1986, 91, 4673. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Mezouar, M. Equations of state of six metals above 94 GPa. Phys. Rev. B 2004, 70, 094112. [Google Scholar] [CrossRef]
- Holzapfel, W.B. Refinement of the ruby luminescence pressure scale. J. Appl. Phys. 2003, 93, 1813. [Google Scholar] [CrossRef]
- Kunc, K.; Loa, I.; Syassen, K. Equation of state and phonon frequency calculations of diamond at high pressures. Phys. Rev. B 2003, 68, 094107. [Google Scholar] [CrossRef]
- Chijioke, A.D.; Nellis, W.J.; Soldatov, A.; Silvera, I.F. The ruby pressure standard to 150GPa. J. Appl. Phys. 2005, 98, 114905. [Google Scholar] [CrossRef]
- Dorogokupets, P.I.; Oganov, A.R. Ruby, metals, and MgO as alternative pressure scales: A semiempirical description of shock-wave, ultrasonic, x-ray, and thermochemical data at high temperatures and pressures. Phys. Rev. B 2007, 75, 024115. [Google Scholar] [CrossRef]
- Sokolova, T.S.; Dorogokupets, P.I.; Litasov, K.D. Self-consistent pressure scales based on the equations of state for ruby, diamond, MgO, B2–NaCl, as well as Au, Pt, and other metals to 4 Mbar and 3000 K. Russ. Geol. Geophys. 2013, 54, 181. [Google Scholar] [CrossRef]
- Shen, G.; Wang, Y.; Dewaele, A.; Wu, C.; Fratanduono, D.E.; Eggert, J.; IPPS Task Group. Toward an international practical pressure scale: A proposal for an IPPS ruby gauge (IPPS-Ruby2020). High Pressure Res. 2020, 40, 299. [Google Scholar] [CrossRef]
- Prut, V.V. Ruby High Pressure Scale. Russ. Phys. J. 2022, 65, 1172. [Google Scholar] [CrossRef]
- Boccato, S.; Torchio, R.; Kantor, I.; Morard, G.; Anzellini, S.; Giampaoli, R.; Briggs, R.; Smareglia, A.; Irifune, T.; Pascarelli, S. The Melting Curve of Nickel Up to 100 GPa Explored by XAS. J. Geophys. Res. Solid Earth 2017, 122, 9921. [Google Scholar] [CrossRef]
- Birch, F. Elasticity and constitution of the Earth’s interior. J. Geophys. Res. 1952, 57, 227. [Google Scholar] [CrossRef]
- Barin, I.; Knacke, O.; Kubaschewski, O. Thermochemical Properties of Inorganic Substances, 2nd ed.; Springer: Berlin, Germany, 1991. [Google Scholar]




| P (GPa) | 300 K | 500 K | 1000 K | 1500 K | 2000 K | 2500 K | 3000 K |
|---|---|---|---|---|---|---|---|
| 0.0001 | 11.0328 | 11.1324 | 11.4000 | 11.7070 | |||
| 10 | 10.4944 | 10.5697 | 10.7763 | 10.9992 | 11.2423 | ||
| 20 | 10.0904 | 10.1468 | 10.2977 | 10.4650 | 10.6542 | ||
| 30 | 9.7656 | 9.8131 | 9.9364 | 10.0679 | 10.2091 | 10.3625 | |
| 40 | 9.4884 | 9.5299 | 9.6365 | 9.7479 | 9.8651 | 9.9890 | |
| 50 | 9.2444 | 9.2809 | 9.3750 | 9.4735 | 9.5758 | 9.6822 | |
| 60 | 9.0317 | 9.0640 | 9.1464 | 9.2321 | 9.3219 | 9.4164 | 9.5146 |
| 70 | 8.8413 | 8.8707 | 8.9454 | 9.0221 | 9.1013 | 9.1835 | 9.2693 |
| 80 | 8.6688 | 8.6956 | 8.7641 | 8.8343 | 8.9063 | 8.9803 | 9.0565 |
| 90 | 8.5127 | 8.5373 | 8.5999 | 8.6641 | 8.7300 | 8.7978 | 8.8674 |
| 100 | 8.3693 | 8.3919 | 8.4498 | 8.5091 | 8.5698 | 8.6321 | 8.6958 |
| 110 | 8.2358 | 8.2567 | 8.3106 | 8.3659 | 8.4225 | 8.4804 | 8.5394 |
| 120 | 8.1127 | 8.1316 | 8.1809 | 8.2323 | 8.2854 | 8.3396 | 8.3949 |
| 130 | 7.9993 | 8.0169 | 8.0622 | 8.1092 | 8.1578 | 8.2080 | 8.2599 |
| 140 | 7.8938 | 7.9103 | 7.9526 | 7.9962 | 8.0411 | 8.0872 | 8.1346 |
| 150 | 7.7946 | 7.8104 | 7.8503 | 7.8912 | 7.9331 | 7.9760 | 8.0200 |
| 160 | 7.7008 | 7.7160 | 7.7540 | 7.7927 | 7.8322 | 7.8725 | 7.9137 |
| 170 | 7.6114 | 7.6261 | 7.6627 | 7.6996 | 7.7371 | 7.7752 | 7.8142 |
| 180 | 7.5258 | 7.5401 | 7.5755 | 7.6110 | 7.6469 | 7.6832 | 7.7202 |
| 190 | 7.4437 | 7.4575 | 7.4920 | 7.5264 | 7.5609 | 7.5958 | 7.6311 |
| 200 | 7.3660 | 7.3790 | 7.4120 | 7.4452 | 7.4786 | 7.5123 | 7.5463 |
| 210 | 7.2928 | 7.3051 | 7.3364 | 7.3680 | 7.4000 | 7.4323 | 7.4651 |
| 220 | 7.2235 | 7.2352 | 7.2648 | 7.2949 | 7.3254 | 7.3563 | 7.3876 |
| 230 | 7.1574 | 7.1685 | 7.1966 | 7.2252 | 7.2544 | 7.2839 | 7.3138 |
| 240 | 7.0936 | 7.1043 | 7.1312 | 7.1586 | 7.1864 | 7.2147 | 7.2435 |
| 250 | 7.0319 | 7.0422 | 7.0681 | 7.0944 | 7.1212 | 7.1484 | 7.1760 |
| 260 | 6.9720 | 6.9820 | 7.0070 | 7.0325 | 7.0584 | 7.0846 | 7.1112 |
| 270 | 6.9141 | 6.9236 | 6.9479 | 6.9726 | 6.9976 | 7.0230 | 7.0487 |
| 280 | 6.8585 | 6.8677 | 6.8910 | 6.9147 | 6.9389 | 6.9635 | 6.9884 |
| 290 | 6.8050 | 6.8138 | 6.8363 | 6.8592 | 6.8825 | 6.9061 | 6.9302 |
| 300 | 6.7534 | 6.7619 | 6.7837 | 6.8058 | 6.8283 | 6.8511 | 6.8742 |
| 310 | 6.7034 | 6.7117 | 6.7329 | 6.7544 | 6.7761 | 6.7981 | 6.8204 |
| 320 | 6.6551 | 6.6632 | 6.6838 | 6.7046 | 6.7257 | 6.7470 | 6.7686 |
| 330 | 6.6085 | 6.6164 | 6.6363 | 6.6565 | 6.6769 | 6.6975 | 6.7185 |
| 340 | 6.5633 | 6.5710 | 6.5904 | 6.6100 | 6.6298 | 6.6498 | 6.6700 |
| 350 | 6.5194 | 6.5269 | 6.5459 | 6.5650 | 6.5842 | 6.6036 | 6.6232 |
| 360 | 6.4767 | 6.4841 | 6.5026 | 6.5212 | 6.5399 | 6.5588 | 6.5779 |
| 370 | 6.4352 | 6.4424 | 6.4605 | 6.4786 | 6.4969 | 6.5154 | 6.5339 |
| 380 | 6.3947 | 6.4017 | 6.4194 | 6.4372 | 6.4551 | 6.4731 | 6.4912 |
| 390 | 6.3551 | 6.3620 | 6.3794 | 6.3968 | 6.4143 | 6.4319 | 6.4496 |
| 400 | 6.3165 | 6.3233 | 6.3403 | 6.3573 | 6.3745 | 6.3917 | 6.4090 |
| 410 | 6.2787 | 6.2853 | 6.3020 | 6.3187 | 6.3356 | 6.3525 | 6.3695 |
| 420 | 6.2416 | 6.2482 | 6.2646 | 6.2810 | 6.2975 | 6.3141 | 6.3308 |
| 430 | 6.2056 | 6.2120 | 6.2279 | 6.2440 | 6.2603 | 6.2766 | 6.2930 |
| 440 | 6.1706 | 6.1768 | 6.1923 | 6.2080 | 6.2239 | 6.2399 | 6.2560 |
| 450 | 6.1364 | 6.1424 | 6.1576 | 6.1730 | 6.1884 | 6.2041 | 6.2198 |
| 460 | 6.1031 | 6.1090 | 6.1238 | 6.1388 | 6.1539 | 6.1692 | 6.1846 |
| 470 | 6.0705 | 6.0763 | 6.0907 | 6.1054 | 6.1202 | 6.1351 | 6.1502 |
| 480 | 6.0387 | 6.0443 | 6.0585 | 6.0727 | 6.0872 | 6.1018 | 6.1165 |
| 490 | 6.0076 | 6.0130 | 6.0269 | 6.0408 | 6.0550 | 6.0692 | 6.0837 |
| 500 | 5.9770 | 5.9824 | 5.9959 | 6.0096 | 6.0234 | 6.0374 | 6.0515 |
| DIA | Campbell et al. [3] | Pigott et al. [4] | |
|---|---|---|---|
| V0 (Å3/atom) | 10.972 (0) | 10.939 | 10.926 |
| K0 (GPa) | 197.256 (0.126) | 179 (3) | 201 (6) |
| K0′ | 4.626 (0.001) | 4.3 (0.2) | 4.4 (0.3) |
| θ0 (K) | / | 415 | 415 |
| γ0 | 2.014 (0.002) | 2.50 (0.06) | 1.98 (0.08) |
| q | 0.745 (0.002) | 1 | 1.3 (0.2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Tian, Y.; Ning, B.; Zhang, H.; Ning, X. Theoretical Predictions for the Equation of State of Metal Nickel at Extreme Conditions. Metals 2025, 15, 582. https://doi.org/10.3390/met15060582
Wu S, Tian Y, Ning B, Zhang H, Ning X. Theoretical Predictions for the Equation of State of Metal Nickel at Extreme Conditions. Metals. 2025; 15(6):582. https://doi.org/10.3390/met15060582
Chicago/Turabian StyleWu, Sihan, Yueyue Tian, Boyuan Ning, Huifen Zhang, and Xijing Ning. 2025. "Theoretical Predictions for the Equation of State of Metal Nickel at Extreme Conditions" Metals 15, no. 6: 582. https://doi.org/10.3390/met15060582
APA StyleWu, S., Tian, Y., Ning, B., Zhang, H., & Ning, X. (2025). Theoretical Predictions for the Equation of State of Metal Nickel at Extreme Conditions. Metals, 15(6), 582. https://doi.org/10.3390/met15060582






