Influence of Deformation Temperature and Strain Rate on Martensitic Transformation of Duplex Stainless Steel and Its Corresponding Kinetic Model
Abstract
1. Introduction
2. Experimental Procedure
3. Results and Discussion
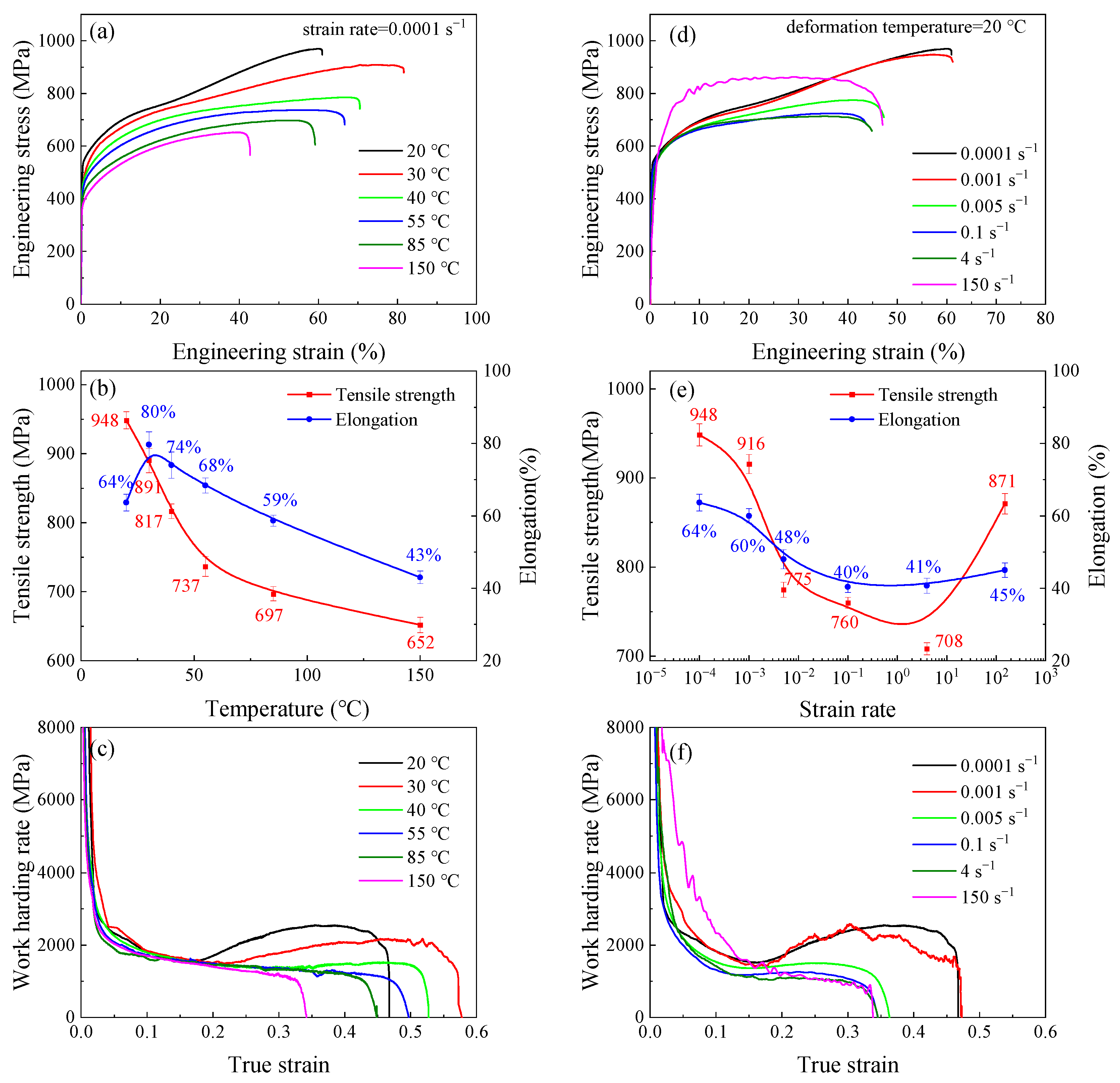
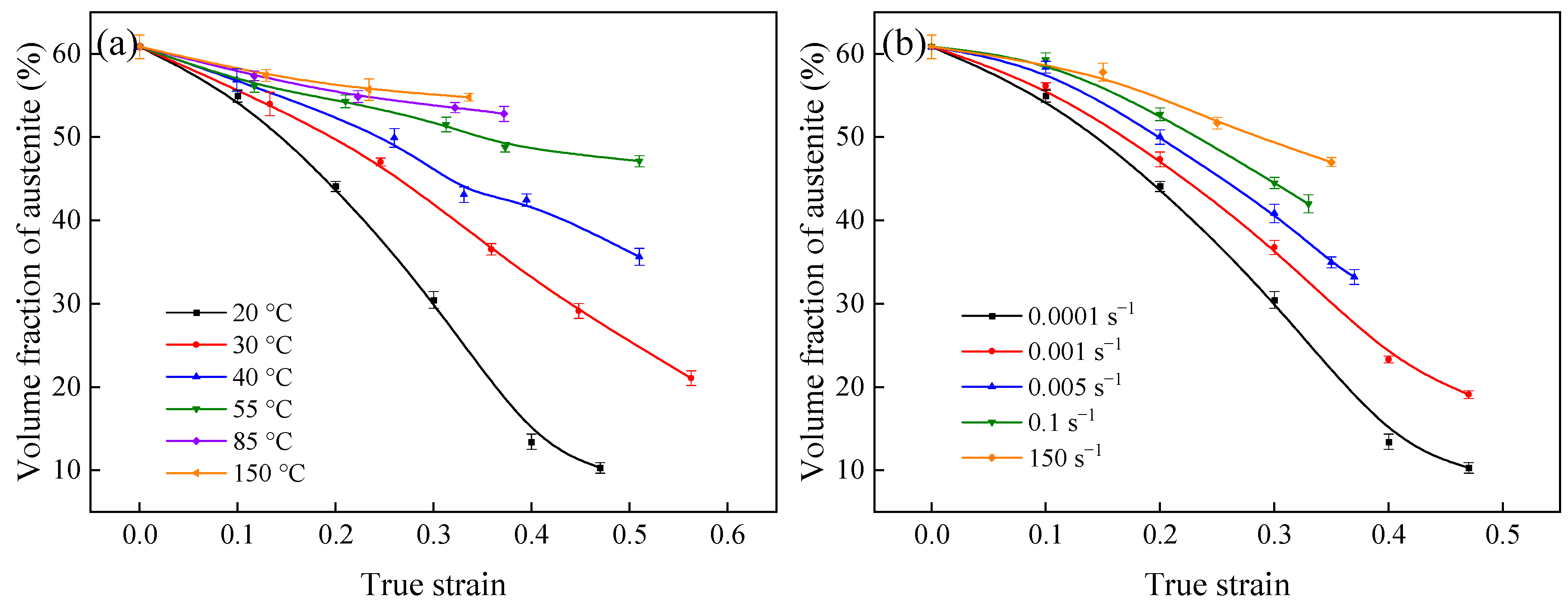
3.1. Microstructure and Mechanical Properties
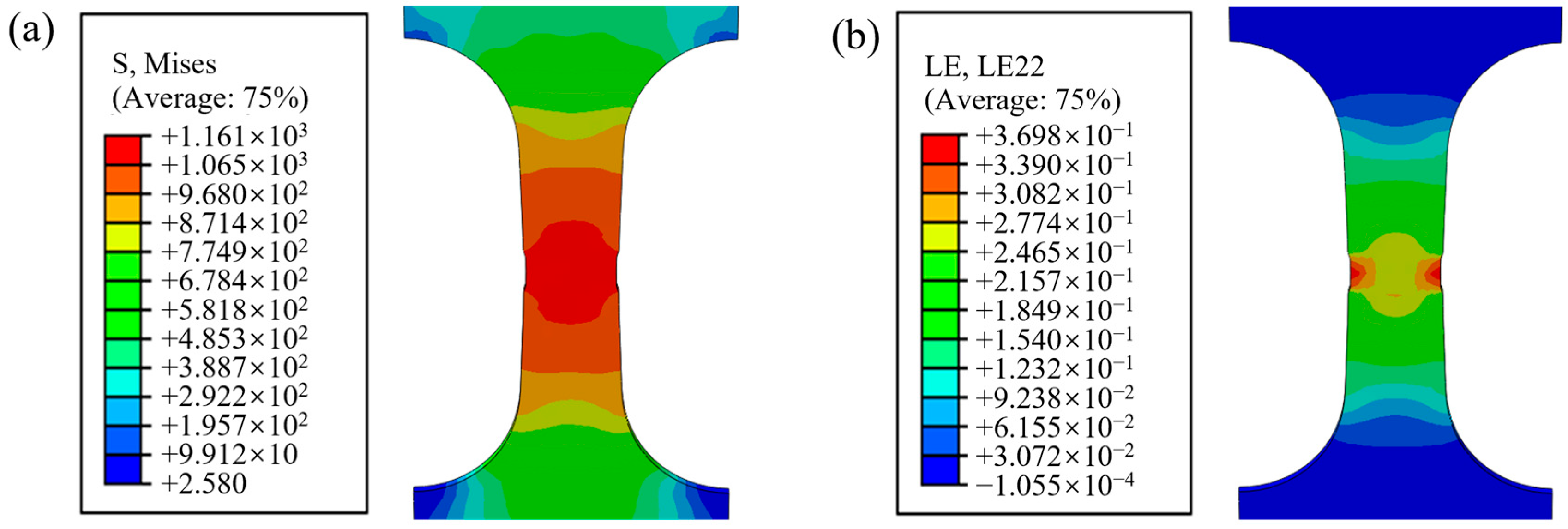
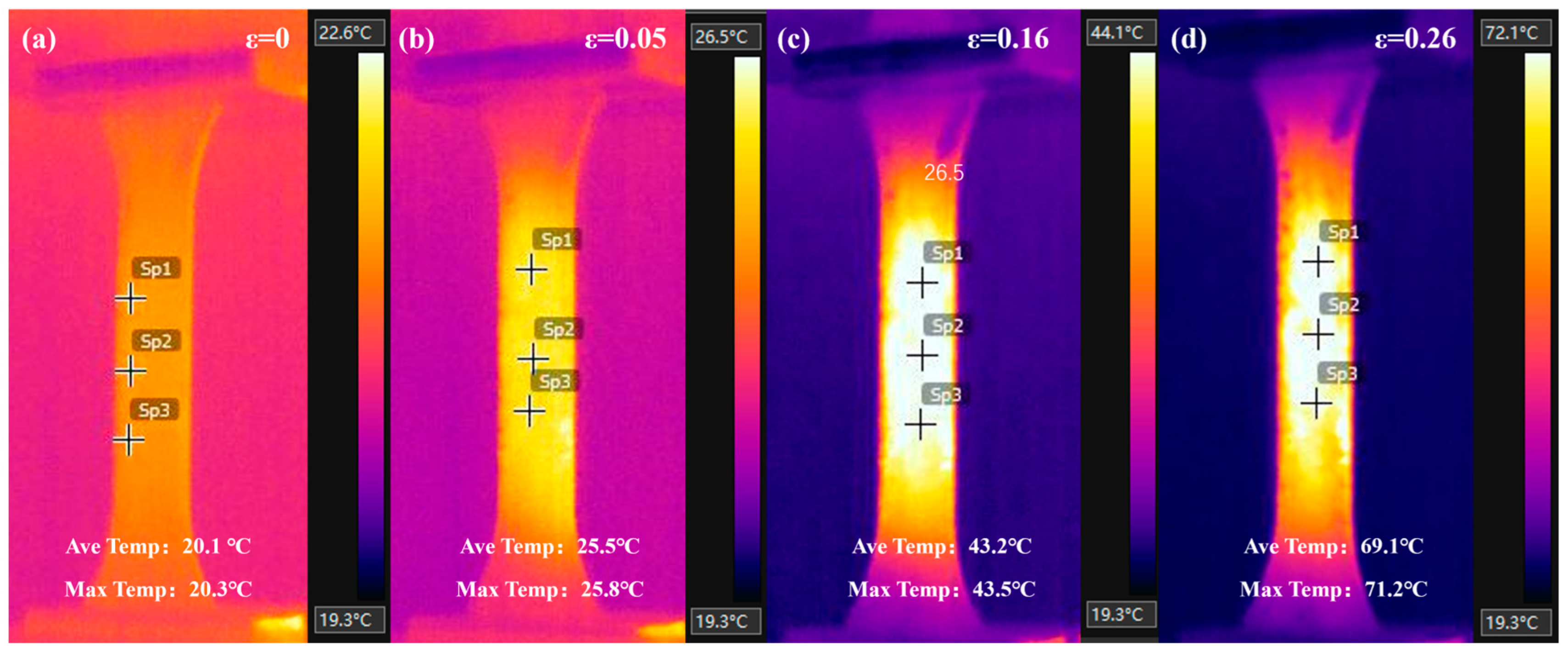
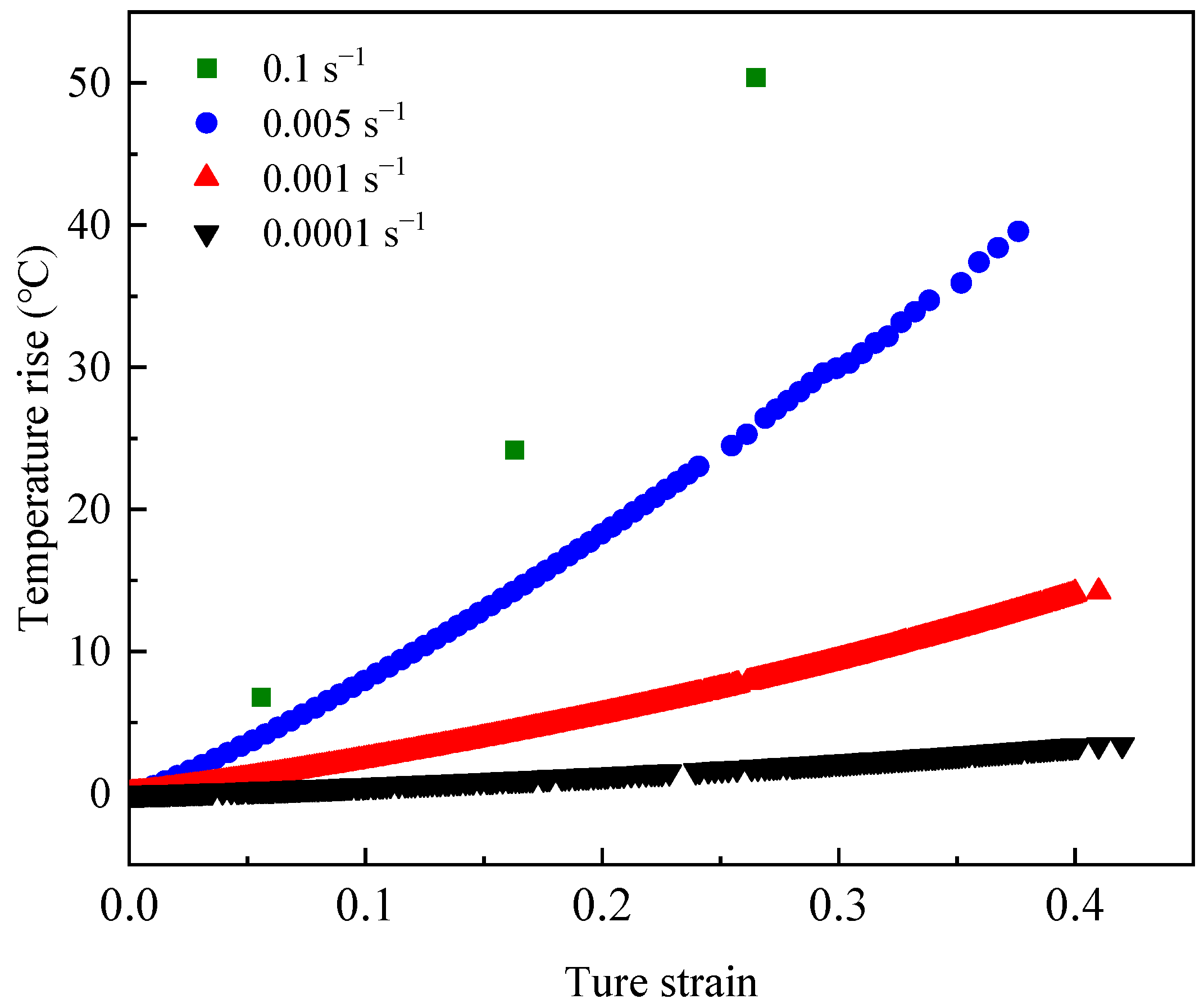
3.2. Measurement of Plastic Temperature Rise
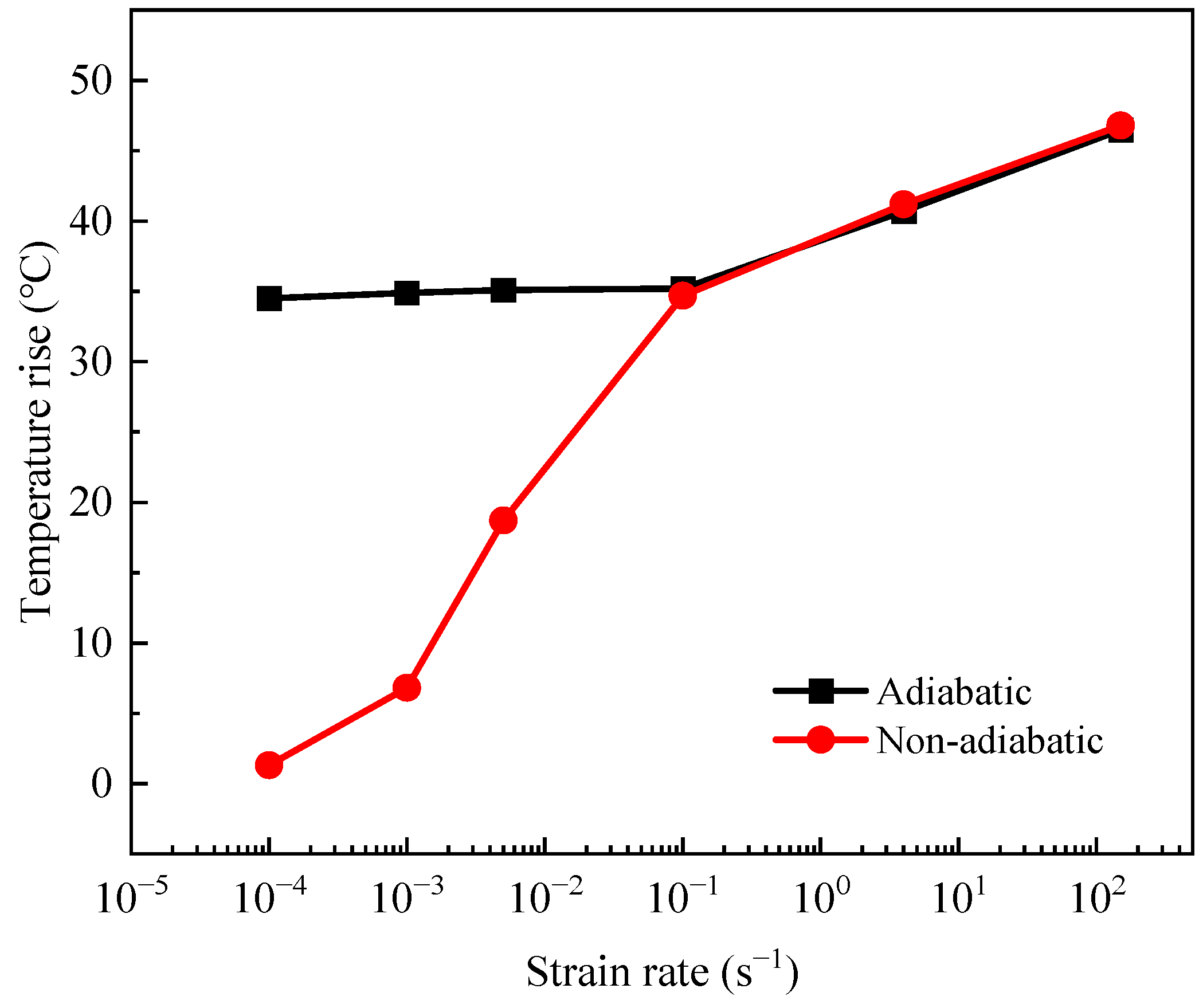
3.3. Plastic Temperature Rise Model
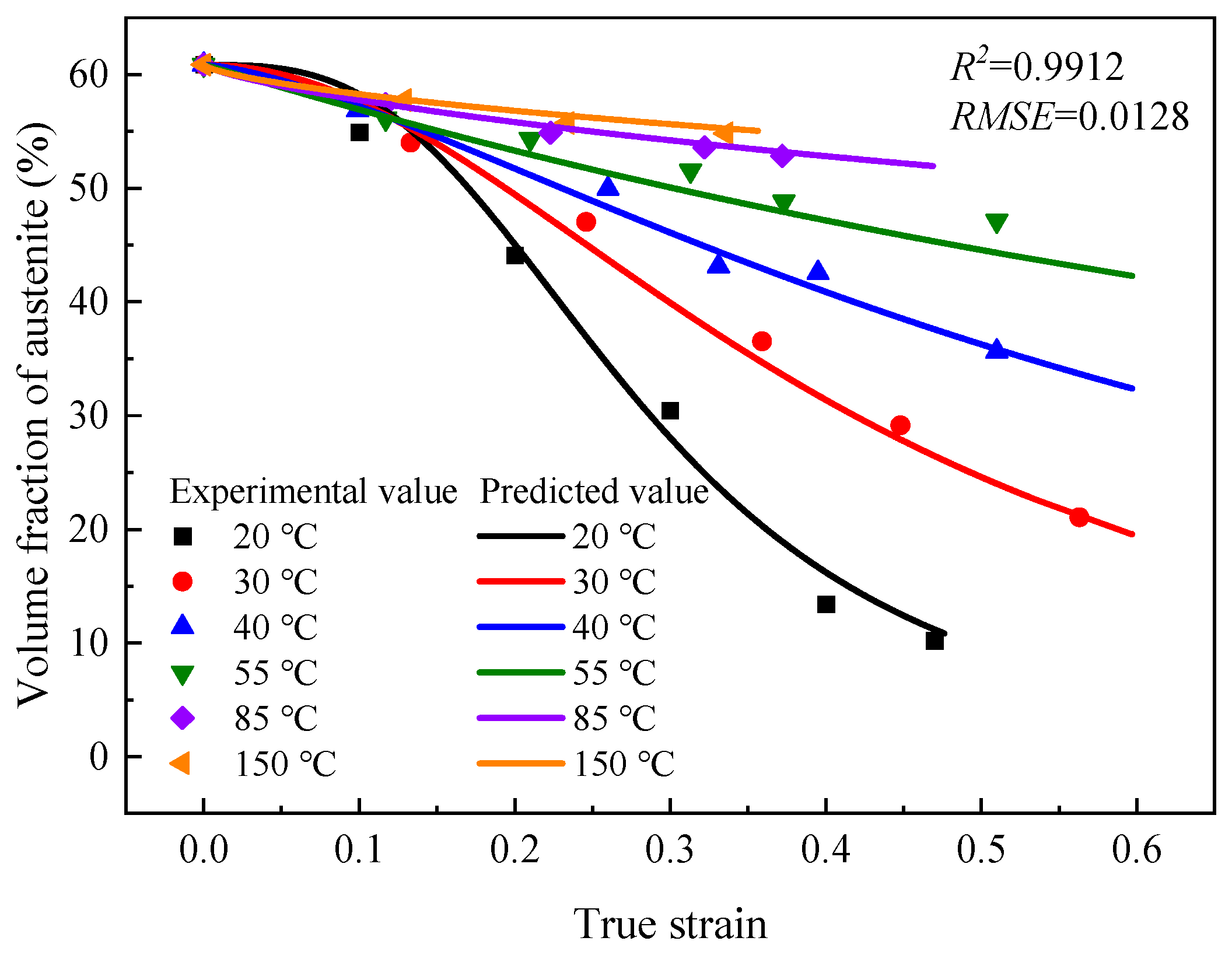
3.4. Kinetic Model of Martensitic Transformation
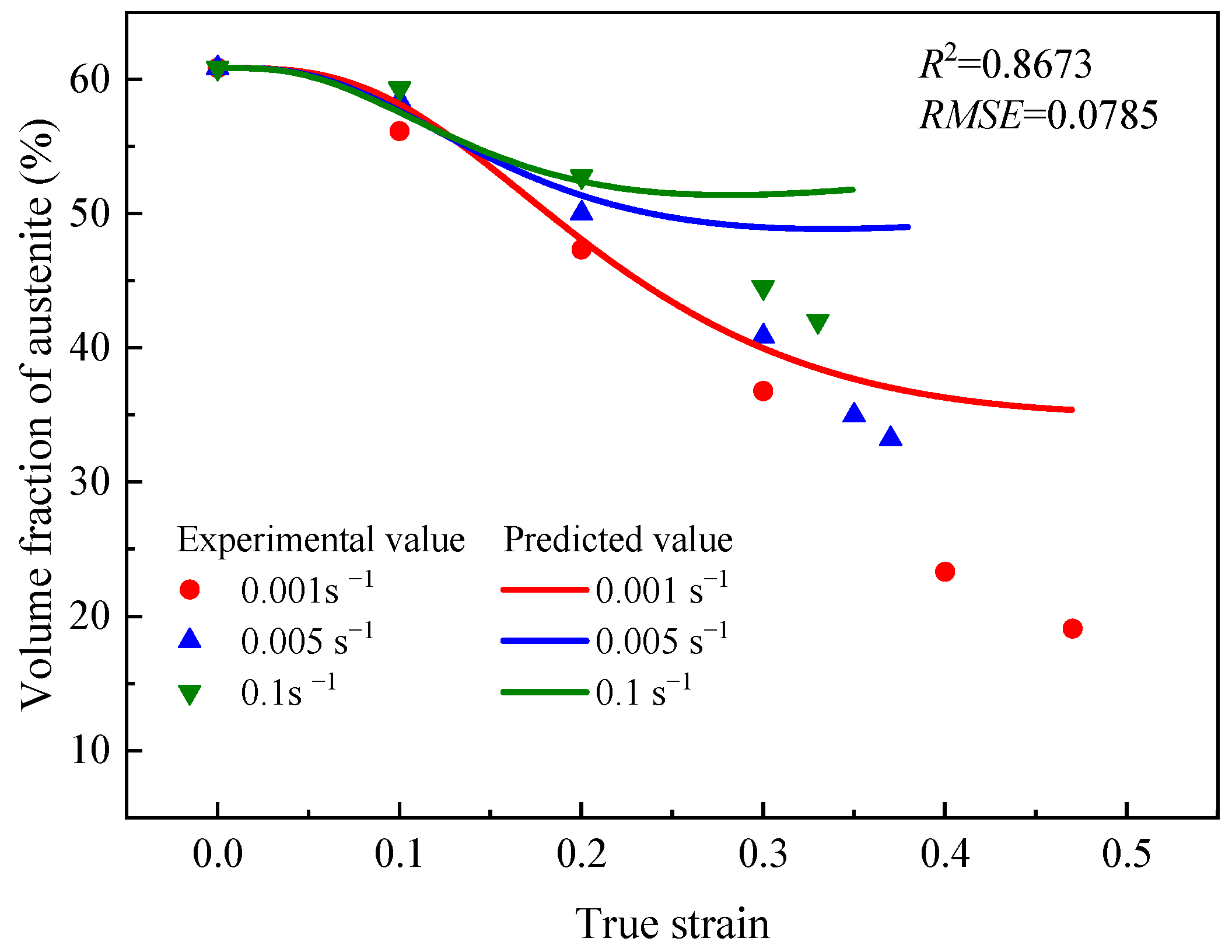
3.4.1. Temperature-Dependent Ludwigson–Berger Model
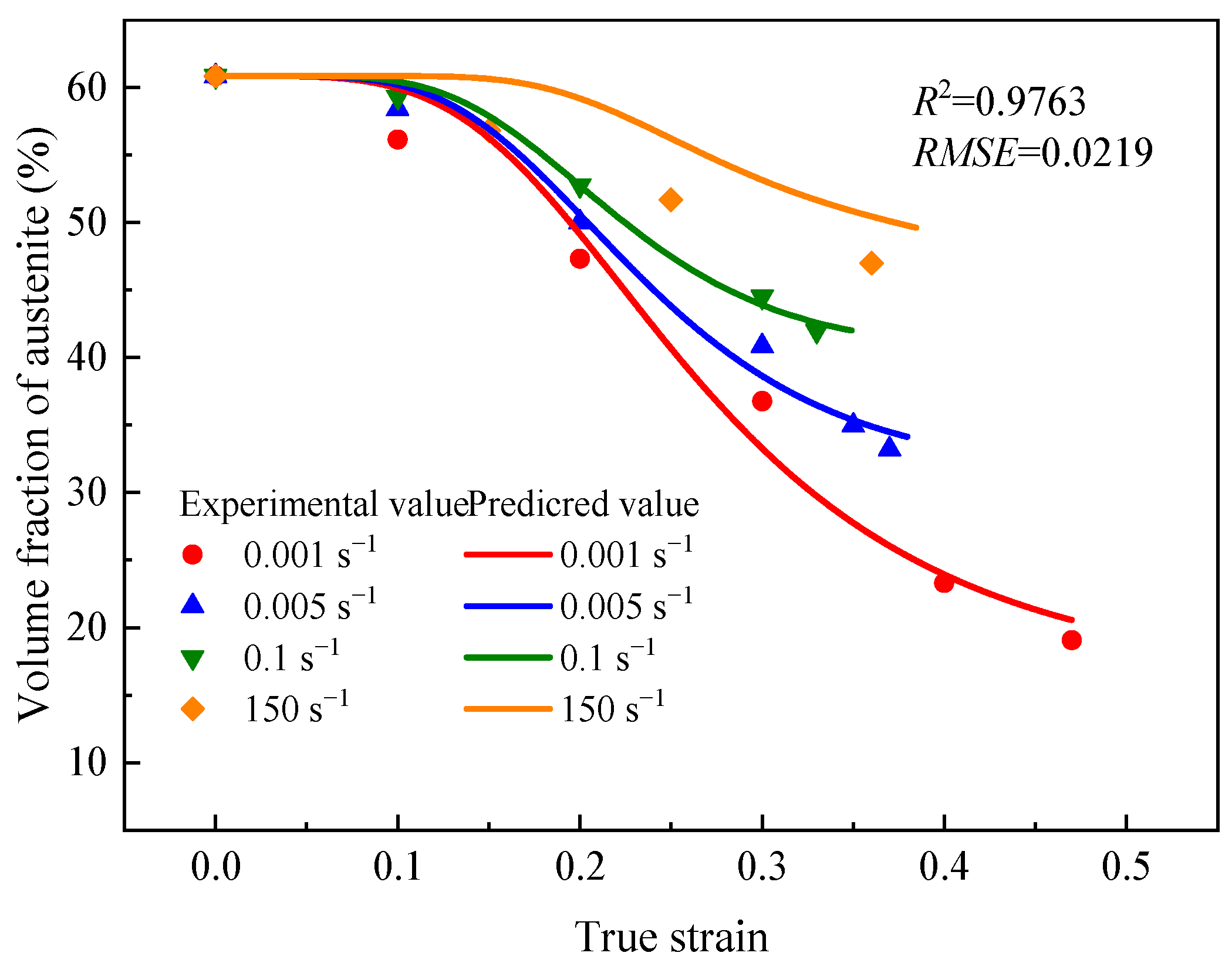
3.4.2. Temperature–Strain Rate Coupled Ludwigson–Berger Model
4. Conclusions
- As the deformation temperature increases from 20 to 150 °C, the strain-induced martensitic transformation is inhibited, and the deformation mechanism transforms from martensitic transformation (20 °C) to the co-occurrence of martensitic transformation and twinning (40–55 °C), and finally twinning was the main deformation mechanism (150 °C). This results in a monotonic decrease in tensile strength from 948 MPa to 652 MPa with increasing deformation temperature, while the elongation first increased from 64% to a range of 68–80% (30–55 °C), then decreased to 43% (150 °C);
- As the strain rate increases from 0.0001 to 150 s−1, martensitic transformation is inhibited. This leads to a monotonic decrease in tensile strength from 948 to 760 MPa and a reduction in elongation from 64% to 40% as the strain rate increases from 0.0001 to 0.1 s−1. However, when the strain rate rises from 4 to 150 s−1, the tensile strength increases monotonically from 708 to 871 MPa due to enhanced resistance to dislocation motion. Meanwhile, the plasticity remains largely unchanged owing to the combined effects of adiabatic softening and suppressed martensitic transformation;
- A plastic temperature rise model is established for newly developed DSSs during tensile deformation. Based on this model, the Ludwigson–Berger model for martensitic transformation was modified to couple the effect of temperature and strain rate by considering the non-uniform distribution of temperature rise within the material and its variation with strain rate, as well as the suppression of dynamic strain rate on martensitic transformation. This new model could accurately describe the characteristics of martensitic transformation in newly developed DSSs over a wide range of deformation temperatures and strain rates.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Badji, R.; Bouabdallah, M.; Bacroix, B.; Kahloun, C.; Belkessa, B.; Maza, H. Phase transformation and mechanical behavior in annealed 2205 duplex stainless steel welds. Mater. Charact. 2008, 59, 447–453. [Google Scholar] [CrossRef]
- Francis, R.; Byrne, G. Duplex stainless steels—Alloys for the 21st century. Metals 2021, 11, 836. [Google Scholar] [CrossRef]
- Balancin, O.; Hoffmann, W.A.M.; Jonas, J.J. Influence of microstructure on the flow behavior of duplex stainless steels at high temperatures. Metall. Mater. Trans. A 2000, 31, 1353–1364. [Google Scholar] [CrossRef]
- Capello, E.; Chiarello, P.; Previtali, B.; Vedani, M. Laser welding and surface treatment of a 22Cr-5Ni-3Mo duplex stainless steel. Mater. Sci. Eng. A 2003, 351, 334–343. [Google Scholar] [CrossRef]
- Gatto, M.L.; Santoni, A.; Santecchia, E.; Spigarelli, S.; Fiori, F.; Mengucci, P.; Cabibbo, M. The potential of duplex stainless steel processed by laser powder bed fusion for biomedical applications: A review. Metals 2023, 13, 949. [Google Scholar] [CrossRef]
- Liu, Y.X.; Chen, H.; Wang, R.Z.; Jia, Y.F.; Zhang, X.C.; Cui, Y.; Tu, S.T. Fatigue behaviors of 2205 duplex stainless steel with gradient nanostructured surface layer. Int. J. Fatigue 2021, 147, 10617. [Google Scholar] [CrossRef]
- De Lacerda, J.C.; Cândido, L.C.; Godefroid, L.B. Effect of volume fraction of phases and precipitates on the mechanical behavior of UNS S31803 duplex stainless steel. Int. J. Fatigue 2015, 74, 81–87. [Google Scholar] [CrossRef]
- Kwon, D.Y.; Na, H.S.; Choi, J.Y.; Kang, J.H. Effect of annealing temperature on tensile and impact properties of S31803 duplex stainless steel. Mater. Sci. Eng. A 2025, 931, 148222. [Google Scholar] [CrossRef]
- Liu, Z.X.; Xie, Y.; Zhang, L.; Zhao, C.; He, H. Effect of aging on the microstructure and properties of ASTM A890 3A duplex stainless steel. Mater. Today Commun. 2023, 35, 106215. [Google Scholar] [CrossRef]
- Herrera, C.; Ponge, D.; Raabe, D. Design of a novel Mn-based 1 GPa duplex stainless TRIP steel with 60% ductility by a reduction of austenite stability. Acta Mater. 2011, 59, 4653–4664. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Li, X.; Zhang, W.N.; Tang, S.; Liu, Z.Y. Effects of Plastic straining on the corrosion resistance of TRIP-aided lean duplex stainless steels. J. Mater. Sci. 2018, 53, 9258–9272. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, W.N.; Liu, X.; Liu, Z.Y.; Wang, G.D. Development of TRIP-aided lean duplex stainless steel by twin-roll strip casting and its deformation mechanism. Metall. Mater. Trans. A 2016, 47, 6292–6303. [Google Scholar] [CrossRef]
- Choi, J.Y.; Ji, J.H.; Hwang, S.W.; Park, K.T. Strain induced martensitic transformation of Fe–20Cr–5Mn–0.2 Ni duplex stainless steel during cold rolling: Effects of nitrogen addition. Mater. Sci. Eng. A 2011, 528, 6012–6019. [Google Scholar] [CrossRef]
- Ran, Q.X.; Xu, Y.L.; Li, J.; Wan, J.Q.; Xiao, X.S.; Yu, H.F.; Jiang, L.Z. Effect of heat treatment on transformation-induced plasticity of economical Cr19 duplex stainless steel. Mater. Des. 2014, 56, 959–965. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, J.C. Effect of Annealing temperature on transformation induced plasticity effect of a lean duplex stainless steel. Mater. Charact. 2013, 79, 37–42. [Google Scholar] [CrossRef]
- Jia, Y.D.; Yin, X.Y.; Xu, Y.L.; Wang, G. Effects of heat treatment on microstructure and mechanical properties of a transformation-induced plasticity-aided economical duplex stainless steel. Metals 2022, 12, 2019. [Google Scholar] [CrossRef]
- Wang, Y.X.; Chen, L.; Shao, L.Z.; Hao, S.; Koyama, M.; Cai, X.Z.; Ma, X.C.; Jin, M. Strain rate-dependent tensile deformation behavior and fracture mechanism of Mn–N bearing lean duplex stainless steel. Mater. Sci. Eng. A 2024, 889, 145832. [Google Scholar] [CrossRef]
- Talonen, J.; Hänninen, H.; Nenonen, P.; Pape, G. Effect of strain rate on the strain-induced γ→ α′-martensite transformation and mechanical properties of austenitic stainless steels. Metall. Mater. Trans. A 2005, 36, 421–432. [Google Scholar] [CrossRef]
- Talonen, J.; Hänninen, H. Formation of shear bands and strain-induced martensite during plastic deformation of metastable austenitic stainless steels. Acta Mater. 2007, 55, 6108–6118. [Google Scholar] [CrossRef]
- Huang, F.; Yang, J.; Guo, Z.H.; Rong, Y.H.; Chen, N.L. Dynamic compression property of a low-carbon quenching and partitioning steel. Mater. Sci. Eng. A 2016, 651, 224–232. [Google Scholar] [CrossRef]
- Lee, W.S.; Lin, C.F. The morphologies and characteristics of impact-induced martensite in 304L stainless steel. Scr. Mater. 2000, 43, 777–782. [Google Scholar] [CrossRef]
- Lee, W.S.; Lin, C.F. Impact properties and microstructure evolution of 304L stainless steel. Mater. Sci. Eng. A 2001, 308, 124–135. [Google Scholar] [CrossRef]
- Cao, B.; Iwamoto, T.; Bhattacharjee, P.P. An experimental study on strain-induced martensitic transformation behavior in SUS304 austenitic stainless steel during higher strain rate deformation by continuous evaluation of relative magnetic permeability. Mater. Sci. Eng. A 2020, 774, 138927. [Google Scholar] [CrossRef]
- Vázquez-Fernández, N.I.; Nyyssönen, T.; Isakov, M.; Hokka, M.; Kuokkala, V.T. Uncoupling the effects of strain rate and adiabatic heating on strain induced martensitic phase transformations in a metastable austenitic steel. Acta Mater. 2019, 176, 134–144. [Google Scholar] [CrossRef]
- Pun, L.; Langi, V.; Ruiz, A.R.; Isakov, M.; Hokka, M. In-situ synchrotron X-ray diffraction study of the effects of grain orientation on the martensitic phase transformations during tensile loading at different strain rates in metastable austenitic stainless steel. Mater. Sci. Eng. A 2024, 900, 146481. [Google Scholar] [CrossRef]
- Langi, V.; Pun, L.; Ruiz, A.R.; Isakov, M.; Hokka, M. Effects of strain rate on martensitic phase transformation in TRIP assisted multiphase steels studied in-situ with X-ray diffraction. Mater. Sci. Eng. A 2025, 923, 147724. [Google Scholar] [CrossRef]
- Rosakis, P.; Rosakis, A.J.; Ravichandran, G.; Hodowany, J. A thermodynamic internal variable model for the partition of plastic work into heat and stored energy in metals. J. Mech. Phys. Solids 2000, 48, 581–607. [Google Scholar] [CrossRef]
- Zaera, R.; Rodríguez-Martínez, J.A.; Rittel, D. On the Taylor–Quinney coefficient in dynamically phase transforming materials. Application to 304 stainless steel. Int. J. Plast. 2013, 40, 185–201. [Google Scholar] [CrossRef]
- Rittel, D.; Zhang, L.H.; Osovski, S. The dependence of the Taylor–Quinney coefficient on the dynamic loading mode. J. Mech. Phys. Solids 2017, 107, 96–114. [Google Scholar] [CrossRef]
- Angel, T. Formation of martensite in austenitic stainless steel. J. Iron Steel Inst. 1954, 177, 165–174. [Google Scholar]
- Ludwigson, D.C.; Berger, J.A. Plastic behaviour of metastable austenitic stainless steel. J. Iron Steel Inst. 1969, 207, 63–69. [Google Scholar]
- Sugimoto, K.I.; Kobayashi, M.; Hashimoto, S.I. Ductility and strain-induced transformation in a high-strength transformation-induce plasticity-aided dual-phase steel. Metall. Mater. Trans. A 1992, 23, 3085–3091. [Google Scholar] [CrossRef]
- Shin, H.C.; Ha, T.K.; Chang, Y.W. Kinetics of deformation induced martensitic transformation in a 304 stainless steel. Scr. Mater. 2001, 45, 823–829. [Google Scholar] [CrossRef]
- Olson, G.B.; Cohen, M. A mechanism for the strain-induced nucleation of martensitic transformations. J. Less Common Met. 1972, 28, 107–118. [Google Scholar] [CrossRef]
- Stringfellow, R.G.; Parks, D.M.; Olson, G.B. A constitutive model for transformation plasticity accompanying strain-induced martensitic transformations in metastable austenitic steels. Acta Metall. Mater. 1992, 40, 1703–1716. [Google Scholar] [CrossRef]
- Iwamoto, T.; Tsuta, T.; Tomita, Y. Investigation on deformation mode dependence of strain-induced martensitic transformation in trip steels and modelling of transformation kinetics. Int. J. Mech. Sci. 1998, 40, 173–182. [Google Scholar] [CrossRef]
- Dan, W.J.; Zhang, W.G.; Li, S.H.; Lin, Z.Q. A model for strain-induced martensitic transformation of TRIP steel with strain rate. Comput. Mater. Sci. 2007, 40, 101–107. [Google Scholar] [CrossRef]
- Beese, A.M.; Mohr, D. Effect of stress triaxiality and lode angle on the kinetics of strain-induced austenite-to-martensite transformation. Acta Mater. 2011, 59, 2589–2600. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Barlat, F.; Kim, D.; Lee, M.G. Experiment and modeling to investigate the effect of stress state, strain and temperature on martensitic phase transformation in TRIP-assisted steel. Acta Mater. 2015, 97, 435–444. [Google Scholar] [CrossRef]
- Wan, J.Q.; He, B.B.; Yang, X.S.; Kong, L.B.; Zuo, X.W.; Jiao, Z.B. Dislocation accumulation-induced strength-ductility synergy in TRIP-aided duplex stainless steel. Int. J. Plast. 2024, 182, 104130. [Google Scholar] [CrossRef]
- Pan, J.X.; Xu, P.D.; Li, W.; Ma, F.C.; Zhang, K. Study of a nearly Ni-free V-containing lean duplex stainless steel and the deformation mechanism. Mater. Sci. Eng. A 2023, 865, 144562. [Google Scholar] [CrossRef]
- Zeng, L.Y.; Song, X.Y.; Chen, N.L.; Rong, Y.H.; Zuo, X.W.; Min, N. A new understanding of transformation induced plasticity (TRIP) effect in austenitic steels. Mater. Sci. Eng. A 2022, 857, 143742. [Google Scholar] [CrossRef]
- Zhang, W.N.; Liu, Z.Y.; Zhang, Z.B.; Wang, G.D. The crystallographic mechanism for deformation induced martensitic transformation observed by high resolution transmission electron microscope. Mater. Lett. 2013, 91, 158–160. [Google Scholar]
- Zhao, M.C.; Hanamura, T.; Qiu, H.; Nagai, K.; Yang, K. Dependence of strength and strength-elongation balance on the volume fraction of cementite particles in ultrafine grained ferrite/cementite steels. Scr. Mater. 2006, 54, 1385–1389. [Google Scholar] [CrossRef]
- Wang, S.H.; Liu, Z.Y.; Wang, G.D. Influence of grain size on the TWIP effect in TWIP steel. Acta Metall. Sin. 2009, 45, 1083–1090. [Google Scholar]
- Choi, J.Y.; Hwang, S.W.; Ha, M.C.; Park, K.T. Extended strain hardening by a sequential operation of twinning induced plasticity and transformation induced plasticity in a low Ni duplex stainless steel. Met. Mater. Int. 2014, 20, 893–898. [Google Scholar] [CrossRef]
- Choi, J.Y.; Lee, J.; Lee, K.; Koh, J.Y.; Cho, J.H.; Han, H.N.; Park, K.T. Effects of the strain rate on the tensile properties of a TRIP-aided duplex stainless steel. Mater. Sci. Eng. A 2016, 666, 280–287. [Google Scholar] [CrossRef]
- Gao, Z.L. Study on Transformation Behavior of Metastable Austenite in Stainless Steel. Master’s Thesis, Northeastern University, Shenyang, China, 2022. [Google Scholar]
- Johnston, W.G.; Gilman, J.J. Dislocation velocities, dislocation densities, and plastic flow in lithium fluoride crystals. J. Appl. Phys. 1959, 30, 129–144. [Google Scholar] [CrossRef]
- Dong, D.Y.; Liu, Y.; Wang, L.; Su, L.J. Effect of strain rate on dynamic tensile deformation behavior of DP780 steel. Acta Metall. Sin. 2013, 49, 159–166. [Google Scholar] [CrossRef]
- Huang, J.N. Research on Novel Heat Treatment and Dynamic Deformation Behavior Under Controllable Strain of High Strength Low Alloy Trip Steel. Ph.D. Thesis, Northeastern University, Shenyang, China, 2020. [Google Scholar]
- Cao, B.; Liu, R.H.; Gao, C.; Sun, Q.; Tan, X.J.; Iwamoto, T.; Sugino, T. An investigation on anomalous deformation behavior in SUS304 austenitic stainless steel: Experiments and simulations. J. Mater. Res. Technol. 2025, 35, 3705–3727. [Google Scholar] [CrossRef]
- De Moor, E.; Lacroix, S.; Clarke, A.J.; Penning, J.; Speer, J.G. Effect of retained austenite stabilized via quench and partitioning on the strain hardening of martensitic steels. Metall. Mater. Trans. A 2008, 39, 2586–2595. [Google Scholar] [CrossRef]
- Zou, D.Q.; Li, S.H.; He, J. Temperature and strain rate dependent deformation induced martensitic transformation and flow behavior of quenching and partitioning steels. Mater. Sci. Eng. A 2017, 680, 54–63. [Google Scholar] [CrossRef]
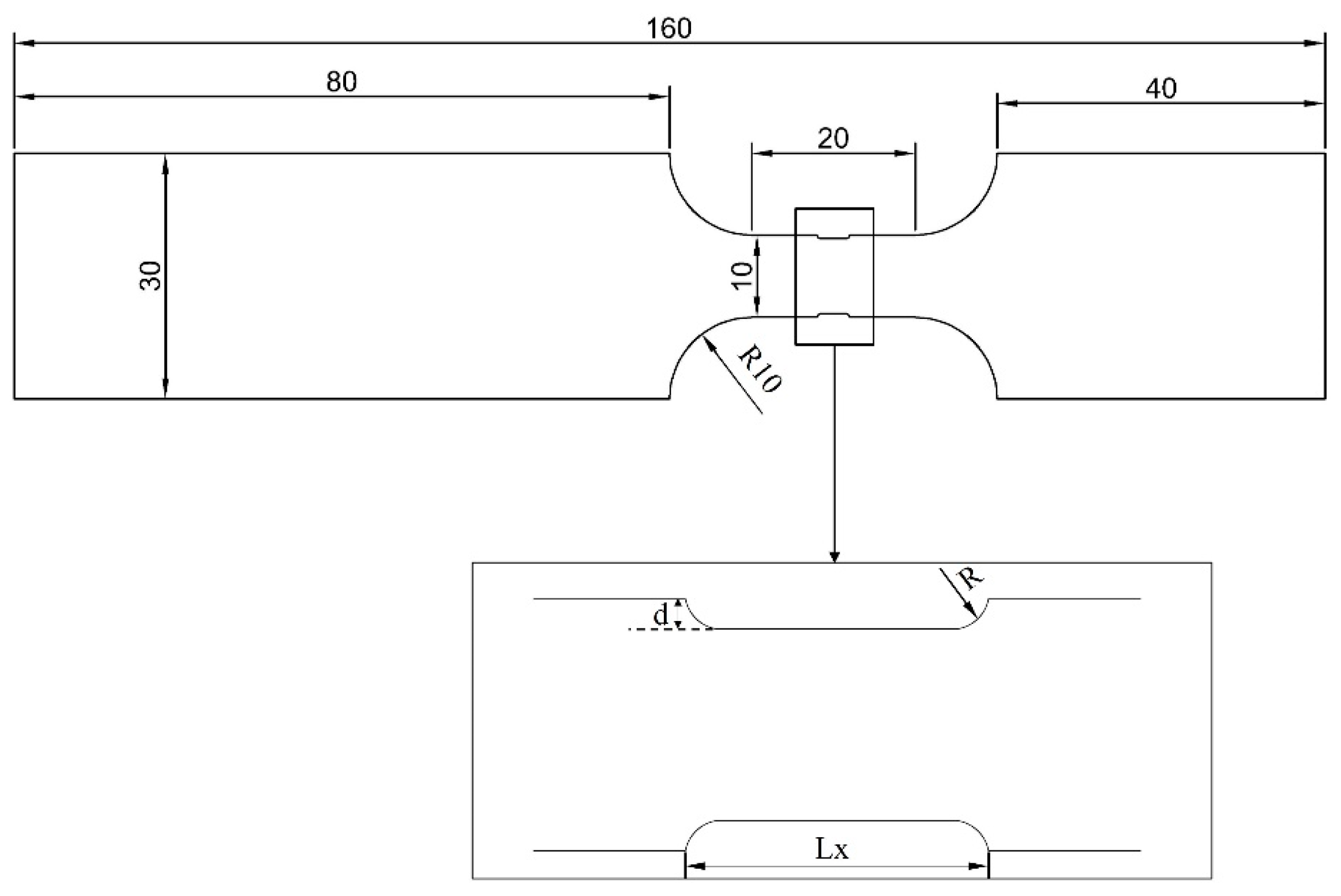




| C | N | Si | Mn | Cr | Ni | Cu | Sn | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.14 | 0.25 | 0.35 | 5 | 20 | 0.4 | 0.5 | 0.2 | Bal. |
| Parameter | Value |
|---|---|
| m1 | −0.6659 |
| m2 | 0.0378 |
| m3 | −214.7257 |
| n1 | 0.6804 |
| n2 | 6.6707 |
| n3 | −0.0534 |
| λ1 | 1.9843 |
| λ2 | 0.1599 |
| η1 | 0.1105 |
| η2 | 0.0139 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Gao, F.; Gao, Z.; Zhang, W.; Tang, S.; Cai, X.; Liu, Z. Influence of Deformation Temperature and Strain Rate on Martensitic Transformation of Duplex Stainless Steel and Its Corresponding Kinetic Model. Metals 2025, 15, 581. https://doi.org/10.3390/met15060581
Zhu Q, Gao F, Gao Z, Zhang W, Tang S, Cai X, Liu Z. Influence of Deformation Temperature and Strain Rate on Martensitic Transformation of Duplex Stainless Steel and Its Corresponding Kinetic Model. Metals. 2025; 15(6):581. https://doi.org/10.3390/met15060581
Chicago/Turabian StyleZhu, Qiyong, Fei Gao, Zilong Gao, Weina Zhang, Shuai Tang, Xiaohui Cai, and Zhenyu Liu. 2025. "Influence of Deformation Temperature and Strain Rate on Martensitic Transformation of Duplex Stainless Steel and Its Corresponding Kinetic Model" Metals 15, no. 6: 581. https://doi.org/10.3390/met15060581
APA StyleZhu, Q., Gao, F., Gao, Z., Zhang, W., Tang, S., Cai, X., & Liu, Z. (2025). Influence of Deformation Temperature and Strain Rate on Martensitic Transformation of Duplex Stainless Steel and Its Corresponding Kinetic Model. Metals, 15(6), 581. https://doi.org/10.3390/met15060581








