Assessment of Rate-Dependency and Adiabatic Heating on the Essential Work of Fracture of Press-Hardening Steels
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
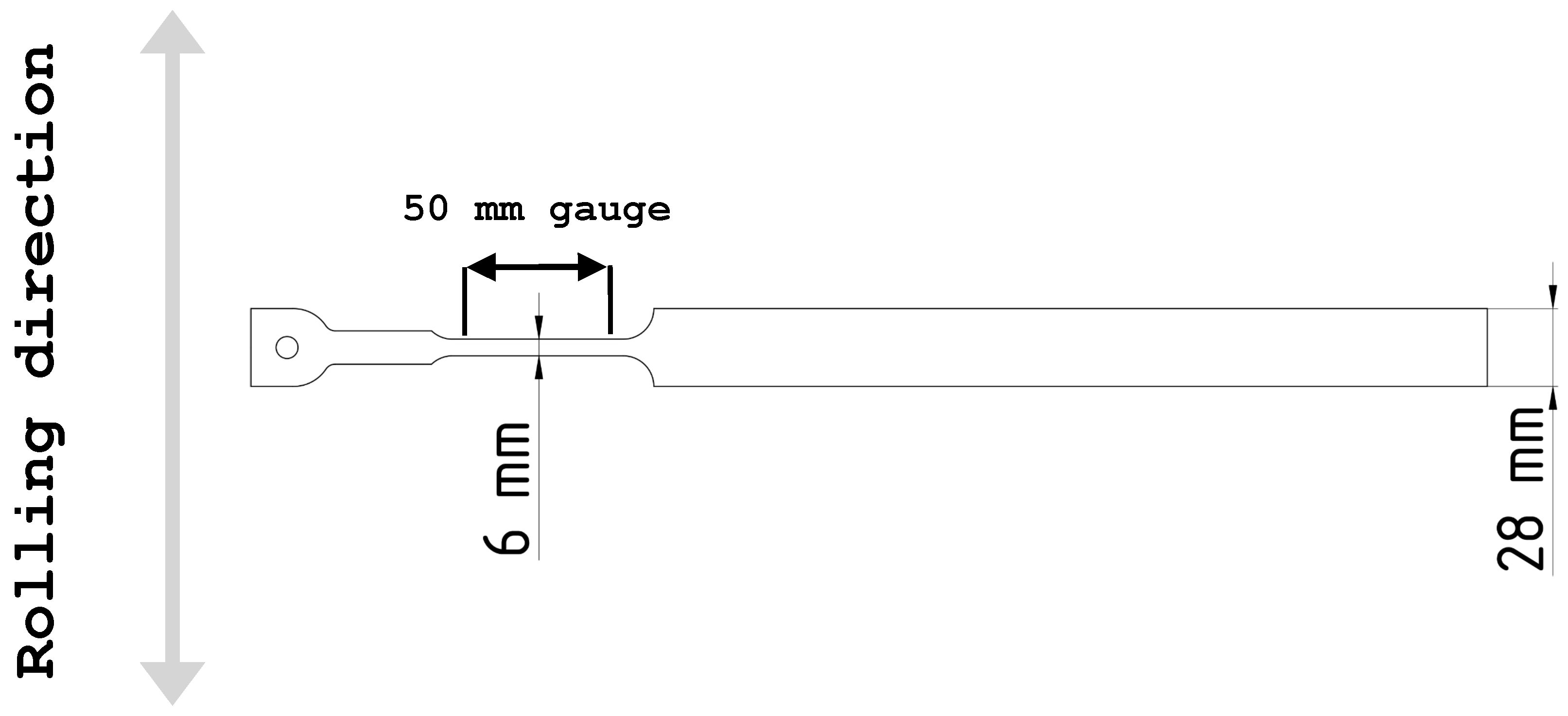
2.2. Tensile Testing
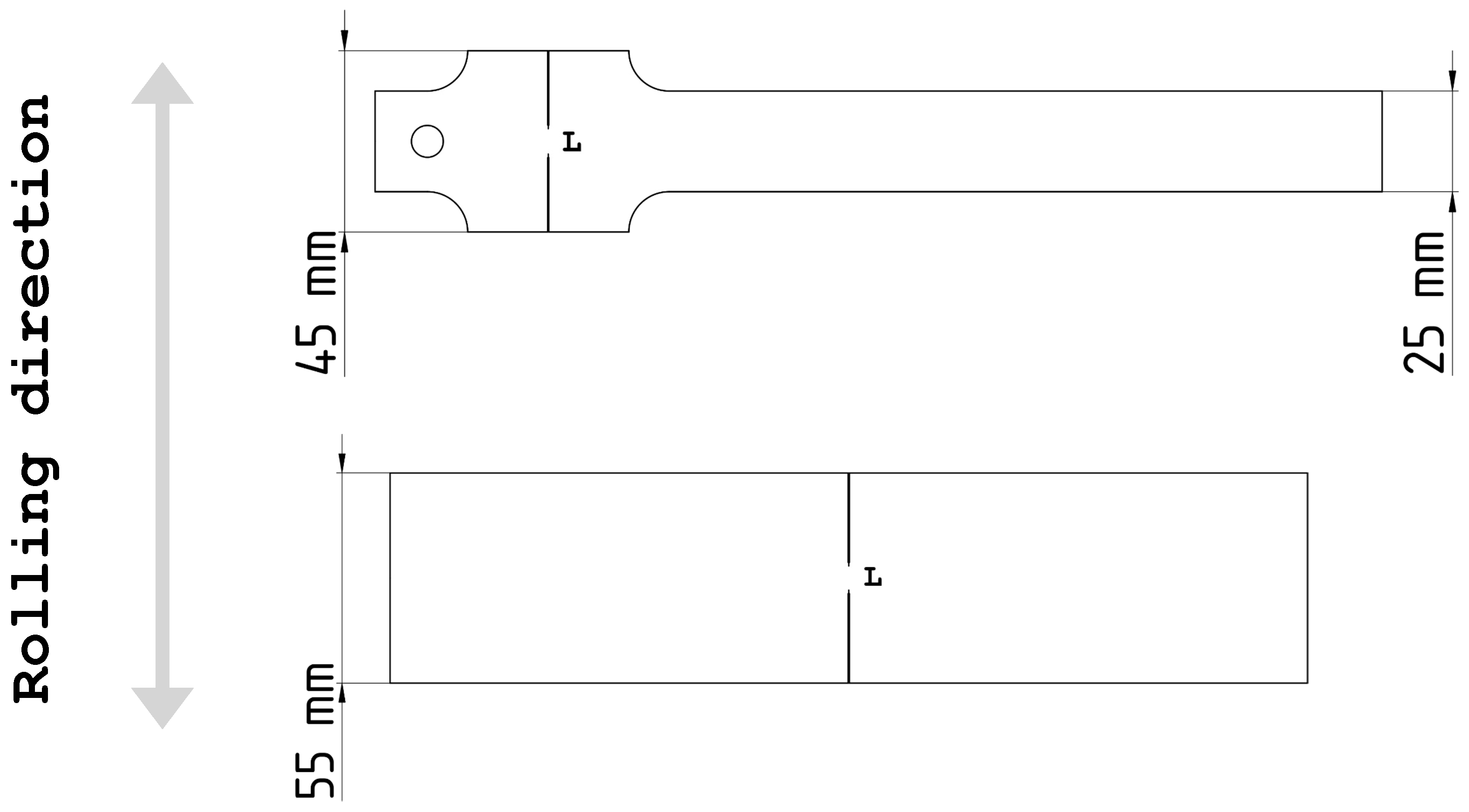
2.3. Essential Work of Fracture
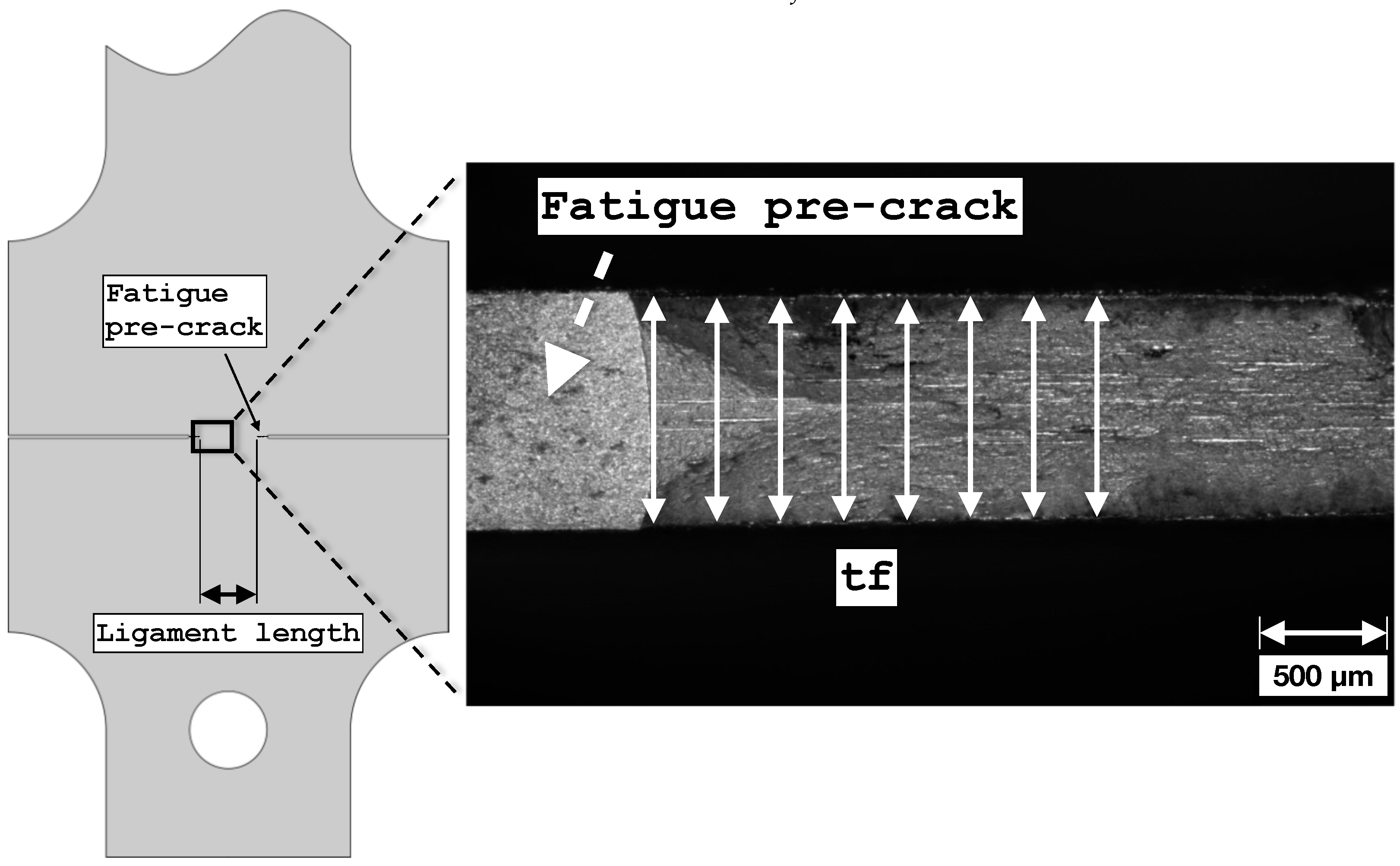
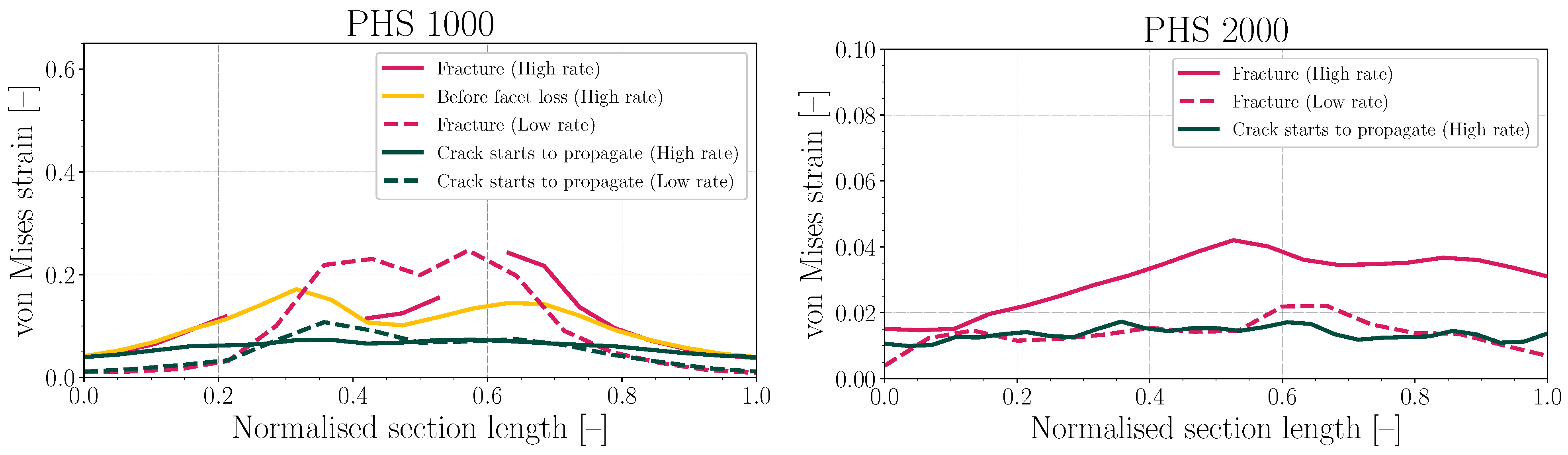
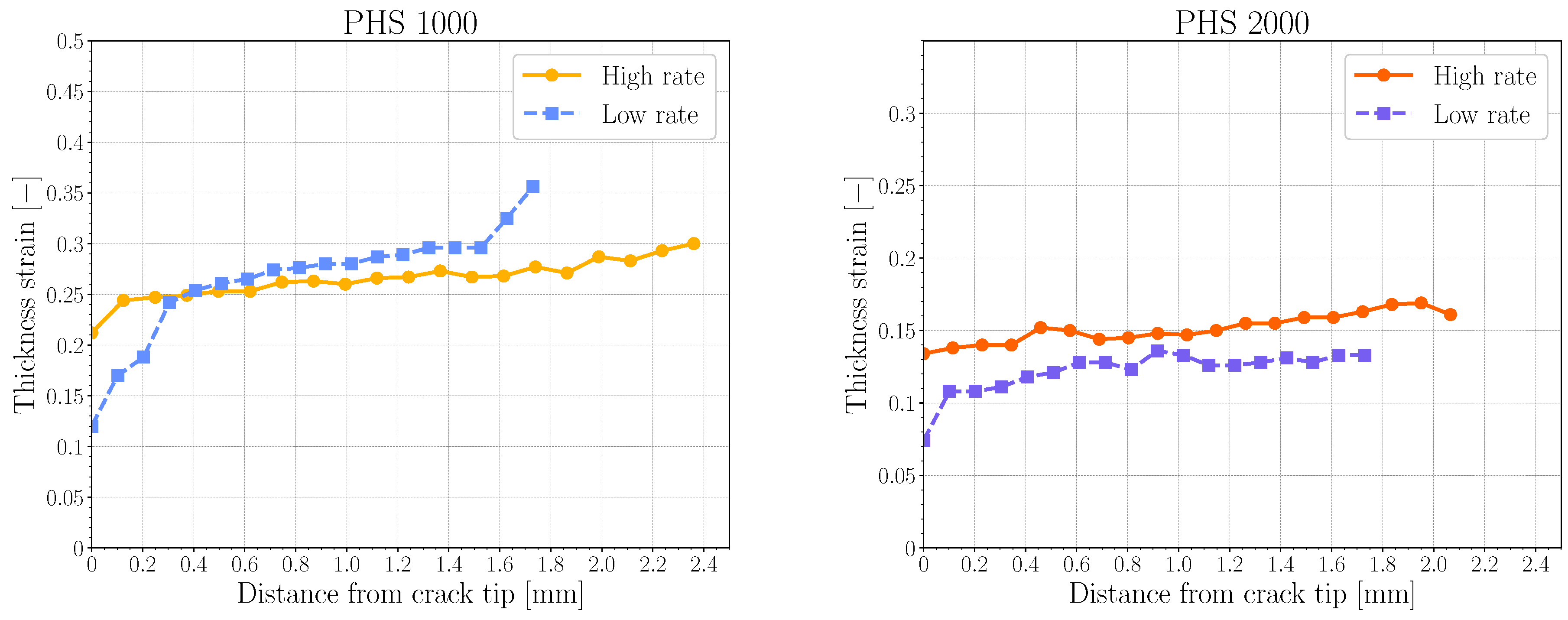
2.4. Thickness Strain
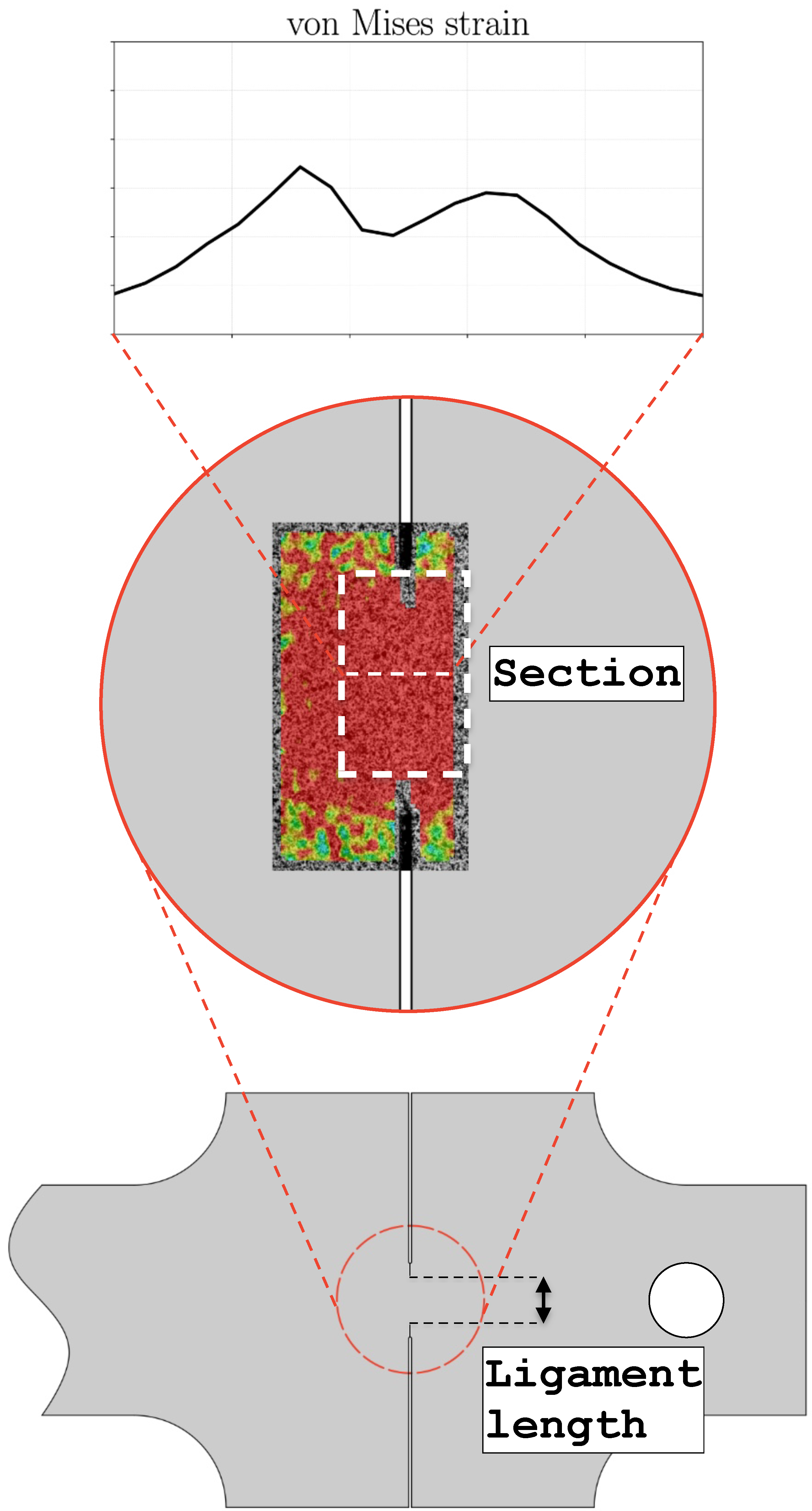
2.5. Digital Image Correlation
2.6. Temperature Measurements
3. Results
3.1. Microstructure and Hardness Measurements
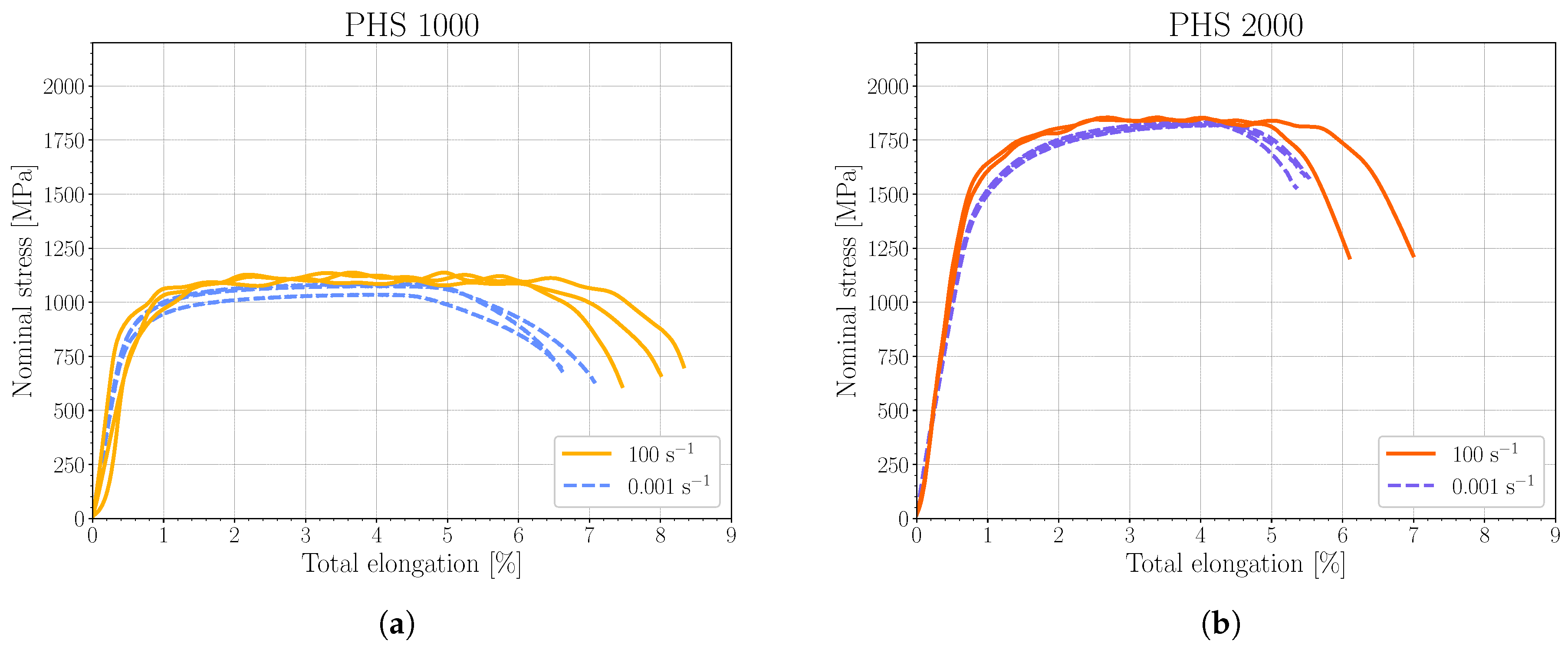
3.2. Uniaxial Tensile Tests
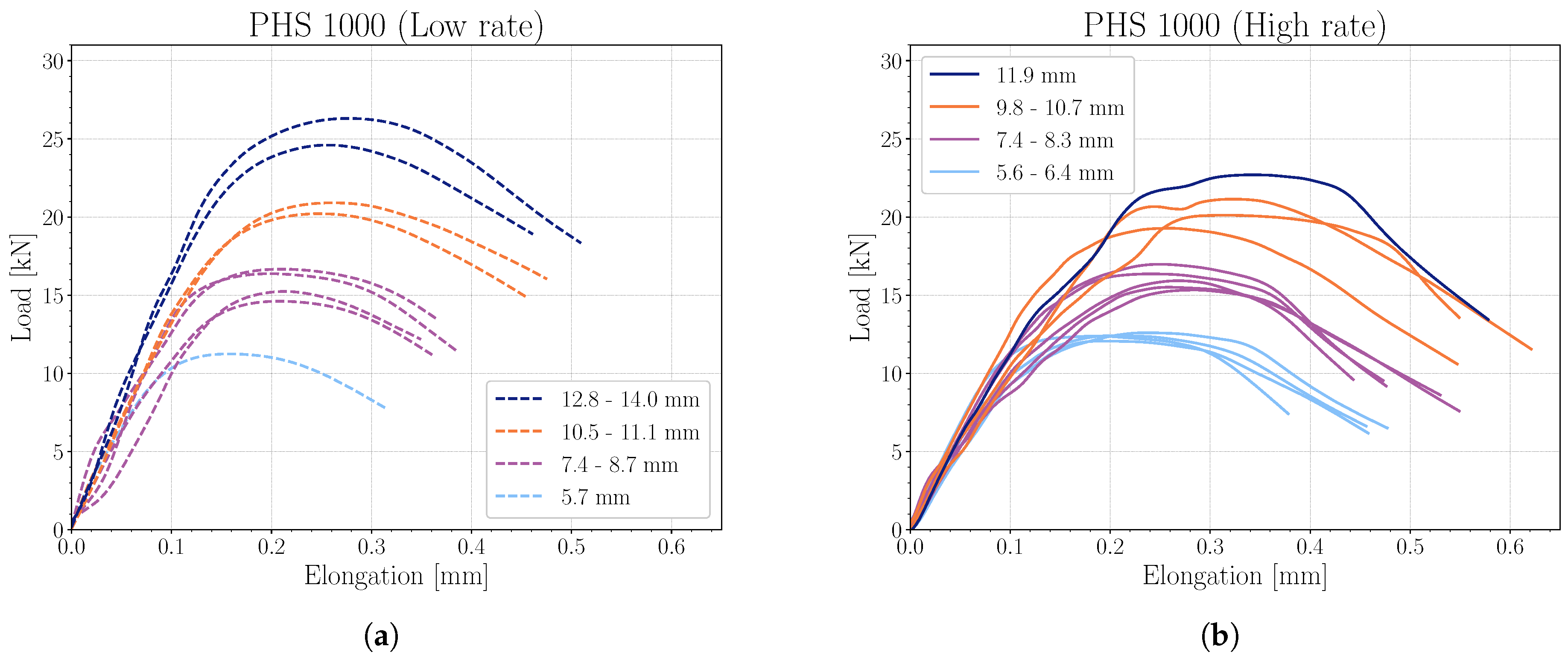
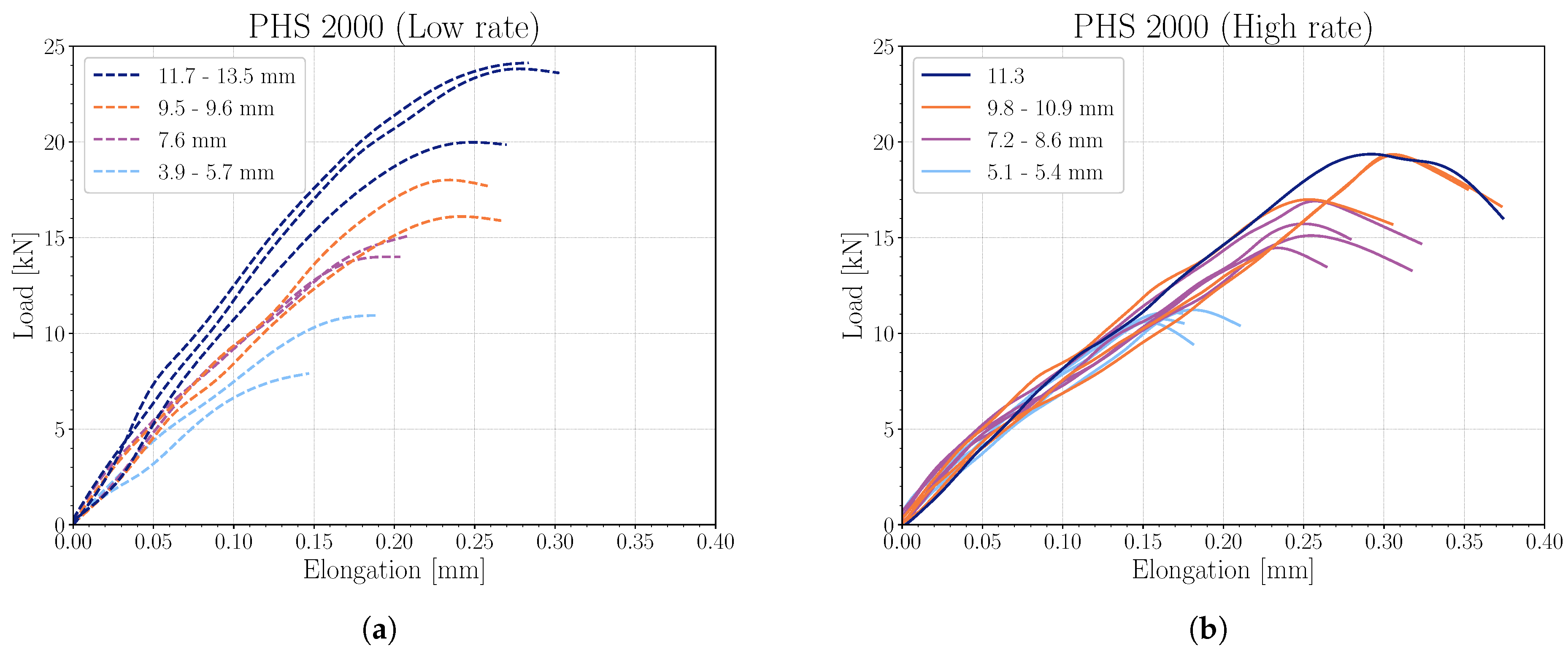
3.3. Essential Work of Fracture
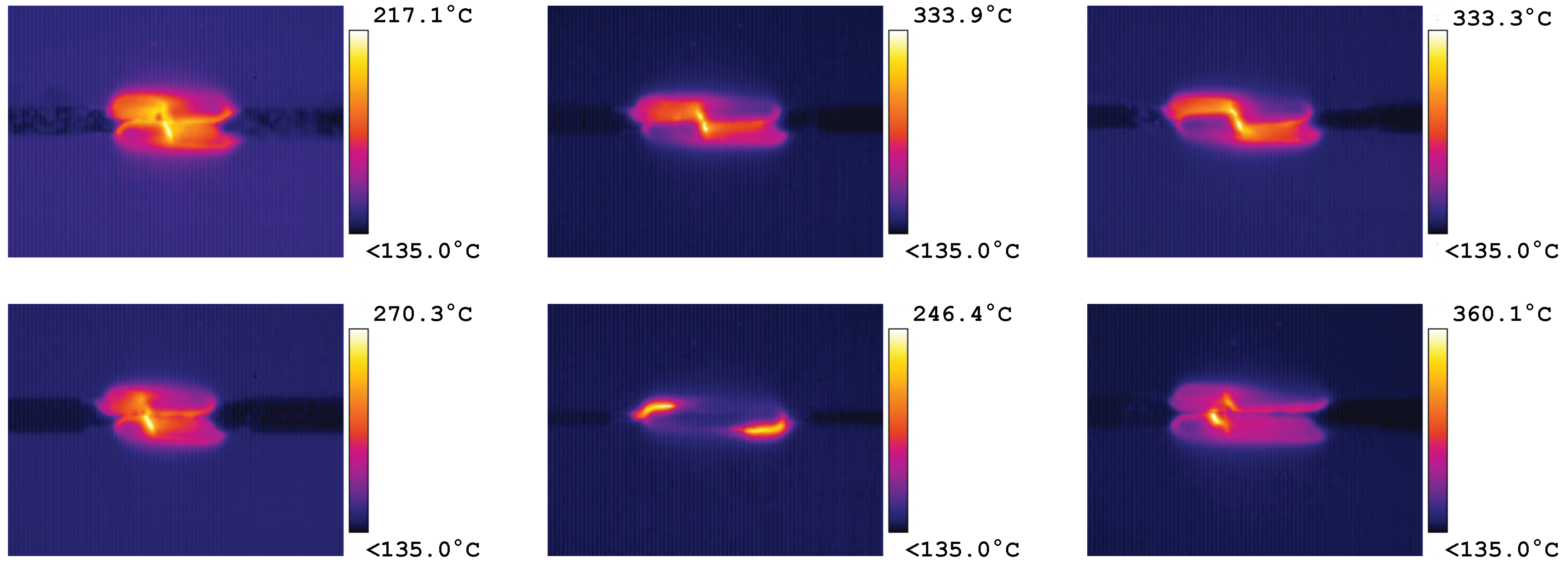
3.4. Thermal Measurements
4. Discussion and Conclusions
- Both grades of PHS showed a moderate increase in YS and UTS measured in uniaxial tensile testing with increasing strain rate, while only PHS 1000 showed a significant increase in fracture toughness with increasing loading rate. No statistically determinable change in fracture toughness could be resolved using the EWF methodology for PHS 2000.
- Both grades showed a significant increase in temperature due to adiabatic heating during the fracture of the DENT specimen, but the temperature for the more ductile PHS 1000 grade increased significantly more. The increase in adiabatic heating might be the cause of the increase in fracture toughness with strain rate in this case. However, more research is needed to draw strong conclusions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EWF | Essential Work of Fracture |
| FPZ | Fracture Process Zone |
| DIC | Digital Image Correlation |
| DENT | Double Edge Notched Tension |
| PHS | Press-Hardening Steel |
| AHSS | Advanced High-Strength Steel |
| UHSS | Ultra-High-Strength Steel |
| BIW | Body-in-White |
| FPZ | Fracture Process Zone |
| YS | Yield Stress |
| UTS | Ultimate Tensile Strength |
| TE | Total Elongation |
| FEG | Field Emission Gun |
| SEM | Scanning Electron Microscope |
References
- Monteforte, M.; Mock, P.; Bernard, M.R.; Tietge, U.; Mulholland, E. European Vehicle Market Statistics Pocketbook 2023/24; Technical Report; International Council on Clean Transportation Europe: Berlin, Germany, 2023. [Google Scholar]
- Noder, J.; Gutierrez, J.E.; Zhumagulov, A.; Dykeman, J.; Ezzat, H.; Butcher, C. A comparative evaluation of third-generation advanced high-strength steels for automotive forming and crash applications. Materials 2021, 14, 4970. [Google Scholar] [CrossRef]
- Barnwal, V.K.; Lee, S.Y.; Choi, J.; Kim, J.H.; Barlat, F. Fracture assessment in dual phase and transformation-induced plasticity steels during 3-point bending. Theor. Appl. Fract. Mech. 2020, 110, 102834. [Google Scholar] [CrossRef]
- Gutierrez, J.E.; Noder, J.; Butcher, C. Experimental characterization and deterministic prediction of in-plane formability of 3rd generation advanced high strength steels. Metals 2020, 10, 902. [Google Scholar] [CrossRef]
- Noder, J.; Gutierrez, J.E.; Zhumagulov, A.; Khameneh, F.; Ezzat, H.; Dykeman, J.; Butcher, C. Constitutive, Formability, and Fracture Characterization of 3rd Gen AHSS with an Ultimate Tensile Strength of 1180 MPa. SAE Int. J. Adv. Curr. Pract. Mobil. 2021, 3, 1395–1407. [Google Scholar] [CrossRef]
- Savic, V.; Hector, L.; Alturk, R.; Enloe, C. High Strain Rate Tensile Behavior of 1180MPa Grade Advanced High Strength Steels. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 2, 1561–1568. [Google Scholar] [CrossRef]
- Kim, J.G.; Enikeev, N.A.; Seol, J.B.; Abramova, M.M.; Karavaeva, M.V.; Valiev, R.Z.; Park, C.G.; Kim, H.S. Superior Strength and Multiple Strengthening Mechanisms in Nanocrystalline TWIP Steel. Sci. Rep. 2018, 8, 11200. [Google Scholar] [CrossRef]
- Ding, H.; Liu, D.; Cai, M.; Zhang, Y. Austenite-Based Fe-Mn-Al-C Lightweight Steels: Research and Prospective. Metals 2022, 12, 1572. [Google Scholar] [CrossRef]
- Bartlett, L.; Van Aken, D. High Manganese and Aluminum Steels for the Military and Transportation Industry. JOM 2014, 66, 1770–1784. [Google Scholar] [CrossRef]
- Zambrano, O. A general perspective of Fe–Mn–Al–C steels. J. Mater. Sci. 2018, 53, 14003–14062. [Google Scholar] [CrossRef]
- Zuazo, I.; Hallstedt, B.; Lindahl, B.; Selleby, M.; Soler, M.; Etienne, A.; Perlade, A.; Hasenpouth, D.; Massardier-Jourdan, V.; Cazottes, S.; et al. Low-Density Steels: Complex Metallurgy for Automotive Applications. JOM 2014, 66, 1747–1758. [Google Scholar] [CrossRef]
- Karbasian, H.; Tekkaya, A. A review on hot stamping. J. Mater. Process. Technol. 2010, 210, 2103–2118. [Google Scholar] [CrossRef]
- Ferrea, M.; De Caro, D.; Baldoin, E.; Tedesco, M.; Barile, B. 2000 PHS Press Hardening Steel Mechanical Characterization and Virtual Simulation of Automotive Crash Applications. In Proceedings of the 8th International Conference on Hot Sheet Metal Forming of High-Performance Steel, CHS2 2022, Barcelona, Spain, 30 May 2022; pp. 95–102. [Google Scholar]
- Kawajiri, K.; Kobayashi, M.; Sakamoto, K. Lightweight materials equal lightweight greenhouse gas emissions?: A historical analysis of greenhouse gases of vehicle material substitution. J. Clean. Prod. 2020, 253, 119805. [Google Scholar] [CrossRef]
- Burd, J.T.J.; Moore, E.A.; Ezzat, H.; Kirchain, R.; Roth, R. Improvements in electric vehicle battery technology influence vehicle lightweighting and material substitution decisions. Appl. Energy 2021, 283, 116269. [Google Scholar] [CrossRef]
- Choi, W.S.; De Cooman, B.C. Characterization of the Bendability of Press-Hardened 22MnB5 Steel. Steel Res. Int. 2014, 85, 824–835. [Google Scholar] [CrossRef]
- Golem, L.; Cho, L.; Speer, J.G.; Findley, K.O. Influence of austenitizing parameters on microstructure and mechanical properties of Al-Si coated press hardened steel. Mater. Des. 2019, 172, 107707. [Google Scholar] [CrossRef]
- Frómeta, D.; Lara, A.; Grifé, L.; Dieudonné, T.; Dietsch, P.; Rehrl, J.; Suppan, C.; Casellas, D.; Calvo, J. Fracture Resistance of Advanced High-Strength Steel Sheets for Automotive Applications. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2021, 52, 840–856. [Google Scholar] [CrossRef]
- Yoon, J.I.; Jung, J.; Joo, S.H.; Song, T.J.; Chin, K.G.; Seo, M.H.; Kim, S.J.; Lee, S.; Kim, H.S. Correlation between fracture toughness and stretch-flangeability of advanced high strength steels. Mater. Lett. 2016, 180, 322–326. [Google Scholar] [CrossRef]
- Frómeta, D.; Lara, A.; Casas, B.; Casellas, D. Fracture toughness measurements to understand local ductility of advanced high strength steels. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 651. [Google Scholar] [CrossRef]
- Frómeta, D.; Lara, A.; Molas, S.; Casellas, D.; Rehrl, J.; Suppan, C.; Larour, P.; Calvo, J. On the correlation between fracture toughness and crash resistance of advanced high strength steels. Eng. Fract. Mech. 2019, 205, 319–332. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, Z.; Wei, Y.; Lu, Q.; Ma, Y.; Wang, J.; Fan, G. Towards the understanding of fracture resistance of an ultrahigh-strength martensitic press-hardened steel. J. Mater. Res. Technol. 2023, 27, 1996–2006. [Google Scholar] [CrossRef]
- Rice, J.R.; Paris, P.C.; Merkle, J.G. Some Further Results of J-Integral Analysis and Estimates. In Progress in Flaw Growth and Fracture Toughness Testing; ASTM International: West Conshohocken, PA, USA, 1973. [Google Scholar] [CrossRef]
- Golling, S.; Frómeta, D.; Casellas, D.; Jonsén, P. Influence of microstructure on the fracture toughness of hot stamped boron steel. Mater. Sci. Eng. A 2019, 743, 529–539. [Google Scholar] [CrossRef]
- Grifé, L.; Frómeta, D.; Parareda, S.; Lara, A.; Casellas, D. An Innovative Rapid Procedure for Fracture Toughness Characterization of Advanced High Strength Steels and Press Hardened Steels. In Proceedings of the 8th International Conference on Hot Sheet Metal Forming of High-Performance Steel, CHS2 2022, Barcelona, Spain, 30 May 2022; pp. 221–228. [Google Scholar]
- Frómeta, D.; Parareda, S.; Pujante, J.; Corón, D.; Galceran, L.; Casellas, D. Influence of Laser Tempering on Fracture Toughness of Press Hardened Steels – Correlation with Components Crash Performance. In Proceedings of the 8th International Conference on Hot Sheet Metal Forming of High-Performance Steel, CHS2 2022, Barcelona, Spain, 30 May 2022; pp. 137–144. [Google Scholar]
- Tarhouni, I.; Frómeta, D.; Casellas, D. Essential Work of Fracture Method for Toughness Evaluation of Thick Press Hardened 22MnB5 Plates. In Proceedings of the 8th International Conference on Hot Sheet Metal Forming of High-Performance Steel, CHS2 2022, Barcelona, Spain, 30 May 2022; pp. 387–394. [Google Scholar]
- Parareda, S.; Casellas, D.; Taiss, E.; Tolotti de Almeida, D.; Frómeta, D. Improved Fatigue and Fracture Resistance of 22MnB5 Steels With Added Nb and Mo. In Proceedings of the 9th International Conference on Hot Sheet Metal Forming of High-Performance Steel, CHS2 2024, Nashville, TN, USA, 27 May 2024; pp. 445–450. [Google Scholar]
- Golling, S.; Frómeta, D.; Casellas, D.; Jonsén, P. Investigation on the influence of loading-rate on fracture toughness of AHSS grades. Mater. Sci. Eng. A 2018, 726, 332–341. [Google Scholar] [CrossRef]
- Larour, P.; Pauli, H.; Kurz, T.; Hebesberger, T. Influence of Post Uniform Tensile and Bending Properties on the Crash Behaviour of AHSS and Press-Hardening Steel Grades. In Proceedings of the IDDRG 2010 Conference (International Deep Drawing Research Group), Graz, Austria, 31 May–2 June 2010; pp. 107–126. [Google Scholar]
- Langi, V.; Soares, G.C.; Ahmed, S.; Peura, P.; Hokka, M. Effects of strain rate and adiabatic heating on mechanical behavior of medium manganese Q&P steels. Mater. Sci. Eng. A 2023, 865, 144659. [Google Scholar] [CrossRef]
- Vázquez-Fernández, N.; Nyyssönen, T.; Isakov, M.; Hokka, M.; Kuokkala, V.T. Uncoupling the effects of strain rate and adiabatic heating on strain induced martensitic phase transformations in a metastable austenitic steel. Acta Mater. 2019, 176, 134–144. [Google Scholar] [CrossRef]
- Peirs, J.; Verleysen, P.; Degrieck, J.; Coghe, F. The use of hat-shaped specimens to study the high strain rate shear behaviour of Ti-6Al-4V. Int. J. Impact Eng. 2010, 37, 703–714. [Google Scholar] [CrossRef]
- Kubair, D.; Ramesh, K.; Swaminathan, P. Effect of shear-void-growth-softening on adiabatic shear-band-spacing in ductile materials. Acta Mech. 2015, 226, 4189–4206. [Google Scholar] [CrossRef]
- Cotterell, B.; Reddel, J. The essential work of plane stress ductile fracture. Int. J. Fract. 1977, 13, 267–277. [Google Scholar] [CrossRef]
- Broberg, K.B. On stable crack growth. J. Mech. Phys. Solids 1975, 23, 443–445. [Google Scholar] [CrossRef]
- Broberg, K.B. Critical review of some theories in fracture mechanics. Int. J. Fract. Mech. 1968, 4, 11–19. [Google Scholar] [CrossRef]
- Broberg, K.B. Crack-growth criteria and non-linear fracture mechanics. J. Mech. Phys. Solids 1971, 19, 407–418. [Google Scholar] [CrossRef]
- Frómeta, D.; Parareda, S.; Lara, A.; Molas, S.; Casellas, D.; Jonsén, P.; Calvo, J. Identification of fracture toughness parameters to understand the fracture resistance of advanced high strength sheet steels. Eng. Fract. Mech. 2020, 229, 106949. [Google Scholar] [CrossRef]
- Clutton, E. Essential work of fracture. In Fracture Mechanics Testing Methods for Polymers, Adhesives and Composites; European Structural Integrity Society; Moore, D., Pavan, A., Williams, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 28, pp. 177–195. [Google Scholar] [CrossRef]
- Pardoen, T.; Hachez, F.; Marchioni, B.; Blyth, P.; Atkins, A. Mode I fracture of sheet metal. J. Mech. Phys. Solids 2004, 52, 423–452. [Google Scholar] [CrossRef]
- Samadian, P.; Abedini, A.; Butcher, C.; Worswick, M.J. Microstructure-Based Modelling of Flow and Fracture Behavior of Tailored Microstructures of Ductibor® 1000-AS Steel. Metals 2022, 12, 1770. [Google Scholar] [CrossRef]
- Zhu, H.; Yin, H.; Sadagopan, S. Study of Microstructural Evolution of Press Hardening Steels using Dilatometer and In-situ Studies for a Simulated Hot Stamping Condition. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1284, 012008. [Google Scholar] [CrossRef]
- Bardelcik, A.; Worswick, M.J.; Wells, M.A. The influence of martensite, bainite and ferrite on the as-quenched constitutive response of simultaneously quenched and deformed boron steel—Experiments and model. Mater. Des. 2014, 55, 509–525. [Google Scholar] [CrossRef]
- Bardelcik, A.; Worswick, M.; Winkler, S.; Wells, M. A strain rate sensitive constitutive model for quenched boron steel with tailored properties. Int. J. Impact Eng. 2012, 50, 49–62. [Google Scholar] [CrossRef]
- Xia, P.; Sabirov, I.; Molina-Aldareguia, J.; Verleysen, P.; Petrov, R. Mechanical behavior and microstructure evolution of a quenched and partitioned steel during drop weight impact and punch testing. Mater. Sci. Eng. A 2018, 737, 18–26. [Google Scholar] [CrossRef]
- Xia, P.; Sanchez Palomar, M.; Sabirov, I. Adiabatic heating and energy absorption capability of an advanced high strength steel during drop weight impact testing. Mater. Sci. Eng. A 2020, 785, 139382. [Google Scholar] [CrossRef]
- Kohar, C.P.; Cherkaoui, M.; Kadiri, H.E.; Inal, K. Numerical modeling of TRIP steel in axial crashworthiness. Int. J. Plast. 2016, 84, 224–254. [Google Scholar] [CrossRef]
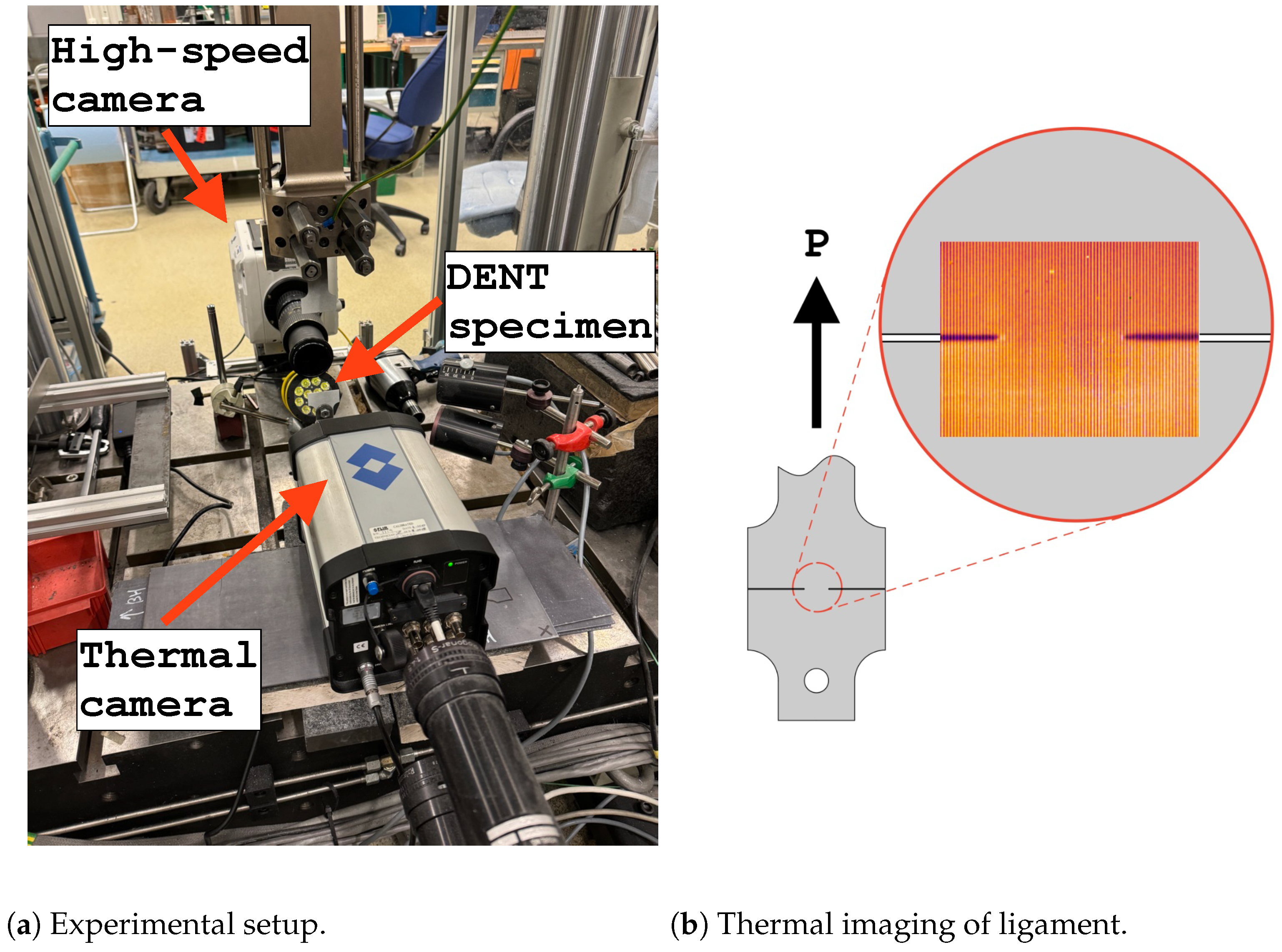



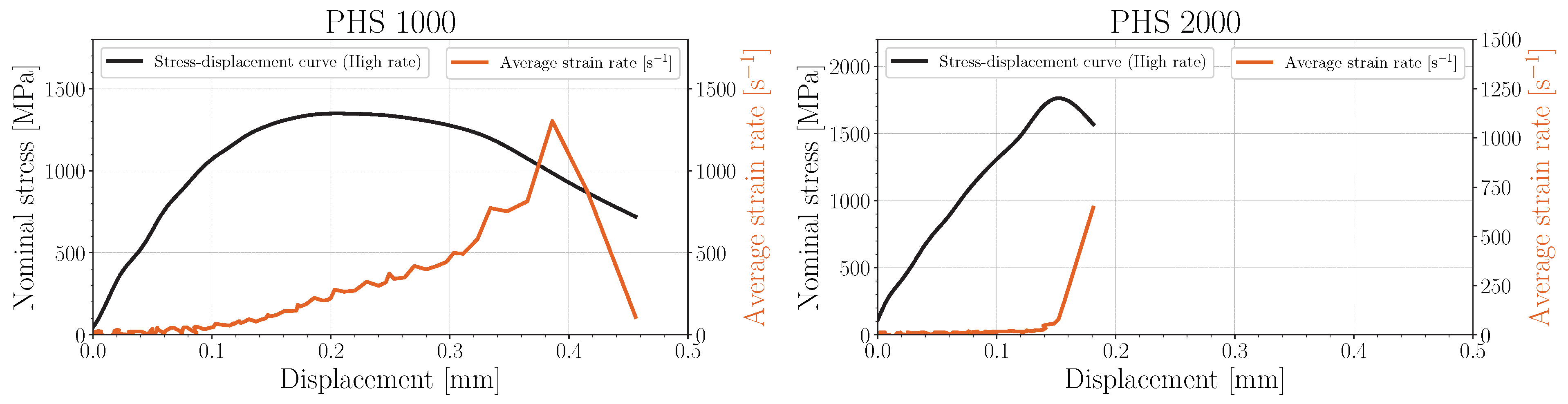

| PHS Grade | C * | Si * | Mn * | P * | S * | Al | Ti * | Nb * | Cu * | B * | Cr * | Mo * |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PHS 1000 | 0.01–0.1 | - | ||||||||||
| PHS 2000 | 0.01–0.06 | 0.02–0.07 |
| PHS Grade | Avg. Vickers Hardness [HV0.5] | Std. Dev. |
|---|---|---|
| PHS 1000 | 364 | 5.3 |
| PHS 2000 | 602 | 5.0 |
| YS (Min/Max) [MPa] | UTS (Min/Max) [MPa] | YS/UTS [–] | TE (Min/Max) [Pct] | UTS × TE [MPa Pct] | |
|---|---|---|---|---|---|
| PHS 1000 (1.55 mm thickness) | |||||
| 0.001 | 901 (878/915) | 1067 (1042/1085) | 0.84 | 6.8 (6.6/7.1) | 7256 |
| 100 | 946 (894/1002) | 1129 (1111/1138) | 0.84 | 8.0 (7.5/8.3) | 9032 |
| PHS 2000 (1.2 mm thickness) | |||||
| 0.001 | 1489 (1482/1496) | 1832 (1820/1842) | 0.81 | 5.5 (5.4/5.5) | 10,076 |
| 100 | 1600 (1583/1617) | 1853 (1850/1855) | 0.86 | 6.6 (6.1/7.0) | 12,230 |
| Low Rate | High Rate | |||||
|---|---|---|---|---|---|---|
| Grade | [kJ/m2] | [MPa] | [kJ/m2] | [MPa] | ||
| PHS 1000 | ||||||
| PHS 2000 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jonsson, S.; Frómeta, D.; Grifé, L.; Larsson, F.; Kajberg, J. Assessment of Rate-Dependency and Adiabatic Heating on the Essential Work of Fracture of Press-Hardening Steels. Metals 2025, 15, 316. https://doi.org/10.3390/met15030316
Jonsson S, Frómeta D, Grifé L, Larsson F, Kajberg J. Assessment of Rate-Dependency and Adiabatic Heating on the Essential Work of Fracture of Press-Hardening Steels. Metals. 2025; 15(3):316. https://doi.org/10.3390/met15030316
Chicago/Turabian StyleJonsson, Simon, David Frómeta, Laura Grifé, Fredrik Larsson, and Jörgen Kajberg. 2025. "Assessment of Rate-Dependency and Adiabatic Heating on the Essential Work of Fracture of Press-Hardening Steels" Metals 15, no. 3: 316. https://doi.org/10.3390/met15030316
APA StyleJonsson, S., Frómeta, D., Grifé, L., Larsson, F., & Kajberg, J. (2025). Assessment of Rate-Dependency and Adiabatic Heating on the Essential Work of Fracture of Press-Hardening Steels. Metals, 15(3), 316. https://doi.org/10.3390/met15030316






