5. Conclusions
The prediction of the fatigue life of 51CrV4 steel for parabolic leaf springs manufactured by hot-forming and subsequent quenching and tempering heat treatment in a probabilistic approach considering the mean stress effect was carried out in this paper. In the analysis performed, specimens produced for three-point in-plane bending and axial tension conditions were considered. The results obtained for different stress ratios were combined with failure data obtained in previous studies for the same category of the material to obtain a larger extensive resistance curve, covering three fatigue regimes: low-cycle fatigue (LCF), high-cycle fatigue (HCF), and very high-cycle fatigue (VHCF).
The estimation of the resistance curves was conducted using a probabilistic approach, where the percentile failure probability curves were obtained for both the normal distribution, considering the Walker SN fatigue model, and the Weibull distribution, considering the ACFC fatigue model. In order to provide a fatigue model for normal loading, bending, and tension loading, a combined fatigue model considering all failure data and run-outs was also developed.
From the initial analysis performed on the strength of 51CrV4 steel, the WSN model showed that 51CrV4 steel is less sensitive to the stress medium under bending loading () than under axial tension loading (). The parameters of the WSN curve, and , did not result in very different values in relation to the Basquin resistance model for specimens tested at a stress ratio of −1. The largest difference observed was 7.97% for the coefficient in specimens tested under uniaxial tension/compression loads.
Regarding the ACFC model, the equivalent strain amplitude parameter, , depending on the applied strain amplitude, the load ratio, and the parameter , proved to be the most suitable for predicting fatigue behavior considering the extension of the fatigue resistance curve from LCF to VHCF. However, to correctly predict this behavior, regarding the damage parameter, , it was necessary to consider the sum of the elastic strain component and the plastic strain component. The results obtained were suitable for the specimen model tested under uniaxial tension/compression loads, with most of the failure data being located between the 5th and 75th failure probability curves, for long and very long lives. For short lives (zone with lower scatter), the failure data are contained within the 25th and 75th failure probability curves. Regarding the statistical estimators, the maximum relative difference occurred in the location parameter (13.68%). In the model of specimens tested under bending loading, non-symmetry of the failure data was observed, with most of the failures occurring between 1 and 75%.
Regarding the combined fatigue model, it was observed from the Walker parameter (Equation (
2)) of the WSN model that, when the bending and uniaxial tension/compression data are combined,
takes the value of
, which is a value that is very close to the
criterion, widely used for steel fatigue modeling. The value of
in the WSN model reduces to 0.4593, which might be strongly associated with outliers fractured for lifetimes greater than
cycles. In contrast, the values of
and
do not change significantly considering the WSN model of specimens under uniaxial tension/compression (no mean stress effect). This result highlighted the great need for knowledge of a material’s resistance in different fatigue regimes.
Regarding the combined ACFC probabilistic model, for short lives, the data remained within the 25th and 75th percentile curves, whereas, for longer lives, increased scatter was observed, with the data located within the 5th and 95th percentile curves. Combining the failure data resulted in the estimators , , and and asymptote values of and .
Regarding the analysis of fracture surfaces, the SEM analysis showed that, for positive stress ratios up to lifetimes of cycles (under tension loads) and cycles (under bending loads), initiation occurs preferentially at the sample surface. This failure mode was observed for stress amplitudes and mean stress greater than 565 and 690 MPa, respectively (for axial tension), and a stress amplitude of 550 MPa for three-point in-plane bending. For lower stress amplitude and mean stress levels, initiation by internal inclusions might occur. In one of the fracture surfaces, with internal initiation from inclusion, the type of non-metallic inclusions found on the fracture surfaces appeared to be Al3O2 with the formation of the FGA zone.
Author Contributions
Conceptualization, V.M.G.G.; methodology, V.M.G.G. and M.A.V.d.F.; software, V.M.G.G. and M.A.V.d.F.; validation, V.M.G.G. and A.M.P.d.J.; formal analysis, V.M.G.G.; investigation, V.M.G.G.; resources, M.A.V.d.F., J.A.F.O.C. and A.M.P.d.J.; data curation, V.M.G.G. and M.A.V.d.F.; writing—original draft preparation, V.M.G.G.; writing—review and editing, V.M.G.G., M.A.V.d.F., J.A.F.O.C. and A.M.P.d.J.; visualization, V.M.G.G., M.A.V.d.F. and A.M.P.d.J.; supervision, M.A.V.d.F., J.A.F.O.C. and A.M.P.d.J.; project administration, A.M.P.d.J.; funding acquisition, J.A.F.O.C. and A.M.P.d.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was co-funded by Doctoral Programme iRail—Innovation in Railway Systems and Technologies—funded by the Portuguese Foundation for Science and Technology, IP (FCT), through the PhD grant PD/BD/143141/2019 and the following research projects: GCYCLEFAT—Giga-cycle fatigue behavior of engineering metallic alloys, with reference PTDC/EME-EME/7678/2020; FERROVIA 4.0, with reference POCI-01-0247-FEDER-046111, co-financed by the European Regional Development Fund (ERDF), through the Operational Programme for Competitiveness and Internationalization (COMPETE 2020), under the PORTUGAL 2020 Partnership Agreement; SMARTWAGONS-DEVELOPMENT OF PRODUCTION CAPACITY IN PORTUGAL OF SMART WAGONS FOR FREIGHT, with reference no. C644940527-00000048; investment project no. 27 from the Incentive System to Mobilising Agendas for Business Innovation, funded by the Recovery and Resilience Plan and by the European funds NextGeneration EU; PRODUCING RAILWAY ROLLING STOCK IN PORTUGAL, with reference no. C645644454-00000065; and investment project no. 55 from the Incentive System to Mobilising Agendas for Business Innovation, funded by the Recovery and Resilience Plan and by the European funds NextGeneration EU.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
The authors want to express their special thanks to CEMUP, “Centro de Materiais da Universidade do Porto”, and the respective technical staff for carrying out the scanning electron microscopy tests.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ISO | International Organization for Standardization |
| ASTM | American Society for Testing and Materials |
| UIC | International Union of Railways |
| CAD | Computer-aided design |
| LCF | Low-cycle fatigue |
| HCF | High-cycle fatigue |
| VHCF | Very high-cycle fatigue or giga-cycle fatigue |
| SN | Stress–number of cycles |
| WSN | Walker stress–number of cycles |
| CFC | Castillo–Fernández–Cantelli |
| ACFC | Apetre and Castillo–Fernández–Cantelli |
| CMB | Coffin–Manson and Basquin |
| SEM | Scanning electron microscopy |
| FGA | Fine granular area zone |
| Probability of failure |
| Stress amplitude |
| Equivalent Walker stress amplitude |
| Number of cycles to failure |
| Stress ratio |
| Strain ratio |
| Coefficient of the Basquin SN model |
| Exponent of the Basquin SN model |
| Walker parameter |
| Dowling parameter |
| SWT | Smith, Watson, and Topper parameter |
| EFRSA | Exponential form for fully equivalent stress amplitude parameter |
| GSA | Generalized strain amplitude parameter |
| , | Constant coefficients of the linearized Basquin SN model |
| , | Linear coefficients of the linearized Basquin SN model with |
| Fatigue limit |
| V | Weibull random variable |
| B | Logarithm of the threshold value for the life |
| C | Logarithm of the threshold of the fatigue life for the fatigue limit |
| Threshold of the fatigue life for the fatigue limit |
| Location parameter of the Weibull distribution model |
| Shape parameter of the Weibull distribution model |
| Scale parameter of the Weibull distribution model |
| RB | Specimens tested under fatigue rotating bending conditions |
| AT | Specimens tested under fatigue uniaxial tension/compression loading conditions |
References
- Zerbst, U.; Beretta, S.; Köhler, G.; Lawton, A.; Vormwald, M.; Beier, H.; Klinger, C.; Černý, I.; Rudlin, J.; Heckel, T.; et al. Safe life and damage tolerance aspects of railway axles—A review. Eng. Fract. Mech. 2013, 98, 214–271. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, B.; Feng, M.; Wang, H. Probabilistic fatigue S–N curves including the super-long life regime of a railway axle steel. Int. J. Fatigue 2009, 31, 1550–1558. [Google Scholar] [CrossRef]
- Xiu, R.; Spiryagin, M.; Wu, Q.; Yang, S.; Liu, Y. Fatigue life assessment methods for railway vehicle bogie frames. Eng. Fail. Anal. 2020, 116, 104725. [Google Scholar] [CrossRef]
- Kassner, M. Fatigue strength analysis of a welded railway vehicle structure by different methods. Int. J. Fatigue 2012, 34, 103–111. [Google Scholar] [CrossRef]
- Yamada, Y. Materials for Springs; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Regional Tensile Stress as a Measure of the Fatigue Strength of Notched Parts; Society, of Materials, Science: Kyoto, Japan, 1972; Volume II.
- Pixabay. Available online: https://pixabay.com/photos/freight-train-tracks-rail-rails-1640349 (accessed on 10 December 2024).
- Bragança, C.; Neto, J.; Pinto, N.; Montenegro, P.; Ribeiro, D.; Carvalho, H.; Calçada, R. Calibration and validation of a freight wagon dynamic model in operating conditions based on limited experimental data. Veh. Syst. Dyn. 2022, 60, 3024–3050. [Google Scholar] [CrossRef]
- Xia, Z.; Kujawski, D.; Ellyin, F. Effect of mean stress and ratcheting strain on fatigue life of steel. Int. J. Fatigue 1996, 18, 335–341. [Google Scholar] [CrossRef]
- Wehner, T.; Fatemi, A. Effects of mean stress on fatigue behaviour of a hardened carbon steel. Int. J. Fatigue 1991, 13, 241–248. [Google Scholar] [CrossRef]
- Sines, G. Failure of Materials Under Combined Repeated Stresses with Superimposed Static Stresses; Technical report; California Univ.: Los Angeles, CA, USA, 1955. [Google Scholar]
- Forrest, P.G. Fatigue of Metals; Pergamon Press: London, UK, 1962. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Walker, K. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum. Eff. Environ. Complex Load Hist. Fatigue Life 1970, 1–14. [Google Scholar] [CrossRef]
- Lu, S.; Su, Y.; Yang, M.; Li, Y. A modified Walker model dealing with mean stress effect in fatigue life prediction for aeroengine disks. Math. Probl. Eng. 2018, 2018, 5148278. [Google Scholar] [CrossRef]
- Smith, K.N.; Watson, P.; Topper, T.H. A Stress-Strain Function for the Fatigue of Metals. J. Materials 1970, 5, 767. [Google Scholar]
- Dowling, N.E.; Calhoun, C.A.; Arcari, A. Mean stress effects in stress-life fatigue and the Walker equation. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 163–179. [Google Scholar] [CrossRef]
- Dowling, N. Mean stress effects in strain-life fatigue. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 1004–1019. [Google Scholar] [CrossRef]
- Özdeş, H.; Tiryakioğlu, M. Walker parameter for mean stress correction in fatigue testing of Al-7% Si-Mg alloy castings. Materials 2017, 10, 1401. [Google Scholar] [CrossRef] [PubMed]
- Kwofie, S. An exponential stress function for predicting fatigue strength and life due to mean stresses. Int. J. Fatigue 2001, 23, 829–836. [Google Scholar] [CrossRef]
- Mahtabi, M.J.; Shamsaei, N. A modified energy-based approach for fatigue life prediction of superelastic NiTi in presence of tensile mean strain and stress. Int. J. Mech. Sci. 2016, 117, 321–333. [Google Scholar] [CrossRef]
- Koh, S.; Stephens, R. Mean stress effects on low cycle fatigue for a high strength steel. Fatigue Fract. Eng. Mater. Struct. 1991, 14, 413–428. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Practical Implementation of the Double Linear Damage Rule and Damage Curve Approach for Treating Cumulative Fatigue Damage. Int. J. Fract. 1981, 17, 169–192. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A modification of Morrow and Smith-Watson-Topper mean stress correction models. Fatigue Fract. Eng. Mater. Struct. 2011, 34, 854–867. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A generalized fatigue damage parameter for multiaxial fatigue life prediction under proportional and non-proportional loadings. Int. J. Fatigue 2014, 62, 34–41. [Google Scholar] [CrossRef]
- Nihei, M.; Heuler, P.; Boller, C.; Seeger, T. Evaluation of mean stress effect on fatigue life by use of damage parameters. Int. J. Fatigue 1986, 8, 119–126. [Google Scholar] [CrossRef]
- Li, J.; Qiu, Y.; Li, C.; Zhang, Z. A Walker exponent corrected model for estimating fatigue life of metallic materials in loading with mean stress. Mater. Werkst. 2019, 50, 1106–1112. [Google Scholar] [CrossRef]
- Correia, J.; Apetre, N.; Arcari, A.; De Jesus, A.; Muniz-Calvente, M.; Calçada, R.; Berto, F.; Fernández-Canteli, A. Generalized probabilistic model allowing for various fatigue damage variables. Int. J. Fatigue 2017, 100, 187–194. [Google Scholar] [CrossRef]
- Meggiolaro, M.A.; de Castro, J.T.P. An improved strain-life model based on the Walker equation to describe tensile and compressive mean stress effects. Int. J. Fatigue 2022, 161, 106905. [Google Scholar] [CrossRef]
- Gomes, V.M.; Fiorentin, F.K.; Dantas, R.; Silva, F.G.; Correia, J.A.; de Jesus, A.M. Probabilistic Modelling of Fatigue Behaviour of 51CrV4 Steel for Railway Parabolic Leaf Springs. Metals 2025, 15, 152. [Google Scholar] [CrossRef]
- Omar, M.A.; Shabana, A.A.; Mikkola, A.; Loh, W.Y.; Basch, R. Multibody system modeling of leaf springs. J. Vib. Control. 2004, 10, 1601–1638. [Google Scholar] [CrossRef]
- Atig, A.; Ben Sghaier, R.; Seddik, R.; Fathallah, R. A simple analytical bending stress model of parabolic leaf spring. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2018, 232, 1838–1850. [Google Scholar] [CrossRef]
- Hassan, T.; Liu, Z. On the difference of fatigue strengths from rotating bending, four-point bending, and cantilever bending tests. Int. J. Press. Vessel. Pip. 2001, 78, 19–30. [Google Scholar] [CrossRef]
- Gomes, V.M.; Souto, C.D.; Correia, J.A.; de Jesus, A.M. Monotonic and Fatigue Behaviour of the 51CrV4 Steel with Application in Leaf Springs of Railway Rolling Stock. Metals 2024, 14, 266. [Google Scholar] [CrossRef]
- EN1993-1-9; Eurocode 3: Design of Steel Structures—Part 1–9: Fatigue. European Commission Standard: Brussels, Belgium, 2005.
- Basquin, O.H. The exponential law of endurance tests. Proc. Am. Soc. Test. Mater. 1910, 10, 625–630. [Google Scholar]
- Castillo, E.; Fernández-Canteli, A. A Unified Statistical Methodology for Modeling Fatigue Damage; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 6th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- ASTM E732-9. Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data. Annu. Book Astm Stand. 2004, 1, 1–7. [Google Scholar]
- Strzelecki, P. Determination of fatigue life for low probability of failure for different stress levels using 3-parameter Weibull distribution. Int. J. Fatigue 2021, 145, 106080. [Google Scholar] [CrossRef]
- Ai, Y.; Zhu, S.; Liao, D.; Correia, J.; Souto, C.; De Jesus, A.; Keshtegar, B. Probabilistic modeling of fatigue life distribution and size effect of components with random defects. Int. J. Fatigue 2019, 126, 165–173. [Google Scholar] [CrossRef]
- Li, H.; Wen, D.; Lu, Z.; Wang, Y.; Deng, F. Identifying the probability distribution of fatigue life using the maximum entropy principle. Entropy 2016, 18, 111. [Google Scholar] [CrossRef]
- Rathod, V.; Yadav, O.P.; Rathore, A.; Jain, R. Probabilistic modeling of fatigue damage accumulation for reliability prediction. J. Qual. Reliab. Eng. 2011, 2011. [Google Scholar] [CrossRef]
- Doh, J.; Lee, J. Bayesian estimation of the lethargy coefficient for probabilistic fatigue life model. J. Comput. Des. Eng. 2018, 5, 191–197. [Google Scholar] [CrossRef]
- Chabod, A.; Czapski, P.; Aldred, J.; Munson, K. Probabilistic fatigue and reliability simulation. Procedia Struct. Integr. 2019, 19, 150–167. [Google Scholar] [CrossRef]
- Wu, Y.L.; Zhu, S.P.; Liao, D.; Correia, J.A.; Wang, Q. Probabilistic fatigue modeling of notched components under size effect using modified energy field intensity approach. Mech. Adv. Mater. Struct. 2022, 29, 6379–6389. [Google Scholar] [CrossRef]
- Castillo, E.; Galambos, J. Lifetime regression models based on a functional equation of physical nature. J. Appl. Probab. 1987, 24, 160–169. [Google Scholar] [CrossRef]
- Castillo, E.; Fernández-Canteli, A.; Ruiz-Tolosa, J.; Sarabia, J. Statistical models for analysis of fatigue life of long elements. J. Eng. Mech. 1990, 116, 1036–1049. [Google Scholar] [CrossRef]
- Castillo, E.; Fernández-Canteli, A. A General Regression Model for Lifetime Evaluation and Prediction. Int. J. Fract. 2001, 107, 117–137. [Google Scholar] [CrossRef]
- Castillo, E.; López-Aenlle, M.; Ramos, A.; Fernández-Canteli, A.; Kieselbach, R.; Esslinger, V. Specimen Length Effect on Parameter Estimation in Modelling Fatigue Strength by Weibull Distribution. Int. J. Fatigue 2006, 28, 1047–1058. [Google Scholar] [CrossRef]
- Castillo, E.; Fernández-Canteli, A.; Ruiz-Ripoll, M.L. A General Model for Fatigue Damage Due to Any Stress History. Int. J. Fatigue 2008, 30, 150–164. [Google Scholar] [CrossRef]
- Correia, J. An Integral Probabilistic Approach for Fatigue Lifetime Prediction of Mechanical and Structural Components. Ph.D. Thesis, Faculty of Engineering of the University of Porto, Porto, Portugal, 2014. [Google Scholar]
- Apetre, N.; Arcari, A.; Dowling, N.; Iyyer, N.; Phan, N. Probabilistic model of mean stress effects in strain-life fatigue. Procedia Eng. 2015, 114, 538–545. [Google Scholar] [CrossRef]
- Fernández-Canteli, A.; Przybilla, C.; Nogal, M.; Aenlle, M.L.; Castillo, E. ProFatigue: A software program for probabilistic assessment of experimental fatigue data sets. Procedia Eng. 2014, 74, 236–241. [Google Scholar] [CrossRef]
- ISO 4287; “Geometrical Product Specifications (gps)—Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 1997.
- UIC517; Wagons—Suspension Gear—Standardisation. The International Union of Railways: Paris, France, 2007.
- ISO 6892-1; Metallic Materials-Tensile Testing-Part 1: Method of Test at Ambient Temperature. ISO: Geneva, Switzerland, 2009.
- Lee, C.; Lee, K.; Li, D.; Yoo, S.; Nam, W. Microstructural influence on fatigue properties of a high-strength spring steel. Mater. Sci. Eng. 1998, 241, 30–37. [Google Scholar] [CrossRef]
- ISO 7438; Metallic Materials: Bend Test. ISO: Geneva, Switzerland, 2005.
- ASTM E466; Standard Practice For Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials. Book of Standards; ASTM: Commonwealth, PA, USA, 2021; Volume 03.01, p. 7. [CrossRef]
- ASTM E606; Standard Test Method for Strain-Controlled Fatigue Testing. Annual Book of ASTM Standards; ASTM: Commonwealth, PA, USA, 1998; pp. 1–15.
- ISO 1143; Metallic Materials—Rotating Bar Bending Fatigue Testing. ISO: Geneva, Switzerland, 2010.
- Dowling, N.E. Mean Stress Effects in Stress-Life and Strain-Life Fatigue. Technical Report; SAE Technical Paper. 2004. Available online: https://www.sae.org/publications/technical-papers/content/2004-01-2227/ (accessed on 6 March 2025).
- Gomes, V.M.; Lesiuk, G.; Correia, J.A.; De Jesus, A.M. Fatigue Crack Propagation of 51CrV4 Steels for Leaf Spring Suspensions of Railway Freight Wagons. Materials 2024, 17, 1831. [Google Scholar] [CrossRef]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions; Elsevier Science: Amsterdam, The Netherlands, 2002. [Google Scholar]
Figure 2.
Microstructure of the chromium–vanadium alloyed steel found for all tested specimens using optical microscopy after surface etching with 2% nitric acid solution (Reprinted from Ref. [
35]).
Figure 3.
Representation of the three-point in-plane bending fatigue testing machine, its structure, and testing specimen.
Figure 4.
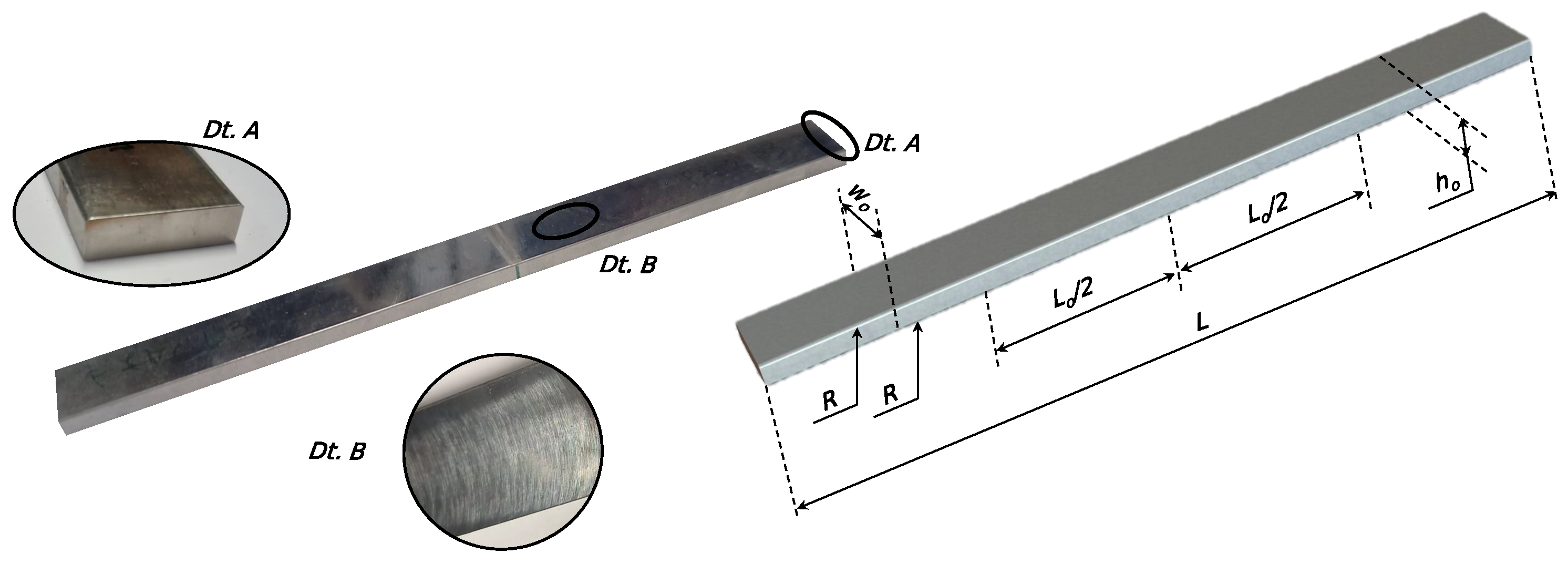
Geometry of the fatigue specimen for three-point in-plane bending testing: left: sample of the actual specimen showing the details of the round corners (Dt. A) and the finishing after milling (Dt. B); right: rendered image of the CAD model showing the dimensions for definition of the specimen geometry.
Figure 5.
Representation of the alternating axial tensile fatigue testing machine, its structure, and testing specimen.
Figure 6.
Geometry of the smooth fatigue specimen for axial tension: left: sample showing details (Dt. A) of the finishing in the analysis zone: Dt. A—machined; right: rendered image of the CAD model showing the dimensions for definition of the specimen geometry.
Figure 7.
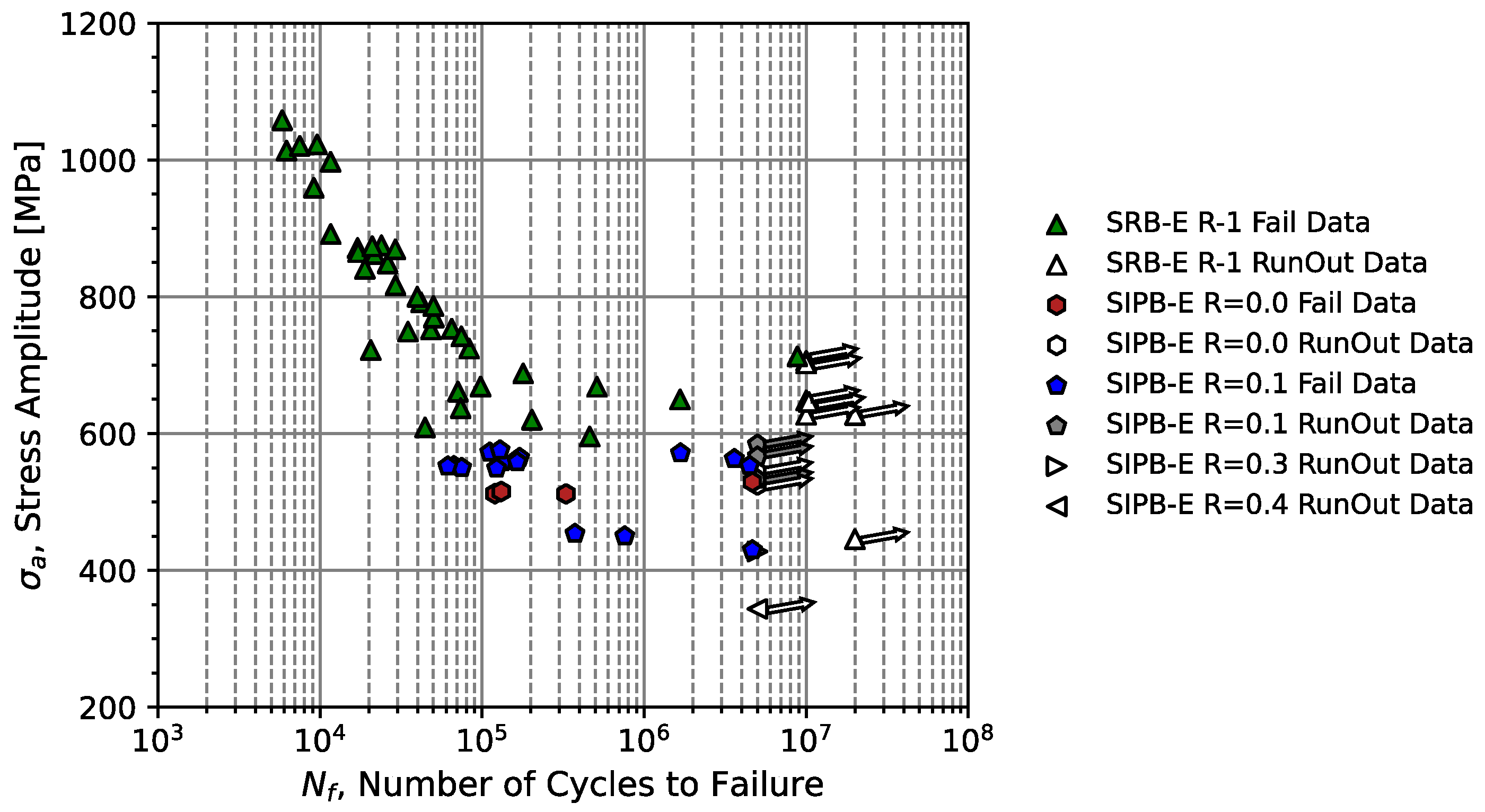
Data pool of fatigue failures and run-outs for specimens tested under rotating and three-point in-plane bending fatigue loadings at different stress ratios. (R—stress ratio, SRB—specimen under rotating bending; SIPB—specimen under in-plane bending; E—elastic regime).
Figure 8.
Data pool of fatigue failures and run-outs for specimens tested under uniaxial tension/compression fatigue loadings at different stress ratios. (R—stress ratio, SAT—specimen under subsonic axial tension; UAT—specimen under ultrasonic axial tension; E—elastic regime; EP—elasto-plastic regime).
Figure 9.
Walker regression and percentile curves of the normal distribution model considering different stress ratios under bending loading. (R—stress ratio; —probability of failure; SRB—specimen under rotating bending; SIPB—specimen under three-point in-plane bending; E—elastic regime; Avg.—average; Dist.—distribution).
Figure 10.
Walker regression and percentile curves of the normal distribution model considering different stress ratios with axial tension/compression loading. (R—stress ratio; —probability of failure; SAT—specimen under subsonic axial tension/compression; UAT—specimen under ultrasonic axial tension/compression; E—elastic conditions; EP—elasto-plastic conditions); Avg.—average; Dist.—distribution.
Figure 11.
PSN field using the ACFC fatigue model considering the mean stress effect due to bending loading conditions. (R—stress ratio; —probability of failure; Est.—estimation for run-out data; RB—specimens under rotating bending (elastic conditions); IPB—specimens under three-point in-plane bending (elastic conditions); Avg.—average; Dist.—distribution, 3p—3 parameters).
Figure 12.
Probabilistic field using the hyperbolic fatigue model considering the mean stress effect due to tensile conditions from low-cycle regime to very high-cycle regime. (R—stress ratio; —probability of failure; Est.—estimation for run-out data; AT (150 Hz)—specimens under axial tension/compression at 150 Hz (elastic conditions); AT (20 kHz)—specimens under axial tension/compression at 20 kHz (elastic conditions); AT (LCF)—specimens under axial tension (elasto-plastic conditions); AT (HCF)—specimens under axial tension (elastic conditions); Avg.—average; Dist.—distribution, 3p—3 parameters).
Figure 13.
Probabilistic field using the extended ACFC fatigue model for tension/compression loading conditions, considering the mean stress effect and the generalized plastic regime: (A)—full-field and (B)—zoom in the axis. (R—stress ratio; —probability of failure; Est.—estimation for run-out data; AT (150 Hz)—specimens under axial tension/compression at 150 Hz (elastic conditions); AT (20 kHz)—specimens under axial tension/compression at 20 kHz (elastic conditions); AT (LCF)—specimens under axial tension (elasto-plastic conditions); AT (HCF)—specimens under axial tension (elastic conditions); Avg.—average; Dist.—distribution, 3p—3 parameters).
Figure 14.
Walker regression and percentile curves of the normal distribution model considering different stress ratios with axial tensile/compression, axial tensile, and bending loading. (R—stress ratio; —probability of failure; SRB—specimen under subsonic rotating bending; SIPB—specimen under subsonic in-plane bending (elastic conditions); SAT—specimen under subsonic axial tension (elastic conditions); UAT—specimen under ultrasonic axial tension (elastic conditions); SATL—specimen under subsonic axial tension (elasto-plastic conditions); Avg.—average; Dist.—distribution.
Figure 15.
Probabilistic field using the extended hyperbolic fatigue model for bending and tensile loading conditions, considering the mean stress effect and the generalized plastic regime: (A)—full-field and (B)—zoom in the vertical axis. (R—stress ratio; —probability of failure; Est.—estimation for run-out data; AT (150 Hz)—specimens under axial tension at 150 Hz (elastic conditions); AT (20 kHz)—specimens under axial tension at 20 kHz (elastic conditions); AT (LCF)—specimens under axial tension (elasto-plastic conditions); AT (HCF)—specimens under axial tension (elastic conditions); RB—specimens under rotating bending at 25 Hz (elastic conditions); IPB—specimens under three-point in-plane bending at 23 Hz (elastic conditions); Avg.—average; Dist.—distribution; 3p—3 parameters).
Figure 16.
Representation of the fracture surface of the rectangular section specimens tested under three-point in-plane bending conditions for a = 515 MPa, = 498 MPa, and .
Figure 17.
Fracture surfaces obtained for different combinations of stress amplitudes and mean stresses under uniaxial loading conditions: (A) = 580 MPa = 710 MPa, (B) = 565 MPa = 690 MPa, (C) = 475 MPa = 580 MPa, (D) = 440 MPa = 540 MPa, (E) = 420 MPa = 515 MPa, and (F) = 420 MPa = 780 MPa.
Figure 18.
Magnification of the fracture surface obtained for case
Figure 17C (
= 475 MPa,
= 580 MPa): left—identification of the initiation zone; right—crack initiation zone from a non-metallic inclusion and formation of a FGA zone.
Table 1.
Standard chemical composition of 51CrV4 steel grade in % wt [
35].
| Material | C | Fe | Si | Mn | Cr | V | S | Pb |
|---|
| 51CrV4 (EN 1.815) | 0.47–0.55 | 96.45–97.38 | ≤0.40 | 0.70–1.10 | 0.90–1.20 | ≤0.10–0.25 | ≤0.025 | ≤0.025 |
Table 2.
Monotonic mechanical properties of the chromium–vanadium alloyed steel, 51CrV4, obtained from ISO 6892-1 standard [
35,
58].
| E [GPa] | [MPa] | [MPa] | [%] | [%] |
|---|
Average
Std. Dev.
[35] | | | | | |
| DIN 51CrV4 (1.8159) | 200 | 1200 | 1350–1650 | 6 | 30 |
Table 3.
Average dimensions of specimens used in three-point in-plane bending fatigue testing according to ISO 7438 standard [
60].
| [mm] | [mm] | | [mm] | L [mm] | R [mm] | [m] |
|---|
| 6.51 ± 0.048 | 22.05 ± 0.058 | 506.97 | 150 | 200 | 1 | 0.664 ± 0.191 |
Table 4.
Average dimensions of smooth specimens used in tensile fatigue test according to ASTM E466-21 standard [
61].
| [mm] | [mm2] | [mm] | R [mm] | Thread [mm] | L [mm] | [mm] | [m] |
|---|
| 3.98 ± 0.24 | 12.41 ± 0.15 | 10 | 75 | M12 | 92 | 20 | 1.075 ± 0.610 |
Table 5.
Summary of the regression models considering the effect of mean stress on bending (rotating bending plus three-point in-plane bending), tension/compression, and tensile fatigue testing data using Walker’s model (Equation (
3)). (IPB—three-point in-plane bending bending; AT—axial tension/compression; RB—rotating bending).
| Fatigue Regime | HCF | LCF + HCF + VHCF | LCF + HCF + VHCF |
|---|
| Testing Conditions
| IPB + RB
| AT
| IPB + RB + AT
|
|---|
| Strength Coefficient, | 3623.26 | 2543.30 | 2282.52 |
| Strength Exponent, | −0.1419 | −0.0886 | −0.0888 |
| Coefficient of Determination, | 0.5729 | 0.6776 | 0.4593 |
| Walker Parameter, | 0.1430 | 0.7758 | 0.5807 |
| Mean Square Error, | 0.2763 | 0.5995 | 0.7221 |
| Coefficient of Interception, | 25.09 | 38.44 | 37.81 |
| Coefficient of Slope 1, | −7.046 | −11.28 | −11.26 |
| Coefficient of Slope 2, | −1.008 | −8.756 | −6.537 |
| Average Ind. Var1, , | 2.834 | 2.772 | 2.802 |
| Std.Ind. Var1, , | 0.102 | 0.010 | 0.106 |
| Average Ind. Var2, , | 0.115 | 0.193 | 0.157 |
| Std.Ind. Var2, , | 0.160 | 0.193 | 0.182 |
| Average Dep. Var, , | 4.965 | 5.463 | 5.235 |
| Std. Dep. Var, , | 0.789 | 1.342 | 1.146 |
Table 6.
Summary of the estimators for ACFC fatigue model on specimens under bending and tension conditions, considering the
fatigue parameter (Equation (
11)). (IPB—three-point in-plane bending bending; AT—axial tension/compression; RB—rotating bending).
| Fatigue Regime | HCF | LCF + HCF + VHCF | LCF + HCF + VHCF | LCF + HCF + VHCF |
|---|
| Testing | Elastic | Elastic | Elasto-Plastic | Elasto-Plastic |
| Conditions | IPB + RB | AT | AT | IPB + RB + AT |
| Dowling Par., | 0.8570 | 0.2242 | 0.2242 | 0.4193 |
| Vert. Asymptote, B | 0.00 (1 [cycle]) | 0.00 (1 [cycle]) | 0.00 (1 [cycle]) | 0.00 (1 [cycle]) |
| Hor. Asymptote, C | −2.47 (0.08 [%]) | −1.87 (0.15 [%]) | −1.90 ( 0.15 [%]) | −2.00 (0.14 [%]) |
| Shape Par., | 1.23 | 3.15 | 3.07 | 1.98 |
| Scale Par., | 4.27 | 7.36 | 7.08 | 6.26 |
| Location Par., | 13.49 | 6.09 | 6.48 | 8.22 |
| Avg. Rand. Var. v, | 17.48 | 12.67 | 12.81 | 13.77 |
| Std. Rand. Var.v, | 10.65 | 5.25 | 5.08 | 8.57 |
| Quantile | 16.67 | 12.64 | 12.76 | 13.42 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).