Microscopic Modeling of Interfaces in Cu-Mo Nanocomposites: The Case Study of Nanometric Metallic Multilayers
Abstract
1. Introduction
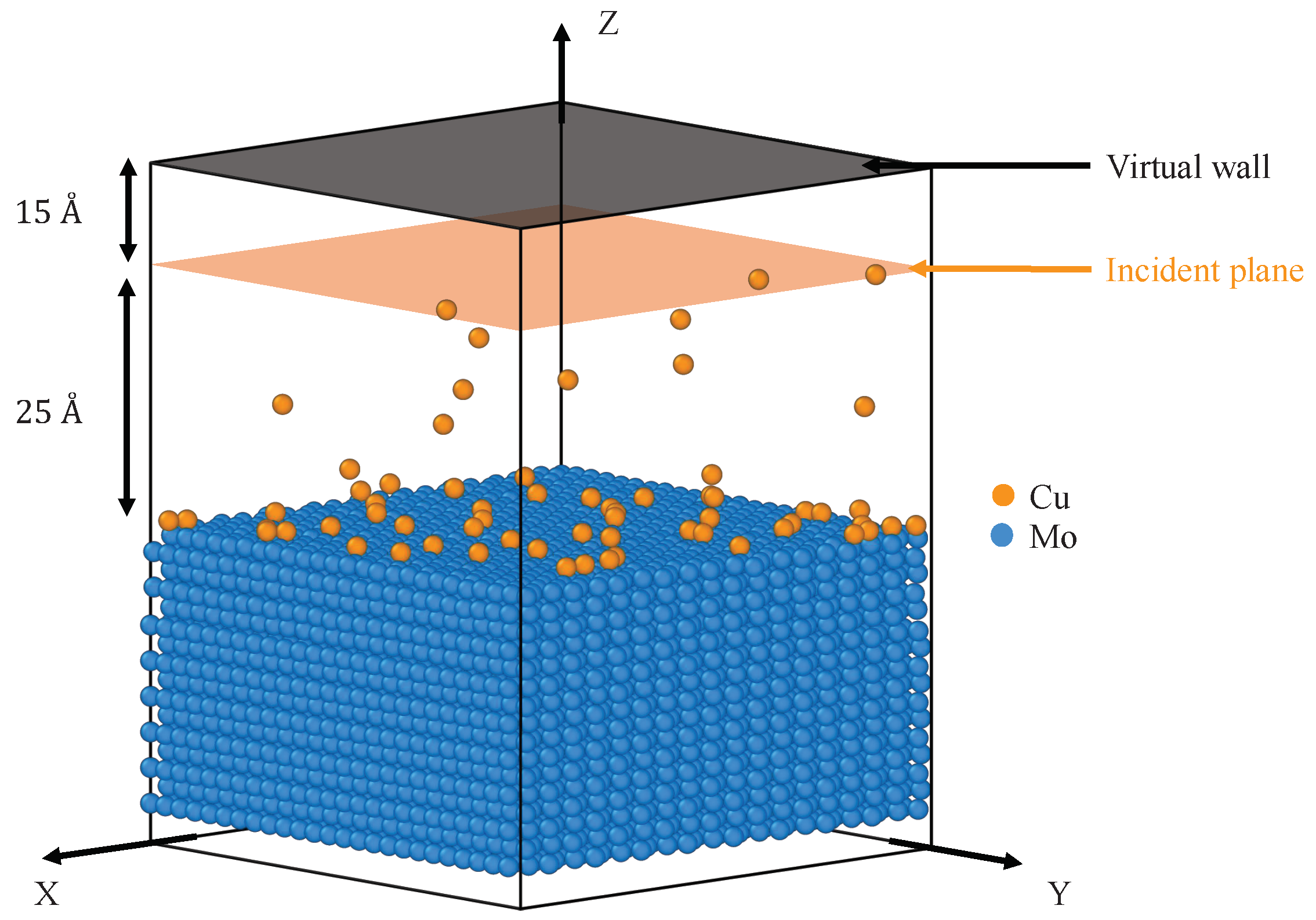
2. Methods
3. Results
3.1. Physical Properties of the Pure Elements in the System
3.1.1. Thermal Expansion
3.1.2. Melting Temperature
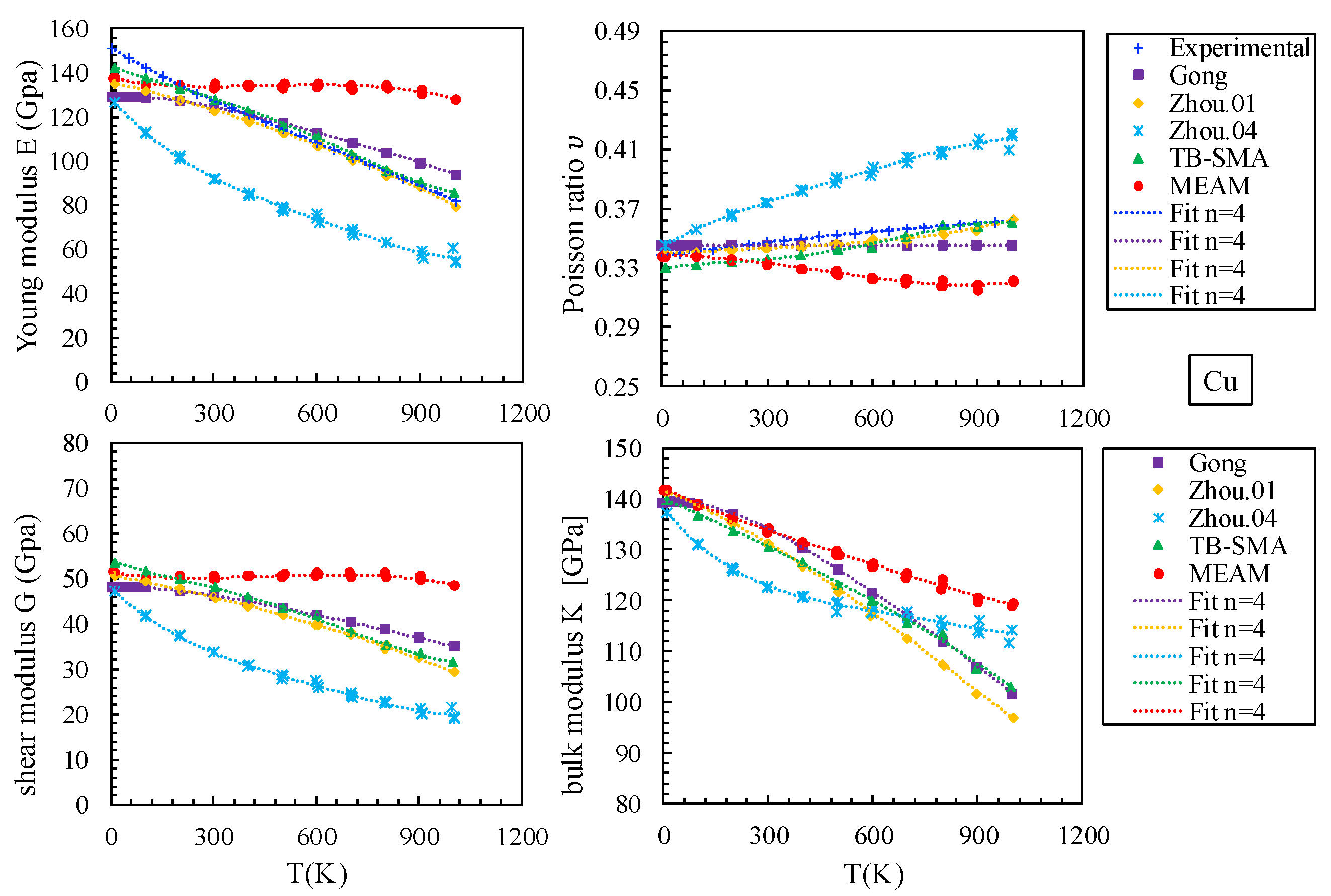
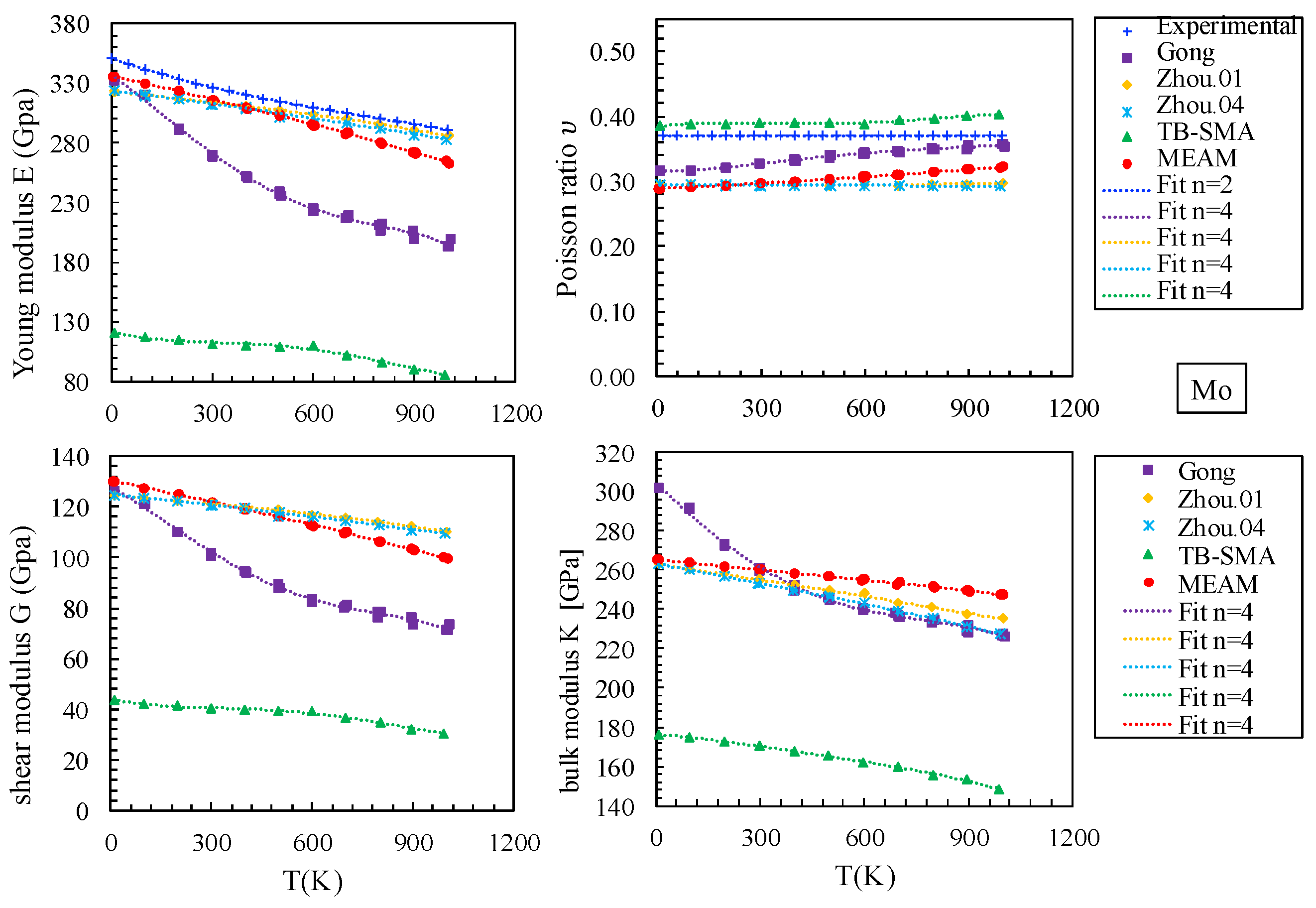
3.1.3. Elastic Constants and Elastic Moduli
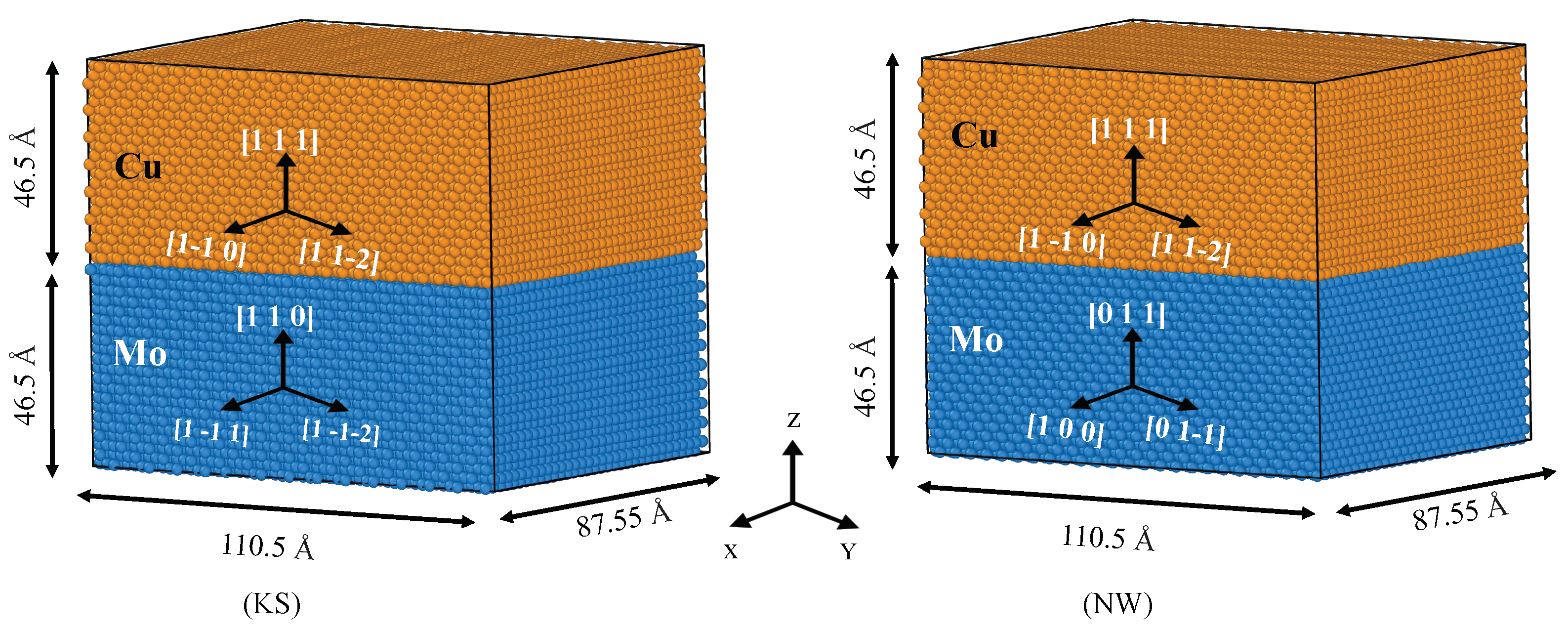
3.2. Modeling of the Cu/Mo Interface
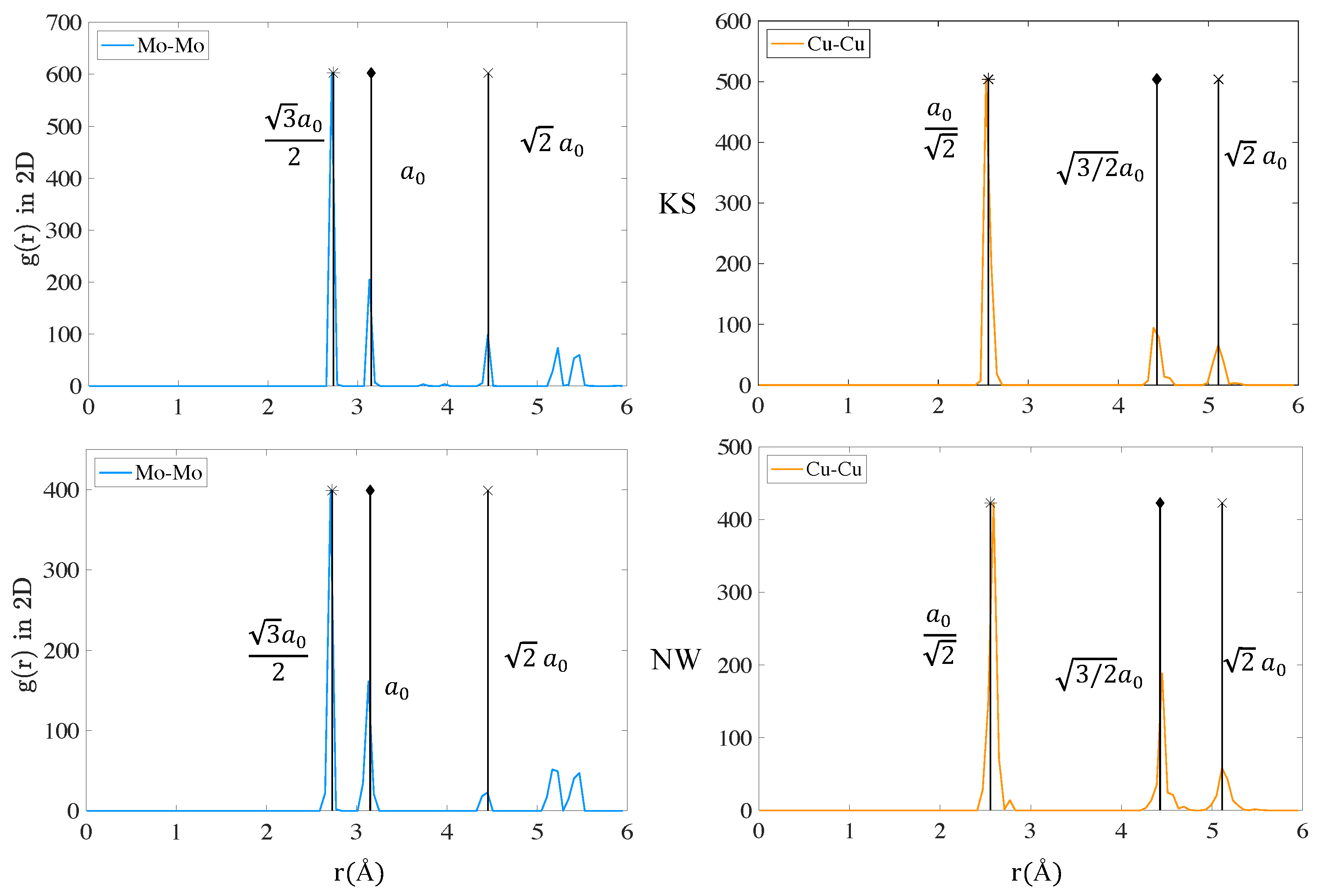
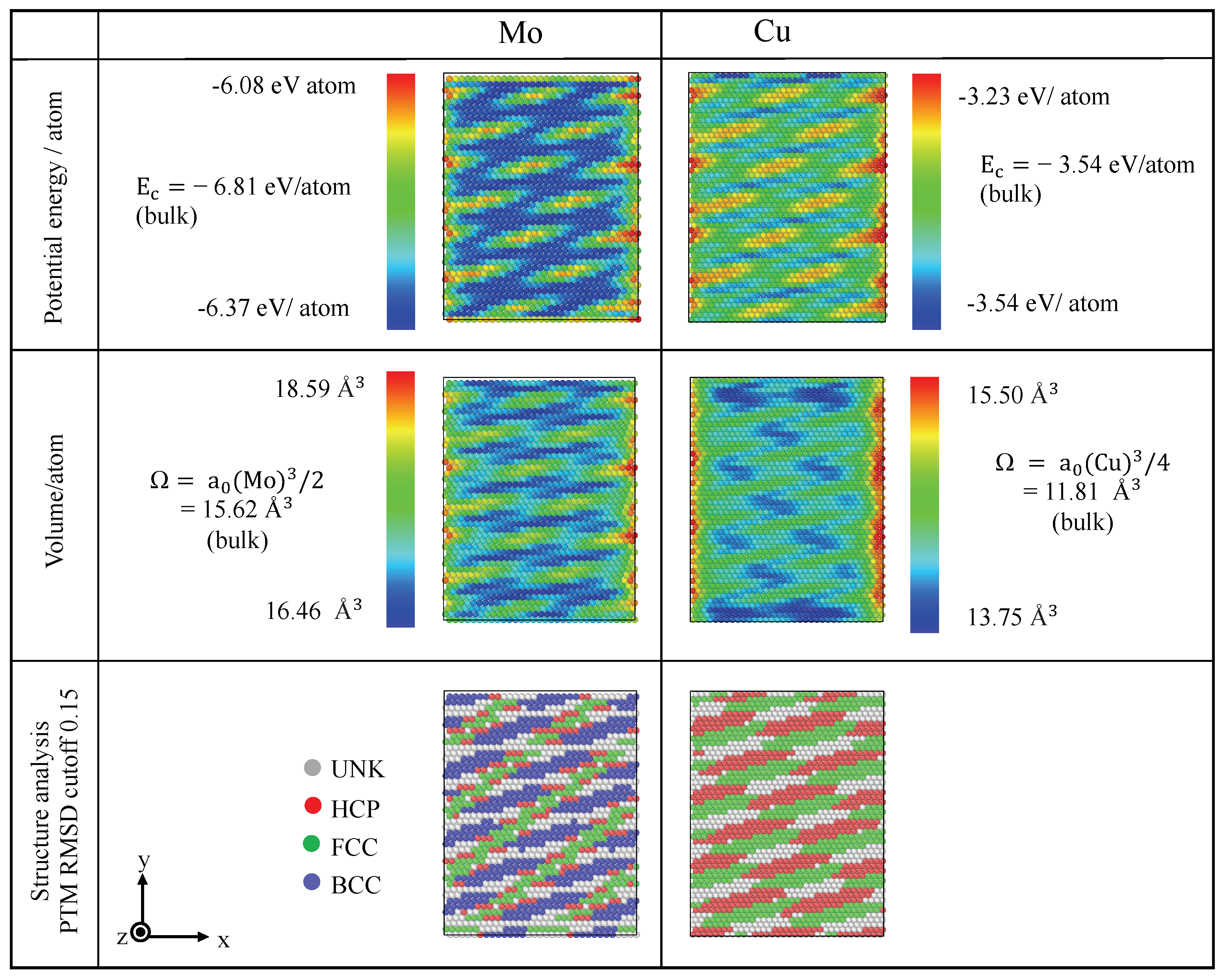
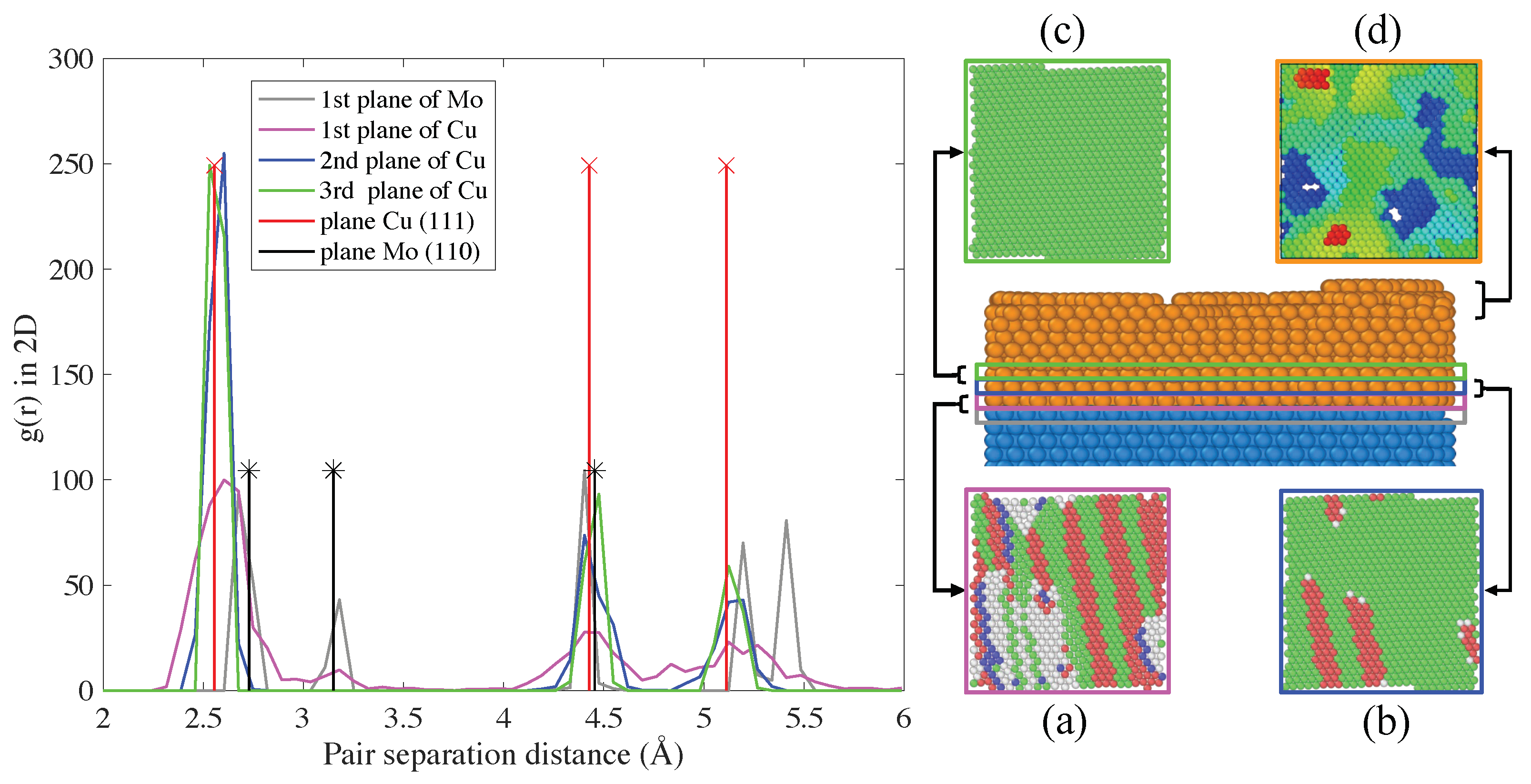
3.2.1. Energy, Atomic Volume and Local Atomic Environment
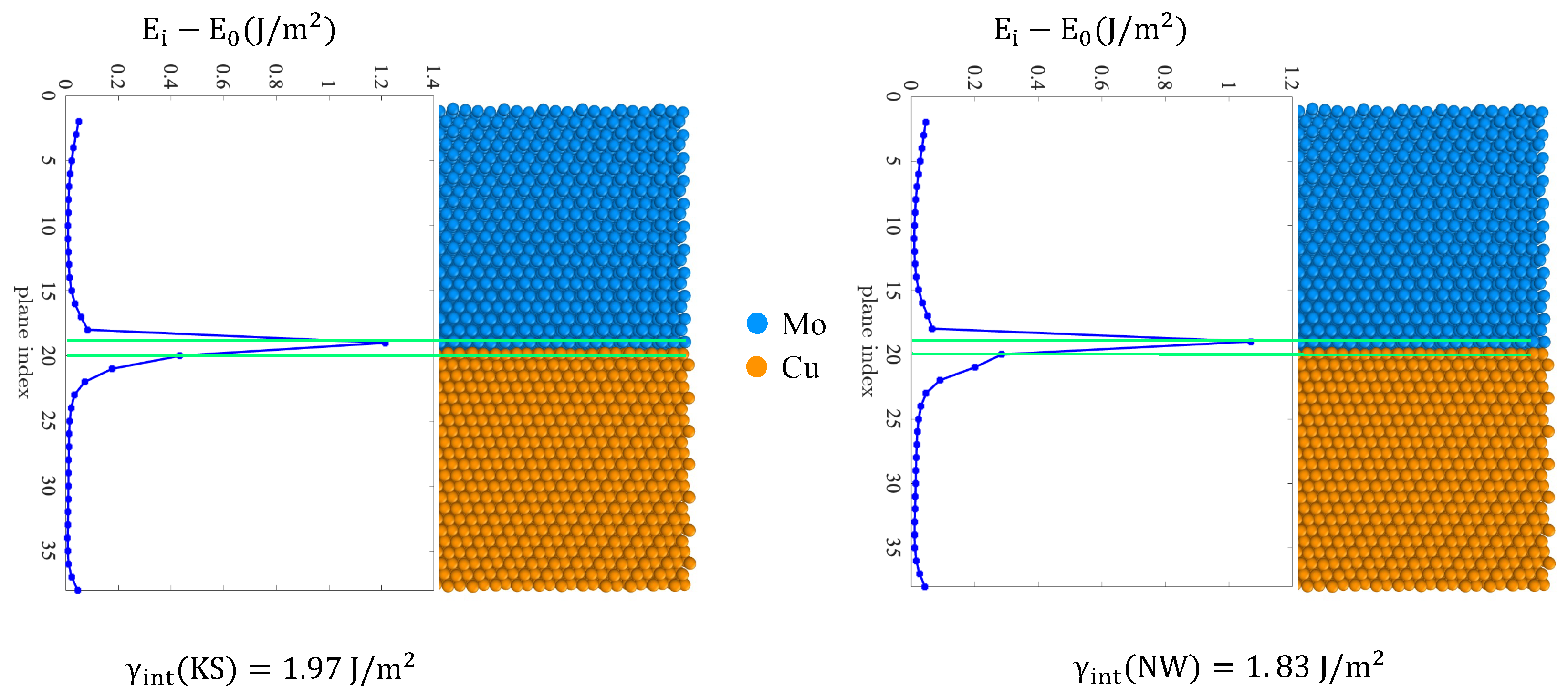
3.2.2. Energy of the Interface
3.2.3. MD Simulation of the Growth of Sputtered Cu Film on Mo Substrate
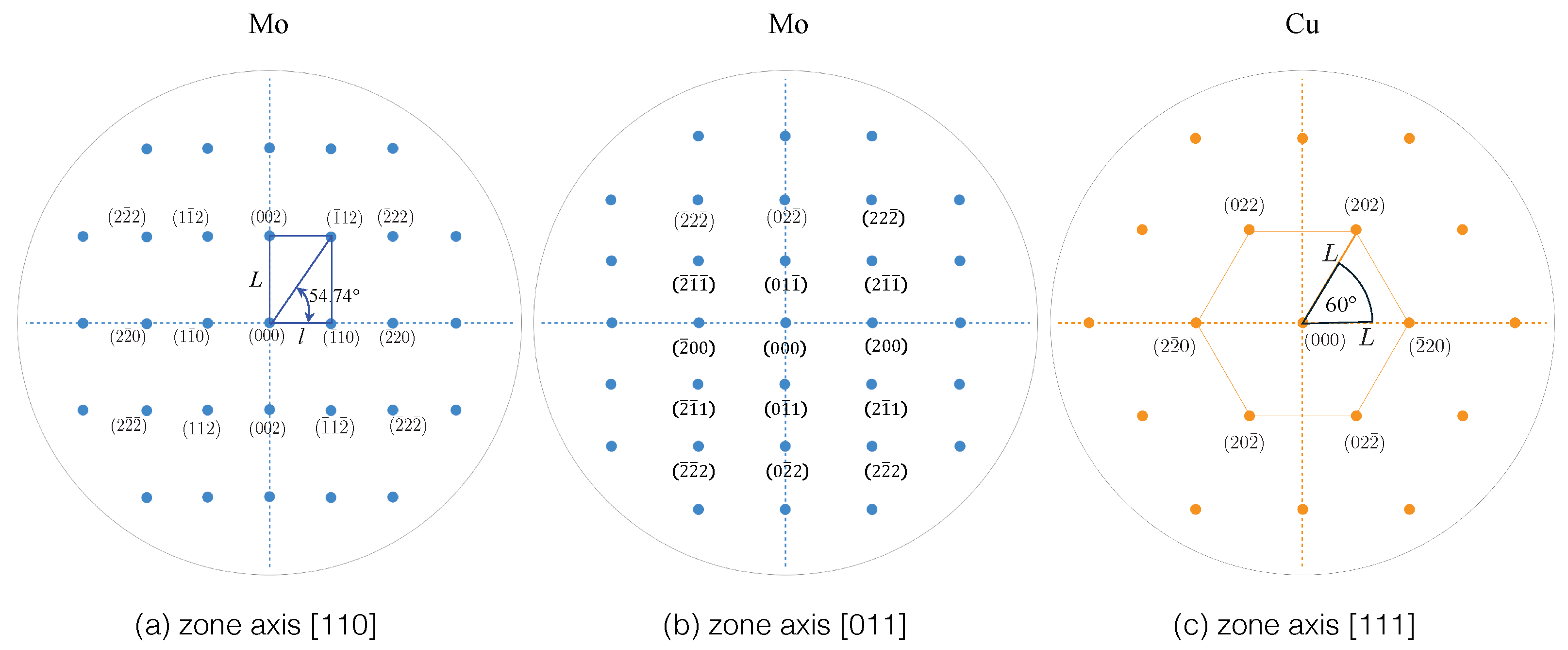
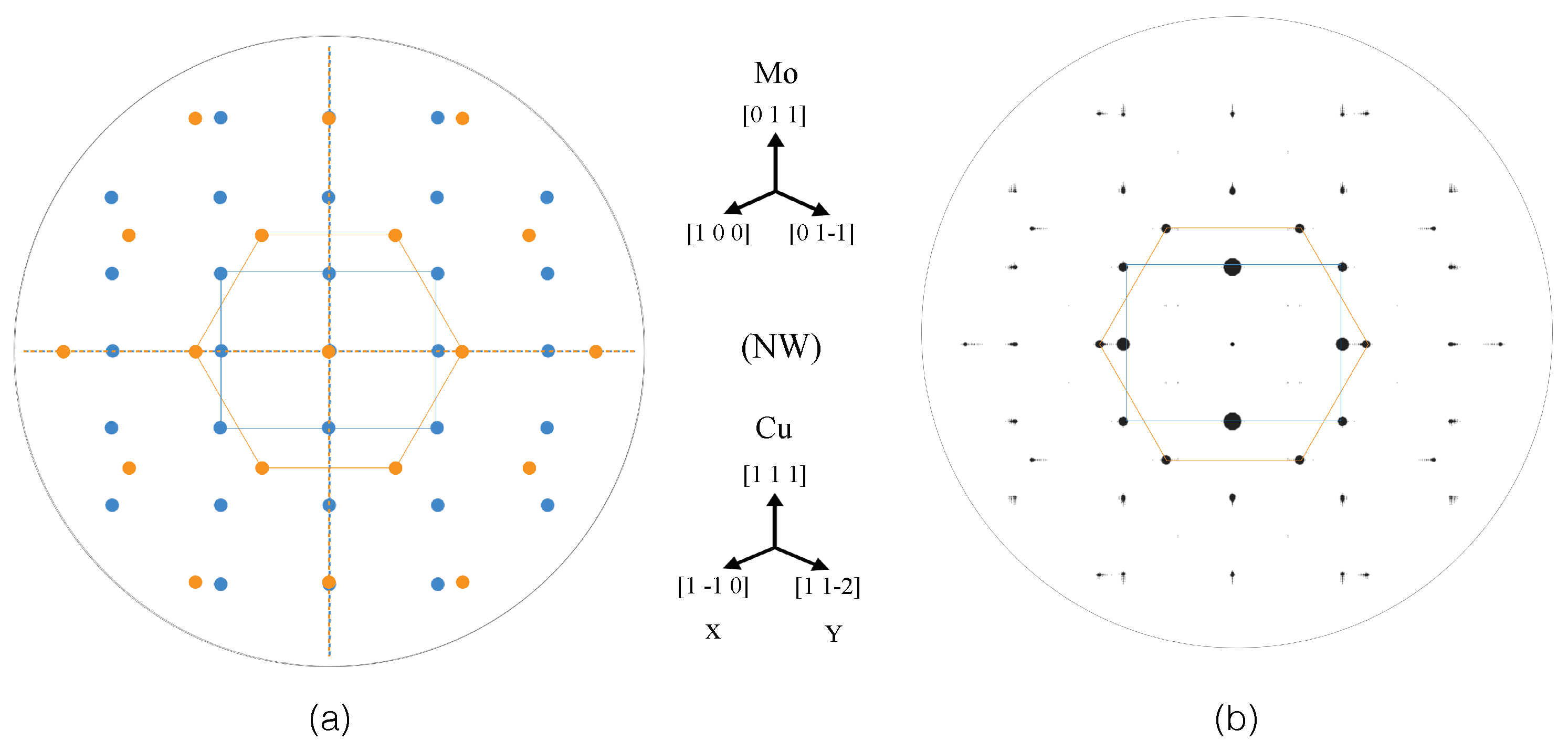
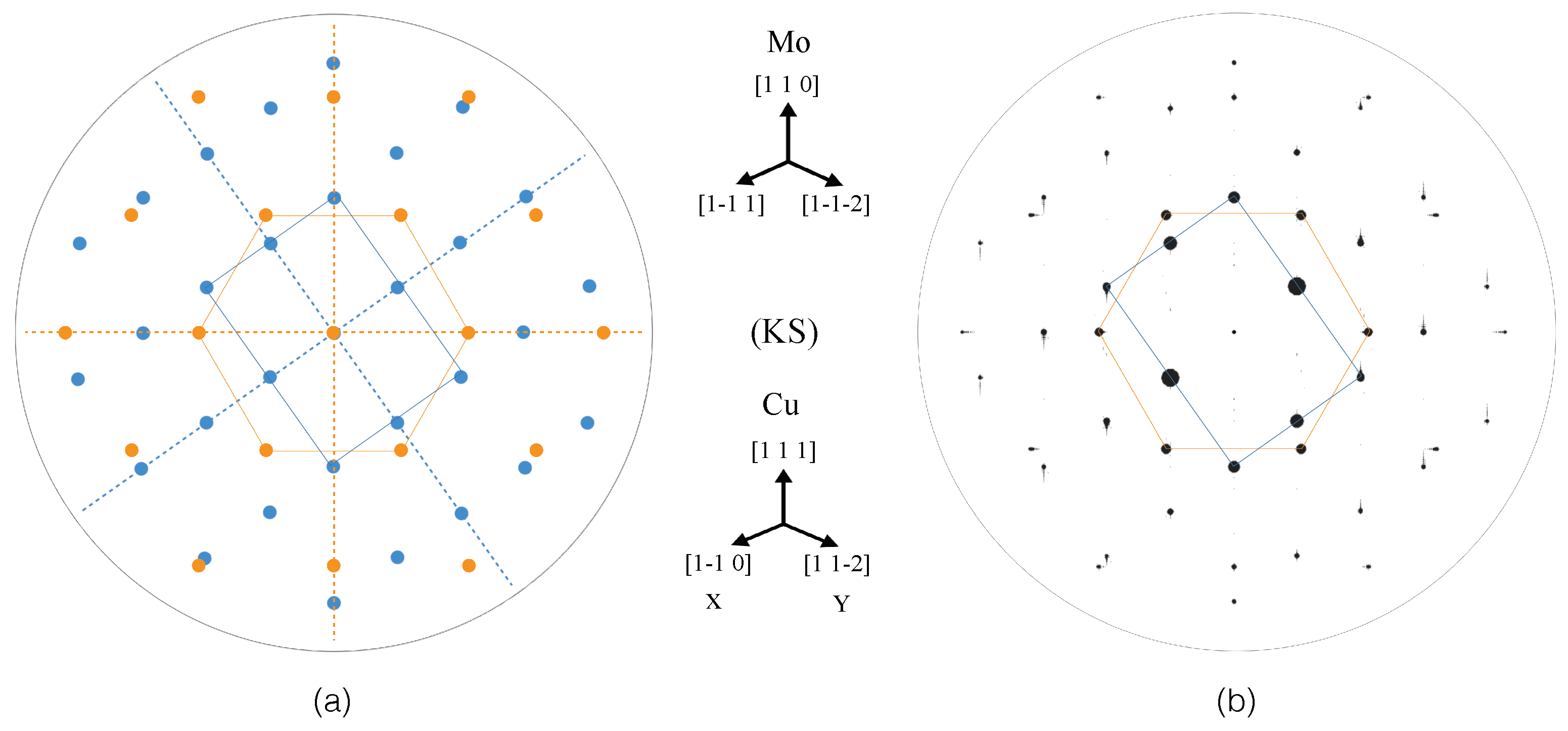
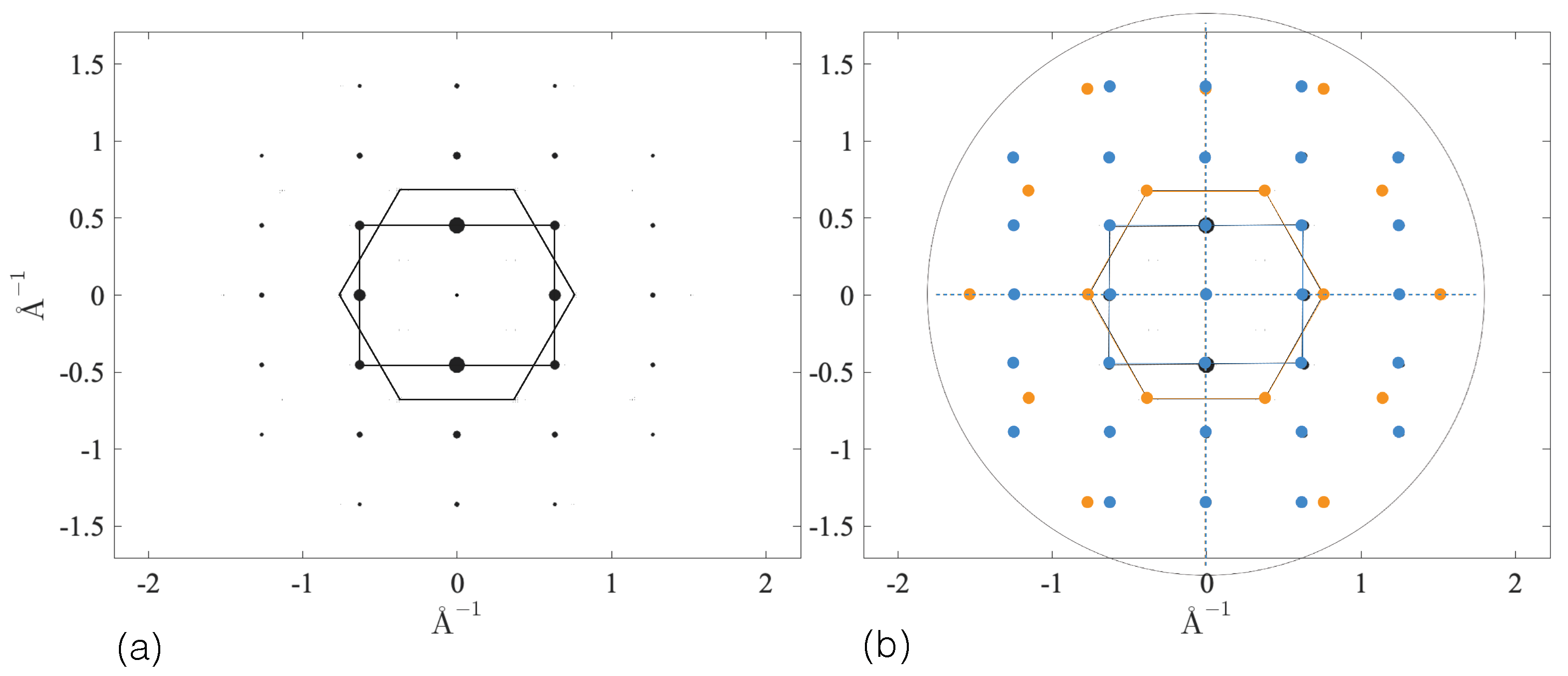
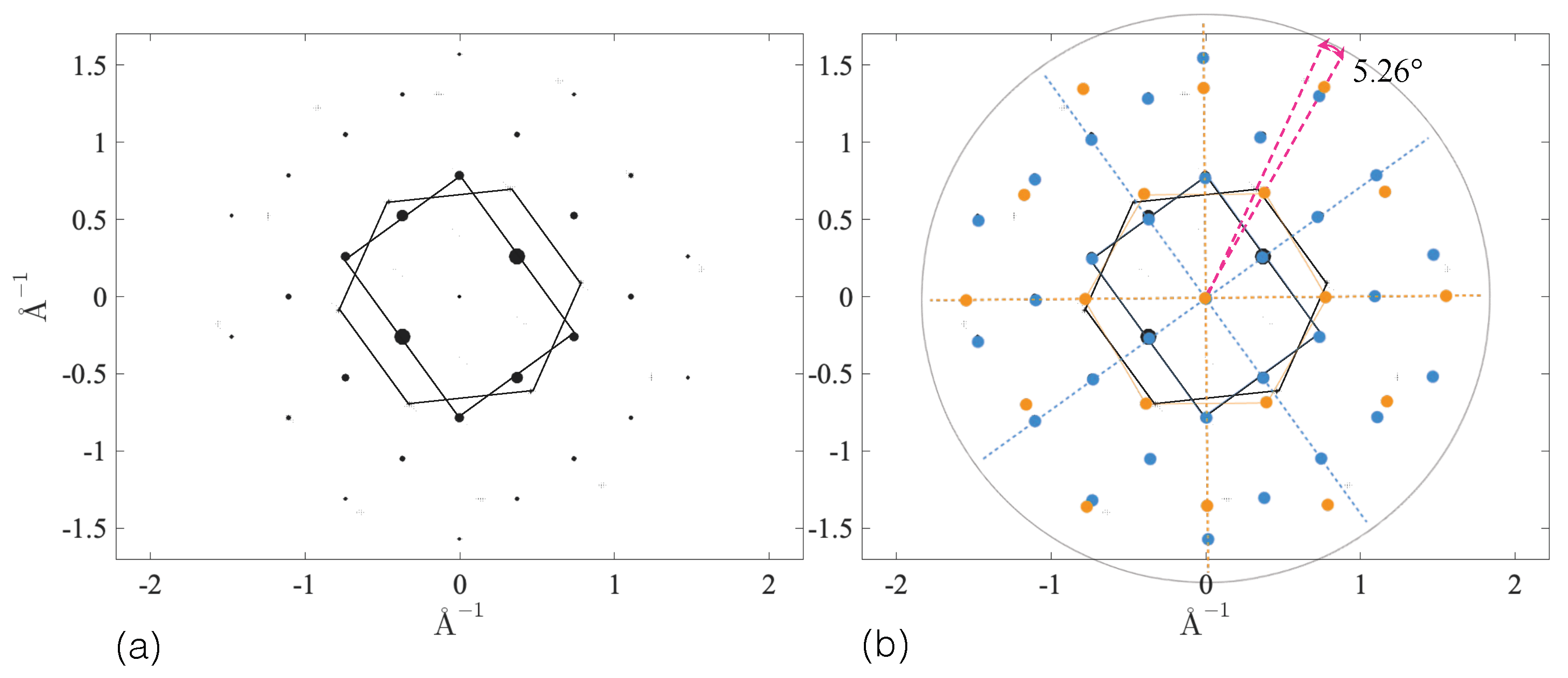
3.2.4. SAED Patterns
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sáenz-Trevizo, A.; Hodge, A.M. Nanomaterials by design: A review of nanoscale metallic multilayers. Nanotechnology 2020, 31, 292002. [Google Scholar] [CrossRef] [PubMed]
- Lewis, A.C.; Josell, D.; Weihs, T.P. Stability in thin film multilayers and microlaminates: The role of free energy, structure, and orientation at interfaces and grain boundaries. Scr. Mater. 2003, 48, 1079–1085. [Google Scholar] [CrossRef]
- Knoedler, H.L.; Lucas, G.E.; Levi, C.G. Morphological stability of copper-silver multilayer thin films at elevated temperatures. Metall. Mater. Trans. 2003, 34A, 1043–1054. [Google Scholar] [CrossRef]
- Ma, Y.J.; Wei, M.Z.; Sun, C.; Cao, Z.H.; Meng, X.K. Length scale effect on the thermal stability of nanoscale Cu/Ag multilayers. Mater. Sci. Eng. A 2017, 686, 142–149. [Google Scholar] [CrossRef]
- Druzhinin, A.V.; Cancellieri, C.; Jeurgens, L.P.H.; Straumal, B.B. The effect of interface stress on the grain boundary grooving in nanomaterials: Application to the thermal degradation of Cu/W nano-multilayers. Scr. Mater. 2021, 199, 113866. [Google Scholar] [CrossRef]
- Moszner, F.; Cancellieri, C.; Chiodi, M.; Yoon, S.; Ariosa, D.; Janczak-Rusch, J.; Jeurgens, L.P.H. Thermal stability of Cu/W nano-multilayers. Acta Mater. 2016, 107, 345–353. [Google Scholar] [CrossRef]
- Troncoso, J.F.; Lorenzin, G.; Cancellieri, C.; Turlo, V. Explaining the effect of in-plane strain on thermal degradation kinetics of Cu/W nano-multilayers. Scr. Mater. 2024, 242, 115902. [Google Scholar] [CrossRef]
- Yeom, J.; Lorenzin, G.; Ghisalberti, L.; Cancellieri, C.; Janczak-Rusch, J. The thermal stability and degradation mechanism of Cu/Mo nanomultilayers. Sci Technol Adv Mater. 2024, 25, 2357536. [Google Scholar] [CrossRef]
- Appleget, C.D.; Riano, J.S.; Hodge, A.M. An Overview of Nano Multilayers as Model Systems for Developing Nanoscale Microstructures. Materials 2022, 15, 382. [Google Scholar] [CrossRef]
- Niu, T.; Zhang, Y.; Cho, J.; Li, J.; Wang, H.; Zhang, X. Thermal stability of immiscible Cu-Ag/Fe triphase multilayers with triple junctions. Acta Mater. 2021, 208, 116679. [Google Scholar] [CrossRef]
- Schweitz, K.O.; Ratzke, K.; Foord, D.; Thomas, P.J.; Greer, A.L.; Geisler, H.; Chevallier, J.; Bottiger, J. The microstructural development of Ag/Ni multilayers during annealing. Phil. Mag. A 2000, 80, 1867–1877. [Google Scholar] [CrossRef]
- Schweitz, K.O.; Bottiger, J.; Greer, A.L.; Thomas, P.J.; Foord, D.T. The mechanism of degradation of Ag/Ni multilayers deposited at different temperatures. Philos. Mag. A 2001, 81, 1–10. [Google Scholar] [CrossRef]
- Baras, F.; Turlo, V.; Politano, O.; Vadchenko, S.G.; Rogachev, A.S.; Mukasyan, A.S. SHS in Ni/Al Nanofoils: A Review of Experiments and Molecular Dynamics Simulations. Adv. Eng. Mater. 2018, 20, 1800091. [Google Scholar] [CrossRef]
- Baloochi, M.; Shekhawat, D.; Riegler, S.S.; Matthes, S.; Glaser, M.; Schaaf, P.; Bergmann, J.P.; Gallino, I.; Pezoldt, J. Influence of Initial Temperature and Convective Heat Loss on the Self-Propagating Reaction in Al/Ni Multilayer Foils. Materials 2021, 14, 7815. [Google Scholar] [CrossRef]
- Politano, O.; Baras, F. Molecular dynamics simulations of self-propagating reactions in Ni–Al multilayer nanofoils. J. Alloys Compd. 2015, 652, 25–29. [Google Scholar] [CrossRef]
- Politano, O.; Baras, F. Reaction front propagation in nanocrystalline Ni/Al composites: A molecular dynamics study. J. Appl. Phys. 2020, 128, 215301. [Google Scholar] [CrossRef]
- Politano, O.; Rogachev, A.S.; Baras, F. Molecular Dynamics Studies in Nanojoining: Self-Propagating Reaction in Ni/Al Nanocomposites. J. Mater. Eng. Perform. 2021, 30, 3160–3166. [Google Scholar] [CrossRef]
- Schwarz, F.; Spolenak, R. Molecular dynamics study of the influence of microstructure on reaction front propagation in Al–Ni multilayers. Appl. Phys. Lett. 2021, 119, 133901. [Google Scholar] [CrossRef]
- Baras, F.; Politano, O.; Li, Y.; Turlo, V. A Molecular Dynamics Study of Ag-Ni Nanometric Multilayers: Thermal Behavior and Stability. Nanomaterials 2023, 13, 2134. [Google Scholar] [CrossRef]
- Lorenzin, G.; Troncoso, J.F.; Liyanage, M.; Druzhinin, A.V.; Jeurgens, L.P.H.; Cancellieri, C.; Turlo, V. Experimental and ab initio derivation of interface stress in nanomultilayered coatings: Application to immiscible Cu/W system with variable in-plane stress. Appl. Surf. Sci. 2024, 661, 159994. [Google Scholar] [CrossRef]
- Wassermann, G. Einflu der—Umwandlung eines irreversiblen Nickelstahls auf Kristallorientierung und Zugfestigkeit. Arch. Eisenhüttenwesen 1933, 6, 347–351. [Google Scholar] [CrossRef]
- Nishiyama, Z. X-ray investigation of the mechanism of the transformation from face centered cubic lattice to body centered cubic. Sci. Rep. Tohoku Univ. 1934, 23, 637. [Google Scholar]
- Kurdjumow, G.; Sachs, G. Über den Mechanismus der Stahlhärtung. Z. Phys. 1930, 64, 325–343. [Google Scholar] [CrossRef]
- Cui, Y.; Derby, B.; Li, N.; Mara, N.A.; Misra, A. Suppression of shear banding in high-strength Cu/Mo nanocomposites with hierarchical bicontinuous intertwined structures. Mater. Res. Lett. 2018, 6, 184. [Google Scholar] [CrossRef]
- Yu-Zhang, K.; Embury, J.D.; Han, K.; Misra, A. Transmission electron microscopy investigation of the atomic structure of interfaces in nanoscale Cu-Nb multilayers. Philos. Mag. 2008, 88, 2559–2567. [Google Scholar] [CrossRef]
- Monclús, M.A.; Karlik, M.; Callisti, M.; Frutos, E.; Lorca, J.L.; Polcar, T.; Molina-Aldareguí, J.M.A. Microstructure and mechanical properties of physical vapor deposited Cu/W nanoscale multilayers: Influence of layer thickness and temperature. Thin Solid Films 2014, 571, 275–282. [Google Scholar] [CrossRef]
- Bodlos, R.; Fotopoulos, V.; Spitaler, J.; Shluger, A.L.; Romaner, L. Energies and structures of Cu/Nb and Cu/W interfaces from density functional theory and semi-empirical calculations. Materialia 2022, 21, 101362. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef]
- Gong, H.R.; Kong, L.T.; Liu, B.X. Metastability of an immiscible Cu-Mo system calculated from first-principles and a derived n-body potential. Phys. Rev. B 2004, 69, 024202. [Google Scholar] [CrossRef]
- Zhou, X.; Johnson, R.A.; Wadley, H.N.G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef]
- Zhou, X.; Johnson, R.A.; Wadley, H.N.G. Atomic scale structure of sputtered metal multilayers. Acta Mater. 2004, 49, 4005–4015. [Google Scholar] [CrossRef]
- Zhou, X.W.; Wadley, H.N.G. Misfit dislocations in gold/Permalloy multilayers. Philos. Mag. 2004, 84, 193–212. [Google Scholar] [CrossRef]
- Wadley, H.; Zhou, X.; Butler, W.H. Atomic Assembly of Magnetoresistive Multilayers; Springer: Berlin/Heidelberg, Germany, 2008; Volume 109, pp. 497–559. [Google Scholar] [CrossRef]
- Karolewski, M.A. Tight-binding potentials for sputtering simulations with fcc and bcc metals, Radiation Effects and Defects in Solids. Radiat. Eff. Defects Solids 2001, 153, 239–255. [Google Scholar] [CrossRef]
- Wang, J.; Lee, B.-J. Second-nearest-neighbor modified embedded-atom method interatomic potential for V-M (M=Cu, Mo, Ti) binary systems. Comput. Mater. Sci. 2021, 188, 110177. [Google Scholar] [CrossRef]
- Oh, S.-H.; Lu, X.-G.; Chen, Q.; Lee, B.-J. Pressure dependence of thermodynamic interaction parameters for binary solid solution phases: An atomistic simulation study. Calphad 2021, 75, 102342. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Kirby, R.K.; Taylor, R.E.; Desai, P.D. Thermophysical properties of matter-the tprc data series. In Thermal Expansion Metallic and Elements and Alloys; Plenum Press: New York, NY, USA, 1975; Volume 12. [Google Scholar]
- Luo, F.; Chen, X.; Cai, L.; Ji, G. Solid–Liquid Interfacial Energy and Melting Properties of Nickel Under Pressure from Molecular Dynamics. J. Chem. Eng. Data Data 2010, 55, 5149–5155. [Google Scholar] [CrossRef]
- Rassoulinejad-Mousavi, S.M.; Mao, Y.; Zhang, Y. Evaluation of copper, aluminum, and nickel interatomic potentials on predicting the elastic properties. J. Appl. Phys. 2016, 119, 244304. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate, Proceedings of the Physical Society. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Simmons, G.; Wang, H.F. Single Crystal Elastic Constants and Calculated Aggregate Properties. In A Handbook, 2nd ed.; M.I.T. Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Bujard, P.; Sanjinés, R.; Walker, E.; Ashkenazi, J.; Peter, M. Elastic constants in Nb-Mo alloys from zero temperature to the melting point: Experiment and theory. J. Phys. Met. Phys. 1981, 11, 775–786. [Google Scholar] [CrossRef]
- ASM Handbook Committee. Properties and Selection: Nonferrous Alloys and Special-Purpose Materials; ASM International: New York, NY, USA, 1952. [Google Scholar] [CrossRef]
- Simon, N.J.; Drexler, E.S.; Reed, R.P. Properties of Copper and Copper Alloys at Cryogenic Temperatures; NIST Monograph: Boulder, CO, USA, 1992. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Li, Z.; Ding, P.; Wang, R.; Wang, C.; Li, Q.; Sun, B.; Zhang, Y. First-principles investigation on the effects of alloying elements on Cu/Mo interface. Chem. Phys. Lett. 2023, 832, 140895. [Google Scholar] [CrossRef]
- Coleman, S.P.; Spearot, D.E.; Capolungo, L. Virtual diffraction analysis of Ni [010] symmetric tilt grain boundaries. Model. Simul. Mater. Sci. Eng. 2013, 21, 055020. [Google Scholar] [CrossRef]

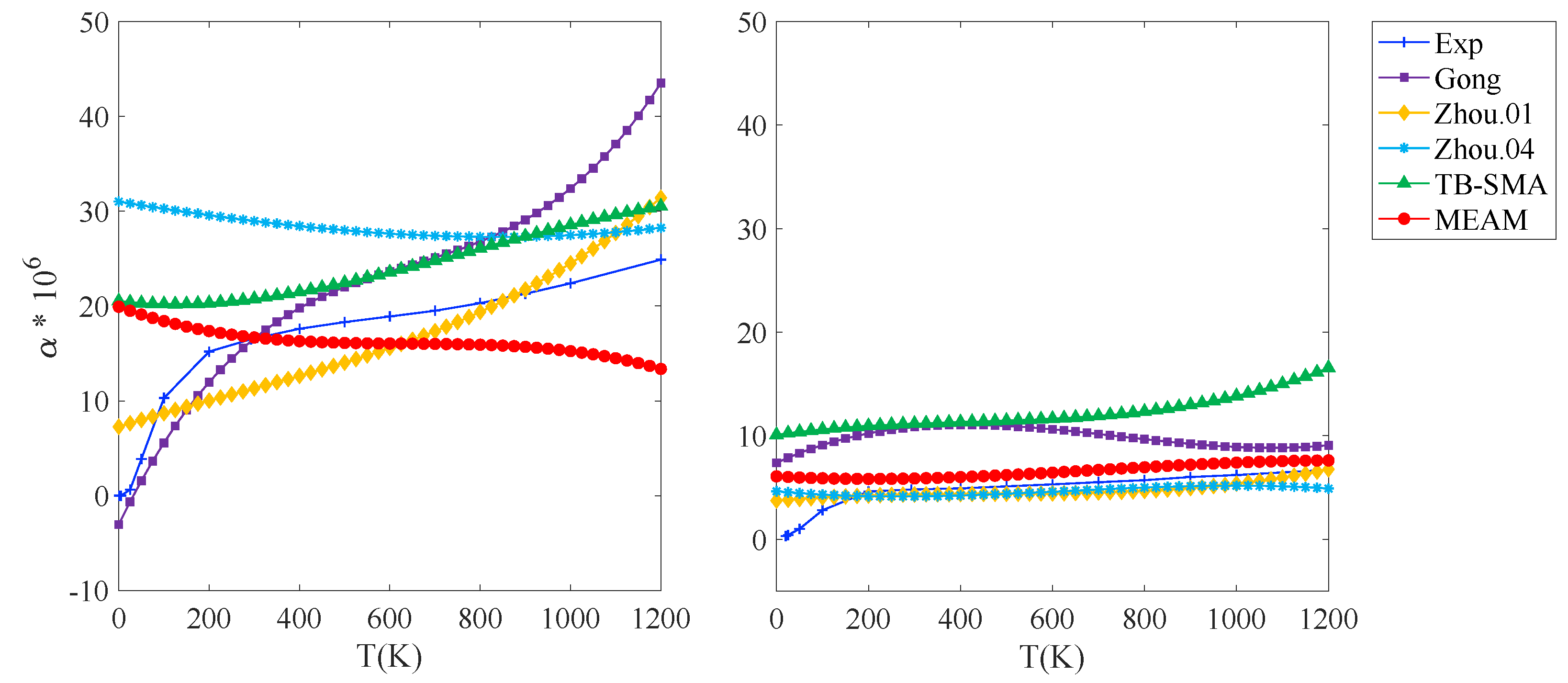
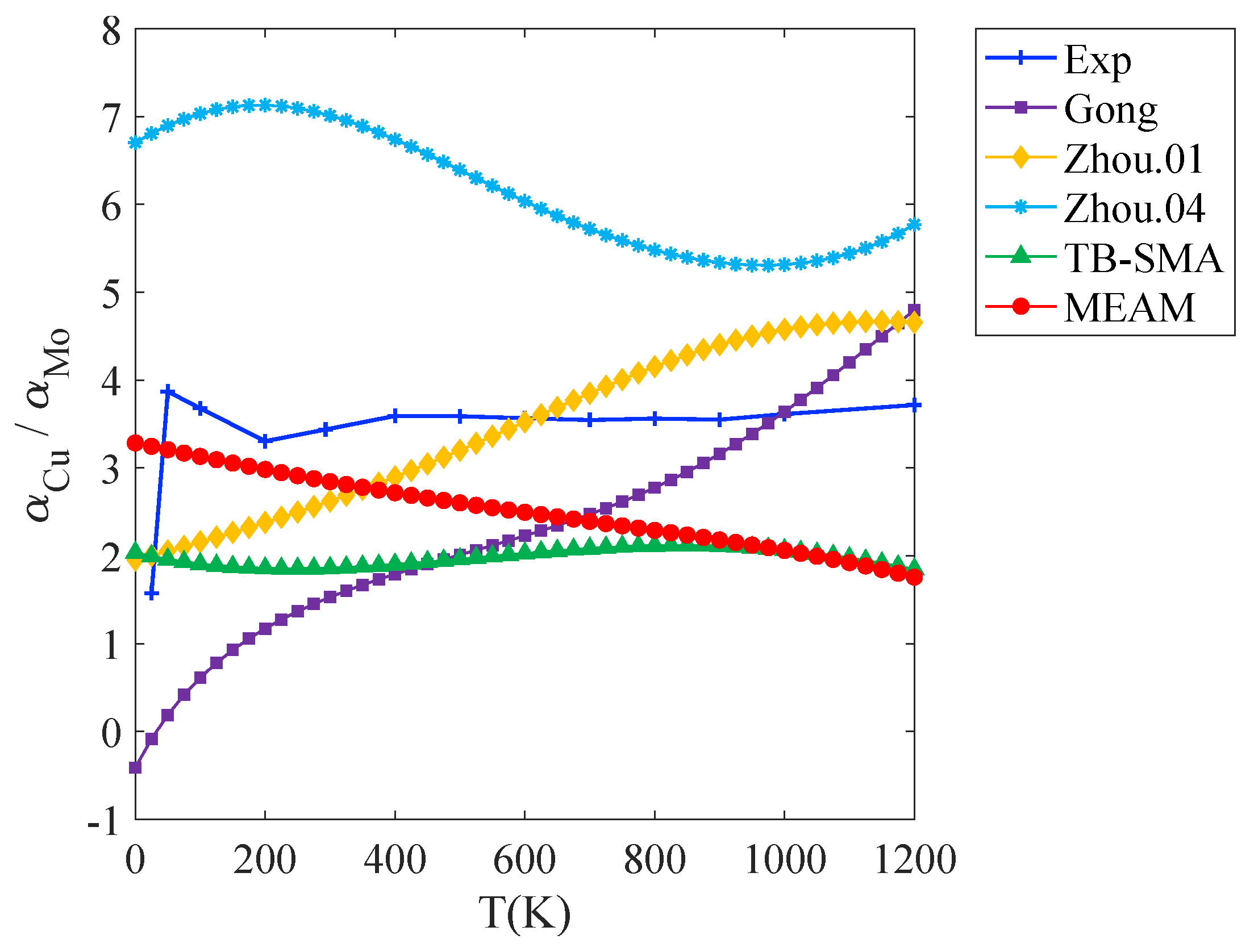

| Potential | Ref | Type | Notation | Performance (ns/Day) |
|---|---|---|---|---|
| Gong et al. | [30] | EAM | Gong | 20.51 |
| Zhou et al. 2001 | [31] | EAM | Zhou.01 | 8.66 |
| Zhou et al. 2004 | [32] | EAM | Zhou.04 | 9.71 |
| M. A. Karolewski et al. | [35] | TB-SMA | TB-SMA | 12.77 |
| J. Wang et al. | [36] | MEAM | MEAM | 0.76 |
| (K) | Cu | Mo | ||
|---|---|---|---|---|
| This Work | Experimental | This Work | Experimental | |
| Gong | 1085 | 3143 | ||
| Zhou.01 | 1131 | 3404 | ||
| Zhou.04 | 1153 | 1358 | 3420 | 2896 |
| TB-SMA | 1332 | 2236 | ||
| MEAM | 1572 | 2778 | ||
| Material | Method | (GPa) | (GPa) | (GPa) | E (GPa) | (GPa) | (GPa) | G (GPa) | K (GPa) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Cu | Experimental | 170 [42] | 122.5 [42] | 75.8 [42] | 128.31 | 54.98 | 40.39 | 47.69 | 138.33 | 0.35 |
| Gong | 170.03 | 122.50 | 75.80 | 128.34 | 54.99 | 40.41 | 47.70 | 138.34 | 0.35 | |
| Zhou.01 | 182.84 | 121.15 | 70.64 | 135.79 | 54.72 | 46.59 | 50.66 | 141.71 | 0.34 | |
| Zhou.04 | 169.62 | 122.13 | 75.74 | 128.21 | 54.94 | 40.38 | 47.66 | 137.96 | 0.35 | |
| TB-SMA | 176.03 | 121.71 | 83.63 | 141.99 | 61.04 | 45.66 | 53.35 | 139.82 | 0.33 | |
| MEAM | 176.13 | 124.90 | 81.76 | 137.67 | 59.30 | 43.56 | 51.43 | 141.98 | 0.34 | |
| Mo | Experimental | 464.7 [43] | 161.5 [43] | 108.9 [43] | 322.20 | 125.98 | 122.73 | 124.35 | 262.57 | 0.30 |
| Gong | 500.18 | 196.94 | 108.92 | 327.55 | 126.00 | 122.75 | 124.37 | 298.02 | 0.32 | |
| Zhou.01 | 456.59 | 166.55 | 113.11 | 323.64 | 125.87 | 124.03 | 124.95 | 263.23 | 0.30 | |
| Zhou.04 | 456.56 | 166.55 | 113.11 | 323.63 | 125.87 | 124.02 | 124.94 | 263.22 | 0.30 | |
| TB-SMA | 182.84 | 173.35 | 123.76 | 121.07 | 76.15 | 11.22 | 43.69 | 176.51 | 0.39 | |
| MEAM | 474.79 | 160.51 | 115.10 | 336.13 | 131.92 | 128.89 | 130.40 | 265.27 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akarou, A.; Baras, F.; Politano, O. Microscopic Modeling of Interfaces in Cu-Mo Nanocomposites: The Case Study of Nanometric Metallic Multilayers. Metals 2025, 15, 282. https://doi.org/10.3390/met15030282
Akarou A, Baras F, Politano O. Microscopic Modeling of Interfaces in Cu-Mo Nanocomposites: The Case Study of Nanometric Metallic Multilayers. Metals. 2025; 15(3):282. https://doi.org/10.3390/met15030282
Chicago/Turabian StyleAkarou, Abdelhafid, Florence Baras, and Olivier Politano. 2025. "Microscopic Modeling of Interfaces in Cu-Mo Nanocomposites: The Case Study of Nanometric Metallic Multilayers" Metals 15, no. 3: 282. https://doi.org/10.3390/met15030282
APA StyleAkarou, A., Baras, F., & Politano, O. (2025). Microscopic Modeling of Interfaces in Cu-Mo Nanocomposites: The Case Study of Nanometric Metallic Multilayers. Metals, 15(3), 282. https://doi.org/10.3390/met15030282







