Numerical Simulation of Arc Characteristics of VP-CMT Aluminum Alloy Arc Additive Manufacturing

Abstract

In this study, simulations and analyses of arc characteristics in EP (positive polarity) and EN (negative polarity) stages (including the arc polarity transition stage) of variable polarity cold metal transition (VP-CMT) during arc additive manufacturing of aluminum alloys are carried out. Temperature field, potential field, and current density distribution of arc plasma at different stages are systematically investigated by establishing a numerical model of arc heat–force coupling in combination with single-layer single-pass additive manufacturing experiments. The results indicate that the arc’s high-temperature zone in EP stage shows the wider distribution range, with enhanced heat transfer efficiency, reaching a surface temperature of up to 11,555.8 K at 2 mm from the substrate. In contrast, the arc during the EN stage demonstrates a more concentrated high-temperature zone, attributed to a more pronounced electromagnetic contraction effect, resulting in reduced heat input and a lower peak substrate temperature in comparison with EP stage. As revealed by analysis of potential and current density distribution, the arc in EP stage shows the “bell-shaped” expansion pattern with widely distributed current density, whereas the EN stage arc displays a “wrapped” contraction pattern with a more concentrated current density. The transition from EN to EP stage exhibits greater arc stability than the reverse transition. Moreover, electrode spacing significantly influences arc characteristics; a reduction in spacing leads to a more focused high-temperature zone and a substantial increase in peak current density. This study elucidates the dynamic variations in heat transfer behavior between the EP and EN stages, offering a theoretical foundation for optimizing process parameters in aluminum alloy arc additive manufacturing.

1. Introduction

Cold metal transfer (CMT) technology combines droplet transition with wire pumping. The welding (additive) current will decrease to nearly zero after the extinguishing of arc, thus substantially decreasing arc heat input. The process is very suitable for low melting point metal (aluminum alloy) additive manufacturing research. The primary distinction between VP CMT and DC CMT lies in the incorporation of a reverse polarity arc; the complete VP CMT waveform alternates between positive polarity EP and reverse polarity EN phases. As illustrated in Figure 1, which depicts a typical VP CMT waveform and corresponding arc morphology, the droplet transfer cycle during the positive polarity phase is segmented into an ignition phase and a short-circuit phase. The ignition phase is further divided into a peak current phase and a base current phase. The EN phase is partitioned in the same manner as the EP phase, maintaining consistency in the cycle structure between both polarities In the EP stage; the welding wire is terminated to the positive electrode, and the workpiece is connected to the negative electrode. The arc heat input range is wide and the heat input is high, which has the effect of cathode cleaning. In the EN stage, the welding wire is terminated with the negative electrode, and the workpiece is connected with the positive electrode. The arc heat input range is small and the heat input is low, which has the effect of reducing heat input and cooling. Compared with DC CMT, the addition of the EN stage further decreases heat input and further strengthens the control of heat, so it is more suitable for arc additive manufacturing.

In arc welding and additive manufacturing, arc plasma controls melt droplet transition and melt pool evolution through coupling of electromagnetic-thermal-force fields, which directly affects molding quality and performance. However, quantitatively obtaining the internal physical information of high-temperature arcs, melt droplets, and melt pools using traditional experimental methods is difficult. With the development of computational technology, the combination of numerical simulation and experimental methods has become the key to revealing the synergistic mechanism of multiple physical fields and realizing breakthroughs from empirical qualitative to scientific quantitative research.

Hsu et al. [1] comprehensively solved the equations of energy conservation, momentum conservation, mass conservation, and Maxwell’s system of equations to establish the first numerical model of a two-dimensional TIG arc plasma, verified and analyzed the results of the experimental and simulation calculations, and found that the heat transfer behavior of the arc is controlled mainly by the electric current. Murphy et al. [2,3], through experiments and numerical calculations, obtained the thermophysical parameters of the thermal physical properties of the argon gas in the arc combustion process. On the basis of the assumption of local thermodynamic equilibrium, many studies have been carried out on heat transfer mechanism underlying TIG arc plasma, including considering the influence mechanism of different types of metal vapors, different protective gases, etc., on the arc plasma, and the established numerical model of the arc accurately calculates and predicts the distribution of heat flow as well as weld morphology, which lays an important foundation for subsequent research. Professor Fan Ding’s team at Lanzhou University of Technology [4] developed a three-dimensional fixed-point numerical model for analyzing the interaction between the TIG arc and the molten pool, with particular emphasis on the influence of metal vapor on arc plasma behavior. Their findings revealed that metal vapor primarily accumulates near the molten pool upper surface, exerting the pronounced constriction on arc plasma, while its impact on plasma velocity and potential remains minimal. Xiao et al. [5,6] constructed a fixed-point unsteady-state numerical models for heat transfer in TIG and MIG arcs, respectively, incorporating the effects of metal vapor and externally applied axial magnetic fields (EAMF). By computing the temperature, electromagnetic, and flow fields, along with metal vapor distribution, they demonstrated that both metal vapor and EAMF significantly affect the heat transfer characteristics of TIG and MIG arcs, as well as the flow field and the spatial distribution of critical physical quantities. The TIG-applied magnetic field promotes arc contraction and reduces the melting depth, and the MIG-applied magnetic field expands the arc plasma outward, promotes discrete metal vapor, and then forms a low-temperature cavity. Xu et al. [7] constructed a three-dimensional fixed-point numerical model of P-MIG arc–droplet coupling by considering the effects of metal vapor and droplet transition to study the temperature field of the arc plasma and the distribution of the metal vapor under the effects of different current waveforms. The droplet transition directly affects the arc morphology, the peak plasma temperature appears around the anode droplet, and the metal vapor is concentrated on the surface of the droplet.

Domestic and foreign scholars have carried out much research concerning the TIG and MIG arc plasma heat transfer behaviors, including Zhang et al. in 2017 [8]. The effect of the melt droplet transition on the arc was ignored, and a two-dimensional fixed-point rotational symmetry model of CMT arc was established. Their results show that the arc tends to compress during the fuse feeding process and that the temperature first remains constant until the end of fuse feeding, when the temperature instantly decreases to a minimum; the arc morphology expands when the fuse is pumped back, and the temperature gradually increases to the maximum temperature and remains constant until the end of pumping back. In 2020, Cadiou et al. [9] comprehensively considered heat and mass transfer phenomena observed in arc, the melt drop transition, and the melt pool. They proposed a numerical model of 304 stainless steel wires strongly coupled with CMT arc additive manufacturing to calculate the electromagnetic force, shear force, arc pressure, and Joule heat effect. However, their results were more inclined toward the description of the state of melt droplet and melt pool, ignoring arc plasma heat transfer behavior of the quantitative analysis. Lv Feiyue [10] analyzed the mechanism by which physical factors including the Lorentz force and current density inside the arc affected the transition of the molten droplet under different current bands and process parameters. In turn, arc width and Lorentz force determine the force magnitude of molten droplet in arc discharge, which in turn determines the size of the molten droplet and its transition frequency. In 2023, Zhao et al. [11] established China’s first three-dimensional numerical model for the fully coupled simulation of the CMT arc–droplet–melt pool system, incorporating the effects of arc plasma heat transfer, droplet transition, melt pool evolution, metal vapor behavior, mechanical motion of filler wire, and relative movement between filler wire and substrate. Their study highlights that the arc characteristics are jointly influenced by the transient current and electrode spacing during wire motion, and that arc plasma significantly affects the temperature distribution and flow dynamics of the molten metal under the influence of peak current.

The following authors have recently contributed to WAAM additive manufacturing: Thangamani, G. et al. [12,13,14] have demonstrated that in directed energy deposition-arc (DED-Arc) fabricated SS308L, laser shock peening (LSP) significantly refines the coarse columnar and equiaxed dendritic microstructure, leading to notable improvements in ultimate tensile strength, yield strength, and hardness, while effectively reducing porosity. Similarly, for NiTi shape memory alloys produced via WAAM, LSP induces microstructural refinement and phase stabilization, which concurrently enhance tensile strength and fracture toughness. Moreover, in the case of SS316L medical bone screws, LSP not only strengthens mechanical properties but also improves corrosion resistance and imparts remarkable antibacterial capabilities by suppressing biofilm formation. These collective findings underscore the significant potential of integrating LSP with DED-Arc and WAAM processes to advance the performance of additively manufactured metallic components across industrial and biomedical applications

In the research of CMT-PADV arc additive manufacturing for 4043 aluminum alloy, Zhang L. [15] built a system platform integrating high-speed camera and electrical signal acquisition. It was found that the matching of wire feeding speed and walking speed had a key influence on process stability. Excessive wire feeding speed could easily lead to energy accumulation and droplet transfer instability, while an excessive proportion of the EN-CMT stage would cause arc offset and splash. The electrode polarity conversion further affects the arc shape and weld pool behavior. The EP-Pulse stage is beneficial to the flow of the weld pool, while the EN-CMT stage concentrates the heat on the wire. In terms of forming, the increase in wire feeding speed will reduce the forming accuracy, and the optimization of AC frequency and positive and negative polarity ratio (such as 7:7 frequency and 13:7 ratio) can significantly improve the sidewall roughness and effective width.

Scotti [16], FM16 combines the CMT Advanced process with the near-immersed active cooling (NIAC) technology to deposit the aluminum alloy wall preform by changing the positive and negative polarity ratio (EP/EN) in the CMT Advanced process and the layer edge to water distance (LEWD) in the NIAC technology. The results clearly show that the EP/EN parameters have a greater influence on the control layer size and the surface waviness of the preform. The LEWD parameter has a greater effect on reducing heat accumulation. Therefore, as the number of deposited layers increases, it is ensured that the wall will not become wider. Finally, it is inferred that the possibility of using two independent thermal management tools to affect the thermal cycle and geometry of the resulting preform expands the window for finding the best deposition parameters in WAAM.

In summary, there are many experiments in WAAM, and it is widely used in practical applications. The conclusions related to controlling the forming size, forming accuracy, and mechanical properties of the cladding layer are more abundant. However, the current study concerning arc plasma’s heat transfer behavior during additive manufacturing processes is dominated by TIG and MIG, and heat transfer behavior of CMT arc plasma is relatively less investigated. Research on the mechanism of the influence of the shielding gas composition, the applied magnetic field, and the metal vapor, etc., on the morphology of the arc and the distribution of its temperature field, electromagnetic field, and flow field tends to be conducted. However, owing to the more complex heat transfer behavior of the VP-CMT composite arc additive arc plasma, few domestic and international investigations regarding heat transfer behavior of the VP-CMT composite arc plasma have been reported, mostly because the transformation of non-steady state processes in different stages of VP-CMT composite arc plasma can hardly be realized, resulting in the arc characteristics under the synergistic effect of mechanical movement of CMT wire and variable polarity current remaining unclear.

2. Additive Processes and Modeling of Arc Plasma Heat Transfer

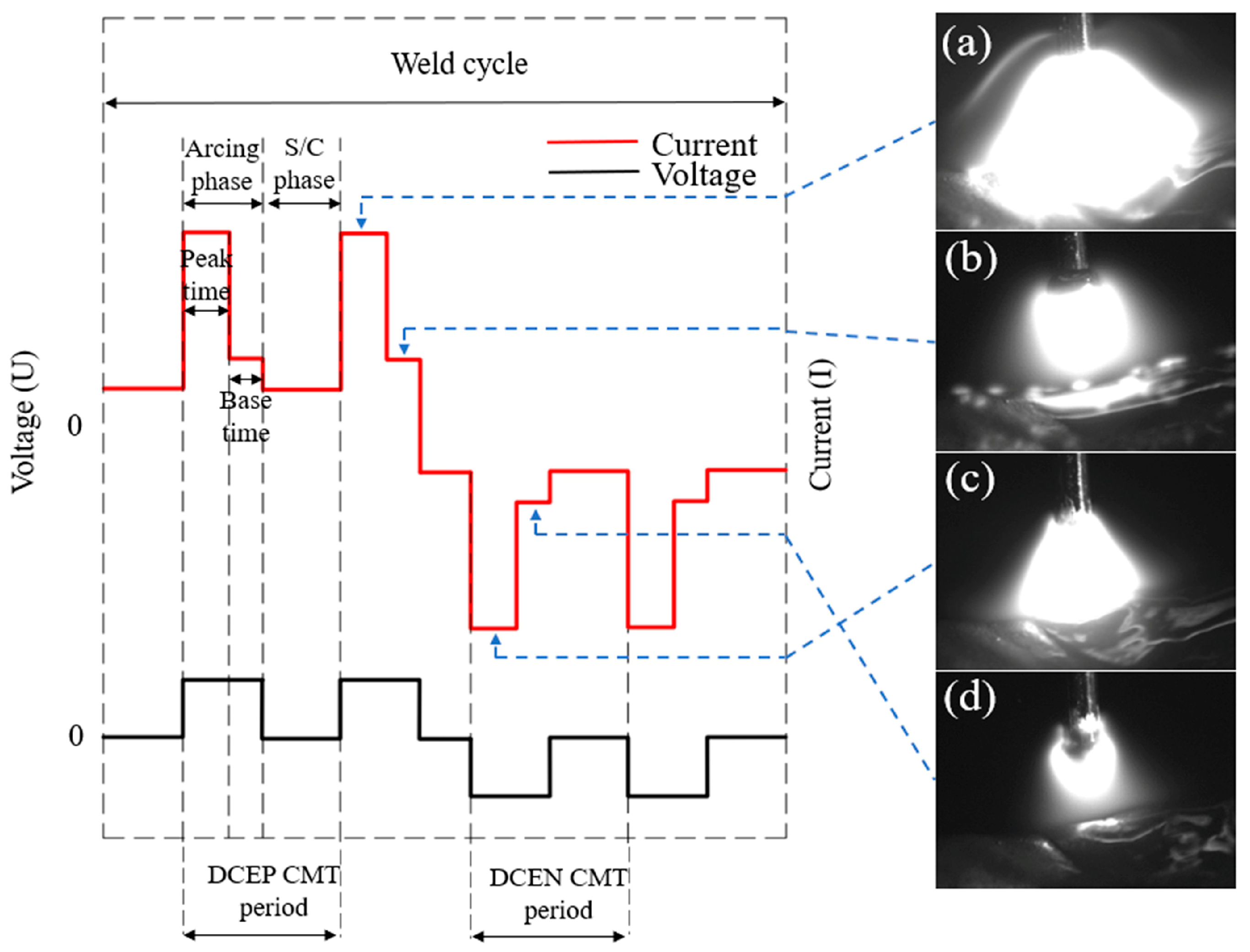
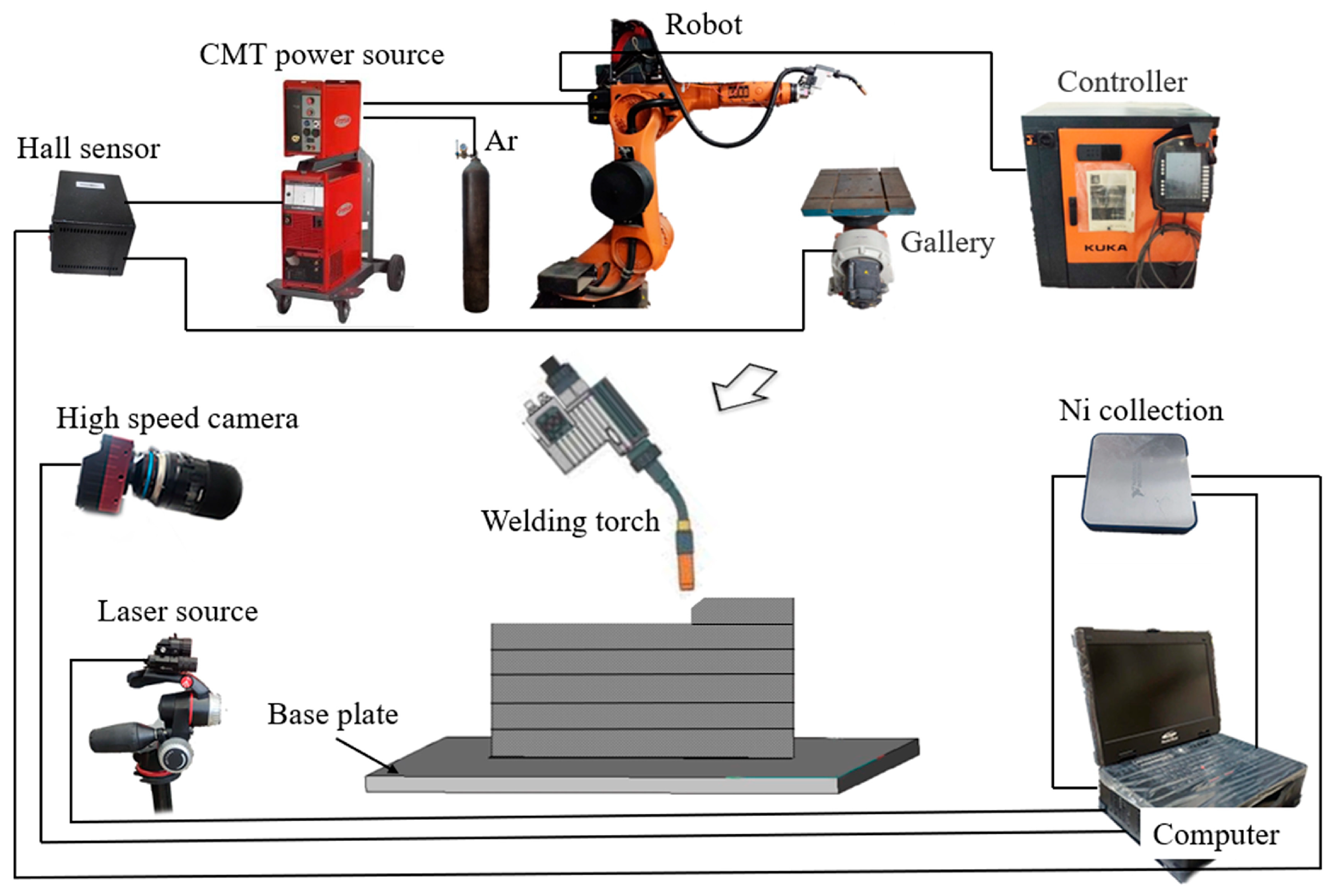
2.1. Experimental Materials and Additive Processes

In this experiment, aluminum alloy welding wire-grade ER5356 was used as the additive material (diameter, 1.2 mm) and a substrate of 250 mm × 100 mm × 8 mm 6061 aluminum alloy plate.

A single-pass, single-layer test under the optimal process parameters (wire feed speed at 4.0 m/min, travel speed at 8 mm/s, protective gas flow rate at 15 L/min) was selected on the substrate, and the current and voltage signals, arc, and melt-drop transition behaviors in the additive process were also captured using a high-speed camera system, as shown in Figure 2.

2.2. Modeling of Arc Plasma Heat Transfer Underlying Assumption

To better reveal the heat transfer mechanism underlying the arc plasma in two different phases, EP and EN, and to decrease computation time and improve the stability of the solution process, it is necessary to simplify it to a certain extent according to the actual situation and to make the following basic assumption during the numerical simulation process [9].

For an arc plasma:

(1)

Arc plasma serves as the continuous, laminar Newtonian fluid under atmospheric pressure.

(2)

Arc plasma reaches the local thermodynamic equilibrium, i.e., it is characterized by the same particle temperature without considering the variability of the electron and heavy ion temperatures.

(3)

The arc plasma satisfies the optical thinness property.

For metal electrodes:

(4)

The variation in multiphysics field within the welding wire and metal mass transfer process are neglected.

(5)

The melt pool is a laminar, unsteady, incompressible fluid.

(6)

The melt pool is treated with enthalpy–porosity for the mushy zone, and a Boussinesq approximate solution is applied for the buoyancy effect in the melt pool.

(7)

There is no free deformation of the surface of the melt pool, and mass and heat losses due to evaporation of the metal are not taken into account.

2.3. Governing Equations (Math.)

On the basis of the above assumption, the control equations of the numerical model of the coupled arc-melt pool fixed-point heat transfer for VP-CMT composite arc additive manufacturing were established.

Mass Continuity Equation.

$${\displaystyle \frac{\mathsf{\partial }\rho }{\mathsf{\partial }t}}+\nabla \cdot (\rho v)=0$$

(1)

Conservation of Momentum Equation.

$${\displaystyle \frac{\mathsf{\partial }(\rho v)}{\mathsf{\partial }t}}+\nabla \cdot (\rho vv)=-\nabla P+\nabla \cdot \tau +\rho g+J\times B+F_{Darcy}$$

(2)

in which ρ represents density, v stands for velocity vector, τ suggests viscous stress tensor, J denotes current density, B represents magnetic induction, g demonstrates gravitational acceleration, while F_Darcy indicates the source term for momentum decay in mushy region.

Energy Conservation Equation.

$${\displaystyle \frac{\mathsf{\partial }\left(\rho C_{p}T\right)}{\mathsf{\partial }t}}+\nabla \cdot \left(\rho v{C}_{p}T\right)=\nabla \cdot (k\nabla T)+S_{\mathrm{p}}+S_{\mathrm{c}}$$

(3)

in which C_p represents specific heat capacity, k stands for the fluid thermal conductivity, T indicates temperature, and S_p illustrates arc plasma’s energy source term, whereas S_c represents the substrate’s energy source term. To deal with the electromagnetic field distribution in both arc plasma and substrate, it is also necessary to calculate it in conjunction with Maxwell’s system of equations and its associated theory.

Current continuity equation:

$$\nabla \cdot (\sigma \nabla \phi )=0$$

(4)

Ohm’s Law:

$$J=-\sigma \nabla \phi$$

(5)

Poisson’s equation for magnetic vector potential is determined by Ampere–Maxwell law and Coulomb norm condition:

$${\nabla }^{2}A=-{\mu }_{0}J$$

(6)

Helmholtz’s theorem relates magnetic induction to magnetic vector potential:

$$B=\nabla \times A$$

(7)

where σ stands for electrical conductivity, φ demonstrates electric potential, A illustrates magnetic vector potential, while μ₀ suggests vacuum permeability.

The energy source term S_p for an arc plasma in Equation (3) comprises Joule heating, electron transport enthalpy, and net radiative heat loss [17], which can be determined below:

$$S_{\mathrm{p}}={\displaystyle \frac{{\left|J\right|}^2}{\sigma }}+{\displaystyle \frac{5k_{\mathrm{B}}}{2e}}J\cdot \nabla T-4\pi {\epsilon }_{\mathrm{n}}$$

(8)

in which k_B indicates Boltzmann constant, e represents electron charge, while ε_n suggests net radiation coefficient. The energy source term S_e for substrate contains latent heat of fusion and Joule heat and is determined below:

$$S_c={\displaystyle \frac{\mathsf{\partial }\left(\rho fL\right)}{\mathsf{\partial }t}}+\nabla \cdot \left(\rho vfL\right)+{\displaystyle \frac{{\left|J\right|}^2}{\sigma }}$$

(9)

in which f suggests liquid volume fraction of paste region, which varies linearly with temperature, and L represents latent heat of melting.

$$f=\left\{\begin{array}{ll}0\hfill & \mathrm{if} T<T_{\mathrm{s}}\hfill \\ {\displaystyle \frac{T-T_{\mathrm{s}}}{T_{\mathrm{l}}-T_{\mathrm{s}}}}\hfill & \mathrm{if} T_{\mathrm{s}}\le T\le T_1\hfill \\ 1\hfill & \mathrm{if} T>T_1\hfill \end{array}\right.$$

(10)

The solid–liquid interface of a mushy region is tracked by an enthalpy–porosity approach, and the mushy region is considered to be the porous medium with an identical porosity to liquid volume fraction. A decrease in liquid-metal volume fraction results in momentum decay, and is determined by

$$F_{\mathrm{Darcy}}={\displaystyle \frac{A_{\mathrm{mush}}{(1-f)}^2}{{(f+C)}^3}}v$$

(11)

where A_mush is the paste parameter; a larger paste parameter results in a greater |gradient of change between liquid to solid phase regions|. Additionally, the calculation will be more easily dispersed, generally taking a value of 1 × 10⁵~ between 1 × 10⁸, where the value is 1.6 × 10⁶. T_s and T_l are the solid phase line and the liquid phase line, respectively, and C stands for the small constant to ensure the non-zero of denominator, thus preventing solution divergence, which is taken as 0.00118.

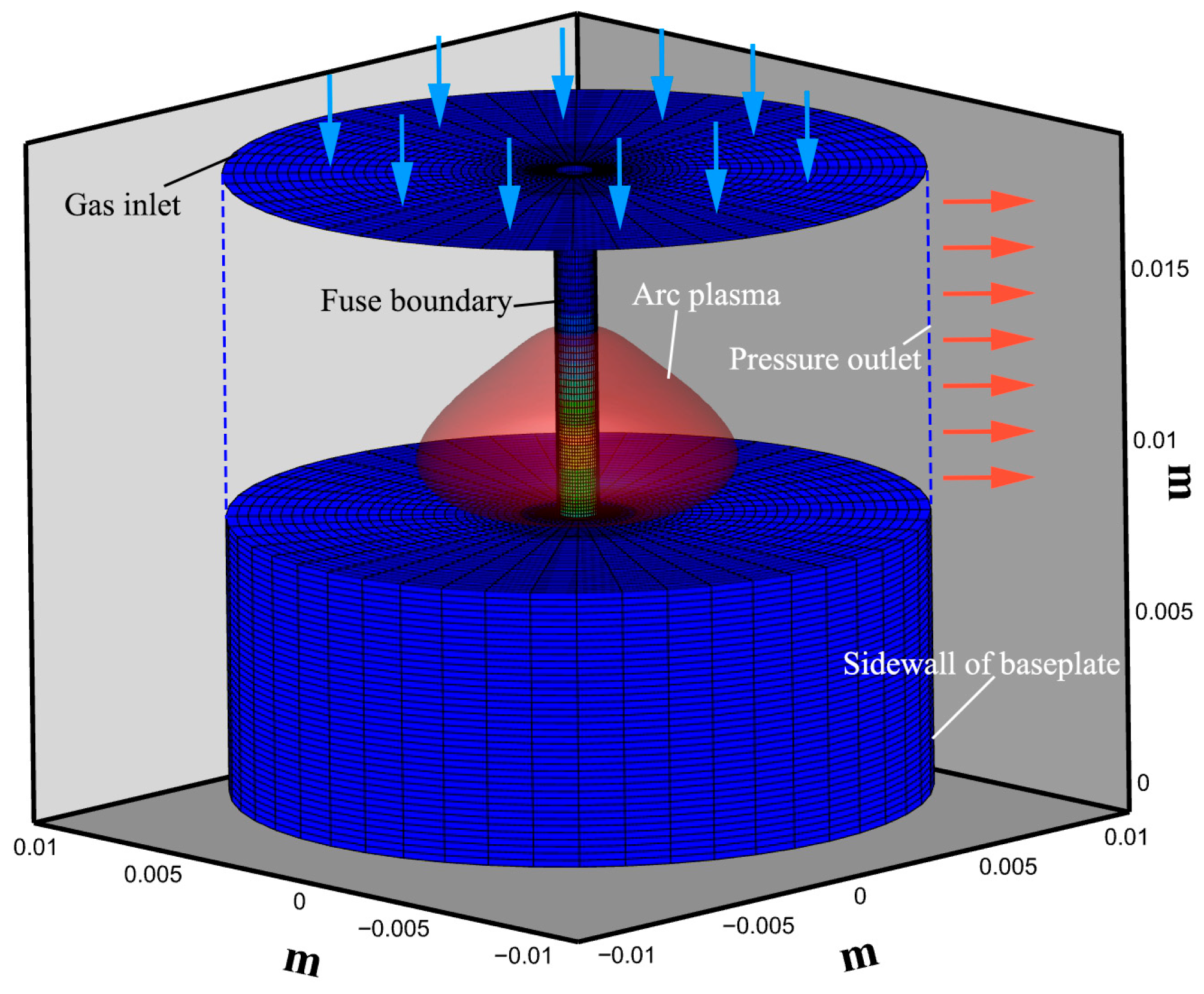
2.4. Computational Domain and Boundary Conditions

Figure 3 presents a 3D geometric model of the VP-CMT arc-melt pool computational domain, comprising wire boundary, substrate domain, and shielding gas domain. During numerical simulation, a dynamic mesh technique can be employed for controlling wire tip motion, enabling the simulation of wire feeding and retraction processes characteristic of the CMT stage. The model primarily investigates the influence of wire mechanical motion and input current on arc plasma’s heat transfer behavior, while neglecting internal physical reactions within the wire.

An electrode sheath layer deviating from thermodynamic equilibrium state exists at the junction of the arc plasma and the substrate. Thermal boundary conditions at the surface near substrate can be described by Equation (12).

$$q_{\mathrm{c}}=-k_{\mathrm{eff}}\left({\displaystyle \frac{T_{\mathrm{cw}}-T_{\mathrm{cp}}}{{\delta }_{\mathrm{c}}}}\right)-\left|J_e\right|{\Phi }_{\mathrm{m}}+J_i{V}_i-{\epsilon }_0{\sigma }_0(T_{\mathrm{cw}}^4-T_{\mathrm{cp}}^4)$$

(12)

In the formula, the terms from left to right represent heat conduction, the effect of electron cooling on heat transfer, and thermal radiation. k_eff represents effective thermal conductivity of the sheath from the arc plasma to the metal substrate. T_cw and T_cp denote electrode surface temperature and arc plasma temperature near electrode surface, separately. δ_c indicates the conductive space layer thickness. J_e suggests current density used for calculating heat flux onto the substrate surface, Φ_m indicates the work function, ε₀ represents the radiation coefficient, while σ₀ serves as the Stefan–Boltzmann constant [18]. The baseplate is the cold cathode, sustaining arc plasma primarily through field-emitted electrons.

Equation (13) gives the calculation method of J_e current density.

$$J_e=A{T}_{\mathrm{cw}}^2\cdot \exp \left(-{\displaystyle \frac{e{\Phi }_{\mathrm{m}}}{k_{\mathrm{B}}{T}_{\mathrm{cw}}}}\right)$$

(13)

In which A stands for Richardson’s constant, T_cw represents substrate surface temperature, e suggests elementary charge, Φ_m illustrates the effective work function of the electrode, while k_B represents Boltzmann’s constant [9,17,19]. In the JiVi term of Equation (12), Ji is the ion current density and Vi is the ionization potential of the gas. It is assumed that if the calculated current density Je is greater than the current density generated by the hot electron emission, the excess is partially provided by the ions transferred from the plasma to the cathode. The ion current density can be expressed as [20]:

$$J_i=\left\{\begin{array}{c}\begin{array}{cc}{J}_C-J_e& if\left(J_C-J_e>0\right)\end{array}\\ \begin{array}{cc}0& if(not)\end{array}\end{array}\right.$$

(14)

As described in the literature [21], the current density’s normal component on the surface dominates, so the J_C is defined as $J_C=\left|\overrightarrow{J}\cdot \overrightarrow{n}\right|$.

Referring to Zhao [11], the sheath near the positive and negative electrodes is considered, and the equilibrium state near the thermodynamics near the anode is considered.

$$q_c=\left\{\begin{array}{c}-k_{\mathrm{eff}}\left({\displaystyle \frac{T_{\mathrm{cw}}-T_{\mathrm{cp}}}{{\delta }_{\mathrm{c}}}}\right)-\left|J_e\right|(Vf-{\Phi }_{\mathrm{m}})+J_i{V}_i-{\epsilon }_0{\sigma }_0(T_{\mathrm{cw}}^4-T_{\mathrm{cp}}^4)(EPstage)\\ -k_{\mathrm{eff}}\left({\displaystyle \frac{T_{\mathrm{cw}}-T_{\mathrm{cp}}}{{\delta }_{\mathrm{c}}}}\right)-\left|J_e\right|{\Phi }_{\mathrm{m}}+J_i{V}_i-{\epsilon }_0{\sigma }_0(T_{\mathrm{cw}}^4-T_{\mathrm{cp}}^4)(ENstage)\end{array}\right.\begin{array}{c}\\ \end{array}$$

(15)

Considering effects of arc plasma shear and Marangoni convection inside the substrate melt zone, we define momentum boundary conditions below:

For x-direction:

$${\tau }_x={\tau }_{\mathrm{p}x}+{\tau }_{\mathrm{M}x}=-{\mu }_{\mathrm{p}}{\displaystyle \frac{\mathsf{\partial }{v}_x}{\mathsf{\partial }z}}+{\displaystyle \frac{\mathsf{\partial }\gamma }{\mathsf{\partial }T}}{\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }x}}$$

(16)

For y-direction:

$${\tau }_y={\tau }_{\mathrm{p}y}+{\tau }_{\mathrm{M}y}=-{\mu }_{\mathrm{p}}{\displaystyle \frac{\mathsf{\partial }{v}_y}{\mathsf{\partial }z}}+{\displaystyle \frac{\mathsf{\partial }\gamma }{\mathsf{\partial }T}}{\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }y}}$$

(17)

In which τ_M denotes the Marangoni force, τ_p denotes the plasma flow shear, v_x and v_y suggest velocity components at x- and y-directions, separately, and γ indicates surface tension coefficient.

Table 1. Internal boundary conditions.

Physical Field	Internal Boundary of the Cathode
electromotive force	be coupled (with sth)
magnetic fields	be coupled (with sth)
energies	arc plasma side: Tcp; substrate side: Equation (12)
momentum	baseboard side: Equations (16) and (17)

presents additional internal boundary conditions within the substrate.

At the substrate bottom and sidewalls, heat dissipation boundary conditions are as follows:

$$-k{\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }n}}=-h_{\mathrm{c}}\left(T_{\mathrm{w}}-T_0\right)-{\epsilon }_0{\sigma }_0\left(T_{\mathrm{w}}^4-T_0^4\right)$$

(18)

In which h_c stands for metal thermal conductivity, T_w represents substrate side and bottom temperatures, and T₀ represents the reference temperature.

Both current and voltage data used for the simulations are shown in Figure 4 and Figure 5.

3. Simulation Results and Discussion

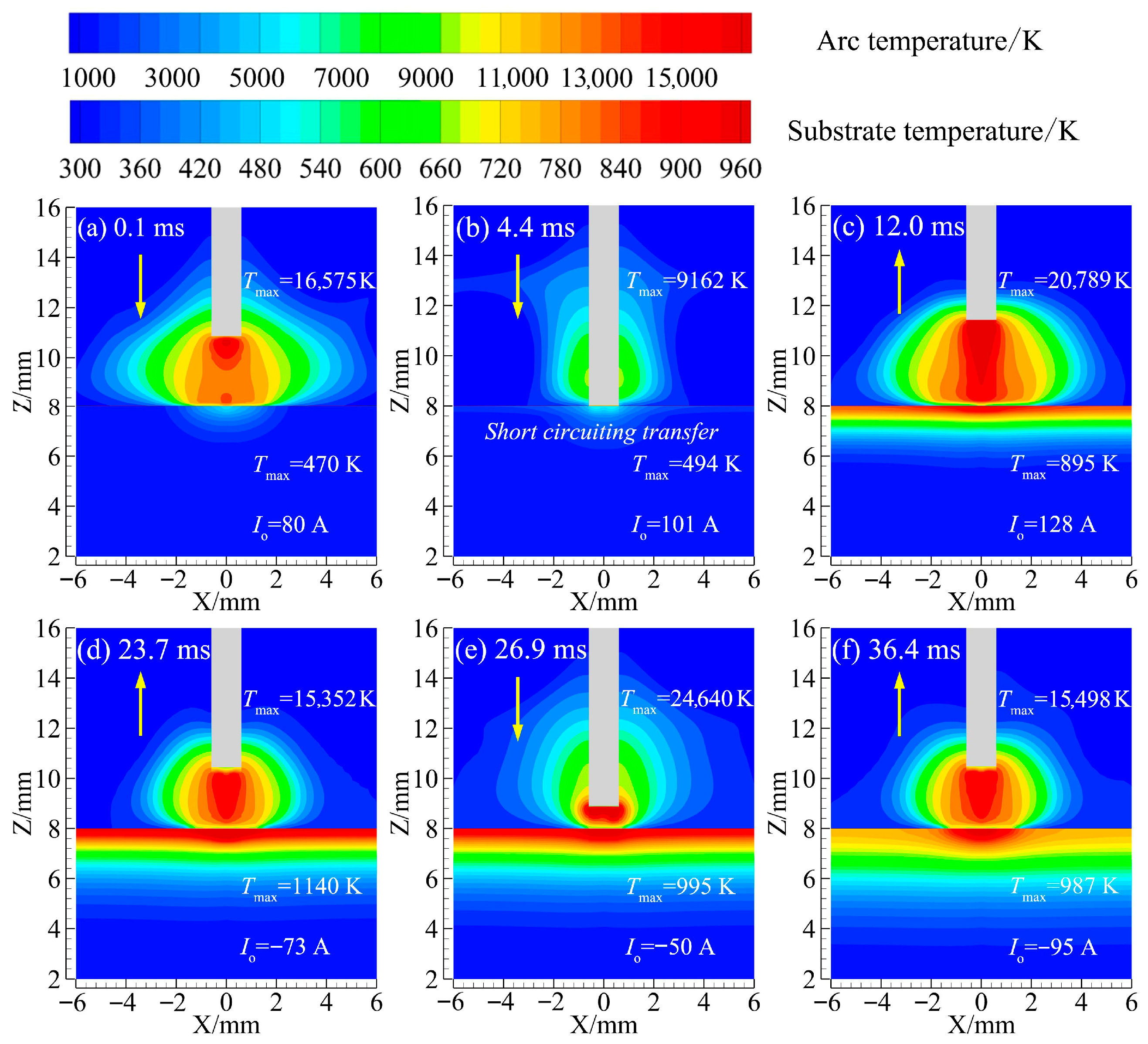
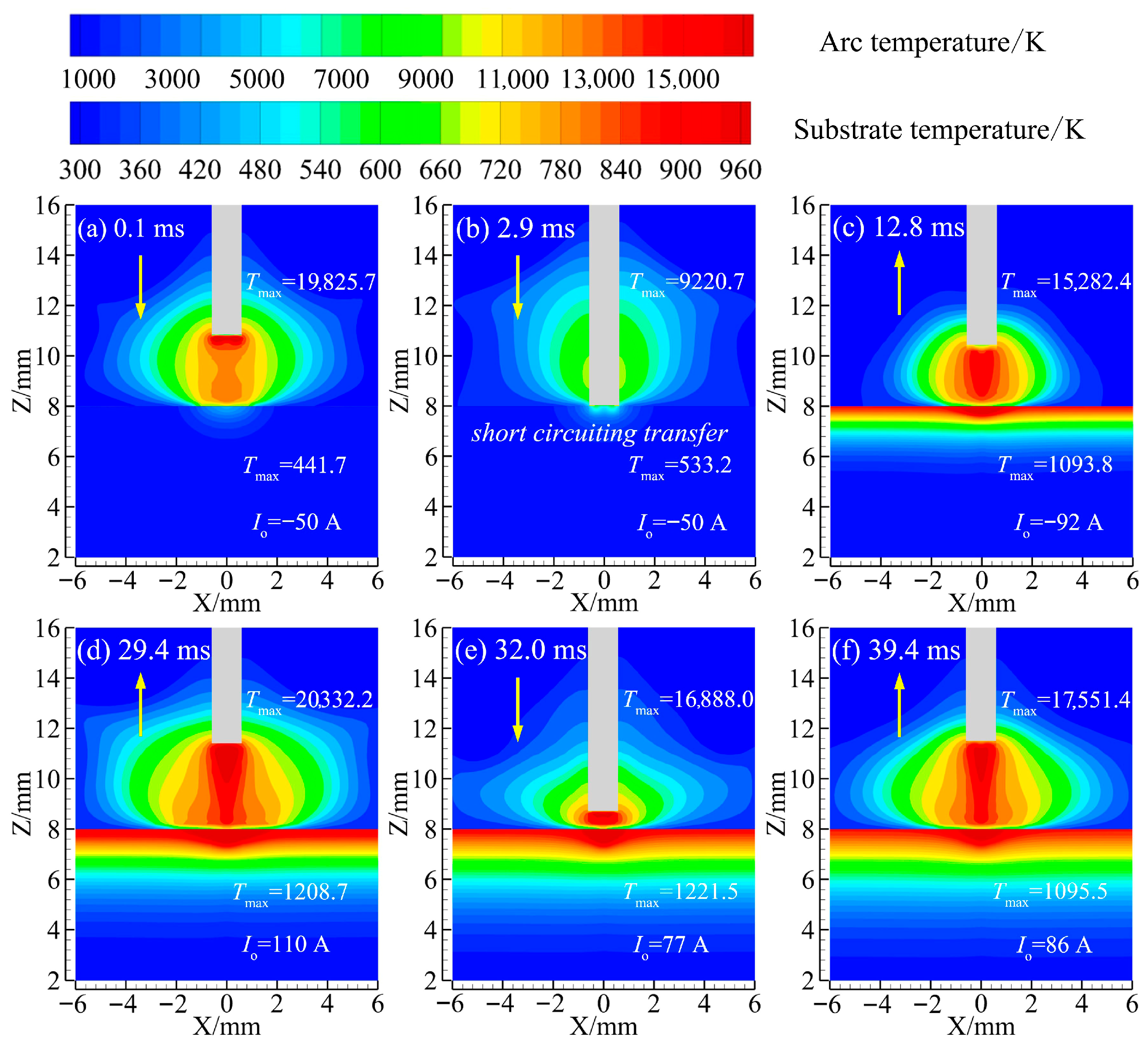
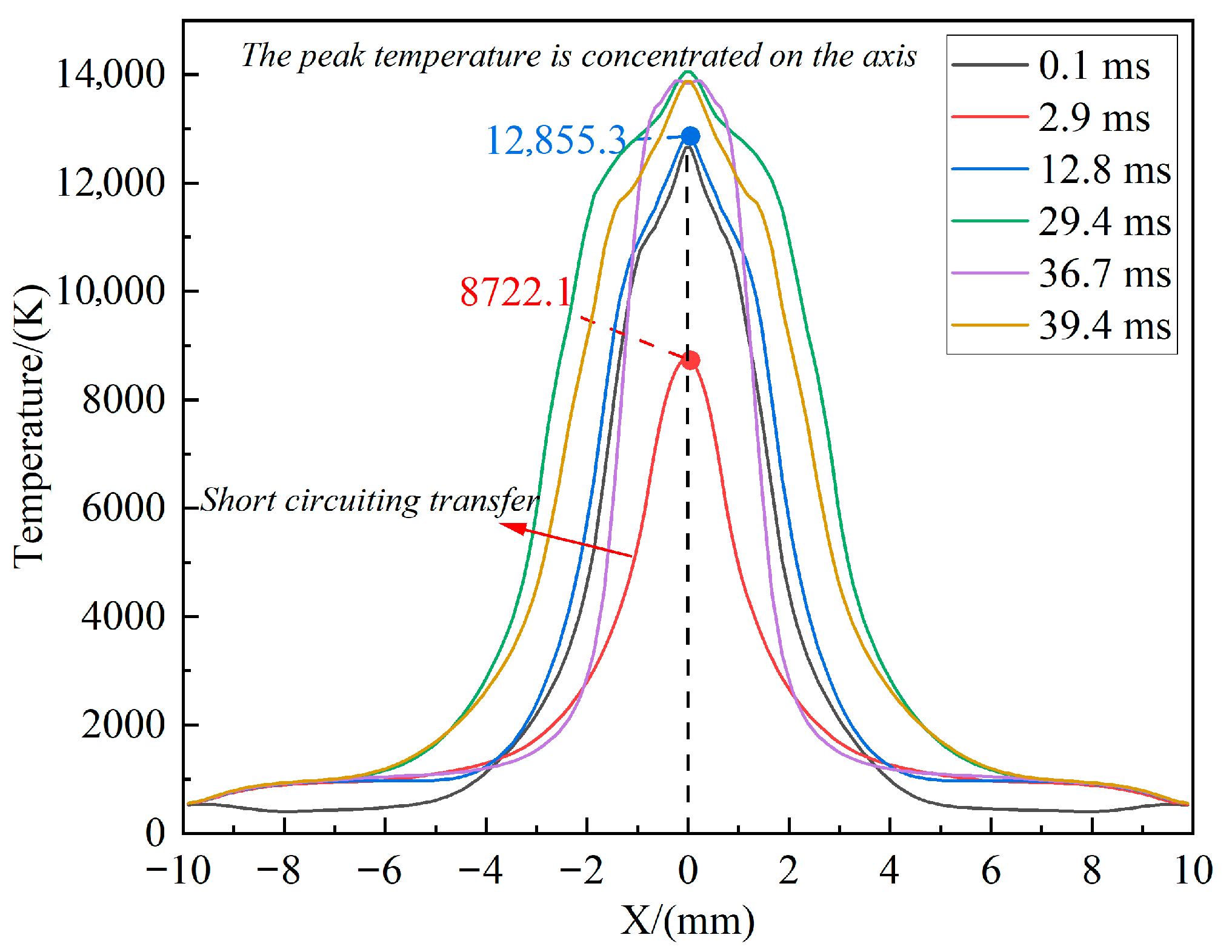
3.1. Arc Isolation

Mechanism of Temperature Distribution in Heat Transfer Process of a Substrate

The arc plasma temperature field in transition from EP to EN stages is shown in Figure 6. At 0.1 ms, the welding wire serves as the anode and the substrate as the cathode. The input current is 80 A, corresponding to the base current stage of the CMT process. Ionization of the particles between the electrodes forms an arc plasma, which assumes a stable conical shape due to thermal contraction and electromagnetic forces, with the temperature peak concentrated at the wire end at 16,575.3 K. At 4.4 ms, the wire makes short contact with the substrate, extinguishing the arc; however, the instantaneous current reaches 101 A, and the temperature peak drops to 9162.7 K, the lowest observed during the CMT stage. During this phase, arc plasma encircles the wire, driven by temperature and pressure gradients to minimize heat loss. At 12 ms, arc plasma re-ignites as the wire retracts, with peak plasma temperature rising to 20,789.2 K under a peak current of 128 A, nearing the maximum temperature for the CMT stage. By 23.7 ms, the arc has transitioned into the EN stage with a current of −73 A, resulting in a decrease in arc plasma temperature to 15,352.8 K, while the substrate peak temperature rises to 1140 K due to cumulative heat input. At 26.9 ms, the wire is fed close to the substrate, and owing to the small electrode spacing, the arc plasma presents an ellipsoidal shape wrapped the wire end, and peak temperature can even reach 24,640.3 K. A higher temperature zone of arc plasma is concentrated when the electrode spacing is small. After the short-circuit transition, the wire is pumped back to the starting position of the EN stage, and arc plasma has a peak temperature of 15,498.6 K under a current of −95 A, which is 145.8 K greater than the peak temperature at 23.7 ms, and the distribution areas are all conical in shape.

The arc plasma temperature field from EN to EP phases is shown in Figure 7. The current in the base current stage at 0.1 ms is −50 A, which is 30 A less than the current at the corresponding moment in Figure 6. At this time, the wire is the cathode, and the substrate is the anode. By comparing Figure 6a and Figure 7a, it is evident that the arc in EN stage shows increased convergence compared with EP stage. The peak temperature of 19,825.7 K further indicates that the electromagnetic contraction at the arc initiation in the EN stage is stronger, resulting in a more concentrated high-temperature region. At 2.9 ms, the arc enters a short-circuit state, assuming an ellipsoidal shape that envelops the wire, with the high-temperature zone appearing about 2 mm above the wire tip. At 12.8 ms, as the wire retracts, the temperature peak beneath the wire reaches 15,282.4 K under a current of −92 A. A substantial volume of plasma overcomes electromagnetic contraction through the effects of temperature and pressure gradients, gradually expanding outward. The substrate peak temperature rises to 1093.8 K, initiating melting and forming a small molten pool. At 29.4 ms, EN phase transitions back to EP phase, and under a peak current of 110 A, the outer arc column exhibits a flat-top morphology, while the inner high-temperature zone displays a bell-shaped profile. The peak temperature beneath the wire tip reaches 20,332.2 K, contributing to further expansion of the molten pool on the substrate. At 32.0 ms, the wire reaches the substrate feed, and with the gradual reduction in electrode spacing, the arc at this moment presents a “flying saucer” shape, although the electrode spacing is close; however, the arc distribution range is larger, which is close to the electrode moment with the EN stage “wrapped” type of arc difference. This is different from the “wrapped” arc at the near electrode moment in the EN stage. At 39.4 ms, the wire was withdrawn to the same starting position of the EP phase as in Figure 7d, the arc plasma temperature peaked at 17,551.4 K, and the arc column was conical and compressed toward the substrate.

Temperature data at 0.2 mm above the substrate surface were taken to further analyze the substrate surface temperature at six moments to reveal the heat transfer mechanism underlying the VP-CMT arc plasma. Figure 8 shows the substrate surface temperature distribution results at six characteristic moments from EP to EN stages. Temperature peaks at different moments reach a maximum near the wire axis with an approximate Gaussian distribution, the temperature peak of the substrate surface is the largest at 12.0 ms at 11,555.8 K, and the temperature peak reaches a minimum at 6193.7 K during the short-circuit transition.

Figure 9 presents the temperature distribution on the substrate surface at six characteristic moments during the transition from EN to EP phases. Similarly to the pattern observed in Figure 8, the temperature distribution on the substrate surface remains consistent, with temperature peaks concentrated along the wire axis. The lowest peak temperature occurs during the short-circuit transition at 2.9 ms, reaching 8722.1 K. However, the difference is that the substrate surface temperature at 12.8 ms in the EN stage is lower than that at the three moments in EP stage, indicating the greater arc energy in EP relative to EN stages and the greater heat transfer efficiency. In addition, it can be found in Figure 8 and Figure 9 that the substrate surface temperature is less than 1000 K at 6 mm away from the axis of the wire, which indicates that the main area of action of the arc is within a circle with a radius of 6 mm.

From Figure 8 and Figure 9, EP and EN stages of peak arc temperature are close to each other, but the EP stage of the high-temperature zone range is wider, and the EN stage is narrower than the 4000 K arc high-temperature zone distribution range of the EP stage, which increases relative to EN stage of arc radius distribution of 1 mm. In EN to EP stages, the EP stage of peak arc temperature is slightly greater than the EN stage, and high-temperature zone distribution range distribution in the same EP stage is wider. In addition, a more than 4000 K arc high-temperature zone distribution range of EP stage can be observed, whereas the EN stage distribution radius is greater, up to 1.5 mm.

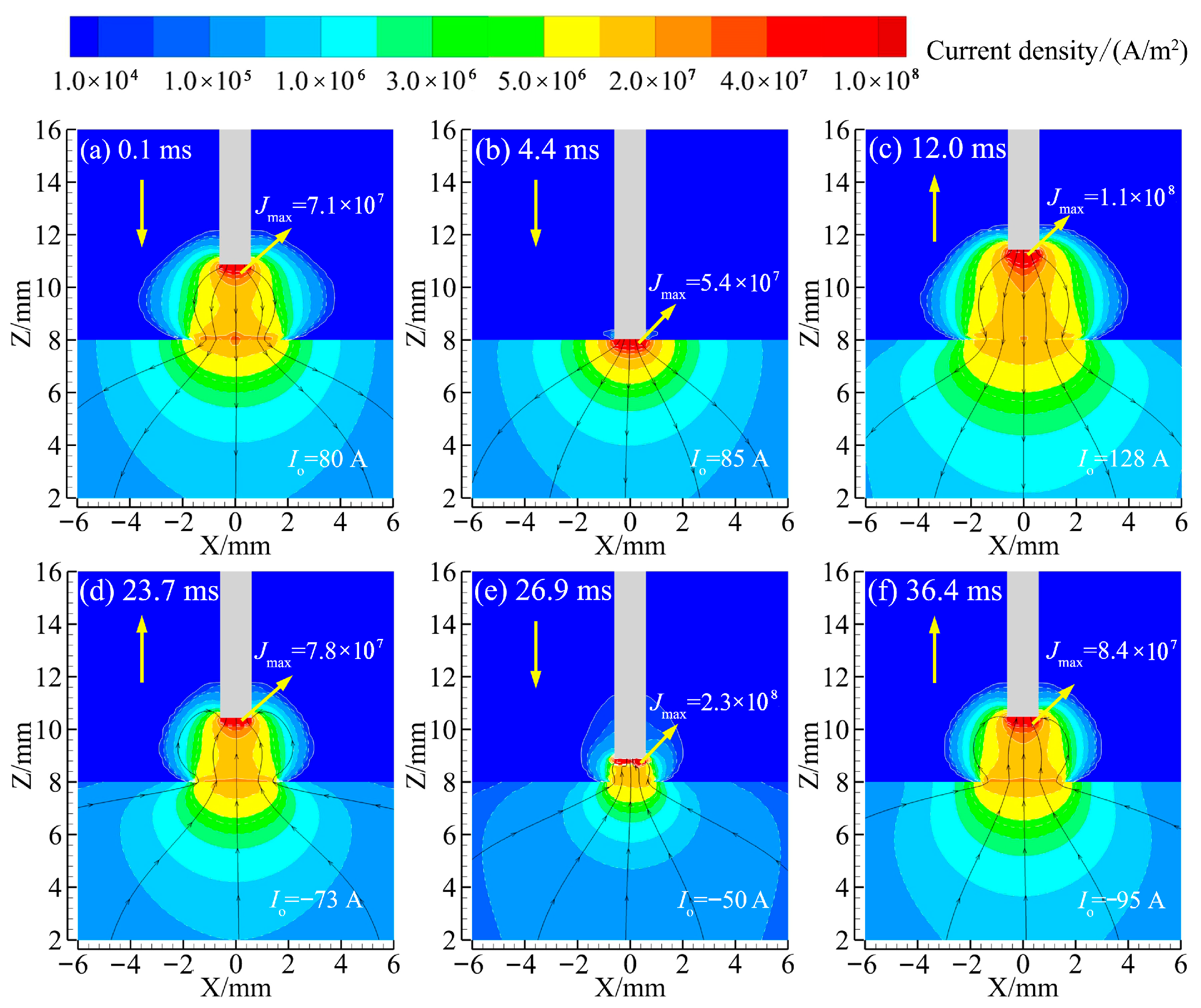
3.2. Electromagnetic Field Evolution Laws for Arc Plasma Heat Transfer Processes

The results of the potential field distribution of the arc plasma for the EP stage to EN stage are shown in Figure 10. The potential distribution pattern is consistent with the temperature field. At 0.1 ms, the potential profile exhibits a bell-shaped structure, with multiple high-potential regions located at the outer edge of the arc column, and a peak potential of 9.1 V at the filament tip. At 4.4 ms, due to the expansion of the arc plasma above the filament tip and the formation of a low-potential cavity, the peak potential decreases to 5.0 V, as shown in Figure 10b. At 12.0 ms, the potential field distribution closely mirrors the temperature field, with a peak potential of 10.8 V at the anode filament end, gradually decreasing toward the substrate. Upon entering the EN stage, the potential field in the arc column region adopts a stable, circular plateau configuration at 23.7 ms and 36.4 ms, with the cathode filament end potentials reaching −8.3 V and −9.7 V, respectively. Notably, the potential is only distributed in the form of a cone with a −2 V at 26.9 ms, although the temperature peak reaches 24,640.3 K. This suggests that the temperature of the arc column (Figure 6) is not dominated by the electrode spacing and the current only but is also affected by the thermal contraction effect due to the different arc characteristics between the EP and EN stages.

The results of the potential field distribution of the arc plasma from the EN stage to the EP stage are shown in Figure 11. At 0.1 ms, the potential in the arc column area is conically distributed under the −50 A current, the peak potential at the cathode filament end is −8.6 V, and the potential gradually increases toward the substrate. With the feeding of the filament, the arc was extinguished at 2.9 ms, and the potential distribution in the arc-column region was similar to that in Figure 10e, with a conical distribution of less than −1 V. The potential of the arc-column region was also distributed in a conical shape at 12.8 ms. At 12.8 ms, the electromagnetic contraction of the arc plasma increased significantly under the −92 A current, and the arc compressed toward the substrate. A comparison of the potential distribution of the EP stage with that of Figure 10a–c reveals that the potential distribution of the CMT arc is more stable in EN relative to EP stages in the previous stage of CMT arc action, indicating that the thermal action of the arc is correspondingly more stable. In the EP stage, at 29.4 ms, 36.7 ms, and 39.4 ms, the potential distribution characteristics are basically consistent with the temperature distribution characteristics of Figure 7d–e. Moreover, from the comparison between Figure 10c and Figure 11f, the peak potential of Figure 11f is 13% greater than that of Figure 10c for high-current action with the wire at the same position maintaining the same electrode spacing.

The arc plasma current density distributions from EP to EN stages are further analyzed, as shown in Figure 12. In the EP stage of Figure 12a–c, the current flows from the anode filament end to the cathode substrate; in the EN stage of Figure 12d–f, the current flows from the cathode substrate to the anode filament end. The current density is conically distributed except for the short-circuit moment at 4.4 ms. In addition, the electrode spacing affects the current flow more at different moments. The larger the electrode spacing is, the wider the current density distribution is; the smaller the electrode spacing is, as shown in Figure 12e, the more concentrated the current density distribution is, and at 26.9 ms in the EN stage, the action current is only −50 A. However, because the electrode spacing is only 0.4 mm or so, the peak current density can reach 8 × 10^2.3A/m². In contrast, at 12.0 ms of the EP stage, the electrode spacing is around 2.6 mm, and the applied current is 128 A, but the peak current density is 8 × 10^1.1A/m², which is 8 × 10^1.2A/m² smaller than that at 26.9 ms.

The results of the arc plasma current density distribution from the EN stage to the EP stage are shown in Figure 13. Owing to the small electrode spacing and low current in the EN stage, less Joule heat is generated, and the thermal diffusion motion of the arc plasma is weaker than that in the EP stage. Figure 13d–f shows that the current density is concentrated not only at the anode filament end but also at the substrate surface under high-temperature and high-pressure environments and electromagnetic contraction forces. Especially at 32.0 ms in Figure 13e, the peak current density is as high as 8 × 10^6.2 A/m² under a 77 A current.

Figure 14 shows the arc plasma potential distribution on substrate surface from EP stage to EN stage. At 0.1 ms and 12.0 ms in the EP stage, the potential on the substrate surface reaches a peak of 3 V at 3 mm from the wire axis, whereas it has a low potential distribution of about 1 V on the wire axis. According to Gou et al. [18], the potential was concave downward inside the center axis region, whereas current density is convex upward because the high wire axis temperature corresponding to molten region promotes electron field emission, which in turn causes more electrons to be emitted inside the molten region than in the unmelted region; thus, the large number of electrons on the surface of the substrate leads to a low potential and high current density in the molten pool. Similarly, in the EN stage, the potential on substrate surface shows a same trend as that in the EP stage due to the smaller electrode spacing and opposite polarity, but the peak potentials at 29.4 ms and 39.4 ms appear at 2 mm from the wire axis, which also indicates that the arc has a smaller range of action and a lower heat output in EN relative to EP stages.

Figure 15 displays the arc plasma current density distribution on substrate surface from EP to EN stages. The current density distribution is clearly concentrated mainly near the wire axis, which is negatively correlated with the Figure 14 potential distribution. In addition, the current density is not a completely axisymmetric distribution. In the actual additive process, the molten droplet and molten pool morphology affects the arc distribution law, but considering the electromagnetic thermal effect of arc plasma, arc plasma further burns until the stabilization of the electron emission in the process. On the basis of thermal contraction effect and minimum voltage principle, arc plasma gradually converges in the direction of the axis. During arc plasma contraction, the molten pool is subjected to fluctuations in the arc force.

Figure 16 shows the arc plasma potential distribution onto substrate surface in transition from EN to EP stages. In contrast to Figure 14 positive potentials are observed on the substrate surface at 0.1 ms and 2.9 ms during the EN stage. This is because the edge of the arc plasma is not fully compressed to the substrate surface but presents a circular arc line tangent to the substrate surface (Figure 11a), which creates a localized potential difference. In addition, in the EP stage, the low potential at the wire axis is also due to the higher electron emission density, which reduces the potential at the substrate surface, and it is smaller than the low potential region in Figure 15 which indicates that the arc action will be wider and that the additive efficiency will be higher after switching from the EN stage to the EP stage.

Figure 17 presents the arc plasma current density distribution on substrate surface during the transition from the EN to EP phase. At each moment across the different phases, the peak current density on substrate surface is concentrated along the wire axis. This distribution correlates with the current flow lines between the electrodes, which are oriented parallel to the axis shown in Figure 12 and Figure 13. The current density between the electrodes is more focused due to the relatively limited influence of the circumferential electromagnetic force, which acts perpendicular to the wire axis and has a reduced effect on the plasma concentrated along the axis. In addition, unlike Figure 16 the current density distribution on substrate surface from EN stage to EP stage is significantly more concentrated than that from EP to EN stages, suggesting the superior stability of this transition.

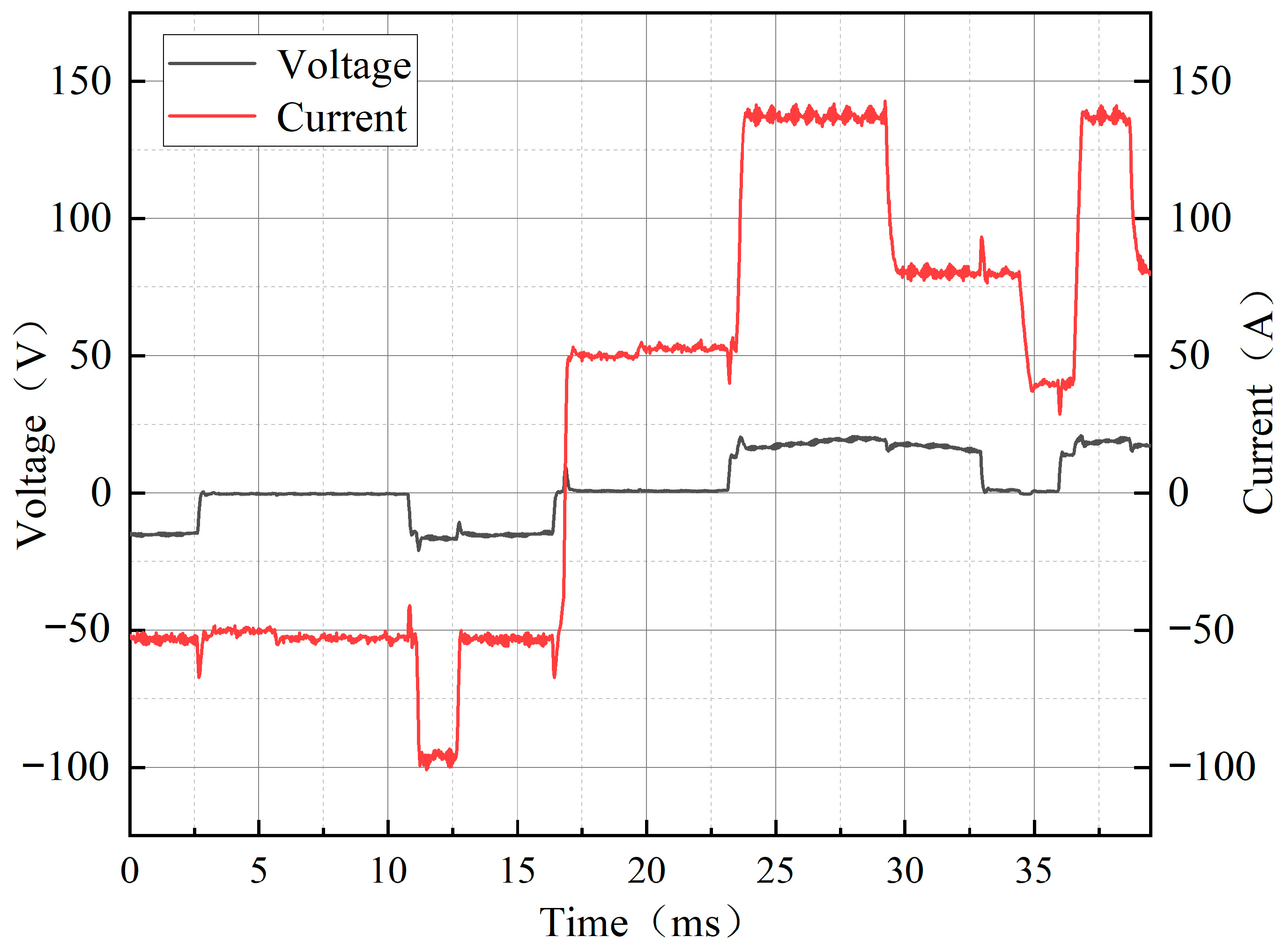
3.3. Comparison of Experimental and Simulation Results

According to the high-speed camera of EP to EN stage process in the experimental process, the simulation results were compared with arc images obtained using a high-speed camera at six moments inside the temperature field, 0.1 ms, 4.4 ms, 12.0 ms, 23.7 ms, 26.9 ms, and 36.4 ms, as shown in Figure 18. It can be observed that the contour of the arc-illuminated region in the arc image corresponds closely with the high-temperature region exceeding 10,000 K of simulation results, while the high-exposure region in the arc image aligns well with the high-temperature region above 12,000 K in the simulation. To sum up, based on these comparisons, the model demonstrates high accuracy in capturing arc plasma characteristics in the VP-CMT arc heat source, providing a theoretical basis for further investigation of the VP-CMT process.

4. Conclusions

(1)

In the EP to EN stages, EP and EN stages of the peak arc temperature are close, but the EP stage of the high-temperature zone range is wider, and the EN stage is narrower, with a more than 4000 K arc high-temperature zone distribution range of the EP stage. Meanwhile, the EN stage of the arc distribution radius is larger than 1 mm, increasing 40%., and the overall arc temperature is also higher. In addition, from EN to EP stages, the EP stage arc peak temperature is slightly greater than that in the EN stage, the distribution range of the high-temperature zone distribution in the same EP stage is wider, and the distribution range of the high-temperature zone distribution range in the EP stage is greater than that in the EN stage, reaching 1.5 mm and increasing 60%, and the overall arc temperature is greater than that in EN stage.

(2)

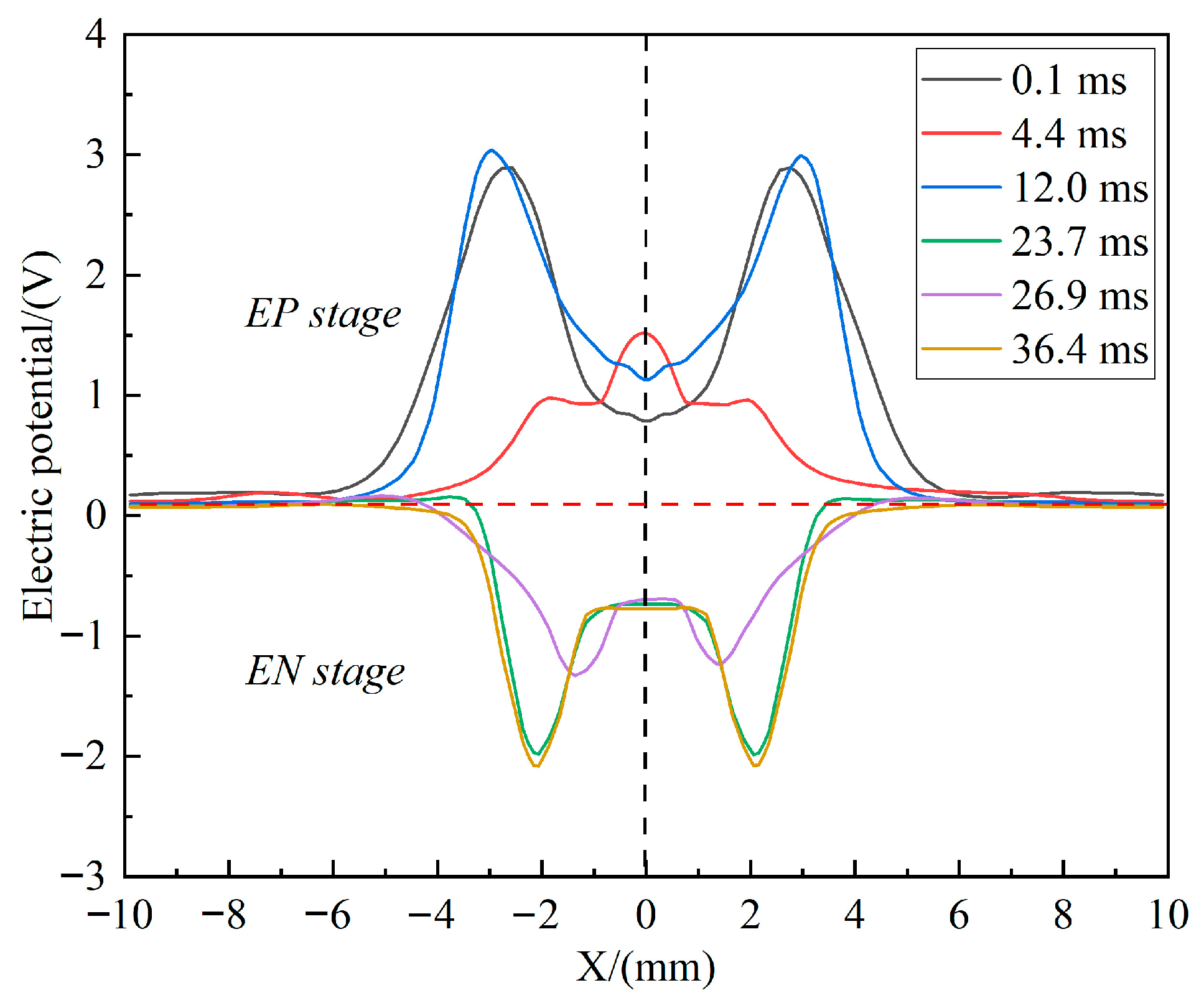
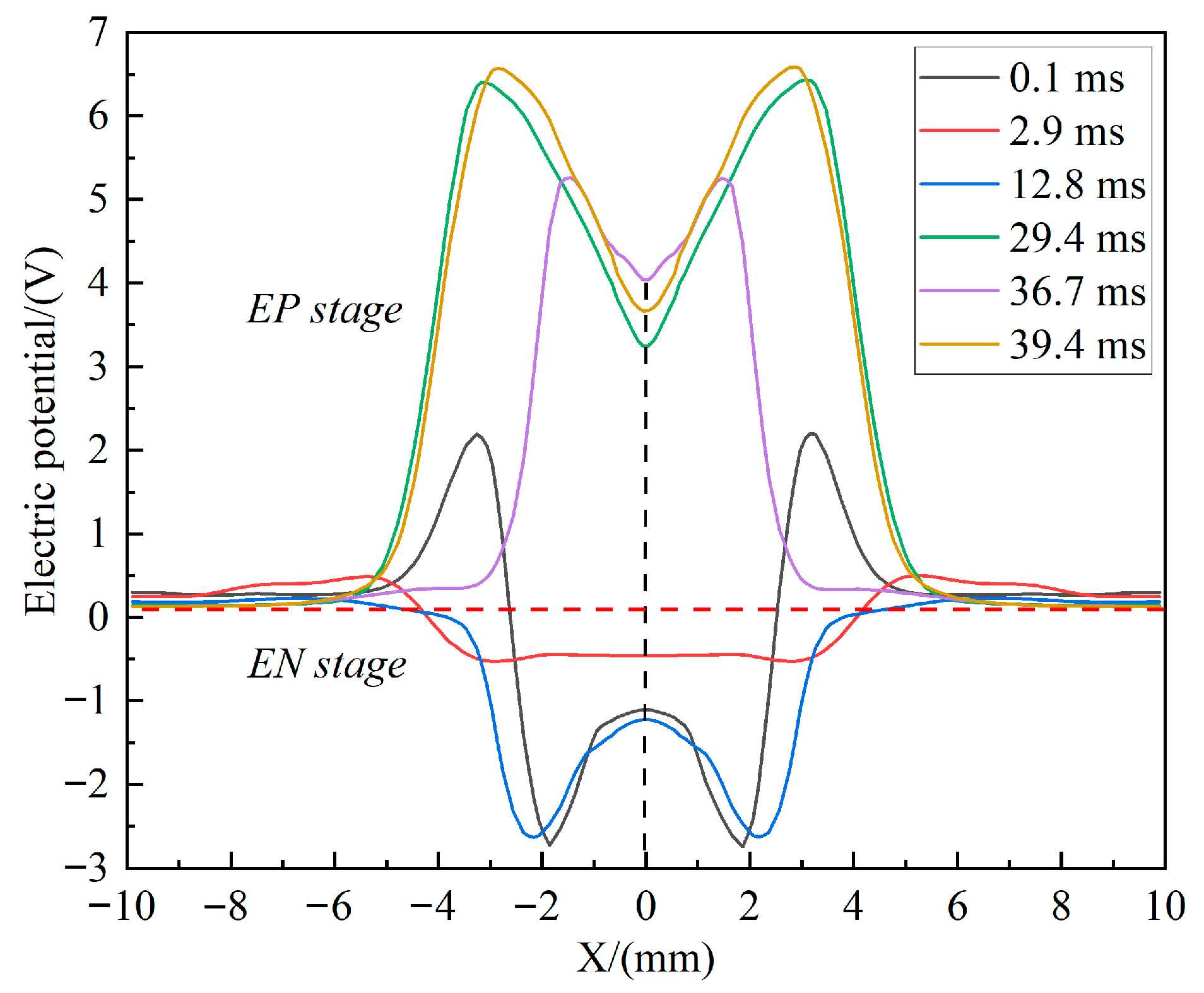
Compared with EP stage, EN stage exhibits distinct arc characteristics due to the opposite polarity of the electrodes. As shown in the potential distribution diagrams, the arc during the EN stage forms a “wrapped” contraction arc, resulting in a smaller heat transfer area within the molten pool (characterized by a narrower high-potential region). In contrast, the arc during the EP stage assumes a more “bell-shaped” expansion form, leading to a larger heat transfer area at the bottom of molten pool (indicated by a wider high-potential region). Additionally, arc stability is greater during the EN to EP transition than during the EP to EN transition, as evidenced by the more linear current density distribution converging toward the axis.

(3)

Electrode spacing significantly affects arc characteristics. During the EN stage, a reduction in electrode spacing results in a more concentrated high-temperature region, with the peak temperature increasing markedly from 15,352.8 K at high spacing to 24,640.3 K at low spacing, an increase of 60.5%. Similarly, the peak current density rises substantially from 7.8 × 10⁷ A/m² at high spacing to 2.3 × 10⁸ A/m² at low spacing, increasing 295%.