Probabilistic Modeling of Fatigue Life Prediction of Notched Specimens Combining Highly Stressed Volume and Theory of Critical Distance Approach
Abstract
1. Introduction
2. Theoretical Background
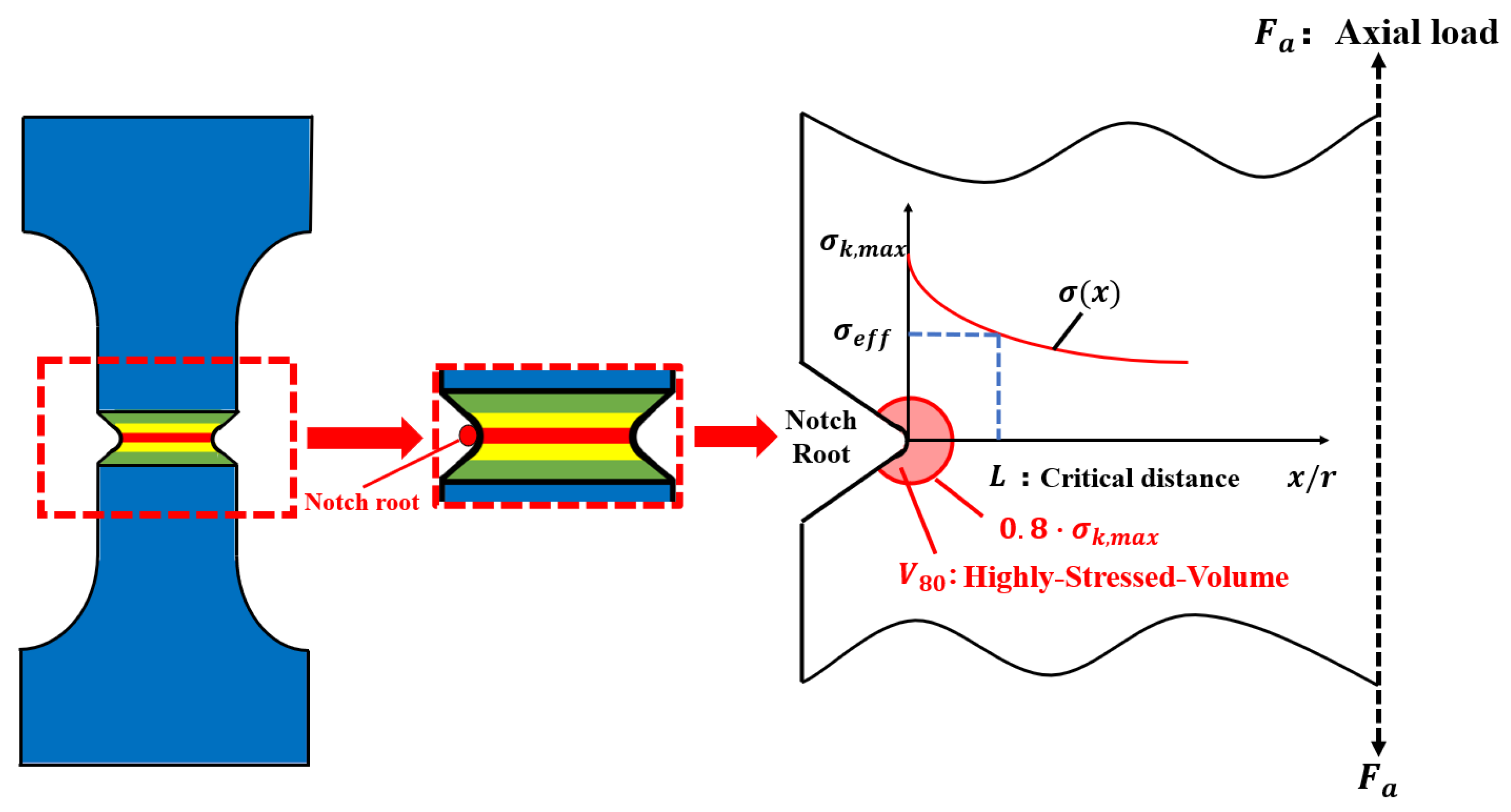
2.1. Theory of Critical Distance
2.2. Highly Stressed Volume
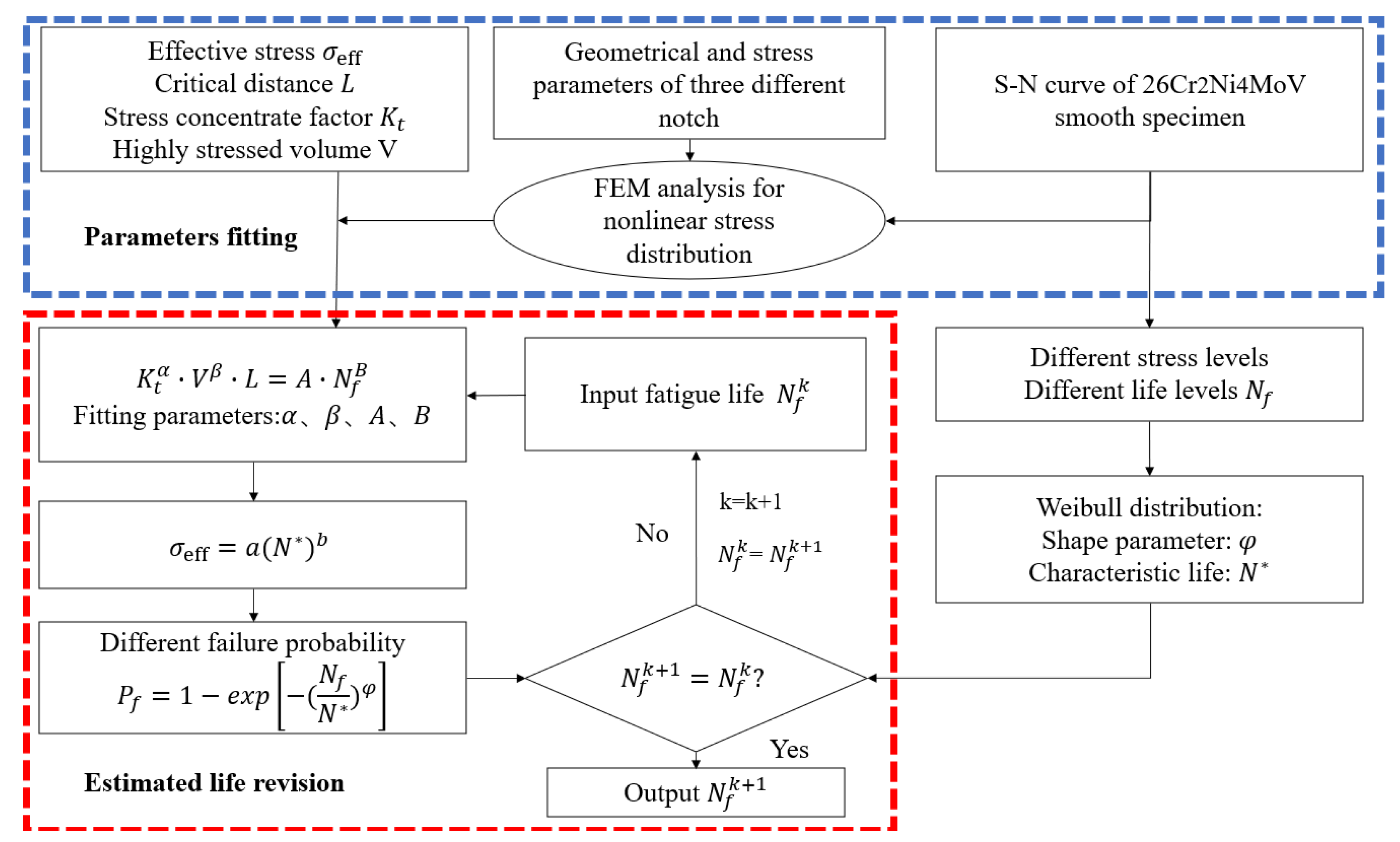
2.3. Theoretical Model Construction
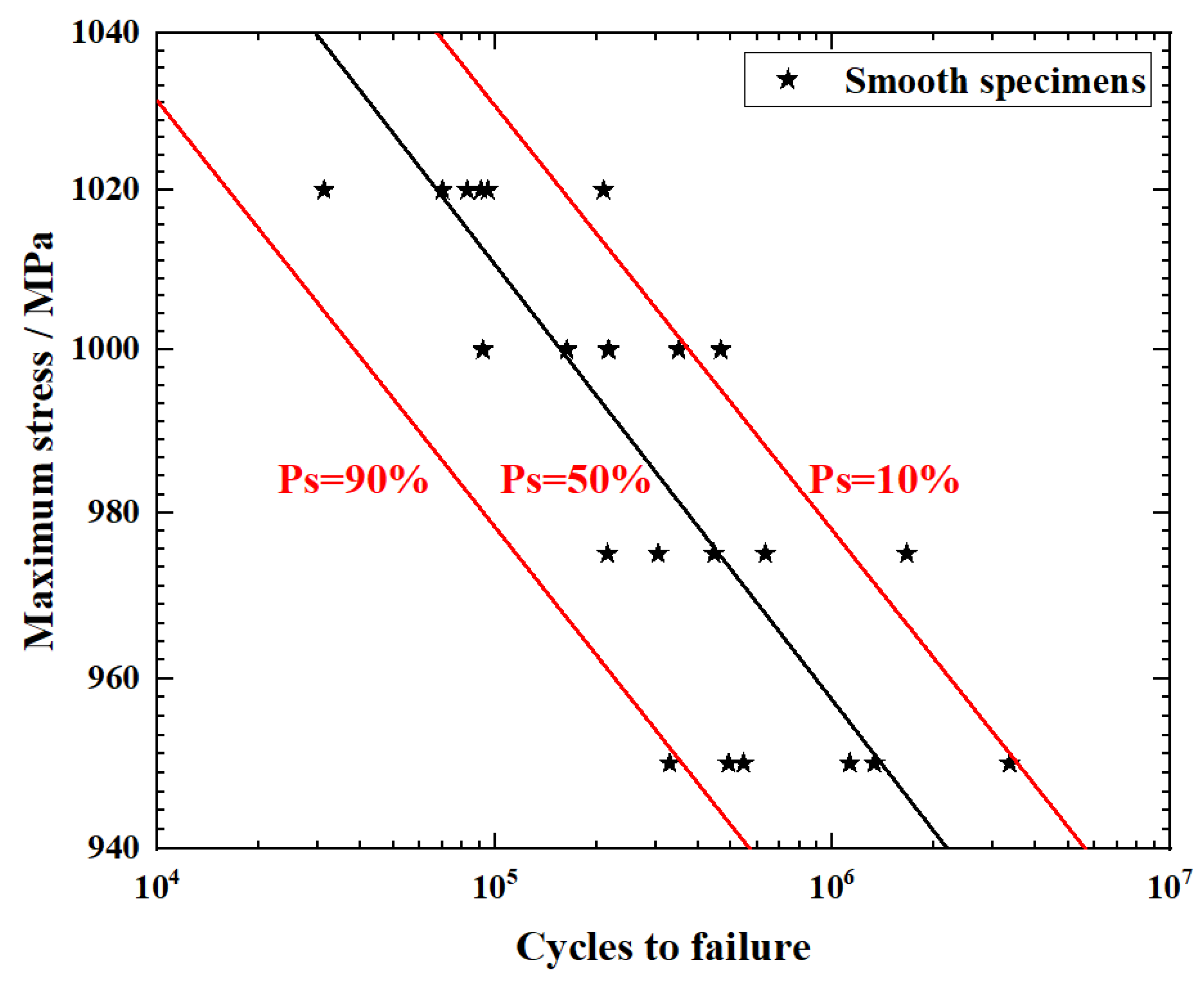
2.4. Weibull Probabilistic Analysis
- Use the Weibull distribution to describe the dispersion of fatigue life of the smooth specimens, and obtain the Weibull scale parameters and shape parameters ;
- Perform finite element analysis on the notched specimens to obtain the linear elastic stress distribution at the notch root and calculate the effective stress ;
- Obtain fatigue life distribution of the predicted notched specimen. The expression is as follows:
2.5. Parameter Determination
- Based on the fatigue data of smooth and notched specimen, and the FEM analysis for linear stress distribution of different notches. The , are determined by smooth specimen under different stress levels and , , , and can be fitted by the data of highly stressed volume V, stress concentration factor Kt and critical distance L;
- Input life , calculated L, receive , and compute through Equation (14);
- Determine value of and , and output the if above two values are equal. If not, repeat this calculation cycle until .
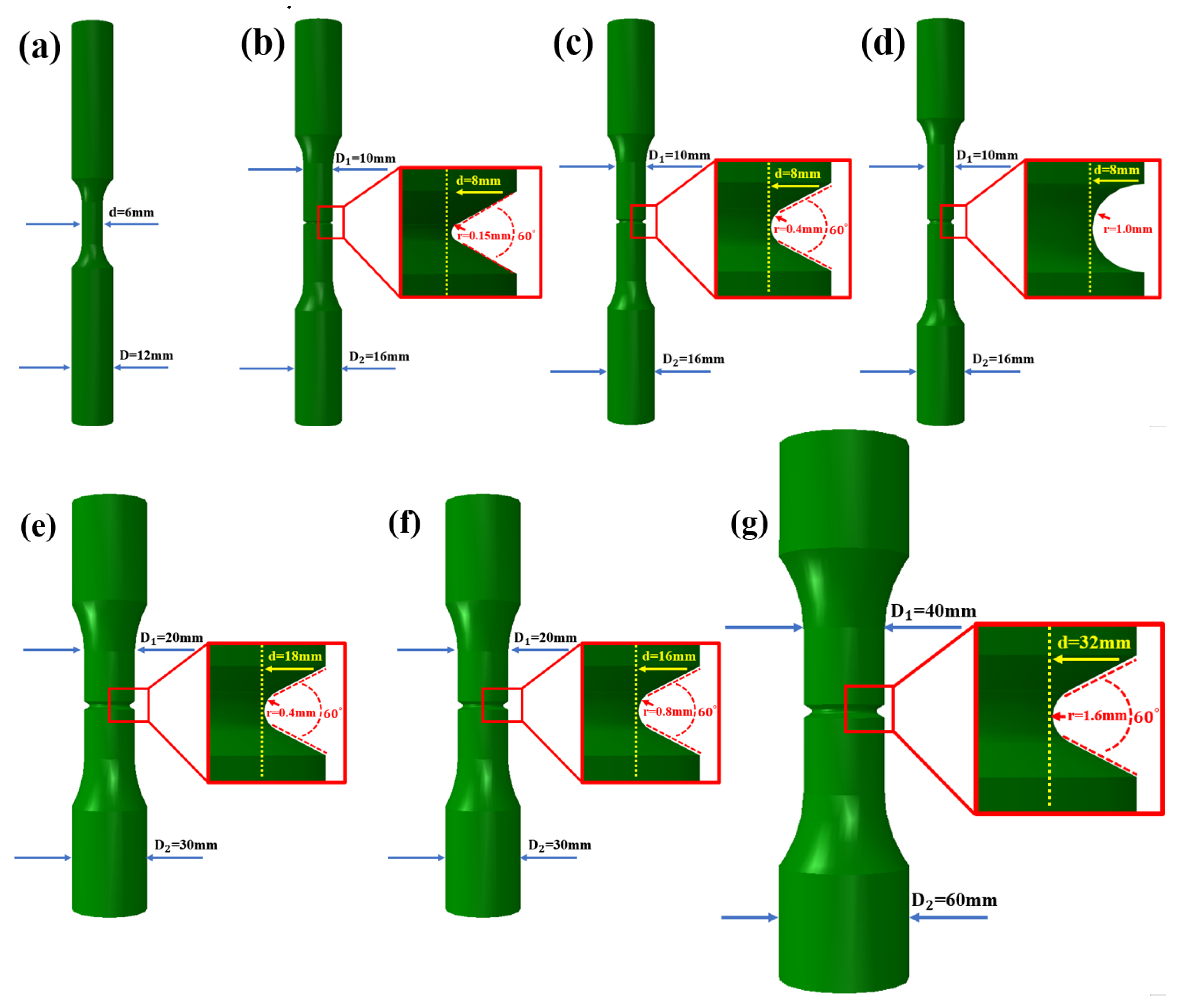
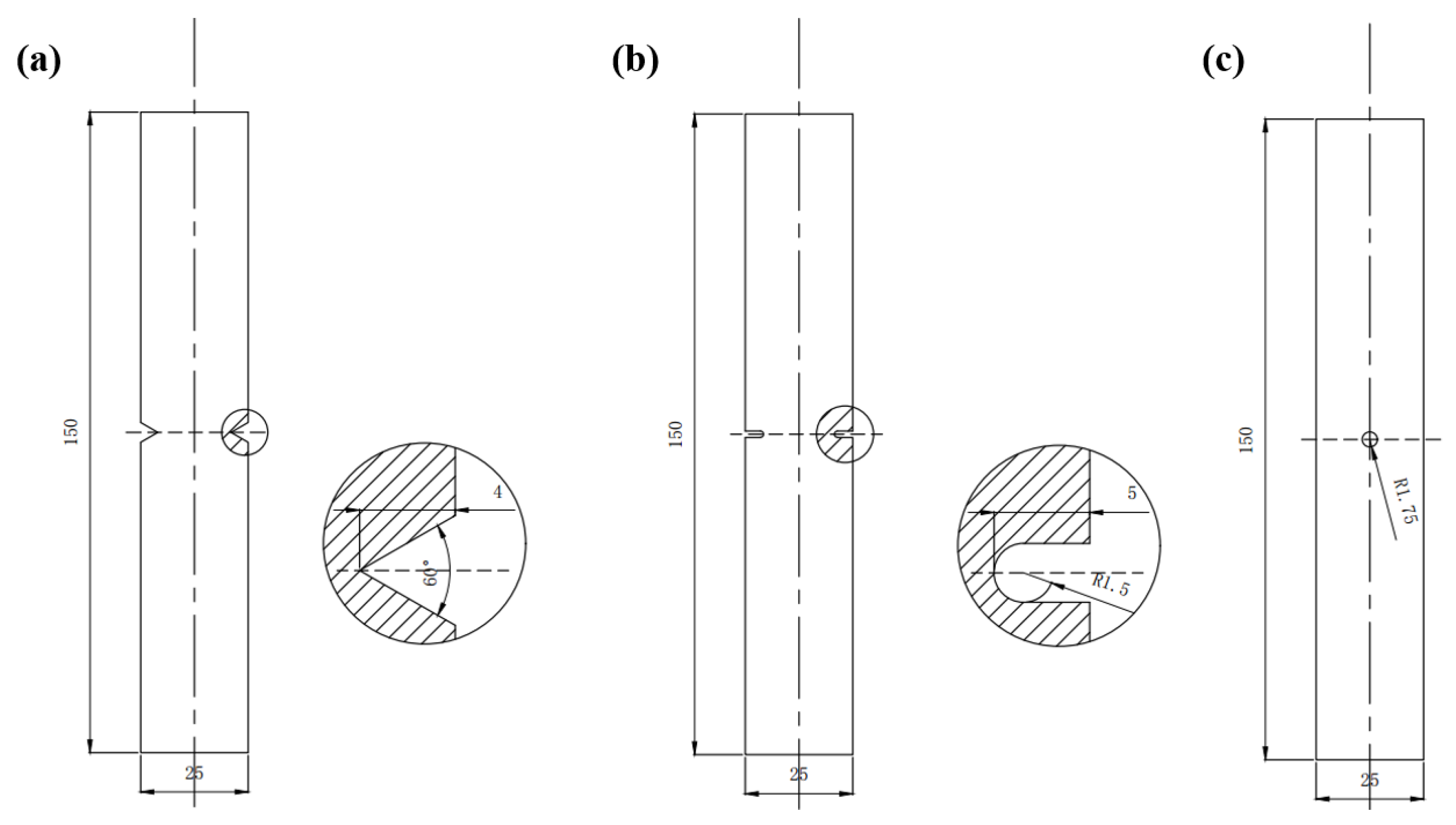
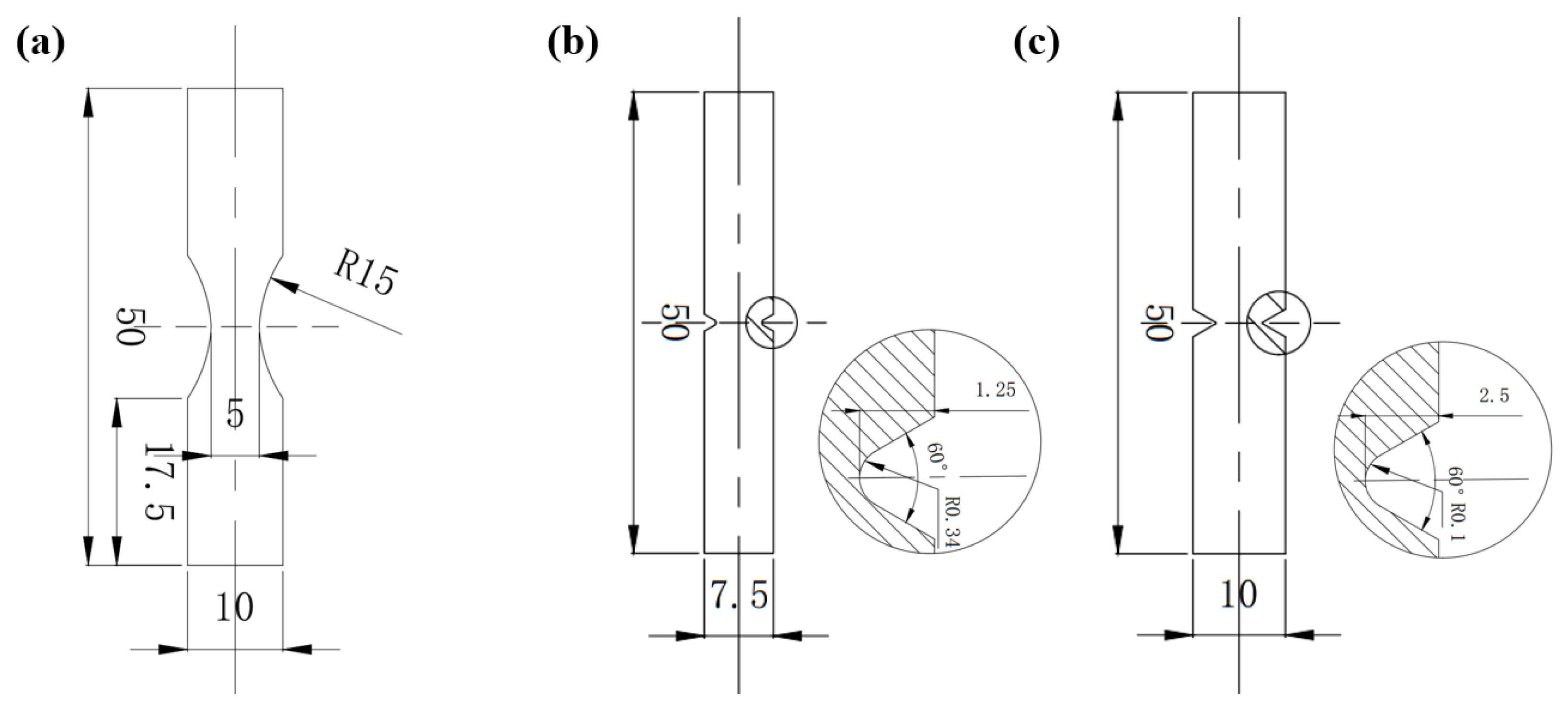
3. Materials and Methods
3.1. Material
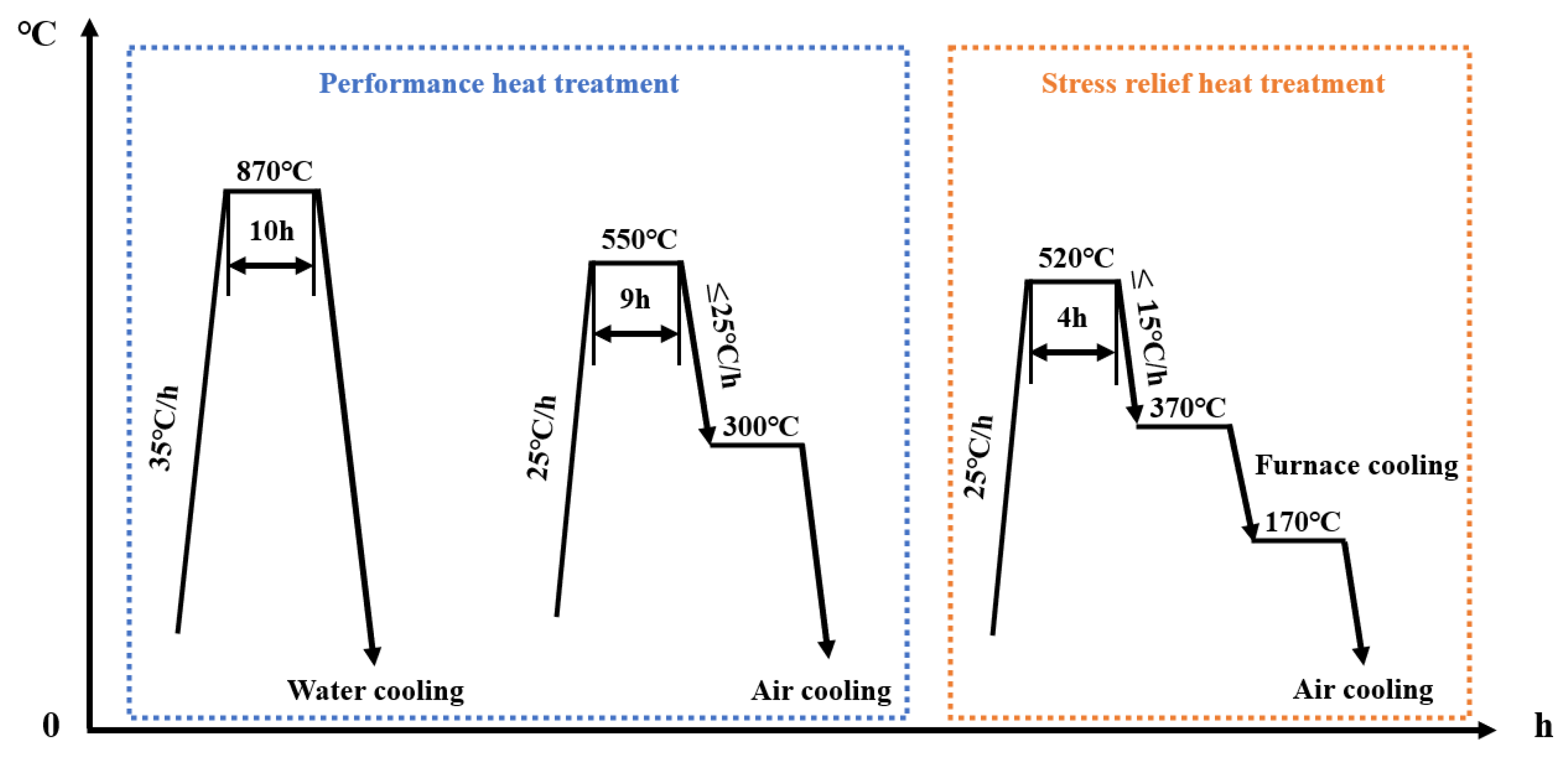
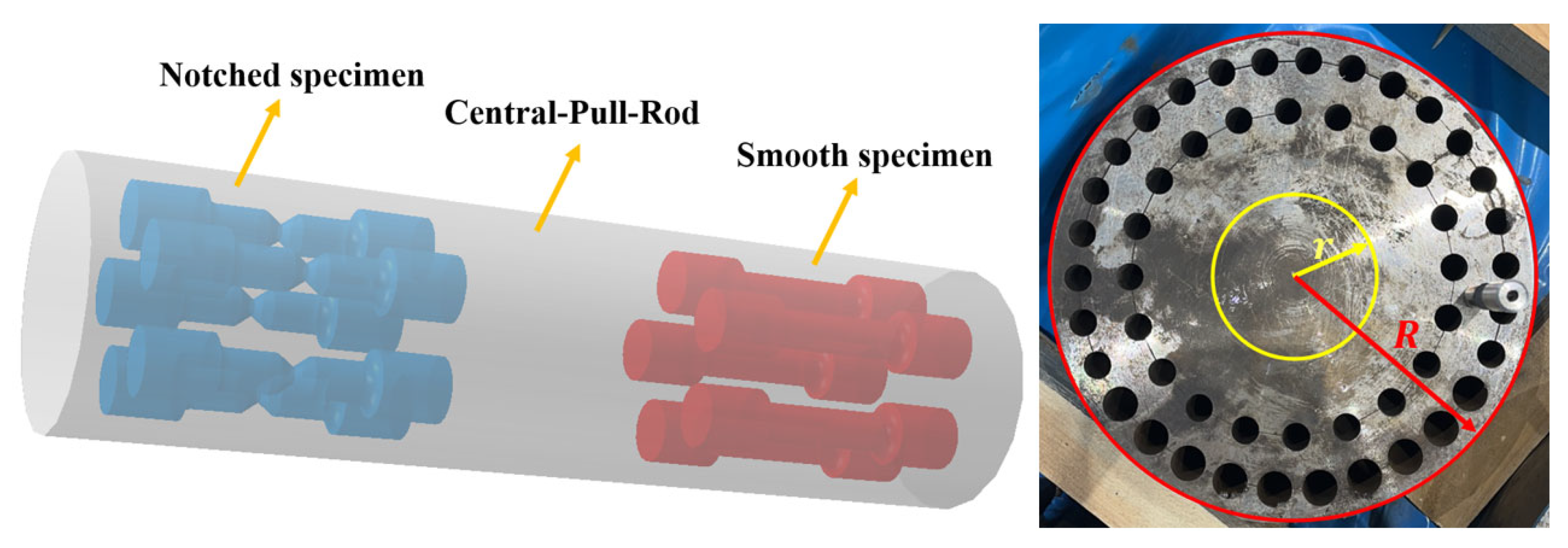
3.2. Test Condition and Methods
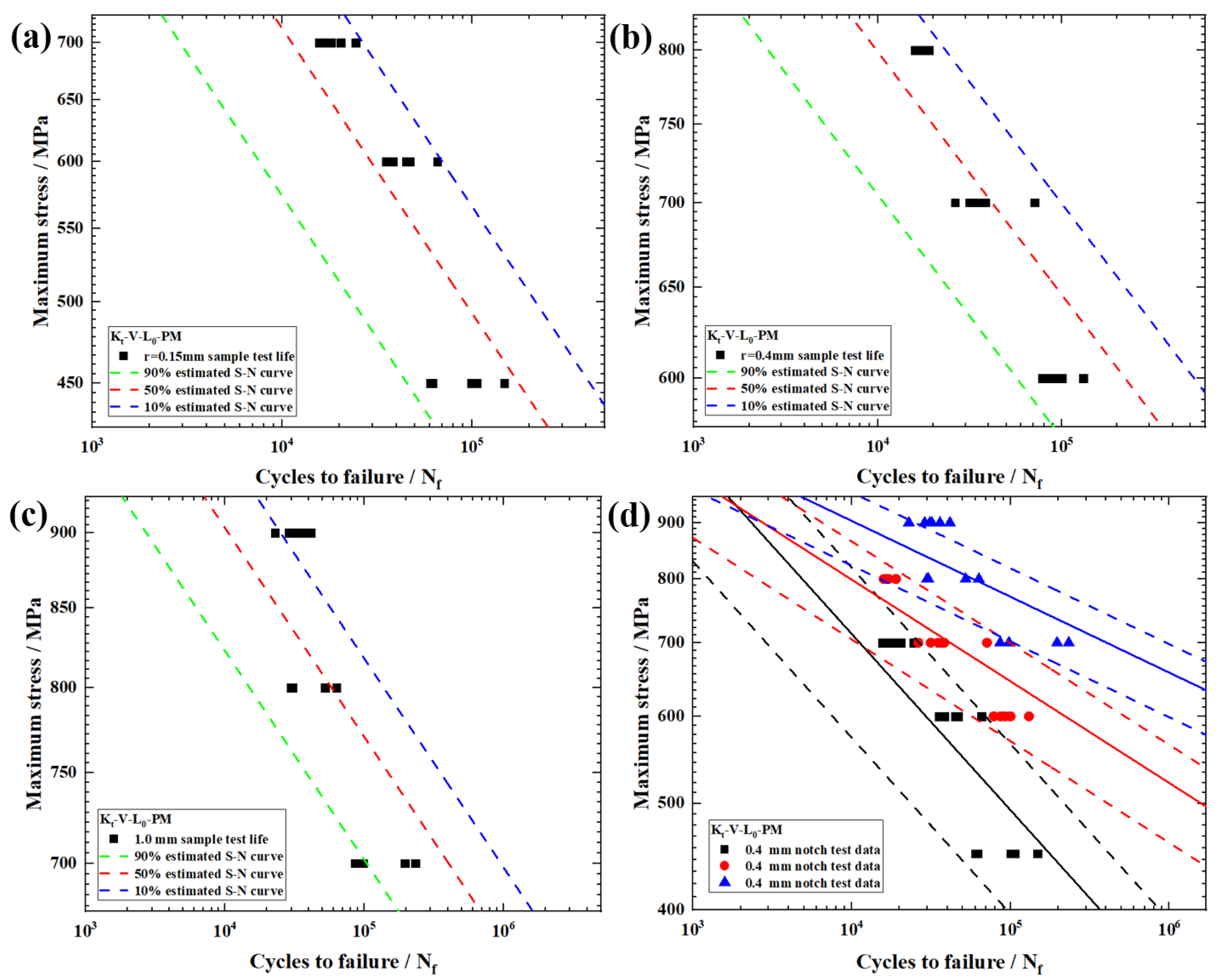
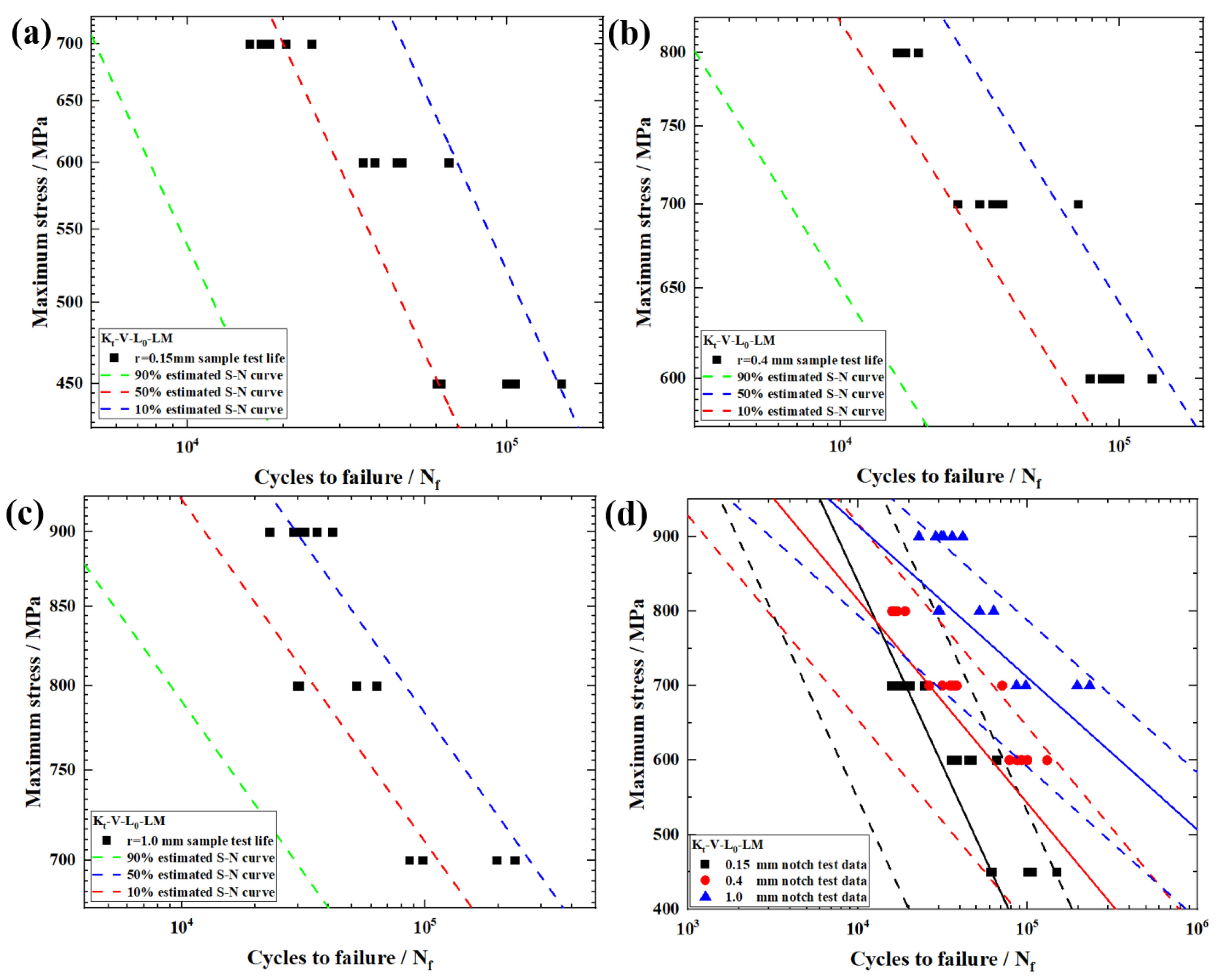
4. Results and Discussion
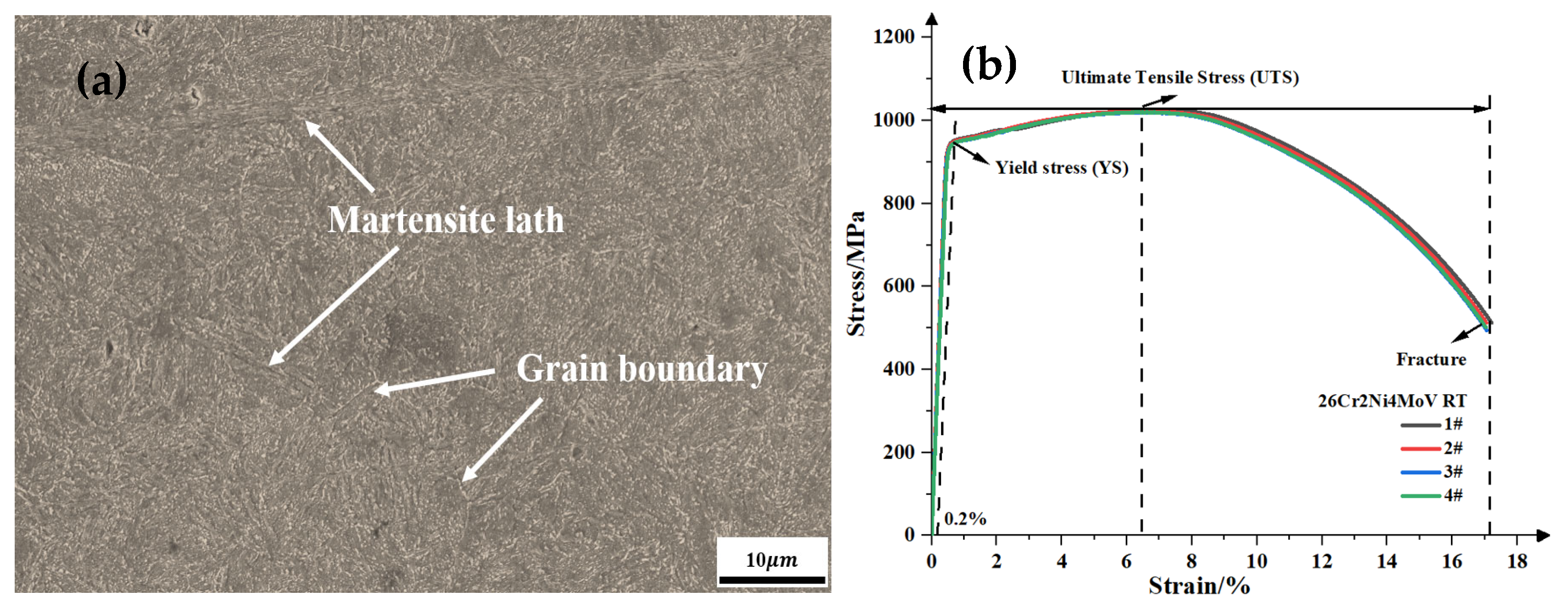
4.1. Microstructure and Tensile Properties
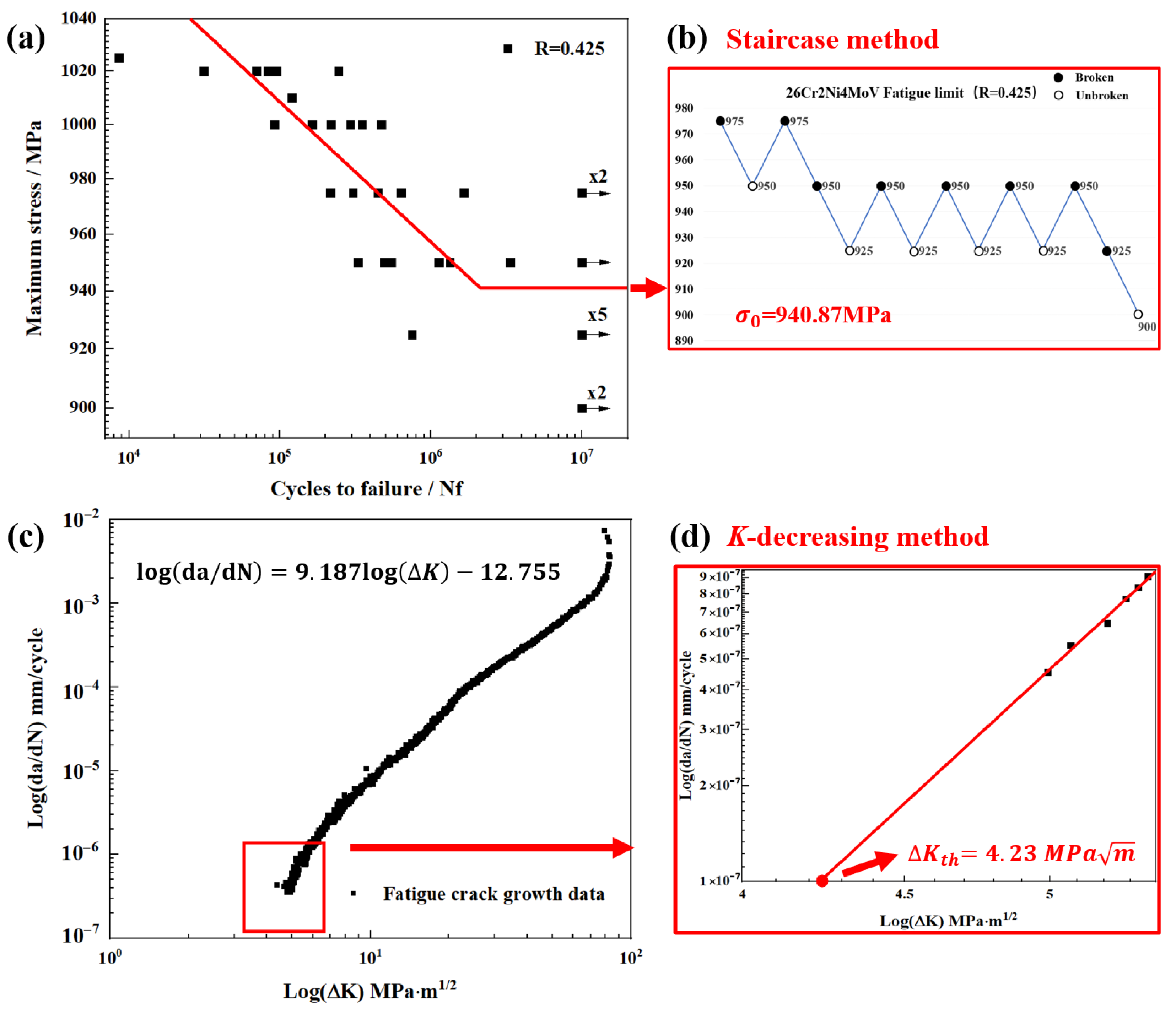
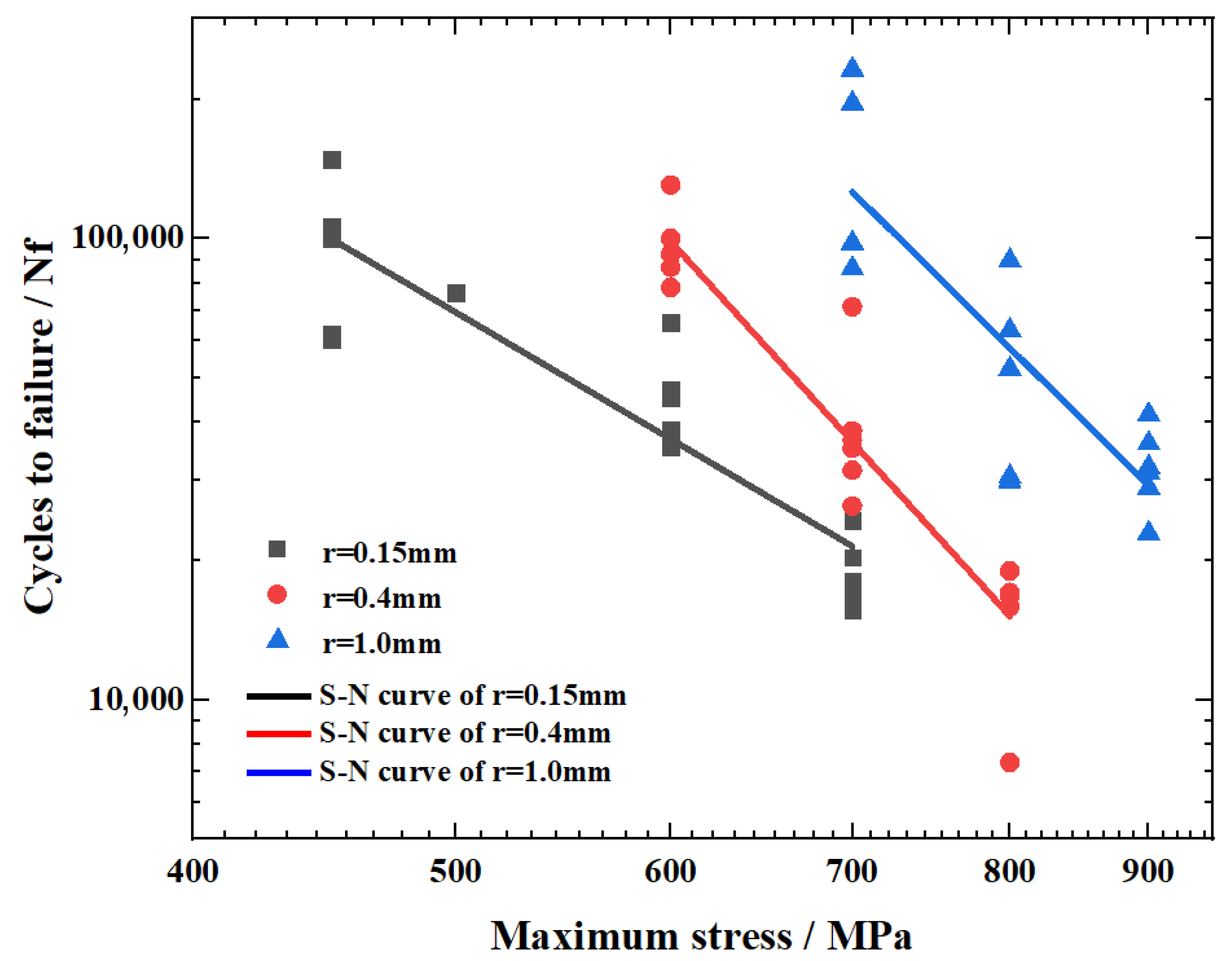
4.2. Fatigue Properties
4.3. Fatigue Fracture Analysis
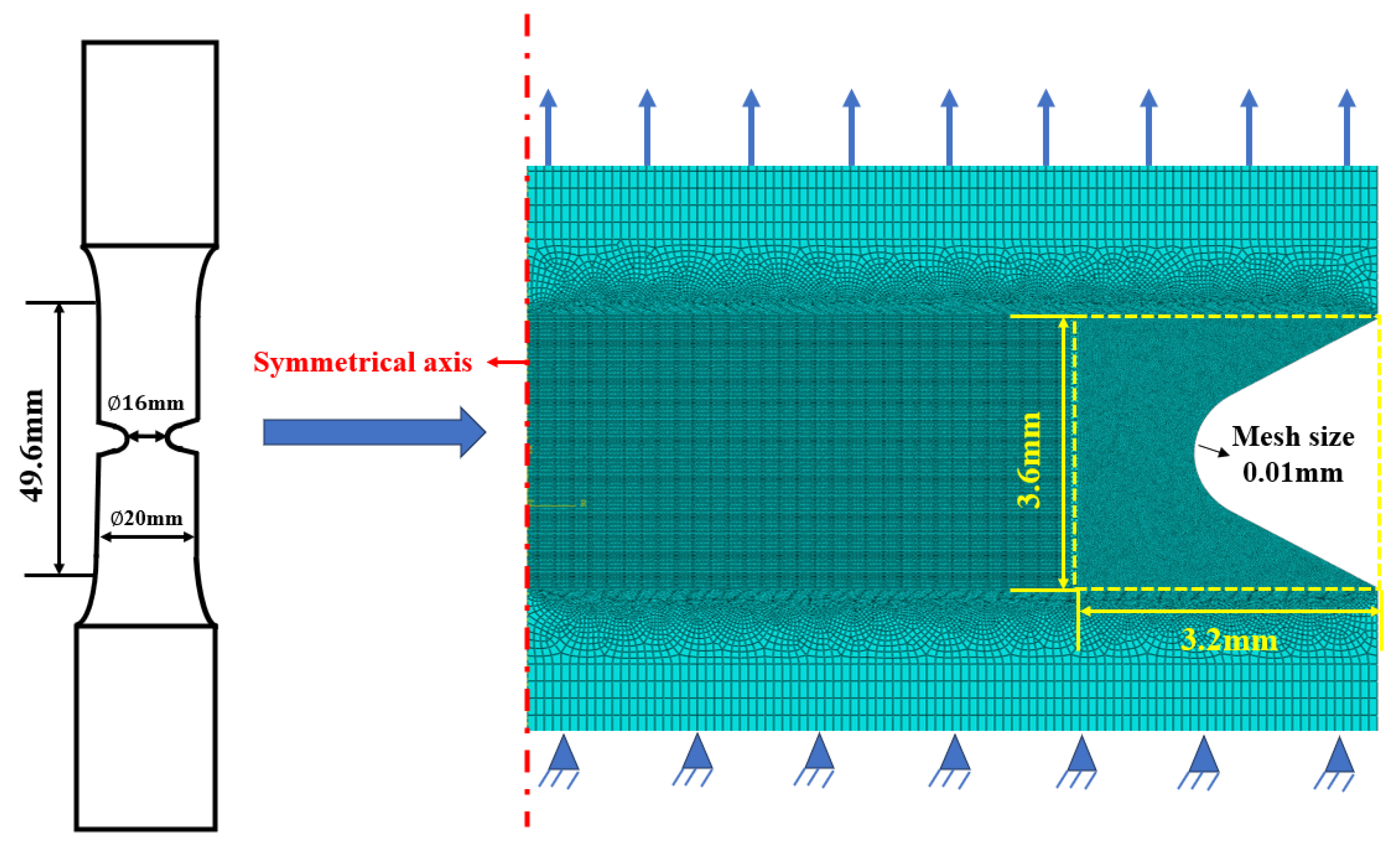
4.4. Finite Element Result
- Perform axisymmetric finite element analysis on notched specimens in ABAQUS to extract the maximum stress;
- Second item; extract the cross-sectional area ()of the high-stress region;
- Import the cross-sectional area after obtaining high stress into AutoCAD;
- Perform axisymmetric rotation and calculate volume ().
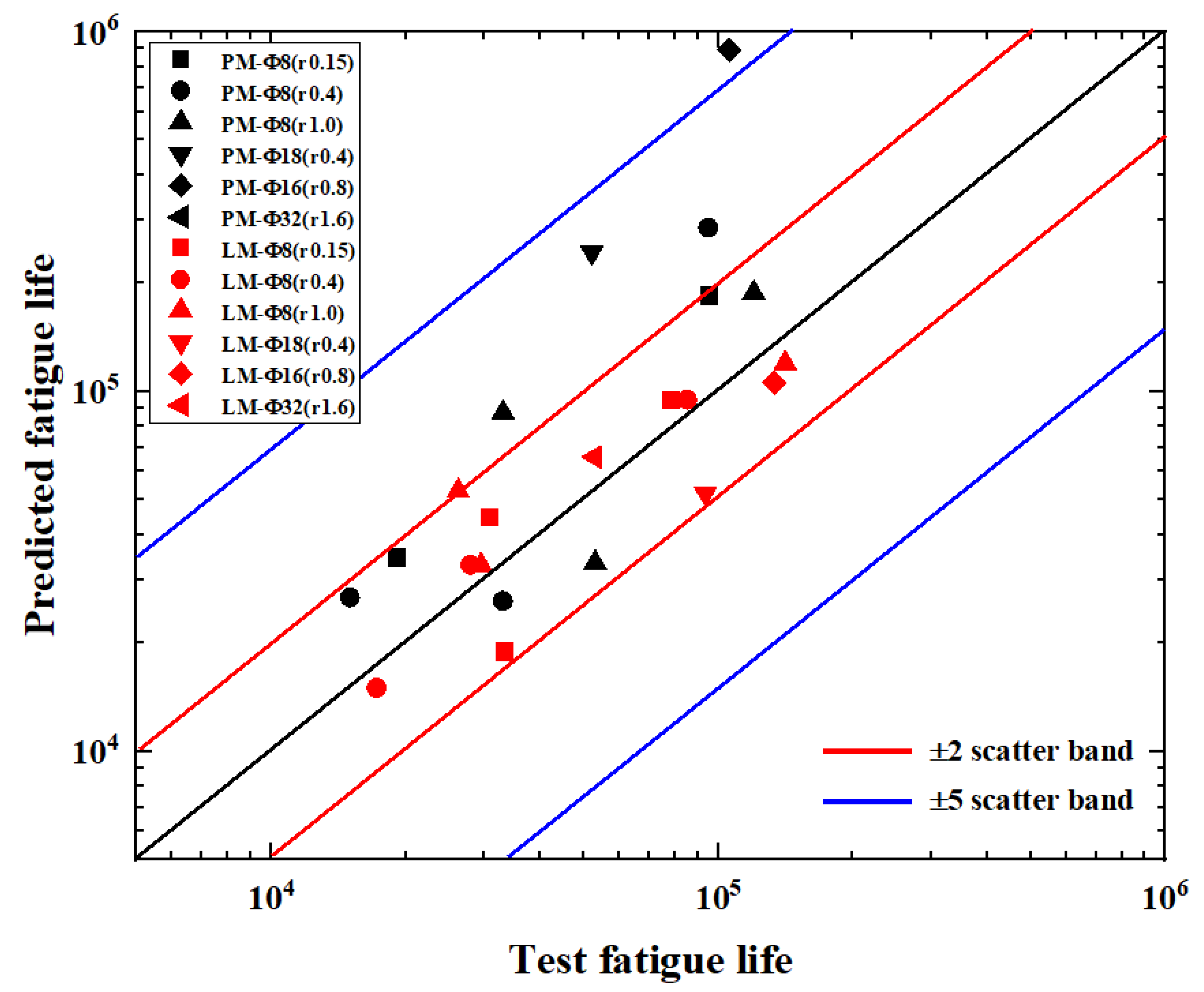
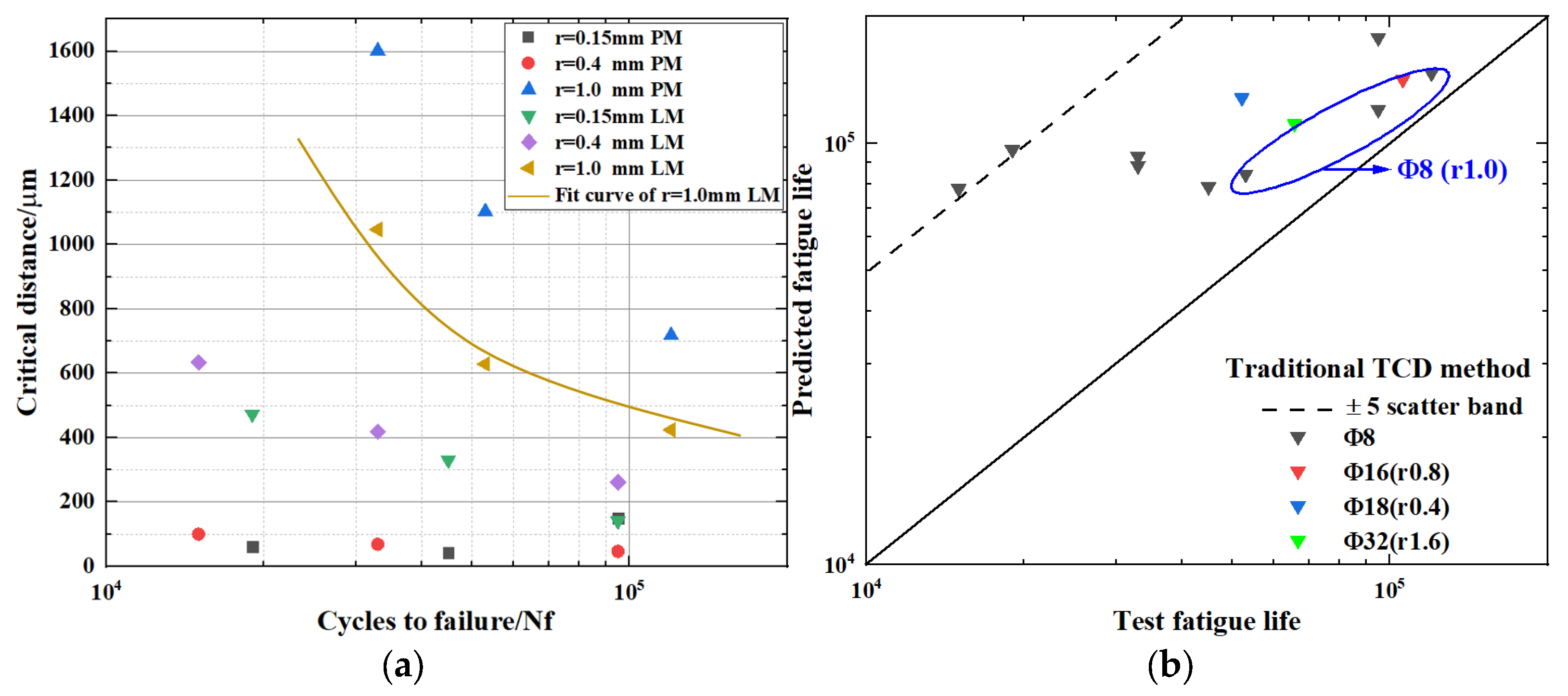
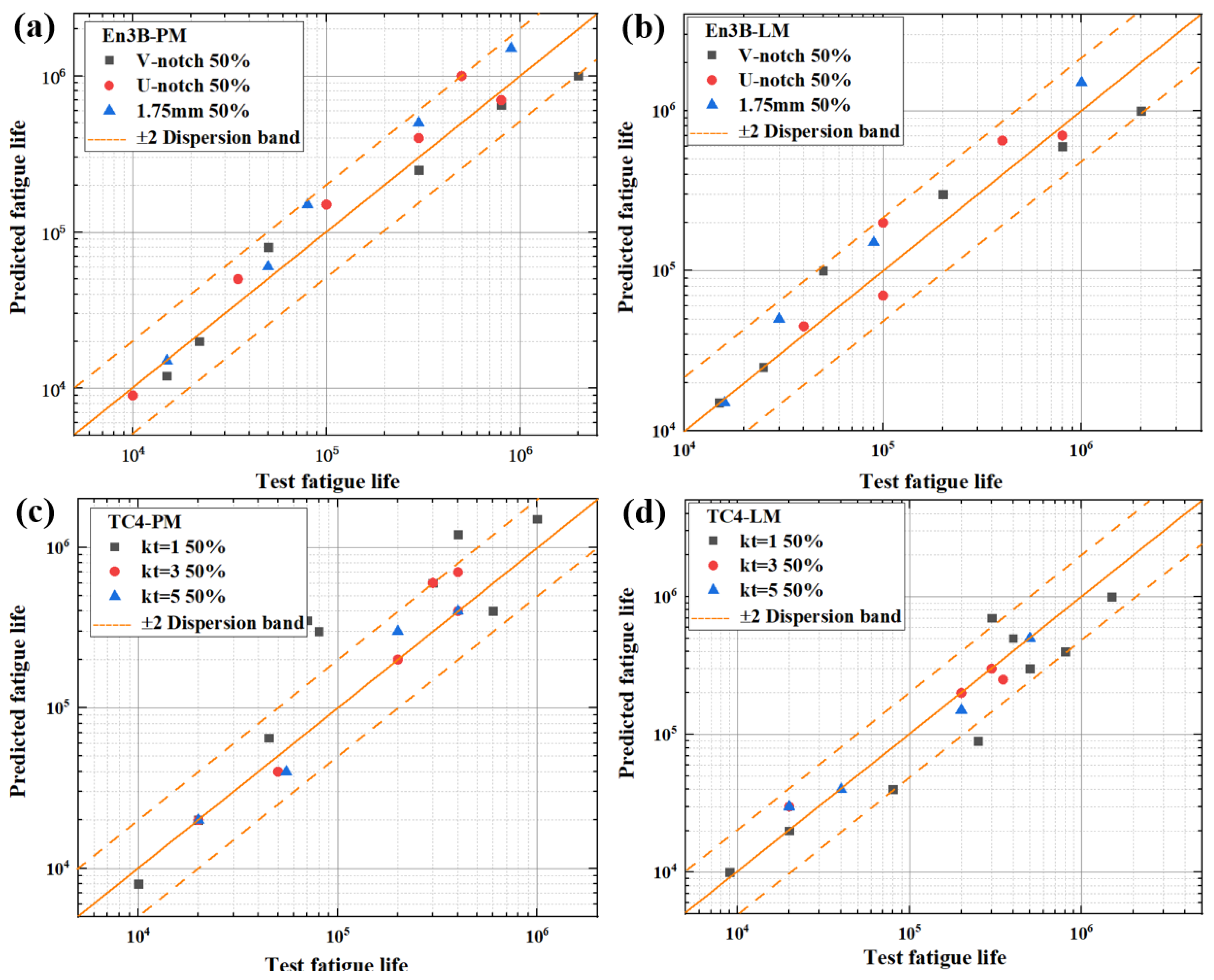
5. Model Validation and Comparison
- PM (26Cr2Ni4MoV):
- LM (26Cr2Ni4MoV):
- En3B PM:
- En3B LM:
- TC4 PM:
- TC4 LM:
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LCF | Low cycle fatigue |
| MCF | Middle cycle fatigue |
| HSV | Highly stressed volume |
| TCD | Theory of critical distances |
| SCF | Stress concentration factor |
| PM | Point Method |
| LM | Line Method |
| AM | Area Method |
| VM | Volume Method |
| FEM | Finite element method |
| FCG | Fatigue crack propagation |
| FS | Crack initiation zone |
| CP | Crack propagation zone |
| FF | Rapid fracture zone |
| LES | Linear elastic stress |
| ICP | Inductively coupled plasma emission spectroscopy |
References
- Härkegård, G.; Denk, J.; Stärk, K. Growth of naturally initiated fatigue cracks in ferritic gas turbine rotor steels. Int. J. Fatigue 2005, 27, 715–726. [Google Scholar] [CrossRef]
- Tang, Y.; Song, Y.; Yin, G.; Nie, Y. Notch fatigue life prediction model considering stress gradient influence depth and weight function. Metals 2023, 13, 539. [Google Scholar] [CrossRef]
- He, J.C.; Zhu, S.P.; Niu, X.P.; Liao, D.; Wang, Q.Y. Notch fatigue life prediction under size effect: Stress gradient-based theory of critical distance. J. Mech. Eng. 2023, 59, 90–106. [Google Scholar]
- Ni, H.; Guo, S.; Zhang, S.; Lei, H. Experimental and Numerical Investigation of Constant-Amplitude Fatigue Performance in Welded Joints of Steel Tubular Flange Connections for Steel Structures. Buildings 2025, 15, 1574. [Google Scholar] [CrossRef]
- Xu, W.; Ren, Y.; Xiao, S.; Liu, B. A finite crack growth energy release rate for elastic-plastic fracture. J. Mech. Phys. Solids 2023, 181, 105447. [Google Scholar] [CrossRef]
- Mirzaei, A.M.; Mirzaei, A.H.; Sapora, A.; Cornetti, P. Strain based finite fracture mechanics for fatigue life prediction of additively manufactured samples. Int. J. Fract. 2025, 249, 44. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Hembara, O.; Chepil, O.; Hrynenko, M.; Hembara, T. A new energy approach to predicting fracture resistance in metals. Materials 2023, 16, 1566. [Google Scholar] [CrossRef]
- Amsterdam, E.; Wiegman, J.W.E.; Nawijn, M.; De Hosson, J.T.M. On the strain energy release rate and fatigue crack growth rate in metallic alloys. Eng. Fract. Mech. 2023, 286, 109292. [Google Scholar] [CrossRef]
- De Jesus, A.M.P.; Pereira, H.F.S.G.; Ribeiro, A.S.; Fernandes, A.A. Cyclic elastoplastic analysis of structures concerning a fatigue assessment according to the local strain approach: An overview. J. Press. Vessel. Technol. 2008, 130, 034503. [Google Scholar] [CrossRef]
- Pan, X.; Liu, J.; Li, Y.; Hua, F.; Chen, X.; Zhang, Z. Finite element analysis of stress field and fatigue life prediction of notched specimens under multiaxial load. Int. J. Struct. Integr. 2023, 14, 663–680. [Google Scholar] [CrossRef]
- Rice, J.R.; Rosengren, G.F. Plane strain deformation near a crack tip in a power-law hardening material. J. Mech. Phys. Solids 1968, 16, 1–12. [Google Scholar] [CrossRef]
- Neuber, H. Theory of Notch Stresses: Principles for Exact Stress Calculation; J.W. Edwards: Braintree, MA, USA, 1946. [Google Scholar]
- Taylor, D. Geometrical effects in fatigue: A unifying theoretical model. Int. J. Fatigue 1999, 21, 413–420. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, K.; Hu, Z.; Chen, T.; Zhang, W.; Jin, K.; Sun, C.; Susmel, L.; Wei, B. A modified highly stressed volume (HSV) method to predict fatigue life considering the critical crack size. Int. J. Fatigue 2023, 172, 107644. [Google Scholar] [CrossRef]
- He, J.C.; Zhu, S.P.; Luo, C.; Li, W.; Liu, Q.; He, Y.; Wang, Q. Probabilistic notch fatigue assessment under size effect using micromechanics-based critical distance theory. Int. J. Fatigue 2024, 183, 108280. [Google Scholar] [CrossRef]
- Shuai, Z.; Zhu, S.P.; He, J.C.; Liao, D.; Correia, J.; Macek, W.; Branco, R.; Wang, Q. Fatigue life prediction of notched components under size effect using strain energy reformulated critical distance theory. Int. J. Fatigue 2023, 175, 107805. [Google Scholar] [CrossRef]
- Liu, J.; Lu, J.; Zhou, F.; Zhao, H.; Wang, J. Multiaxial fatigue life prediction model for notched specimen based on modified energy gradient and critical plane method. Theor. Appl. Fract. Mech. 2023, 125, 103880. [Google Scholar] [CrossRef]
- Taylor, D.; O’Donnell, M. Notch geometry effects in fatigue: A conservative design approach. Eng. Fail. Anal. 1994, 1, 275–287. [Google Scholar] [CrossRef]
- Susmel, L. On the estimation of the material fatigue properties required to perform the multiaxial fatigue assessment. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 565–585. [Google Scholar] [CrossRef]
- He, J.C.; Zhu, S.P.; Taddesse, A.T.; Niu, X. Evaluation of critical distance, highly stressed volume, and weakest-link methods in notch fatigue analysis. Int. J. Fatigue 2022, 162, 106950. [Google Scholar] [CrossRef]
- Fryer, Y.D.; Bailey, C.; Cross, M.; Lai, C.H. A control volume procedure for solving the elastic stress-strain equations on an unstructured mesh. Appl. Math. Model. 1991, 15, 639–645. [Google Scholar] [CrossRef]
- Marques, J.M.E.; Mžourek, M.; Papuga, J.; Růžička, M.; Benasciutti, D. A probabilistic stress-life model supported by weakest link principle and highly-stressed volume/surface area concepts. Int. J. Fatigue 2024, 178, 108006. [Google Scholar] [CrossRef]
- Ghazal, M.G.M. A new extension of the modified Weibull distribution with applications for engineering data. Probabilistic Eng. Mech. 2023, 74, 103523. [Google Scholar] [CrossRef]
- Strzelecki, P. Determination of fatigue life for low probability of failure for different stress levels using 3-parameter Weibull distribution. Int. J. Fatigue 2021, 145, 106080. [Google Scholar] [CrossRef]
- Shahriari, M.; Shahrasbi, H.; Zaretalab, A. Reliability analysis of lifetime systems based on Weibull distribution. Int. J. Nonlinear Anal. Appl. 2024, 15, 321–329. [Google Scholar]
- Karolczuk, A. Validation of the weakest link approach and the proposed Weibull based probability distribution of failure for fatigue design of steel welded joints. Eng. Fail. Anal. 2016, 67, 46–62. [Google Scholar] [CrossRef]
- China Aeronautical Materials Handbook Editorial Committee. China Aeronautical Materials Handbook vol. 4 Titanium Alloy; China Standards Press: Beijing, China, 2002. [Google Scholar]
- Susmel, L.; Taylor, D. A novel formulation of the theory of critical distances to estimate lifetime of notched components in the medium-cycle fatigue regime. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 567–581. [Google Scholar] [CrossRef]
- Susmel, L.; Taylor, D. On the Use of the Theory of Critical Distances to Estimate KIc and ∆ Kth from Experimental Results Generated by Testing Standard Notches. Key Eng. Mater. 2010, 417, 25–28. [Google Scholar]
- Lipp, K.; Baumgartner, J.; Beiss, P. Fatigue design of sintered steel components: Effect of stress concentrations and mean stresses on local strength using highest stressed volume approach. Powder Metall. 2013, 56, 337–341. [Google Scholar] [CrossRef]
- Sonsino, C.M.; Moosbrugger, E. Fatigue design of highly loaded short-glass-fibre reinforced polyamide parts in engine compartments. Int. J. Fatigue 2008, 30, 1279–1288. [Google Scholar] [CrossRef]
- Akiniwa, Y.; Miyamoto, N.; Tsuru, H.; Tanaka, K. Notch effect on fatigue strength reduction of bearing steel in the very high cycle regime. Int. J. Fatigue 2006, 28, 1555–1565. [Google Scholar] [CrossRef]
- Ren, W.; Nicholas, T. Notch size effects on high cycle fatigue limit stress of Udimet 720. Mater. Sci. Eng. A 2003, 357, 141–152. [Google Scholar] [CrossRef]
- Cunningham, B.M.D.; Evangelou, A.; You, C.; Morris, A.; Wise, J.; Reed, P.A.; Hamilton, A.R. Fatigue crack initiation and growth behavior in a notch with periodic overloads in the low-cycle fatigue regime of FV566 ex-service steam turbine blade material. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 546–564. [Google Scholar] [CrossRef]
- Sakane, M.; Zhang, S.; Kim, T.J. Notch effect on multiaxial low cycle fatigue. Int. J. Fatigue 2011, 33, 959–968. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.P.; Correia, J.A.F.O.; De, J.A.M.; Berto, F. Recent advances on notch effects in metal fatigue: A review. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 637–659. [Google Scholar] [CrossRef]
- Mäde, L.; Schmitz, S.; Gottschalk, H.; Beck, T. Combined notch and size effect modeling in a local probabilistic approach for LCF. Comput. Mater. Sci. 2018, 142, 377–388. [Google Scholar] [CrossRef]
- Ai, Y.; Zhu, S.P.; Liao, D.; Correia, J.A.; De, J.A.M.; Keshtegar, B. Probabilistic modelling of notch fatigue and size effect of components using highly stressed volume approach. Int. J. Fatigue 2019, 127, 110–119. [Google Scholar] [CrossRef]
- Wang, R.; Li, D.; Hu, D.; Meng, F.; Liu, H.; Ma, Q. A combined critical distance and highly-stressed-volume model to evaluate the statistical size effect of the stress concentrator on low cycle fatigue of TA19 plate. Int. J. Fatigue 2017, 95, 8–17. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, Z.; Deng, W.; Wang, F.; Wang, Z. A novel line method of the theory of critical distance for predicting the notched specimen’s fatigue life based on the relative stress gradient variation. Appl. Phys. A 2025, 131, 1–15. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Wang, P.; Chen, H.; Wang, Y.; Liu, Z.; Liu, X. The plastic strain energy density-based fatigue life prediction method incorporating geometric-mechanical-microstructural characteristic parameters of machined surface integrity. Results Eng. 2025, 28, 107299. [Google Scholar] [CrossRef]
- Jirandehi, A.P.; Khonsari, M.M. On the determination of cyclic plastic strain energy with the provision for microplasticity. Int. J. Fatigue 2021, 142, 105966. [Google Scholar] [CrossRef]
- Lyu, H.; Hamid, M.; Ruimi, A.; Zbib, H.M. Stress/strain gradient plasticity model for size effects in heterogeneous nano-microstructures. Int. J. Plast. 2017, 97, 46–63. [Google Scholar] [CrossRef]
- As’ad, F.; Avery, P.; Farhat, C. A mechanics-informed artificial neural network approach in data-driven constitutive modeling. Int. J. Numer. Methods Eng. 2022, 123, 2738–2759. [Google Scholar] [CrossRef]
- Conoscenti, M.A.; Smith, N.J.; Fanselow, M.S. Dissociable consequences of moderate and high volume stress are mediated by the differential energetic demands of stress. PLoS ONE 2022, 17, e0273803. [Google Scholar] [CrossRef]
- Braun, M.; Müller, A.M.; Milaković, A.S.; Fricke, W.; Ehlers, S. Requirements for stress gradient-based fatigue assessment of notched structures according to theory of critical distance. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1541–1554. [Google Scholar] [CrossRef]
- Benedetti, M.; Santus, C. Statistical properties of threshold and notch derived estimations of the critical distance according to the line method of the theory of critical distances. Int. J. Fatigue 2020, 137, 105656. [Google Scholar] [CrossRef]
- Cicero, S.; Madrazo, V.; Carrascal, I.A. Analysis of notch effect in PMMA using the Theory of Critical Distances. Eng. Fract. Mech. 2012, 86, 56–72. [Google Scholar] [CrossRef]
- Neuber, H. Theory of Notch Stresses: Principles for Exact Calculation of Strength with Reference to Structural Form and Material; J.W. Edwards: Braintree, MA, USA, 1961. [Google Scholar]
- Peterson, T.D. A refined technique for measuring crystal size distributions in thin section. Contrib. Mineral. Petrol. 1996, 124, 395–405. [Google Scholar] [CrossRef]
- Taylor, D. Applications of the theory of critical distances in failure analysis. Eng. Fail. Anal. 2011, 18, 543–549. [Google Scholar] [CrossRef]
- Bellett, D.; Taylor, D.; Marco, S.; Mazzeo, E.; Guillois, J.; Pircher, T. The fatigue behaviour of three-dimensional stress concentrations. Int. J. Fatigue 2005, 27, 207–221. [Google Scholar] [CrossRef]
- Yang, X.; Wang, J.; Liu, J. High temperature LCF life prediction of notched DS Ni-based superalloy using critical distance concept. Int. J. Fatigue 2011, 33, 1470–1476. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X. HCF strength estimation of notched Ti–6Al–4V specimens considering the critical distance size effect. Int. J. Fatigue 2012, 40, 97–104. [Google Scholar] [CrossRef]
- Al, Z.I.; Razavi, S.M.J.; Berto, F.; Susmel, L. The critical distance method to estimate the fatigue strength of notched additively manufactured titanium alloys. Procedia Struct. Integr. 2020, 28, 994–1001. [Google Scholar] [CrossRef]
- Kuguel, R. A relation between theoretical stress concentration factor and fatigue notch factor deduced from the concept of highly stressed volume. Proc. ASTM 1961, 61, 732–748. [Google Scholar]
- Lin, C.K.; Lee, W.J. Effects of highly stressed volume on fatigue strength of Austempered Ductile Irons. Int. J. Fatigue 1998, 20, 301–307. [Google Scholar] [CrossRef]
- Susmel, L.; Taylor, D. The Theory of Critical Distances as an alternative experimental strategy for the determination of KIc and ΔKth. Eng. Fract. Mech. 2010, 77, 1492–1501. [Google Scholar] [CrossRef]


| C | Cr | Ni | Mo | V | Mn | Si |
|---|---|---|---|---|---|---|
| 0.3 | 1.5 ~ 2.0 | 3.25 ~ 3.75 | 0.3 ~ 0.6 | 0.07 ~ 0.15 | 0.2 ~ 0.4 | 0.17 ~ 0.37 |
| Material | /MPa | /MPa | Elongation/% | Reduction in Area/% |
|---|---|---|---|---|
| 26Cr2Ni4MoV | 950 | 1025 | 21.5 | 73 |
| 959 | 1023 | 19.5 | 73 | |
| 945 | 1019 | 21.0 | 76 | |
| 946 | 1020 | 20.5 | 74 | |
| Average | 947 | 1022 | 20.5 | 74 |
| Specimens Notch Diameter (Root Radius) | /MPa | /MPa | Maximum Stress Reduction Path | ||
|---|---|---|---|---|---|
| 8 (r = 0.15 mm) | 512 | 120 | 4.2 |  | 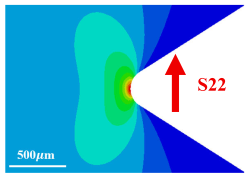 |
| 8 (r = 0.4 mm) | 337 | 120 | 2.8 | 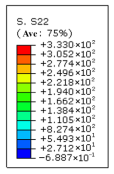 |  |
| 8 (r = 1.0 mm) | 250 | 120 | 2.1 |  |  |
| 16 (r = 0.8 mm) | 425 | 120 | 3.5 | 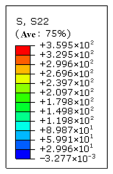 |  |
| 18 (r = 0.4 mm) | 340 | 120 | 2.8 | 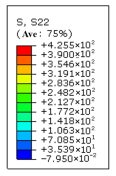 | 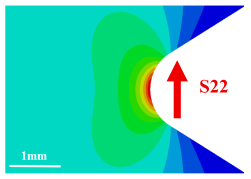 |
| 32 (r = 1.6 mm) | 331 | 120 | 2.8 | 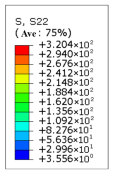 | 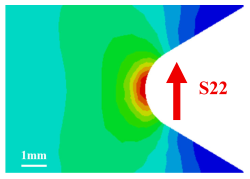 |
| Material | Ratio of High-Stress Zones | Notch Diameter (Root Radius) | Maximum Stress/ MPa | HAS—High-Stress Area /mm2 | HSV /mm3 |
|---|---|---|---|---|---|
| 26Cr2Ni4MoV | V-notch | 8 (r = 0.15 mm) | 450 | 0.021 | 0.546 |
| 600 | 0.068 | 1.633 | |||
| 700 | 0.168 | 3.995 | |||
| 8 (r = 0.4 mm) | 600 | 0.098 | 2.442 | ||
| 700 | 0.169 | 4.309 | |||
| 800 | 0.406 | 9.893 | |||
| 8 (r = 1.0 mm) | 700 | 0.328 | 8.024 | ||
| 800 | 0.527 | 14.128 | |||
| 900 | 1.659 | 39.403 | |||
| 18 (r = 0.4 mm) | 600 | 0.195 | 10.972 | ||
| 16 (r = 0.8 mm) | 600 | 0.379 | 19.377 | ||
| 32 (r = 1.6 mm) | 600 | 1.553 | 146.725 |
| Notch Type | Maximum Stress ( ) and Critical Distance () | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 8 (r = 0.15 mm) PM | Maximum Stress/ MPa | 700 | 600 | 450 | 400 | ||||
| /mm | 0.294 | 0.224 | 0.116 | 0.0184 | |||||
| 8 (r = 0.4 mm) PM | Maximum Stress/ MPa | 800 | 700 | 600 | |||||
| 0.468 | 0.332 | 0.226 | |||||||
| 8 (r = 1.0 mm) PM | Maximum Stress/ MPa | 900 | 800 | 700 | |||||
| 0.812 | 0.563 | 0.400 | |||||||
| 8 (r = 0.15 mm) LM | Maximum Stress/ MPa | 700 | 600 | 450 | 400 | ||||
| 0.107 | 0.091 | 0.049 | 0.046 | ||||||
| 8 (r = 0.4 mm) LM | Maximum Stress/ MPa | 800 | 700 | 600 | |||||
| 0.183 | 0.129 | 0.071 | |||||||
| 8 (r = 1.0 mm) LM | Maximum Stress/ MPa | 900 | 800 | 700 | |||||
| 0.281 | 0.208 | 0.128 | |||||||
| Material | R | |||
|---|---|---|---|---|
| 26Cr2Ni4MoV | 1341.219 | −0.0229 | 1.3904 | 0.9396 |
| Material | Notch Type | PM ()/mm | PM ()/mm |
|---|---|---|---|
| 26Cr2Ni4MoV | 16 (r = 0.8 mm) | 0.504 | 0.156 |
| 18 (r = 0.4 mm) | 0.409 | 0.129 | |
| 32 (r = 1.6 mm) | 1.087 | 0.340 |
| Material | E/MPa | /MPa | /MPa | /MPa | |
|---|---|---|---|---|---|
| En3B | 197,400 | 638.5 | 606.2 | 890.7 | 0.1635 |
| TC4 | 107,000 | 950.0 | 902.0 | 1032.0 | 0.0729 |
| Material | Notch Type | Kt |
|---|---|---|
| En3B | V-4 mm notch | 16.2 |
| U-R1.5 mm notch | 6.1 | |
| central hole-R1.75 mm | 3.1 | |
| TC4 | smooth | 1.0 |
| R0.34 mm notch | 3.0 | |
| R0.1 mm notch | 5.0 |
| Material | |||
|---|---|---|---|
| En3B | 873 | −0.119 | 2.47 |
| TC4 | 943 | 0.152 | 2.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Liu, P.; Cheng, Y.; Wang, X.; Ren, X. Probabilistic Modeling of Fatigue Life Prediction of Notched Specimens Combining Highly Stressed Volume and Theory of Critical Distance Approach. Metals 2025, 15, 1300. https://doi.org/10.3390/met15121300
Li B, Liu P, Cheng Y, Wang X, Ren X. Probabilistic Modeling of Fatigue Life Prediction of Notched Specimens Combining Highly Stressed Volume and Theory of Critical Distance Approach. Metals. 2025; 15(12):1300. https://doi.org/10.3390/met15121300
Chicago/Turabian StyleLi, Bin, Peng Liu, Yuan Cheng, Xiaodi Wang, and Xuechong Ren. 2025. "Probabilistic Modeling of Fatigue Life Prediction of Notched Specimens Combining Highly Stressed Volume and Theory of Critical Distance Approach" Metals 15, no. 12: 1300. https://doi.org/10.3390/met15121300
APA StyleLi, B., Liu, P., Cheng, Y., Wang, X., & Ren, X. (2025). Probabilistic Modeling of Fatigue Life Prediction of Notched Specimens Combining Highly Stressed Volume and Theory of Critical Distance Approach. Metals, 15(12), 1300. https://doi.org/10.3390/met15121300







