Equation of State for Aluminum at High Entropies and Internal Energies in Shock Waves
Abstract
1. Introduction
2. Equation-of-State Model
2.1. TEC Model
2.2. STEC Model
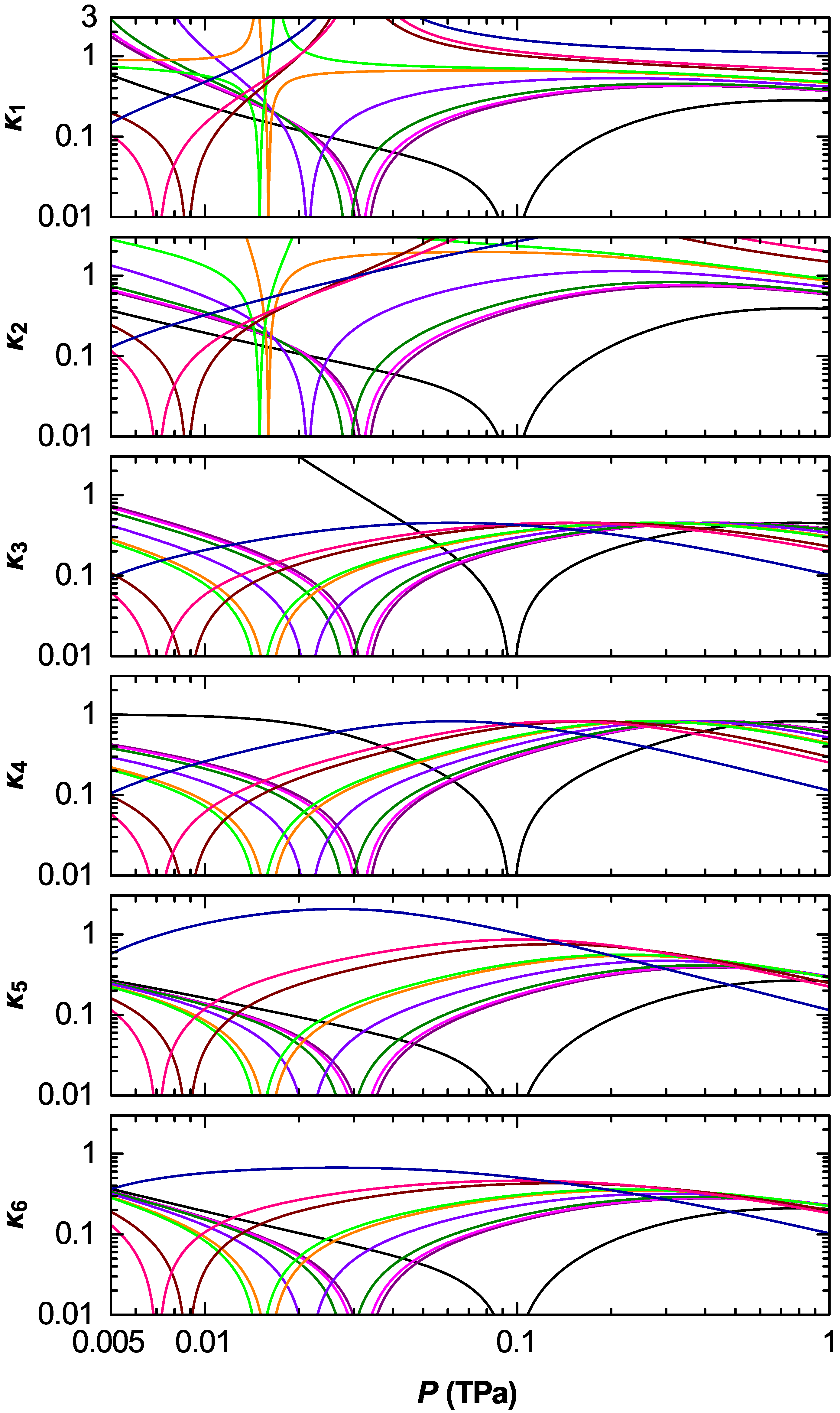
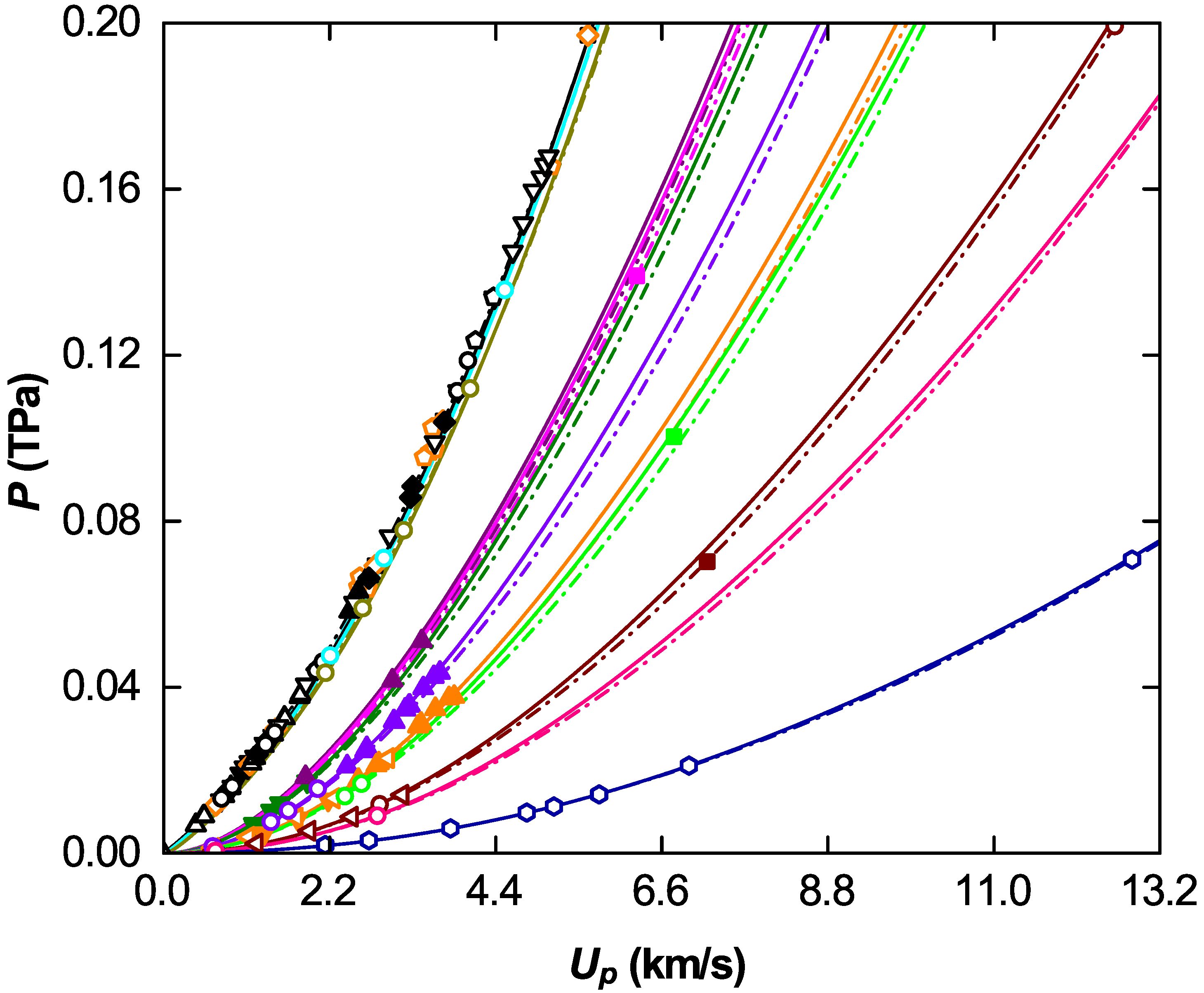
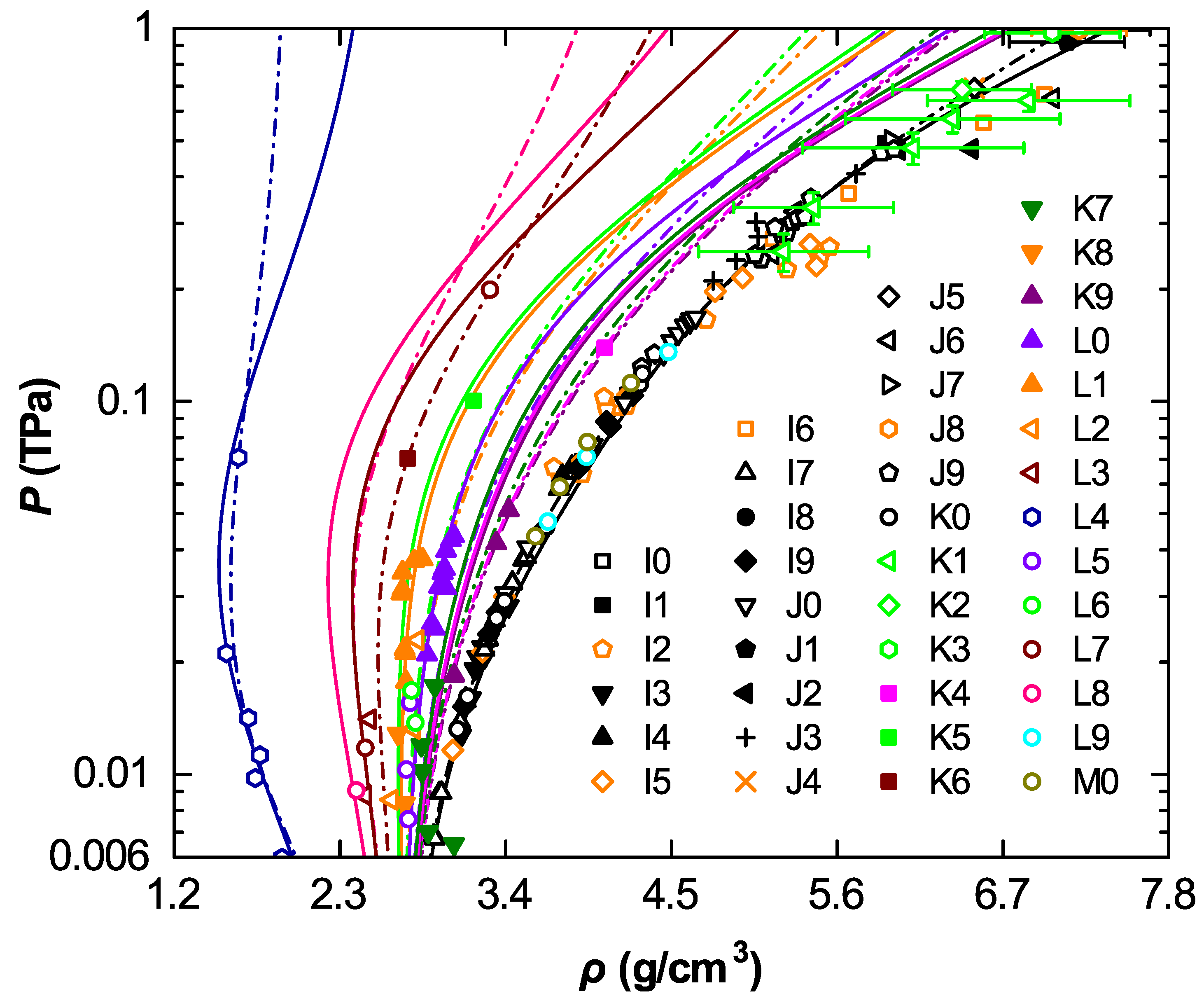
3. Thermodynamic Characteristics of Aluminum in Shock Waves
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Thermodynamic Inconsistency of the TEC Model
References
- Zel’dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Bushman, A.V.; Fortov, V.E.; Kanel’, G.I.; Ni, A.L. Intense Dynamic Loading of Condensed Matter; Taylor & Francis: Washington, DC, USA, 1993. [Google Scholar]
- Fortov, V. Intense Shock Waves on Earth and in Space; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Agureikin, V.A.; Anisimov, S.I.; Bushman, A.V.; Kanel’, G.I.; Karyagin, V.P.; Konstantinov, A.B.; Kryukov, B.P.; Minin, V.F.; Razorenov, S.V.; Sagdeev, R.Z.; et al. Thermo-physical and gas-dynamic studies of the meteorite shield for the Vega spacecraft. High Temp. 1984, 22, 761–778. [Google Scholar]
- Povarnitsyn, M.E.; Khishchenko, K.V.; Levashov, P.R. Hypervelocity impact modeling with different equations of state. Int. J. Impact Eng. 2006, 33, 625–633. [Google Scholar] [CrossRef]
- Povarnitsyn, M.E.; Khishchenko, K.V.; Levashov, P.R. Simulation of shock-induced fragmentation and vaporization in metals. Int. J. Impact Eng. 2008, 13, 1723–1727. [Google Scholar] [CrossRef]
- Charakhch’yan, A.A.; Khishchenko, K.V.; Fortov, V.E.; Frolova, A.A.; Milyavskiy, V.V.; Shurshalov, L.V. Shock compression of some porous media in conical targets: Numerical study. Shock Waves 2011, 21, 35–42. [Google Scholar] [CrossRef]
- Khishchenko, K.V.; Charakhch’yan, A.A.; Fortov, V.E.; Frolova, A.A.; Milyavskiy, V.V.; Shurshalov, L.V. Hydrodynamic simulation of converging shock waves in porous conical samples enclosed within solid targets. J. Appl. Phys. 2011, 110, 053501. [Google Scholar] [CrossRef]
- Popova, T.V.; Mayer, A.E.; Khishchenko, K.V. Evolution of shock compression pulses in polymethylmethacrylate and aluminum. J. Appl. Phys. 2018, 123, 235902. [Google Scholar] [CrossRef]
- Aleksandrov, V.V.; Branitskii, A.V.; Grabovski, E.V.; Laukhin, Y.N.; Oleinik, G.M.; Tkachenko, S.I.; Frolov, I.N.; Khishchenko, K.V. Study of the impact of a duralumin flyer with a tungsten target at the Angara-5-1 facility. Plasma Phys. Rep. 2019, 45, 421–426. [Google Scholar] [CrossRef]
- Khishchenko, K.V.; Mayer, A.E. High- and low-entropy layers in solids behind shock and ramp compression waves. Int. J. Mech. Sci. 2021, 189, 105971. [Google Scholar] [CrossRef]
- Wen, K.; Chen, X.W.; Lu, Y.G. Research and development on hypervelocity impact protection using Whipple shield: An overview. Def. Technol. 2021, 17, 1864–1886. [Google Scholar] [CrossRef]
- Radchenko, P.A.; Radchenko, A.V.; Batuev, S.P.; Kanutkin, A.V. Application of the finite element method to evaluate the effectiveness of spacecraft protective screens. Acta Astronaut. 2025, 229, 466–470. [Google Scholar] [CrossRef]
- Rodionov, E.S.; Cherepanov, A.Y.; Fazlitdinova, A.G.; Sultanov, T.T.; Lupanov, V.G.; Mayer, P.N.; Mayer, A.E. Dynamic plasticity and fracture of Al 7075 and V95T1 alloys: High-velocity impact experiments. Dynamics 2025, 5, 6. [Google Scholar] [CrossRef]
- Abdelmaola, M.; Thurston, B.; Panton, B.; Vivek, A.; Daehn, G. Influence of augmentation compositions and confinement layers on flyer velocity in laser impact welding. Metals 2025, 15, 190. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Prokhorov, A.M.; Fortov, V.E. The use of powerful lasers for the study of matter under superhigh pressures. Usp. Fiz. Nauk 1984, 142, 395–434. [Google Scholar] [CrossRef]
- Batani, D.; Koenig, M.; Benuzzi, A.; Krasyuk, I.K.; Pashinin, P.P.; Semenov, A.Y.; Lomonosov, I.V.; Fortov, V.E. Problems in the optical measurement of dense plasma heating in laser shock wave compression. Plasma Phys. Control. Fusion 1999, 41, 93–103. [Google Scholar] [CrossRef]
- Povarnitsyn, M.E.; Itina, T.E.; Khishchenko, K.V.; Levashov, P.R. Multi-material two-temperature model for simulation of ultra-short laser ablation. Appl. Surf. Sci. 2007, 253, 6343–6346. [Google Scholar] [CrossRef]
- Abrosimov, S.A.; Bazhulin, A.P.; Voronov, V.V.; Krasyuk, I.K.; Pashinin, P.P.; Semenov, A.Y.; Stuchebryukhov, I.A.; Khishchenko, K.V. Study of mechanical properties of aluminum, AMg6M alloy, and polymethyl methacrylate at high strain rates under the action of picosecond laser radiation. Dokl. Phys. 2012, 57, 64–66. [Google Scholar] [CrossRef]
- Inogamov, N.A.; Zhakhovsky, V.V.; Khokhlov, V.A.; Demaske, B.J.; Khishchenko, K.V.; Oleynik, I.I. Two-temperature hydrodynamic expansion and coupling of strong elastic shock with supersonic melting front produced by ultrashort laser pulse. J. Phys. Conf. Ser. 2014, 500, 192023. [Google Scholar] [CrossRef]
- Shu, H.; Huang, X.; Ye, J.; Jia, G.; Wu, J.; Fu, S. Absolute equation of state measurement of aluminum using laser quasi-isentropic-driven flyer plate. Laser Part. Beams 2017, 35, 145–153. [Google Scholar] [CrossRef]
- Gus’kov, S.Y.; Krasyuk, I.K.; Semenov, A.Y.; Stuchebryukhov, I.A.; Khishchenko, K.V. Extraction of the shock adiabat of metals from the decay characteristics of a shock wave in a laser experiment. JETP Lett. 2019, 109, 516–520. [Google Scholar] [CrossRef]
- Semenov, A.Y.; Stuchebryukhov, I.A.; Khishchenko, K.V. Modeling of shock-wave processes in aluminum under the action of a short laser pulse. Math. Montis. 2021, 50, 108–118. [Google Scholar] [CrossRef]
- Belov, I.A.; Bel’kov, S.A.; Bondarenko, S.V.; Vergunova, G.A.; Voronin, A.Y.; Garanin, S.G.; Golovkin, S.Y.; Gus’kov, S.Y.; Demchenko, N.N.; Derkach, V.N.; et al. Shock-wave pressure transfer to a solid target with porous absorber of high-power laser pulse. J. Exp. Theor. Phys. 2022, 134, 340–349. [Google Scholar] [CrossRef]
- Semenov, A.Y.; Abrosimov, S.A.; Stuchebryukhov, I.A.; Khishchenko, K.V. Studying the dynamics of wave processes of compression and expansion in palladium under picosecond laser action. High Temp. 2023, 61, 502–507. [Google Scholar] [CrossRef]
- Shen, Z.; Xu, Q.; Yu, Y.; Liu, D.; Ji, J. Fabrication of papillary composite microstructured aluminum surfaces by laser shock imprinting and ablation. Metals 2024, 14, 1346. [Google Scholar] [CrossRef]
- Romashevskiy, S.A.; Ashitkov, S.I.; Khokhlov, V.A.; Inogamov, N.A. Study of energy relaxation in a nickel nanofilm after ultrafast heating of the electronic subsystem by a femtosecond laser pulse. High Temp. 2024, 62, 795–800. [Google Scholar] [CrossRef]
- Nakanii, N.; Mori, Y.; Inoue, S.; Sano, T. Ultrafast observation of shock wave formation in aluminum under direct femtosecond laser irradiation. J. Appl. Phys. 2025, 137, 153108. [Google Scholar] [CrossRef]
- Weber, M.; Raffray, Y.; Loison, D.; Aubert, B.; Benuzzi-Mounaix, A.; Berthe, L.; Harmand, M.; Jodar, B.; Videau, L.; Vinci, T.; et al. Experimental and numerical investigation of laser intensity distribution influence on laser pressure loading. J. Appl. Phys. 2025, 138, 033104. [Google Scholar] [CrossRef]
- Khomich, V.Y.; Shakhmatov, E.V.; Sviridov, K.N. Laser-optical technologies for space debris removal. Acta Astronaut. 2025, 226, 78–85. [Google Scholar] [CrossRef]
- Bushman, A.V.; Romanov, G.S.; Smetannikov, A.S. Theoretical modeling of the initial-stage of a pulsed layer discharge including the real equation of state of the conductor. High Temp. 1984, 22, 658–664. [Google Scholar]
- Korobenko, V.N.; Rakhel, A.D.; Savvatimski, A.I.; Fortov, V.E. Measurement of the electrical resistivity of hot aluminum passing from the liquid to gaseous state at supercritical pressure. Phys. Rev. B 2005, 71, 014208. [Google Scholar] [CrossRef]
- Rososhek, A.; Efimov, S.; Nitishinski, M.; Yanuka, D.; Tewari, S.V.; Gurovich, V.T.; Khishchenko, K.; Krasik, Y.E. Spherical wire arrays electrical explosion in water and glycerol. Phys. Plasmas 2017, 24, 122705. [Google Scholar] [CrossRef]
- Oreshkin, E.V.; Barengolts, S.A.; Oreshkin, V.I. The specific current action integral for conductors exploded by high-frequency currents. Phys. Plasmas 2024, 31, 033904. [Google Scholar] [CrossRef]
- Yang, L.; Rehwald, M.; Kluge, T.; Laso Garcia, A.; Toncian, T.; Zeil, K.; Schramm, U.; Cowan, T.E.; Huang, L. Dynamic convergent shock compression initiated by return current in high-intensity laser–solid interactions. Matter Radiat. Extrem. 2024, 9, 047204. [Google Scholar] [CrossRef]
- Li, Y.; Ren, H.; Liu, S. Influence of the glycidyl azide polymer on the energy release of aluminum sub-micron particles under ultrafast heating rates stimulated by electric explosion and solid laser. Metals 2024, 14, 786. [Google Scholar] [CrossRef]
- Grikshtas, R.; Asmedianov, N.; Belozerov, O.; Efimov, S.; Strucka, J.; Yao, Y.; Lukic, B.; Rack, A.; Bland, S.N.; Krasik, Y.E. Electrothermal instabilities observed by x-ray radiography of underwater sub-microsecond electrical explosions of aluminum, silver, and molybdenum wires. Phys. Plasmas 2025, 32, 032705. [Google Scholar] [CrossRef]
- Bushman, A.V.; Fortov, V.E.; Lomonosov, I.V. Investigations of metals in the liquid and plasma states by use of shock waves. J. Non-Cryst. Solids 1993, 156–158, 631–638. [Google Scholar] [CrossRef]
- Lomonosov, I.V.; Fortova, S.V. Wide-range semiempirical equations of state of matter for numerical simulation on high-energy processes. High Temp. 2017, 55, 585–610. [Google Scholar] [CrossRef]
- Maler, D.; Liziakin, G.; Belozerov, O.; Efimov, S.; Rakhmilevich, D.; Cohen, K.; Krasik, Y.E. Comparing magnetic pushing to underwater explosions for flyer acceleration. J. Appl. Phys. 2023, 134, 185902. [Google Scholar] [CrossRef]
- Tkachenko, S.I.; Levashov, P.R.; Khishchenko, K.V. Analysis of electrical conductivity measurements in strongly coupled tungsten and aluminum plasmas. Czech. J. Phys. 2006, 56, B419–B424. [Google Scholar] [CrossRef]
- Tkachenko, S.I.; Levashov, P.R.; Khishchenko, K.V. The influence of an equation of state on the interpretation of electrical conductivity measurements in strongly coupled tungsten plasma. J. Phys. A Math. Gen. 2006, 39, 7597–7603. [Google Scholar] [CrossRef]
- Hangai, Y.; Kaneko, Y.; Amagai, K. Continuous fabrication process of aluminum foam from foaming to press forming. Metals 2025, 15, 633. [Google Scholar] [CrossRef]
- Bushman, A.V.; Fortov, V.E. Models of equation of the matter state. Usp. Fiz. Nauk 1983, 140, 177–232. [Google Scholar] [CrossRef]
- Khishchenko, K.V. The equation of state for magnesium at high pressures. Tech. Phys. Lett. 2004, 30, 829–831. [Google Scholar] [CrossRef]
- Mead, P.T.; Rogers, J.A.; Williams, T.N.; Wilkerson, J.W.; Lacy, T.E., Jr. EPIC simulations of hypervelocity impacts of aluminum spheres into high-density polyethylene plates. J. Dynamic Behavior Mater. 2025. [Google Scholar] [CrossRef]
- Kolgatin, S.N.; Khachatur’yants, A.V. Interpolation equations of state of metals. High Temp. 1982, 20, 380–384. [Google Scholar]
- Al’tshuler, L.V. Use of shock waves in high-pressure physics. Usp. Fiz. Nauk 1965, 85, 197–258. [Google Scholar]
- Trunin, R.F. Shock compression of condensed matters in strong shock-waves caused by underground nuclear-explosions. Usp. Fiz. Nauk 1994, 164, 1215–1237. [Google Scholar] [CrossRef]
- Kadatskiy, M.A.; Khishchenko, K.V. Comparison of Hugoniots calculated for aluminum in the framework of three quantum-statistical models. J. Phys. Conf. Ser. 2015, 653, 012079. [Google Scholar] [CrossRef]
- Orlov, N.Y.; Kadatskiy, M.A.; Denisov, O.B.; Khishchenko, K.V. Application of quantum-statistical methods to studies of thermodynamic and radiative processes in hot dense plasmas. Matter Radiat. Extrem. 2019, 4, 054403. [Google Scholar] [CrossRef]
- Karakulov, V.V.; Skripnyak, V.A. About mechanical behavior and effective properties of metal matrix composites under shock wave loading. In Behavior of Materials Under Impact, Explosion, High Pressures and Dynamic Strain Rates; Orlov, M.Y., Visakh, P.M., Eds.; Advanced Structured Materials; Springer: Cham, Switzerland, 2023; Volume 176, pp. 53–68. [Google Scholar] [CrossRef]
- Cao, R.; Chen, J.; Song, X.; Feng, D.; Peng, C.; Li, Z. Numerical simulation of the damage characteristics of carbon fiber-reinforced aluminum laminates under hypervelocity impact based on the FE-SPH adaptive method. Appl. Compos. Mater. 2025, 32, 817–847. [Google Scholar] [CrossRef]
- Zou, G.; Yang, Y.; Chang, Z.; Wu, S.; Wang, X. Analytical and numerical investigation on the penetration resistance of PUE/honeycomb aluminum composite structures. Acta Mech. Solida Sin. 2024, 37, 771–785. [Google Scholar] [CrossRef]
- Dadoura, M.H.; Farahat, A.I.Z.; Taha, M.R.; Elshaer, R.N. Enhancement of quasi-static compression strength for aluminum closed cell foam blocks shielded by aluminum tubes. Sci. Rep. 2023, 13, 6929. [Google Scholar] [CrossRef]
- Wu, F.; Miao, B.; Tian, Y.; Zhang, F.; Zhang, C. Aluminum foam as buffer layer used in soft rock tunnel with large deformation. J. Mt. Sci. 2025, 22, 324–336. [Google Scholar] [CrossRef]
- Hao, T.; Yang, X.; Xie, A.; Deng, S.; Yu, B.; Sun, Q. A novel aluminum foam structure for combined excellent wave attenuation and ventilation performance. Sci. Rep. 2025, 15, 7346. [Google Scholar] [CrossRef]
- Thorat, M.; Kumar, G.; Sahu, S.N.; Menezes, V.; Gokhale, A.A. Cell wall fracture in shock-loaded aluminum foams. J. Mater. Eng. Perform. 2025, 34, 10810–10818. [Google Scholar] [CrossRef]
- Shepelev, V.V. Hydrodynamic modeling of laser-induced shock waves in aluminum in a cylindrically symmetric statement. J. Appl. Ind. Math. 2023, 17, 385–395. [Google Scholar] [CrossRef]
- Sharma, A.; Song, J.; Furfari, D.; Mannava, S.R.; Vasudevan, V.K. Influence of laser shock peening and ultrasonic nanocrystal surface modification on residual stress, microstructure, and corrosion–fatigue behavior of aluminum 7075-T6. Metall. Mater. Trans. A 2023, 54, 4233–4252. [Google Scholar] [CrossRef]
- Bakulin, I.A.; Kuznetsov, S.I.; Panin, A.S.; Tarasova, E.Y.; Yaresko, S.I.; Novikov, V.A. Effect of preliminary heat treatment on the formation of structure and residual stresses in the AMg6 alloy at laser shock peening without coating. J. Russ. Laser Res. 2024, 45, 237–248. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, Z.; Zhou, J.; Song, F.; Zhao, X.; Wu, W.; Gao, F.; Cai, J.; Xue, W.; Liu, Y. Study on the wear resistance of 2024-T351 aluminum alloy strengthened by ultrasonic-assisted laser shock peening. J. Mater. Sci. 2025, 60, 5954–5976. [Google Scholar] [CrossRef]
- Song, P.F.; Cao, M.Y.; Fu, M.; Li, B.; Wu, L.J.; Li, Y.F.; Liu, Z. Effect of ultrasonic vibration modes on the residual stress relaxation and mechanical properties of aluminum alloy. J. Cent. South Univ. 2025, 32, 1008–1023. [Google Scholar] [CrossRef]
- Pikuz, S.A.; Tilikin, I.N.; Romanova, V.M.; Mingaleev, A.R.; Shelkovenko, T.A. Development of instabilities in thin aluminum foils exploded using generator with current of up to 10 kA. Plasma Phys. Rep. 2024, 50, 792–799. [Google Scholar] [CrossRef]
- Walsh, J.M.; Rice, M.H.; McQueen, R.G.; Yarger, F.L. Shock-wave compressions of twenty-seven metals. Equations of state of metals. Phys. Rev. 1957, 108, 196–216. [Google Scholar] [CrossRef]
- Kormer, S.B.; Urlin, V.D. Interpolation equations for the condition of metals at super high pressures. Dokl. Akad. Nauk SSSR 1960, 131, 542–545. [Google Scholar]
- Leont’ev, A.A.; Fortov, V.E. Melting and evaporation of metals in an unloading wave. J. Appl. Mech. Tech. Phys. 1974, 15, 417–420. [Google Scholar] [CrossRef]
- Godwal, B.K.; Sikka, S.K.; Chidambaram, R. Equation of state theories of condensed matter up to about 10 TPa. Phys. Rep. 1983, 102, 121–197. [Google Scholar] [CrossRef]
- Young, D.A.; Wolford, J.K.; Rogers, F.J.; Holian, K.S. Theory of the aluminum shock equation of state to 104 Mbar. Phys. Lett. A 1985, 108, 157–160. [Google Scholar] [CrossRef]
- Holian, K.S. A new equation of state for aluminum. J. Appl. Phys. 1986, 59, 149–157. [Google Scholar] [CrossRef]
- Kerley, G.I. Theoretical equation of state for aluminum. Int. J. Impact Eng. 1987, 5, 441–449. [Google Scholar] [CrossRef]
- Wu, Q.; Jing, F.Q. Thermodynamic equation of state and application to Hugoniot predictions for porous materials. J. Appl. Phys. 1996, 80, 4343–4349. [Google Scholar] [CrossRef]
- Geng, H.Y.; Wu, Q.; Tan, H.; Cai, L.C.; Jing, F.Q. Extension of the Wu–Jing equation of state for highly porous materials: Calculations to validate and compare the thermoelectron model. J. Appl. Phys. 2002, 92, 5917–5923. [Google Scholar] [CrossRef]
- Chisolm, E.D.; Crockett, S.D.; Wallace, D.C. Test of a theoretical equation of state for elemental solids and liquids. Phys. Rev. B 2003, 68, 104103. [Google Scholar] [CrossRef]
- Lomonosov, I.V. Multi-phase equation of state for aluminum. Laser Part. Beams 2007, 25, 567–584. [Google Scholar] [CrossRef]
- Gordeev, D.G.; Gudarenko, L.F.; Zhernokletov, M.V.; Kudel’kin, V.G.; Mochalov, M.A. Semi-empirical equation of state of metals. Equation of state of aluminum. Combust. Explos. Shock Waves 2008, 44, 177–189. [Google Scholar] [CrossRef]
- Kinelovskii, S.A.; Maevskii, K.K. Simple model for calculating shock adiabats of powder mixtures. Combust. Explos. Shock Waves 2011, 47, 706–714. [Google Scholar] [CrossRef]
- Medvedev, A.B.; Trunin, R.F. Shock compression of porous metals and silicates. Phys. Usp. 2012, 55, 773–789. [Google Scholar] [CrossRef]
- Liu, H.; Song, H.; Zhang, G. The single phase and two-phase equations of state for aluminum. AIP Conf. Proc. 2012, 1426, 832–835. [Google Scholar] [CrossRef]
- Minakov, D.V.; Levashov, P.R.; Khishchenko, K.V. First-principle simulation of shock-wave experiments for aluminum. AIP Conf. Proc. 2012, 1426, 836–839. [Google Scholar] [CrossRef]
- Shemyakin, O.P.; Levashov, P.R.; Khishchenko, K.V. Equation of state of Al based on the Thomas–Fermi model. Contrib. Plasma Phys. 2012, 52, 37–40. [Google Scholar] [CrossRef]
- Mishra, V.; Chaturvedi, S. Equation of state of Al for compressed and expanded states from first-principles calculations. Phys. B 2012, 407, 2533–2537. [Google Scholar] [CrossRef]
- Li, Y.H.; Chang, J.Z.; Li, X.M.; Zhang, L. Multiphase equation of states of the solid and liquid phases of Al and Ta. Chin. Phys. Lett. 2012, 29, 046201. [Google Scholar] [CrossRef]
- Gordeev, D.G.; Gudarenko, L.F.; Kayakin, A.A.; Kudel’kin, V.G. Equation of state model for metals with ionization effectively taken into account. Equation of state of tantalum, tungsten, aluminum and beryllium. Combust. Explos. Shock Waves 2013, 49, 92–104. [Google Scholar] [CrossRef]
- Minakov, D.V.; Levashov, P.R.; Khishchenko, K.V.; Fortov, V.E. Quantum molecular dynamics simulation of shock-wave experiments in aluminum. J. Appl. Phys. 2014, 115, 223512. [Google Scholar] [CrossRef]
- Kinelovskii, S.A.; Maevskii, K.K. Model of the behavior of aluminum and aluminum-based mixtures under shock-wave loading. High Temp. 2014, 52, 821–829. [Google Scholar] [CrossRef]
- Kinelovskii, S.A.; Maevskii, K.K. Estimation of the thermodynamic parameters of a shock-wave action on high-porosity heterogeneous materials. Tech. Phys. 2016, 61, 1244–1249. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, D.; Shi, Z.Q.; Shi, Y.J.; Wang, T.H.; Zhang, Y. Equation of state for aluminum in warm dense matter regime. Chin. Phys. B 2019, 28, 016401. [Google Scholar] [CrossRef]
- Gilev, S.D. Low-parametric equation of state of aluminum. High Temp. 2020, 58, 166–172. [Google Scholar] [CrossRef]
- Bogdanova, Y.A.; Gubin, S.A.; Maklashova, I.V. Calculation of thermodynamic properties of metals and their binary alloys by the perturbation theory. Metals 2021, 11, 1548. [Google Scholar] [CrossRef]
- Kozyrev, N.V.; Gordeev, V.V. Thermodynamic properties and equation of state for solid and liquid aluminum. Metals 2022, 12, 1346. [Google Scholar] [CrossRef]
- Khishchenko, K.V. Equation of state for aluminum at high pressures. High Temp. 2023, 61, 440–443. [Google Scholar] [CrossRef]
- Wu, M.Z.; Zhang, Q.M.; Zhong, X.Z.; Ren, S.Y. An improved multiphase equation of state for aluminum in hypervelocity impact. Int. J. Impact Eng. 2024, 192, 105031. [Google Scholar] [CrossRef]
- Belkheeva, R.K. A simple equation of state for describing the behavior of solid and porous aluminum samples under shock compression and isentropic unloading. Zh. Tekh. Fiz. 2025, 95, 1303–1312. [Google Scholar]
- Zhao, Y.; Wang, L.F.; Zhang, Q.; Zhang, L.; Song, H.; Gao, X.; Sun, B.; Liu, H.; Song, H. A thermodynamically complete multi-phase equation of state for dense and porous metals at wide ranges of temperature and pressure. Chin. Phys. B 2025, 34, 036401. [Google Scholar] [CrossRef]
- Anand, R.K. On the convergence of strong cylindrical and spherical shock waves in solid materials. Proc. Natl. Acad. Sci. India Sect. A 2025, 95, 103–112. [Google Scholar] [CrossRef]
- Fortov, V.E. Equations of state of condensed media. J. Appl. Mech. Tech. Phys. 1972, 13, 894–902. [Google Scholar] [CrossRef]
- Bushman, A.V.; Lomakin, B.N.; Sechenov, V.A.; Fortov, V.E.; Shchekotov, O.E.; Sharipdzhanov, I.I. Thermodynamics of nonideal cesium plasma. Zh. Eksp. Teor. Fiz. 1975, 69, 1624–1632. [Google Scholar]
- Lomonosov, I.V.; Fortov, V.E.; Khishchenko, K.V. Model of wide-range equations of polymer materials state under high-energy densities. Khim. Fiz. 1995, 14, 47–52. [Google Scholar]
- Khishchenko, K.V. Equation of state for titanium at high pressures. High Temp. 2024, 62, 150–153. [Google Scholar] [CrossRef]
- Seredkin, N.N.; Khishchenko, K.V. Equation of state for the hafnium–zirconium alloy at high pressures and temperatures in shock waves. High Temp. 2024, 62, 450–453. [Google Scholar] [CrossRef]
- Boyarskikh, K.A.; Khishchenko, K.V. Algorithm for finding parameters of equations of state by particle swarm optimization. Bull. Russ. Acad. Sci. Phys. 2024, 88, 1446–1451. [Google Scholar] [CrossRef]
- Bazarov, I.P. Thermodynamics; MacMillan: New York, NY, USA, 1964. [Google Scholar]
- Charakhch’yan, A.A.; Gryn’, V.I.; Khishchenko, K.V. On the role of heat conduction in the formation of a high-temperature plasma during counter collision of rarefaction waves of solid deuterium. J. Appl. Mech. Tech. Phys. 2011, 52, 501–516. [Google Scholar] [CrossRef]
- Bushman, A.V.; Fortov, V.E.; Sharipdzhanov, I.I. Equation of state for metals in a wide range of parameters. Teplofiz. Vys. Temp. 1977, 15, 1095–1097. [Google Scholar]
- Kinelovskii, S.A.; Maevskii, K.K. Modeling shock loading of multicomponent materials including bismuth. High Temp. 2016, 54, 675–681. [Google Scholar] [CrossRef]
- Maevskii, K.K.; Kinelovskii, S.A. Thermodynamic parameters of mixtures with silicon nitride under shock-wave impact in terms of equilibrium model. High Temp. 2018, 56, 853–858. [Google Scholar] [CrossRef]
- Maevskii, K.K. Numerical study of shock-wave loading of the W- and WC-based metal composites. Tech. Phys. 2021, 66, 749–754. [Google Scholar] [CrossRef]
- Maevskii, K.K. Modeling of shock wave loading FeO to 1000 GPa. J. Appl. Phys. 2025, 137, 055901. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Al’tshuler, L.V.; Kormer, S.B.; Bakanova, A.A.; Trunin, R.F. Equation of state for aluminum, copper, and lead in the high-pressure region. Zh. Eksp. Teor. Fiz. 1960, 38, 790–798. [Google Scholar]
- Kormer, S.B.; Funtikov, A.I.; Ulrin, V.D.; Kolesnikova, A.N. Dynamic compression of porous metals and the equation of state with variable specific heat at high temperatures. Zh. Eksp. Teor. Fiz. 1962, 42, 686–702. [Google Scholar]
- Skidmore, I.C.; Morris, E. Experimental equation-of-state data for uranium and its interpretation in the critical region. In Thermodynamics of Nuclear Materials; IAEA: Vienna, Austria, 1962; pp. 173–216. [Google Scholar]
- Morgan, D.T.; Rockowitz, M.; Atkinson, A.L. Measurement of the Grueneisen Parameter and the Internal Energy Dependence of the Solid Equation of State for Aluminum and Teflon; Tech. Rep. AFWL-TR-65-117; Air Force Weapons Laboratory, Kirtland Air Force Base: Albuquerque, NM, USA, 1965. [Google Scholar]
- Anderson, G.D.; Doran, D.G.; Fahrenbruch, A.L. Equation of State of Solids: Aluminum and Teflon; Tech. Rep. AFWL-TR-65-147; Air Force Weapons Laboratory, Kirtland Air Force Base: Albuquerque, NM, USA, 1965. [Google Scholar]
- Al’tshuler, L.V.; Chekin, B.S. Metrology of high impulse pressure. In Reports of the 1st All-Union Symposium on Pulse Pressures; VNIIFTRI: Moscow, Russia, 1974; Volume 1, pp. 5–22. [Google Scholar]
- Al’tshuler, L.V.; Kalitkin, N.N.; Kuz’mina, L.V.; Chekin, B.S. Shock adiabats for ultrahigh pressures. Zh. Eksp. Teor. Fiz. 1977, 72, 317–325. [Google Scholar]
- Marsh, S.P. (Ed.) LASL Shock Hugoniot Data; University of California Press: Berkeley, CA, USA, 1980. [Google Scholar]
- Volkov, L.P.; Voloshin, N.P.; Vladimirov, A.S.; Nogin, V.N.; Simonenko, V.A. Shock compressibility of aluminum at a pressure of 10 Mbar. JETP Lett. 1980, 31, 588–592. [Google Scholar]
- Al’tshuler, L.V.; Bakanova, A.A.; Dudoladov, I.P.; Dynin, E.A.; Trunin, R.F.; Chekin, B.S. Shock adiabatic curves of metals. New data, statistical analysis, and general laws. J. Appl. Mech. Tech. Phys. 1981, 22, 145–169. [Google Scholar] [CrossRef]
- Mitchell, A.C.; Nellis, W.J. Shock compression of aluminum, copper, and tantalum. J. Appl. Phys. 1981, 52, 3363–3374. [Google Scholar] [CrossRef]
- Simonenko, V.A.; Voloshin, N.P.; Vladimirov, A.S.; Nagibin, A.P.; Nogin, V.N.; Popov, V.A.; Salnikov, V.A.; Shoidin, Y.A. Absolute measurements of shock compressibility of aluminum at pressures P≳1 TPa. Zh. Eksp. Teor. Fiz. 1985, 88, 1452–1459. [Google Scholar]
- Trunin, R.F. Compressibility of various substances at high shock pressures: An overview. Izv. Acad. Sci. USSR. Phys. Solid Earth 1986, 22, 103–114. [Google Scholar]
- Glushak, B.L.; Zharkov, A.P.; Zhernokletov, M.V.; Ternovoi, V.Y.; Filimonov, A.S.; Fortov, V.E. Experimental investigation of the thermodynamics of dense plasmas formed from metals at high energy concentrations. Zh. Eksp. Teor. Fiz. 1989, 96, 1301–1318. [Google Scholar]
- Trunin, R.F.; Panov, N.V.; Medvedev, A.B. Shock compressibilities of iron, aluminum and tantalum at terapascal pressures. Khim. Fiz. 1995, 14, 97–99. [Google Scholar]
- Trunin, R.F.; Panov, N.V.; Medvedev, A.B. Shock compressibility of iron, aluminum, and tantalum under terapascal pressures in laboratory conditions. High Temp. 1995, 33, 328–329. [Google Scholar]
- Trunin, R.F.; Podurets, M.A.; Simakov, G.V.; Popov, L.V.; Sevast’yanov, A.G. New data, obtained under strong shock wave conditions from an underground nuclear explosion, on the compressibility of aluminum, plexiglass, and quartz. Zh. Eksp. Teor. Fiz. 1995, 108, 851–861. [Google Scholar]
- Avrorin, E.N.; Vodolaga, B.K.; Voloshin, N.P.; Kovalenko, G.V.; Kuropatenko, V.F.; Simonenko, V.A.; Chernovolyuk, B.T. Experimental study of the influence of electron shell structure on shock adiabats of condensed materials. Zh. Eksp. Teor. Fiz. 1987, 93, 613–626. [Google Scholar]
- Trunin, R.F.; Panov, N.V.; Medvedev, A.B. Compressibility of iron, aluminum, molybdenum, titanium, and tantalum at shock-wave pressures of 1–2.5 TPa. JETP Lett. 1995, 62, 591–594. [Google Scholar]
- Knudson, M.D.; Lemke, R.W.; Hayes, D.B.; Hall, C.A.; Deeney, C.; Asay, J.R. Near-absolute Hugoniot measurements in aluminum to 500 GPa using a magnetically accelerated flyer plate technique. J. Appl. Phys. 2003, 94, 4420–4431. [Google Scholar] [CrossRef]
- Trunin, R.F.; Gudarenko, L.F.; Zhernokletov, M.V.; Simakov, G.V. Experimental Data on Shock Compression and Adiabatic Expansion of Condensed Matter; RFNC-VNIIEF: Sarov, Russia, 2006. [Google Scholar]
- Bakanova, A.A.; Dudoladov, I.P.; Sutulov, Y.N. Shock compressibility of porous tungsten, molybdenum, copper, and aluminum in the low pressure domain. J. Appl. Mech. Tech. Phys. 1974, 15, 241–245. [Google Scholar] [CrossRef]
- Trunin, R.F.; Simakov, G.V.; Panov, N.V. Shock compression of porous aluminum and nickel at megabar pressures. High Temp. 2001, 39, 401–406. [Google Scholar] [CrossRef]
- Song, P.; Cai, L.; Wang, Q.; Zhou, X.; Li, X.; Zhang, Y.; Yuan, S.; Weng, J.; Li, J. Sound velocity, temperature, melting along the Hugoniot and equation of state for two porosity aluminums. J. Appl. Phys. 2011, 110, 103522. [Google Scholar] [CrossRef]
- Al’tshuler, L.V.; Trunin, R.F.; Urlin, V.D.; Fortov, V.E.; Funtikov, A.I. Development of high-pressure dynamical measurement techniques in Russia. Usp. Fiz. Nauk 1999, 169, 323–344. [Google Scholar] [CrossRef]
- Bushman, A.V.; Krasyuk, I.K.; Pashinin, P.P.; Prokhorov, A.M.; Ternovoi, V.Y.; Fortov, V.E. Dynamic compressibility and thermodynamics of a dense aluminum plasma at megabar pressures. JETP Lett. 1984, 39, 411–413. [Google Scholar]
- Al’tshuler, L.V.; Trunin, R.F.; Krupnikov, K.K.; Panov, N.V. Explosive laboratory devices for shock wave compression studies. Usp. Fiz. Nauk 1996, 166, 575–581. [Google Scholar] [CrossRef]
- Funtikov, A.I. Explosive laboratory measurement of the dynamical compressibility of porous substances in the pressure range from 0.1 to 1 TPa. Usp. Fiz. Nauk 1997, 167, 1119–1120. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Zhang, R.; Yang, G.; Luo, G.; Shen, Q. Equation of state remeasurements for aluminum and copper under low-impact loading. AIP Adv. 2023, 13, 045202. [Google Scholar] [CrossRef]
- Gan, Y.; Nan, X.; Wu, D.; Yang, S.; Li, X.; Geng, H.; Shen, Y.; Yu, Y.; Hu, J. Dynamic yield behaviors of aluminum under shock and ramp compression: Experiments and models. J. Appl. Phys. 2025, 137, 215902. [Google Scholar] [CrossRef]
- Ragan, C.E., III. Shock compression measurements at 1 to 7 TPa. Phys. Rev. A 1982, 25, 3360–3375. [Google Scholar] [CrossRef]
- Ragan, C.E., III. Shock-wave experiments at threefold compression. Phys. Rev. A 1984, 29, 1391–1402. [Google Scholar] [CrossRef]
- Avrorin, E.N.; Vodolaga, B.K.; Simonenko, V.A.; Fortov, V.E. High-intensity shock-waves and the extreme states of matter. Usp. Fiz. Nauk 1993, 163, 1–34. [Google Scholar] [CrossRef]
- He, Z.; Fang, Z.; Huang, X.; Xie, Z.; Ye, J.; Dong, J.; Shu, H.; Wang, P.; Jia, G.; Zhang, F.; et al. Sound velocity measurement based on laser-induced microflyers. AIP Adv. 2024, 14, 105315. [Google Scholar] [CrossRef]
- Al’tshuler, L.V.; Il’kaev, R.I.; Fortov, V.E. Use of powerful shock and detonation waves to study extreme states of matter. Phys. Usp. 2021, 64, 1167–1179. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khishchenko, K.V.; Boyarskikh, K.A.; Obruchkova, L.R.; Seredkin, N.N. Equation of State for Aluminum at High Entropies and Internal Energies in Shock Waves. Metals 2025, 15, 1189. https://doi.org/10.3390/met15111189
Khishchenko KV, Boyarskikh KA, Obruchkova LR, Seredkin NN. Equation of State for Aluminum at High Entropies and Internal Energies in Shock Waves. Metals. 2025; 15(11):1189. https://doi.org/10.3390/met15111189
Chicago/Turabian StyleKhishchenko, Konstantin V., Kseniya A. Boyarskikh, Liliya R. Obruchkova, and Nikolai N. Seredkin. 2025. "Equation of State for Aluminum at High Entropies and Internal Energies in Shock Waves" Metals 15, no. 11: 1189. https://doi.org/10.3390/met15111189
APA StyleKhishchenko, K. V., Boyarskikh, K. A., Obruchkova, L. R., & Seredkin, N. N. (2025). Equation of State for Aluminum at High Entropies and Internal Energies in Shock Waves. Metals, 15(11), 1189. https://doi.org/10.3390/met15111189




