Abstract
Erosion wear is a primary factor in material failure and is widely observed in hydropower, petroleum, aerospace, and other industrial fields. It is evident from the findings of numerous research studies that both the characteristics of particles and the fluid dynamic parameters are significantly associated with the occurrence of erosion damage. However, there has been a paucity of research into the correlation between the mechanical properties of materials and their erosion wear behaviour. This review methodically summarises the latest understanding of erosion wear mechanisms and influencing factors, with a specific focus on how the mechanical properties of materials regulate erosion processes. Furthermore, it provides a concise overview of erosion mechanisms and fluid dynamic factors, while undertaking a critical evaluation of the discrepancies observed among various erosion wear rate prediction models. The overarching objective of this research is to enhance mechanistic comprehension, facilitate the integration of prediction models with material property databases, and furnish a theoretical foundation for the design of erosion-resistant materials and the development of industrial protection strategies.
1. Introduction
Erosion wear is a long-standing area of research in materials engineering [1,2,3]. This phenomenon is characterised by the progressive detachment of material arising from repetitive mechanical interactions between target surfaces and solid particles transported by a fluid undergoing impingement. As a common failure mechanism, erosion wear has occurred in many industrial sectors in recent years, including hydroelectric power systems [4,5,6,7], petroleum extraction infrastructure [8,9,10], coal processing facilities [11,12], and aerospace propulsion components [13,14]. The sustained impact of abrasive particles induces incremental material degradation through microcutting and deformation mechanisms, which may ultimately result in catastrophic equipment failure. Industrial survey data reveals that erosion wear accounts for around 8% of total wear-related economic losses in industrial operations [15], highlighting its significant impact on maintenance expenditure and operational reliability.
Finnie’s foundational investigations formulated a numerical analysis framework for single-particle erosion through systematic kinematic modelling and idealised mechanical postulations [16,17,18,19,20,21,22]. Despite these seminal advancements, the underlying micromechanisms governing the physics of erosive material removal remain incompletely characterised, particularly concerning the synergistic interactions between cutting-dominated and deformation-induced wear regimes. Contemporary research identifies erosion wear as a multivariate phenomenon influenced by over 100 interdependent parameters spanning operational conditions and material attributes, as systematically categorised in Meng’s parametric taxonomy [23,24]. The critical governing factors that must be considered when analysing the erosive interactions in question include the impact angle [25], the particle kinetic energy (encompassing velocity [26,27] and diameter [28,29]), and the target surface hardness [30]. Furthermore, recent studies on erosion have also revealed that other mechanical properties besides hardness are equally significant (such as elastic modulus [31], composite functions of certain mechanical properties [32], elemental composition [33], etc.). These factors collectively illustrate the multidimensional complexity inherent in erosive interactions. The development of computationally efficient predictive models necessitates precise quantification of multiphase interaction mechanics and rigorous parametric sensitivity analysis. Advancements in methodology would facilitate the optimisation of the selection of materials resistant to erosion and the strategic design of maintenance protocols. This, in turn, would advance operational sustainability through the adoption of balanced safety–economic efficiency paradigms.
Erosion prediction models are the core tools connecting “fundamental mechanisms” and “engineering applications”. The development of these models has gradually expanded coverage from “ideal working conditions” to “complex industrial scenarios”, as evidenced by the progression from Finnie’s single-particle cutting model to Oka’s multi-parameter adaptive model, and then to Mansouri’s liquid–solid flow correction model. However, extant models still lack sufficient adaptability to special conditions and suffer from insufficient accuracy; they need to be further optimised by incorporating the dynamic changes in material mechanical parameters (e.g., dynamic hardness, elastic modulus, etc.). This constitutes a pivotal focal point within the scope of this review.
The author’s research team has a long-standing focus on the study of erosion–corrosion behaviour in various materials [34,35,36,37,38,39,40,41,42,43]. This review methodically summarises the regulatory effects of material mechanical properties, drawing upon extant research and the team’s own contributions. It thereby provides a reference point for the optimisation of the accuracy of erosion damage prediction models.
The present review delineates three primary objectives: firstly, to systematically synthesise current understandings of parametric influences and modelling methodologies in solid particle-induced erosion wear; secondly, to clarify fundamental correlations between intrinsic material properties and erosive degradation patterns; and thirdly, to identify critical research voids through comparative evaluation of predictive model competencies. The organisational structure of this review is delineated as follows: Section 2 investigates the fundamental micromechanical mechanisms governing erosive material removal, with a specific focus on the interactive effects between corrosive media and erosive processes.
Section 3 applies multivariate analysis to assess operational parameters and material response characteristics. Section 4 conducts a critical evaluation of continuum-based, discrete element, and hybrid computational models. Section 5 integrates current research trajectories and proposes a mechanistic framework linking bulk mechanical properties to microstructural evolution during cumulative erosive damage.
2. Erosion Wear Mechanism
2.1. Mechanical Damage Mechanism
The micromechanical processes that occur during solid particle impingement result in the generation of diagnostic surface topographies. These surfaces have been shown to serve as empirical indicators of erosive damage mechanisms [44]. As demonstrated in Figure 1, these impact-induced surface morphologies provide the experimental foundation for the classification of material removal physics. Finnie’s pioneering investigations [16,17,18,19,20,21,22] established fundamentally distinct damage progression pathways between ductile and brittle substrates. In ductile materials, erosive mass loss occurs through repetitive cycles of plastic indentation and microcutting mechanisms. These mechanisms involve the induction of particle kinetic energy, which in turn induces localised material displacement via shear-driven chip formation. Conversely, brittle materials exhibit subsurface fracture propagation triggered by hertzian contact stresses, with lateral crack networks coalescing under cyclic loading to produce conchoidal spallation.
Subsequent studies have refined this mechanistic dichotomy. In the energy partitioning model proposed by Bitter [45,46], the angle-dependent dominance of wear modes is elucidated as follows: low-angle impacts (θ < 30°) preferentially instigate microcutting-dominated regimes, whereas high-angle collisions (θ > 60°) induce a transition toward plastic deformation-controlled material extrusion. For metallic substrates, Levy [47] proposed a three-stage failure progression: initial work hardening of near-surface layers, followed by subsurface platelet formation through cumulative strain accumulation, ultimately culminating in fatigue-driven delamination orthogonal to the impact trajectory.
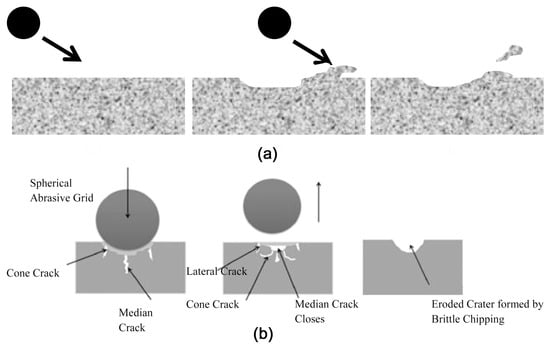
Figure 1.
Erosion wear mechanism of (a) plastic materials and (b) brittle materials. Reprinted with permission from Ref [48], Copyright 2014, Elsevier.
Material ductility has been shown to interact significantly with impact angle, thereby governing erosion wear mechanisms and resulting in the classification of erosive processes into ductile and brittle regimes. In the case of ductile materials, oblique impacts predominantly induce material removal through cutting/ploughing mechanisms. Conversely, normal impacts result in craters with extruded material lips that subsequently fail via ductile fracture [20,49,50,51,52,53,54,55]. Conversely, brittle materials undergo erosive damage through the initiation and interlinkage of subsurface crack networks [56]. While multiple mechanisms often coexist during the process of erosion, the dominant process is ultimately determined by the combined effects of impact conditions (i.e., velocity, angle, and particle characteristics) and intrinsic material properties (i.e., hardness, toughness, and ductility).
Recent investigations have systematically characterised three dominant erosion wear mechanisms under varying operational conditions [34,35,57,58,59,60,61,62]. These mechanisms are illustrated schematically in Figure 2a.
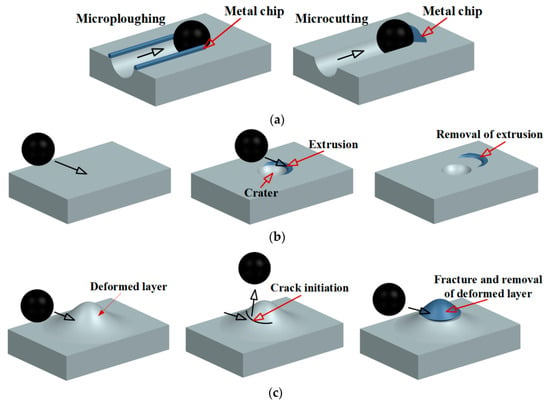
Figure 2.
Three erosion mechanisms. (a) cutting wear, (b) deformation wear, (c) fatigue wear. Adapted from Ref. [63].
- (a)
- Cutting wear: This phenomenon is governed by low-angle particle impingement (θ < 30°). The process entails the removal of material through microcutting methodologies, wherein abrasive particles result in the generation of continuous shear chips through plastic deformation. The effects of adjacent ploughing have been shown to induce lateral material displacement along the peripheries of impact scars (see Figure 2a).
- (b)
- Deformation wear: The phenomenon under discussion is most prevalent at high impact angles (θ > 60°). This phenomenon occurs when transient contact stresses exceed the material’s yield strength, resulting in localised plastic deformation. Subsequent impacts of particles result in the progressive detachment of accumulated surface extrusions through a process of cyclic material removal (see Figure 2b).
- (c)
- Fatigue wear: The mechanism is characterised by stress concentration amplification under cyclic particle bombardment, which initiates microcrack nucleation at stress raiser sites. The process of crack propagation occurs when the cumulative strain energy exceeds the material’s fracture toughness, resulting in spallation failure (see Figure 2c). This particular form of wear is most commonly observed in brittle materials. However, ductile materials may exhibit localised fatigue damage via strain localisation, where cyclic plasticity exceeds the fatigue limit, despite the material possessing the capacity for bulk plastic energy dissipation.
2.2. Corrosion-Assisted Damage Mechanism
In industrial operational contexts, ion-laden fluid flows initiate surface degradation via coupled erosive–corrosive mechanisms, wherein mechanical erosion enhances electrochemical corrosion kinetics and leads to synergistic material degradation [64,65,66]. Tribocorrosion is defined as the interaction between tribological and electrochemical corrosion effects, which can lead to a significantly higher material corrosion rate than that under static conditions. As illustrated in Figure 3, the zones where erosion–corrosion interactions may occur across different flow regimes and corrosion scenarios are delineated. The most significant zones are: zone A, involving the superposition of turbulent slurry flow and corrosion; zone B, featuring the synergistic effect of hydrodynamically induced cavitation and corrosion, where the combined action of turbulence and corrosion causes flow-accelerated corrosion that may induce erosion–corrosion; and zone C, defined as turbulent corrosion rather than erosion–corrosion [67].
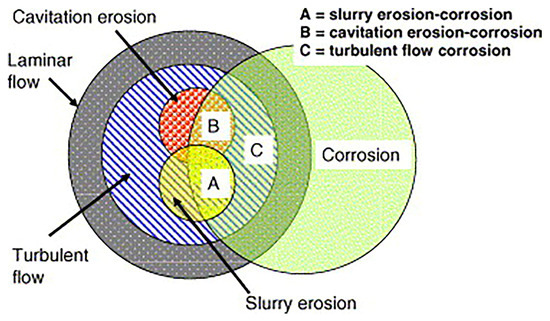
Figure 3.
Venn diagram illustrating the possible regions of erosion–corrosion interactions between different flow regimes and corrosion: (A) slurry erosion–corrosion, (B) cavitation erosion–corrosion and (C) turbulent flow or flow enhanced erosion–corrosion. Reprinted with permission from Ref. [67], Copyright 2006, Elsevier.
Empirical studies confirm that the erosion–corrosion synergy (S) can be mathematically expressed as:
where T denotes the total mass loss rate; E represents the pure erosion rate under inert conditions; and C signifies the isolated corrosion rate in the absence of mechanical erosion.
S = T − (E + C)
This coupling phenomenon emanates from three primary interaction mechanisms: (1) the erosive removal process of protective passive layers, (2) strain-induced increased corrosion susceptibility in plastically deformed zones, and (3) hydrodynamic modulation of localised corrosion kinetics.
Electrochemical dissolution establishes three synergistic pathways for erosive acceleration at material interfaces:
- Topographical roughening enhances stress concentration during particle impingement;
- Localised hardness decrement occurs via selective element depletion in anodic regions;
- Preferential corrosion accelerates damage progression along plastic strain gradients [65,68].
As demonstrated by Zheng et al. [69], the integrity of the surface is compromised by corrosive media through a sequence of degradation mechanisms. The initial stage of degradation is chemical dissolution, which weakens the near-surface atomic bonds. This is followed by mechanical stripping of the destabilised matrix during particle impacts. This oxide film degradation process is the fundamental cause of erosion–corrosion synergism, by virtue of the continuous exposure of fresh metallic surfaces to coupled chemical and mechanical attack. Contemporary research employs in situ electrochemical microscopy to quantify the dynamic interplay between surface passivation kinetics and erosive depassivation events.
The damage mechanism of erosion wear has been clearly defined in Section 2. However, in actual industrial scenarios, the erosion intensity, rate, and dominant mechanism are not fixed; instead, they are dynamically regulated by multi-dimensional factors such as the intrinsic properties of particles, fluid flow behaviour, and intrinsic material properties. For instance, the presence of sharp particles has been demonstrated to enhance micro-cutting, while elevated temperatures have been shown to alter material hardness and corrosion rate. The subsequent chapter will therefore systematically analyse the key influencing factors, quantify the action laws of each parameter on the erosion rate, and focus particularly on the core influence of material mechanical properties. This is both an extension of the “mechanism” and the foundation for the subsequent improvement of the accuracy of prediction models.
3. Factors Affecting Erosion Wear
The intensity, rate, and dominant mechanism of erosion wear are not determined by a single factor, but rather dynamically regulated by parameters across three key dimensions: namely, particle characteristics, hydrodynamic factors, and mechanical properties of materials. In this study, the damage potential of the impact source is defined by the characteristics of the particles (e.g., the degree of stress concentration). The interaction mode between particles and the target material is influenced by hydrodynamic factors (e.g., impact velocity, impact angle, and energy transfer efficiency). The damage resistance of the target material is determined by its mechanical properties (e.g., resistance to cutting, deformation, and crack propagation). Collectively, these three aspects shape the final erosive damage outcome by altering the microscopic mechanisms of erosion (e.g., micro-cutting, plastic deformation, crack propagation, or erosion–corrosion synergy), as will be elaborated on below.
3.1. Particle Properties
3.1.1. Particle Size
The dynamics of erosive impacts are profoundly influenced by the density matching between particles and the carrier fluid [42]. When the particle-to-fluid density ratio approaches unity, submicron particulates exhibit nearly perfect trajectory compliance with fluid flow, leading to attenuated erosive damage during particle–wall interactions due to reduced relative impact velocities [70]. However, the effects of particle size on erosion wear involve competing physical mechanisms. While it is true that finer particles possess lower kinetic energy per impact, their higher surface-area-to-mass ratio enhances chemical reactivity in corrosive environments. This intricate interplay gives rise to a non-linear, size-dependent wear rate profile that resists simplistic characterisation [71,72,73]. The non-linear dependency is often described by means of Stokes number, particle Reynolds number, and material hardness ratios.
Finnie [17] demonstrated that erosion wear exhibits size independence for particles larger than approximately 100 μm. The erosion rate exhibited a monotonous decrease in conjunction with a reduction in particle size below this critical dimension. Subsequent research across multiple studies has corroborated the phenomenon of a critical particle size. It has been demonstrated that, for particles of smaller size, the erosion kinetics diverge significantly from those of larger particles. This threshold indicates a fundamental transition from quasi-static indentation-dominated processes for supercritical particles to strain rate-sensitive microplasticity effects governing subcritical particle interactions.
Nguyen et al. [74] found that when particle size exceeded a specific threshold, further increases in particle size could reduce mass loss. The stagnation pressure tended to deflect small particles outward due to their low inertia, whereas large particles maintained their trajectories. In the initial phase, an increase in the magnitude of the particles is indicative of an elevated degree of erosion wear intensity. However, as the particle size increased beyond a certain threshold, large rebound particles accumulated in the central impact area, interacted with incoming particles, and consequently reduced the frequency of solid particle-wall collisions. Conversely, the presence of small rebound particles resulted in a dispersal of the particles in an outward direction, thereby leading to a reduction in the frequency of particle–particle collisions. This dynamic elucidates the existence of a particle size threshold above which erosion wear diminishes. Desale et al. [28] identified a critical particle size of 200 μm for aluminium alloy (AA 6063). They documented a transition from erosion wear to three-body abrasion as particles reach minimum kinetic energy. This transition also induced a shift in material removal mechanisms from impact-driven erosion to abrasive ploughing.
3.1.2. Particle Shape
The morphology of the particles is a contributing factor to the process of erosion wear. Research has indicated that the effect of particle shape on erosion may be comparable to, or even greater than, that of particle size [29]. The phenomenon under investigation has been shown to result in the formation of localised stress concentrations, which in turn can trigger a process of material removal that is dominated by microcutting. This process occurs as a result of acute contact geometries. Conversely, spherical particles have been shown to promote homogenised stress distributions, thereby favouring cyclic deformation wear through rolling-contact fatigue mechanisms. This morphology-driven modulation of contact mechanics has the potential to alter erosive intensity by factors of 2–5 across typical industrial particulate systems. It is evident that they have been a primary control parameter in the design of erosive systems [75,76]. As demonstrated in Figure 4, the removal of materials is facilitated by spherical and flaky particles [77].
Figure 4.
Removal of material by (a) spherical particles and (b) flaky particles. Reprinted with permission from Ref. [77], Copyright 2019, Elsevier.
Researchers employ diverse methodologies to characterise particle shape such as shape factor or circularity. The shape factor is defined as the ratio of a particle’s projected area (Ap) to the square of its projected perimeter (Pp). It can be mathematically expressed as shown below:
where Fs is the shape factor of the particle.
The particle shape factor ranges from 0 to 1, where 1 indicates that the shape of the particle is round, and the lower the value, the sharper the shape of the particle.
The morphology of particles has been demonstrated to exert a significant influence on the intensity of erosion wear. It is an established fact that angular particulates can exhibit superior material removal efficiency in comparison to their spherical counterparts. Empirical investigations have documented that sharp-edged particles induce 2–3 times higher erosive damage on a per-unit-mass basis than rounded particles [78]. Leguizamón et al. [79] recorded 225% greater mass loss for angular versus spherical particulates under identical impact conditions. This disparity can be attributed to fundamental differences in contact mechanics: acute particle geometries concentrate impact stresses into localised micro-zones, facilitating efficient microcutting, whereas spherical morphologies induce distributed plastic deformation with diminished cutting efficiency.
3.1.3. Particle Feed Rate
The sand content is a pivotal factor in the erosion process of liquid–solid two-phase flow, directly influencing the collision frequency between solid particles and the material surface, as well as the efficiency of energy transfer. The influence law on erosion has been systematically verified in experimental and simulation studies on various engineering components, such as casings, radiator pipes, and high-pressure manifolds. The range of sand content is subject to variation across different application scenarios. However, it is generally accepted that “erosion rate increases with the rise of sand content”, accompanied by local special phenomena. For instance, the “particle shielding effect” is observed under high sand content, leading to a sharp increase in the collision frequency between particles. Some particles lose the energy to impact the pipe wall due to mutual rebound, and at the same time, the “buffer layer” formed by particle groups reduces the probability of direct collision between subsequent particles and the pipe wall, thereby indirectly alleviating erosion damage [80].
In the study carried out by Zhu et al. [81], resin coatings, metal coatings and 125 V matrix casings were selected as the research objects. The construction of a liquid–solid two-phase flow environment was then undertaken, with quartz sand (45 kg/m3, 80–120 mesh, particle size 0.125–0.18 mm) utilised as the medium. The investigation into the effect of sand content was conducted using a self-developed erosion test device. The findings indicated a positive correlation between sand content and erosion rate: with an increase in sand content, the erosion rates of the three casing materials increased significantly, though to a lesser extent than that caused by flow velocity. Within the same experimental parameters (i.e., an erosion angle of 90° and a flow velocity of 15 m/s), it was observed that for every 10% increase in sand content, there was an approximate 8–12% increase in the erosion rate of both the resin and metal coatings. In contrast, for every 2 m/s increase in flow velocity, the erosion rate increased by up to 25–30%.
Wang et al. [82] conducted a study on red copper elbows, utilising a range of sand content gradients (0, 0.2, 0.6, and 1.0 wt.%) and employing quartz sand (with a particle size ranging from 0.212 to 0.85 mm) as the medium for the solid phase. The erosion rate was monitored over the course of a 24 h erosion cycle. The experiment established that an increase in sand content directly intensified the collision effect between quartz sand and the outer arch side of the elbow. When the sand content increased from 0 to 0.6 wt.%, the erosion rate of the 45° outer arch side of the elbow (the most severely eroded area) increased from nearly 0 to 10.53 g/(m2·h), showing a linear growth trend in the increase magnitude. As the sand content was increased to 1.0 wt.%, the erosion rate increased significantly to 28.52 g/(m2·h). Furthermore, under conditions of a flow velocity of 8 m/s and a particle size of 0.85 mm, erosion pits with a depth of up to 650 μm appeared on the elbow surface. These pits exhibited a combination of damage from “cutting–extrusion–spalling” (obvious grooves and traces of plastic deformation were visible on the surface). The phenomenon can be summarised as follows: an increase in sand content results in a higher number of particles colliding with the pipe wall per unit time. The synergistic impact effect between particles (e.g., the secondary scraping of pre-formed erosion pits by subsequent particles) further amplifies material loss. This effect is more significant under high flow velocity. At the same sand content of 1.0 wt.%, the erosion rate at a flow velocity of 8 m/s is 42 times that at a flow velocity of 2 m/s.
3.2. Fluid Mechanical Factors
3.2.1. Fluid Velocity
Particle impact velocity determinedly governs material erosion rates [37,38,39,83,84]. At elevated impact velocities, even smaller particles can induce significant erosive damage. Numerous studies have established a positive correlation between velocity and erosion rate [25,26,27], which can be mathematically described by the power-law relationship:
where n denotes the power-law exponent linking velocity to erosion kinetics; ER is the erosion rate to represent the material damage rate (all ERs thereafter represent the erosion rate).
ER ∝ (Velocity)n
Finnie [20] derived n = 2 from theoretical mechanics frameworks, while Oka [26,27] demonstrated through empirical observations that n was contingent upon both material hardness and particle properties (e.g., shape, density). In Yang et al.’s study [85], at an impact angle of 30°, the power exponent relating erosion rate to flow velocity was 2.053 (Figure 5).
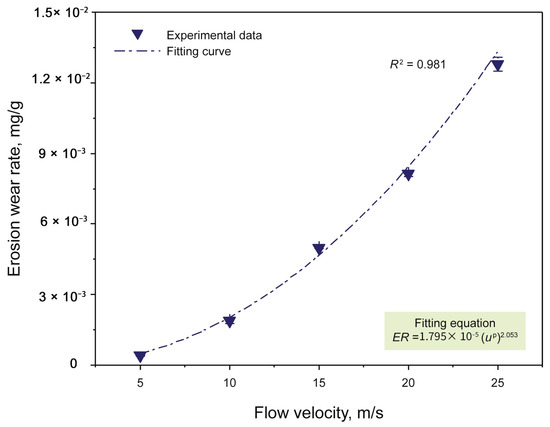
Figure 5.
Erosion rates at different flow velocities. Adapted from Ref. [85].
3.2.2. Angle of Impact
The impingement angle (θ) is defined as the acute angle between the particle velocity vector and the target surface normal (As shown in Figure 6). The phenomenon under scrutiny has been demonstrated to exert a critical influence on erosion wear mechanisms through the process of angle-dependent energy partitioning [40,41,43,86]. Ductile and brittle materials exhibit fundamentally distinct angular dependencies in erosive response:
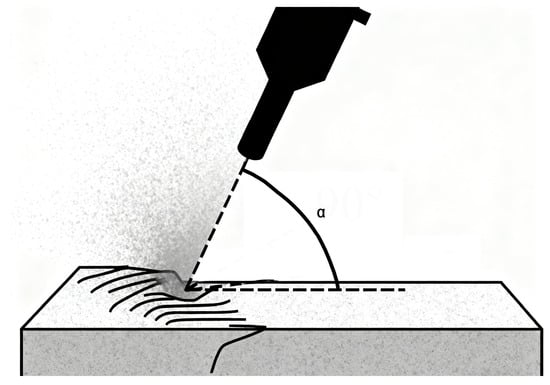
Figure 6.
The impingement angle.
Ductile material erosion: Maximum erosive loss occurs at intermediate angles (θ = 15–30°) due to optimal microcutting–ploughing efficiency. Wear rates progressively attenuate toward normal incidence (θ = 90°) as plastic deformation transitions to indentation-dominated energy dissipation [25,87].
Brittle material erosion: Erosive damage has been shown to increase monotonically with impact obliquity, reaching a peak at normal incidence (θ = 90°). The maximum tensile stress components activate fracture-dominated material removal via subsurface crack network formation [87].
3.2.3. Stand-Off Distance
The stand-off distance is a pivotal operational parameter in the context of erosion tests and engineering applications. It exerts a direct influence on the erosion damage characteristics and extent of the target material by modifying the impact flux, kinetic energy distribution, and impact area morphology of eroding particles. The following section details the specified influence laws:
Ben-Mansour et al. [88] conducted a computational analysis on the underwater jet erosion of 316 stainless steel. The findings demonstrated that when the stand-off distance fluctuated within the range of 5–20 mm, the minimum stand-off distance (5 mm) led to the maximum peak loss of erosion thickness. This phenomenon was attributed to the concentrated impact of particles on a small central area of the target with high impact density. As the stand-off distance increased to 20 mm, the expansion of the impact area led to a reduction in local impact density, thereby decreasing the peak loss; however, the area of the significant erosion region expanded accordingly.
As demonstrated by Chowdhury et al. [89], this rule was further verified through experiments on copper alloys. Within the stand-off distance range of 15–25 mm, the erosion rate decreased continuously with increasing stand-off distance: at the short stand-off distance of 15 mm, particles impacted in a beam-like manner, resulting in a small impact area (only 66.62 mm2) with high flux. Conversely, at the extended stand-off distance of 25 mm, the impact area increased to 234.54 mm2, and particles displayed V-shaped dispersed impact. This resulted in substantial attenuation of both flux and kinetic energy, consequently leading to more dispersed erosion damage.
Amaro et al. [90] revealed that as the stand-off distance increased from 75 mm to 125 mm, the erosion weight loss of the composite material decreased by 24.4%, and the erosion depth decreased by 43%. This study covered a stand-off distance range of 75–125 mm. At the short stand-off distance (75 mm), particles impacted in a high-energy beam form a small yet deep erosion area. However, at the long stand-off distance (125 mm), the dissipation of particle kinetic energy and the reduction in impact flux resulted in a large but shallow damage area. Furthermore, this parameter exerts an indirect influence on the impact fatigue life of the material subsequent to erosion. At short stand-off distances (i.e., <100 mm), the relatively profound damage resulted in analogous and diminished fatigue lives. Conversely, at the extended stand-off distance of 125 mm, the more superficial damage exhibited a substantial enhancement in the fatigue life.
3.2.4. Temperature
Temperature exerts material-specific effects on erosion by regulating material properties, surface behaviours, and interaction with the medium, as detailed below:
Miao et al. [91] focused on 304 stainless steel with ridge-like bionic units prepared via laser cladding of WC-NiCrBSiFe. In the temperature range from room temperature to 1000 °C, the erosion rate of the bionic samples exhibited a general trend of “slow increase—local decrease in the range of 400–600 °C—re-increase after 600 °C”. At a temperature of 1000 °C, the erosion rate of the bionic samples was only 50% of that of the untreated samples. The underlying mechanisms are as follows: at low temperatures, the hard phases resisted deformation while the soft phases absorbed impact energy; at medium temperatures, the formation of dense oxide films by Ni and Cr reduced erosion; at high temperatures, although the oxide films spalled off, the “air cushion effect” and “shielding effect” of the bionic structure still inhibited the aggravation of erosion.
Li et al. [92] conducted a study on SiC-Si3N4 composite ceramics fabricated by nitridation reaction sintering. In the temperature range from ambient temperature to 1400 °C, the volumetric erosion rate exhibited a U-shaped curve, with an initial increase followed by a subsequent decrease. The rate reached a maximum of 0.22 mm3/g at 800 °C and a minimum of 0.05 mm3/g at 1400 °C. Specifically, the material exhibited brittleness at low temperatures, leading to the fracture and spallation of aggregates due to the loss of support caused by matrix erosion; after 800 °C, the softening of the matrix intensified erosion; above 800 °C, SiC and Si3N4 were oxidised to form SiO2 glass films. When considered in conjunction with the enhanced thermal expansion compatibility between aggregates and the matrix, this led to a substantial reduction in the erosion rate.
As stated in the work of Wu et al. [93], the focus of the study was 20G steel. In a pure air environment at temperatures ranging from 350 to 450 °C, the erosion rate exhibited only a marginal increase (with a mass loss increment of 6.7%), suggesting a negligible effect of temperature. In the presence of ammonia, the material’s critical erosion temperature exhibited an increase from 348 °C to 398 °C. Below the critical temperature, ammonia inhibited oxidation and alleviated erosion. Conversely, above the critical temperature (400–450 °C), ammonia accelerated the reduction and spallation of the oxide film, resulting in an erosion depth that was 1.18 times that observed in the pure air environment. This finding suggests that the erosion–corrosion coupling process has exacerbated the damage to the material.
3.3. Mechanical Properties of Materials
The present body of research has been chiefly concerned with extrinsic factors, such as environmental conditions and hydrodynamic parameters. However, the intrinsic mechanical properties of materials are equally pivotal in determining erosion wear resistance. A substantial body of research has previously been conducted on the external influences in question, including but not limited to flow dynamics and particle kinematics. Nevertheless, the constitutive material attributes governing stress accommodation mechanisms remain fundamental. These include strain hardening capacity, fracture toughness, and deformation energy dissipation efficiency. Such attributes dictate the progression of erosive damage by modulating microstructural failure pathways.
3.3.1. Material Hardness
The erosion wear resistance of target materials is highly dependent on their mechanical properties. Hardness is a typical mechanical property influencing the erosion process. Extensive experimental studies have established hardness as the dominant mechanical property influencing erosive degradation. These were systematically documented in the reference [94].
The relationship between material hardness and erosion wear rate has been shown to exhibit pronounced angle-dependent characteristics. Whilst the prevailing wisdom posits an inverse correlation between hardness and erosion rate, Chang et al. [95] revealed a dual-phase response governed by impact geometry (see Table 1 for details of the mechanical properties of the experimental ductile iron):

Table 1.
Mechanical properties of the experimental ductile irons. Reprinted with permission from Ref. [95], Copyright 2005, Elsevier.
Low-angle erosion (θ < 30°): Higher hardness suppresses erosion wear by enhancing resistance to microcutting and ploughing mechanisms, since harder surfaces impede particle-induced shear deformation.
High-angle erosion (θ > 60°): The erosion can increase with the increasing hardness of the target material as high impingement angle. This is because the increasing hardness can reduce the capacity of plastic deformation and retard the dissipation of impact energy through localised yielding. Instead, stress concentrations promote brittle fracture and subsurface crack propagation under normal-impact loading.
This duality underscores the critical interplay between material microstructure and impact mechanics. On the one hand, the optimisation of hardness in low-angle cutting-dominated regimes has been shown to enhance wear resistance. Conversely, it has been observed that the material exhibits a compromise in energy dissipation within scenarios dominated by high-angle deformation.
In stainless steel alloys, a direct linear correlation exists between material hardness and erosion rate. Jia [30] confirmed experimentally that increasing martensite content enhanced both material hardness and strength. The erosion rate showed a linear dependence on hardness (the composition of steel elements used is shown in Table 2), as depicted in Figure 7. Slurry erosion-induced work-hardening further increases surface hardness, thereby improving the material’s resistance to erosion. Concurrently, Mondal et al. [96] confirmed that the erosion resistance of martensitic steels is primarily governed by their hardness (the composition of steel elements used is shown in Table 3).

Table 2.
Chemical composition of the dual-phase steel (wt. %). Reprinted with permission from Ref. [30], Copyright 2024, Elsevier.
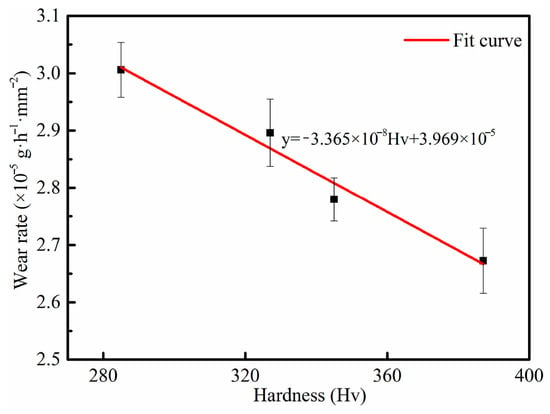
Figure 7.
Correlation between slurry erosion rate and material hardness. Reprinted with permission from Ref. [30], Copyright 2024, Elsevier.

Table 3.
The alloy composition of investigated steel. Reprinted with permission from Ref. [96], Copyright 2022, Elsevier.
In the context of alloy systems, material hardness is a pivotal factor in determining erosion resistance, primarily through microstructural strengthening mechanisms. A study by Gou et al. [97] demonstrated that the addition of 0.432 wt.% nano-additives to Fe-Cr-C-B hardfacing alloys results in a substantial enhancement of erosion resistance. In comparison with conventional alloys, this results in a 31.8% reduction in wear rate. The enhancement can be attributed to two synergistic effects: Firstly, it is evident that nanoparticles at carbide–matrix interfaces impede dislocation mobility. Secondly, carbide size is refined by 25–40%, thereby optimising stress distribution patterns. Furthermore, strain hardening during erosion increases surface hardness by approximately 20%. This effectively suppresses the initiation and propagation of microcracks.
Mehrabadi et al. [98] demonstrated that yttrium additions increase alloy hardness by 80% through solid solution strengthening and grain boundary strengthening. The former was achieved via the dissolution of yttrium atoms in the gamma–iron matrix. The latter is attributable to yttrium oxide nanoprecipitates. The modified alloys exhibited 45–60% higher erosion resistance, attributed to enhanced resistance against subsurface delamination and crack branching.
Surface engineering via thermal spraying highlights significant potential for enhancing material surface hardness and erosion resistance [99,100,101,102]. Sharma et al. [103] utilised high-velocity oxygen fuel (HVOF) spraying to deposit Fe-Cr-Ti-Mo-C-Si alloy coatings on 316L stainless steel substrates. This process achieved a 58% increase in hardness (from 220 HV to 348 HV), which directly led to a 3.2-fold enhancement in erosion resistance under slurry flow conditions.
As demonstrated by Huang et al. [104], the application of optimised heat treatment has been shown to promote microstructural densification and nanocrystalline phase formation on iron-based amorphous coatings. The coating hardness was increased from 746 HV0.1 to 917 HV0.1, which resulted in a 67% reduction in erosion rates. Yang et al. [105] further validated the correlation between hardness and erosion resistance in iron-based amorphous coatings. The findings of this study demonstrated that these coatings exhibited 4.16-fold higher erosion resistance than uncoated substrates at 30° impingement angles. The enhanced performance is ascribed to the coating’s ultrafine microstructure (50–100 nm grain size) and 1.8 GPa nanoindentation hardness, which efficiently dissipate impact energy through controlled plastic deformation rather than brittle fracture.
Temporal dynamics are complex in corrosive environments due to the triple influences of hardness, erosion, and corrosion [106,107,108,109,110]. Owen et al. [111] conducted experimental studies to investigate the damage of X65 carbon steel in CO2-saturated aqueous environments. As demonstrated in Figure 8, the study revealed that surface hardness underwent degradation under conditions of combined erosion and corrosion. This deterioration process manifests in two distinct operational phases. The initial corrosion-dominant regime is characterised by an 18% loss in hardness over 48 h, primarily through anodic dissolution and pit nucleation mechanisms. This is followed by an accelerated erosion–corrosion coupling phase, during which micro-galvanic interactions at active corrosion sites induce an additional 32% hardness reduction over 152 h.
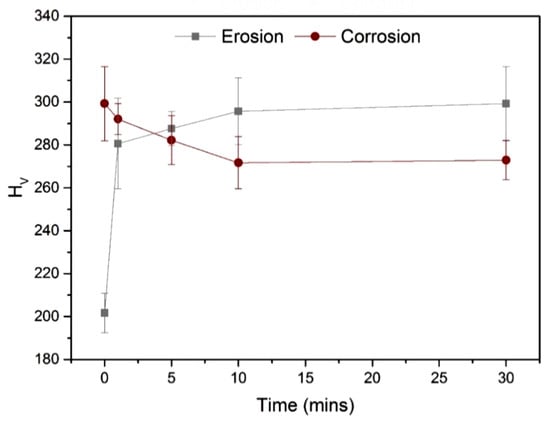
Figure 8.
Variation in material surface hardness with erosion and corrosion time. Reprinted with permission from Ref. [111], Copyright 2018, Elsevier.
The decrease in hardness is directly linked to microstructural changes, including preferential dissolution of the ferrite phase [112] and hydrogen-induced degradation of mechanical properties at pearlite interfaces [113]. These mechanisms fundamentally shift the material’s failure mode. The study explicitly demonstrates that corrosion-induced surface embrittlement not only accelerates erosion wear but also alters the failure mechanisms of the material by destabilising its crystalline structure [114].
3.3.2. Combination Function of Hardness and Other Mechanical Properties
Whilst material hardness has historically been regarded as the primary factor determining metallic wear resistance, recent studies have emphasised the critical distinction between initial hardness (H1) and strain-hardened hardness (H2) in erosive environments. Ji et al. [115] proposed a novel methodology for the evaluation of wear resistance. In this study, post-erosion strain-hardened hardness (H2) was utilised in lieu of the conventional initial hardness (H1). The post-erosion strain-hardened hardness-to-elastic modulus ratio (H2/E) exhibited a more robust correlation with experimental erosion rates in comparison to the conventional H1/E parameter. The comprehensive validation process (see Figure 9) demonstrated a reduction in prediction errors to below 10%.
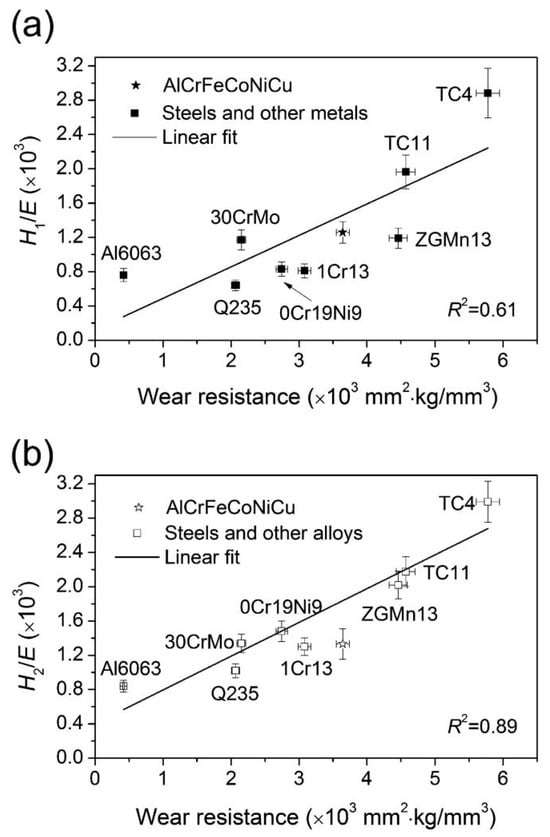
Figure 9.
Effect of hardness on the relationship between erosion wear resistance and H/E ratio, which is calculated, respectively, using (a) original hardness, and (b) strain-hardened hardness. Reprinted with permission from Ref [115], Copyright 2018, Elsevier.
Material erosion resistance shows strong correlations with composite mechanical parameters that integrate hardness and complementary material properties. It is reported that [31,116] the plasticity index (H/E) and plastic deformation resistance parameter (H3/E2) were well used in predicting erosion wear performance. These dimensionless ratios encapsulate critical facets of a material’s response to erosive impacts. The H/E ratio reflects the balance between surface penetration resistance and elastic recovery capacity, while H3/E2 quantifies the energy required to initiate permanent deformation under multi-cycle loading conditions.
Selvam et al. [32] investigated the erosion wear behaviour of austenitic stainless steel 316L via an innovative immersion stir friction processing (ISFP) technique. The findings demonstrated a direct proportional relationship between hardness and erosion wear resistance under low-angle (30°) impacts. Furthermore, the H/E (hardness-to-elastic modulus) ratio exhibited a stronger correlation with erosion wear rates at normal incidence (90°), as illustrated quantitatively in Figure 10. This angular dichotomy is attributed to the transition between cutting-dominated (low-angle) and deformation-controlled (high-angle) material removal regimes. In this context, strain-hardened microstructures generated by the ISFP process achieve a 40–60% reduction in wear through two mechanisms: increased dislocation density and grain refinement.
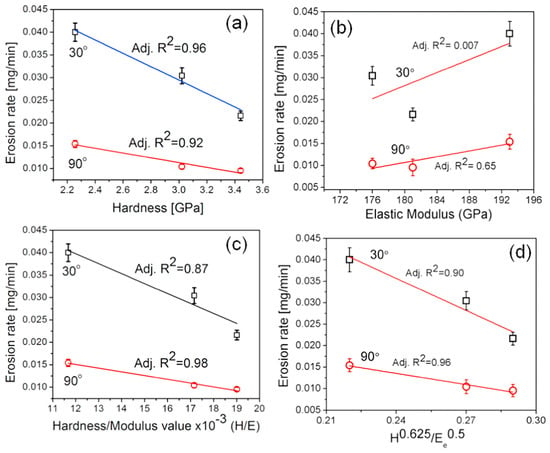
Figure 10.
Correlation of erosion rate and the combined function of hardness and elastic modulus: (a) Correlation of erosion rate at 30° and 90° impingement angles with hardness for the as-cast SS316L, friction stir processed SS316L under ambient cooling (1800A) and submerged cooling (1800C); (b) Correlation of erosion rate at 30°and 90° impingement angle with elastic modulus; (c) Correlation of erosion rate at 30° and 90° impingement angle with hardness to elastic modulus (H/E) ratio; (d) Correlation of erosion rate at 30° and 90° impingement angle with H0.625/Ee0.5 for the as-cast SS316L, 1800A and 1800C specimens. Reprinted with permission from Ref. [32], Copyright 2017, Elsevier.
Beyond the established correlations between hardness and elastic modulus, a synergistic interaction between material hardness and tensile toughness was identified as a contributing factor to slurry erosion. It has been demonstrated that an optimal balance of hardness and toughness is exhibited, which has been shown to result in a 67% improvement in erosion resistance compared to the substrate [117]. This finding indicates that the dual-property relationship is a more appropriate approach for presenting the slurry erosion resistance in ductile alloy systems.
The development of multivariate mechanical indices extends beyond dual-property frameworks for erosion wear prediction. Studies have identified stronger correlations through composite parameters integrating three or more fundamental material properties. Mann et al. [118] exemplified this through modified ultimate resilience (MUR) analysis on surface-treated 13Cr4Ni stainless steel. The MUR parameter synthesises microhardness, ultimate tensile strength (UTS), and elastic modulus (E) via a hierarchical formulation:
where H denotes Vickers hardness measurements. This multi-parametric approach achieved 92% correlation accuracy with experimental erosion data, outperforming conventional single-property predictors. The enhanced predictive capability stems from MUR’s integration of both hardness gradients and elastic resilience. In another word, the synergistic effects of work hardening and residual stress distribution is also a sign of erosion resistance.
UR = UTS2/2E
MUR = URsubstrate × (Hardnesstop surface/Hardnesssubstrate)2
Wan et al. [119] developed a comprehensive model to evaluate the erosion resistance of cermets. The model is presented in Equation (6). It integrates indentation fracture toughness (KIC), hardness (H), and transverse rupture strength (TRS).
where E is the erosion rate, C is the proportional constant; KIC is the indentation fracture toughness, H is the hardness, m and n are −1.3 and −0.25, respectively.
There is also a significant correlation between the erosion rate and the hardness ratio of material hardness (Hm) to erodent hardness (He). Desale et al. [120] conducted erosion wear tests at a normal (90°) impact angle using seven ductile materials (aluminium alloy, copper, brass, mild steel, AISI 304L stainless steel, AISI 316L stainless steel, and turbine blade steel) and three erodent particles (quartz, alumina, and silicon carbide). Their study categorised the target material-to-erodent hardness ratio (Hm/He) into three distinct regions: 4.2–5.2, 6.9–12.1, and 12.5–27.5 (Figure 11). Notably, the erosion rate remained nearly constant within each defined hardness ratio range, indicating threshold-like behaviour in material response to erodent abrasion across these intervals.
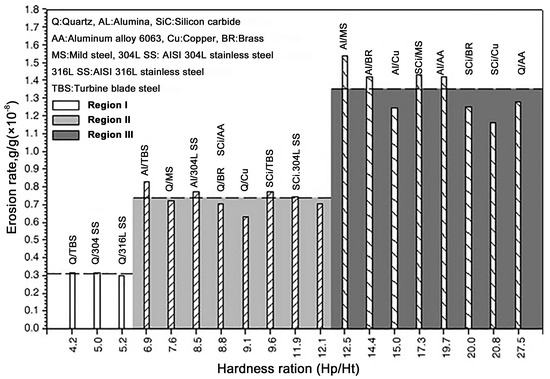
Figure 11.
Effect of hardness ratio on erosion rate of ductile materials at normal impact of 550 μm size particulate mixture at 10 wt% concentration and 3 m/s velocity. Reprinted with permission from Ref. [120], Copyright 2008, Elsevier.
3.3.3. Other Mechanical Properties
It is evident that mechanical properties, in addition to hardness, play a significant role in determining the erosion rate. The erosion process is primarily initiated by the impact of small particles on the surface of the target material, as previously documented [121]. This process establishes an intrinsic relationship between material properties, such as tensile strength and elongation, and the erosion rate. As demonstrated by Shimizu et al. [122], the erosion rate of SUS403 is twice that of SUS630 at a 30° impact angle and a test temperature of 1173 K. This finding indicates that materials with higher elongation tend to form protrusions under shallow-angle impacts, which are subsequently removed by particle impingement. In their seminal study, Chang et al. [123] investigated the erosion behaviour of isothermally quenched nodular cast iron under various heat treatment parameters at normal (90°) impact angles. The findings of the study demonstrated that the erosion rate exhibited a positive correlation with hardness and tensile strength, while being inversely proportional to elongation and mechanical energy density (Figure 12).
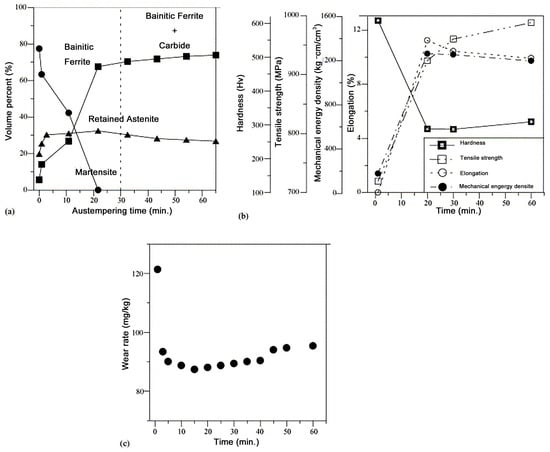
Figure 12.
Variation in (a) microstructures, (b) mechanical properties, and (c) erosion rate with austempering time (austempering temperature, 420 °C). Reprinted with permission from Ref. [123], Copyright 2006, Elsevier.
In addition to material strength and elongation, the impact toughness also exhibits a significant correlation with the erosion rate. Zambrano et al. [124] conducted a review of the literature on the influence of impact toughness and fracture toughness on erosion mechanisms. Zheng et al. [125] modified the hardness and impact toughness of iron–chromium alloys by varying the chromium content. As the chromium content increased, the alloy hardness rose monotonically, while the impact toughness decreased in an inverse trend (see Figure 13). The erosion test results demonstrated that high-hardness alloys exhibited a predominant effect on the early-stage erosion resistance, characterised by the impediment of particle indentation. However, the reduction in impact toughness enhanced the probability of material fracture under sustained erosive loading. This underscores a pivotal trade-off between hardness and toughness. While initial hardness enhances resistance to surface abrasion, inadequate toughness can precipitate structural failure through crack propagation under cyclic impact. Consequently, the inadequate toughness ultimately negates the benefits of high hardness in long-term erosion scenarios.
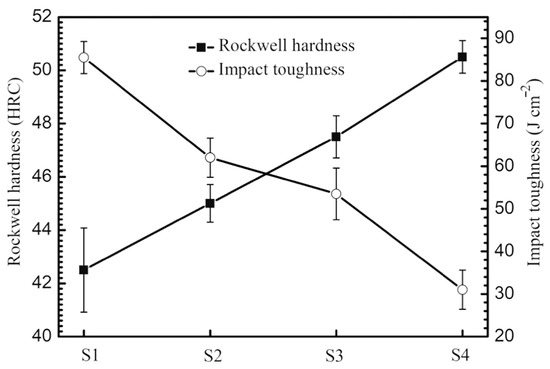
Figure 13.
Rockwell hardness and impact toughness of the alloys with different Cr contents. Adapted from Ref. [125].
Porosity is a fundamental microstructural characteristic of thermal spray coatings (including High-Velocity Oxygen Fuel (HVOF), atmospheric plasma spraying, and supersonic plasma spraying coatings) and directly affects the erosion resistance of coatings. The content demonstrates a substantial negative correlation with erosion resistance, exhibiting specific patterns as outlined below:
In HVOF-sprayed coatings (for geothermal drilling scenarios), WC-CoCr (0.9 ± 0.3%) and CrC-NiCr (1.1 ± 0.1%) coatings with low porosity (<1.5%) demonstrated no evident corrosion penetration and delamination following 24 h simulated drilling fluid erosion. Conversely, the Fe-based amorphous coating exhibited electrolyte penetration due to through pores, forming a 20 μm-thick corrosion layer and undergoing delamination [126]. It has been demonstrated that low porosity has the capacity to impede medium penetration, thereby diminishing the synergistic effect of erosion and corrosion.
In atmospheric plasma-sprayed NiTi coatings (for aviation scenarios), a significant decrease in the erosion rate was observed when the porosity decreased from 3.5% to below 1.0%. In conditions of normal erosion at temperatures below 90°, coatings with high porosity (>2.5%) exhibited a deficiency in support at the pore edges, thereby rendering them susceptible to material spallation induced by abrasive particles. The erosion rate of these coatings was observed to be 30–50% higher compared to coatings with low porosity. In the context of oblique erosion at an angle of less than 45°, the formation of pores has been shown to induce a phenomenon referred to as the “concave surface effect”. This effect has been demonstrated to intensify the process of material removal, which is predominantly governed by shear forces [127].
In supersonic plasma-sprayed AT13 ceramic coatings (for resin matrix protection scenarios), the 60° oblique erosion rate of the AT13-1 coating (porosity: 12.77%) was 21% higher than that of the AT13-2 coating (porosity: 8.21%), specifically 8.45 × 10−3 mm3·g−1 versus 6.97 × 10−3 mm3·g−1. In conditions of normal erosion at temperatures below 90°, the AT13-1 coating was found to be penetrated by abrasive particles due to its high porosity. Furthermore, its erosion rate (11.61 × 10−3 mm3·g−1) was determined to be 2.08 times that of the AT13-2 coating (5.57 × 10−3 mm3·g−1) [128]. It has been demonstrated that high porosity has the effect of weakening the support of hard phases, thus leading to their detachment.
In summary, porosity affects erosion resistance through the “channel effect” (promoting medium penetration) and “stress concentration effect” (accelerating damage propagation).
3.3.4. Effect of Element Content on Erosion
Firstly, regarding permanent mould cast austempered ductile iron (PMADI) alloyed with manganese (Mn) [129], Mn content regulates graphite morphology and matrix phase composition to influence erosion performance, exhibiting a “first-improving-then-worsening” trend: When Mn content ranges from 1% to 2%, erosion volume loss decreases gradually, with the 2% Mn sample showing optimal erosion resistance—its resistance at a 45° impact angle is ~20% higher than that of the 1% Mn sample; when Mn content increases to 3%, erosion loss rises instead.
Mechanistically, 2% Mn promotes the refinement and uniform distribution of graphite nodules (484 nodules/mm2, 8.6 μm in size), while facilitating the uniform precipitation of a bainitic matrix and retaining 28–34% retained austenite (this austenite transforms into martensite via work hardening during erosion). In contrast, 3% Mn induces the precipitation of large quantities of Fe3C carbides in the matrix, disrupting matrix continuity and causing brittle spallation.
Secondly, for high-chromium cast iron under high-temperature (1173 K) erosion [130], molybdenum (Mo) content must reach 3% to significantly enhance erosion resistance: 16Cr-3Mo has a 36% lower erosion rate than Mo-free 16Cr, and 26Cr-3Mo has a 28% lower rate than Mo-free 26Cr; notably, these two Mo-bearing alloys have identical erosion rates (1.8 × 10−3 cm3/kg). In contrast, 1% Mo has no significant effect—the erosion rate difference between the 1% Mo sample and Mo-free samples is less than 5%.
Mechanistically, 3% Mo dissolves into M7C3 carbides (dissolution amount: 4.2–4.9%) to inhibit their high-temperature softening, while inducing the precipitation of M2C carbides—these carbides possess a high hardness of 2200 HV and a high melting point of 2790 K. These two effects act synergistically to resist particle impact. For the 1% Mo sample, insufficient Mo dissolution in M7C3 and inadequate M2C precipitation fail to optimise erosion resistance.
Thirdly, regarding the erosion behaviour of high-chromium cast iron in as-cast (AC) and quenched-tempered (QT: 1323 K quenching + 726 K tempering) states [33], heat treatment modulates how chromium (Cr) content affects erosion rate: In the AC state, as Cr content increases from 12% to 27%, erosion rate decreases continuously—12Cr-AC exhibits the highest erosion rate (5.59 cm3/kg), and 27Cr-AC the lowest. In the QT state, erosion rate stabilises once Cr content reaches 17%, with the rate difference among 17Cr-QT, 22Cr-QT, and 27Cr-QT being less than 30%.
Mechanistically, the Cr/C ratio determines carbide type: When Cr < 17%, the matrix is dominated by low-hardness M3C carbides (prone to plastic deformation during erosion); when Cr ≥ 17%, high-hardness M7C3 carbides (1200–1600 HV at room temperature, with good high-temperature stability) become dominant. QT treatment promotes the transformation of M3C to M7C3 in the 17Cr sample, enabling “low Cr content with high erosion resistance”.
As demonstrated in Section 3, the “parameter-erosion response” has been shown to exhibit quantitative correlations, including the power-law relationship with flow velocity and the angle dependence of hardness. However, in industrial applications, it is necessary to integrate these dispersed parameter relationships into computable predictive tools in order to enable equipment service life assessment and the selection of erosion-resistant materials. The subsequent chapter will concentrate on contemporary mainstream erosion prediction models, appraising their theoretical underpinnings, parameter inputs, and applicable scenarios. It will also analyse their strengths and limitations in “gas–solid/liquid–solid systems” and “ductile/brittle materials”. This is not only the quantitative integration of “influencing factors” but also the core link for achieving the objective of “promoting the integration of models with material property databases”.
4. Erosion Prediction Model
Erosion prediction models serve as the core tools for the quantitative integration of “erosion mechanisms” and “influencing factors”. The objective is to correlate particle characteristics (size, shape), fluid parameters (velocity, angle), and material properties (hardness, toughness) through mathematical formulas, thereby enabling the quantitative calculation of erosion rate. This provides a basis for the service life assessment of industrial equipment (e.g., oil and gas pipelines, turbine components), the selection of erosion-resistant materials, and the optimisation of protective strategies.
Existing models can be classified according to their theoretical foundations, with the classification system comprising the following categories: “mechanistic models”, “semi-mechanistic-empirical models”, and “empirical models”. The classification of these systems is determined by their applicability to specific operating conditions. Consequently, they can be categorised into three distinct groups: “for gas–solid systems only”, “for liquid–solid systems only”, and “universal for multiple systems”. However, it should be noted that all models have certain limitations (e.g., poor adaptability to brittle materials, low prediction accuracy under complex operating conditions), and thus require selection and optimisation based on specific scenarios.
4.1. Overview of Erosion Prediction Models
Finnie model [131]
The model under discussion is rooted in the erosion mechanism. The postulation asserts that the impingement erosion caused by solid particles is contingent on the kinematic properties of the particles and the mechanical properties of the material. The expression of this model is displayed in Equations (7) and (8). It can be observed that this model is applicable to both high and low impact angles.
where M is the mass of eroding particles, m is the mass of an individual particle, I is the moment of inertia of the particle about its centroid, r is the mean particle radius, α is the angle of impact, V is the particle velocity, p is the horizontal component of the flow pressure, and c is the fraction of particles idealised cutting.
Despite the fact that the Finnie model takes into account both ductile and brittle materials, its application to brittle materials is constrained by its angle function, which has been tailored to the plastic deformation mechanisms that are predominant in ductile materials. Furthermore, certain parameters inherent in the Finnie model are challenging to measure with precision in practical scenarios, thereby limiting its universal predictive capability across material classes.
Oka model [26,27]
The Oka model has been demonstrated to be capable of predicting the rate of erosion in a variety of conditions. The parameters under consideration are numerous and of critical importance. These include the angle of impact, the properties of the particles, the velocity of the impact, and the hardness of the target material. Its specific mathematical formulation—typically expressed as a power-law relationship—synthesises these factors to quantify erosion rates. To illustrate this point, the following model may be considered:
where n1 and n2 are the exponents determined by the material hardness and particle properties. k1, k2, and k3 are the exponential factors related to other parameters, respectively. K denotes the particle characteristic factor such as particle shape (edge angle), particle hardness.
The Oka model is designed for ductile materials, but it can still describe the erosion rate of brittle materials by setting n2 = 0.
E/CRC model [132]
The E/CRC model can also be widely applied to predict erosion rates under various working conditions. It includes Brinell hardness, particle roundness, impact angle, impact velocity, etc. This model is presented below.
where BH is the Brinell hardness of the wall material; Fs is the particle shape coefficient, Fs = 1.0 for sharp (angular), 0.53 for semirounded, or 0.2 for fully rounded sand particles; Vp is the particle impact velocity; θ is the impact angle in radians; and n = 2.41 and C = 2.17 × 10−7 are empirical constants.
Arbanejad model [133]
The model is based on the work of Finnie and Bitter and develops a semi-mechanistic model based on E/CRC. It uses experimental data collected with air as the carrier fluid to explicitly divide erosion damage into cutting and deformation damage. The erosion rate is expressed as:
where ERC denotes material loss caused by cutting; ERD denotes material loss caused by deformation, Fs is shape factor (1 for sharp particles and 0.5 for semi-circular particles), C1, C2, K are empirical constants, V is the particle impact velocity, and α is the particle impact angle.
It is noted that the Arbanejad model is only applicable to the erosion rate prediction under gas–solid conditions.
Mansouri model [134]
Mansouri’s modification of the Arabnejad model was developed on the basis of gas–solid erosion test data. The model incorporates liquid viscosity considerations in the context of slurry erosion, thereby extending its scope to encompass both gas–solid and liquid–solid conditions. Furthermore, a Stokes number function is introduced. The phenomenon is associated with the dimensions of the particles and the viscosity of the carrier fluid. The form is as follows:
It is noticed that Mansouri model could not predict the erosion in the stagnation zone for the particle size of 300 µm and 600 µm. It is because that deformation erosion was not assumed to occur in the liquid–solid flow. However, it was improved by Mansouri and the deformation was considered in the modified model [135].
DNV model [136]:
The DNV model is suitable for the erosion in pipeline system transporting oil, gas, and water. It can predict erosion rates of many materials (e.g., steel, epoxy resin, titanium, etc.). The form is as follows:
Huang model [137]
Huang et al. [137] indicated that the particle impact on the target generates normal and tangential directions, which cause deformation. They considered that the normal component of the force is responsible for “deformation damage elimination” and the tangential component for “cutting elimination”. The following model was proposed:
Neilson and Gilchrist model [138]:
Neilson and Gilchrist proposed an erosion model based on the impact angle, building upon the research conducted by Finnie and Bitter. The researchers established two particle erosion equations for large and small impact angles, respectively, and demonstrated that the total erosion rate is equivalent to the sum of erosion due to deformation and cutting mechanisms. The model was derived from experimental results:
Gnanavelu model [139]
Gnanavelu proposed a model to predict the erosion rate of mud erosion under different particle shapes. This model was developed by integrating experimental data and computational fluid dynamics (CFD) simulations.
4.2. Discussion on Erosion Prediction Models
As clarified in Section 3.3, the erosion resistance of materials correlates strongly with “combined mechanical properties”—including the hardness-to-elastic modulus ratio (H/E), strain-hardened hardness (H2), impact toughness, and hardness–toughness balance—rather than a single hardness parameter. However, the following issues remain prevalent in existing models:
Firstly, many existing models rely solely on a single mechanical parameter, neglecting the critical role of “combined properties”. For instance, most take hardness as the sole input for material mechanical properties (e.g., Oka, E/CRC models). Nevertheless, as noted in Section 3.3.2, the H/E ratio exhibits a significantly higher predictive correlation (R2 = 0.89) under 90° (deformation-dominated) impact than initial hardness (R2 = 0.61); furthermore, H3/E2—a parameter characterising plastic deformation resistance—can more accurately reflect material damage under multi-cycle impacts. Although models such as Finnie and Neilson-Gilchrist implicitly assume “plastic deformation”, they fail to quantify the effect of elastic modulus on energy dissipation. For example, for 304 stainless steel under elevated temperatures (400–600 °C), oxide film formation alters its H/E ratio; existing models, however, cannot capture this dynamic mechanical response, leading to prediction deviations.
Secondly, existing models fail to account for the “dynamic changes” in materials’ mechanical properties. For one thing, in corrosive environments, materials’ mechanical properties degrade significantly—for example, the hardness of X65 carbon steel decreases by 18% after 48 h in a CO2 environment and a further 32% after 152 h. Yet existing models (e.g., Mansouri, DNV) do not incorporate “corrosion–mechanical property coupling” parameters, leaving them unable to reflect the sharp increase in erosion rate caused by reduced hardness. For another, the strain-hardening effect (e.g., a 20% increase in surface hardness after wear) is critical to enhancing erosion resistance (Section 3.3.1), but none of the models replace initial hardness (H1) with “strain-hardened hardness (H2)”, resulting in substantial prediction errors.
Thirdly, existing models completely lack correlation with the mechanical properties of brittle materials. For brittle materials (e.g., SiC-Si3N4 ceramics), their erosion is dominated by “fracture toughness (KIC)” (Section 3.3.3). However, existing models (e.g., Oka, E/CRC) only adapt passively to brittle materials by “setting a parameter (n2 = 0)” and do not proactively correlate KIC with impact energy. For example, changes in the KIC of SiC-Si3N4 at 800 °C reduce its erosion rate from 0.22 to 0.05 mm3/g, a phenomenon existing models cannot account for.
5. Conclusions
This article systematically reviews erosion mechanisms, influencing factors, and erosion models, with emphasis placed on the effects of materials’ mechanical parameters on impingement erosion in multiphase flow. Erosion wear involves complex processes influenced by multiple factors, including particle properties, fluid dynamic parameters, and materials’ mechanical properties. Although numerous factors have been considered to clarify erosion mechanisms, the influence of material parameters on the erosion process remains understudied—most research focuses on environmental conditions. Thus, future research should prioritise the following directions to advance erosion prediction:
First, more attention should be paid to the differences in materials’ responses to erosion and their underlying causes. Work hardening, localised strain, and multi-phase microstructural interactions seem related to erosion resistance. Notably, the combined effects of hardness, elastic modulus, toughness, fracture toughness, and other parameters have been shown to be more directly associated with slurry erosion. For instance, to characterise the cutting wear of ductile materials under low-angle impacts, it is necessary to integrate plastic deformation capacity with hardening behaviour. For brittle materials, coupling fracture toughness with the impact energy dissipation mechanism is crucial for understanding their crack propagation.
Second, most existing models (such as Finnie, Oka, E/CRC, etc.) have been developed primarily for ductile metals or specific operating conditions (e.g., gas–solid/liquid–solid flow), with limited development for brittle materials. Their predictive accuracy remains inadequate, relying on single mechanical parameters while neglecting the critical role of combined characteristics and failing to account for the “dynamic changes” in material mechanical properties. It is therefore recommended to embed materials’ mechanical parameters (e.g., strain-hardened hardness (H2), impact toughness) into model frameworks. Empirical coefficients calibrated using multi-condition experimental data (e.g., different particle shapes, velocities, and corrosive media) are more appropriate for enhancing prediction accuracy. Additionally, it is necessary to develop multiphysics models that couple flow field dynamics, particle trajectories, and material failure mechanisms for complex industrial scenarios—such as multiphase flow in oil and gas pipelines and dusty flue gas in coal-fired power plants.
Author Contributions
W.A.: Conceptualization, Investigation, Writing—original draft, Validation; S.Y.: Project administration, Visualisation, Validation; Z.W.: Formal analysis, Visualisation, Validation; H.P.: Conceptualization, Writing—review and editing, Validation; H.H.: Funding acquisition, Writing—review and editing, Validation.; Y.Z.: Writing—review and editing, Supervision, Validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key R&D Program of China, grant number 2024YFC3013702 and National Natural Science Foundation of China general project, grant number 52571115.
Data Availability Statement
No new data were created or analysed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Allen, C.; Ball, A. A review of the performance of engineering materials under prevalent tribological and wear situations in South African industries. Tribol. Int. 1996, 29, 105–116. [Google Scholar] [CrossRef]
- Goddard, J.; Wilman, H. A theory of friction and wear during the abrasion of metals. Wear 1962, 5, 114–135. [Google Scholar] [CrossRef]
- Richardson, R.C.D. The wear of metals by hard abrasives. Wear 1967, 10, 291–309. [Google Scholar] [CrossRef]
- Ariely, S.; Khentov, A. Erosion corrosion of pump impeller of cyclic cooling water system. Eng. Fail. Anal. 2006, 13, 925–932. [Google Scholar] [CrossRef]
- Kashyap, T.; Thakur, R.; Ngo, G.H.; Lee, D.; Fekete, G.; Kumar, R.; Singh, T. Silt erosion and cavitation impact on hydraulic turbines performance: An in-depth analysis and preventative strategies. Heliyon 2024, 10, e28998. [Google Scholar] [CrossRef]
- Shrivastava, N.; Rai, A.K. Hydro-abrasive erosion in Pelton turbines: Comprehensive review and future outlook. Renew. Sustain. Energy Rev. 2025, 207, 114957. [Google Scholar] [CrossRef]
- Kumar, P.; Singal, S.K.; Gohil, P.P. A technical review on combined effect of cavitation and silt erosion on Francis turbine. Renew. Sustain. Energy Rev. 2024, 190, 114096. [Google Scholar] [CrossRef]
- Amadi, A.; Mohyaldinn, M.; Ridha, S. Sand particle induced erosion in oil and gas screens: A review of influencing factors and wear dynamics. Powder Technol. 2024, 436, 119528. [Google Scholar] [CrossRef]
- Peng, W.; Cao, X.; Ma, L.; Wang, P.; Bian, J.; Lin, C. Sand erosion prediction models for two-phase flow pipe bends and their application in gas-liquid-solid multiphase flow erosion. Powder Technol. 2023, 421, 118421. [Google Scholar] [CrossRef]
- Yao, L.; Liu, Y.; Xiao, Z.; Chen, Y. An algorithm combining sedimentation experiments for pipe erosion investigation. Energy 2023, 270, 126891. [Google Scholar] [CrossRef]
- Zhou, J.W.; Liu, Y.; Liu, S.Y.; Du, C.L.; Li, J.P. Effects of particle shape and swirling intensity on elbow erosion in dilute-phase pneumatic conveying. Wear 2017, 380–381, 66–77. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Liu, Y.; Wei, J.; Liu, X. Effect of abrasive mass flow on the abrasive acceleration and erosion rates of abrasive gas jets. Rock. Mech. Rock. Eng. 2019, 52, 3085–3102. [Google Scholar] [CrossRef]
- Babu Golla, C.; Narasimha Rao, R.; Ismail, S. Variation in wear scar penetration depths due to impact angle on the erosion wear of advanced aluminum matrix nanocomposites. Mater. Lett. 2024, 370, 136843. [Google Scholar] [CrossRef]
- Annamalai, S.; Anand Ronald, B.; Ebenezer, D. Slurry erosive wear behaviour of metal matrix composites—A review. Mater. Today Proc. 2024. [Google Scholar] [CrossRef]
- Yu, H.; Shao, L.; Zhang, S.; Zhang, J.; Han, Z. An innovative strategy of anti-erosion: Combining bionic morphology and bionic arrangement. Powder Technol. 2022, 407, 117653. [Google Scholar] [CrossRef]
- Finnie, I. Some reflections on the past and future of erosion. Wear 1995, 186–187, 1–10. [Google Scholar] [CrossRef]
- Finnie, I. Some observations on the erosion of ductile metals. Wear 1972, 19, 81–90. [Google Scholar] [CrossRef]
- Finnie, I.; Kabil, Y.H. On the formation of surface ripples during erosion. Wear 1965, 8, 60–69. [Google Scholar] [CrossRef]
- Misra, A.; Finnie, I. An experimental study of three-body abrasive wear. Wear 1983, 85, 57–68. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Dupont, F.; Finnie, I. The simulation of sliding wear by cyclic deformation: Microstructural aspects. Wear 1990, 140, 93–106. [Google Scholar] [CrossRef]
- Finnie, I.; Stevick, G.R.; Ridgely, J.R. The influence of impingement angle on the erosion of ductile metals by angular abrasive particles. Wear 1992, 152, 91–98. [Google Scholar] [CrossRef]
- Zhou, X.L.; Guo, Y.B.; Xie, Q.J.; Wang, D.G.; Yoon, H.C. Numerical study on erosion behavior of sliding sleeve ball seat for hydraulic fracturing based on experimental data. Petrol. Sci. 2023, 20, 515–525. [Google Scholar] [CrossRef]
- Meng, H.C.; Ludema, K.C. Wear models and predictive equations: Their form and content. Wear 1995, 181–183, 443–457. [Google Scholar] [CrossRef]
- López, D.; Congote, J.P.; Cano, J.R.; Toro, A.; Tschiptschin, A.P. Effect of particle velocity and impact angle on the corrosion–erosion of AISI 304 and AISI 420 stainless steels. Wear 2005, 259, 118–124. [Google Scholar] [CrossRef]
- Oka, Y.I.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 2: Mechanical properties of materials directly associated with erosion damage. Wear 2005, 259, 102–109. [Google Scholar] [CrossRef]
- Oka, Y.I.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Desale, G.R.; Gandhi, B.K.; Jain, S.C. Particle size effects on the slurry erosion of aluminium alloy (AA 6063). Wear 2009, 266, 1066–1071. [Google Scholar] [CrossRef]
- Lin, N.; Arabnejad, H.; Shirazi, S.A.; McLaury, B.S.; Lan, H. Experimental study of particle size, shape and particle flow rate on Erosion of stainless steel. Powder Technol. 2018, 336, 70–79. [Google Scholar] [CrossRef]
- Jia, Y.; Deng, X.; Wang, Q.; Li, C.; Wang, Z. Correlation between microstructure, mechanical properties, and slurry erosion behavior of hot-rolled dual-phase steel. Wear 2024, 540–541, 205266. [Google Scholar] [CrossRef]
- Hua, L.; Liuhe, L.; Xiaoting, W.; Guodong, L.; Duoduo, L.; Yang, L.; Ling, T.; Mingyue, H. Effect of bias voltage on the erosion performance of TiAlSiN coatings on TC6 substrate by high power impulse magnetron sputtering. Surf. Coat. Technol. 2024, 477, 130263. [Google Scholar] [CrossRef]
- Selvam, K.; Rakesh, B.S.; Grewal, H.S.; Arora, H.S.; Singh, H. High strain deformation of austenitic steel for enhancing erosion resistance. Wear 2017, 376–377, 1021–1029. [Google Scholar] [CrossRef]
- Shimizu, K.; Purba, R.H.; Kusumoto, K.; Yaer, X.; Ito, J.; Kasuga, H.; Gaqi, Y. Microstructural evaluation and high-temperature erosion characteristics of high chromium cast irons. Wear 2019, 426–427, 420–427. [Google Scholar] [CrossRef]
- Hu, H.X.; Zheng, Y.G.; Qin, C.P. Comparison of Inconel 625 and Inconel 600 in resistance to cavitation erosion and jet impingement erosion. Nucl. Eng. Des. 2010, 240, 2721–2730. [Google Scholar] [CrossRef]
- Hu, H.X.; Jiang, S.L.; Tao, Y.S.; Xiong, T.Y.; Zheng, Y.G. Cavitation erosion and jet impingement erosion mechanism of cold sprayed Ni–Al2O3 coating. Nucl. Eng. Des. 2011, 241, 4929–4937. [Google Scholar] [CrossRef]
- Hu, H.X.; Zheng, Y.G.; Liu, C.B. Predicting the preferential sites to liquid droplet erosion of the bellows assemblies by CFD. Nucl. Eng. Des. 2011, 241, 2295–2306. [Google Scholar] [CrossRef]
- Yi, J.Z.; Hu, H.X.; Wang, Z.B.; Zheng, Y.G. Comparison of critical flow velocity for erosion-corrosion of six stainless steels in 3.5 wt% NaCl solution containing 2 wt% silica sand particles. Wear 2018, 416–417, 62–71. [Google Scholar] [CrossRef]
- Yi, J.Z.; Hu, H.X.; Wang, Z.B.; Zheng, Y.G. On the critical flow velocity for erosion-corrosion in local eroded regions under liquid-solid jet impingement. Wear 2019, 422–423, 94–99. [Google Scholar] [CrossRef]
- Yi, J.Z.; Hu, H.X.; Wang, Z.B.; Zheng, Y.G. On the critical flow velocity for erosion-corrosion of Ni-based alloys in a saline-sand solution. Wear 2020, 458–459, 203417. [Google Scholar] [CrossRef]
- Chen, Z.X.; Hu, H.X.; Zheng, Y.G.; Guo, X.M. Effect of groove microstructure on slurry erosion in the liquid-solid two-phase flow. Wear 2021, 466–467, 203561. [Google Scholar] [CrossRef]
- Chen, Z.X.; Hu, H.X.; Guo, X.M.; Zheng, Y.G. Effect of groove depth on the slurry erosion of V-shaped grooved surfaces. Wear 2022, 488–489, 204133. [Google Scholar] [CrossRef]
- Ma, X.G.; Yang, X.D.; Hu, H.X.; Zheng, Y.G. Numerical simulation of particle concentration and size on the slurry erosion on the surface of V-shaped groove microstructure. J. Korean Phys. Soc. 2022, 80, 991–1002. [Google Scholar] [CrossRef]
- Zhao, L.Q.; Hu, H.X.; Zheng, Y.G.; Guo, X.M.; Pu, J.X. Behavior and mechanism of slurry erosion to grooved surface at different angles. Colloid. Surface A 2023, 656, 130410. [Google Scholar] [CrossRef]
- Yıldızlı, K.; Karamış, M.B.; Nair, F. Erosion mechanisms of nodular and gray cast irons at different impact angles. Wear 2006, 261, 622–633. [Google Scholar] [CrossRef]
- Bitter, J.G.A. A study of erosion phenomena: Part II. Wear 1963, 6, 169–190. [Google Scholar] [CrossRef]
- Bitter, J.G.A. A study of erosion phenomena part I. Wear 1963, 6, 5–21. [Google Scholar] [CrossRef]
- Levy, A.V. The platelet mechanism of erosion of ductile metals. Wear 1986, 108, 1–21. [Google Scholar] [CrossRef]
- Parsi, M.; Najmi, K.; Najafifard, F.; Hassani, S.; McLaury, B.S.; Shirazi, S.A. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications. J. Nat. Gas. Sci. Eng. 2014, 21, 850–873. [Google Scholar] [CrossRef]
- Sundararajan, G. A comprehensive model for the solid particle erosion of ductile materials. Wear 1991, 149, 111–127. [Google Scholar] [CrossRef]
- Nguyen, Q.B.; Lim, C.Y.H.; Nguyen, V.B.; Wan, Y.M.; Nai, B.; Zhang, Y.W.; Gupta, M. Slurry erosion characteristics and erosion mechanisms of stainless steel. Tribol. Int. 2014, 79, 1–7. [Google Scholar] [CrossRef]
- Al-Bukhaiti, M.A.; Ahmed, S.M.; Badran, F.M.F.; Emara, K.M. Effect of impingement angle on slurry erosion behaviour and mechanisms of 1017 steel and high-chromium white cast iron. Wear 2007, 262, 1187–1198. [Google Scholar] [CrossRef]
- Hutchings, I.M. A model for the erosion of metals by spherical particles at normal incidence. Wear 1981, 70, 269–281. [Google Scholar] [CrossRef]
- Sheldon, G.L.; Kanhere, A. An investigation of impingement erosion using single particles. Wear 1972, 21, 195–209. [Google Scholar] [CrossRef]
- Levy, A.V.; Yau, P. Erosion of steels in liquid slurries. Wear 1984, 98, 163–182. [Google Scholar] [CrossRef]
- Shimizu, K.; Noguchi, T. Erosion characteristics of ductile iron with various matrix structures. Wear 1994, 176, 255–260. [Google Scholar] [CrossRef]
- Rajahram, S.S.; Harvey, T.J.; Walker, J.C.; Wang, S.C.; Wood, R.J.K. Investigation of erosion–corrosion mechanisms of UNS S31603 using FIB and TEM. Tribol. Int. 2012, 46, 161–173. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, L.; Xie, H.; Zhang, W.; Huang, S.; Yang, Z.; Li, Z.; Mi, X. Enhancing the erosion–corrosion resistance of cupronickel alloy through grain boundary engineering. Corros. Sci. 2023, 219, 111228. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, Y.; Fu, J.; Teng, W.; Wang, H. Erosive wear analysis of bamboo fiber-reinforced high-density polyethylene composites: Effect of aluminum oxide. Polym. Compos. 2022, 43, 3823–3830. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Z.; Zhan, M. An investigation of the erosion–corrosion characteristics of ductile cast iron. Mater. Design 2007, 28, 260–265. [Google Scholar] [CrossRef]
- Zhou, R.; Cao, Y.; Shi, W.; Yang, Y.; Cheng, S.; Wang, Z. Experimental study on surface erosion of Grade-A marine steel with different curvatures by ultra-high pressure water jet. J. Mater. Res. Technol. 2024, 31, 3025–3034. [Google Scholar] [CrossRef]
- Okonkwo, P.C.; Shakoor, R.A.; Ahmed, E.; Mohamed, A.M.A. Erosive wear performance of API X42 pipeline steel. Eng. Fail. Anal. 2016, 60, 86–95. [Google Scholar] [CrossRef]
- Tandel, R.R.; Patel, R.N.; Jain, S.V. Correlation development of erosive wear and silt erosion failure mechanisms for pump as turbine. Eng. Fail. Anal. 2023, 153, 107610. [Google Scholar] [CrossRef]
- Kang, C.; Li, M.; Teng, S.; Liu, H.; Chen, Z.; Li, C. Erosive Wear Caused by Large Solid Particles Carried by a Flowing Liquid: A Comprehensive Review. Processes 2024, 12, 1150. [Google Scholar] [CrossRef]
- Zeng, L.; Zhang, G.A.; Guo, X.P. Erosion–corrosion at different locations of X65 carbon steel elbow. Corros. Sci. 2014, 85, 318–330. [Google Scholar] [CrossRef]
- Islam, M.A.; Farhat, Z. Erosion-corrosion mechanism and comparison of erosion-corrosion performance of API steels. Wear 2017, 376–377, 533–541. [Google Scholar] [CrossRef]
- Chung, R.J.; Jiang, J.; Pang, C.; Yu, B.; Eadie, R.; Li, D.Y. Erosion-corrosion behaviour of steels used in slurry pipelines. Wear 2021, 477, 203771. [Google Scholar] [CrossRef]
- Wood, R.J.K. Erosion–corrosion interactions and their effect on marine and offshore materials. Wear 2006, 261, 1012–1023. [Google Scholar] [CrossRef]
- Lu, B.T.; Lu, J.F.; Luo, J.L. Erosion–corrosion of carbon steel in simulated tailing slurries. Corros. Sci. 2011, 53, 1000–1008. [Google Scholar] [CrossRef]
- Zheng, Z.B.; Zheng, Y.G.; Zhou, X.; He, S.Y.; Sun, W.H.; Wang, J.Q. Determination of the critical flow velocities for erosion–corrosion of passive materials under impingement by NaCl solution containing sand. Corros. Sci. 2014, 88, 187–196. [Google Scholar] [CrossRef]
- Wang, K.; Liu, H.; Wang, L.; Guo, P.; Wang, Y.; Yang, J. Effect of particle size on vortex structure and erosion behavior of semi-open centrifugal pump. Energy 2024, 293, 130576. [Google Scholar] [CrossRef]
- Qiu, J.; Tian, M.; Zhu, D.; Xiao, C.; Wen, B.; Bin, F.; Chen, H.; Wang, D. Numerical Study of Resistance Loss and Erosive Wear during Pipe Transport of Paste Slurry. Sustainability 2023, 15, 11890. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, Y.; Liang, Q.; Xiao, Y.; Liu, Z.; Li, H.; Ye, J.; Yang, N.; Deng, H.; Du, Q. Analysis of sediment erosion in pelton nozzles and needles affected by particle size. Energies 2024, 17, 1635. [Google Scholar] [CrossRef]
- Aponte, R.D.; Teran, L.A.; Ladino, J.A.; Larrahondo, F.; Coronado, J.J.; Rodríguez, S.A. Computational study of the particle size effect on a jet erosion wear device. Wear 2017, 374–375, 97–103. [Google Scholar] [CrossRef]
- Nguyen, V.B.; Nguyen, Q.B.; Zhang, Y.W.; Lim, C.Y.H.; Khoo, B.C. Effect of particle size on erosion characteristics. Wear 2016, 348–349, 126–137. [Google Scholar] [CrossRef]
- Ning, S.M.; Yu, Q.M.; Liu, T.J.; Zhang, K.; Zhang, H.L.; Wang, Y.; Li, Z.H. Influence of particle shape on erosion behavior of EB-PVD thermal barrier coatings. Ceram. Int. 2022, 48, 8627–8640. [Google Scholar] [CrossRef]
- Liu, Z.G.; Wan, S.; Nguyen, V.B.; Zhang, Y.W. A numerical study on the effect of particle shape on the erosion of ductile materials. Wear 2014, 313, 135–142. [Google Scholar] [CrossRef]
- Di, J.; Wang, S.s.; Xie, Y.h. Investigation on the erosion characteristics of martensitic blade steel material 1Cr12W1MoV by micro-particle swarm with high velocity. Powder Technol. 2019, 345, 111–128. [Google Scholar] [CrossRef]
- Lindgren, M.; Perolainen, J. Slurry pot investigation of the influence of erodent characteristics on the erosion resistance of austenitic and duplex stainless steel grades. Wear 2014, 319, 38–48. [Google Scholar] [CrossRef]
- Leguizamón, S.; Jahanbakhsh, E.; Alimirzazadeh, S.; Maertens, A.; Avellan, F. FVPM numerical simulation of the effect of particle shape and elasticity on impact erosion. Wear 2019, 430–431, 108–119. [Google Scholar] [CrossRef]
- Li, Q.; Liu, M.; Gao, K.; Guan, Z.; Xu, Y.; Fan, C. Research on the erosion resistance characteristics of liquid-solid two-phase flow in high-pressure manifolds. Geoenergy Sci. Eng. 2024, 241, 213188. [Google Scholar] [CrossRef]
- Zhu, L.; Luo, J.; Huang, C.; Zhou, L.; Li, L.; Li, Y.; Wang, Z. Erosion resistance of casing with resin and metallic coatings in liquid–solid two-phase flow. Processes 2024, 12, 790. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Wang, T.; Zhang, J.; Li, L.; Zhang, Y. Experimental analysis and model prediction of elbow pipe’s erosion in water-cooled radiator. Sci. Rep. 2024, 14, 6880. [Google Scholar] [CrossRef] [PubMed]
- Rahman, S.; Khan, R.; Niazi, U.M.; Legutko, S.; Khan, M.A.; Ahmed, B.A.; Petrů, J.; Hajnyš, J.; Irfan, M. Performance Prediction of Erosive Wear of Steel for Two-Phase Flow in an Inverse U-Bend. Materials 2022, 15, 5558. [Google Scholar] [CrossRef] [PubMed]
- Liu, E.B.; Huang, S.; Tian, D.C.; Shi, L.M.; Peng, S.B.; Zheng, H. Experimental and numerical simulation study on the erosion behavior of the elbow of gathering pipeline in shale gas field. Petrol. Sci. 2024, 21, 1257–1274. [Google Scholar] [CrossRef]
- Yang, S.Q.; Fan, J.C.; Liu, M.T.; Li, D.N.; Li, J.L.; Han, L.H.; Wang, J.J.; Yang, S.Y.; Dai, S.W.; Zhang, L.B. Research on the solid particle erosion wear of pipe steel for hydraulic fracturing based on experiments and numerical simulations. Petrol. Sci. 2024, 21, 2779–2792. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Hossain, N.; Shahin, M.; Debnath, U.K.; Rahman, M.; Rahman, M.M. Erosion characteristics of stainless steels under different percentage of SiC- Al2O3-Fe2O3 solid particles. Tribol. Int. 2022, 167, 107403. [Google Scholar] [CrossRef]
- Desale, G.R.; Gandhi, B.K.; Jain, S.C. Effect of erodent properties on erosion wear of ductile type materials. Wear 2006, 261, 914–921. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Badr, H.M.; Araoye, A.A.; Toor, I.U.H. Computational analysis of water-submerged jet erosion. Energies 2021, 14, 3074. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Debnath, U.K.; Nuruzzaman, D.M.; Islam, M.M. Study of erosive surface characterization of copper alloys under different test conditions. Surf. Interfaces 2017, 9, 245–259. [Google Scholar] [CrossRef]
- Amaro, A.M.; Loureiro, A.J.R.; Neto, M.A.; Reis, P.N.B. Residual impact strength of glass/epoxy composite laminates after solid particle erosion. Compos. Struct. 2020, 238, 112026. [Google Scholar] [CrossRef]
- Miao, S.S.; Sun, S.C.; Wang, L.; Zhang, P. Effect of Bionic Units Fabricated by WC-NiCrBSiFe Laser Cladding on High-Temperature Erosion Wear Resistance of 304 Stainless Steel. Strength Mater. 2024, 56, 144–154. [Google Scholar] [CrossRef]
- Li, X.; Ding, H.; Huang, Z.; Fang, M.; Liu, B.; Liu, Y.g.; Wu, X.; Chen, S. Solid particle erosion-wear behavior of SiC–Si3N4composite ceramic at elevated temperature. Ceram. Int. 2014, 40, 16201–16207. [Google Scholar] [CrossRef]
- Wu, W.; Wei, B.; Li, G.; Chen, L.; Wang, J.; Ma, J. Study on ammonia gas high temperature corrosion coupled erosion wear characteristics of circulating fluidized bed boiler. Eng. Fail. Anal. 2022, 132, 105896. [Google Scholar] [CrossRef]
- Hattori, S.; Ishikura, R. Revision of cavitation erosion database and analysis of stainless steel data. Wear 2010, 268, 109–116. [Google Scholar] [CrossRef]
- Chang, L.C.; Hsui, I.C.; Chen, L.H.; Lui, T.S. A study on particle erosion behavior of ductile irons. Scr. Mater. 2005, 52, 609–613. [Google Scholar] [CrossRef]
- Mondal, J.; Das, K.; Das, S. The effect of microstructure and mechanical properties on the slurry erosion behavior of carbide-free bainitic and martensitic steel. Wear 2022, 504–505, 204422. [Google Scholar] [CrossRef]
- Gou, J.; Wang, Y.; Wang, C.; Chu, R.; Liu, S. Effect of rare earth oxide nano-additives on micro-mechanical properties and erosion behavior of Fe-Cr-C-B hardfacing alloys. J. Alloys Compd. 2017, 691, 800–810. [Google Scholar] [CrossRef]
- Mehrabadi, H.B.; Korojy, B. The effect of yttrium on the microstructure and wear and mechanical properties of Al-20%Sn. Mater. Lett. 2024, 362, 136247. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, C.; Sun, J.; Zhao, W.; Dong, L.; Li, L.; Meng, F. Erosion behavior of arc sprayed FeTi/CrB MMC coating at elevated temperature. Surf. Coat. Technol. 2015, 262, 141–147. [Google Scholar] [CrossRef]
- Singh, P.K.; Mishra, S.B. Erosion wear characteristics of HVOF Sprayed WC-Co-Cr and CoNiCrAlY coatings on IS-2062 structural steel. Mater. Res. Express 2018, 5, 095508. [Google Scholar] [CrossRef]
- Kaushal, S.; Singh, S. Slurry erosion behavior of plasma sprayed coating on turbine steel. Ind. Lubr. Tribol. 2019, 71, 1–9. [Google Scholar] [CrossRef]
- Ma, A.; Liu, D.; Zhang, X.; Liu, D.; He, G.; Yin, X. Solid particle erosion behavior and failure mechanism of TiZrN coatings for Ti-6Al-4V alloy. Surf. Coat. Technol. 2021, 426, 127701. [Google Scholar] [CrossRef]
- Sharma, R.K.; Das, R.K.; Kumar, S.R. Effect of chromium content on microstructure, mechanical and erosion properties of Fe-Cr-Ti-Mo-C-Si coating. Surf. Interfaces 2021, 22, 100820. [Google Scholar] [CrossRef]
- Huang, F.; Kang, J.J.; Yue, W.; Liu, X.B.; Fu, Z.Q.; Zhu, L.N.; She, D.S.; Ma, G.Z.; Wang, H.D.; Liang, J.; et al. Effect of heat treatment on erosion–corrosion of Fe-based amorphous alloy coating under slurry impingement. J. Alloys Compd. 2020, 820, 153132. [Google Scholar] [CrossRef]
- Yang, J.; Sun, Y.; Su, M.; Yin, X.; Li, H.; Zhang, J. Corrosion and erosion wear behaviors of HVOF-Sprayed Fe-Based amorphous coatings on dissolvable Mg-RE alloy substrates. Materials 2023, 16, 5170. [Google Scholar] [CrossRef]
- Begum, Y.; Doddamani, S. Investigation on the Hardness of Al6061 Alloys: Implications of Seawater Corrosion. JOM 2024, 76, 3734–3742. [Google Scholar] [CrossRef]
- Chekalil, I.; Chadli, R.; Miloudi, A.; Ghazi, A.; Planche, M.-P.; Mekid, S.; Raza, M.S. Effect of corrosion environments on the mechanical properties of friction stir welded aluminum alloy AA3003. J. Mater. Res. Technol. 2024, 33, 2353–2364. [Google Scholar] [CrossRef]
- Patil, A.R.; Vagge, S.T. The Effect of Hot Corrosion and Electrochemical Corrosion on Microhardness of the Coating. High. Temp. Corr. Mater. 2024, 101, 471–483. [Google Scholar] [CrossRef]
- Zhou, Z.; Du, J.; Tian, C.; Peng, X.; Wu, Y.; Lv, X.; Zhang, Y.; Chen, Z. Local mechanical properties of corrosion layers formed on T91 and SS316L steels after exposure to static liquid LBE at 500 °C for 1000 h obtained by nano-indentation. Nucl. Eng. Technol. 2024, 56, 3067–3075. [Google Scholar] [CrossRef]
- Shojai, S.; Schönamsgruber, F.; Köhler, M.; Ghafoori, E. Impact of accelerated corrosion on weld geometry, hardness and residual stresses of offshore steel joints over time. Mater. Des. 2025, 251, 113578. [Google Scholar] [CrossRef]
- Owen, J.; Ramsey, C.; Barker, R.; Neville, A. Erosion-corrosion interactions of X65 carbon steel in aqueous CO2 environments. Wear 2018, 414–415, 376–389. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, X.; Du, L.; Li, J.; Kuang, Y.; Wu, B. Corrosion behavior of low-alloy steel with martensite/ferrite microstructure at vapor-saturated CO2 and CO2-saturated brine conditions. Appl. Surf. Sci. 2015, 351, 610–623. [Google Scholar] [CrossRef]
- Niu, R.; Li, H.; Liu, P.Y.; Burr, P.; Feng, Y.; Yen, H.W.; Huang, C.; Sun, Y.H.; Ma, M.; Guo, A.; et al. Hydrogen-enhanced deformation in pearlite. Acta Mater. 2024, 281, 120327. [Google Scholar] [CrossRef]
- Li, S.; Chen, Z.; Tan, L.; Bobaru, F. Corrosion-induced embrittlement in ZK60A Mg alloy. Mater. Sci. Eng. A 2018, 713, 7–17. [Google Scholar] [CrossRef]
- Ji, X.; Ji, C.; Cheng, J.; Shan, Y.; Tian, S. Erosive wear resistance evaluation with the hardness after strain-hardening and its application for a high-entropy alloy. Wear 2018, 398–399, 178–182. [Google Scholar] [CrossRef]
- El-Rahman, A.M.A.; Wei, R. A comparative study of conventional magnetron sputter deposited and plasma enhanced magnetron sputter deposited Ti–Si–C–N nanocomposite coatings. Surf. Coat. Technol. 2014, 241, 74–79. [Google Scholar] [CrossRef]
- Singh, J.; Nath, S.K. Microstructural characterization and investigation of slurry erosion performance of cyclically heat treated martensite steel. Eng. Fail. Anal. 2022, 131, 105833. [Google Scholar] [CrossRef]
- Mann, B.S. High-Power diode laser-treated 13Cr4Ni stainless steel for hydro turbines. J. Mater. Eng. Perform. 2014, 23, 1964–1972. [Google Scholar] [CrossRef]
- Wan, W.; Xiong, J.; Liang, M. Effects of secondary carbides on the microstructure, mechanical properties and erosive wear of Ti(C,N)-based cermets. Ceram. Int. 2017, 43, 944–952. [Google Scholar] [CrossRef]
- Desale, G.R.; Gandhi, B.K.; Jain, S.C. Slurry erosion of ductile materials under normal impact condition. Wear 2008, 264, 322–330. [Google Scholar] [CrossRef]
- Balan, K.P.; Reddy, A.V.; Joshi, V.; Sundararajan, G. The influence of microstructure on the erosion behaviour of cast irons. Wear 1991, 145, 283–296. [Google Scholar] [CrossRef]
- Shimizu, K.; Xinba, Y.; Araya, S. Solid particle erosion and mechanical properties of stainless steels at elevated temperature. Wear 2011, 271, 1357–1364. [Google Scholar] [CrossRef]
- Chang, L.C.; Hsui, I.C.; Chen, L.H.; Lui, T.S. Effects of heat treatment on the erosion behavior of austempered ductile irons. Wear 2006, 260, 783–793. [Google Scholar] [CrossRef]
- Zambrano, O.A. A review on the effect of impact toughness and fracture toughness on impact-abrasion wear. J. Mater. Eng. Perform. 2021, 30, 7101–7116. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, S.; Long, J.; Zheng, K.; Wang, H.; Li, H. Effect of chromium content on the erosion-corrosion behavior of Fe-Cr alloy produced by ball milling liner in weakly alkaline slurry. Mater. Res. Express 2020, 7, 036510. [Google Scholar] [CrossRef]
- Zhang, F.; Tabecki, A.; Bennett, M.; Begg, H.; Lionetti, S.; Paul, S. Feasibility study of high-velocity Oxy-fuel (HVOF) sprayed cermet and alloy coatings for geothermal applications. J. Therm. Spray Technol. 2023, 32, 339–351. [Google Scholar] [CrossRef]
- Swain, B.; Mantry, S.; Mohapatra, S.S.; Mishra, S.C.; Behera, A. Investigation of tribological behavior of plasma sprayed NiTi coating for aerospace application. J. Therm. Spray Technol. 2022, 31, 2342–2369. [Google Scholar] [CrossRef]
- Wang, C.; Liu, M.; Wang, H.; Jin, G.; Ma, G.; Zhang, J.; Chen, S. Tribological properties and solid particle erosion wear behavior of Al2O3-13 wt%TiO2/Al2O3-PF composite coatings prepared on resin matrix by supersonic plasma spraying. Ceram. Int. 2024, 50, 29987–29996. [Google Scholar] [CrossRef]
- Murthy, K.N.; Sampathkumaran, P.; Seetharamu, S. Abrasion and erosion behaviour of manganese alloyed permanent moulded austempered ductile iron. Wear 2009, 267, 1393–1398. [Google Scholar] [CrossRef]
- Shimizu, K.; Kusumoto, K.; Yaer, X.; Zhang, Y.; Shirai, M. Effect of Mo content on erosive wear characteristics of high chromium cast iron at 1173 K. Wear 2017, 376–377, 542–548. [Google Scholar] [CrossRef]
- Finnie, I.; McFadden, D.H. On the velocity dependence of the erosion of ductile metals by solid particles at low angles of incidence. Wear 1978, 48, 181–190. [Google Scholar] [CrossRef]
- Zhang, Y.; Reuterfors, E.P.; McLaury, B.S.; Shirazi, S.A.; Rybicki, E.F. Comparison of computed and measured particle velocities and erosion in water and air flows. Wear 2007, 263, 330–338. [Google Scholar] [CrossRef]
- Arabnejad, H.; Mansouri, A.; Shirazi, S.A.; McLaury, B.S. Development of mechanistic erosion equation for solid particles. Wear 2015, 332–333, 1044–1050. [Google Scholar] [CrossRef]
- Mansouri, A.; Arabnejad, H.; Shirazi, S.A.; McLaury, B.S. A combined CFD/experimental methodology for erosion prediction. Wear 2015, 332–333, 1090–1097. [Google Scholar] [CrossRef]
- Mansouri, A.; Arabnejad, H.; Karimi, S.; Shirazi, S.A.; McLaury, B.S. Improved CFD modeling and validation of erosion damage due to fine sand particles. Wear 2015, 338–339, 339–350. [Google Scholar] [CrossRef]
- Veritas, D.N. Recommended Practice RP O501 erosive wear in piping systems. DNV Recomm. Pract. 2007, 4, 1–43. [Google Scholar]
- Huang, C.; Chiovelli, S.; Minev, P.; Luo, J.; Nandakumar, K. A comprehensive phenomenological model for erosion of materials in jet flow. Powder Technol. 2008, 187, 273–279. [Google Scholar] [CrossRef]
- Neilson, J.H.; Gilchrist, A. Erosion by a stream of solid particles. Wear 1968, 11, 111–122. [Google Scholar] [CrossRef]
- Gnanavelu, A.; Kapur, N.; Neville, A.; Flores, J.F.; Ghorbani, N. A numerical investigation of a geometry independent integrated method to predict erosion rates in slurry erosion. Wear 2011, 271, 712–719. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).