Abstract
The photocatalytic activity of Bi2WO6 Aurivillius phase has been widely exploited for the degradation of a wide range of gaseous and aqueous molecules, as well as microorganisms, under the influence of visible irradiation. Strategies for the development of doped and co-doped bismuth tungstate materials require the thermodynamic data on this phase. The heat capacity of bismuth tungstate, Bi2WO6, was investigated using a DSC microcalorimeter on polycrystalline powder samples in the temperature range from 313 to 1103 K (40–830 °C) in two separate runs. The samples were synthesized by solid-state reaction from pure binary oxides at 1033 K (760 °C) in a platinum crucible with cover. The high temperature Cp(T) data were fitted by the Maier–Kelley equation and, from this relation, the standard molar heat capacity of γ-Bi2WO6 polymorph was estimated to be at 298.15 K 176.8 ± 3.9 J·K−1·mol−1. A reversible second-order transition of Bi2WO6 phase was observed in the experimental temperature range, with a peak close to 940 K (667 °C). Additionally, the extrapolation of Cp(T) to 0 K was proposed using a method based on the multiple Einstein model. Thermodynamic properties (heat capacity Cp(T), entropy S°(T), enthalpy H°(T), Gibbs energy G°(T)) of crystalline γ-Bi2WO6 were calculated in the temperature range of 298.15–1123 K (25–850 °C).
1. Introduction
Metal oxide semiconductors have been extensively explored as photoanodes over the past two decades. During this time, over one hundred metal oxide phases have been identified in the oxygen evolution reaction. Among them, a class of bismuth-based compounds, primarily BiVO4, Bi2WO6 and BiFeO3, has been identified as promising photoanode materials for the use in solar energy conversion [1,2] due to their chemical and electrochemical stability under oxidizing conditions [3]. These materials have also been found to be useful for producing pure hydrogen, a key step towards a sustainable hydrogen economy. The photocatalytic activity of the Bi2WO6 Aurivillius phase, since its discovery in 1999 [4], has been extensively used to degrade a wide range of gaseous and aqueous molecules and even microorganisms under the influence of visible irradiation [5,6].
Bi2WO6, as a photoanode material, can decompose water into hydrogen and oxygen during water splitting due to its special properties. These special features include suitable band edge positions for potential photoelectrochemical water splitting [7], chemical stability over a wide pH range (from 0.26 to 9) [8,9] and flat band potential below 0.25 V vs. RHE (Reversible Hydrogen Electrode), which is a key benchmark for the behavior of semiconductors in a photoelectron catalysis and solar energy applications [8,10].
Bismuth tungstate, Bi2WO6, the n-type semiconductor (~2.8 eV band gap), has a suitable crystal and electronic structure for photocatalysis under visible light. The layered structure consists of alternating bismuth–oxygen [Bi2O2]2+ ionic layers and perovskite-like [WO4]2− ionic layers [11,12] which promote the separation of photoexcited electron–hole pairs, increasing the photocatalytic efficiency.
The comprehensive review of Bi2WO6-based photocatalysts applied in clean energy production and environmental remedial action was published by Zhu et al. [13].
The ferroelectric Bi2WO6 phase is chemically and structurally complex; therefore, several crystal structure models have been proposed: I4/mmm [14], B2cb [15] and P21ab (referred to as Pca21) [16,17]. At low temperatures, Bi2WO6 is a material with an internally ordered structure that forms an electric dipole and it was assumed that this structure belongs to the polar P21ab space group [18,19,20]. With increasing temperatures, a reconstructive transformation from the polar state to the nonpolar state occurs, and it is not a typical ferroelectric transition. After the end of second-order phase transition ~933 K (660 °C), the orthorhombic phase belongs to the symmetry of the Aba2 space group, described in [18,21,22,23].
At 1233 K (960 °C), the reconstructive reversible transformation between the orthorhombic and monoclinic phase occurs. The monoclinic phase does not belong to Aurivillius structure and is unfavorable from a technical point of view due to its destructive effect on the phase structure. Information on the structural, photophysical and photocatalytic properties is summarized in the review by Elaouni et al. [24].
Although many studies have been carried out on the physical properties and crystal structure of compounds in the pseudobinary Bi2O3–WO3 system, little attention has been paid to their thermodynamic analysis. And so, the phase diagrams reported so far on this system [25,26,27,28] contradict each other in terms of the existence and stability of ternary phases in the system. The Bi2O3–WO3 phase diagram appears to be fairly complicated. Hoda and Chang [26] show the presence of four intermediate ternary oxide phases, namely, Bi14WO24, Bi14W2O27, Bi2WO6 and Bi2W2O9. Additionally, Bi14W2O27 forms an extensive range of solid solutions in the system and Bi14WO24 represents the endmember of an isostructural solid solution extending from compositions around Bi30WO48 [29]. Ling et al. [27] observed two mixed oxide phases in the Bi-rich part of the pseudobinary system, except for the Bi2WO6 congruent melting stoichiometric compound: a stoichiometric phase Bi14WO24 and a solid solution between endmembers Bi42W8O87 and Bi30W4O57. The recent phase equilibria reported on this system [28] using differential thermal analysis (DTA) of bismuth tungsten oxides confirmed broad agreement with phase diagram data of Speranskaya [25] with five stable compounds. Finlayson et al. [28] concluded that other compounds in the Bi2O3–WO3 phase system also show similar optical properties to Bi2WO6, so they also have the potential to exhibit photocatalysis. In particular, Bi7WO13.5 and Bi24WO39 are of interest because their broad tungsten solubility ranges open up the possibility of further optimization. For this purpose, the trusted thermodynamic data of the phases in the Bi2O3–WO3 system are necessary. In 2006, a new Aurivillius bismuth tungstate, Bi3W2O10.5, was synthesized and characterized by single-crystal X-ray diffraction by Muktha and Row [30].
In addition to inconsistent information on phase relations, many thermochemical properties of bismuth tungstates remain poorly recognized. The only available experimental thermochemical data on these compounds, standard molar enthalpy of formation, concern the compound Bi2WO6 [31]. Careful experimental study of thermochemical properties of bismuth tungstates is essential to predicting their stability and effectiveness in reactive environments. It can also enable the assessment of the phase relationships within the pseudobinary system. In general, for many potential applications of materials, knowledge of their thermal properties is of great importance. Thermodynamic data influence photocatalytic applications by determining material stability, reaction efficiency and energy conversion. It is worth noting that heat capacity is a critical factor, for example, in thermoelectric materials, where it is used to calculate the figure of merit (zT). The thermal conductivity of a material can be derived from heat capacity, density and diffusivity data, so heat capacity is an important parameter for designers and used in designing efficient heat management systems and reactor configurations for industrial-scale applications. In addition to the above mentioned thermal properties, the knowledge of one of the most fundamental property, i.e., Gibbs energy (G), is imperative to predict the formation and stability of the compounds in various physicochemical environments. In particular, Gibbs free energy explains the feasibility and direction of the reaction. This also helps in establishing phase diagrams of various systems.
In this context, in this work, for the first time, the heat capacity of Bi2WO6 was measured in a wide temperature range, from 313 to 1103 K (40–830 °C), using a differential scanning calorimeter (DSC). The high-temperature data were described by the well-known Maier–Kelley equation [32]. Additionally, an extrapolation of Cp(T) to 0 K was proposed using a method based on the modified Einstein model [33] to estimate the standard entropy of Bi2WO6, which was necessary to calculate the Gibbs energy function. Furthermore, the second-order phase transition was detected in the temperature range close to 940 K (667 °C). The further investigation of the thermal properties of the system is complicated due to discrepancies in the number of phases, their polymorphs and the characteristic transition temperatures.
2. Literature Data
2.1. Structure Data
Three phase transitions were found in pure bismuth tungstate, Bi2WO6. The first one was found between two polar and nonpolar orthorhombic phases (γ ⟶ γ‴), which occur in the temperature range 640–660 °C (913–933 K) with a space group change from P21ab to B2cb (nonstandard setting of Aba2). It corresponds to a second-order transition (the propagation of displacive modes along c axis is related to this difference). Next, ferroelectric transition between the polar and nonpolar orthorhombic phase (γ‴ ⟶ γ″) occurs at about 1203 K (930 °C) [24], and a first-order phase transition (γ″ ⟶ γ′) to monoclinic nonferroelectric phase with the space group A2/m at 1233 K (960 °C) was observed [34,35,36,37]. In the case of room temperature structure (γ form), the nonstandard setting of space group Pca21 was also used [17,20] to be consistent with the convention adopted in Aurivillius phase ferroelectrics, according to which the long axis is designated as c and the polar axis as a. It was confirmed by the use of high-resolution powder neutron diffraction [34] that a transition from space group P21ab (γ form) to B2cb (γ‴ form) in Bi2WO6 compound corresponds to the loss of one octahedral tilt mode within the perovskite-like WO4 layer of the orthorhombic structure. The medium-temperature form γ‴ has a higher B2cb symmetry, but its structure is similar to the orthorhombic γ phase.
The second-order phase transition between polar and nonpolar phases, corresponding to the ferroelectric Curie point, occurs around 1203 K (930 °C). Lastly, first-order transition before melting with significant reorganization of the crystal structure, involving the breaking and reforming of primary chemical bonds, takes place at 1233 K (960 °C). This high-temperature monoclinic γ′ phase is very complex [34].
2.2. Thermodynamic Data
The DTA study of Newkirk et al. [38] showed a reversible first-order thermal effect at 1208 ± 5 K (935 °C) with a heat of transition of 4.184 kJ·mol−1. The experimental error in measuring the transition enthalpy by the DTA method is usually significant.
Phapale et al. [31] measured the standard molar enthalpy of formation of solid Bi2WO6 compounds, using a Calvet calorimeter (HT-1000, Setaram, Lyon, France) with the liquid Na2O+MoO3 (3:4 M) solvent. The purity of the solid compound was determined by the XRD method. The obtained result was amended in the corrigendum [31]. Using the standard molar enthalpies of formation of pure Bi2O3 and WO3 from the literature [39], the value of Bi2WO6 was recalculated to be –1440.53 ± 8.38 kJ·mol−1 [31].
3. Experiment
3.1. Material and Synthesis
Bismuth tungstate, Bi2WO6, was prepared by solid-state reaction using pure oxides, Bi2O3 (99.9995%, USA) and WO3 (99.99%, USA), respectively, as starting materials. A stoichiometric oxide mixture was ground in the cyclic mortar (30 cycles/min) with 10 mm ceramic balls (zirconia) and pressed into 5 mm diameter pellets, then fired in air at 1033 K (760 °C) for 24 h in a platinum crucible. To drive the solid reaction to completion, the samples were reground, pressed and annealed twice. The phase composition of samples was determined by the XRD (X-Ray Diffraction) method using Rigaku diffractometer (Mini Flex II) (Rigaku, Tokyo, Japan) with Cu Kα radiation. XRD patterns were collected in angular range 2θ from 10° to 100°, with scan step 0.01.
The results are presented in Figure 1. The lattice parameters of Bi2WO6 were determined by Rietveld refinement using software GSAS II version 5800 (Argonne National Laboratory, Lemont, IL, USA) [40]. The pseudo-Voigt peak shape function was adopted. The short vertical markers represent the peak positions from [41] database. The parameters of oxygen atoms are difficult to refine because of their small scattering factors [18]. The lattice constants of Bi2WO6 structure are as follows: a = 5.43391(1) Å, b = 16.42596(2) Å, c = 5.45620(1) Å, (Z = 4, V = 487.005 Å3), which proved that this product is orthorhombic. The lattice parameters of powder material were found to be similar with these reported in JCPDS card no. 01-079-2381. The obtained structure of the low-temperature polar (orthorhombic) phase of russellite agrees very well with the literature data of Knight [17] with powder neutron diffraction and Okudera et al. [20] with the Weissenberg method: 5.43726; 16.43018; 5.45842 (code ID 9011799) and 5.4345; 16.4324; 5.4558 (code ID 2108252), respectively [35]. No impurity lines from pure binary oxides or any other impurities were observed in the XRD spectrum of Bi2WO6.
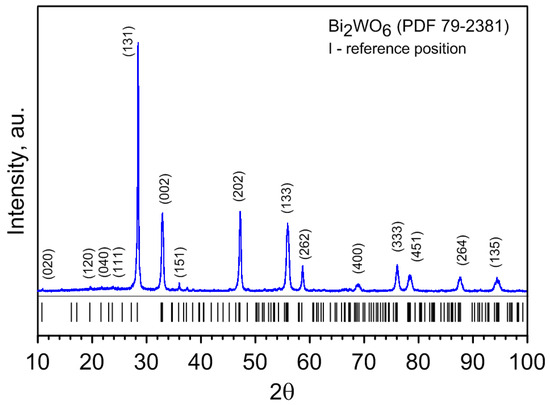
Figure 1.
The XRD of Bi2WO6 compound material from solid-state synthesis of pure oxides at 760 °C (1033 K). Indexes of several characteristic reflexes are pointed out.
The typical morphology of Bi2WO6 powder samples is shown in Figure 2. Microstructural studies were carried out on the Hitachi SU-70 scanning microscope (SEM) (Hitachi High-Technologies Corporation, Tokyo, Japan). No other impurity phases were detected.

Figure 2.
SEM micrograph image of the typical morphology of Bi2WO6 powder sample.
3.2. Experimental Procedure
The molar heat capacity of lead tungstate Bi2WO6 has been measured using Netzsch 401 F1 Pegasus differential microcalorimeter DSC (Netzsch GmbH, Selb, Germany), calibrated by measuring the temperature of fusion of several pure (99.999%) metals (In, Sn, Zn, Al, Ag, Au) on heating. The measured melting point (onset) of these metals is compared with the known melting point temperature. By definition, the calibration point used is the extrapolated melting peak onset, as it is independent of the sample mass. Each metallic standard was measured three times. The temperature uncertainty obtained from calibration in this work is ±1 K, and the temperature detection sensitivity of DSC (the S-thermocouple resolution) is 0.01 K.
Temperature calibration is necessary because the thermocouple measuring the sample temperature is located on the probe holder below the contact surface of the calorimetric pan. Additionally, at the high-temperature range, the uncertainty increases due to radiation. To minimize other factors of influence, all single calibrations should be performed in the same conditions.
The high-temperature calibration on pure copper gave results even ~5 K lower that the nominal melting point. Therefore, only gold meets the high requirements of accurate temperature calibration.
To determine the high-temperature dependence of Cp(T), the method recommended by the American Society for Testing and Materials (ASTM) E1269 [42,43] was adopted. To evaluate the heat capacity, three successive scans on the DSC apparatus are required under the same experimental conditions. The platinum pans with Pt lids were applied as a sample and reference crucibles in Cp(T) measurements. The same pair of crucibles were used for the baseline, standard and sample measurements. The accuracy of the heat capacity measurement was increased by using the calorimetric pans with masses placed as close to each other as possible and placed in the same positions on the platinum DSC sensor for each scan. For accurate heat capacity experiments, the baseline scan should be repeated three times to ensure stability and reproducibility of DSC measurements. The first scan is an obligatory run with the empty platinum pans to establish a baseline of the apparatus. Following good practice, both sample and the reference Pt crucibles were covered with Pt lids.
As a heat capacity reference, the Cp(T) of synthetic sapphire standard disk of 5.2 mm diameter and 1 mm thick (certified by Netzsch GmbH, Selb, Germany) was established during the second run (Appendix A, Table A1). In such cases, in the experimental temperature range, the heat flow was calibrated to the Cp(T) of sapphire comparing the obtained DSC results with tabled values [42,43].
To stabilize the instrument system and correct the baseline drift, ten-minute isothermal segments at the beginning and at the end of every calibration heat cycle were adopted. This stabilization period ensures the temperature is uniform before a measurement begins and allows any instrument drift to be characterized, which is crucial for accurate data analysis and heat capacity calculations.
In the third scan, the sample of the testing material was investigated.
As required, the measurements for the baseline, samples and reference material (sapphire) were performed in three separate heating cycles. Only curves with a difference between the second and third run of less than 1% were considered in further Cp(T) analysis. The heat capacity of synthetic sapphire calculated from the third curve compared to the values in the NBS (National Bureau of Standards) tables [42,43] can be considered as a test of the sensitivity and accuracy of the current sample measurement. Therefore, the relative error of the observed values against the corresponding values of NBS certificate was found to be less than ±1% and this value was adopted as uncertainty of measurements.
The measurements were carried out with heating and cooling rates of 10 K·min−1 on the sample disks to maximize the thermal contact with the pan. To ensure good contact with the bottom of platinum pan and good heat flow, the samples were polished on one side by successive steps of finer and finer abrasives (polishing disk and the polishing cloth) to progressively create a smooth light-reflecting surface. No aqueous suspensions were used to ensure no contamination from polishing agents.
DSC measurement precision is limited not only by instrument calibration but also by experimental factors like heating rate and sample mass. The mass of the 5 mm diameter sample was comparable to the mass of the sapphire standard which was 84.5 mg. To determine heat capacity, the heating runs were assumed in the following cycles: thermal equalization at 313 K (40 °C) for 10 min, heating up to 1103 K (830 °C) with an isothermal stop for 10 min after heating. A cooling rate of 10 K·min−1 was applied to temperature of 313 K (40 °C). The heating and cooling procedure was also repeated three times.
At the beginning of each DSC experiment, the apparatus was evacuated and filled twice with argon. The small orifices in the platinum lids guarantee the gas exchange in Pt crucibles during DSC tube evacuation and protective gas flow. The controlled 20 mL/min argon (Ar 6+, Air Products, Warsaw, Poland) flux flow was performed in all the experiments on the Netzsch DSC 404 instrument in the experimental temperature range. After the experiment, no traces of reaction were noticed between the samples and the bottom of the platinum calorimetric pan. Moreover, after the experiment, no traces of Bi2WO6 (neither Bi2O3 or WO3 oxides) evaporation or deposition on the crucible or cover were observed. The weighted mass losses due to vaporization were less than 0.03%, showing insignificant mass change. The maximal difference between Cp values obtained in two separate temperature runs (run I and run II) was about 0.8%.
According to described procedure, the heat capacity function Cp(T) of the studied material was determined from three scans of continuous temperature change using the Netzsch Proteus ver. 5.2.1 (Netzsch, Germany) software with sensitivity related to sapphire.
4. Results and Discussion
The results of the heat capacity Cp(T) measurements obtained during two separate runs in the temperature range from 313 to 1103 K (40–830 °C) are shown in Figure 3 and are collected in Table A2 (in Appendix A) with consecutive ten degree intervals. In fact, every registered DSC signal consists of several hundred points. Molar mass of Bi2WO6 equal to 697.7972 g·mol–1 was taken for the Cp(T) calculations.
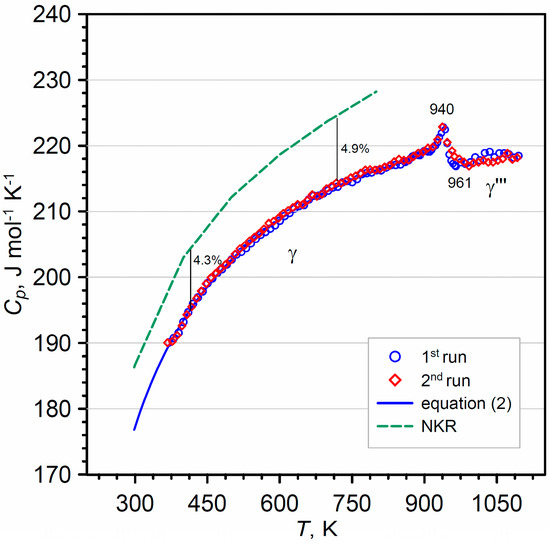
Figure 3.
Experimental heat capacity Cp(T) data of γ-Bi2WO6 (Appendix A, Table A2) fitted by parameters of Equation (2). The values calculated by NKR approximation were superimposed.
The DSC signal shows weak endothermic heat effect up to the temperature 961 K (688 °C) (Figure 3). The Cp signal shows the peak at temperature Tmax = 940 ± 1 K (667 °C). The continuous variation in the molar heat capacity in the vicinity of the extremum allows it to be considered as a second-order phase transition, and the λ-shaped heat capacity peak suggests that thermodynamic fluctuations affect the molar heat capacity of Bi2WO6 near the phase transition. The heat capacity jump in the phase transition region is ΔCp(Tmax) ≈ 6 J·mol–1·K–1. Yanovskii et al. [37] observed an inflection at 913 K (640 °C) and 933 K (660 °C) during the DSC heating scans of Bi2WO6 ceramic. A similar, very weak signal near 935 K (662 °C) was at the DTA curve detected by Watanabe [44]. From the earlier studies on the bismuth tungstate polymorphs [37,44], it has been proven that the phase transition is second-order in nature (polar–nonpolar [35]) and involves structural reversible order–disorder transition from P21ab to B2cb [24] (γ ⟶ γ‴).
4.1. High-Temperature Heat Capacity Function
The heat capacity of pure phases in the high-temperature range (T ≥ 298.15 K) listed in the reviews are the outcomes of various preliminary fitting and smoothing procedures for enthalpies, H(T), and the respective heat capacities, Cp(T) = (dH(T)/dT)p. Instead of real experimental values, these Cp(T) values are based on relatively simple analytical expressions. For example, the well-known Maier–Kelley [32] equation is adopted:
where a, b, c and d are the empirical parameters (as a rule a and b are positive and c is negative).
At high temperatures, the dominating effects such as lattice anharmonicity and expansion effects are described by the linear term in Equation (1). The quadratic term is required in many cases to describe the nonlinear behavior of the Cp(T) dependences close to the melting point. In the present analysis, Equation (1) was fitted with three and four terms, respectively, defined by a, b, c, d parameters (Figure 3) depending on the temperature range. The part of temperature dependence of heat capacity below the second-order transformation has been described by four terms Equation (2). In the case of detected phase transitions, the excess heat capacity ΔexCp related to this phase transition can be determined by subtracting the measured heat capacity values [45] and the heat capacity derived from the modeled line of the Cp = f(T) for both γ and γ‴ phases.
Taking into account the experimental heat capacity in the region of the γ phase stability (370–855 K), the fitted function of Cp(T) (Equation (1)) has the following form:
The correlation coefficient for Equation (2) was determined to be 0.99946. The confidence intervals of parameters of fitting to high-temperature data are also attached. All values obtained in this extrapolation are characterized by Student’s t-distribution with 95% confidence intervals.
In Figure 3, the experimental temperature dependence of heat capacity of γ-Bi2WO6 is compared with calculated Cp values from Equation (2). The standard heat capacity at 298.15 K for one mole of Bi2WO6 was estimated to be 176.8 ± 3.9 J·mol−1·K−1 on the basis of Equation (2). The result calculated from Equation (2) is lower than the standard heat capacity calculated from the Neumann–Kopp rule (NKR) [46] = 184.9 J·K−1·mol−1. The values of standard molar heat capacity of pure oxides, and , necessary for calculation of NKR, were taken from the review of Leitner et al. [47]. The difference between determined from NKR and from present data is ~4.5%.
Additionally, the values of Bi2WO6 heat capacity estimated by Neumann–Kopp’s rule (NKR) using the Cp data for pure oxides [48] were compared with the measured data in Figure 3. As shown in this figure, the heat capacity of NKR is greater than the experimentally obtained Cp values, and the percentage difference is ~4.3% at 400 K. The deviation increases with increasing temperature and is ~4.9% at 700 K.
These results can be compared, for example, with the differences in the experimental and calculated heat capacity of orthorhombic Bi2MoO6 using the Neumann–Kopp method [49]. The experimental heat capacity is lower than the estimated data, so that at the mid-range temperature, the percentage deviation is 3.3% at 568 K and increases with increasing temperature to 6.1% at 754 K. Also, Aiswarya et al. [50] compared the of triclinic CuV2O6 obtained by experimental measurements and the values calculated by NKR approximation and found that they were 157.6 and 174.9 J·K−1·mol−1, respectively. This means that the percentage difference is ~10% at 298.15 K. Negative deviation increases with increasing temperature.
Heat capacity data of BaTa2O6 ceramic were estimated by using NKR at the temperatures ranging from 298.15 to 1300 K and compared with experimental data of Ilhan et al. [51]. A good agreement was observed between the values fitted to experimental data and NKR heat capacities with an average positive deviation of less than 1%. The fitted and NKR calculated values of BaTa2O6 were estimated to be 182.3 J·K−1·mol−1 and 184.9 J·K−1·mol−1, respectively. Fitted standard heat capacity value showed good agreement with NKR with the mean error of 1.4%.
Aiswarya et al. [49] also show the variation in heat capacity of Bi2Mo3O12 and Bi6Mo2O15 compounds with temperature. For both compounds, the negative deviation from NKR was observed, (from 2.7% at 370 K to 7.0% at 800 K) and (from 1.4% at 380 K to 2.4% at 750 K), respectively.
Aiswarya et al. [50] also estimated the heat capacity of copper vanadates by the NKR method. For the case of orthorhombic Cu2V2O7 phase, good agreement with experimental data was found. However, Cu2V2O7 computed from experimental data and obtained by the NKR method shows a negative deviation, and are 202.2 J·K−1·mol−1, and 217.2 J·K−1·mol−1, respectively (difference 6.9% at 298.15 K). On the other hand, significant negative deviation was also observed in the data reported by Denisova et al. [52] in the entire temperature range. The experimental Cp data of Cu5V2O10 are also compared with estimated by NKR and those reported by Denisowa et al. [53]. A positive deviation from NKR was observed in almost the entire experimental temperature range [50]. Again, at 298.15 K, the Cp deviation is negative and differs by ~5.7%, and Denisova data [53] show lower values over almost the entire experimental temperature range. It should be noted here that Cp(T) data for complex oxides obtained by different scientific groups often differ by more than 15%.
The heat capacity values of Cu11V6O26 compound at 298.15 K are 793.4 J·K−1·mol−1 based on the experimental expression and 862.7 J·K−1·mol−1 from the NKR estimation, respectively (difference 8.7% at 298.15 K). The experimental heat capacity values [50] are slightly lower than those predicted by NKR, and in the mid-range of the measured temperatures, there is good agreement between the experimental and estimated data. The above examples show that 4% is an acceptable difference between NKR and experimental data. It also emphasized that heat capacities of binary oxides are difficult to compare with Cp of the constituent elements, because one of them is oxygen.
Both positive and negative deviations from the Neumann–Kopp rule are possible, reflecting changes in the vibrational frequencies of atoms in the mixed oxide compounds compared to their component binary oxides. Predicting the heat capacity of compound oxides from the heat capacities of the constituent pure oxides works well in cases of the same crystal structures of the compound and the constituent components. At room temperature, both Bi2O3 and WO3 polymorphs occur in a monoclinic structure compared to the orthorhombic structure of bismuth tungstate. Therefore, deviations are expected in case of significant difference between the molar volumes of the compound and constituent oxides.
The sources of the difference between experimental values of the heat capacity and those obtained from NKR estimation were discussed by Leitner et al. [54]. They proposed an additive expression for Cp(T) which takes into account several factors influencing the isobaric molar heat capacity of the solids, such as phonon contribution , lattice dilatations term and —the other contributions originating from electrons, vacancy formation, magnetic order, etc. In the case of Bi2WO6 ionic crystals, the influence of oxygen nonstoichiometry related to the formation of vacancy cannot be excluded. However, the small contributions of electrons and the formation of vacancies are expected. The phonon contribution Cph was considered [54], as the sum of heat capacities modeled by the harmonic approximation and term describing the anharmonicity of vibration modes.
The dilatation term Cdil can be expressed as a function of temperature, molar volume Vm, the isothermal compressibility, β and isobaric volume expansion α. Negative deviation ~4% obtained in this work can be connected with the negative value of the dilatation term. If the formation of a ternary oxide results in a lower volume expansion coefficient or higher compressibility compared to the sum of its constituents, the dilatation contribution to the heat capacity will be negative. It should also be noted that in the Bi2WO6 phase, the additional effect on Cp will be related to electrical polarization, as it is a ferroelectric material with a noncentrosymmetric crystal structure up to Curie temperature 930 K (1203 °C). That causes spontaneous polarization, giving it piezoelectric properties and potential applications in memory devices. Leitner et al. [54] showed that for the combination Δα < 0 and Δβ > 0, the mixed oxide will exhibit the negative deviations from NKR, while for other combinations, this cannot be directly determined.
In analysis, the term related to the phase polarization can be identified with the excess heat capacity, ΔexCp. The entropy change calculated by the integration of the ratio ΔexCp/T in the phase transition region [45] is ΔS ≈ 0.6 J·K−1·mol−1.
The contribution of harmonic phonon vibrations, which dominate at low temperatures, approaches the Dulong–Petit limit of 3sR (s is the number of atoms per formula unit and R is the universal gas constant) at high temperatures. It is known from the literature [54] that at elevated temperatures, the dilatation and anharmonic correction terms are responsible for the deviation from the NKR predictions. Discussing the deviation of heat capacity of Bi2MoO6 from NKR according to the analysis of Leitner et al. [54], Aiswarya et al. [49] pointed out that the bond distances in binary oxides are relatively shorter than those in ternary oxides, because the binary oxides are more closely packed [49]. Therefore, for ternary oxides, when comparing the experimental Cp with heat capacity value obtained using NKR, the lower experimental heat capacity is expected.
In general, the difference observed between the measured and NKR estimated data of heat capacities could be attributed to the differences arising in the dilatation terms due to expansion or contraction in the molar volumes of the unit cells, as well as due to variation in the isothermal compressibility and isobaric volume expansion [54]. Especially at high temperatures, the relations between Vm, α and β as well as the internal anharmonic corrections are important. It should be noted that an accurate calculation of the dilatation contribution is only possible based on rarely available high-temperature data on the α and β parameters of binary and ternary oxides.
It should also be mentioned that the molar heat capacity of Bi2WO6 (Table A2) in the entire analyzed temperature range does not exceed the limit of 3sR (s = 9 for Bi2WO6), resulting from Dulong–Petit law, 224.5 J·K−1·mol−1. The heat capacity of mixed oxides can be lower than the high-temperature Dulong–Petit limit due to the difference in their dilatation contributions to heat capacity. At high temperatures, the heat capacity of many materials is dominated by lattice vibrations, but anharmonicity, thermal expansion and other contributions become significant. In mixed oxides, a negative deviation in the dilatation contribution compared to the sum of their constituent oxides can cause the total heat capacity to be lower than the expected Dulong–Petit value.
4.2. Extrapolation of Heat Capacity Function
To estimate the heat capacities of binary oxides in the solid state, empirical contribution methods as the sum of contributions of individual atoms or ions are used. For various groups of substances, such contributions are evaluated from the experimental data by an optimization procedure. The earliest attempts to physically predict the heat capacity data from the low (helium) region up to the 298.15 K were proposed by Einstein and Debye [34] who modeled the Cp as a function of T due to harmonic acoustic and optical phonons. To take into account the anharmonicity of the crystal lattice vibrations, a hybrid description combining the Debye and Einstein models was proposed [55,56,57,58,59,60,61].The use of the Debye function is quite difficult to implement in thermodynamic databases. Therefore, the method of assuming multiple Einstein temperatures proposed by Voronin and Kutsenok [62] is convenient for extrapolating Cp data in modeling multicomponent systems. After excluding any magnetic transitions, the molar heat capacity of the crystalline phase, Cp(T), can be expressed as follows:
where s is a number of atoms per formula unit (for Bi2WO6, s = 9) and (i = 1, 2, 3…) are adjustable parameters obtained from Cp(T) experimental data fit. is the Einstein temperature for the ith mode of vibration and fi is the corresponding pre-factor. The additional term for mutual low- and high-temperature fitting, aT, is an electronic part of heat capacity, which represents non-thermodynamic information of the electron density of states at the Fermi level. The term bTn in Equation (3) accounts for high-order anharmonic lattice vibrations. In this case, the polynomial representation also accounts for the conversion from CV to Cp. To be able to match a wider phase spectrum, Chen and Sundman [63] adopted the bT4 term instead of the initially recommended [64] bT2 term. Onderka [65] adopted Equation (3) with k = 1 and n = 2 to estimate the heat capacity of bismuth silicates. It turned out that extrapolation for k = 1 is not sufficiently accurate because of Einstein function limitations. Therefore, in the present work, assuming no phase transitions in γ-Bi2WO3 phase below 300 K, the high-temperature experimental heat capacity data were extrapolated to 0 K using Equation (3) with k = 2 and n = 4. The parameters for extrapolating Cp(T) to 0 K based on the multiple Einstein model (3) are summarized in Table 1. The standard molar heat capacity, calculated from Equation (3) is 177.6 ± 5.7 J·K−1·mol−1.

Table 1.
Parameters of experimental Cp data fit according Equation (3). The confidence intervals are attached.
It should be emphasized that the value of standard molar heat capacity calculated from this extrapolation is in good agreement with the value estimated by the Neumann-Kopp method, which is 184.9 J·K−1·mol−1 [46,47] (giving a difference of ~4%). Furthermore, the difference between values calculated from Equations (2) and (3) is only 0.4%.
It should be noted that such determined standard molar heat capacity of Bi2WO6 is close similar to that obtained by Aiswarya et al. [49] for monoclinic Bi2MoO6 compound given as 177.1 J·K−1·mol−1. The values of triclinic CuV2O6 [50] and tetragonal BaTa2O6 [51] compounds obtained by experimental measurements are 157.6 J·K−1·mol−1 and 182.3 J·K−1·mol−1, respectively.
Using Equation (3), the standard molar entropy of Bi2WO6, was estimated to be 226.3 ± 8.3 J·K−1mol−1. This value is comparable to the entropy approximated [66] by NKR from the sum of the entropies of the component binary oxides [67,68], which is found to be 225.4 J·K−1mol−1. The attempts to estimate using modified Einstein equation for k = 1 and modified Debye equation [65] gave the results ~38% lower. The difference between estimated and approximated values using Equations (2) and (3) is only 0.4%, which shows that the Cp(T) function (3) can be used to estimate the standard entropy of the Bi2WO6 phase. Taking into account the difference between the obtained result of the NKR and Einstein estimates (k = 2), in the absence of low-temperature Cp data [69], the data estimated by the Einstein equation were adopted for further thermodynamic calculations.
It should be emphasized again that calculating the exact standard molar entropy from the heat capacity function [69,70] requires experimental data on the Cp(T) of this compound at low temperatures.
4.3. Thermodynamic Functions of Bi2WO6
Using Equation (3) in conjunction with known thermodynamic relations, the thermodynamic functions of Bi2WO6 were calculated using standard molar entropy, determined from low-temperature approximation and standard molar enthalpy of formation, of Phapale et al. [31]. The values of molar—heat capacity, entropy So(T), enthalpy Ho(T) and Gibbs energy Go(T) of γ-Bi2WO6 phase—are summarized in Table 2.

Table 2.
Molar heat capacity data and calculated thermodynamic functions of γ-Bi2WO6.
5. Conclusions
The heat capacity of bismuth tungstate Bi2WO6 was determined for the first time using a DSC on a powder sample synthesized by solid-state reaction in the temperature range from 313 to 1103 K (40–830 °C). The Cp of Bi2WO6 at 298.15 K (25 °C), estimated in this study from the Maier–Kelley model (Equation (2)) is 176.8 ± 3.9 J·K−1·mol−1.
The modified Einstein model [62,63] (k = 2) was proposed to extrapolate the of bismuth tungstate on the basis of high-temperature data set. The standard molar heat capacity, calculated from this extrapolation (Equation (3)) is 177.6 ± 5.7 J·K–1·mol–1. The difference between the standard molar heat capacities calculated from Equations (2) and (3) is about 0.4%. The standard molar entropy of compound Bi2WO6, approximated from Equation (3) is 226.3 ± 8.3 J·K−1mol−1.
Thermodynamic functions of Bi2WO6 were calculated using standard molar entropy determined in this work and standard molar enthalpy of formation of Phapale et al. [31]. The values of calculated molar heat capacity and thermodynamic molar functions of entropy So(T), enthalpy Ho(T) and Gibbs energy Go(T) over the temperature range of 298.15–1123 K (25–850 °C) are presented Table 2. More accurate thermodynamic data can be obtained after analysis of calorimetric low-temperature data (4–300 K).
A reversible second-order phase transition (polar–nonpolar [45]) was observed in the experimental temperature range, with a maximum at 940 ± 1 K (667 °C). The end of the weak endothermic thermal effect was observed near 961 K (688 °C).
Recent works are ongoing to develop new heat capacity estimation techniques using machine learning algorithms. For example, Kauwe et al. [71] described the development of a high-throughput supervised machine learning-based tool that allows the prediction of temperature-dependent heat capacity by correlating with a range of elemental and atomic properties. The conventionally accepted heat capacity prediction methods, such as DFT-based (Density Functional Theory) calculations [72], cation/anion contribution methods [73] and NKR estimates are limited by accuracy or speed. Therefore, the most reliable thermodynamic data, which is the experimental heat capacity, should be used to increase the accuracy of computer throughput calculations.
Machine learning methods enable extremely fast prediction of the heat capacity of thousands of compounds, which allows for easy implementation in integrated computational materials engineering (ICME) [74,75,76]. In this context, it is being considered as a replacement for Neumann–Kopp predictions as a high-throughput screening tool to help identify new materials suitable for engineering processes.
Author Contributions
Conceptualization, B.O.; Methodology, B.O.; Formal analysis, B.O.; Investigation, B.O. and A.K.; Writing—original draft, B.O.; Writing—review and editing, B.O. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Experimental data for the sapphire obtained at P = 0.1 MPa 1.
Table A1.
Experimental data for the sapphire obtained at P = 0.1 MPa 1.
| T, K | Cp(T) 2, J·mol−1·K−1 | T, K | Cp(T) 2, J·mol−1·K−1 | T, K | Cp(T) 2, J·mol−1·K−1 |
|---|---|---|---|---|---|
| 324 | 84.3 | 604 | 112.9 | 884 | 122.6 |
| 334 | 86.1 | 614 | 113.3 | 894 | 122.3 |
| 344 | 87.8 | 624 | 113.9 | 904 | 122.7 |
| 354 | 89.4 | 634 | 114.2 | 914 | 123.5 |
| 364 | 90.9 | 644 | 114.7 | 924 | 123.1 |
| 374 | 92.5 | 654 | 115.2 | 934 | 123.3 |
| 384 | 94.0 | 664 | 115.3 | 944 | 123.4 |
| 394 | 95.2 | 674 | 116.0 | 954 | 124.0 |
| 404 | 96.5 | 684 | 116.4 | 964 | 124.3 |
| 414 | 97.7 | 694 | 116.9 | 974 | 124.2 |
| 424 | 98.9 | 704 | 117.0 | 984 | 124.4 |
| 434 | 100.1 | 714 | 117.3 | 994 | 124.7 |
| 444 | 101.1 | 724 | 117.8 | 1004 | 124.4 |
| 454 | 102.0 | 734 | 118.2 | 1014 | 125.0 |
| 464 | 103.0 | 744 | 118.6 | 1024 | 125.0 |
| 474 | 104.0 | 754 | 118.9 | 1034 | 125.4 |
| 484 | 104.8 | 764 | 119.0 | 1044 | 125.5 |
| 494 | 105.6 | 774 | 119.4 | 1054 | 125.3 |
| 504 | 106.4 | 784 | 120.1 | 1064 | 126.0 |
| 514 | 107.1 | 794 | 120.2 | 1074 | 125.8 |
| 524 | 107.9 | 804 | 120.2 | 1084 | 126.0 |
| 534 | 108.6 | 814 | 120.6 | 1094 | 126.4 |
| 544 | 109.3 | 824 | 120.8 | 1104 | 126.7 |
| 554 | 109.8 | 834 | 121.3 | 1114 | 126.8 |
| 564 | 110.4 | 844 | 121.3 | 1124 | 126.9 |
| 574 | 111.1 | 854 | 121.6 | 1134 | 126.8 |
| 584 | 111.7 | 864 | 121.8 | 1144 | 126.7 |
| 594 | 112.4 | 874 | 122.1 | 1154 | 127.0 |
1 Standard uncertainties, are u(T) = 1 K and u(P) = 0.85 kPa. 2 The extended uncertainty of u(Cp) is 0.02 Cp(T).

Table A2.
Experimental data for the Bi2WO6 obtained by ASTM 1269 method at P = 0.1 MPa 1.
Table A2.
Experimental data for the Bi2WO6 obtained by ASTM 1269 method at P = 0.1 MPa 1.
| First Run 2 | Second Run 2 | ||||||
|---|---|---|---|---|---|---|---|
| T, K | Cp(T), J·K−1·mol−1 | T, K | Cp(T), J·K−1·mol−1 | T, K | Cp(T), J·K−1·mol−1 | T, K | Cp(T), J·K−1·mol−1 |
| 379 | 190.5 | 749 | 215.4 | 375 | 190 | 745 | 214.7 |
| 389 | 191.3 | 759 | 215.8 | 385 | 191 | 755 | 214.6 |
| 399 | 192.7 | 769 | 215.8 | 395 | 192 | 765 | 215.4 |
| 409 | 194.1 | 779 | 216.8 | 405 | 194 | 775 | 215.7 |
| 419 | 195.6 | 789 | 216.4 | 415 | 195 | 785 | 215.9 |
| 429 | 196.8 | 799 | 216.3 | 425 | 197 | 795 | 215.6 |
| 439 | 197.7 | 809 | 216.5 | 435 | 197 | 805 | 216.5 |
| 449 | 198.6 | 819 | 216.6 | 445 | 198 | 815 | 216.4 |
| 459 | 199.5 | 829 | 216.9 | 455 | 200 | 825 | 217.1 |
| 469 | 200.4 | 839 | 217.5 | 465 | 200 | 835 | 217.0 |
| 479 | 201.1 | 849 | 217.6 | 475 | 201 | 845 | 217.2 |
| 489 | 201.7 | 859 | 218.0 | 485 | 202 | 855 | 217.4 |
| 499 | 202.4 | 869 | 218.2 | 495 | 202 | 865 | 217.7 |
| 509 | 203.1 | 879 | 218.3 | 505 | 203 | 875 | 218.4 |
| 519 | 203.6 | 889 | 219.0 | 515 | 204 | 885 | 218.6 |
| 529 | 204.3 | 899 | 218.8 | 525 | 204 | 895 | 219.0 |
| 539 | 205.0 | 909 | 219.8 | 535 | 205 | 905 | 219.0 |
| 549 | 205.7 | 919 | 220.5 | 545 | 205 | 915 | 219.4 |
| 559 | 206.1 | 929 | 221.4 | 555 | 206 | 925 | 220.2 |
| 569 | 206.8 | 939 | 223.0 | 565 | 207 | 935 | 221.9 |
| 579 | 207.3 | 949 | 219.7 | 575 | 207 | 945 | 221.5 |
| 589 | 208.1 | 959 | 219.2 | 585 | 208 | 955 | 217.7 |
| 599 | 208.8 | 969 | 218.2 | 595 | 208 | 965 | 216.9 |
| 609 | 209.4 | 979 | 217.6 | 605 | 209 | 975 | 217.5 |
| 619 | 209.7 | 989 | 217.1 | 615 | 210 | 985 | 217.2 |
| 629 | 210.4 | 999 | 217.0 | 625 | 210 | 995 | 217.5 |
| 639 | 210.8 | 1009 | 217.2 | 635 | 211 | 1005 | 218.2 |
| 649 | 211.1 | 1019 | 217.3 | 645 | 211 | 1015 | 217.8 |
| 659 | 211.7 | 1029 | 217.0 | 655 | 211 | 1025 | 218.9 |
| 669 | 212.1 | 1039 | 217.1 | 665 | 212 | 1035 | 219.1 |
| 679 | 212.5 | 1049 | 217.2 | 675 | 212 | 1045 | 218.2 |
| 689 | 213.0 | 1059 | 217.3 | 685 | 213 | 1055 | 218.8 |
| 699 | 213.4 | 1069 | 217.4 | 695 | 213 | 1065 | 218.9 |
| 709 | 213.5 | 1079 | 217.9 | 705 | 213 | 1075 | 218.7 |
| 719 | 213.6 | 1089 | 217.5 | 715 | 214 | 1085 | 218.2 |
| 729 | 214.3 | 1099 | 218.0 | 725 | 214 | 1095 | 218.5 |
| 739 | 214.7 | 735 | 214 | ||||
1 Standard uncertainties are u(T) = 1 K and u(P) = 0.85 kPa. 2 The extended uncertainty of u(Cp) is 0.02·Cp (T).
References
- Bhat, S.S.M.; Jang, H.W. Recent Advances in Bismuth-Based Nanomaterials for Photoelectrochemical Water Splitting. ChemSusChem 2017, 10, 3001–3018. [Google Scholar] [CrossRef]
- Lee, D.K.; Lee, D.; Lumley, M.A.; Choi, K.-S. Progress on Ternary Oxide-Based Photoanodes for Use in Photoelectrochemical Cells for Solar Water Splitting. Chem. Soc. Rev. 2019, 48, 2126–2157. [Google Scholar] [CrossRef]
- Zhou, L.; Shinde, A.; Guevarra, D.; Haber, J.A.; Persson, K.A.; Neaton, J.B.; Gregoire, J.M. Successes and Opportunities for Discovery of Metal Oxide Photoanodes for Solar Fuels Generators. ACS Energy Lett. 2020, 5, 1413–1421. [Google Scholar] [CrossRef]
- Aurivillius, B. Mixed bismuth oxides with layer lattices. 2. Structure of Bi4Ti3O12. Arkiv. Kemi 1950, 1, 499–512. [Google Scholar]
- Fu, H.; Pan, C.; Yao, W.; Zhu, Y. Visible-Light-Induced Degradation of Rhodamine B by Nanosized Bi2WO6. J. Phys. Chem. B 2005, 109, 22432–22439. [Google Scholar] [CrossRef]
- Ren, J.; Wang, W.; Zhang, L.; Chang, J.; Hu, S. Photocatalytic inactivation of bacteria by photocatalyst Bi2WO6 under visible light. Catal. Commun. 2009, 10, 1940–1943. [Google Scholar] [CrossRef]
- Kudo, A.; Hijii, S. H2 or O2 Evolution from Aqueous Solutions on Layered Oxide Photocatalysts Consisting of Bi3+ with 6s2 Configuration and D0 Transition Metal Ions. Chem. Lett. 1999, 28, 1103–1104. [Google Scholar] [CrossRef]
- Hill, J.C.; Choi, K.-S. Synthesis and Characterization of High Surface Area CuWO4 and Bi2WO6 Electrodes for Use as Photoanodes for Solar Water Oxidation. J. Mater. Chem. A 2013, 1, 5006–5014. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, T.; Chang, X.; Li, A.; Gong, J. Fabrication of Porous Nanoflake BiMOx (M = W, V, and Mo) Photoanodes via Hydrothermal Anion Exchange. Chem. Sci. 2016, 7, 6381–6386. [Google Scholar] [CrossRef]
- Chae, S.Y.; Lee, E.S.; Jung, H.; Hwang, Y.J.; Joo, O.-S. Synthesis of Bi2WO6 Photoanode on Transparent Conducting Oxide Substrate with Low Onset Potential for Solar Water Splitting. RSC Adv. 2014, 4, 24032–24037. [Google Scholar] [CrossRef]
- Buttrey, D.J.; Vogt, T.; Wildgruber, U.; Robinson, W.R. Structural Refinement of the High Temperature Form of Bi2MoO6. J. Solid State Chem. 1994, 111, 118–127. [Google Scholar] [CrossRef]
- Bégué, P.; Enjalbert, R.; Galy, J.; Castro, A. Single-crystal X-ray investigations of the structures of γ(H)Bi2MoO6 and its partially substituted As3+ and Sb3+ homologues. Solid State Sci. 2000, 2, 637–653. [Google Scholar] [CrossRef]
- Zhu, Z.; Wan, S.; Zhao, Y.; Qin, Y.; Ge, X.; Zhong, Q.; Bu, Y. Recent progress in Bi2WO6-based photocatalysts for clean energy and environmental remediation: Competitiveness, challenges, and future perspectives. Nano Sel. 2021, 2, 187–215. [Google Scholar] [CrossRef]
- Frit, B.; Mercurio, J.P. The Crystal Chemistry and Dielectric Properties of the Aurivillius Family of Complex Bismuth Oxides with Perovskite-Like Layered Structures. J. Alloys Compd. 1992, 188, 27–35. [Google Scholar] [CrossRef]
- Wolfe, R.W.; Newham, R.E.; Kay, M.I. Crystal structure of Bi2WO6. Solid State Commun. 1969, 7, 1797–1801. [Google Scholar] [CrossRef]
- Islam, M.S.; Lazure, S.; Vannier, R.-N.; Nowogrocki, G.; Mairesse, G. Structural and Computational Studies of Bi2WO6 Based Oxygen Ion Conductors. J. Mater. Chem. 1998, 8, 655–660. [Google Scholar] [CrossRef]
- Knight, K.S. The crystal structure of russellite; a re-determination using neutron powder diffraction of synthetic Bi2WO6. Min. Mag. 1992, 56, 399–409. [Google Scholar] [CrossRef]
- Yoneda, Y.; Kohara, S.; Takeda, H.; Tsurumi, T. Local Structure Analysis of Bi2WO6. Jap. J. Appl. Phys. 2012, 51, 09LE06. [Google Scholar] [CrossRef]
- Djani, H.; Hermet, P.; Ghosez, P. First-Principles Characterization of the P21ab Ferroelectric Phase of Aurivillius Bi2WO6. J. Phys. Chem. C 2014, 118, 13514–13524. [Google Scholar] [CrossRef]
- Okudera, H.; Sakai, Y.; Yamagata, K.; Takeda, H. Structure of Russellite (Bi2WO6): Origin of Ferroelectricity and the Effect of the Stereoactive Lone Electron Pair on the Structure. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2018, 74, 295–303. [Google Scholar] [CrossRef]
- Rae, A.D.; Thompson, J.G.; Withers, R.L. Structure refinement of commensurately modulated bis muth tungstate, Bi2WO6. Acta Crystallogr. Sect. B. 1991, 47, 870–881. [Google Scholar] [CrossRef]
- Knight, K.S. The Crystal Structure of Ferroelectric Bi2WO6 at 961 K. Ferroelectrics 1993, 150, 319–330. [Google Scholar] [CrossRef]
- Mohn, C.E.; Stølen, S. Influence of the Stereochemically Active Bismuth Lone Pair Structure on Ferroelectricity and Photocalytic Activity of Aurivillius Phase Bi2WO6. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 014103. [Google Scholar] [CrossRef]
- Elaouni, A.; El Ouardi, M.; BaQais, M.; Arab, M.; Saadi, M.; Ahsaine, H.A. Bismuth tungstate Bi2WO6: A review on structural, photophysical and photocatalytic properties. RSC Adv. 2023, 13, 17476. [Google Scholar] [CrossRef] [PubMed]
- Speranskaya, E.I. The Bi2O3–WO3 System. Inorg. Mater. 1970, 6, 127–129. [Google Scholar]
- Hoda, Y.N.; Chang, L.L.Y. Phase Relations in the System Bi2O3-WO3. J. Am. Ceram. Soc. 1974, 57, 323–326. [Google Scholar] [CrossRef]
- Ling, C.D.; Withers, R.L.; Schmid, S.; Thompson, J.G. A Review of Bismuth-Rich Binary Oxides in the Systems Bi2O3–Nb2O5, Bi2O3–Ta2O5, Bi2O3–MoO3, and Bi2O3–WO3. J. Solid State Chem. 1998, 137, 42–61. [Google Scholar] [CrossRef]
- Finlayson, A.P.; Ward, E.; Tsaneva, V.N.; Glowacki, B.A. Bi2O3–WO3 compounds for photocatalytic applications by solid state and viscous processing. J. Power Sources 2005, 145, 667–674. [Google Scholar] [CrossRef]
- Zhou, W. Defect Fluorite Superstructures in the Bi2O3-WO3 System. J. Solid State Chem. 1994, 108, 381–394. [Google Scholar] [CrossRef]
- Muktha, B.; Row, T.N.G. Crystal structure and ionic conductivity of a new bismuth tungstate, Bi3W2O10.5. J. Chem. Sci. 2006, 118, 43–46. [Google Scholar] [CrossRef]
- Phapale, S.; Das, D.; Mishra, R. Standard molar enthalpy of formation of Bi2WO6(s) and Bi2W2O9(s) compounds. J. Chem. Thermodyn. 2013, 63, 74–77, Erratum in J. Chem. Thermodyn. 2015, 89, 312–313. [Google Scholar] [CrossRef]
- Maier, C.G.; Kelley, K.K. An equation for the representation of high-temperature heat content data. J. Am. Chem. Soc. 1932, 54, 3243–3246. [Google Scholar] [CrossRef]
- Gamsjager, E.; Wiessner, M. Low temperature heat capacities and thermodynamic functions described by Debye-Einstein integrals. Monatsh. Chem. 2018, 149, 357–368. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N.A.; Knight, K.S.; Lightfoot, P. Unusual High-Temperature Structural Behaviour in Ferroelectric Bi2WO6. Chem. Eur. J. 2006, 12, 1493–1499. [Google Scholar] [CrossRef] [PubMed]
- Voronkova, V.I.; Kharitonova, E.P.; Rudnitskaya, O.G. Refinement of Bi2WO6 and Bi2MoO6 polymorphism. J. Alloys Compd. 2009, 487, 274–279. [Google Scholar] [CrossRef]
- Mączka, M.; Macalik, L.; Hermanowicz, K.; Kępiński, L.; Tomaszewski, P. Phonon properties of nanosized bismuth layered ferroelectric material—Bi2WO6. J. Raman Spectrosc. 2010, 41, 1059–1066. [Google Scholar] [CrossRef]
- Yanovskii, V.K.; Voronkova, V.I. Polymorphism and Properties of Bi2WO6 and Bi2MoO6. Phys. Stat. Sol. 1986, 93, 57–66. [Google Scholar] [CrossRef]
- Newkirk, H.W.; Quadflieg, P.; Liebertz, J.; Kockel, A. Growth, crystallography and dielectric properties of Bi2WO6. Ferroelectrics 1972, 4, 51–55. [Google Scholar] [CrossRef]
- Kubaschewski, O.; Alcock, C.B.; Spencer, P.J. Materials Thermochemistry, 6th ed.; Pergamon Press: Oxford, UK, 1993; pp. 267–323. [Google Scholar]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystal. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Day, N. Open-Access Collection of Crystal Structures of Organic, Inorganic, Metal-Organic Compounds and Minerals, Excluding Biopolymers. COD—Crystallography Open Database, University of Cambridge. Available online: http://www.crystallography.net/cod/result.php (accessed on 1 July 2025).
- ASTM Standard E1269-05; Determining Specific Heat Capacity by DSC. ASTM International: Philadelphia, PA, USA, 2007. [CrossRef]
- ASTM Standard E1269-11; Standard Test Method for Determining Specific Heat Capacity by Differential Scanning Calorimetry. ASTM International: Philadelphia, PA, USA, 2011. [CrossRef]
- Watanabe, A. Polymorphism in Bi2WO6. J. Solid State Chem. 1982, 41, 160–165. [Google Scholar] [CrossRef]
- Denisova, L.T.; Izotov, A.D.; Chumilina, L.G.; Kargin, Y.F.; Denisov, V.M. Heat capacity and thermodynamic properties of bismuth orthovanadate in the temperature range 356–980 K. Dokl. Phys. Chem. 2016, 467, 41–43. [Google Scholar] [CrossRef]
- Kopp, H. III. Investigations of the specific heat of solid bodies. Phil. Trans. R Soc. Lond. 1865, 155, 71–202. [Google Scholar] [CrossRef]
- Leitner, J.; Chuchvalec, P.; Semidubský, D.; Strejc, A.; Abrman, P. Estimation of heat capacities of solid mixed oxides. Thermochem. Acta 2003, 395, 27–46. [Google Scholar] [CrossRef]
- Barin, I. Thermochemical Data of Pure Substances, 3rd ed.; VCH: Weinheim, Germany, 1995; pp. 202+1160. [Google Scholar]
- Aiswarya, P.M.; Kumar, S.S.; Ganesan, R.; Gnanasekaran, T. Determination of thermodynamic properties of Bi2Mo3O12 (s), Bi2MoO6 (s) and Bi6Mo2O15 (s). J. Chem. Thermodyn. 2019, 139, 105886. [Google Scholar] [CrossRef]
- Aiswarya, P.M.; Narang, S.; Dawar, R.; Babu, P.D.; Mishra, R. Calorimetric investigation of ternary oxides in the CuO–V2O5 system. J. Therm. Anal. Calorim. 2025. [Google Scholar] [CrossRef]
- Ilhan, M.; Mergen, A.; Sarıoglu, C.; Yaman, C. Heat capacity measurements on BaTa2O6 and derivation of its thermodynamic functions. J. Therm. Anal. Calorim. 2017, 128, 707–711. [Google Scholar] [CrossRef]
- Denisova, L.T.; Belousova, N.V.; Denisov, V.M.; Galiakhmetova, N.A. High-temperature heat capacity of oxides of the CuO–V2O5 system. Phys. Solid State. 2017, 59, 1270–1274. [Google Scholar] [CrossRef]
- Denisova, L.T.; Kargin, Y.F.; Belousova, N.V.; Galiakhmetova, N.A.; Denisov, V.M. Synthesis and investigation of thermodynamic properties of Cu5V2O10. Russ. J. Inorg. Chem. 2019, 64, 725–728. [Google Scholar] [CrossRef]
- Leitner, J.; Vonka, P.; Sedmidubsky, D.; Svoboda, P. Application of Neumann-Kopp rule for the estimation of heat capacity of mixed oxides. Thermochim. Acta 2010, 497, 7–13. [Google Scholar] [CrossRef]
- Demidenko, A.F.; Koshchenko, V.I.; Medvedeva, Z.S.; Radchenko, A.F. Thermal capacities and thermodynamic functions of BAs and B6As. Izv. Akad. Nauk. SSSR Neorg. Mater. 1975, 11, 2117–2119. [Google Scholar]
- Danilchenko, B.A.; Paszkiewicz, T.; Wolski, S.; Jezowski, A.; Plackowski, T. Heat capacity and phonon mean free path of wurtzite GaN. Appl. Phys. Lett. 2006, 89, 061901. [Google Scholar] [CrossRef]
- Sedmidubsky, D.; Leitner, J. Calculation of the thermodynamic properties of AIII nitrides. J. Cryst. Growth 2006, 286, 66–70. [Google Scholar] [CrossRef]
- Sedmidubsky, D.; Leitner, J.; Svoboda, P.; Sofer, Z.; Macháček, J. Heat capacity and phonon spectra of AIIIN. J. Therm. Anal. Calorim. 2009, 95, 403–407. [Google Scholar] [CrossRef]
- Pässler, R. Non-Debye heat capacity formula refined and applied to GaP, GaAs, GaSb, InP, InAs, and InSb. AIP Adv. 2013, 3, 82108. [Google Scholar] [CrossRef]
- Szytuła, A.; Baran, S.; Przewoźnik, J.; Tyvanchuk, Y.; Kalychak, Y. Magnetic properties and specific heat data of R11Ni4In9 (R = Pr, Nd, Sm, Gd and Tb) compounds. J. Alloys Comp. 2014, 601, 238–244. [Google Scholar] [CrossRef]
- Jendrzejczyk-Handzlik, D.; Przewoźnik, J.; Onderka, B.; Kapusta, C.; Handzlik, P.; Fitzner, K. Thermodynamic properties of the novel photocatalyst BiSbO4 phase determined from 1.8 K to 1073 K. Ceram. Intern. 2017, 48, 29686–29694. [Google Scholar] [CrossRef]
- Voronin, G.F.; Kutsenok, I.B. Universal Method for Approximating the Standard Thermodynamic Functions of Solids. J. Chem. Eng. Data 2013, 58, 2083–2094. [Google Scholar] [CrossRef]
- Chen, Q.; Sundman, B. Modelling of thermodynamic properties for Bcc, Fcc, liquid, and amorphous iron. J. Phase Equil. 2001, 22, 631–644. [Google Scholar] [CrossRef]
- Chase, M.W.; Ansara, I.; Dinsdale, A.; Eriksson, G.; Grimvall, G.; Höglund, L.; Yokokawa, H. Workshop on thermodynamic models and data for pure elements and other endmembers of solutions, Schloss Ringberg. Calphad 1995, 19, 437–447. [Google Scholar] [CrossRef]
- Onderka, B. The heat capacity of bismuth silicates. Thermochim. Acta. 2015, 601, 68–74. [Google Scholar] [CrossRef]
- Mrovĕc, M.; Leitner, J.; Nevřiva, M.; Sedmidubský, D.; Stejskal, J. Thermochemical properties of MeCuO2 and Me2CuO3 (Me=Ca, Sr, Ba) mixed oxides. Thermochim. Acta 1998, 318, 63–70. [Google Scholar] [CrossRef]
- Aspiala, M.; Sukhomlinov, D.; Taskinen, P. Standard thermodynamic properties of Bi2O3 by a solid-oxide electrolyte EMF technique. J. Chem. Thermodyn. 2014, 75, 8–12. [Google Scholar] [CrossRef]
- Han, B.-Y.; Khoroshilov, A.V.; Tyurin, A.V.; Baranchikov, A.E.; Razumov, M.I.; Ivanova, O.S.; Gavrichev, K.S.; Ivanov, V.K. WO3 thermodynamic properties at 80–1256 K revisited. J. Therm. Anal. Calorim. 2020, 142, 1533–1543. [Google Scholar] [CrossRef]
- Harvey, J.-P.; Lebreux-Desilets, F.; Marchand, J.; Oishi, K.; Bouarab, A.-F.; Robelin, C.; Gheribi, A.E.; Pelton, A. On the Application of the FactSage Thermochemical Software and Databases in Materials Science and Pyrometallurgy. Processes 2020, 8, 1156. [Google Scholar] [CrossRef]
- Leitner, J.; Jakeš, V.; Sofer, Z.; Semidubský, D.; Ružicka, K.; Svoboda, P. Heat capacity, enthalpy and entropy of ternary bismuth tantalum oxides. J. Solid State Chem. 2011, 184, 241–245. [Google Scholar] [CrossRef]
- Kauwe, S.K.; Graser, J.; Vazquez, A.; Sparks, T.D. Machine Learning Prediction of Heat Capacity for Solid Inorganics. Integr. Mater. Manuf. Innov. 2018, 7, 43–51. [Google Scholar] [CrossRef]
- Chihaia, V.; Alexiev, V.; AlMatrouk, H.S. Assessment of the Heat Capacity by Thermodynamic Approach Based on Density Functional Theory Calculations. In Applications of Calorimetry; Rivera-Armenta, J.L., Flores-Hernández, C.G., Eds.; IntechOpen: London, UK, 2022. [Google Scholar] [CrossRef]
- Mostafa, A.T.M.G.; Eakman, J.M.; Montoya, M.M.; Yarbro, S.L. Prediction of heat capacities of solid inorganic salts from group contributions. Ind. Eng. Chem. Res. 1996, 35, 343–348. [Google Scholar] [CrossRef]
- Gaultois, M.W.; Oliynyk, A.; Mar, A.; Sparks, T.D.; Mulholland, G.J.; Meredig, B. Perspective: Web-based machine learning models for real-time screening of thermoelectric materials properties. APL Mater. 2016, 4, 053213. [Google Scholar] [CrossRef]
- Seshadri, R.; Sparks, T.D. Perspective: Interactive material property databases through aggregation of literature data. APL Mater. 2016, 4, 053206. [Google Scholar] [CrossRef]
- Sparks, T.D.; Gaultois, M.W.; Oliynyk, A.; Brgoch, J.; Meredig, B. Data mining our way to the next generation of thermoelectrics. Scr. Mater. 2016, 111, 10–15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).