Thin Film Fragmentation Testing: A Refined Screening Method for Estimating Relative Intrinsic Ductility of Refractory Metals
Abstract
1. Introduction
2. Methods
3. Results and Discussion
- The film–substrate adhesion must be sufficiently strong to force the film to undergo the strain imposed on it by the substrate, and thereby ensure uniform deformation before failure. If adhesion is weak, the film may delaminate in certain areas and partially behave like a free-standing film, which would fracture differently than a substrate-supported film [60]. Magnetron sputtering is capable of generating excellent film adhesion, for pure metals as well as for alloys including RHEAs and other multi-principal element alloys [61]. Strong adhesion can be achieved by maintaining a high-quality vacuum in the chamber prior to sputtering [62], selecting an appropriate substrate material, and surface etching before deposition [60,63]. In the current study, the base pressure before deposition was maintained at 5 × 10−8 torr (or better). Kapton substrates were used because of their excellent adhesion with metal coatings. Finally, the substrates were plasma cleaned by applying RF bias to the substrate before deposition, to further improve adhesion.
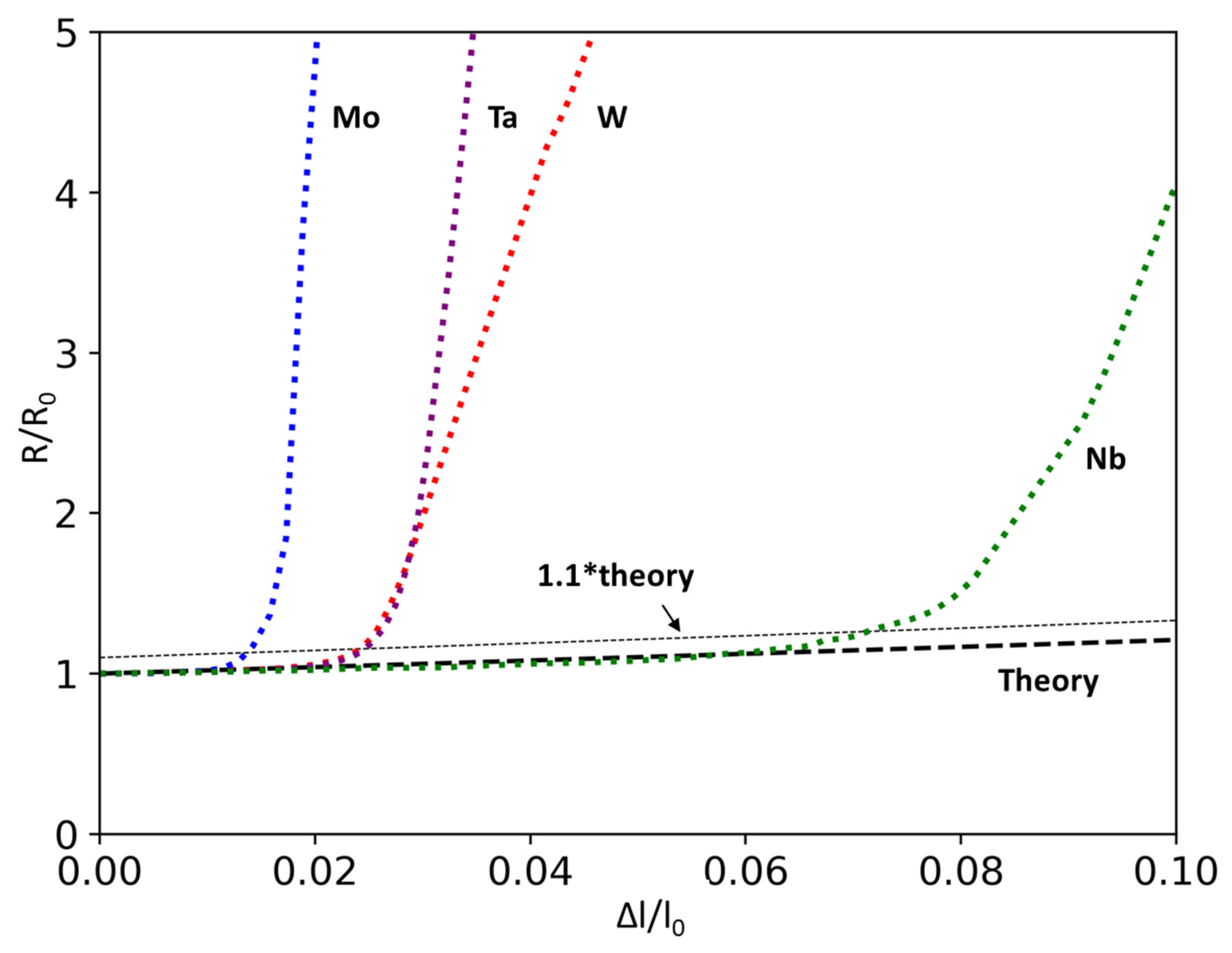
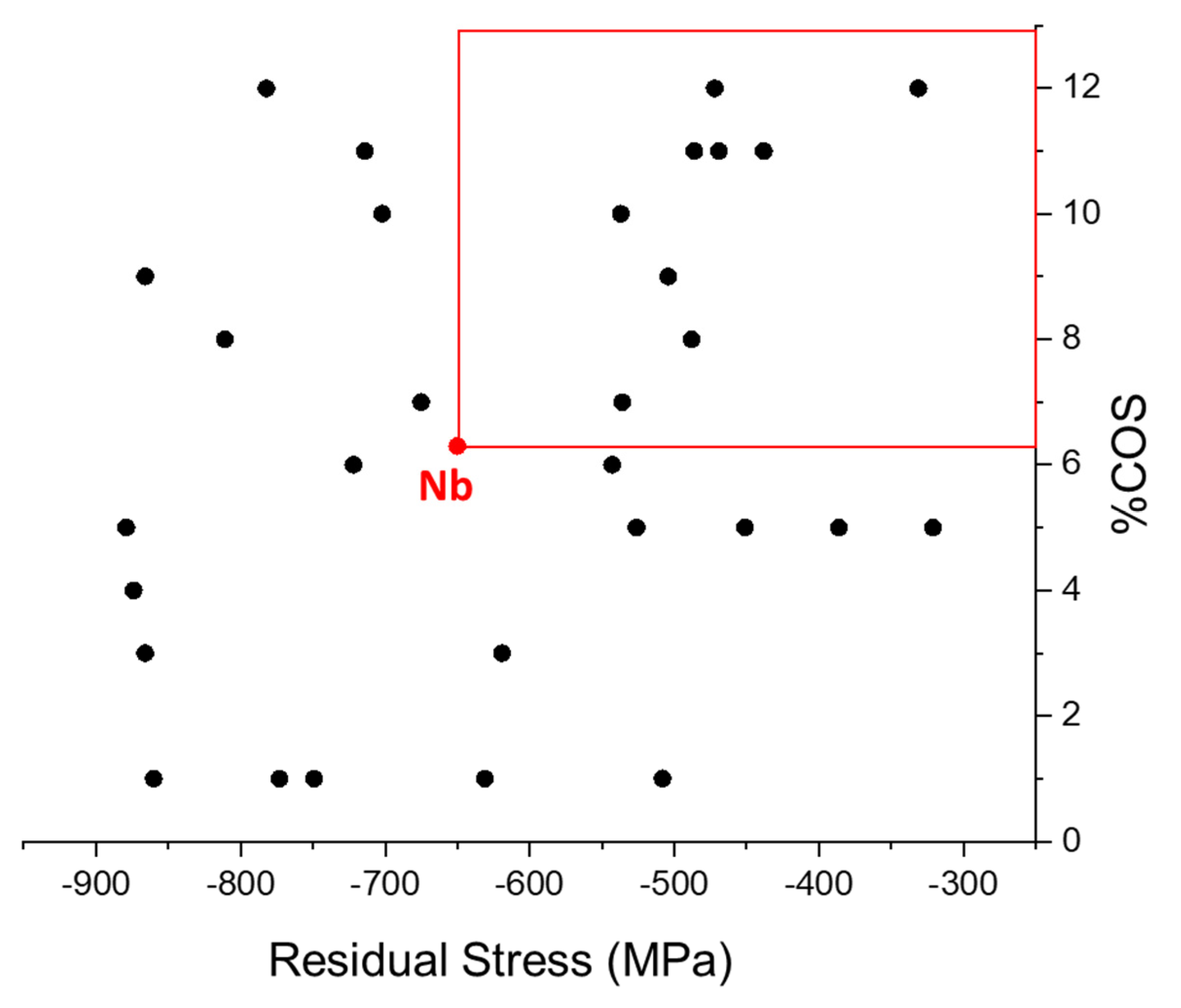
- It is important to match, as closely as possible, the residual film stress levels for the metals and alloys being compared. Residual stress can be controlled by adjusting factors such as chamber pressure and deposition power, or by applying a substrate bias during the deposition process. All films in the current study have a compressive stress of approximately −650 MPa. The particular combination of fabrication parameters can also affect the COS of a film. Among the four metals studied here, only Mo was deposited using a substrate bias. Results indicate that using a substrate bias led to a reduction in COS. In contrast to the ductility levels of their bulk counterparts, Mo films exhibited a lower COS than W films. This indicates that both the stress state and fabrication parameters should be carefully considered in order to obtain reliable comparisons between different metal films.
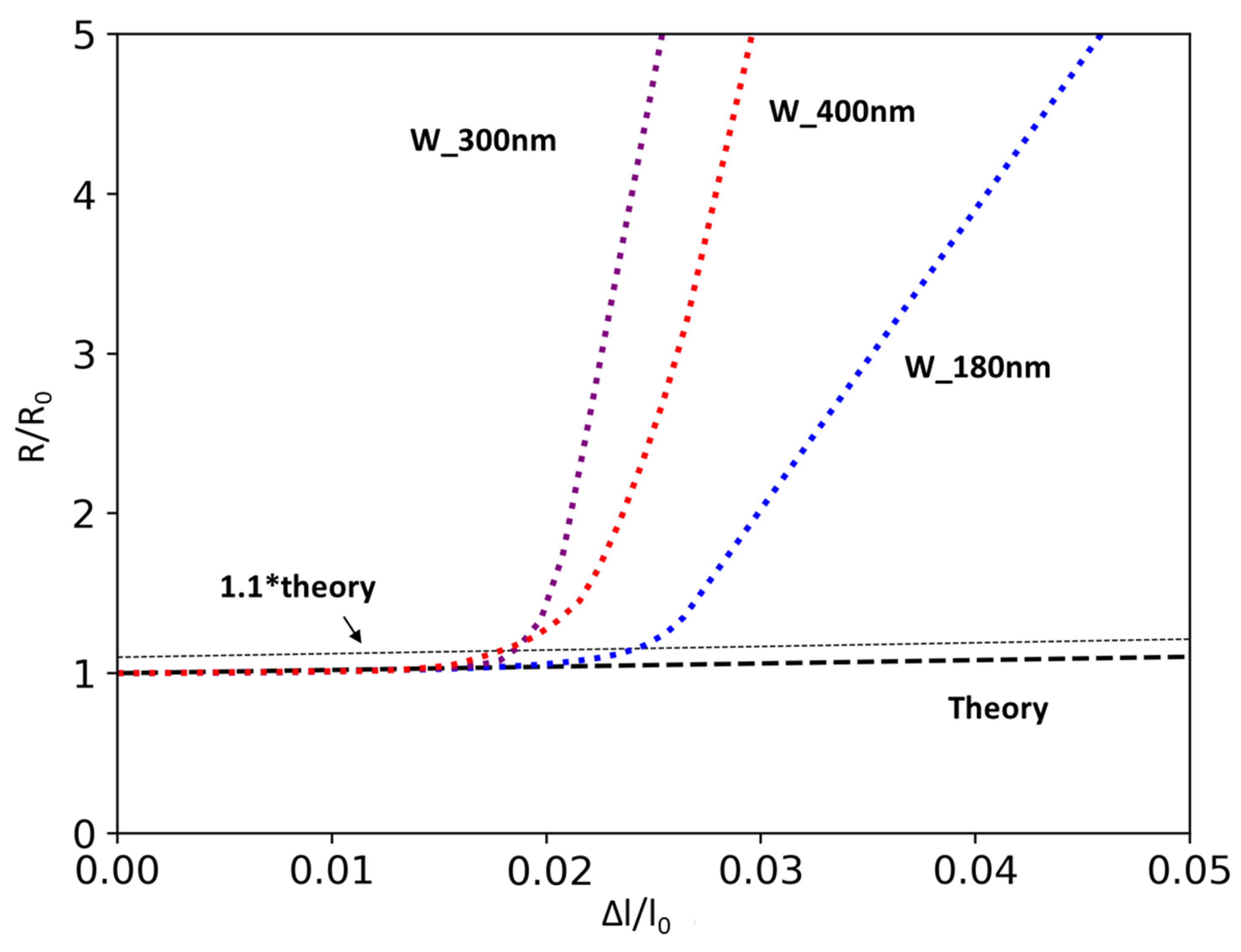
- The thickness of a film influences its COS in two ways. First, variations in thickness alter the film’s cross-sectional area, which in turn affects the local stress and thereby the fracture behavior of the film. Second, film thickness can modify the residual stress in the film [42,64]. Moreover, this study highlights that a change in film thickness can even alter the dependence of COS on residual stress. Therefore, to compare film compositions, it is necessary to ensure a consistent thickness for all films. This can be readily achieved by controlling the deposition time for each metal film.
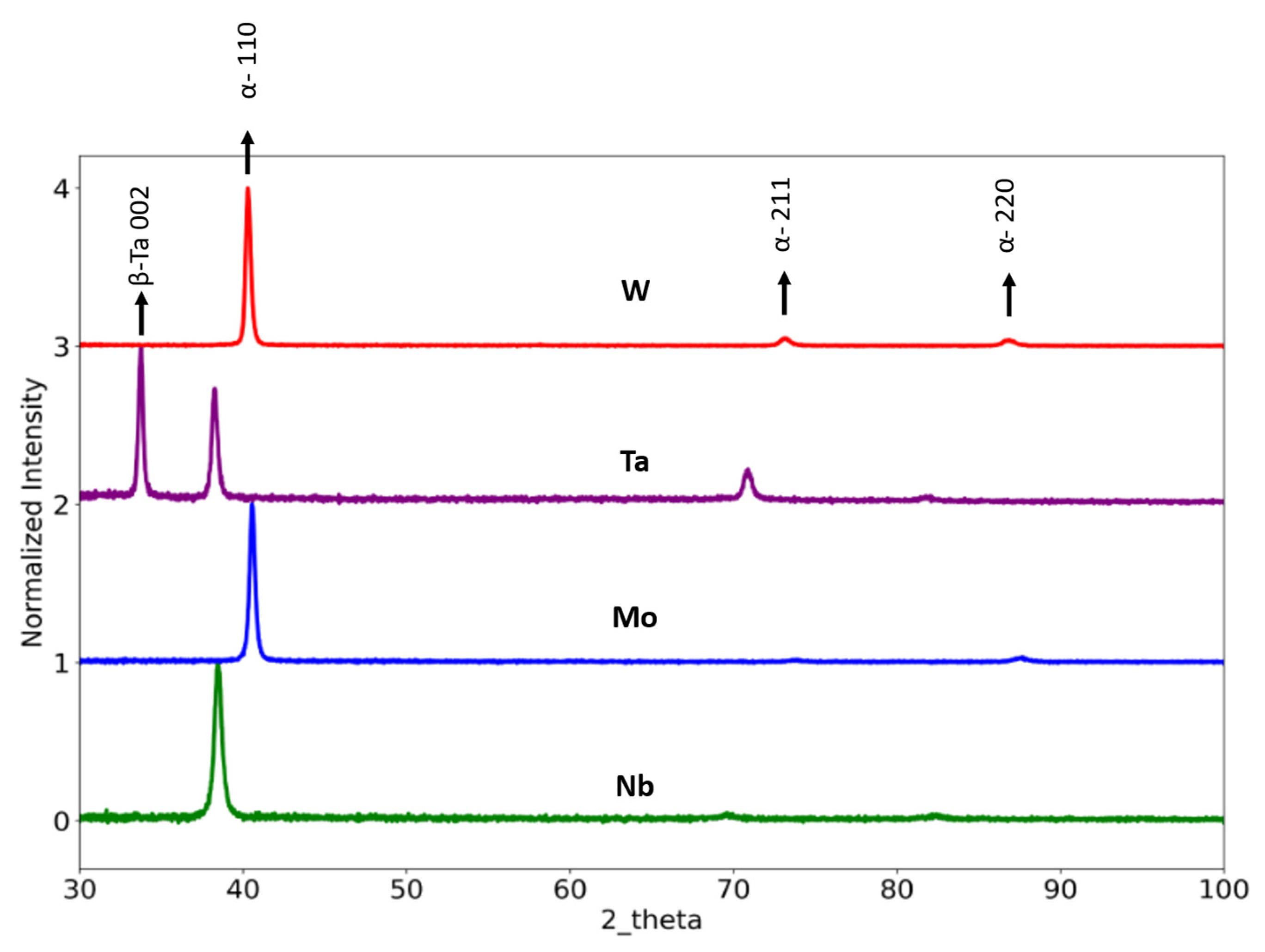
- The contributions from film microstructure should be considered carefully. This includes grain size, crystal structure, and defects such as inclusions. While sputtered thin films can exhibit dense, inclusion-free, nanocrystalline grain structures, it is also possible for unfavorable fabrication parameters to result in metastable phases or strong crystallographic texture that may differ for each metal. For a comprehensive comparison between thin film and bulk counterparts, the crystal structure and texture should be considered. The current study shows that metastable β Ta is brittle and does not follow the ductility trend of bulk refractory BCC metals. On the other hand, W and Nb thin films with the same BCC structure and texture do reflect their relative levels of bulk ductility.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Senkov, O.N.; Tsakiropoulos, P.; Couzinié, J.-P. Special Issue “Advanced Refractory Alloys”: Metals, MDPI. Metals 2022, 12, 333. [Google Scholar] [CrossRef]
- Soni, V.; Senkov, O.N.; Gwalani, B.; Miracle, D.B.; Banerjee, R. Microstructural Design for Improving Ductility of An Initially Brittle Refractory High Entropy Alloy. Sci. Rep. 2018, 8, 8816. [Google Scholar] [CrossRef] [PubMed]
- Qi, L.; Chrzan, D.C. Tuning Ideal Tensile Strengths and Intrinsic Ductility of bcc Refractory Alloys. Phys. Rev. Lett. 2014, 112, 115503. [Google Scholar] [CrossRef]
- Winter, I.S.; de Jong, M.; Montoya, J.; Rothchild, E.; Chrzan, D.C. Intrinsic ductility of random substitutional alloys from nonlinear elasticity theory. Phys. Rev. Mater. 2019, 3, 113608. [Google Scholar] [CrossRef]
- Raza, H.; Cheng, J.; Wang, J.; Kandasamy, S.; Zheng, G.; Chen, G. Titanium-containing high entropy oxide (Ti-HEO): A redox expediting electrocatalyst towards lithium polysulfides for high performance Li-S batteries. Nano Res. Energy 2024, 3, e9120116. [Google Scholar] [CrossRef]
- Qin, Y.; Du, Z.; Liu, X.; Yu, J. Research Progress of High Entropy Carbides. J. Wuhan Univ. Technol.-Mat. Sci. Ed. 2024, 39, 1440–1448. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Li, B.; Yuan, Z.; Yang, T.; Liu, Y.; Gao, H.; Xu, L.; Yu, X.; Luo, Q.; et al. Enhanced energy storage in high-entropy ferroelectric polymers. Nat. Mater. 2025, 24, 1066–1073. [Google Scholar] [CrossRef]
- Senkov, O.N.; Miracle, D.B.; Chaput, K.J.; Couzinie, J.-P. Development and exploration of refractory high entropy alloys—A review. J. Mater. Res. 2018, 33, 3092–3128. [Google Scholar] [CrossRef]
- Zhuo, L.; Xie, Y.; Chen, B. A review on recent progress of refractory high entropy alloys: From fundamental research to engineering applications. J. Mater. Res. Technol. 2024, 33, 1097–1129. [Google Scholar] [CrossRef]
- Hu, Y.-J.; Sundar, A.; Ogata, S.; Qi, L. Screening of generalized stacking fault energies, surface energies and intrinsic ductile potency of refractory multicomponent alloys. Acta Mater. 2021, 210, 116800. [Google Scholar] [CrossRef]
- Tandoc, C.; Hu, Y.-J.; Qi, L.; Liaw, P.K. Mining of lattice distortion, strength, and intrinsic ductility of refractory high entropy alloys. npj Comput. Mater. 2023, 9, 53. [Google Scholar] [CrossRef]
- Lee, C.; Xie, D.; Kyle Derby, B.; Kevin Baldwin, J.; Tandoc, C.; EI Atwani, O.; Hu, Y.-J.; Valdez, J.A.; Li, N.; Fensin, S.J. An experimentally driven high-throughput approach to design refractory high-entropy alloys. Mater. Des. 2022, 223, 111259. [Google Scholar] [CrossRef]
- Li, Z.; Ludwig, A.; Savan, A.; Springer, H.; Raabe, D. Combinatorial metallurgical synthesis and processing of high-entropy alloys. J. Mater. Res. 2018, 33, 3156–3169. [Google Scholar] [CrossRef]
- He, J.; Li, Z.; Lin, J.; Zhao, P.; Zhang, H.; Zhang, F.; Wang, L.; Cheng, X. Machine learning-assisted design of refractory high-entropy alloys with targeted yield strength and fracture strain. Mater. Des. 2024, 246, 113326. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Pei, Z. Machine learning for high-entropy alloys: Progress, challenges and opportunities. Prog. Mater. Sci. 2023, 131, 101018. [Google Scholar] [CrossRef]
- Miracle, D.; Majumdar, B.; Wertz, K.; Gorsse, S. New strategies and tests to accelerate discovery and development of multi-principal element structural alloys. Scr. Mater. 2017, 127, 195–200. [Google Scholar] [CrossRef]
- Ribeiro, B.L.; Monclús, M.A.; Barbosa, M.; Torralba, J.M.; Malheiros, L.F.; Santos, R.F.; Sequeiros, E.W. High-throughput screening of MoNbTaW-based Refractory High-Entropy Alloys through Direct Energy Deposition in-situ alloying. Mater. Charact. 2024, 217, 114346. [Google Scholar] [CrossRef]
- Less Common Nonferrous Metals. In Materials Handbook: A Concise Desktop Reference; Cardarelli, F., Ed.; Springer: London, UK, 2008; pp. 213–454. ISBN 978-1-84628-669-8. [Google Scholar]
- Chen, Y.; Li, Y.; Cheng, X.; Wu, C.; Cheng, B.; Xu, Z. The Microstructure and Mechanical Properties of Refractory High-Entropy Alloys with High Plasticity. Materials 2018, 11, 208. [Google Scholar] [CrossRef]
- Chen, B.; Zhuo, L. Latest progress on refractory high entropy alloys: Composition, fabrication, post processing, performance, simulation and prospect. Int. J. Refract. Met. Hard Mater. 2023, 110, 105993. [Google Scholar] [CrossRef]
- Baëtens, T.; Pallecchi, E.; Thomy, V.; Arscott, S. Cracking effects in squashable and stretchable thin metal films on PDMS for flexible microsystems and electronics. Sci. Rep. 2018, 8, 9492. [Google Scholar] [CrossRef]
- Chen, X.; Kirsch, B.L.; Senter, R.; Tolbert, S.H.; Gupta, V. Tensile testing of thin films supported on compliant substrates. Mech. Mater. 2009, 41, 839–848. [Google Scholar] [CrossRef]
- Cordill, M.J.; Glushko, O.; Kreith, J.; Marx, V.M.; Kirchlechner, C. Measuring electro-mechanical properties of thin films on polymer substrates. Microelectron. Eng. 2015, 137, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Jörg, T.; Music, D.; Hauser, F.; Cordill, M.J.; Franz, R.; Köstenbauer, H.; Winkler, J.; Schneider, J.M.; Mitterer, C. Deformation behavior of Re alloyed Mo thin films on flexible substrates: In situ fragmentation analysis supported by first-principles calculations. Sci. Rep. 2017, 7, 7374. [Google Scholar] [CrossRef]
- Xia, A.; Dedoncker, R.; Glushko, O.; Cordill, M.J.; Depla, D.; Franz, R. Influence of the nitrogen content on the structure and properties of MoNbTaVW high entropy alloy thin films. J. Alloys Compd. 2021, 850, 156740. [Google Scholar] [CrossRef]
- Tuhser, T.B.N.; Winter, I.S.; Chrzan, D.; Balk, T.J. Enhancing intrinsic ductility in VNbMoTaW high entropy alloy: A combinatorial investigation with experimental evaluation of theoretical predictions. J. Mater. Res. Technol. 2025, 35, 3645–3654. [Google Scholar] [CrossRef]
- Xia, A.; Glushko, O.; Cordill, M.J.; Franz, R. Electromechanical properties of cathodic arc deposited high entropy alloy thin films on polymer substrates. J. Vac. Sci. Technol. A 2018, 37, 010601. [Google Scholar] [CrossRef]
- ASTM Standard D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2022. [CrossRef]
- Glushko, O.; Cordill, M.J. Electrical Resistance of Metal Films on Polymer Substrates Under Tension. Exp. Tech. 2016, 40, 303–310. [Google Scholar] [CrossRef]
- Cordill, M.J.; Kreiml, P.; Mitterer, C. Materials Engineering for Flexible Metallic Thin Film Applications. Materials 2022, 15, 926. [Google Scholar] [CrossRef]
- Cordill, M.J.; Glushko, O.; Putz, B. Electro-Mechanical Testing of Conductive Materials Used in Flexible Electronics. Front. Mater. 2016, 3, 11. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X.; Zhang, X.; Zhang, W.; Li, J.; Chen, Y.; Liu, H.; Yan, Y. Mechanical Properties of Tensile Cracking in Indium Tin Oxide Films on Polycarbonate Substrates. Coatings 2022, 12, 538. [Google Scholar] [CrossRef]
- Lu, N.; Wang, X.; Suo, Z.; Vlassak, J. Metal films on polymer substrates stretched beyond 50%. Appl. Phys. Lett. 2007, 91, 221909. [Google Scholar] [CrossRef]
- Leterrier, Y.; Médico, L.; Demarco, F.; Månson, J.-A.E.; Betz, U.; Escolà, M.F.; Kharrazi Olsson, M.; Atamny, F. Mechanical integrity of transparent conductive oxide films for flexible polymer-based displays. Thin Solid Films 2004, 460, 156–166. [Google Scholar] [CrossRef]
- Jörg, T.; Cordill, M.J.; Franz, R.; Glushko, O.; Winkler, J.; Mitterer, C. The electro-mechanical behavior of sputter-deposited Mo thin films on flexible substrates. Thin Solid Films 2016, 606, 45–50. [Google Scholar] [CrossRef]
- Kreiml, P.; Rausch, M.; Terziyska, V.L.; Köstenbauer, H.; Winkler, J.; Mitterer, C.; Cordill, M.J. Balancing the electro-mechanical and interfacial performance of Mo-based alloy films. Materialia 2020, 12, 100774. [Google Scholar] [CrossRef]
- Akbari, A. Combinatorial Screening Approach in Developing Non-Equiatomic High Entropy Alloys. Ph.D. Thesis, University of Kentucky Libraries, Lexington, KY, USA, 2018. [Google Scholar]
- Chen, S.; Wang, J.; Wu, R.; Wang, Z.; Li, Y.; Lu, Y.; Zhou, W.; Hu, P.; Li, H. Insights into the nucleation, grain growth and phase transformation behaviours of sputtered metastable β-W films. J. Mater. Sci. Technol. 2021, 90, 66–75. [Google Scholar] [CrossRef]
- Shen, Y.G.; Mai, Y.W.; Zhang, Q.C.; McKenzie, D.R.; McFall, W.D.; McBride, W.E. Residual stress, microstructure, and structure of tungsten thin films deposited by magnetron sputtering. J. Appl. Phys. 2000, 87, 177–187. [Google Scholar] [CrossRef]
- Sun, H.L.; Song, Z.X.; Guo, D.G.; Ma, F.; Xu, K.W. Microstructure and Mechanical Properties of Nanocrystalline Tungsten Thin Films. J. Mater. Sci. Technol. 2010, 26, 87–92. [Google Scholar] [CrossRef]
- Rossnagel, S.M.; Noyan, I.C.; Cabral, C. Phase transformation of thin sputter-deposited tungsten films at room temperature. J. Vac. Sci. Technol. B 2002, 20, 2047. [Google Scholar] [CrossRef]
- Vink, T.J.; Walrave, W.; Daams, J.L.C.; Dirks, A.G.; Somers, M.A.J.; van den Aker, K.J.A. Stress, strain, and microstructure in thin tungsten films deposited by dc magnetron sputtering. J. Appl. Phys. 1993, 74, 988–995. [Google Scholar] [CrossRef]
- Li, H.; Gao, D.; Xie, S.; Zou, J. Effect of magnetron sputtering parameters and stress state of W film precursors on WSe 2 layer texture by rapid selenization. Sci. Rep. 2016, 6, 36451. [Google Scholar] [CrossRef]
- Alfonso, J.A.; Greaves, E.D.; Lavelle, B.; Sajo-Bohus, L. Effect of sputtering pressure on residual stress in Ni films using energy-dispersive x-ray diffraction. J. Vac. Sci. Technol. A 2003, 21, 846–850. [Google Scholar] [CrossRef]
- El Khakani, M.A.; Chaker, M.; Le Drogoff, B. Iridium thin films deposited by radio-frequency magnetron sputtering. J. Vac. Sci. Technol. A 1998, 16, 885–888. [Google Scholar] [CrossRef]
- Vüllers, F.T.N.; Spolenak, R. Alpha- vs. beta-W nanocrystalline thin films: A comprehensive study of sputter parameters and resulting materials’ properties. Thin Solid Films 2015, 577, 26–34. [Google Scholar] [CrossRef]
- Djaziri, S.; Renault, P.-O.; Le Bourhis, E.; Goudeau, P.; Faurie, D.; Geandier, G.; Mocuta, C.; Thiaudière, D. Comparative study of the mechanical properties of nanostructured thin films on stretchable substrates. J. Appl. Phys. 2014, 116, 093504. [Google Scholar] [CrossRef]
- Tuhser, T.B.N. Advancing Combinatorial Screening of Refractory High Entropy Alloys Through Intrinsic Ductility Assessment via Thin Film Fragmentation Testing. Ph.D. Thesis, University of Kentucky, Lexington, KY, USA, 2024. [Google Scholar] [CrossRef]
- Choi, D.; Wang, B.; Chung, S.; Liu, X.; Darbal, A.; Wise, A.; Nuhfer, N.T.; Barmak, K.; Warren, A.P.; Coffey, K.R.; et al. Phase, grain structure, stress, and resistivity of sputter-deposited tungsten films. J. Vac. Sci. Technol. A 2011, 29, 051512. [Google Scholar] [CrossRef]
- Hofer, A.M.; Schlacher, J.; Keckes, J.; Winkler, J.; Mitterer, C. Sputtered molybdenum films: Structure and property evolution with film thickness. Vacuum 2014, 99, 149–152. [Google Scholar] [CrossRef]
- Cordill, M.J.; Taylor, A.A.; Schmidegg, K. Thickness Effects on the Fracture of Chromium Films on Polyethylene Terephthalate. BHM Berg- Hüttenmänn. Monatsh. 2011, 156, 434–437. [Google Scholar] [CrossRef]
- Colin, J.J.; Abadias, G.; Michel, A.; Jaouen, C. On the origin of the metastable β-Ta phase stabilization in tantalum sputtered thin films. Acta Mater. 2017, 126, 481–493. [Google Scholar] [CrossRef]
- Chen, W.-C.; Wang, Z.-Y.; Yu, C.-Y.; Liao, B.-H.; Lin, M.-T. A study of the phase transformation of low temperature deposited tantalum thin films using high power impulse magnetron sputtering and pulsed DC magnetron sputtering. Surf. Coat. Technol. 2022, 436, 128288. [Google Scholar] [CrossRef]
- Al-masha’al, A.; Bunting, A.; Cheung, R. Evaluation of residual stress in sputtered tantalum thin-film. Appl. Surf. Sci. 2016, 371, 571–575. [Google Scholar] [CrossRef]
- Zhang, J.; Huai, Y.; Chen, L.; Zhang, J. Formation of low resistivity alpha Ta by ion beam sputtering. J. Vac. Sci. Technol. B 2003, 21, 237. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley: Hoboken, NJ, USA, 2005; Available online: https://www.wiley.com/en-us/Introduction+to+Solid+State+Physics%2C+8th+Edition-p-9780471415268 (accessed on 13 December 2020).
- Ni, Z.; Zhong, Y.; Tao, X.; Li, W.; Gao, H.; Yao, Y. Effects of Radio Frequency Bias on the Structure Parameters and Mechanical Properties of Magnetron-Sputtered Nb Films. Crystals 2022, 12, 256. [Google Scholar] [CrossRef]
- Yang, Z.-H.; Wu, P.-C.; Chuang, T.-H. Effects of substrate bias on the sputtering of high density (111)-nanotwinned Cu films on SiC chips. Sci. Rep. 2022, 12, 15408. [Google Scholar] [CrossRef] [PubMed]
- Frank, S.; Gruber, P.A.; Handge, U.A.; Spolenak, R. In situ studies on the cohesive properties of α- and β-Ta layers on polyimide substrates. Acta Mater. 2011, 59, 5881–5892. [Google Scholar] [CrossRef]
- Xiang, Y.; Li, T.; Suo, Z.; Vlassak, J.J. High ductility of a metal film adherent on a polymer substrate. Appl. Phys. Lett. 2005, 87, 161910. [Google Scholar] [CrossRef]
- Li, C.H.; Dedoncker, R.; Li, L.W.; Sedghgooya, F.; Zighem, F.; Ji, V.; Depla, D.; Djemia, P.; Faurie, D. Mechanical properties of CoCrCuFeNi multi-principal element alloy thin films on Kapton substrates. Surf. Coat. Technol. 2020, 402, 126474. [Google Scholar] [CrossRef]
- Tian, B.; Yu, Q.; Zhang, Z.; Du, Z.; Ren, W.; Shi, P.; Jiang, Z. Effect of magnetron sputtering parameters on adhesion properties of tungsten-rhenium thin film thermocouples. Ceram. Int. 2018, 44, S15–S18. [Google Scholar] [CrossRef]
- Tanaka, K.; Stossel, M.; Jiang, H.; Arola, D.; Wang, J. Engineering the Interface: Effects of Interfacial Adhesion and Substrate Thickness on the Ductility of Polymer-supported Metal Films. Exp. Mech. 2022, 62, 49–58. [Google Scholar] [CrossRef]
- Xi, Y.; Gao, K.; Pang, X.; Yang, H.; Xiong, X.; Li, H.; Volinsky, A.A. Film thickness effect on texture and residual stress sign transition in sputtered TiN thin films. Ceram. Int. 2017, 43, 11992–11997. [Google Scholar] [CrossRef]
- Pradeep, K.G.; Tasan, C.C.; Yao, M.J.; Deng, Y.; Springer, H.; Raabe, D. Non-equiatomic high entropy alloys: Approach towards rapid alloy screening and property-oriented design. Mater. Sci. Eng. A 2015, 648, 183–192. [Google Scholar] [CrossRef]
- Wilson, P.; Field, R.; Kaufman, M. The use of diffusion multiples to examine the compositional dependence of phase stability and hardness of the Co-Cr-Fe-Mn-Ni high entropy alloy system. Intermetallics 2016, 75, 15–24. [Google Scholar] [CrossRef]
- Balar, N.; O’Connor, B.T. Correlating Crack Onset Strain and Cohesive Fracture Energy in Polymer Semiconductor Films. Macromolecules 2017, 50, 8611–8618. [Google Scholar] [CrossRef]
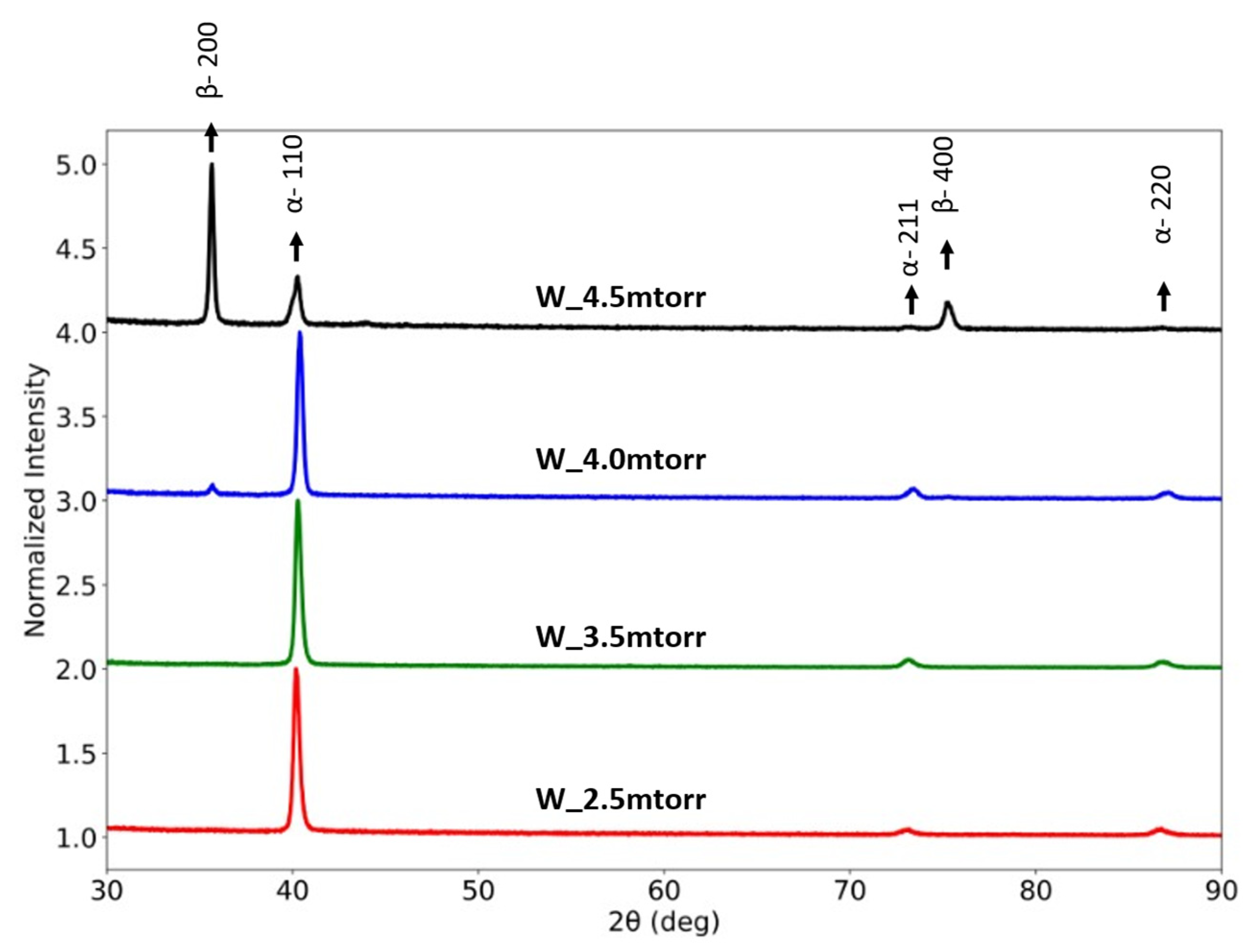
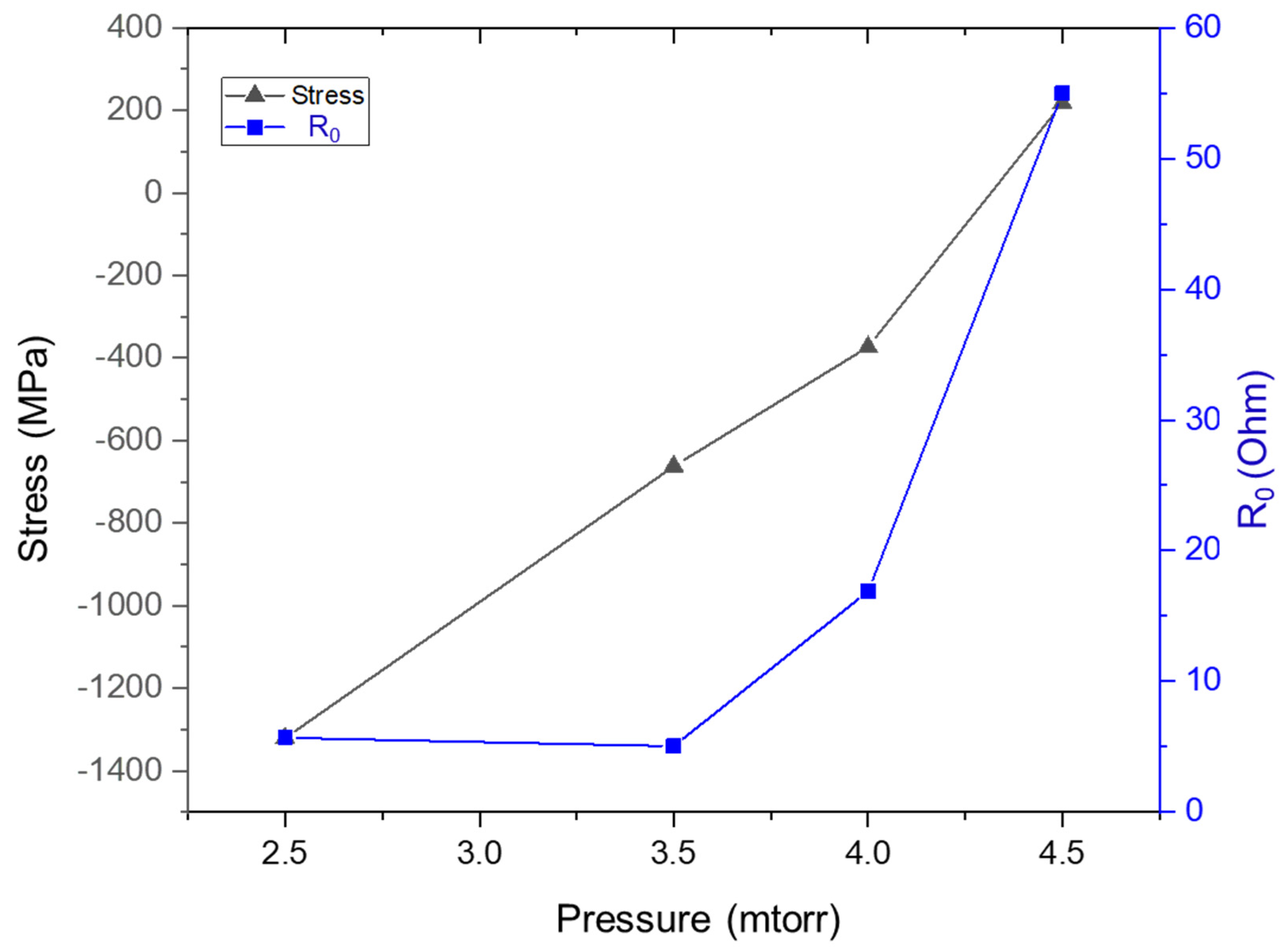
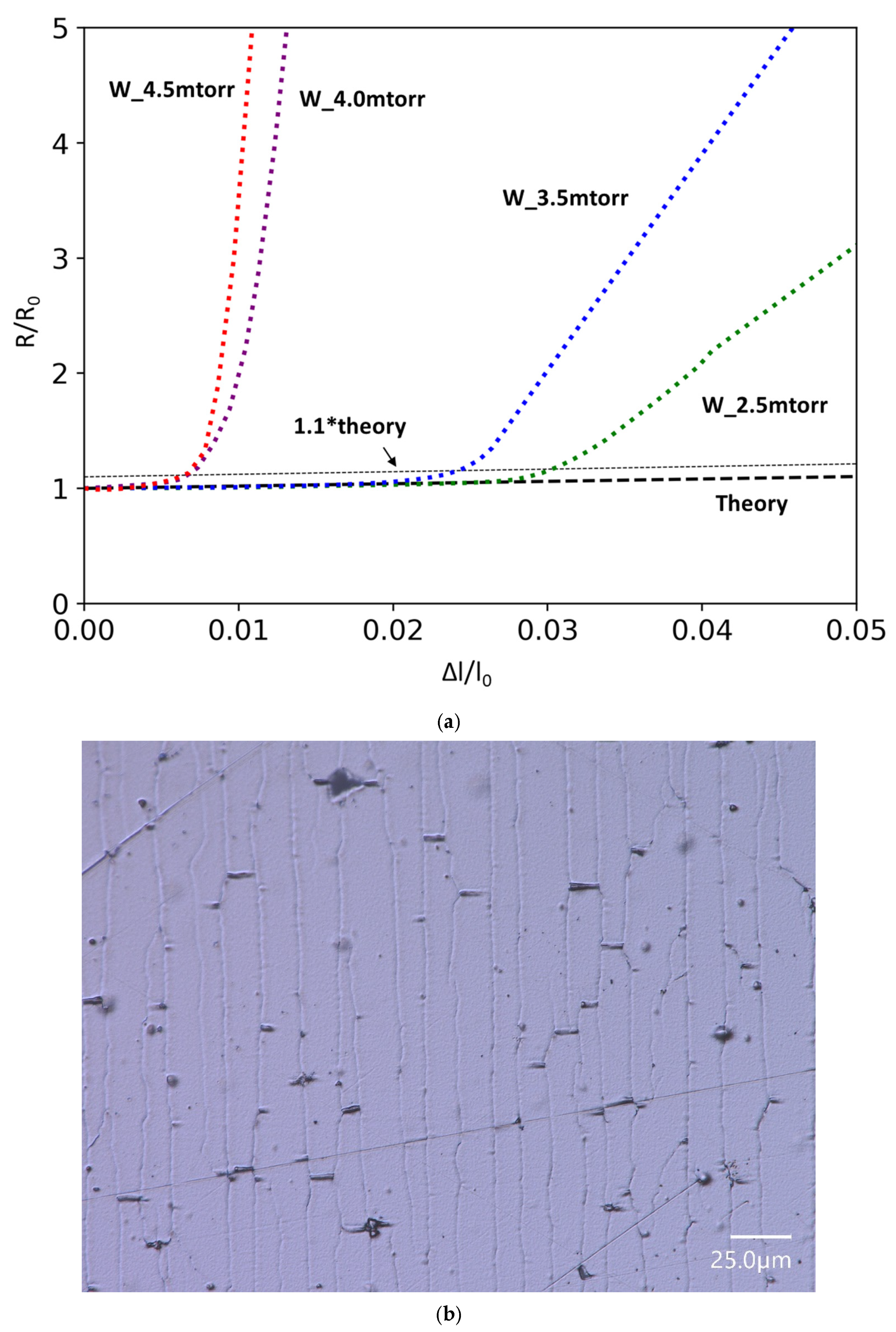
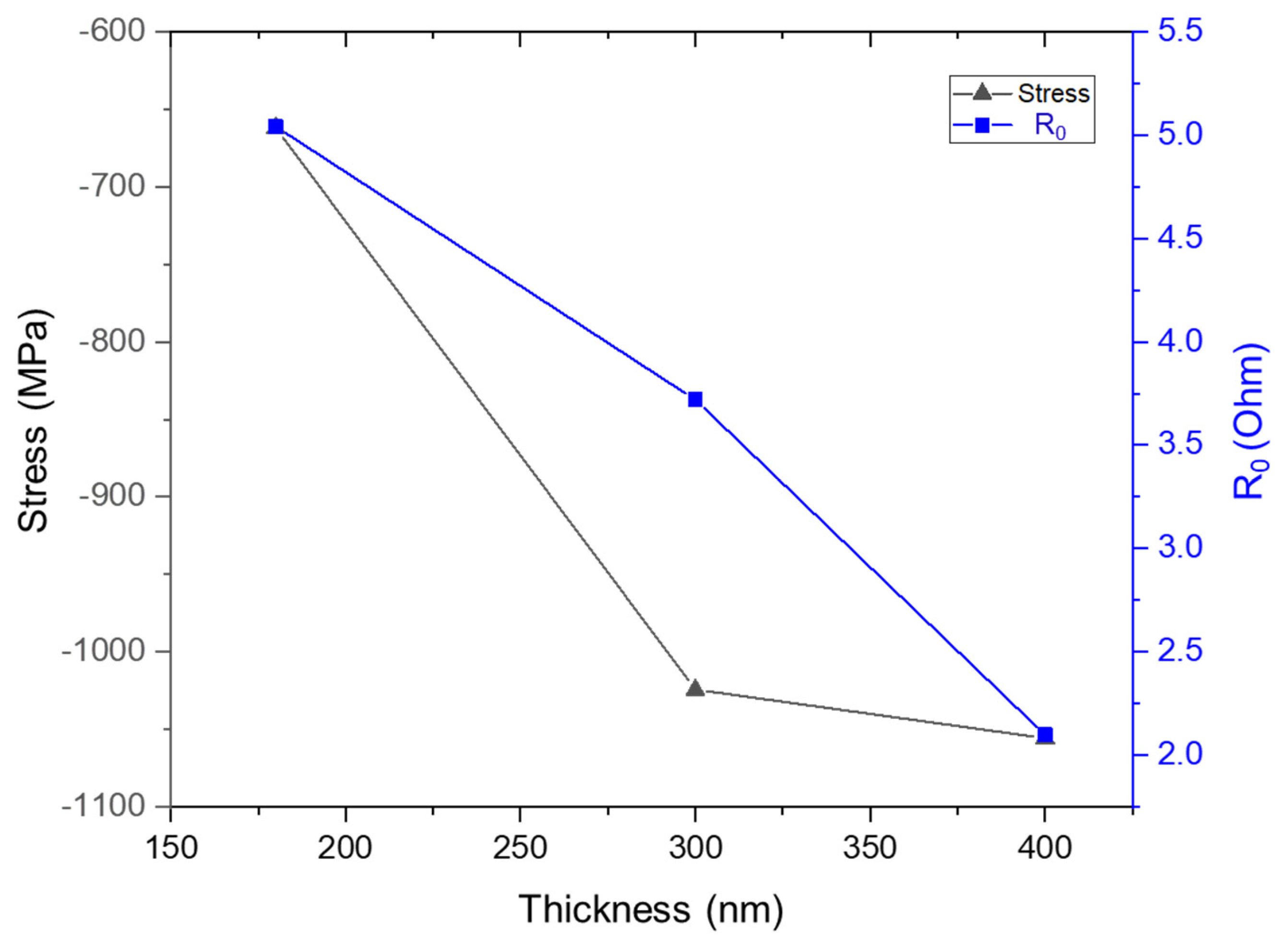
| Material ID | Pressure (mtorr) | Thickness (nm) | Stress (MPa) | R0 (Ω) | COS (Δl/l0 × 100) % | Crystallite Size (nm) |
|---|---|---|---|---|---|---|
| W_2.5mtorr | 2.5 (0.33 Pa) | 180 | −1304 ± 35 | 5.68 | 2.70 | 25 |
| W_3.5mtorr/ W_180nm * | 3.5 (0.47 Pa) | 180 | −670 ± 20 | 5.04 | 2.20 | 26 |
| W_4.0mtorr | 4.0 (0.53 Pa) | 180 | −360 ± 13 | 16.9 | 0.72 | 27 |
| W_4.5mtorr | 4.5 (0.60 Pa) | 180 | 211 ± 12 | ~55 | 0.66 | 18 (α) 42 (β) |
| W_300nm | 3.5 (0.47 Pa) | 300 | −1024 ± 14 | 3.72 | 1.87 | 33 |
| W_400nm | 3.5 (0.47 Pa) | 400 | −1055 ± 29 | 2.1 | 1.69 | 29 |
| Material | Pressure (mtorr) | Thickness (nm) | Stress (MPa) | Phase | Crystallite Size (nm) | COS (Δl/l0 × 100) % | R0 (Ω) | Bulk Resistivity ** (×10−8 Ω-m) |
|---|---|---|---|---|---|---|---|---|
| W | 3.5 (0.47 Pa) | 180 | −670 ± 20 | α | 26 | 2.20 | 5.04 | 5.3 |
| Ta | 3.5 (0.47 Pa) | 180 | −641 ± 7 | α + β | 30(β) | 2.63 | 33.75 | 13.1 |
| Mo * | 2.5 (0.33 Pa) | 180 | −677 ± 22 | α | 24 | 1.61 | 6.30 | 5.3 |
| Nb | 1.8 (0.24 Pa) | 180 | −650 ± 32 | α | 17 | 6.37 | 8.77 | 14.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuhser, T.B.N.; Balk, T.J. Thin Film Fragmentation Testing: A Refined Screening Method for Estimating Relative Intrinsic Ductility of Refractory Metals. Metals 2025, 15, 1144. https://doi.org/10.3390/met15101144
Tuhser TBN, Balk TJ. Thin Film Fragmentation Testing: A Refined Screening Method for Estimating Relative Intrinsic Ductility of Refractory Metals. Metals. 2025; 15(10):1144. https://doi.org/10.3390/met15101144
Chicago/Turabian StyleTuhser, Taohid Bin Nur, and Thomas John Balk. 2025. "Thin Film Fragmentation Testing: A Refined Screening Method for Estimating Relative Intrinsic Ductility of Refractory Metals" Metals 15, no. 10: 1144. https://doi.org/10.3390/met15101144
APA StyleTuhser, T. B. N., & Balk, T. J. (2025). Thin Film Fragmentation Testing: A Refined Screening Method for Estimating Relative Intrinsic Ductility of Refractory Metals. Metals, 15(10), 1144. https://doi.org/10.3390/met15101144






