Multi-Dimensional Uniform Cooling Process for Ship Plate Steel Continuous Casting

Abstract

In slab continuous casting, achieving uniform cooling in the secondary cooling zone is essential for ensuring both surface integrity and internal quality. To optimize the process for ship plate steel, a solidification heat transfer model was developed, incorporating radiation, water film evaporation, spray impingement, and roll contact. The influence of secondary cooling water flow on slab temperature distribution was systematically investigated from multiple perspectives. The results show that a weak cooling strategy is crucial for maintaining higher surface temperatures and aligning the solidification endpoint with the soft reduction zone. Along the casting direction, a “strong-to-weak” cooling pattern effectively prevents abrupt temperature fluctuations, while reducing the inner-to-outer arc water ratio from 1.0 to 0.74 mitigates transverse thermal gradients. In addition, shutting off selected nozzles in the later stage of secondary cooling at medium and low casting speeds increases the slab corner temperature in the straightening zone by approximately 50 °C, thereby avoiding brittle temperature ranges. Overall, the proposed multi-dimensional uniform cooling strategy reduces temperature fluctuations and significantly improves slab quality, demonstrating strong potential for industrial application.

1. Introduction

Secondary cooling is a crucial stage that directly influences slab quality and has therefore been extensively studied worldwide. To ensure high slab quality, it is generally desirable for the slab to undergo uniform cooling in the secondary cooling zone. Insufficient uniformity often leads to defects such as cracks and segregation [1,2,3,4,5]. However, uniform cooling is not a one-dimensional process but is affected by multiple factors in different directions. For example, cooling must be considered along both the casting direction and slab width [6,7,8,9]. Poor uniformity in the width direction can readily cause corner cracks [10,11], whereas inadequate uniformity in the thickness and casting directions may allow surface cracks to propagate into internal cracks [12,13,14]. These challenges impose stringent requirements on heat transfer during solidification in secondary cooling, thereby necessitating a multi-dimensional approach to ensure uniform cooling and high-quality slabs.

In recent years, several scholars have investigated slab uniform cooling from different dimensional perspectives. Along the slab width direction, Yanyan Bi et al. [15] analyzed the surface temperature distribution of round billets in the secondary cooling zone and proposed a new nozzle arrangement, thereby eliminating the adverse effects of nonuniform surface temperature on slab quality. Similarly, C. Ji et al. [16] constructed a solidification heat transfer model for wide-thick slabs, optimized the nozzle layout, and demonstrated that the improved spray pattern reduced corner crack defects. To ensure slab surface temperatures remain above the brittle range during straightening, Y. J. Lu et al. [3] optimized the secondary cooling system by adopting an asymmetric nozzle arrangement, which significantly lowered the incidence of corner cracks. Min Jiang et al. [17] redistributed the water flow among transverse nozzles by reducing flow from central nozzles and increasing flow from edge nozzles, enabling synchronous solidification, enhancing the soft reduction effect, and reducing porosity defects. In addition, Yanshen Han [18] optimized nozzle arrangement to improve transverse water flow distribution, thereby increasing corner temperature, ensuring more uniform cooling across the slab width, and enhancing corner quality.

From the casting direction, Qiang Liu et al. [19] investigated secondary cooling water distribution in beam blanks, focusing on the effects of specific water flow, water Flow Rate in Each Secondary Cooling Zone, and inner-to-outer arc water ratios on the slab temperature field. Hongming Wang et al. [20] showed that directly reducing cooling water in each secondary cooling zone, as well as shutting down or lowering water flow at the zone end, effectively increased slab surface temperature. This not only improved slab quality but also enabled hot-slab continuous casting–rolling production. Josef Stetina et al. [21] demonstrated that replacing large-flow nozzles with smaller ones reduced nozzle flow while maintaining cooling intensity, thereby increasing slab surface temperature at the straightening point and ensuring product quality. Xiaogang Yang et al. [22] applied a similar approach by reducing water flow in selected zones, which raised surface temperature at the straightening point. Industrial trials confirmed that this optimization effectively decreased the incidence of corner cracks. Jingbo Yang et al. [10] further optimized water distribution in certain zones to control slab surface temperature in the straightening region, which refined overall grain size uniformity, improved corner ductility, and enhanced corner quality.

Nevertheless, comprehensive studies on multi-dimensional uniform cooling of slabs in the secondary cooling zone remain limited. Most existing research has focused on single-dimensional effects, without fully considering the combined influence of different cooling directions on slab surface temperature.

In this study, a slab continuous caster from a steel plant was selected as the research object, and a two-dimensional solidification heat transfer model was developed using the finite difference method. Through numerical simulations, the solidification heat transfer process of ship plate steel was investigated from multiple dimensional perspectives, leading to the development of a secondary cooling model. This model ensures uniform cooling along the slab width, thickness, and casting directions, effectively controls surface temperature, and thereby guarantees slab quality.

2. Mathematical Model of Slab Solidification Heat Transfer

2.1. Governing Equations for Heat Transfer

Considering the high specific heat capacity and low thermal conductivity of steel, the heat transfer along the casting direction is negligible. Therefore, the present model was constructed using the slice method [23]. The present model was constructed based on the slice method. Since the two halves of the slab, divided along the centerline of the wide face, are symmetric with respect to both temperature field and cooling conditions, only half of the slab was considered in the simulations.

The following simplifications were adopted in the model: the heat transfer process in the secondary cooling zone was simplified to two-dimensional heat transfer; dimensional changes caused by shrinkage during solidification were neglected; the solidification heat transfer process was treated as a steady-state process; the effect of forced convection was incorporated by modifying the effective thermal conductivity of molten steel; the transverse distribution of water flux was represented by its average value, neglecting the influence of nozzle arrangement on lateral cooling uniformity; and the latent heat of solidification was averaged into the specific heat of the mushy zone. An equivalent specific heat C_e was introduced to replace the actual specific heat C, expressed as: C_e = C − ρ·∂z/∂τ, where f_s is the solid fraction in the mushy zone.

Based on the relationship v = ∂z/∂τ and the aforementioned assumptions, the fundamental differential equation of slab solidification heat transfer during continuous casting was derived [11,18,24,25]:

$$C_e\rho {\displaystyle \frac{\partial t}{\partial \tau }}={\displaystyle \frac{\partial }{\partial x}}({\lambda }_e{\displaystyle \frac{\partial t}{\partial x}})+{\displaystyle \frac{\partial }{\partial y}}({\lambda }_e{\displaystyle \frac{\partial t}{\partial y}})$$

(1)

where C_e is the equivalent specific heat (J/kg·°C); ρ is the density of molten steel (kg/m³); t is the temperature (°C); τ is the time (s); and λ is the thermal conductivity (W/(m·K)).

In the slab continuous casting process, the geometry is relatively regular, which makes the finite difference method (FDM) well suited for discretization with structured grids. FDM ensures numerical stability while providing efficient computation, enabling rapid solutions that meet the requirements of multi-condition simulations in industrial practice. In addition, FDM has been widely applied and proven in the field of heat transfer modeling for continuous casting, making it more consistent with the modeling objectives and practical needs of this study. Therefore, the finite difference method was employed to solve the governing heat transfer equations in this work.

2.2. Selection of Spatial and Temporal Step Sizes

In the calculation of the finite difference equations, the spatial and temporal step sizes must satisfy the stability condition of the equations:

$${\displaystyle \frac{\mathsf{\Delta }\tau }{\rho C{(\mathsf{\Delta }x)}^2}}\left({\lambda }_1+{\lambda }_3+2h\mathsf{\Delta }x\right)\le {\displaystyle \frac{1}{2}}$$

(2)

The selection of the time step is mainly based on two considerations. First, given the historically limited computational resources, the time step should be appropriately controlled to improve calculation efficiency. Second, to ensure computational accuracy, the time step must satisfy the stability requirements of the finite difference scheme. A smaller spatial step requires a correspondingly smaller time step. For a given spatial step, convergence can be assessed through simulation to determine a reasonable time step. In addition, the time step varies with casting speed to ensure accuracy and comparability of results under different casting conditions. In this study, the spatial steps were set as Δx = 10 mm, Δy = 5 mm.

2.3. Heat Transfer Boundary Conditions

During continuous casting, molten steel passes through the mold and the secondary cooling zone, where the heat transfer boundary conditions are relatively complex. In the secondary cooling zone, cooling water does not fully cover the entire slab, so heat transfer between the slab and the environment occurs partially through radiation. Direct water impingement on the slab surface constitutes the primary heat transfer mode in this zone, also referred to as water impact cooling. The sprayed water does not evaporate immediately; part of it accumulates on the inner arc of the slab, while water on the outer arc flows off the surface under gravity. Heat transfer also occurs through direct contact between the slab and the rolls, which depends on the slab surface temperature, casting speed, and contact area. Therefore, the slab in the secondary cooling zone is mainly subjected to four heat transfer mechanisms [6]: radiation, water film evaporation, water impingement, and roll contact. In the model, the entire slab surface between any two adjacent pairs of rolls is divided along the casting direction into four corresponding cooling zones: the radiation zone, the water film evaporation zone, the water impingement zone, and the roll contact zone [26]. A schematic diagram of the four heat transfer modes is shown in Figure 1.

In establishing the heat transfer boundary conditions for the mold and secondary cooling zone, numerous previous studies and practical applications were referenced, and the conditions were ultimately verified and determined based on the specific characteristics of the study object.

2.3.1. Mold Cooling Heat Transfer

Assuming that the temperature at the meniscus is equal to the pouring temperature, the boundary conditions for heat transfer in the mold are specified as follows [27,28,29]:

$$q_m=2392560-263156\sqrt{\tau } \mathrm{W}/{\mathrm{m}}^2$$

(3)

where τ is the residence time of a slab section in the mold (s), and qm is the heat flux density in the mold (W/m²).

Considering that the slab corners are most significantly affected by air gaps and the differences in cooling conditions between the wide and narrow faces of the mold, the heat flux at corner nodes was set to 0.55 times the average heat flux of the corresponding surface [10].

$$q_{corner}=0.55q_{side} \mathrm{W}/{\mathrm{m}}^2$$

(4)

Along the wide face, the heat flux density gradually increases from 55% at the corner to 100% at a distance of 50 mm from the corner or 1/8 of the slab width (whichever is smaller); the same approach is applied to the narrow face. This setting better reflects the continuity of air gap formation and ensures a smooth transition of heat flux.

2.3.2. Radiation Heat Transfer

The radiation heat transfer mode is located between the roll contact and water impingement zones, and the radiation heat flux is expressed as [30,31,32]:

$$q_{\mathrm{rad}}=\epsilon \delta \left[{(Tw+273)}^4-{(T_0+273)}^4\right] \mathrm{W}/{\mathrm{m}}^2$$

(5)

where ε is the emissivity of the slab surface (0.8); δ is the Stefan–Boltzmann constant, 5.67 × 10⁻⁸ W/m²·K⁴; and T₀ is the ambient temperature (°C).

2.3.3. Water Evaporation Heat Transfer

The heat transfer due to water film evaporation between adjacent rolls is considered as a multiple of the radiation heat flux between the same rolls:

$$q_g=b\cdot q_{rad} \mathrm{W}/{\mathrm{m}}^2$$

(6)

where q_g is the heat flux due to water film evaporation between adjacent rolls, typically treated as a constant; q_rad is the total radiation heat flux between adjacent rolls; and b is the proportional coefficient, with b = 4 in the first secondary cooling zone and b = 3.5~1 in the subsequent zones.

The above formula assumes that the heat flux from water film evaporation is the same for both the inner and outer arcs. However, in actual production, the curved geometry of the caster causes the heat flux to differ between the inner and outer arcs. Sprayed water on the inner arc tends to flow along the slab and accumulate at the rolls, while water on the outer arc detaches from the slab under gravity. Consequently, the heat flux from water film evaporation is higher on the inner arc than on the outer arc. Due to the complexity of this process and the limited research available, the same formula is applied to both arcs in the simulation, which results in a slightly larger temperature difference between the inner and outer arcs than observed in practice.

2.3.4. Spray Water Heat Transfer

Water nozzles are used for the foot roll section and its sides, while air–water nozzles are applied in the remaining secondary cooling zones. Since the heat transfer efficiencies of water nozzles and air–water nozzles differ, different boundary conditions are applied accordingly [11].

(a)

Secondary Cooling Zone 1 (Water Spray Nozzles)

$$h=712.425\times T{w}^{-0.13}\times W^{-0.55}$$

(7)

(b)

Secondary Cooling Zones 2–10 (Air-Mist Nozzles)

$$h=1176.475\times T{w}^{-0.11}\times W^{-0.65}$$

(8)

where W is the water flow density (L/m²·S) and Tw is the slab surface temperature (°C).

2.3.5. Roll Contact Heat Transfer

In the roll contact zone, heat transfer primarily includes conduction from the slab surface to the rolls during roll rotation and radiation from the high-temperature slab surface to the rolls. The roll contact heat flux is expressed as [15]:

$$q_{roll}=1919T{w}^{-0.76}{V}^{-0.20}{(2\alpha )}^{-0.17} \mathrm{W}/{\mathrm{m}}^2$$

(9)

$$2\alpha =0.3116+4.6105Z$$

(10)

where Tw is the slab surface temperature (°C); V is the casting speed (m/min); 2α is the contact angle between the roll and the slab (°); and Z is the distance from the meniscus (m). When Z exceeds 2 m, it is taken as 2 m and kept constant.

The longitudinal length of the roll contact zone along the slab is related to the roll radius [26]. For the foot roll section and the upper part of the zero section, the length is given by

$$U=1.047(2\alpha )\cdot 0.001 \mathrm{m}$$

(11)

For the lower part of the zero section, when the distance to the mold meniscus is 4.5 m:

$$U=1.221(2\alpha )\cdot 0.001 \mathrm{m}$$

(12)

When the distance from the mold meniscus Z exceeds 4.5 m, the value given by Equation (12) is kept constant.

2.4. Model Validation

To verify the accuracy of the model and boundary conditions, nail-shooting experiments and temperature measurements were conducted for validation.

Nail-shooting experimental procedure: Nail-shooting was carried out at a position 23 m below the meniscus, located at one-quarter of the slab width on the right side of the wide face. Experiments were conducted at casting speeds of 1.1, 1.2, and 1.3 m/min, respectively. The shell thickness at the nail-shooting location was obtained, from which the solidification coefficient was calculated and subsequently used to estimate the final solidification end point.

The solidification end point obtained from the nail-shooting test was compared with the simulation results, as shown in

Table 1. Comparison of solidification end point between nail-shooting experiment and simulation.

Casting Speed (m/min)	1.1	1.2	1.3
Solidification end point from nail-shooting (m)	24.2	24.9	24.8
Solidification end point from simulation (m)	23.8	26.2	28.6
Accuracy (%)	99.3	97.4	99.6

.

It can be seen from Table 1 that the simulated solidification end point agrees well with the nail-shooting results, with an overall accuracy of 98.8%. This indicates that the model can realistically reflect the solidification end point of slabs during the continuous casting process.

Slab surface temperature measurement scheme: Surface temperature measurements of characteristic points on the slab were performed at 15.6, 17.8, and 20 m below the meniscus. Considering measurement conditions, three characteristic positions were selected: the slab corner, the slab side-face center, and one-eighth of the slab width on the wide face. During the measurement, regions with iron oxide scale were avoided, and to reduce the influence of water vapor on the readings, the maximum temperature recorded during the experiment was adopted as the measured value.

For the temperature validation, the measured temperature data were compared with the simulated values, as shown in

Table 2. Comparison of measured and simulated surface temperatures at different positions.

Casting Speed (m/min)		1.2
Distance from meniscus (mm)		15,610	17,775	19,959
Measured temperature (°C)	Wide face 1/8	947.0	929.0	955.0
	Side center	990.0	967.0	919.0
	Corner	921.0	902.0	865.0
Simulated temperature (°C)	Wide face 1/8	934.0	965.0	966.0
	Side center	994.0	963.0	932.0
	Corner	913.0	891.0	872.0
Accuracy (%)		99.1	98.2	98.9

.

As shown in Table 2, the simulated surface temperatures of the slab are close to the measured values, with an overall accuracy of 98.7%. This demonstrates that the model can realistically reproduce the surface temperature evolution of slabs during the continuous casting process.

3. Structural Parameters of the Slab Continuous Caster

A slab continuous caster from a steel plant was selected as the research object. The caster is a straight-arc type continuous bending machine with a main radius of 9500 mm and a mechanical length of 37,961.1 mm. It can produce slabs with widths ranging from 1300 to 1930 mm and thicknesses of 230 or 250 mm. The caster is divided into ten secondary cooling zones. Secondary cooling zones 1 to 4 correspond to the vertical section. The bending start point, located 4219 mm from the meniscus, is in secondary cooling zone 5, while the straightening start point, 16,822.1 mm from the meniscus, lies in secondary cooling zones 8. Secondary cooling zones 9 to 10 correspond to the horizontal section. The lengths of the secondary cooling zones and their distances from the meniscus are listed in

Table 3. Lengths of the Secondary Cooling Zones.

Secondary Cooling Zones	Secondary Cooling Zone Length (mm)	Distance from the Last Roll to the Meniscus (mm)
I	163	1063
II	720	1783
III	1083	2866
IV	1582	4448
V	1925	6373
VI	3860	10,233
VII	6271	16,504
VIII	4377.1	20,881.1
IX	8540	29,421.1
X	8540	37,961.1

. The positions of the secondary cooling zones are shown in Figure 2.

The slab continuous caster is equipped with a light reduction process, which can be applied in secondary cooling zones 7 to 10, corresponding to distances of 10,528 mm to 37,961.1 mm from the meniscus. Light reduction is activated when the slab solid fraction is between 0.3 and 0.8, and the number of segments undergoing reduction varies with casting speed. An increase in casting speed extends the length of the slab within the 0.3–0.8 solid fraction range, thereby increasing the number of segments subjected to light reduction. In practice, 2–4 secondary cooling segments are typically reduced, with reduction amounts set at 3 mm or 5 mm depending on the steel grade. During light reduction, the rolls in the affected segments can either be adjusted to separate or lifted as needed.

4. Simulation Analysis of Multi-Dimensional Uniform Cooling Process

The secondary cooling model used in this study is a static control model, in which the water flow in each circuit of the secondary cooling zones follows a quadratic relationship with the casting speed. This model is also widely employed in many industrial applications [33].

$$Q_i=K_i(a_i+b_{i}v+c_i{v}^2)$$

(13)

where Q_i is the water flow rate in the i-th secondary cooling circuit (L/min); v is the casting speed (m/min); a_i, b_i, c_i are constant parameters; and K_i is a coefficient, generally ranging from 0.9 to 1.1, with a default value of 1.0.

By considering the slab’s uniform cooling from multiple dimensions during the secondary cooling process, heat transfer simulations of the continuous casting process were performed to determine the water flow rates in each secondary cooling zone. Using the method of least squares, the relationship between water flow in each circuit and casting speed was fitted to determine the parameters a_i, b_i, c_i. The multi-dimensional analysis of uniform cooling in the secondary cooling zones resulted in a model capable of ensuring high slab quality.

The simulation of the multi-dimensional uniform cooling process was carried out through the following five aspects: (1) the water-to-slab ratio in secondary cooling; (2) variation curves of cooling water flow in each secondary cooling zone with casting speed; (3) the ratio of inner-arc to outer-arc cooling water; (4) the distribution of cooling water along the casting direction; and (5) the shutdown strategy of cooling water at medium and low casting speeds.

Simulations were conducted using Q235B steel with a superheat of 25 °C and a slab cross-section of 1820 × 230 mm at casting speeds of 0.8, 1.2, 1.6, and 2.0 m/min. The resulting water flow model is applicable for casting speeds in the range of 0.8–2.0 m/min.

4.1. Specific Water Flow

Different steel grades require varying cooling intensities, and the specific water flow directly affects both the cooling intensity and the slab’s surface temperature as well as the solidification endpoint. Based on extensive research experience, a relatively weak secondary cooling is applied for ship plate steel to maintain a high slab surface temperature during continuous casting. At the same time, to prevent casting accidents such as steel leakage in the initial stage of secondary cooling, a higher water flow is set in secondary cooling zone 1. Considering a large number of simulation results and ensuring that the solidification endpoint matches the light reduction range of the slab at different casting speeds, the specific water flow for four casting speeds were determined. The specific water flow and solidification endpoints for these four speeds are listed in

Table 4. Specific Water Flow and Solidification End Point Across Different Casting Speeds.

Casting Speeds (m/min)	Specific Water Flow (L/kg)	Solidification End Position (m)	fs = 0.3~0.9 (Zone)	Solidification Fraction
0.8	0.27	13.4	VI~VII (10.3~13.2 m)	28.1
1.2	0.39	20.9	VII~VIII (16.5~20.6 m)	27.56
1.6	0.48	27.9	IX (21.9~27.5 m)	27.54
2.0	0.55	34.6	IX~X (27.3~34.1 m)	27.65

.

From Table 4, it can be seen that at a casting speed of 0.8 m/min, a two-stage light reduction mode can be implemented; at 1.2 and 1.6 m/min, a three-stage light reduction mode is achievable; and at 2.0 m/min, a four-stage light reduction mode can be applied. The solidification endpoints align well with the light reduction range of the caster, and the reduction amount generally meets the requirements, which is beneficial for the central quality of the slab.

Table 5. Average Center Temperature on the Inner-Curve Wide Face of Slabs in Each Secondary Cooling Zone at Different Casting Speeds (°C).

Casting Speeds (m/min)	0.8	1.2	1.6	2.0
I	1077.5	1070.9	1080.9	1088.3
II	1011.2	994.3	989.9	989.5
III	989.5	974.5	969.3	969.2
IV	982.0	975.5	972.6	971.9
V	965.9	959.9	956.6	954.7
VI	965.2	957.9	954.3	949.3
VII	976.1	967.5	960.2	953.7
VIII	971.7	985.9	974.8	964.5
IX	907.9	999.8	985.7	972.3
X	822.8	951.6	996.3	977.9
Straightening Start Point	975.8	988.7	979.4	970.7

lists the average inner-arc wide-face temperatures of the slab in each secondary cooling zone, along with the corresponding specific water flow and the slab surface temperatures at the straightening start point, for different casting speeds.

From Table 5, it can be seen that under the current water-to-slab ratio conditions, the inner-arc wide-face center temperature of the slab at the straightening start point exceeds 900 °C. This relatively high temperature allows the slab to avoid the brittle range of ship plate steel [11], ensuring that the slab surface temperature does not fall into the brittle zone during straightening and thereby improving surface quality.

4.2. Cooling Heat Transfer in the Casting Direction

According to metallurgical criteria, the slab surface center temperature along the casting direction must remain stable, with temperature fluctuations minimized. To ensure slab quality, the maximum surface cooling rate is strictly limited to below 100 °C/m, guaranteeing uniform solidification and preventing internal cracks or surface defects caused by sudden temperature changes.

In secondary cooling zones 1 and 2, the slab shell is relatively thin upon exiting the mold, requiring higher cooling intensity to avoid steel leakage. Therefore, larger water flows are applied in zones 1 and 2. During the secondary cooling process, the slab shell gradually thickens along the casting direction. If the cooling intensity in each zone does not gradually decrease along this direction, a large internal temperature gradient may develop, adversely affecting slab quality. To prevent the slab surface temperature from entering the brittle range in the straightening zone, the distribution of cooling water in each secondary cooling zone must be carefully regulated. The cooling intensity in the secondary cooling zones can be represented by the water flow per unit length along the inner arc (i.e., the inner-arc water flow divided by the zone length).

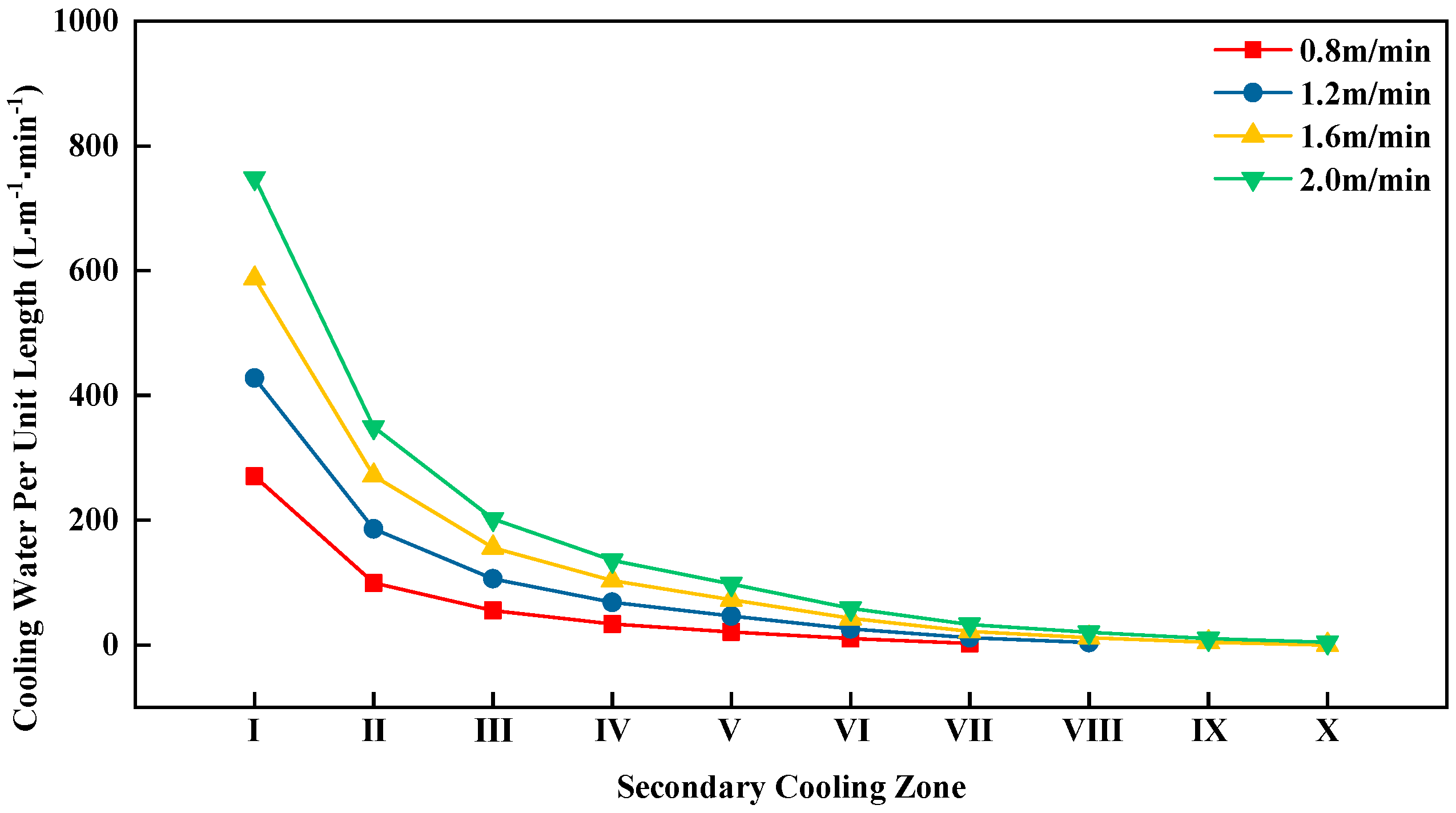
The water flow per unit length in each secondary cooling zone is shown in Figure 3.

From Figure 3, it can be seen that for all four casting speeds, the inner-arc water flow per unit length in the secondary cooling zones gradually decreases along the casting direction.

Table 6. Average Inner-Curve Surface Center Temperature of the Slab and Straightening Start Temperature in Each Secondary Cooling Zone at Different Casting Speeds (°C).

Casting Speeds (m/min)	0.8	1.2	1.6	2.0
I	1077.5	1070.9	1080.9	1088.3
II	1011.2	994.3	989.9	989.5
III	989.5	974.5	969.3	969.2
IV	977.7	969.6	965.8	964.5
V	963.7	956.9	953.0	950.7
VI	962.9	957.6	955.5	951.6
VII	971.9	965.1	959.9	956.3
VIII	969.7	984.2	974.1	964.9
IX	906.9	999.3	985.1	972.1
X	822.1	951.9	996.7	978.9
Straightening start point	972.7	986.6	979.3	972.8

lists the average inner-arc surface center temperatures of the slab in each secondary cooling zone, as well as the slab surface temperatures at the straightening start point, for the different casting speeds.

From Table 6, it can be seen that the inner-arc surface center temperature of the slab at the straightening point is well above 900 °C. This high surface temperature helps the slab avoid the brittle range, ensuring slab quality.

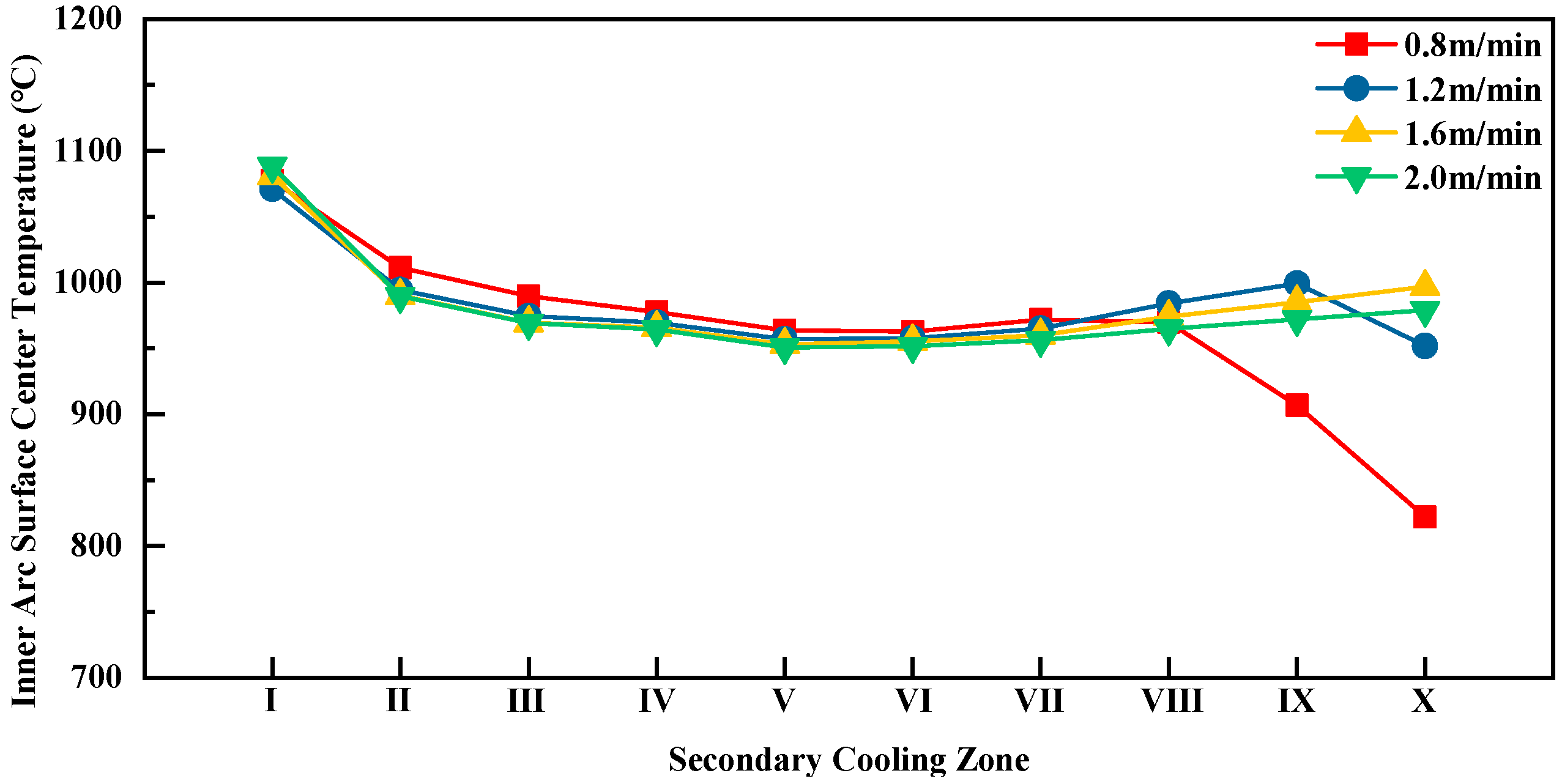
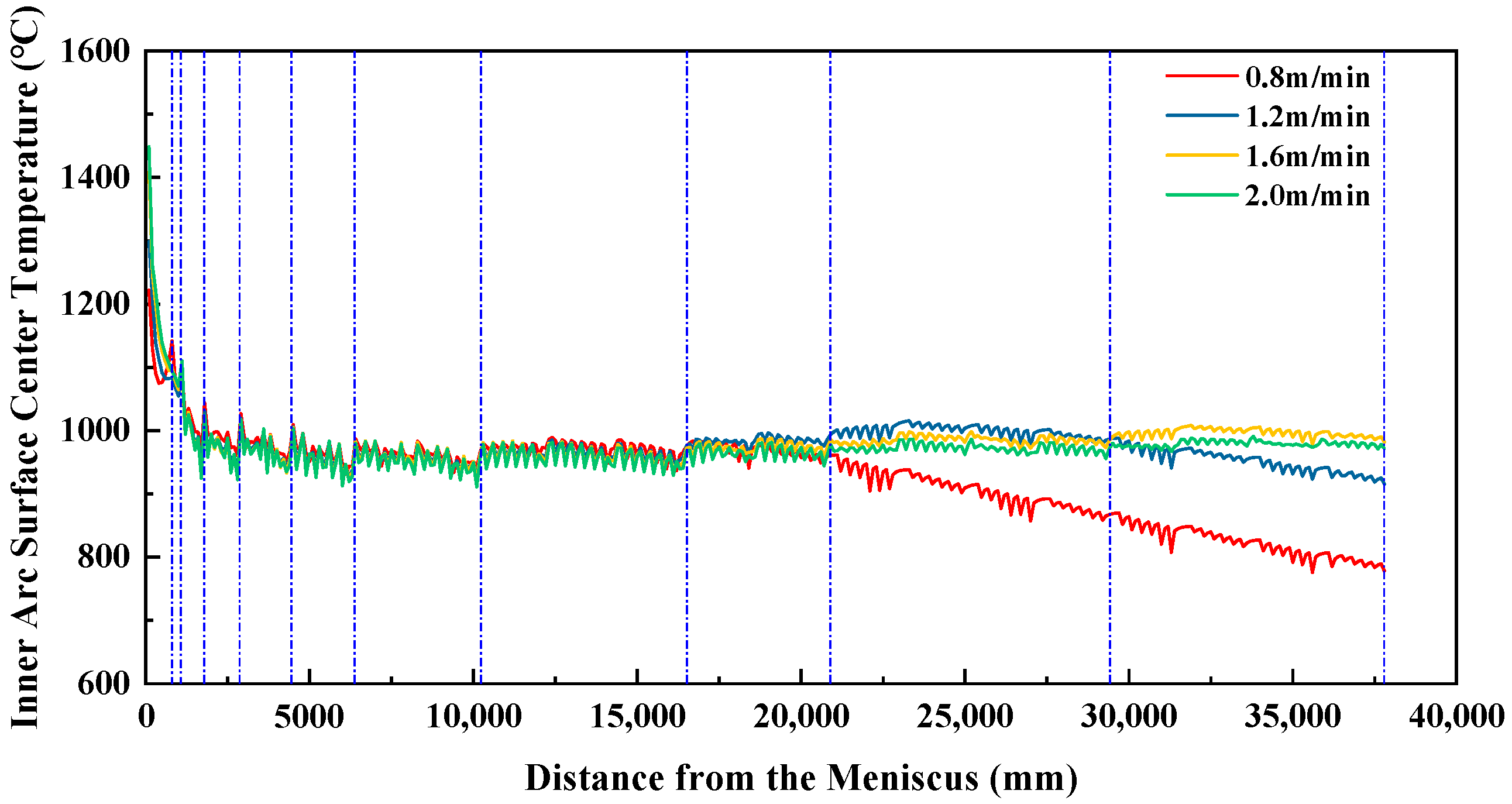
The variation curves of the average inner-arc surface center temperatures along the casting direction for each secondary cooling zone at different casting speeds are shown in Figure 4, while the inner-arc surface center temperature profiles along the casting direction for different casting speeds are presented in Figure 5.

From the above two figures, it can be observed that the cooling rates in each zone conform to the design principles of secondary cooling. In the initial stage of secondary cooling, the inner-arc surface center temperature of the slab drops rapidly, preventing shell breakage. Subsequently, the slab surface temperature decreases more slowly as the shell gradually thickens. In secondary cooling zones 6 to 8, a slight temperature rebound is observed, which helps ensure that the slab surface temperature at the straightening point avoids the low-ductility range.

In secondary cooling zones 9 and 10, there is a significant difference in the inner-arc surface center temperature of the slab at different casting speeds. This is because the solidification endpoint varies with casting speed: at lower speeds, the slab solidifies earlier, releasing latent heat sooner, which results in a lower surface temperature in the later stages of secondary cooling.

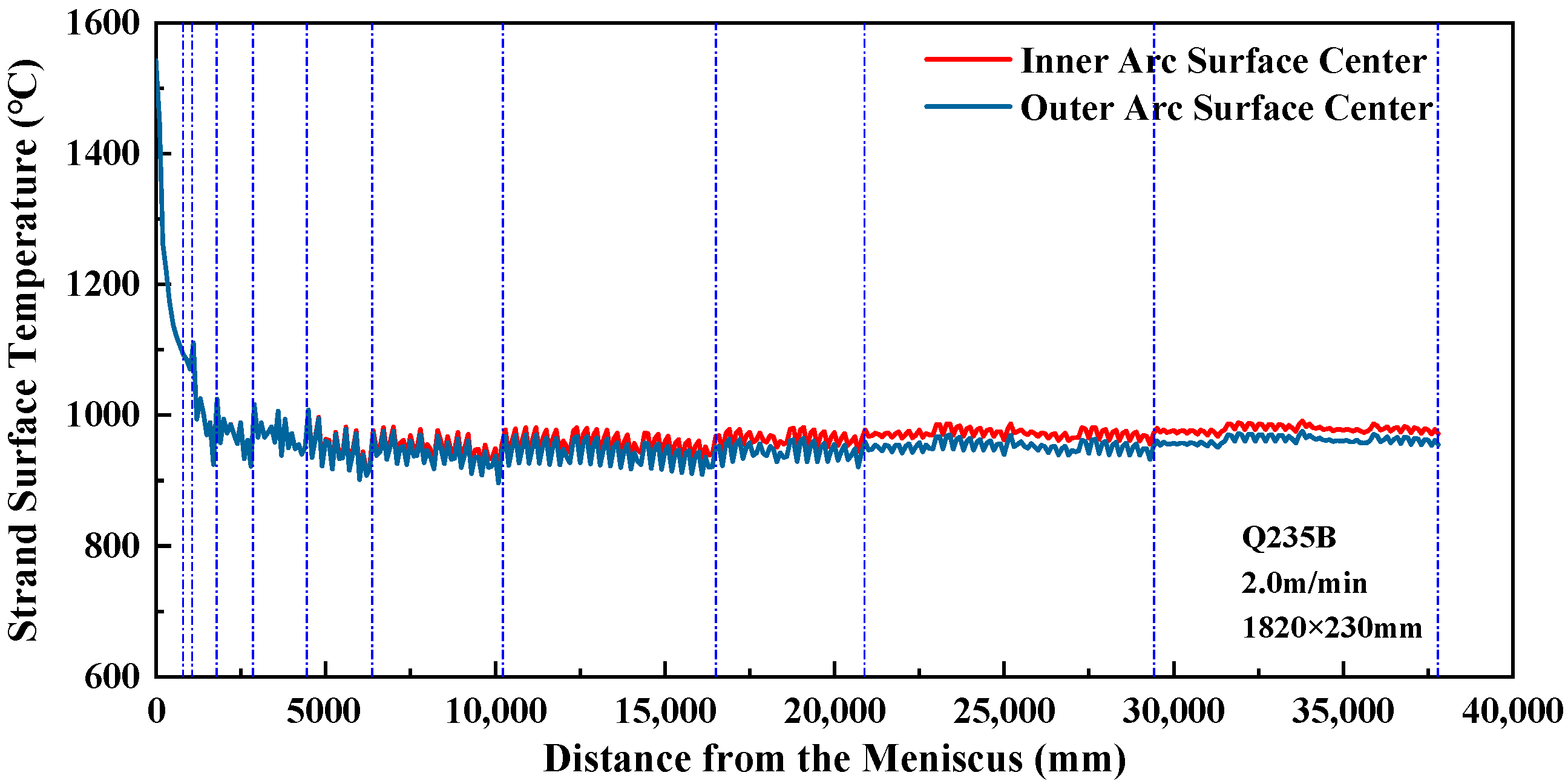
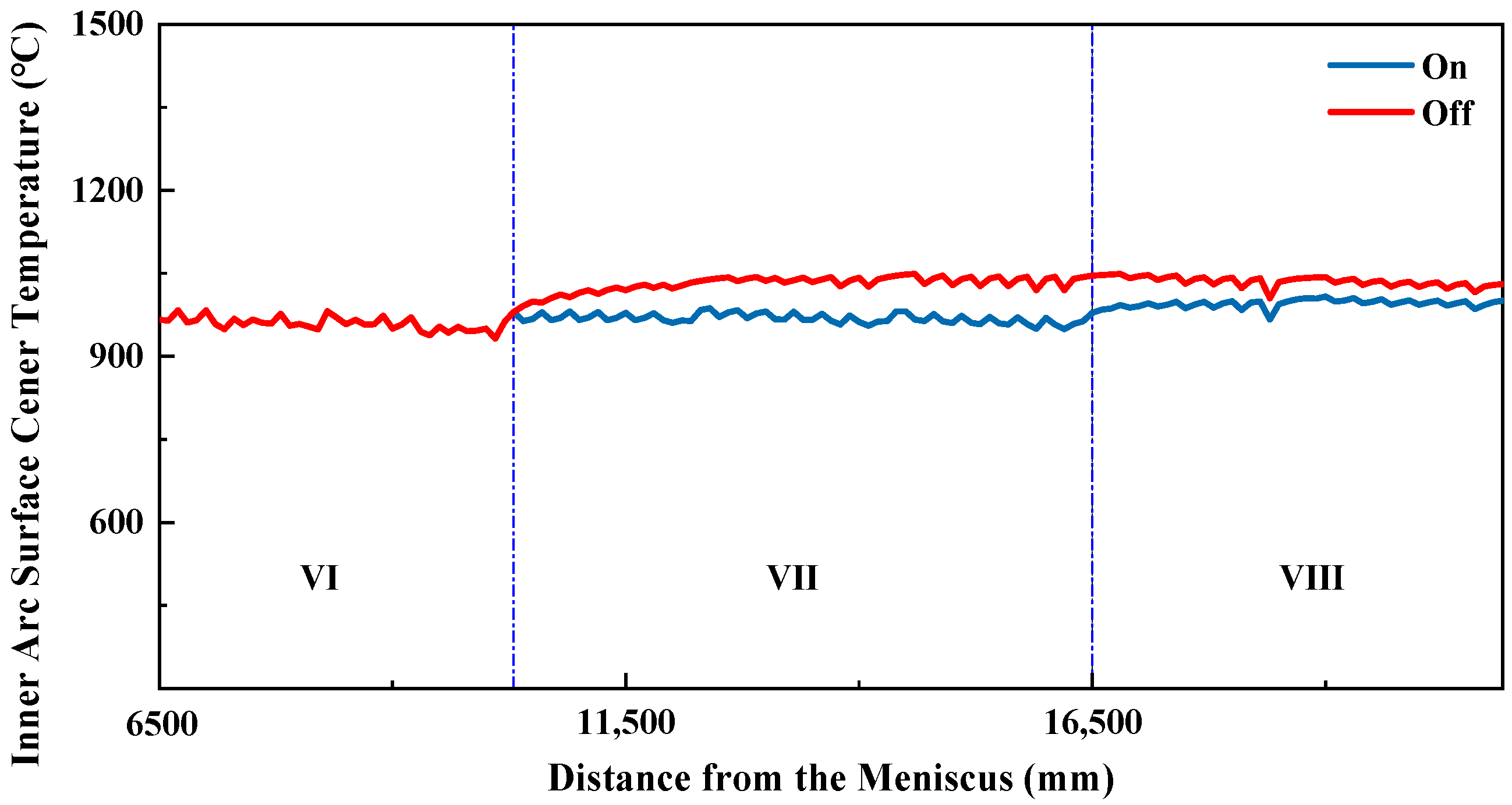
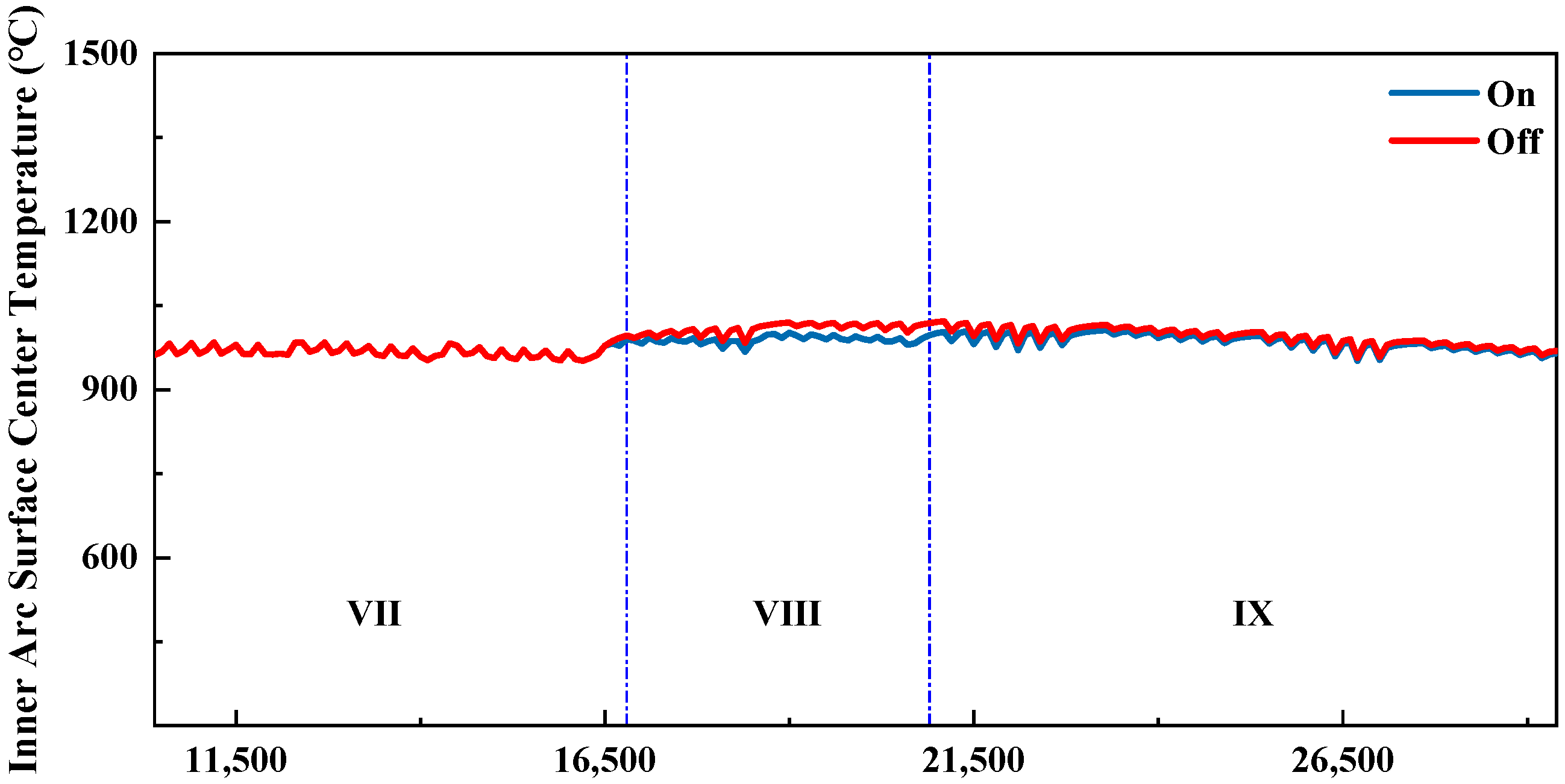
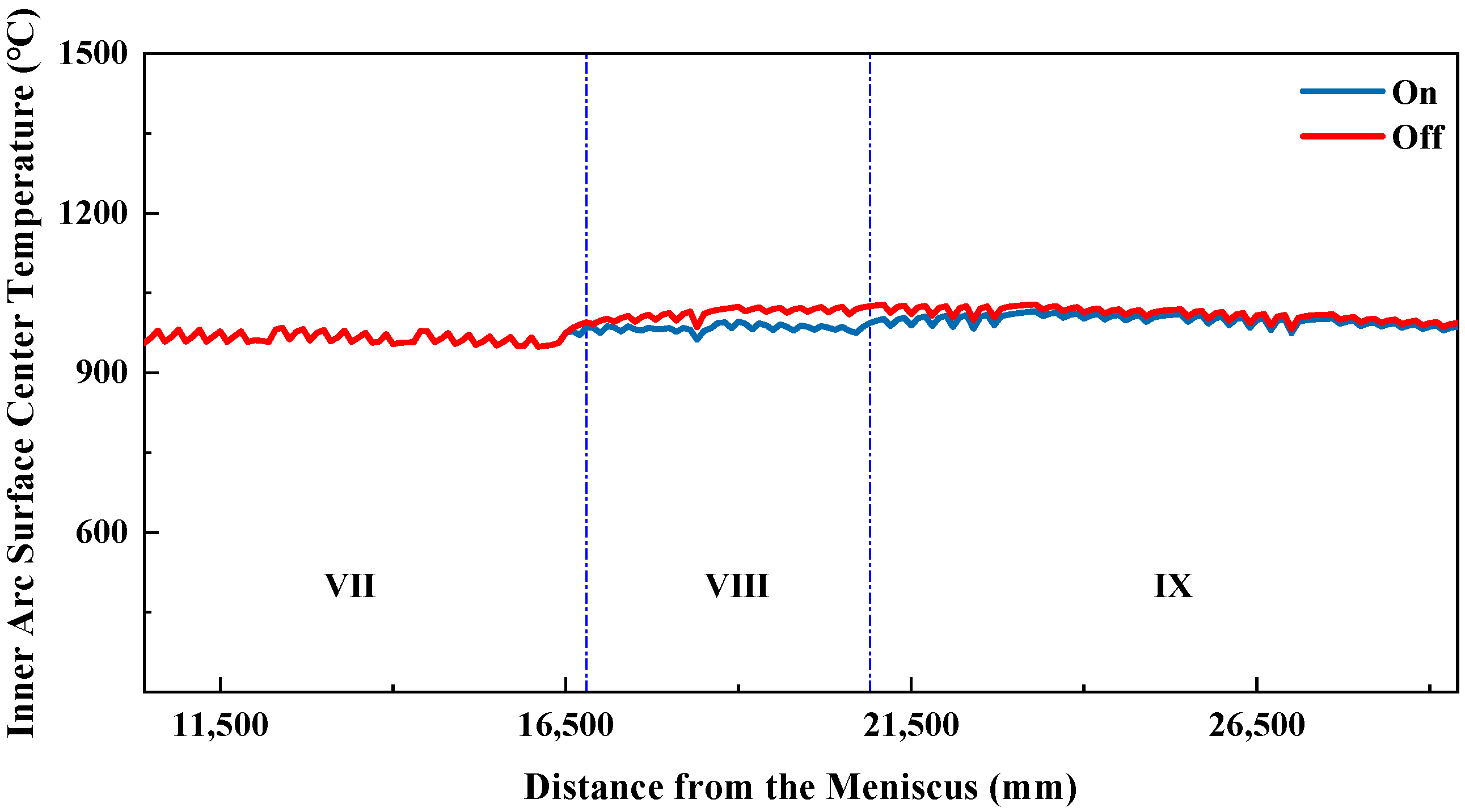
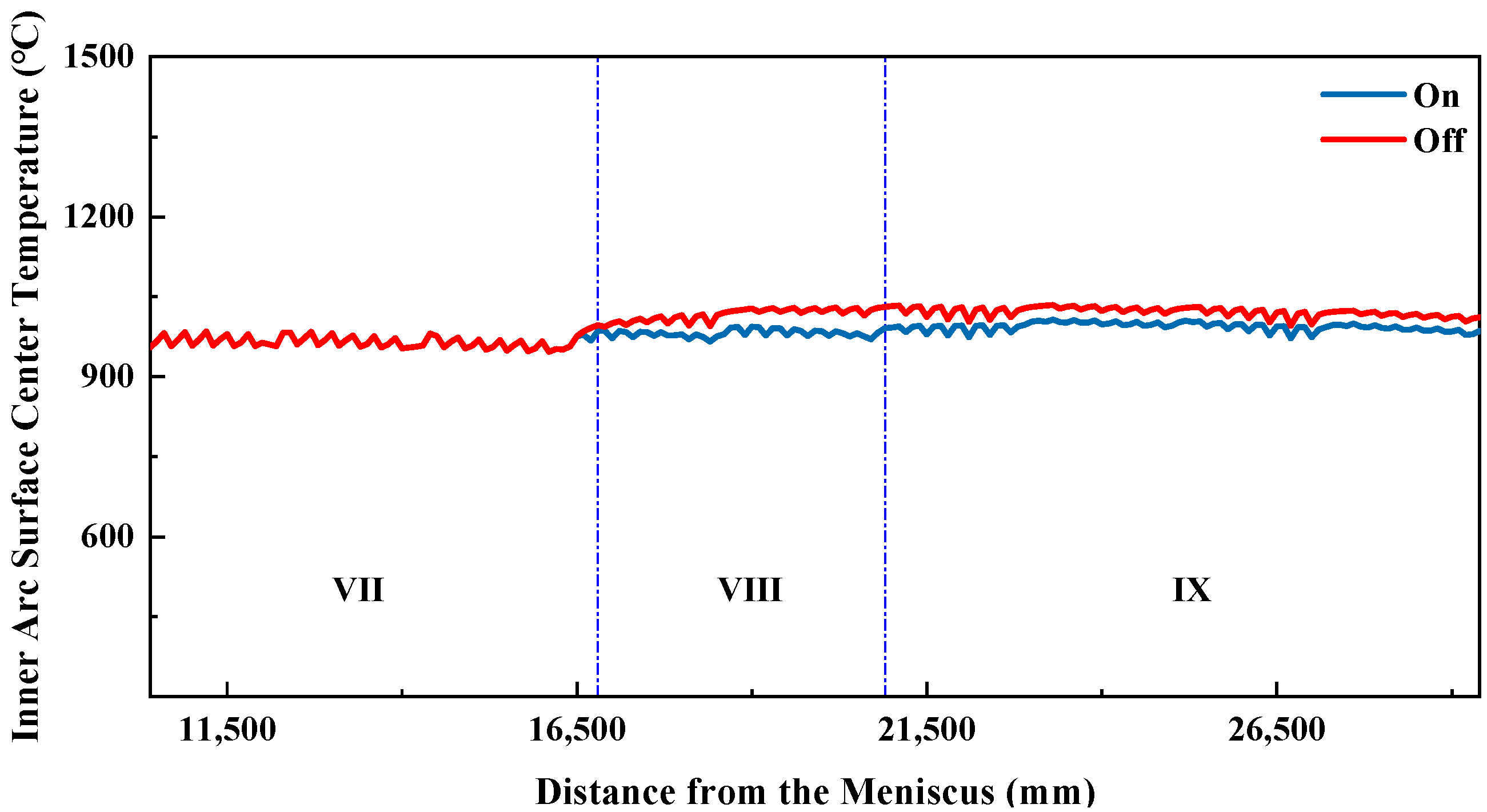
4.3. Analysis of Inner-Arc and Outer-Arc Cooling Differences

During slab production on a straight-arc continuous casting machine, the heat transfer efficiency differs between the inner and outer arcs of the slab in the curved sections, primarily in the water pooling and evaporation heat transfer from the spray water. On the inner arc, the spray water flows along the slab surface and accumulates at the contact interface with the guide rolls, resulting in more water pooling and evaporation heat transfer. On the outer arc, however, gravity causes the sprayed water to fall immediately after contacting the slab surface, preventing accumulation and thus providing little or no water pooling and evaporation heat transfer.

This process is complex; therefore, in establishing the mathematical model for simulation, this difference in heat transfer was not considered, and the inner and outer arcs were assumed to have the same heat transfer efficiency in this aspect. As a result, the simulated temperature difference between the inner and outer arcs is larger than the actual difference. To address this, the inner-to-outer arc water flow ratio was adjusted to maintain the temperature difference within 20 °C.

Since the temperature difference between inner and outer arcs increases with casting speed, this study focuses on a casting speed of 2.0 m/min. The inner-to-outer arc water flow ratio is defined as the inner-arc water flow divided by the outer-arc water flow.

Based on the basic structure of the caster, secondary cooling zones 1 to 4 are vertical sections where the heat transfer efficiency of the inner and outer arcs is similar. In these zones, the inner and outer arc water flows are set equal, i.e., the inner-to-outer arc water flow ratio is 1. When the slab enters the curved section in secondary cooling zone 5, the heat transfer efficiency of the inner and outer arcs begins to differ. Because the inner arc has higher heat transfer efficiency, its water flow is lower than that of the outer arc, i.e., the inner-to-outer arc water flow ratio is <1. As the slab curvature increases, the difference in heat transfer efficiency between the inner and outer arcs gradually grows, reaching a maximum in the horizontal section. Consequently, the difference in inner- and outer-arc water flow should also increase along the casting direction, meaning that the inner-to-outer arc water flow ratio gradually decreases along the casting direction. When the slab straightens in zone 8 and enters the horizontal section, the inner-to-outer arc water flow ratio in zone 8 can be set similar to that of the horizontal section. Zones 9 and 10 are both horizontal, so their inner-to-outer arc water flow ratios should be the same.

The determined inner-to-outer arc water flow ratios are listed in

Table 7. Inner-to-Outer Curve Water Flow Ratio in the Secondary Cooling Zones.

Secondary Cooling Zone	I~IV	V	VI	VII	VIII	IX	X
Inner-to-outer arc water ratio	1	0.94	0.88	0.82	0.76	0.74	0.74

.

The simulated slab surface temperatures of the inner and outer arcs, as well as their temperature differences, are listed in

Table 8. Average Inner- and Outer-Curve Surface Center Temperatures and Temperature Differences in the Slab in Each Secondary Cooling Zone at 2 m/min Casting Speed.

Secondary Cooling Zone	Inner Arc Average Temperature (°C)	Outer Arc Average Temperature (°C)	Temperature Difference (°C)
V	948.7	944.1	4.6
VI	952.9	941.9	11.0
VII	956.2	940.2	16.0
VIII	964.8	945.4	19.4
IX	972.0	952.2	19.8
X	978.9	961.8	17.2

. Since differences in inner- and outer-arc water flow begin in secondary cooling zone 5, only the average surface temperatures and temperature differences for zone 5 and the subsequent secondary cooling zones are presented.

From Table 8, it can be seen that the temperature difference between the inner and outer arcs gradually increases from secondary cooling zone 5 to zone 9, reaching a maximum of 19.8 °C in zone 9, and then decreases in zone 10. The designed inner-to-outer arc water flow ratio effectively keeps the temperature difference within 20 °C.

The variation curves of the inner- and outer-arc surface center temperatures are shown in Figure 6.

4.4. Cooling Heat Transfer in the Slab Width Direction

There are various causes of slab corner cracks, among which the temperature during the straightening process is a major factor [3]. Applying relatively weak secondary cooling [34] can increase the corner temperature [35], improve corner ductility [36], reduce the temperature gradient across the slab width, enhance uniform cooling, and ensure corner quality. The uniformity of cooling in the width direction is evaluated by comparing the center and corner temperatures of the slab wide face.

The temperature differences between the wide-face center and corners at different casting speeds are shown in Figure 7.

From Figure 7, it can be observed that the temperature difference between the slab wide-face center and corners decreases as the casting speed increases. At a relatively low casting speed of 0.8 m/min, the temperature difference gradually increases along the casting direction, reaching a maximum in secondary cooling zone 8. This is because at low casting speeds, slab solidification occurs earlier, with the solidification end point located in zone 7. After complete solidification, the latent heat within the slab continues to release outward, causing the corner temperature to decrease further and thus increasing the center-to-corner temperature difference. During the early stages of secondary cooling, the temperature difference between the wide-face center and corners is kept within 150 °C, indicating good uniformity of cooling across the slab width.

Under medium to high casting speeds, a noticeable reduction in the center-to-corner temperature difference occurs in zone 7. This is because the slab corners in this zone are not covered by spray water, leading to a slight temperature rise, while the wide face continues to be cooled by spray water, resulting in a temperature decrease. Consequently, the temperature difference between the wide face and corners decreases in zone 7. Prior to zone 8, the temperature difference is maintained within 150 °C, ensuring good uniform cooling across the slab width and maintaining corner quality.

4.5. Study on the Cooling Water Shutdown System at Medium and Low Casting Speeds

During slab continuous casting, under low casting speed conditions, the water flow in some secondary cooling zones is relatively low. When the water allocated to each nozzle is below the minimum required for normal operation, the nozzle cannot spray effectively. Based on extensive research experience, the minimum water flow per nozzle corresponds to an air pressure of 0.2 MPa and a water pressure of 0.05 MPa.

At low casting speeds, the solidification end point of the slab occurs relatively early, with some end points located before secondary cooling zone 8 (the straightening zone). Shutting off water in certain secondary cooling zones can help raise the slab surface temperature at the straightening zone without causing significant temperature rebound, thus ensuring slab quality.

Considering that turning off secondary cooling water may induce a temperature rebound in the slab, simulations were performed under two scenarios: with the secondary cooling water turned on and with it turned off.

4.5.1. Effect of Shutting off Secondary Cooling Water at Low Casting Speeds on Slab Temperature Rebound

Simulations were carried out at casting speeds of 0.8, 0.9, and 1.0 m/min for two conditions: with cooling water in secondary cooling zones 7 to 10 turned on and turned off. The resulting inner-arc surface center temperatures and solidification end positions of the slab in each secondary cooling zone are listed in

Table 9. Inner-Curve Surface Center Average Temperature (°C) and Solidification Endpoint of the Slab with or without Cooling Water in Secondary Cooling Zones 7–10 at Different Casting Speeds.

Casting Speeds (m/min)	0.8		0.9		1.0
Whether to Turn on the Cooling Water in Zone VIII	On	Off	On	Off	On	Off
VI	963.1	963.1	963.2	963.3	959.7	959.7
VII	972.8	1013.2	971.2	1024.7	968.5	1031.6
VIII	969.9	991.6	992.6	1021.3	995.3	1035.4
IX	907.1	920.7	947.9	964.9	970.5	992.1
X	822.3	833.9	867.1	881.7	899.5	917.3
the entry of the straightening zone	973.1	1005.8	983.4	1028.1	992.9	1049.1
metallurgical length (m)	13.4 Mid of VII	13.4 Mid of VII	15.8 End of VII	16 End of VII	17.5 Front of VIII	17.9 Front of VIII

.

From Table 9, it can be seen that at a casting speed of 0.8 m/min, shutting off the cooling water in secondary cooling zones 7 to 10 increases the inner-arc surface center temperature in the straightening zone by 21.7 °C. For casting speeds of 0.9 m/min and 1.0 m/min, the corresponding temperature increases are 28.7 °C and 40.1 °C, respectively. Shutting off the cooling water in zones 7 to 10 has almost no effect on the solidification end positions at these three casting speeds.

At a casting speed of 1.0 m/min, the solidification end point is located in the early part of secondary cooling zone 8. The slab interior still contains a small amount of liquid core, so turning off the cooling water in zones 7 to 10 does not significantly affect slab quality, while it can increase the corner temperature in the straightening zone.

Figure 8, Figure 9 and Figure 10 compare the effects of turning on or off the cooling water in secondary cooling zones 7 to 10 on the inner-arc surface center temperature along the casting direction under different casting speeds.

From Figure 8, Figure 9 and Figure 10, it can be observed that at different casting speeds, turning off the cooling water in secondary cooling zones 7 to 10 causes the inner-arc surface center temperature of the slab to rise starting from zone 7. However, the rate and magnitude of the temperature increase do not vary significantly, meeting the metallurgical criteria. Therefore, for casting speeds below 1.0 m/min, the cooling water in zones 7, 8, 9, and 10 can be turned off.

4.5.2. Effect of Shutting off Secondary Cooling Water on Slab Reheating at Medium Casting Speeds

For casting speeds of 1.1, 1.2, and 1.3 m/min, simulation calculations were conducted under two conditions: with the cooling water in secondary cooling zones 8 to 10 turned on, and with it turned off. The inner-arc surface center temperature and solidification end positions of the slab in each secondary cooling zone are listed in

Table 10. Inner-Curve Surface Center Temperature (°C) and Solidification Endpoint of the Slab under Different Casting Speeds with or without Cooling Water in Secondary Cooling Zones 8–10.

Casting Speeds (m/min)	1.1		1.2		1.3
Whether to Turn on the Cooling Water in ZONE VIII	On	Off	On	Off	On	Off
VII	967.2	967.2	965.0	965.0	964.7	964.7
VIII	988.8	1007.7	983.8	1011.0	981.2	1015.3
IX	985.5	993.6	999.1	1010.7	993.8	1021.6
X	929.9	934.4	951.7	957.9	968.6	983.3
the entry of the straightening zone	990.4	996.4	986.0	995.2	985.9	996.8
metallurgical length (m)	19.2 End of VIII	19.2 End of VIII	21 Front of IX	21 Front of IX	22.8 Front of IX	22.9 Front of IX

.

From Table 10, it can be seen that at a casting speed of 1.1 m/min, turning off the cooling water in secondary cooling zones 8 to 10 increases the inner-arc surface center temperature in the straightening zone by 18.9 °C. For casting speeds of 1.2 and 1.3 m/min, the corresponding temperature increases are 27.2 °C and 34.1 °C, respectively. For all three casting speeds, whether the cooling water in zones 8 to 10 is turned off has almost no effect on the solidification end positions. This is because the increased casting speed and the reduced cooling intensity in the later secondary cooling stages have little impact on the solidification end.

The effect of turning off the cooling water in secondary cooling zones 8 to 10 on the inner-arc surface center temperature along the casting direction is compared in Figure 11, Figure 12 and Figure 13.

From Figure 11, Figure 12 and Figure 13, it can be seen that after turning off the cooling water in secondary cooling zones 8 to 10, the inner-arc surface center temperature of the slab rises upon entering zone 8, and both the rate and magnitude of temperature recovery fully comply with metallurgical technical requirements. Therefore, for casting speeds below 1.3 m/min, the cooling water in zones 7, 8, 9, and 10 is turned off.

Based on the above analysis, when the casting speed is below 1 m/min, the cooling water in zones 7 to 10 is turned off; when the casting speed is below 1.3 m/min, the cooling water in zones 8 to 10 is turned off. This scheme effectively increases the temperature in the straightening zone, improves slab quality, and significantly reduces the probability of crack formation.

4.6. Multidimensional Uniform Cooling Process System

The secondary cooling model used in this study is a static control model, in which the water flow in each secondary cooling zone is controlled as a quadratic function of the casting speed. The variation in water flow with casting speed differs among zones. If the water flow changes significantly with casting speed, it may cause fluctuations in the slab surface temperature. In practical production, since the casting speed is not constant, large variations in water flow with speed can lead to significant fluctuations in the slab surface temperature, which is detrimental to surface quality.

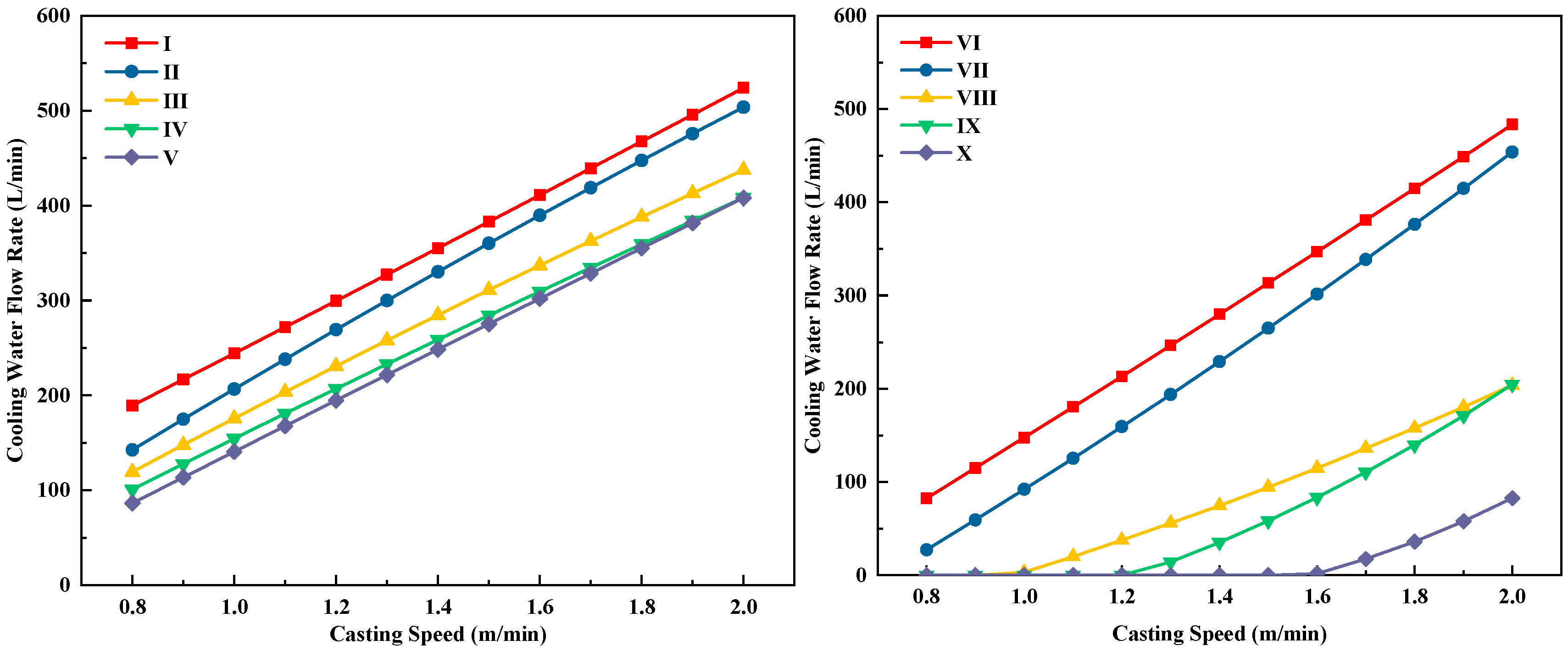
After extensive simulation calculations, the variation in water flow with casting speed for each secondary cooling zone was determined. The curves of water flow versus casting speed for zones 1 to 10 are shown in Figure 14.

From Figure 14, it can be seen that the variation curves of water flow in each loop with casting speed follow the general cooling principle that higher casting speeds require larger water flow. For secondary cooling zones 1 to 5, the quadratic curves of water flow versus casting speed are almost linear, while for zones 6 to 10, the quadratic curves show a slight concave shape. According to continuous casting solidification and cooling theory, to achieve the same cooling effect, an increase in casting speed at high speeds requires a larger increase in water flow than the same speed increment at low speeds. Therefore, the slight concavity of the quadratic curve of water flow versus casting speed is reasonable.

The inner-arc surface center temperatures and temperature differences of the slab in each secondary cooling zone under different casting speeds are listed in

Table 11. Average Center Temperature and Temperature Difference in Slab Inner-Curve Surface in Secondary Cooling Zones at Different Casting Speeds.

Secondary Cooling Zone	Inner-Arc Surface Center Temperature (°C)				Temperature Difference (°C)
Casting Speeds (m/min)	0.8	1.2	1.6	2.0	0.8	1.6	2.0
I	1077.5	1070.9	1080.9	1088.3	6.6	10.0	17.4
II	1011.2	994.3	989.9	989.5	16.9	−4.4	−4.8
III	989.5	974.5	969.3	969.2	15.0	−5.2	−5.3
IV	979.9	972.7	969.4	968.5	7.2	−3.3	−4.2
V	962.9	955.9	951.9	949.5	7.1	−3.9	−6.3
VI	963.5	958.4	956.6	952.9	5.1	−1.8	−5.5
VII	973.4	968.0	964.0	960.7	5.3	−4.1	−7.3
VIII	970.2	986.0	976.8	968.2	−15.8	−9.2	−17.9
IX	907.1	1000.1	986.7	974.1	−93.0	−13.4	−25.9
X	822.1	952.2	997.4	979.6	−130.0	45.3	27.4

. The temperature differences between different speeds are calculated using the slab surface temperature at 1.2 m/min as the reference.

From Table 11, it can be seen that, under different casting speeds, the inner-arc surface center temperature differences in secondary cooling zones 1 to 8 are all controlled within 20 °C. The small temperature differences help prevent large fluctuations in slab surface temperature caused by changes in casting speed during production, thereby ensuring surface quality. The larger temperature differences in zones 9 and 10 are due to variations in the slab solidification end positions at different speeds; at lower speeds, the solidification end occurs earlier, resulting in lower slab surface temperatures in the later stages of secondary cooling. Zones 9 and 10 are horizontal segments, where it is not necessary to maintain a high slab surface temperature. Instead, the goal is to ensure that the slab is fully solidified before the end of secondary cooling at high casting speeds.

Except for Zone 1, the slab surface temperature exhibits a slight decrease with increasing casting speed. This phenomenon arises because higher casting speeds require an increase in cooling water flow in the secondary cooling zones, which lowers the slab surface temperature. Meanwhile, the reduced residence time of the slab in the secondary cooling zone at higher casting speeds necessitates an appropriate increase in cooling water to ensure that the shell thickness is sufficient to withstand the ferrostatic pressure of the molten steel, thereby preventing breakout. Nevertheless, excessive cooling intensity may lead to an overcooling of the slab surface, and in severe cases, the surface temperature in the straightening zone may fall within the third brittle temperature range, exerting a detrimental effect on slab quality. In practice, casting speed is also adjusted according to production requirements. Fluctuations in casting speed cause variations in cooling water flow and, consequently, in surface temperature, and excessive temperature fluctuations can impair surface quality. The proposed multi-dimensional uniform cooling strategy is designed to ensure adequate shell thickness under high casting speeds, while maximizing the slab surface temperature and minimizing its fluctuation with casting speed, thereby achieving stable and improved slab quality.

Finally, the water flow rates for each secondary cooling zone corresponding to different casting speeds were fitted using the least-squares method, resulting in a multi-dimensional uniform cooling process model, as shown in

Table 12. Multi-dimensional uniform cooling strategy.

Qi = Ki(ai + biv + civ2) (L/min)
Secondary Cooling Zone	Casting Speed (m/min)
	0.8	0.9	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2
I io	142.2	162.8	183.5	204.2	225.0	245.9	266.9	287.9	308.9	330.0	351.2	372.5	393.8
I s	47.0	53.9	60.7	67.6	74.4	81.3	88.3	95.2	102.2	109.1	116.1	123.2	130.2
II io	142.5	174.7	206.6	238.1	269.2	299.8	330.1	360.0	389.5	418.6	447.4	475.7	503.6
III io	119.2	147.6	175.7	203.4	230.8	257.9	284.6	310.9	336.9	362.6	388.0	412.9	437.6
IV io	105.2	133.4	161.4	189.1	216.6	243.9	271.0	297.8	324.4	350.8	376.9	402.8	428.5
V i	39.8	52.3	64.8	77.2	89.6	102.0	114.4	126.7	139.0	151.3	163.5	175.8	188.0
V o	42.4	55.7	68.9	82.2	95.4	108.5	121.7	134.8	147.9	160.9	174.0	187.0	199.9
VI i	38.6	53.8	69.1	84.4	99.9	115.4	131.0	146.7	162.4	178.3	194.2	210.2	226.3
VI o	43.9	61.2	78.5	96.0	113.5	131.1	148.9	166.7	184.6	202.6	220.7	238.9	257.2
VII i	12.3	26.8	41.5	56.5	71.8	87.4	103.2	119.4	135.9	152.6	169.6	186.9	204.5
VII o	15.1	32.7	50.6	68.9	87.6	106.6	125.9	145.6	165.7	186.1	206.8	227.9	249.4
VIII i	0.0	0.0	1.4	8.7	16.2	24.1	32.3	40.8	49.6	58.7	68.2	77.9	88.0
VIII o	0.0	0.0	1.9	11.4	21.4	31.7	42.5	53.7	65.3	77.3	89.7	102.5	115.8
IX i	0.0	0.0	0.0	0.0	0.0	6.2	15.0	24.8	35.5	47.0	59.5	72.8	87.1
IX o	0.0	0.0	0.0	0.0	0.0	8.3	20.3	33.5	47.9	63.5	80.4	98.4	117.6
X i	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.4	7.0	14.9	24.2	34.7
X o	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.5	9.4	20.2	32.7	47.0
Specific water flow (kg/min)	0.270	0.306	0.336	0.364	0.388	0.411	0.432	0.451	0.469	0.487	0.504	0.520	0.536

. i represents the cooling water flow on the inner arc of the slab, o represents the cooling water flow on the outer arc, s represents the cooling water flow on the slab sides, and io denotes the cooling water flow equally distributed between the inner and outer arcs.

5. Conclusions

This study aimed at achieving uniform secondary cooling of ship plate steel and investigated, from multiple dimensions, the effects of secondary cooling parameters on slab temperature distribution. The main conclusions are as follows:

(1)

In this study, a two-dimensional slab solidification heat transfer model based on the finite difference method was developed. The model incorporates four types of boundary heat transfer conditions—radiation, water film evaporation, spray impingement, and roll contact—while applying reasonable simplifications through slab symmetry and steady-state assumptions. This model can efficiently and accurately capture the temperature evolution of slabs in the secondary cooling zone, providing a theoretical basis for optimizing secondary cooling strategies. It enables precise simulation of the slab cooling process and guides the design of an optimal secondary cooling scheme, thereby ensuring uniform temperature distribution and improving slab quality.

(2)

A multi-dimensional uniform cooling strategy was proposed. By adopting weaker cooling intensity, the surface temperature of the slab can be maintained at a higher level, ensuring that the solidification end point aligns with the range of soft reduction in the caster, while simultaneously reducing the temperature difference between the slab center and corners across the width. Along the casting direction, a gradually decreasing water distribution model was applied to prevent abrupt temperature drops. Across the thickness, the water flow ratio between the inner and outer arcs was reduced stepwise from 1.0 to 0.74, which helps decrease the temperature difference between the inner and outer arc surface centers. In addition, at medium and low casting speeds, shutting off some spray zones in the secondary cooling system can raise the slab surface temperature by about 50 °C (keeping it outside the brittle temperature range), thereby effectively improving slab quality. Collectively, these measures make the slab temperature field more uniform, reduce fluctuations, and significantly lower the risk of surface and internal quality defects.

(3)

From an industrial perspective, the overall framework of the multi-dimensional uniform cooling strategy shows strong applicability, as it provides guidance for water distribution in different cooling zones under various casting speeds and steel grades, enabling flexible process adjustments. By optimizing cooling water allocation (and shutting off certain spray zones when conditions allow), the slab surface temperature in the straightening zone can be increased, while overall water consumption and energy usage are reduced. More importantly, by maintaining the slab surface temperature outside the brittle range, slab plasticity is effectively improved, and the occurrence of defects and associated cracks is reduced. In summary, the proposed multi-dimensional uniform cooling strategy has considerable practical application value, effectively improving product quality and offering useful reference for implementation across different steel grades and caster configurations.