Residual Temperature Prediction in Selective Laser Melting by Deep Neural Networks
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Prior Work
1.3. Research Gap, Aim, and Contributions
- (i)
- a benchmark part that concentrates representative geometric features to generate diverse training and evaluation cases,
- (ii)
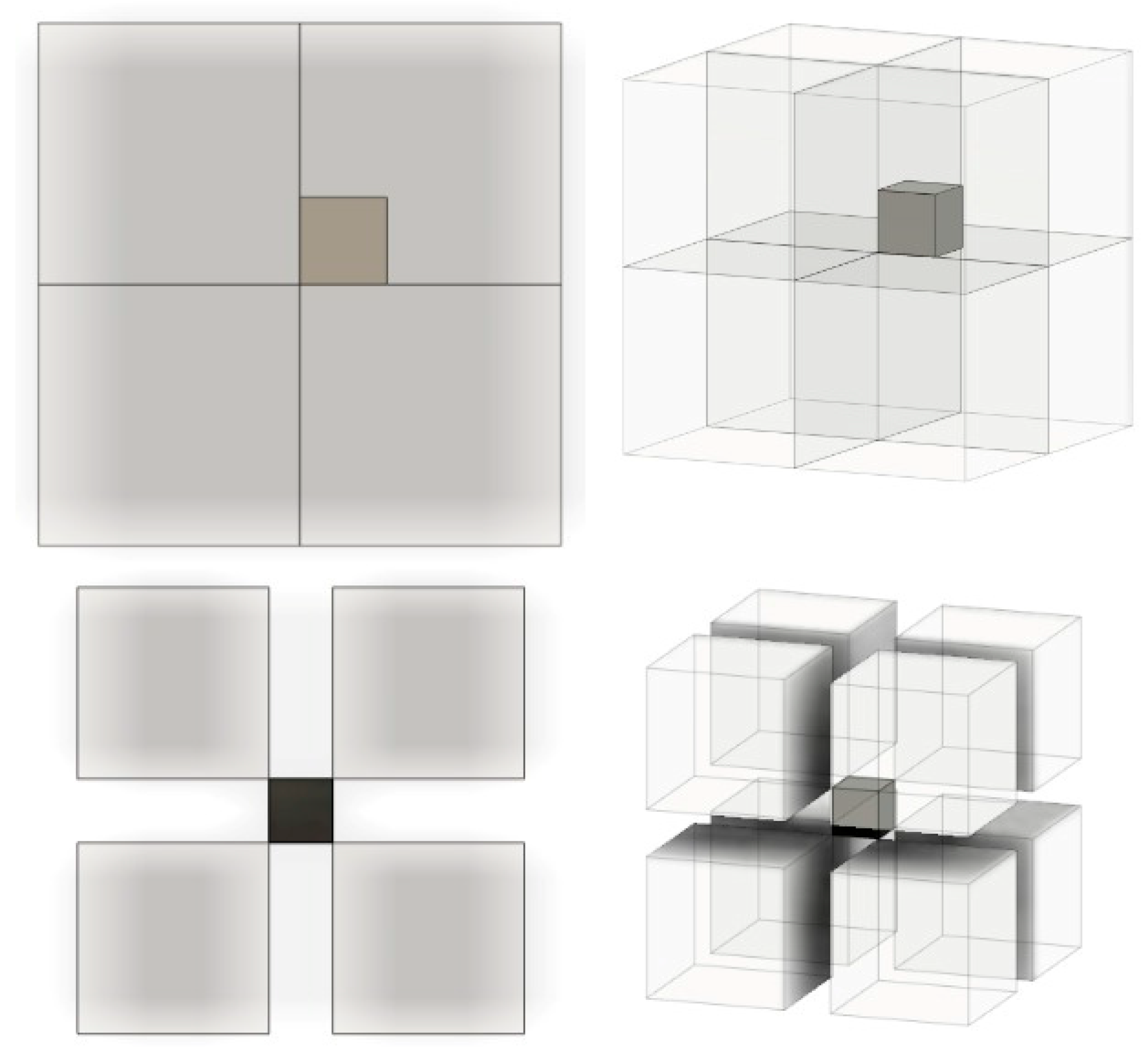
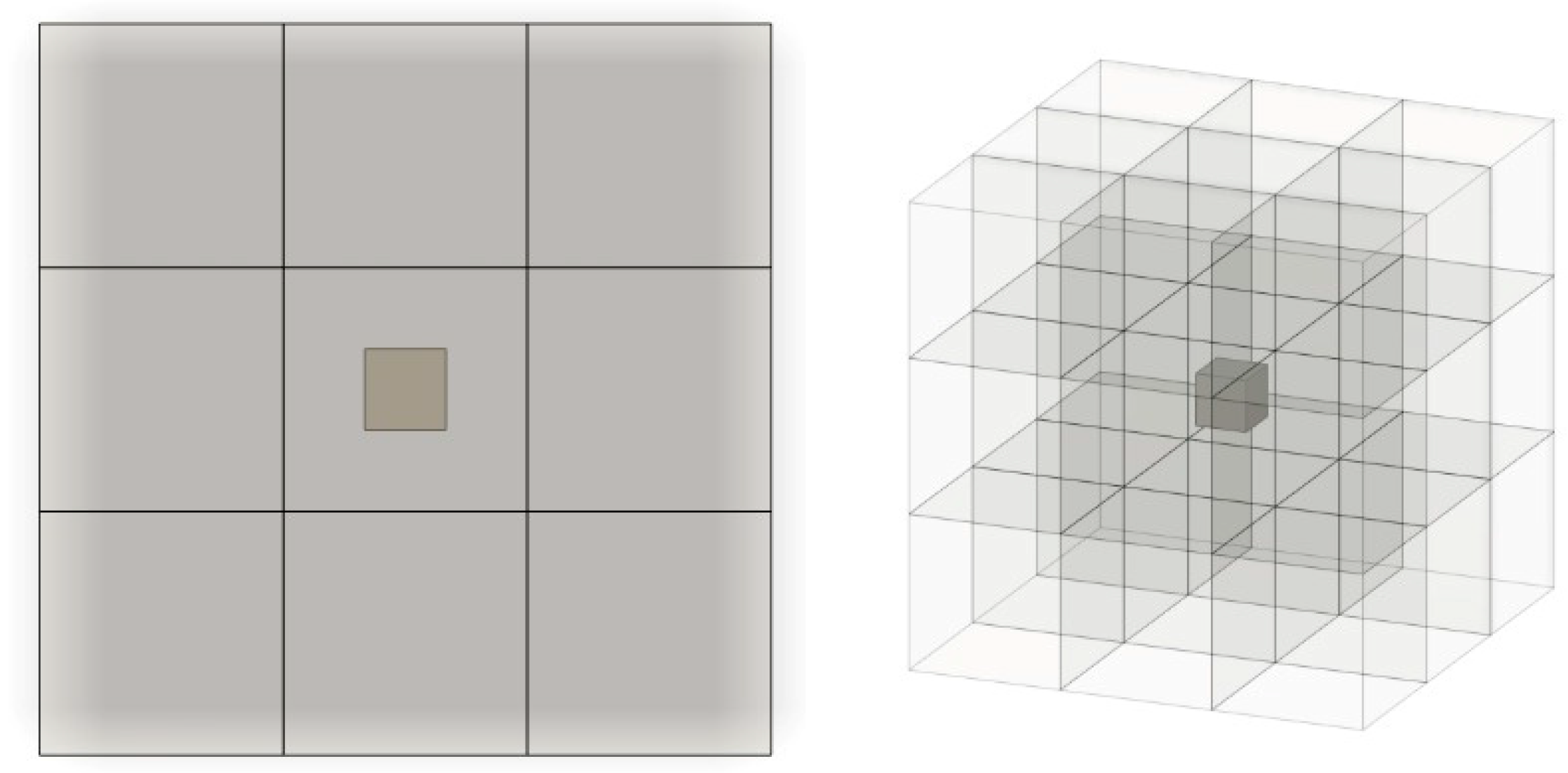
- a geometry-abstraction algorithm that yields per-location descriptors via intersections between predefined control volumes (CVs) and the part, and
- (iii)
- a deep neural network trained on simulation-generated data to predict residual temperature at arbitrary locations, enabling full-field prediction far more efficiently than finite-element analysis.
2. Part Shape Modeling
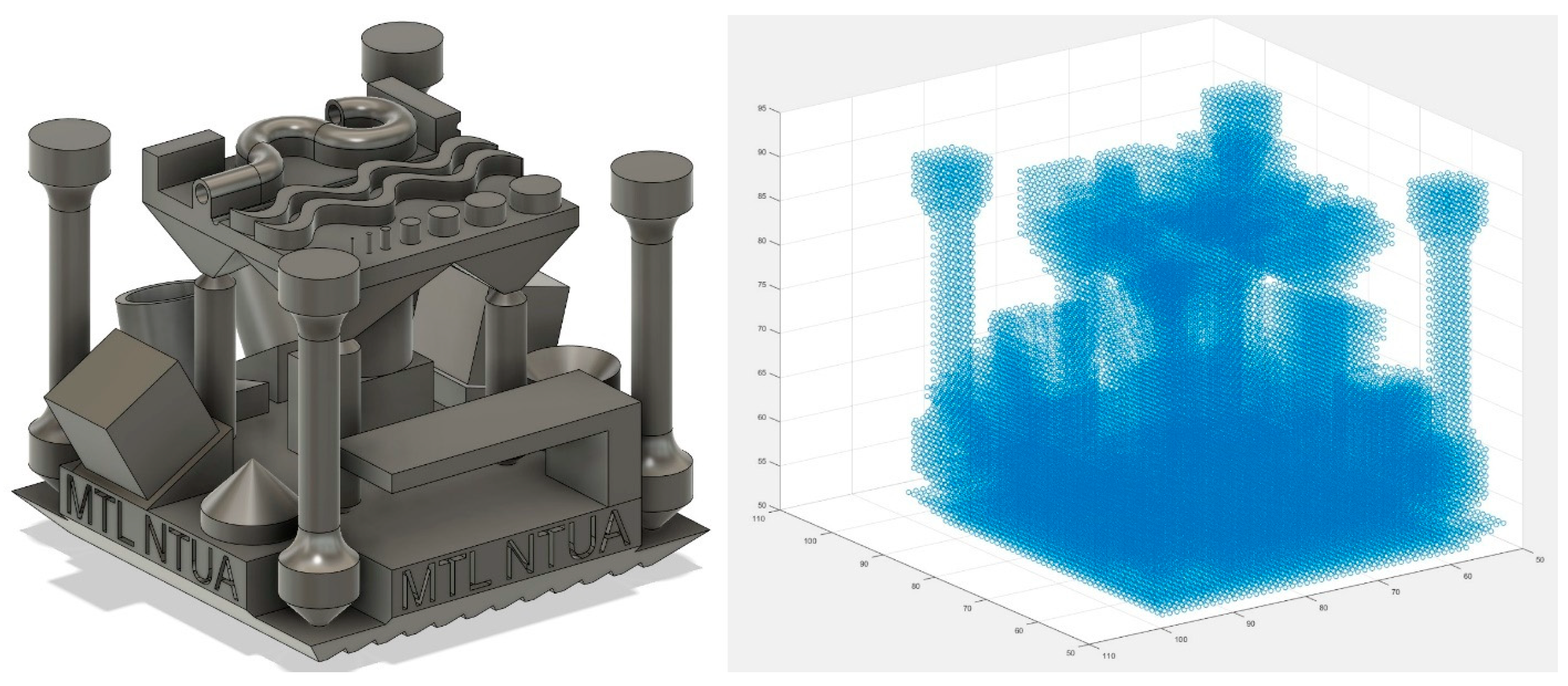
2.1. Benchmark Part Design
- Contain a variety of geometric features in order to provide varying data to train the neural network
- Have a reasonable degree of asymmetry
- Fit within a relatively small-sized bounding box
- Allow for post-printing measurement
- Provide material for mechanical testing
- Minimize geometry below a 1 mm voxel resolution so that analysis remains computationally viable
2.2. Geometry Abstraction
2.3. CV Positioning and Calculation
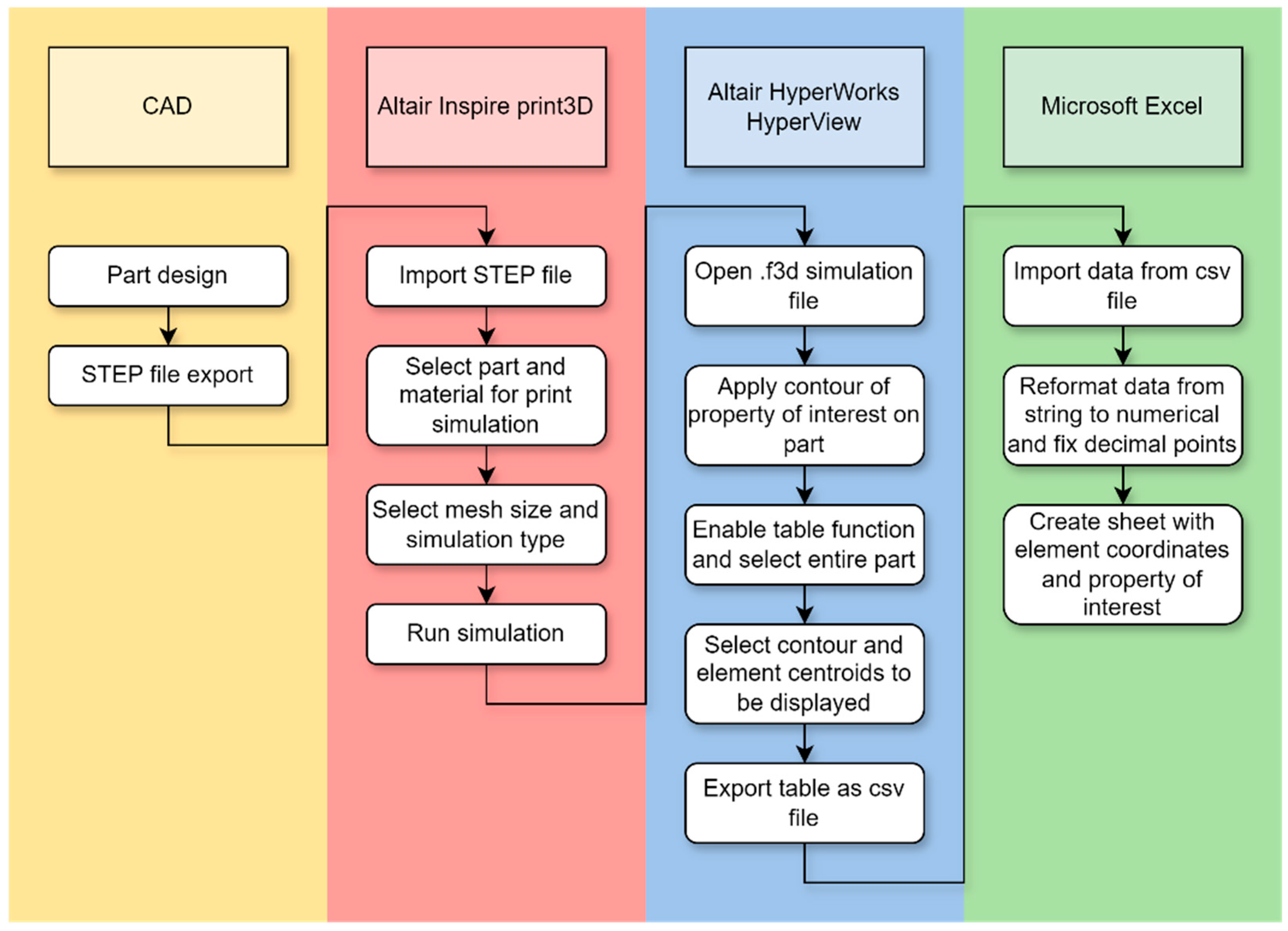
2.4. Code Implementation
- Subtraction of the minimum coordinate value per axis in order to make all coordinates positive, while maintaining identical relative distances and creating a zero point in the process to serve as an origin point
- Division of all coordinate values by element size, resulting in integers
- Addition of a set integer to all coordinates in order to create an offset from the origin point
- Creation of a 3D zero array with each dimension’s size equal to the sum of the size of the part along that dimension and the offset integer multiplied by 2
- Population of the array by setting the values whose array index coincides with a coordinate set from the transformed initial data to 1
3. Deep Neural Network Development
3.1. DNN Configuration
3.2. Dataset Generation from Process Simulations
3.3. Testing Scenarios
4. Results
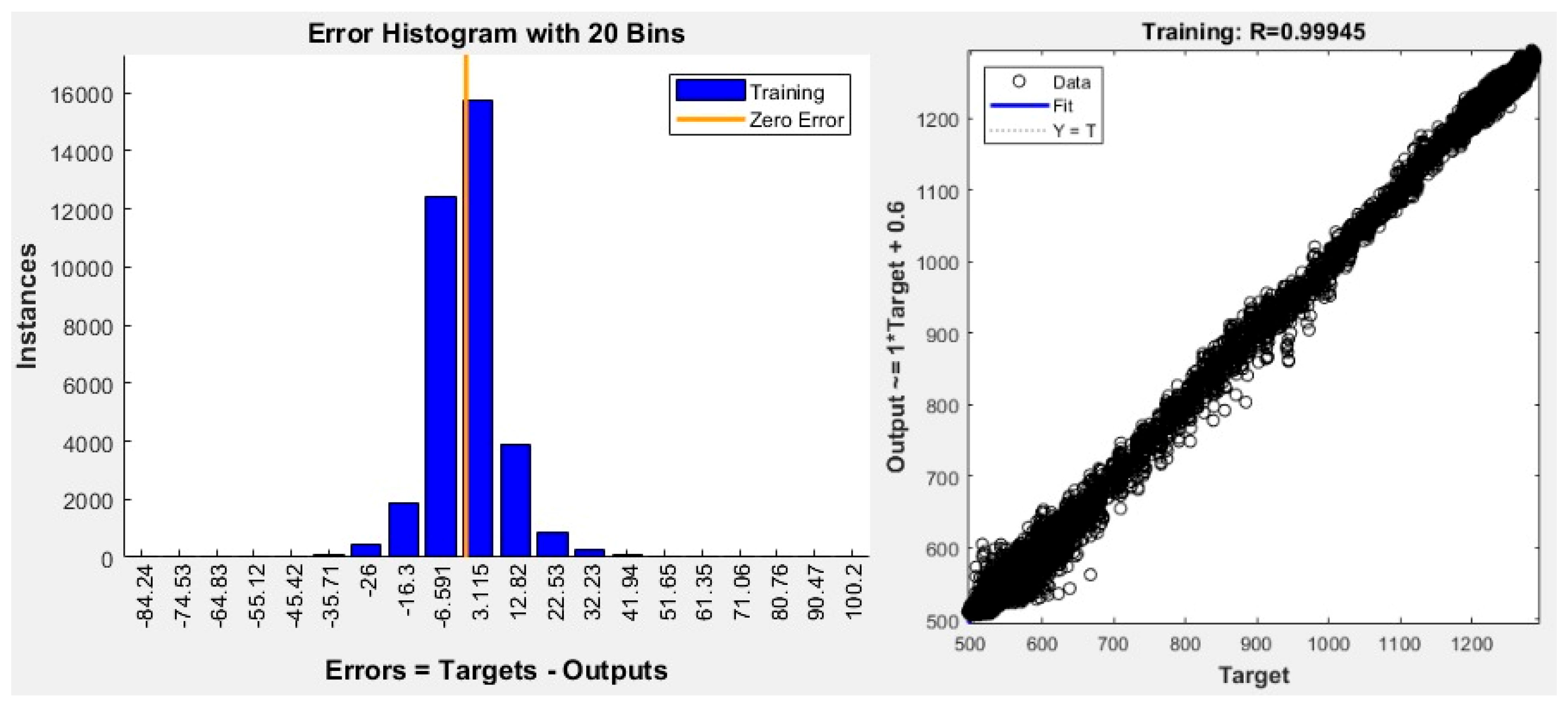
4.1. Baseline Prediction
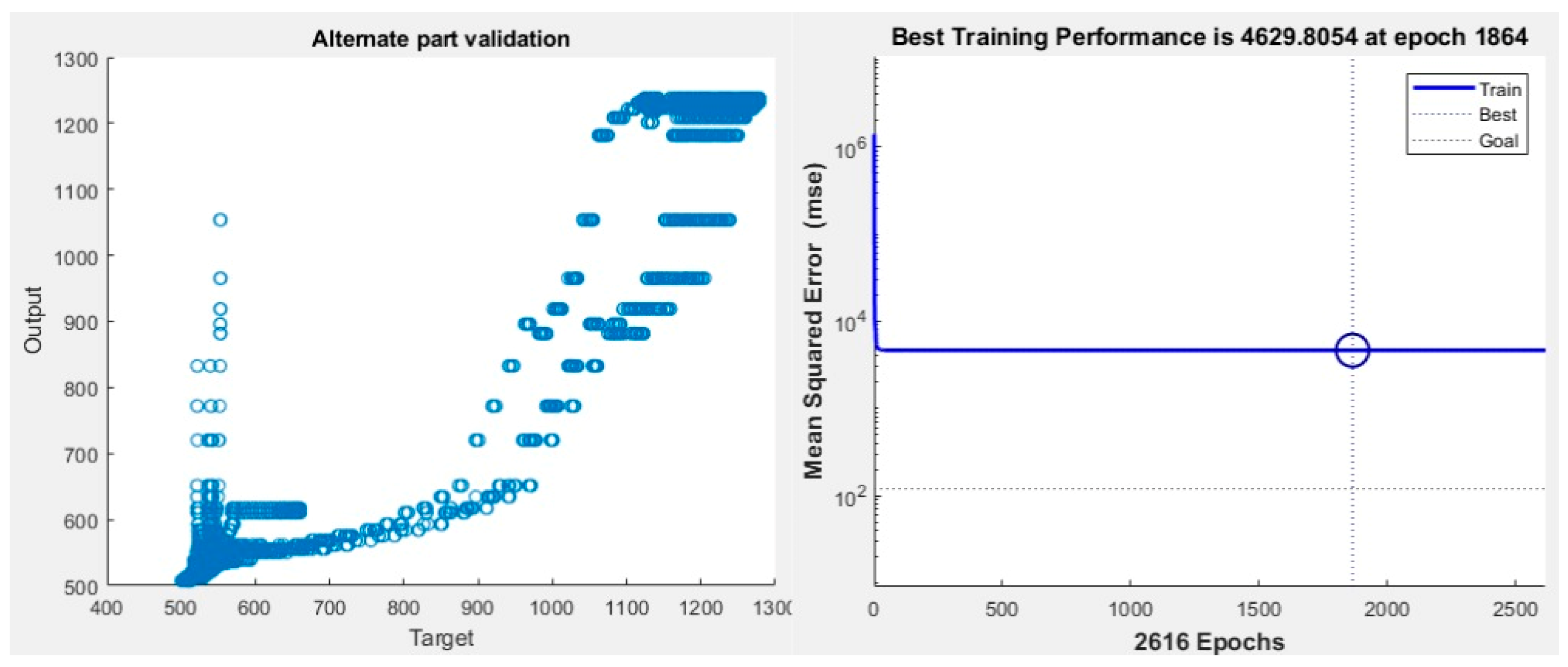
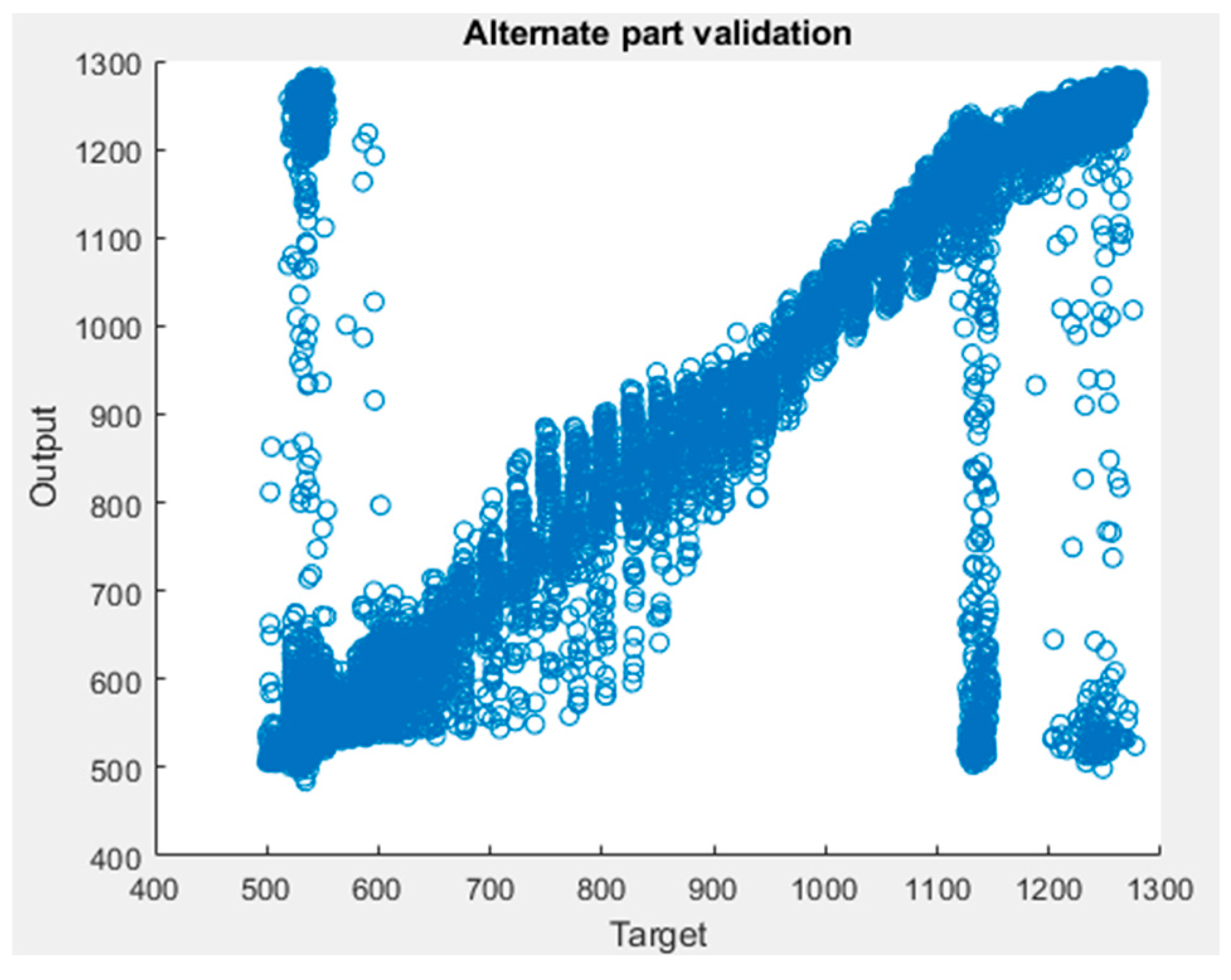
4.2. Robustness to Geometry Changes
4.3. Input Significance Verification
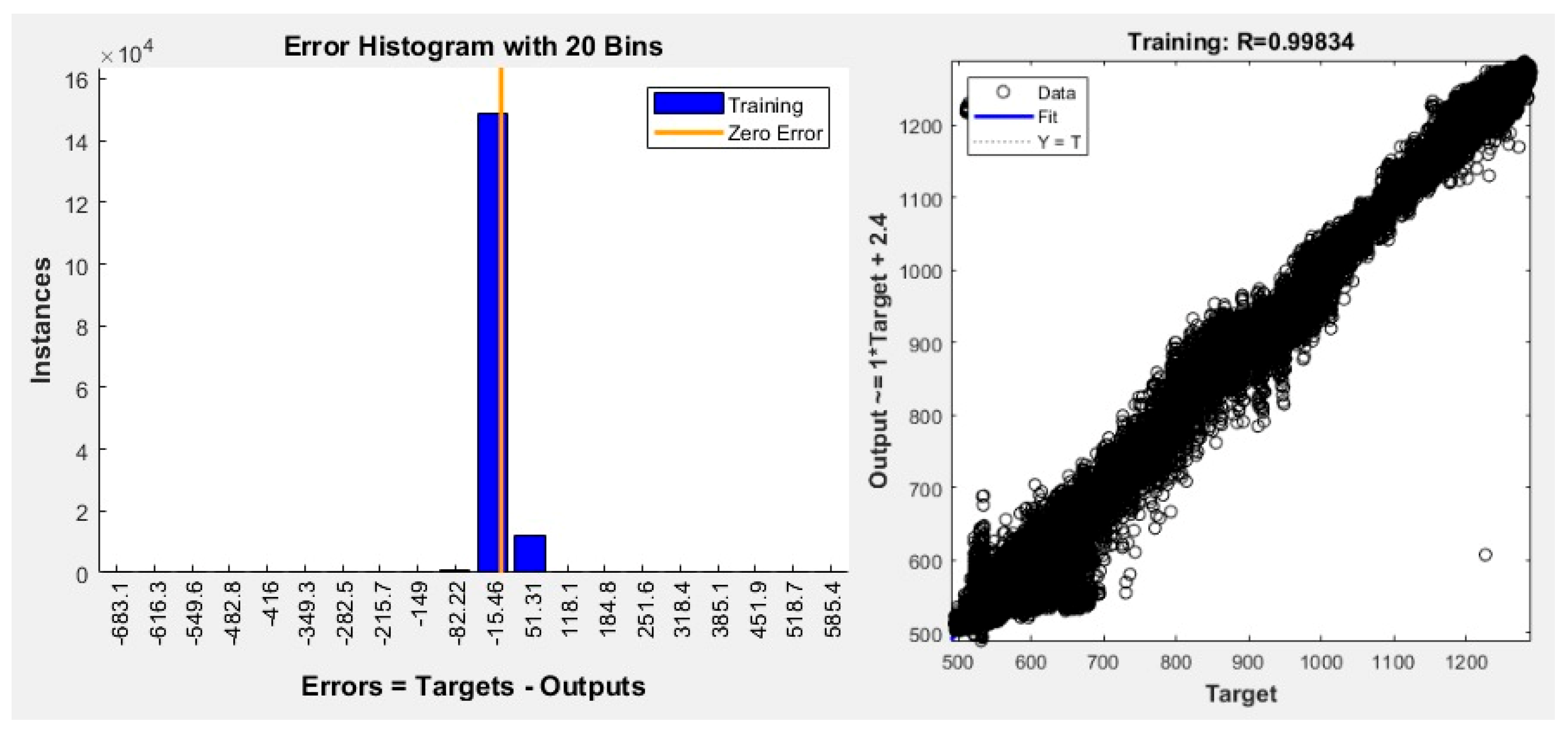
4.4. Multi-Size Dataset Test
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SLM | Selective Laser Melting |
| FE | Finite-Element |
| NN | Neural Network |
| GD&T | Geometric Dimensioning and Tolerancing |
| DNN | Deep Neural Network |
| MSE | Mean Squared Error |
| MRE | Mean Relative Error |
| MAE | Mean Absolute Error |
| CSV | Comma-Separated Values |
References
- Kurzynowski, T.; Pawlak, A.; Smolina, I. The Potential of SLM Technology for Processing Magnesium Alloys in Aerospace Industry. Arch. Civ. Mech. Eng. 2020, 20, 23. [Google Scholar] [CrossRef]
- Buchbinder, D.; Schleifenbaum, H.; Heidrich, S.; Meiners, W.; Bültmann, J. High Power Selective Laser Melting (HP SLM) of Aluminum Parts. Phys. Procedia 2011, 12, 271–278. [Google Scholar] [CrossRef]
- Loh, L.-E.; Chua, C.-K.; Yeong, W.-Y.; Song, J.; Mapar, M.; Sing, S.-L.; Liu, Z.-H.; Zhang, D.-Q. Numerical Investigation and an Effective Modelling on the Selective Laser Melting (SLM) Process with Aluminium Alloy 6061. Int. J. Heat Mass Transf. 2015, 80, 288–300. [Google Scholar] [CrossRef]
- King, W.; Anderson, A.T.; Ferencz, R.M.; Hodge, N.E.; Kamath, C.; Khairallah, S.A. Overview of Modelling and Simulation of Metal Powder Bed Fusion Process at Lawrence Livermore National Laboratory. Mater. Sci. Technol. 2015, 31, 957–968. [Google Scholar] [CrossRef]
- Ganeriwala, R.K.; Hodge, N.E.; Solberg, J.M. Towards Improved Speed and Accuracy of Laser Powder Bed Fusion Simulations via Multiscale Spatial Representations. Comput. Mater. Sci. 2021, 187, 110112. [Google Scholar] [CrossRef]
- Jimenez Abarca, M.; Darabi, R.; de Sa, J.C.; Parente, M.; Reis, A. Multi-Scale Modeling for Prediction of Residual Stress and Distortion in Ti–6Al–4V Semi-Circular Thin-Walled Parts Additively Manufactured by Laser Powder Bed Fusion (LPBF). Thin-Walled Struct. 2023, 182, 110151. [Google Scholar] [CrossRef]
- Nagesha, B.K.; Anand Kumar, S.; Vinodh, K.; Pathania, A.; Barad, S. A Thermo-Mechanical Modelling Approach on the Residual Stress Prediction of SLM Processed HPNGV Aeroengine Part. Mater. Today Proc. 2021, 44, 4990–4996. [Google Scholar] [CrossRef]
- Qi, X.; Chen, G.; Li, Y.; Cheng, X.; Li, C. Applying Neural-Network-Based Machine Learning to Additive Manufacturing: Current Applications, Challenges, and Future Perspectives. Engineering 2019, 5, 721–729. [Google Scholar] [CrossRef]
- Feng, F.; Zhu, T.; Yang, B.; Zhou, S.; Xiao, S. A Physics-Informed Neural Network Approach for Predicting Fatigue Life of SLM 316L Stainless Steel Based on Defect Features. Int. J. Fatigue 2024, 188, 108486. [Google Scholar] [CrossRef]
- Demir, K.; Zhang, Z.; Ben-Artzy, A.; Hosemann, P.; Gu, G.X. Laser Scan Strategy Descriptor for Defect Prognosis in Metal Additive Manufacturing Using Neural Networks. J. Manuf. Process 2021, 67, 628–634. [Google Scholar] [CrossRef]
- Xing, W.; Lyu, T.; Chu, X.; Rong, Y.; Lee, C.-G.; Sun, Q.; Zou, Y. Recognition and Classification of Single Melt Tracks Using Deep Neural Network: A Fast and Effective Method to Determine Process Windows in Selective Laser Melting. J. Manuf. Process 2021, 68, 1746–1757. [Google Scholar] [CrossRef]
- Gao, J.; Wang, C.; Hao, Y.; Wang, X.; Zhao, K.; Ding, X. Prediction of Molten Pool Temperature and Processing Quality in Laser Metal Deposition Based on Back Propagation Neural Network Algorithm. Opt. Laser Technol. 2022, 155, 108363. [Google Scholar] [CrossRef]
- Wang, C.; Tan, X.P.; Tor, S.B.; Lim, C.S. Machine Learning in Additive Manufacturing: State-of-the-Art and Perspectives. Addit. Manuf. 2020, 36, 101538. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, W.; Liu, Q.; Zhao, Y.; Liu, P.; Wu, D.; Banu, M.; Chen, L. Data-Driven Modeling of Process, Structure and Property in Additive Manufacturing: A Review and Future Directions. J. Manuf. Process 2022, 77, 13–31. [Google Scholar] [CrossRef]
- Wu, S.-H.; Tariq, U.; Joy, R.; Sparks, T.; Flood, A.; Liou, F. Experimental, Computational, and Machine Learning Methods for Prediction of Residual Stresses in Laser Additive Manufacturing: A Critical Review. Materials 2024, 17, 1498. [Google Scholar] [CrossRef] [PubMed]
- Belongie, M. Matching with Shape Contexts. In Proceedings of the IEEE 2000 Proceedings Workshop on Content-based Access of Image and Video Libraries, Washington, DC, USA, 16 June 2000; pp. 20–26. [Google Scholar]
- Angrish, A.; Bharadwaj, A.; Starly, B. MVCNN++: Computer-Aided Design Model Shape Classification and Retrieval Using Multi-View Convolutional Neural Networks. J. Comput. Inf. Sci. Eng. 2021, 21, 011001. [Google Scholar] [CrossRef]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. A Systematic Review of Voxelization Method in Additive Manufacturing. Mech. Ind. 2019, 20, 630. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, F. VoxSegNet: Volumetric CNNs for Semantic Part Segmentation of 3D Shapes. IEEE Trans. Vis. Comput. Graph. 2020, 26, 2919–2930. [Google Scholar] [CrossRef]
- Giganto, S.; Martínez-Pellitero, S.; Cuesta, E.; Zapico, P.; Barreiro, J. Proposal of Design Rules for Improving the Accuracy of Selective Laser Melting (SLM) Manufacturing Using Benchmarks Parts. Rapid Prototyp. J. 2022, 28, 1129–1143. [Google Scholar] [CrossRef]
- Taylor, H.C.; Garibay, E.A.; Wicker, R.B. Toward a Common Laser Powder Bed Fusion Qualification Test Artifact. Addit. Manuf. 2021, 39, 101803. [Google Scholar] [CrossRef]
- Subbaian Kaliamoorthy, P.; Subbiah, R.; Bensingh, J.; Kader, A.; Nayak, S. Benchmarking the Complex Geometric Profiles, Dimensional Accuracy and Surface Analysis of Printed Parts. Rapid Prototyp. J. 2019, 26, 319–329. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, L.; Tang, Y.; Singh, J.P.; Bouguila, N.; Wang, C.; Wang, H.; Du, J. Fast Neighbor Search by Using Revised K-d Tree. Inf. Sci. 2019, 472, 145–162. [Google Scholar] [CrossRef]
- Hanzl, P.; Zetek, M.; Bakša, T.; Kroupa, T. The Influence of Processing Parameters on the Mechanical Properties of SLM Parts. Procedia Eng. 2015, 100, 1405–1413. [Google Scholar] [CrossRef]
- Yadav, P.; Rigo, O.; Arvieu, C.; Le Guen, E.; Lacoste, E. Data Treatment of In Situ Monitoring Systems in Selective Laser Melting Machines. Adv. Eng. Mater. 2021, 23, 2001327. [Google Scholar] [CrossRef]






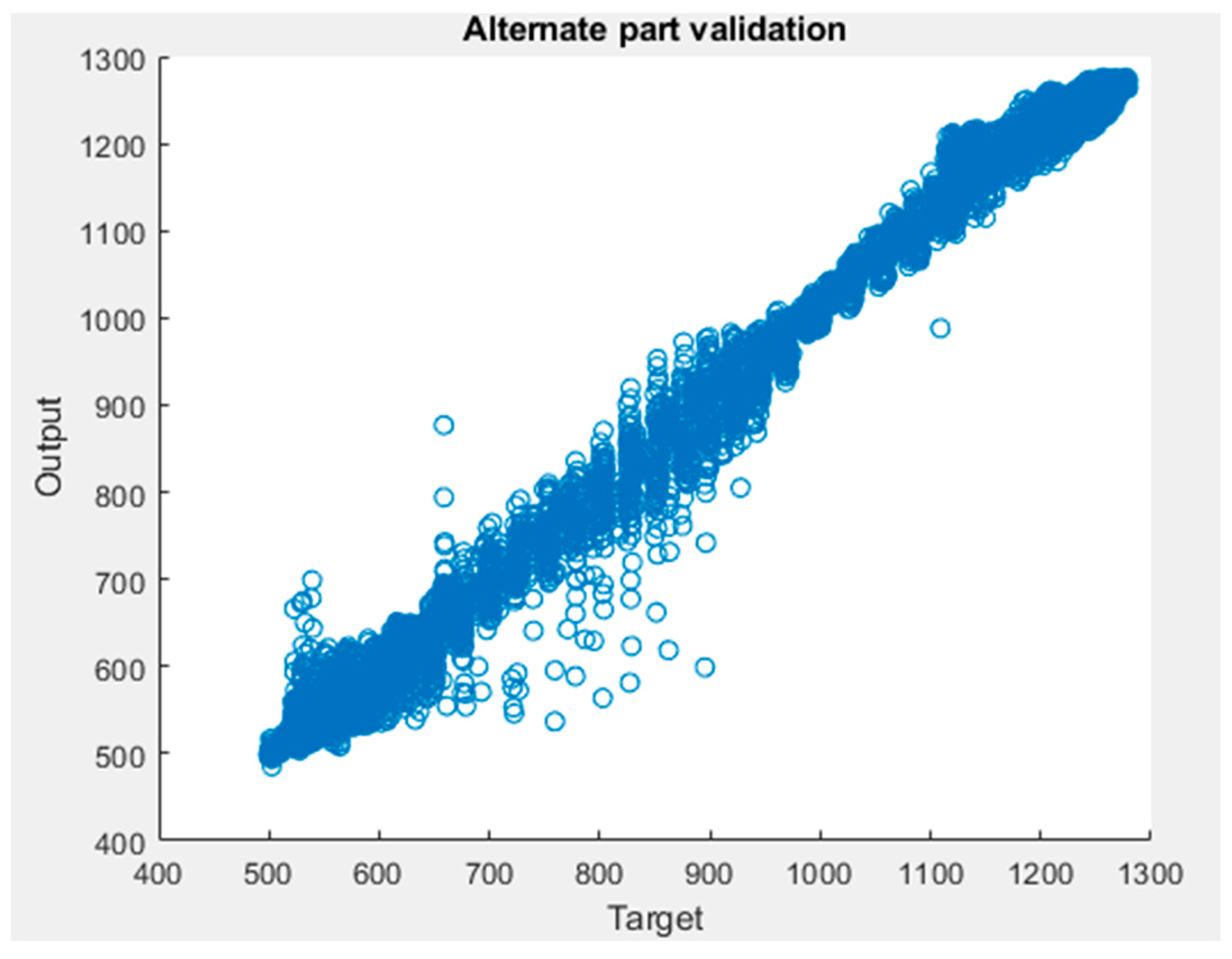
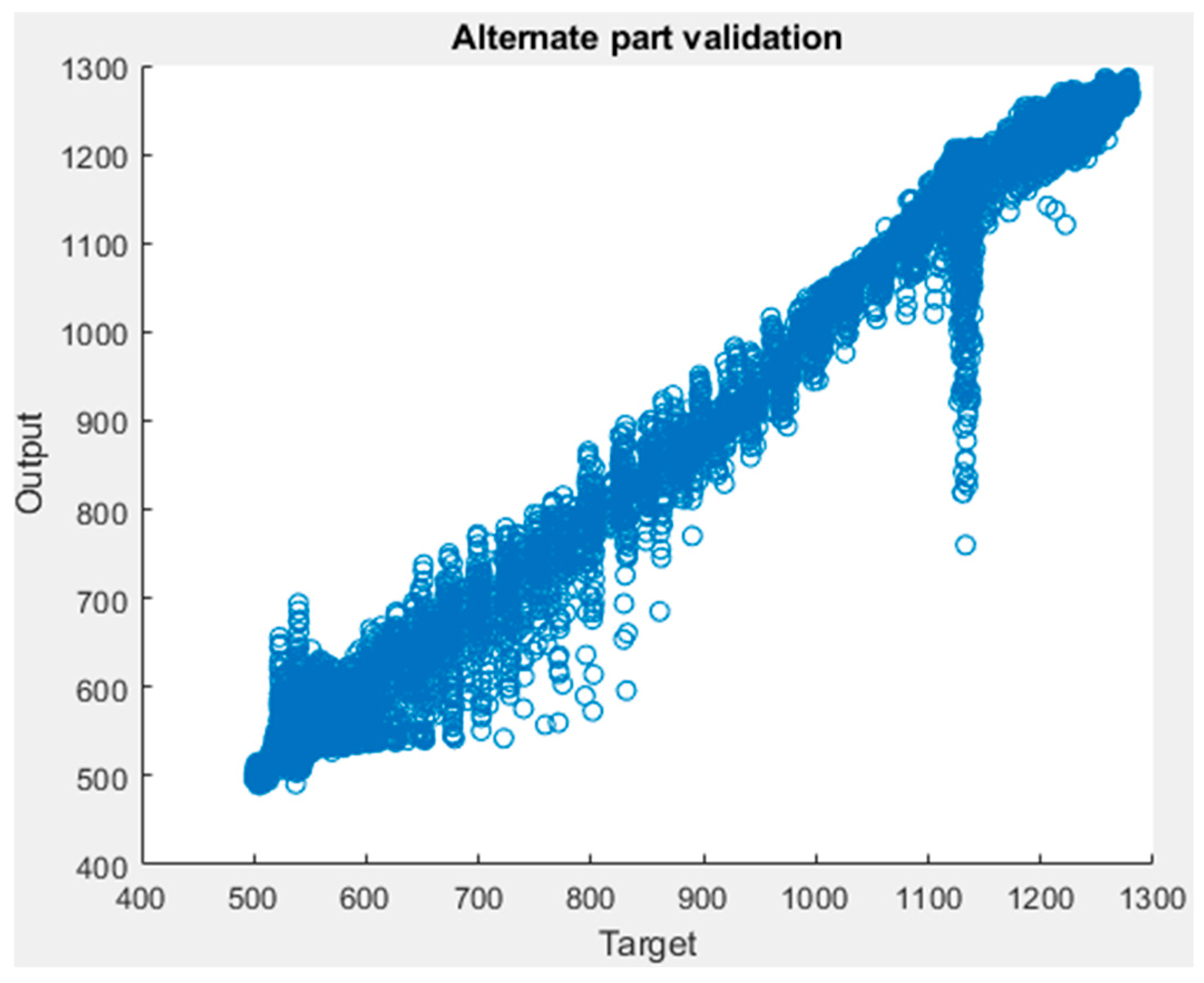
| Parameter | Value |
|---|---|
| Analysis type | Thermo-mechanical |
| Velocity | 1.2 m/s |
| Laser power | 600 W |
| Powder layer thickness | 3 × 10−5 m |
| Powder absorption | 9% |
| Cooling time | 10 s |
| Base temperature | 298 K |
| Element size (length and height) | 0.001 m |
| Epochs | MSE (K2) | MRE | MAE (K) |
|---|---|---|---|
| 1000 | 398.26 | 1.58% | 11.87 |
| 2000 | 354.76 | 1.39% | 10.67 |
| 3000 | 355.90 | 1.36% | 10.39 |
| 4000 | 339.80 | 1.31% | 10.15 |
| 5000 | 300.47 | 1.27% | 9.73 |
| 6000 | 356.58 | 1.34% | 10.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadimitriou, N.; Stathatos, E.; Vosniakos, G.-C. Residual Temperature Prediction in Selective Laser Melting by Deep Neural Networks. Metals 2025, 15, 1119. https://doi.org/10.3390/met15101119
Papadimitriou N, Stathatos E, Vosniakos G-C. Residual Temperature Prediction in Selective Laser Melting by Deep Neural Networks. Metals. 2025; 15(10):1119. https://doi.org/10.3390/met15101119
Chicago/Turabian StylePapadimitriou, Nikolaos, Emmanuel Stathatos, and George-Christopher Vosniakos. 2025. "Residual Temperature Prediction in Selective Laser Melting by Deep Neural Networks" Metals 15, no. 10: 1119. https://doi.org/10.3390/met15101119
APA StylePapadimitriou, N., Stathatos, E., & Vosniakos, G.-C. (2025). Residual Temperature Prediction in Selective Laser Melting by Deep Neural Networks. Metals, 15(10), 1119. https://doi.org/10.3390/met15101119








