Formation of Stainless Steel Welded Joints Produced with the Application of Laser and Plasma Energy Sources
Abstract
1. Introduction
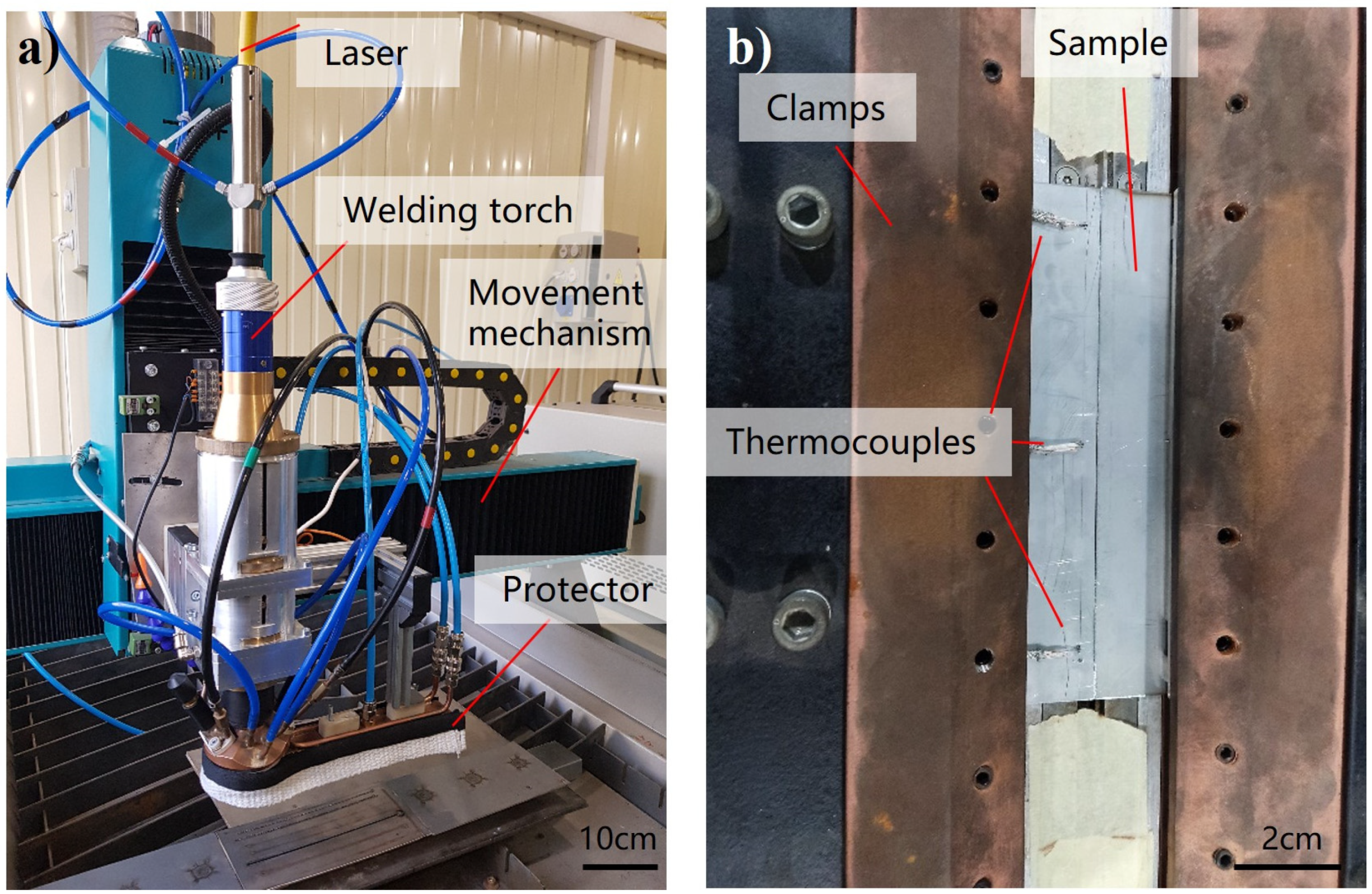
2. Materials and Methods
3. Results
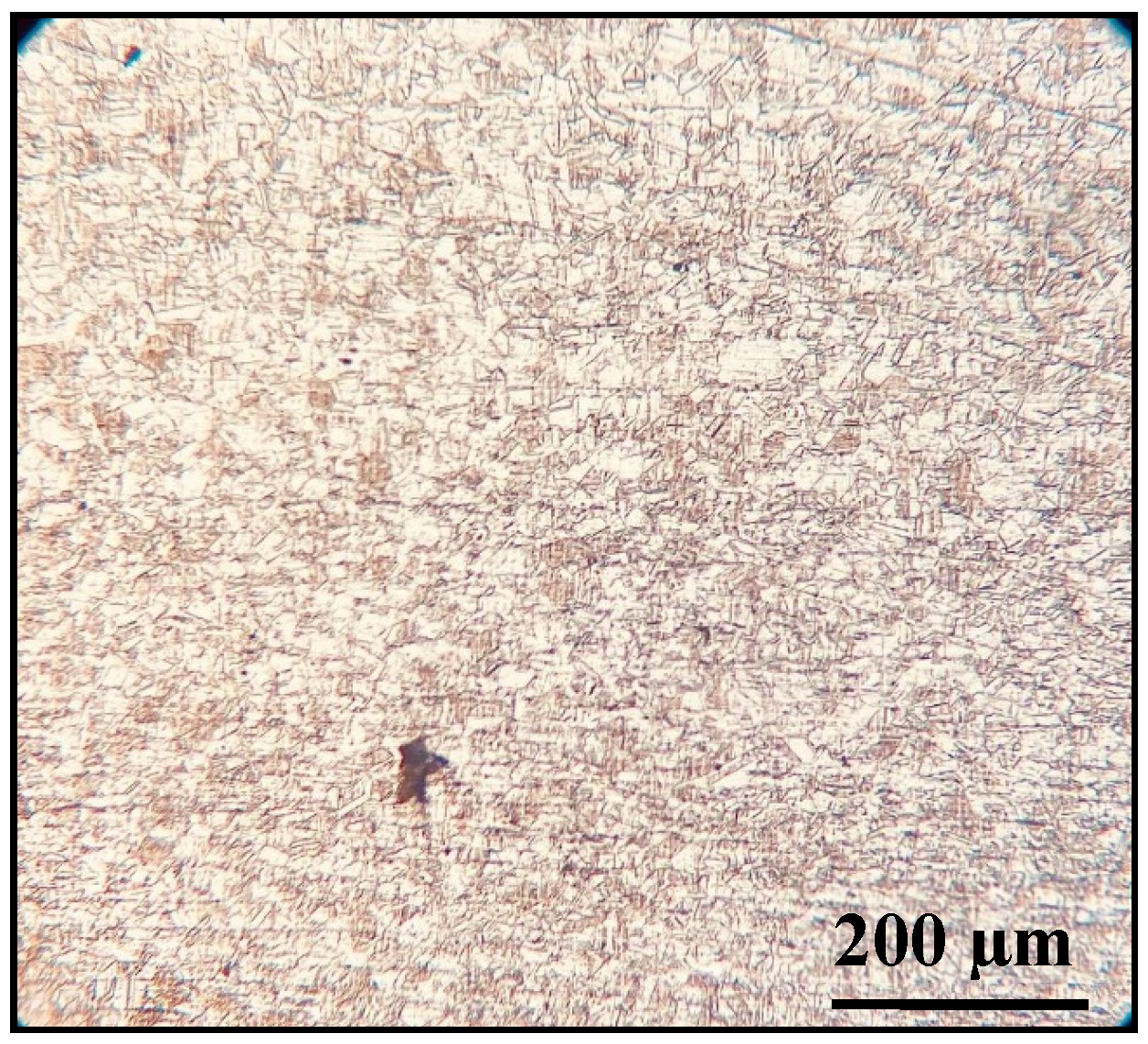
3.1. Investigation of Weld Structure Produced by Laser, Plasma, and Laser–Plasma Welding
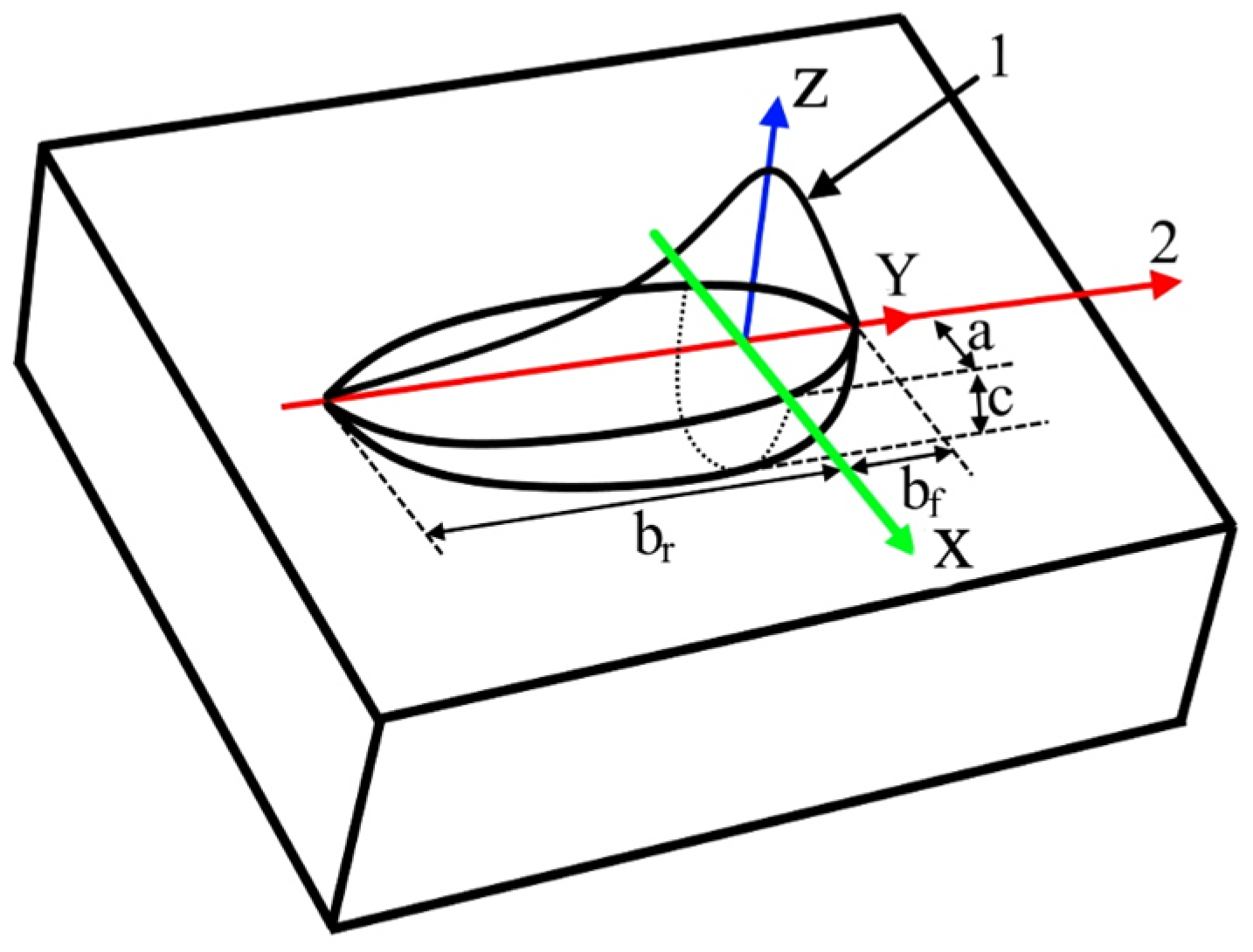
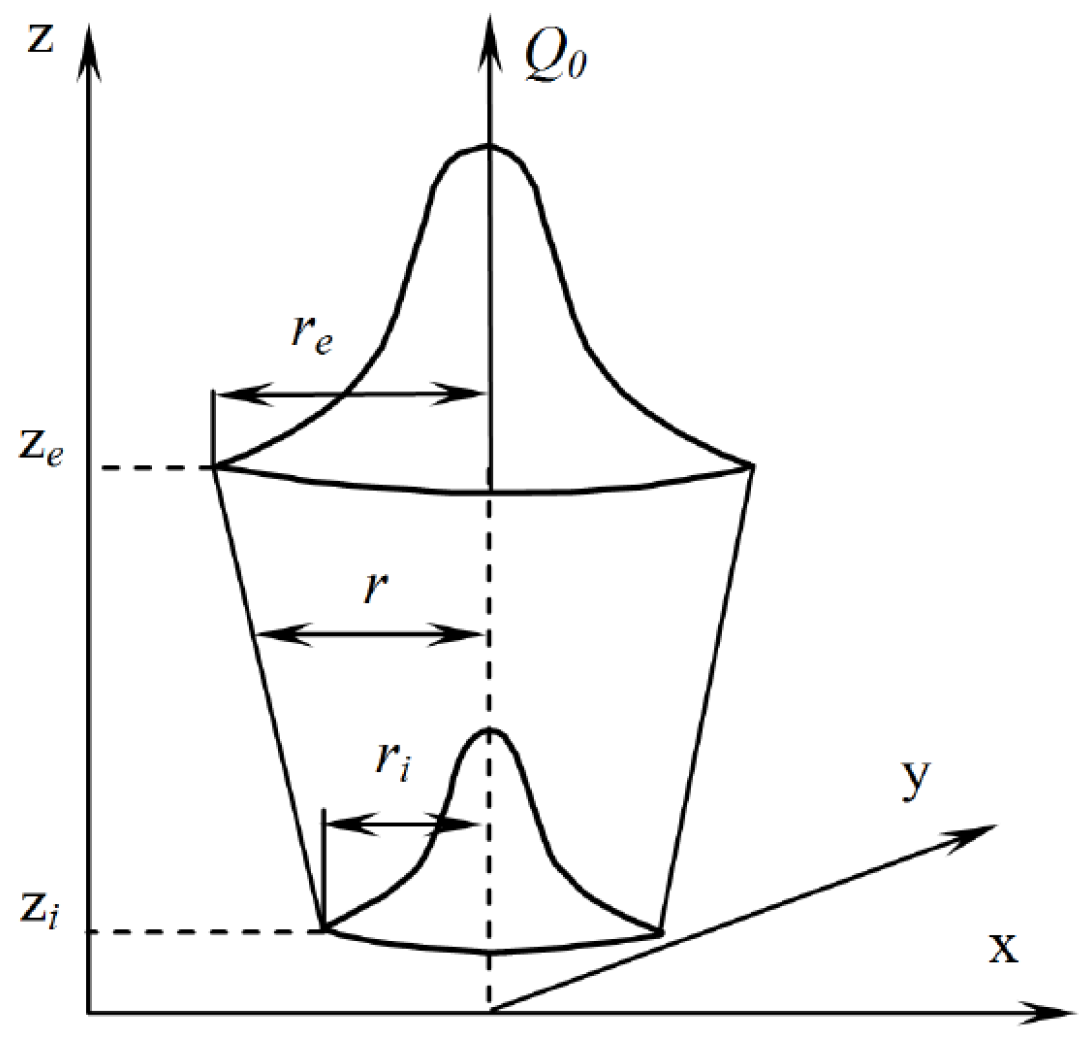
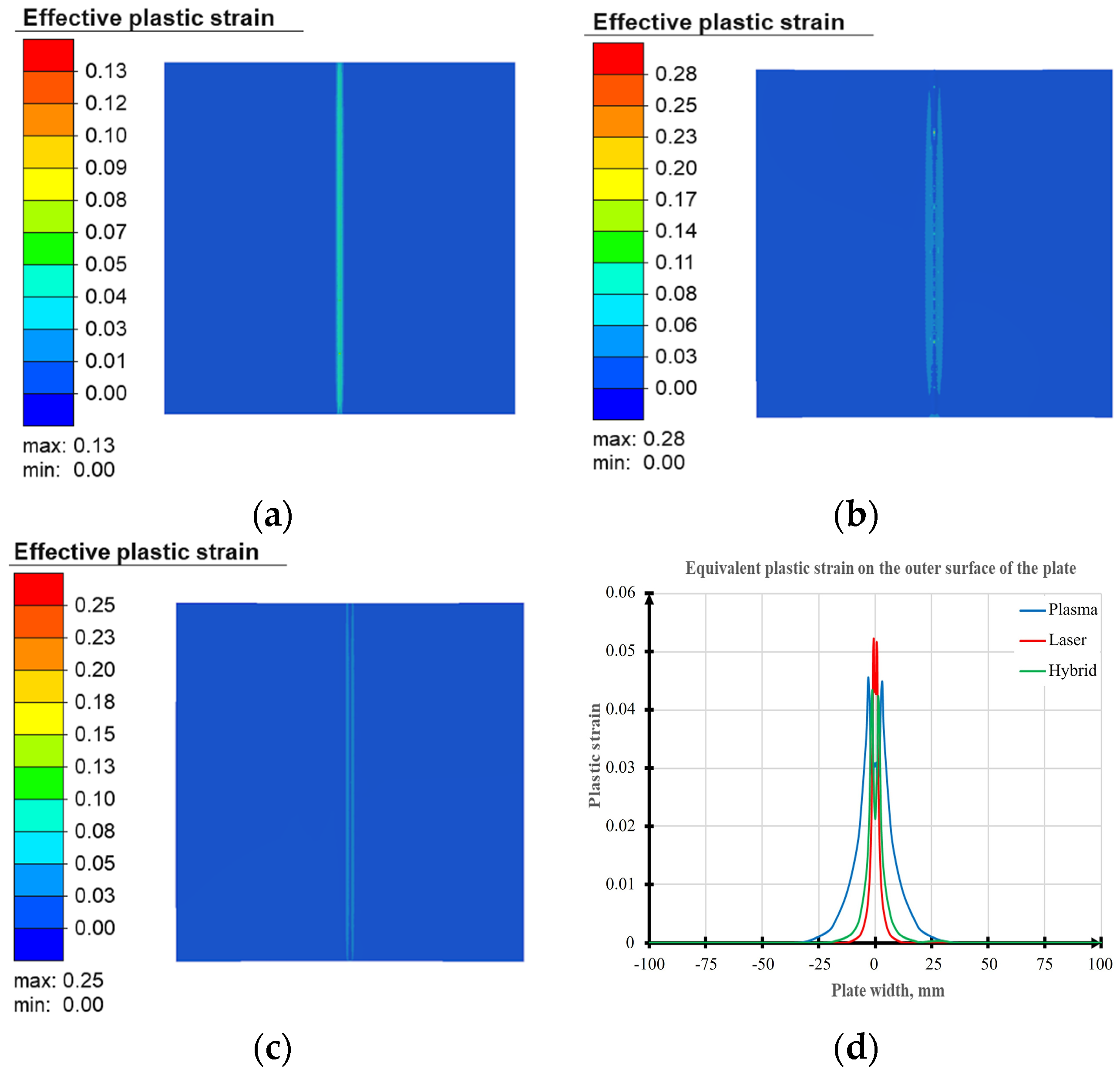
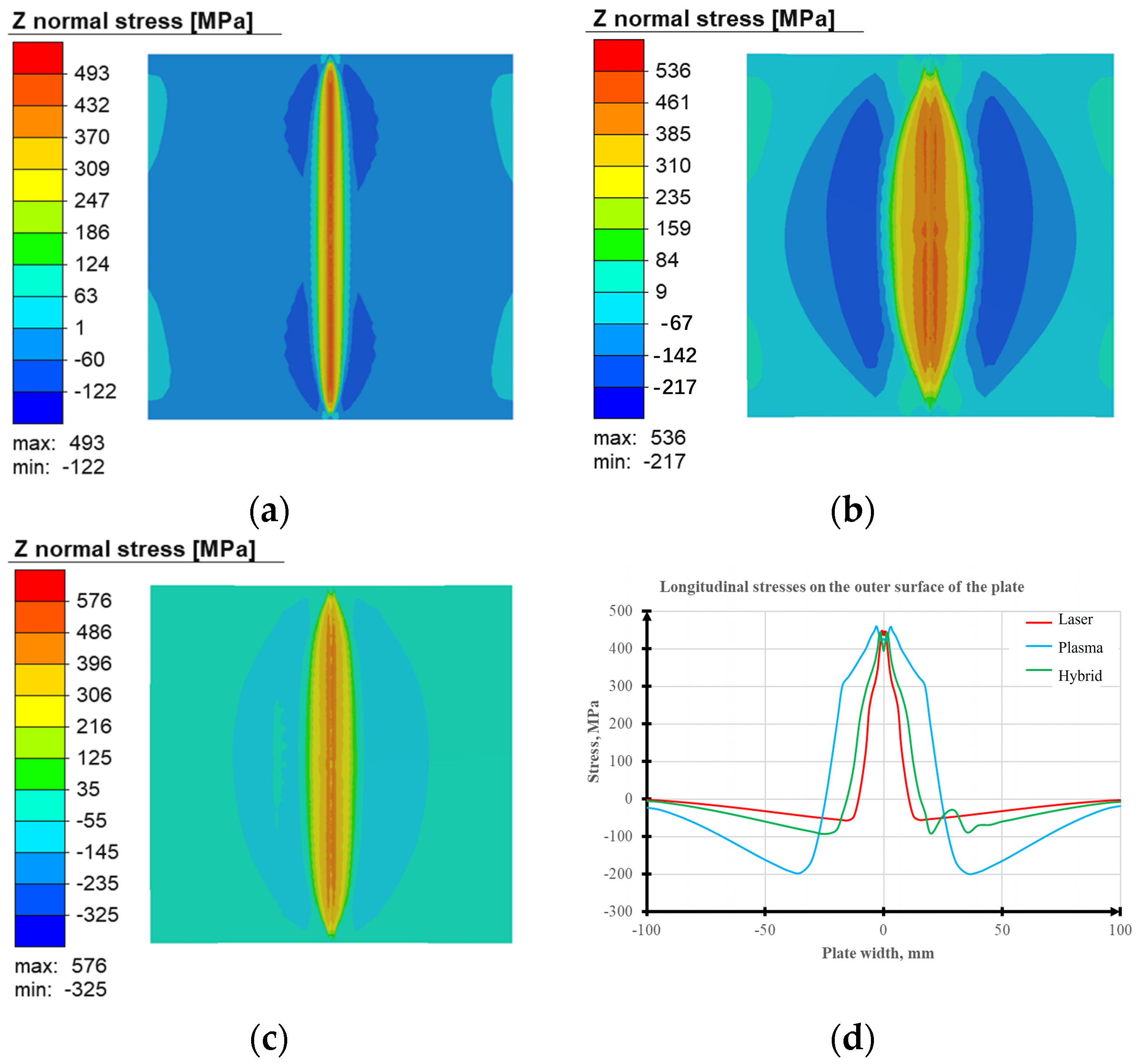
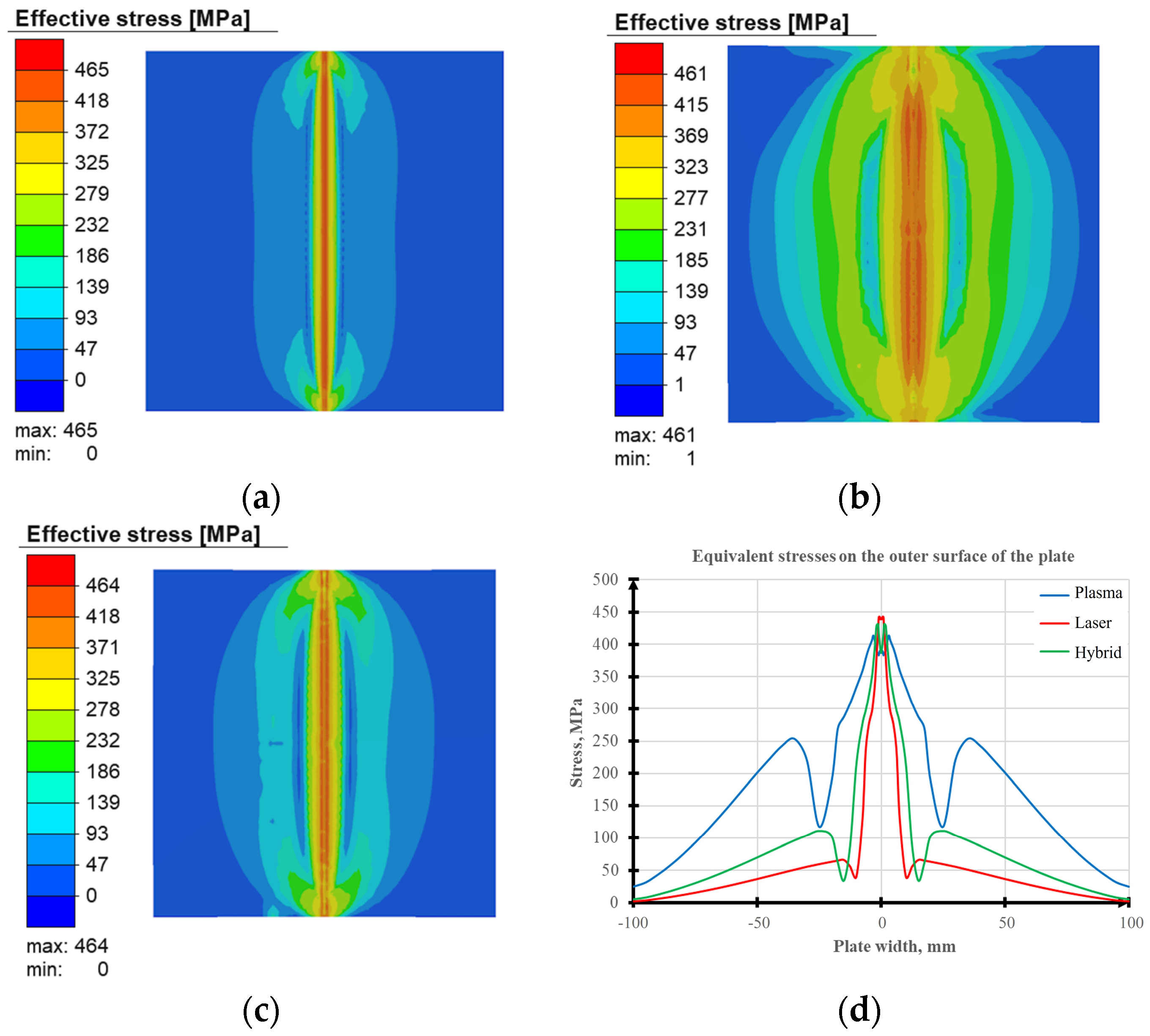
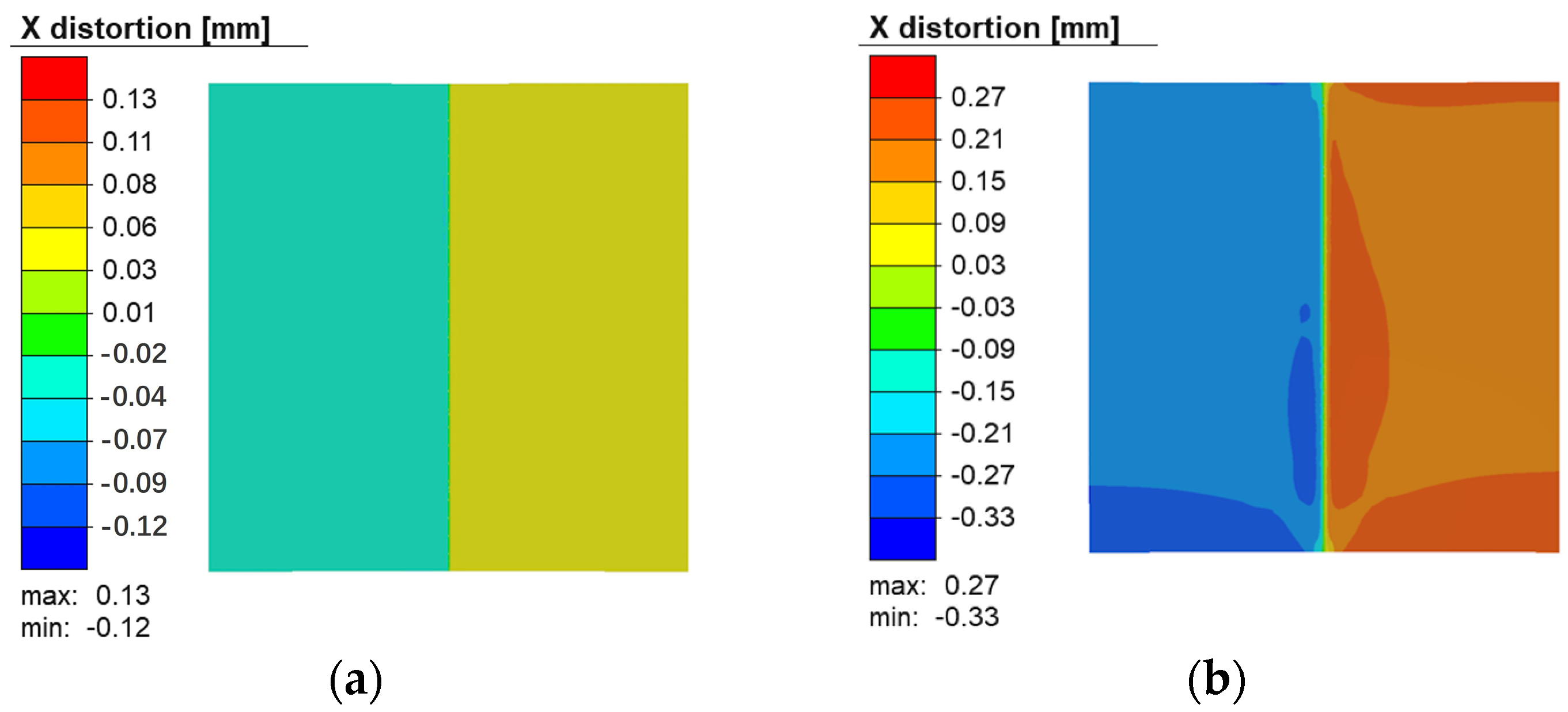
3.2. Modeling the Stress–Strain State of Welded Joints Produced by Laser, Plasma and Hybrid Laser–Plasma Processes
3.3. Experimental Evaluation of Residual Stresses in Welded Joints and Verification of Modeling Results
3.4. Influence of the Conditions of the Technology and Process of Welding on the Physical–Mechanical Properties of the Produced Joints
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Acherjee, B. Hybrid laser arc welding: State-of-art review. Opt. Laser Technol. 2018, 99, 60–71. [Google Scholar] [CrossRef]
- Gook, S.; El-Batahgy, A.M.; Gumenyuk, A.; Biegler, M.; Rethmeier, M. Application of Hybrid Laser Arc Welding for Construction of LNG Tanks Made of Thick Cryogenic 9% Ni Steel Plates. Lasers Manuf. Mater. Process. 2023, 10, 659–680. [Google Scholar] [CrossRef]
- Stelling, K.; Schobbert, H.; Kannengiesser, T.; Boellinghaus, T. Vertical-up and -down Laser Plasma Powder Hybrid Welding of a High Nitrogen Austenitic Stainless Steel. Weld. World 2013, 49, 45–49. [Google Scholar] [CrossRef]
- Mu, Z.; Chen, X.; Zheng, Z.; Huang, A.; Pang, S. Laser cooling arc plasma effect in laser-arc hybrid welding of 316L stainless steel. Int. J. Heat Mass Transfer. 2019, 132, 861–870. [Google Scholar] [CrossRef]
- Górka, J.; Stano, S. Microstructure and Properties of Hybrid Laser Arc Welded Joints (Laser Beam-MAG) in Thermo-Mechanical Control Processed S700MC Steel. Metals 2018, 8, 132. [Google Scholar] [CrossRef]
- Schultz, V.; Woizeschke, P. High Seam Surface Quality in Keyhole Laser Welding: Buttonhole Welding. J. Manuf. Mater. Process. 2018, 2, 78. [Google Scholar] [CrossRef]
- Han, J.; Shi, Y.; Zhang, G.; Korzhyk, V.; Le, W.-Y. Minimizing defects and controlling the morphology of laser welded aluminum alloys using power modulation-based laser beam oscillation. J. Manuf. Process. 2022, 83, 49–59. [Google Scholar] [CrossRef]
- Svenungsson, J.; Choquet, I.; Kaplan, A.F.H. Laser Welding Process—A Review of Keyhole Welding Modelling. Phys. Procedia 2015, 78, 182–191. [Google Scholar] [CrossRef]
- Emmelmann, C.; Kirchhoff, M.; Petri, N. Development of Plasma-Laser-Hybrid Welding Process. Phys. Procedia 2011, 12, 194–200. [Google Scholar] [CrossRef]
- Swanson, P.T.; Page, C.J.; Read, E.; Wu, H.Z. Plasma augmented laser welding of 6 mm steel plate. Sci. Technol. Weld. Join. 2007, 12, 153–160. [Google Scholar] [CrossRef]
- Xu, Y.; Hou, X.; Shi, Y.; Zhang, W.; Gu, Y.; Feng, C.; Korzhyk, V. Correlation between the microstructure and corrosion behaviour of copper/316 L stainless-steel dissimilar-metal welded joints. Corros. Sci. 2021, 191, 109729. [Google Scholar] [CrossRef]
- Gu, Y.; Xu, Y.; Shi, Y.; Feng, C.; Korzhyk, V. Corrosion resistance of 316 stainless steel in a simulated pressurized water reactor improved by laser cladding with chromium. Surf. Coat. Technol. 2022, 441, 128534. [Google Scholar] [CrossRef]
- Mahrle, A.; Rose, S.; Schnick, M.; Beyer, E.; Füssel, U. Laser-assisted plasma arc welding of stainless steel. J. Laser Appl. 2013, 25, 032006. [Google Scholar] [CrossRef]
- Clemens, M.; Warnecke, L.; Olschok, S.; Reisgen, U.; Steiner, M.F. Direction-independent laser-GMA hybrid welding with coaxial wire feed and annular beam. Weld. World 2023, 67, 89–97. [Google Scholar] [CrossRef]
- Markashova, L.I.; Poznyakov, V.D.; Shelyagin, V.D.; Berdnikova, E.N.; Bernatsky, A.V.; Alekseenko, T.A. Effect of metal structure on service properties of high-strength steel welded joints produced using different methods of welding. Paton Weld. J. 2018, 2, 7–13. [Google Scholar] [CrossRef]
- Hipp, D.; Mahrle, A.; Beyer, E.; Jäckel, S.; Hertel, M.; Füssel, U. Thermal Efficiency Analysis for Laser-Assisted Plasma Arc Welding of AISI 304 Stainless Steel. Materials 2019, 12, 1460. [Google Scholar] [CrossRef] [PubMed]
- Deng, D. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects. Mater. Des. 2009, 30, 359–366. [Google Scholar] [CrossRef]
- Evin, E.; Tomáš, M. The Influence of Laser Welding on the Mechanical Properties of Dual Phase and Trip Steels. Metals 2017, 7, 239. [Google Scholar] [CrossRef]
- Yu, T.; Zhong, F.; Zhang, F.; Ying, C.; Geng, G. Application of Scanning Electron Microscopy in Metal Material Detection. J. Phys. Conf. Ser. 2021, 2002, 012010. [Google Scholar] [CrossRef]
- Lobanov, L.M.; Pivtorak, V.A.; Savitsky, V.V.; Tkachuk, G.I. Procedure for determination of residual stresses in welded joints and structural elements using electron speckle-interferometry. Paton Weld. J. 2006, 1, 24–29. [Google Scholar]
- Korzhyk, V.M.; Grynyuk, A.A.; Khaskin, V.Y.; Illiashenko, Y.V.; Klochkov, I.M.; Ganushchak, O.V.; Yu, X.; Liuyi, H. Improving the efficiency of robotic fabrication of steel truss welded structures. Paton Weld. J. 2021, 5, 12–18. [Google Scholar] [CrossRef]
- Anca, A.; Cardona, A.; Risso, J.; Fachinotti, V.D. Finite element modeling of welding processes. Appl. Math. Model. 2011, 35, 688–707. [Google Scholar] [CrossRef]
- Tritt, T.M. Thermal Conductivity: Theory, Properties, and Applications; Physics of Solids and Liquids (PSLI); Springer: New York, NY, USA, 2004; 290p. [Google Scholar] [CrossRef]
- Khudyakov, A.; Korobov, Y.; Danilkin, P.; Kvashnin, V. Finite element modeling of multiple electrode submerged arc welding of large diameter pipes. IOP Conf. Ser. Mater. Sci. Eng. 2019, 681, 012025. [Google Scholar] [CrossRef]
- Goldak, J.A.; Akhlagi, M. Computational Welding Mechanics; Springer: New York, NY, USA, 2005; 322р. [Google Scholar] [CrossRef]
- Li, Y.; Bushby, A.J.; Dunstan, D.J. The Hall–Petch effect as a manifestation of the general size effect. Proc. Math. Phys. Eng. Sci. 2016, 472, 20150890. [Google Scholar] [CrossRef] [PubMed]
- Asgari, M.; Kouchakzadeh, M.A. An equivalent von Mises stress and corresponding equivalent plastic strain for elastic-plastic ordinary peridynamics. Meccanica 2019, 54, 1001–1014. [Google Scholar] [CrossRef]
- Lobanov, L.; Pivtorak, V.; Savitsky, V.; Tkachuk, G. Technology and Equipment for Determination of Residual Stresses in Welded Structures Based on the Application of Electron Speckle-Interferometry. Mater. Sci. Forum 2013, 768–769, 166–173. [Google Scholar] [CrossRef]
- Lobanov, L.M.; Pivtorak, V.A.; Savitsky, V.V.; Tkachuk, G.I. Determination of residual stresses in structural elements based on application of electronic speckle-interferometry and finite element method. In Proceedings of the 13th International Conference on Fracture, Beijing, China, 16–21 June 2013. [Google Scholar]
- Korzhyk, V.; Khaskin, V.; Savitsky, V.; Klochkov, I.; Kvasnytsyi, V.; Perepichay, A.; Peleshenko, S.; Grynyuk, A.; Aloshyn, A.; Shutkevych, O. Calculation-experimental procedure for determining welding deformations and stresses based on a digital image correlation method. East.-Eur. J. Enterp. Technol. 2022, 5, 44–52. [Google Scholar] [CrossRef]
- Lobanov, L.M.; Kondratenko, I.P.; Mikhalskyi, V.M.; Pashchin, M.O.; Karlov, O.M.; Chopyk, V.V.; Mykhodui, O.L. Electrotechnical Complex for Electrodynamic Processing of Welded Joints. Tech. Electrodyn. 2020, 2020, 1–3. [Google Scholar] [CrossRef]
- Lobanov, L.; Savitsky, V. Residual Stresses Determination with Plasticity Effects by Electron Speckle-Interferometry Hole-Drilling Method. Mater. Res. Proc. 2016, 2, 389–394. [Google Scholar] [CrossRef][Green Version]
- Zhang, W.; Xu, Y.; Shi, Y.; Su, G.; Gu, Y.; Korzhyk, V. Intergranular corrosion characteristics of high-efficiency wire laser additive manufactured Inconel 625 alloys. Corros. Sci. 2022, 205, 110422. [Google Scholar] [CrossRef]
- Viňáš, J.; Brezinová, J.; Sailer, H.; Brezina, J.; Sahul, M.; Maruschak, P.; Prentkovskis, O. Properties Evaluation of the Welded Joints Made by Disk Laser. Materials 2021, 14, 2002. [Google Scholar] [CrossRef] [PubMed]
- ISO 6892-1:2019; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. ISO: Geneva, Switzerland, 2019.
- Viňáš, J.; Brezinová, J.; Brezina, J.; Maruschak, P.O. Structural and Mechanical Features of Laser-Welded Joints of Zinc-Coated Advanced Steel Sheets. Mater. Sci. 2019, 55, 46–51. [Google Scholar] [CrossRef]
- Meng, Y.; Fengping, Z.; Liuyi, H.; Shuo, J.; Chao, P.; Korzhyk, V. Study on Efficient Determination of the Content of Key Elements in Thin Stainless Steel by Spark Discharge Optical Emission Spectrometry with Contrivable Sample Thickening. J. Phys. Conf. Ser. 2023, 2539, 012068. [Google Scholar] [CrossRef]
- Hafez, K.M. The influence of shielding gases on keyhole-induced porosity and nitrogen absorption in SS 304 stainless steel fiber laser welds. Int. J. Adv. Manuf. Technol. 2023, 127, 1887–1894. [Google Scholar] [CrossRef]
- Sun, J.; Nie, P.; Feng, K.; Li, Z.; Guo, B.; Jiang, E. The elimination of pores in laser welds of AISI 304 plate using different shielding gases. J. Mater. Process. Technol. 2017, 248, 56–63. [Google Scholar] [CrossRef]




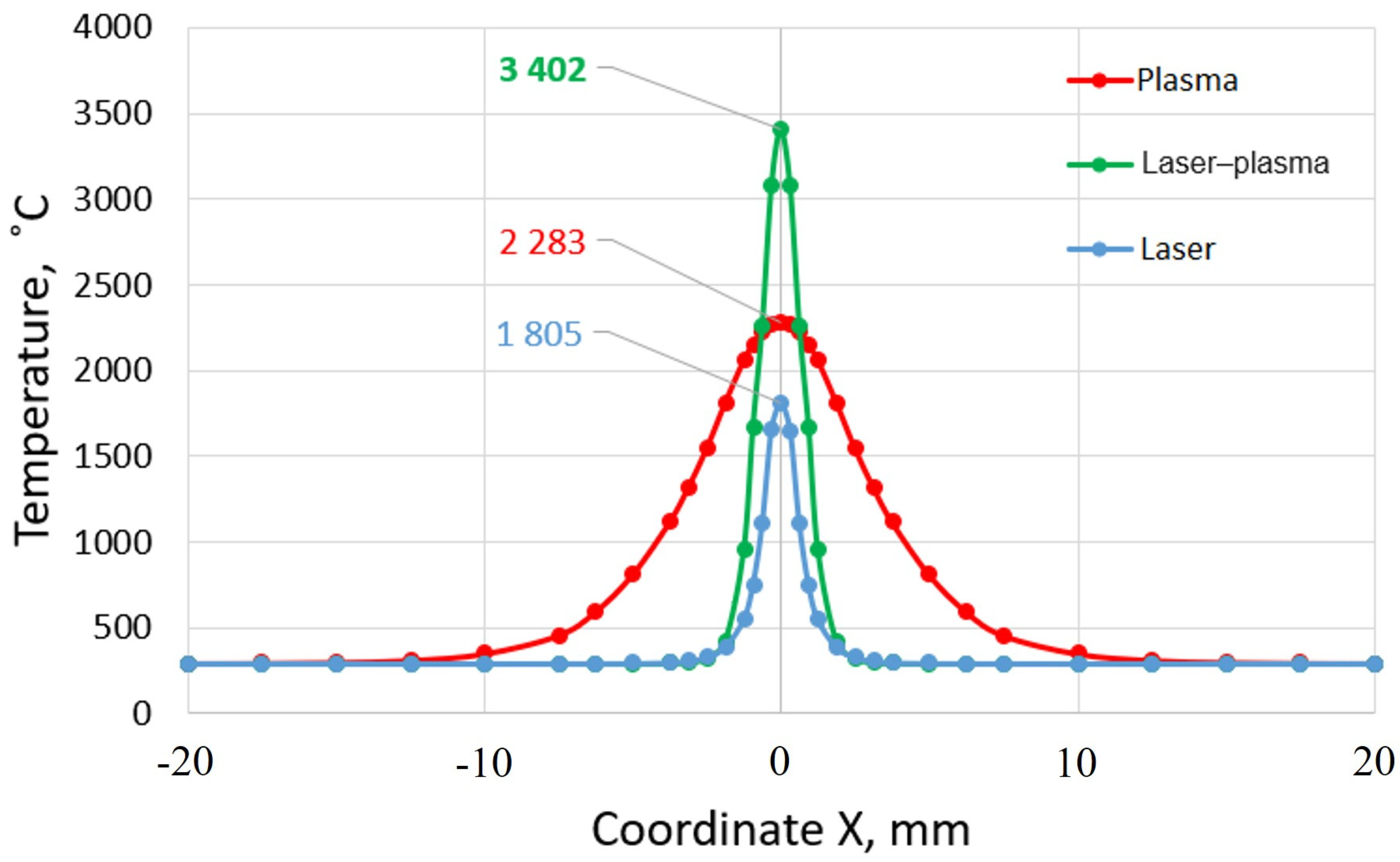
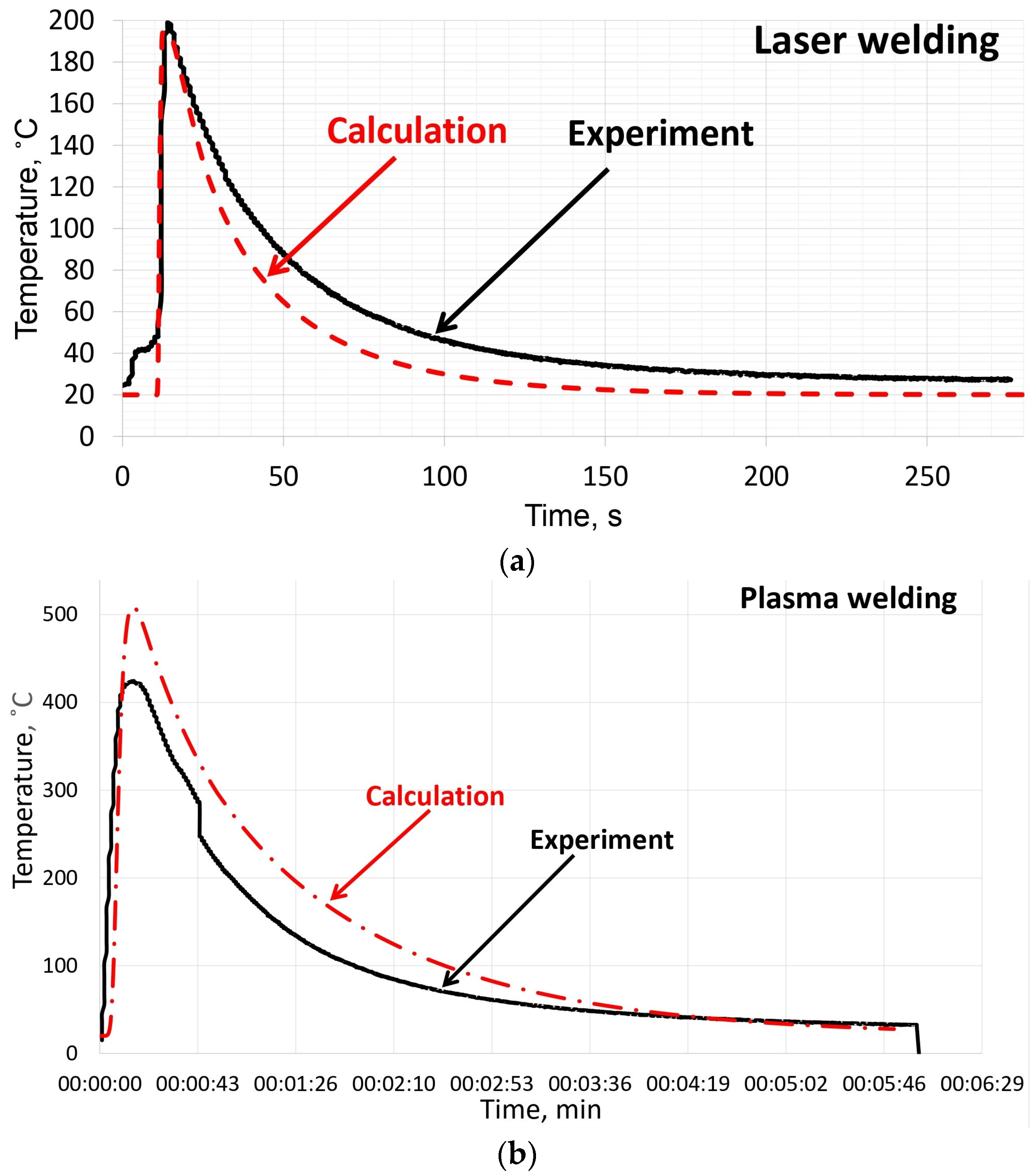
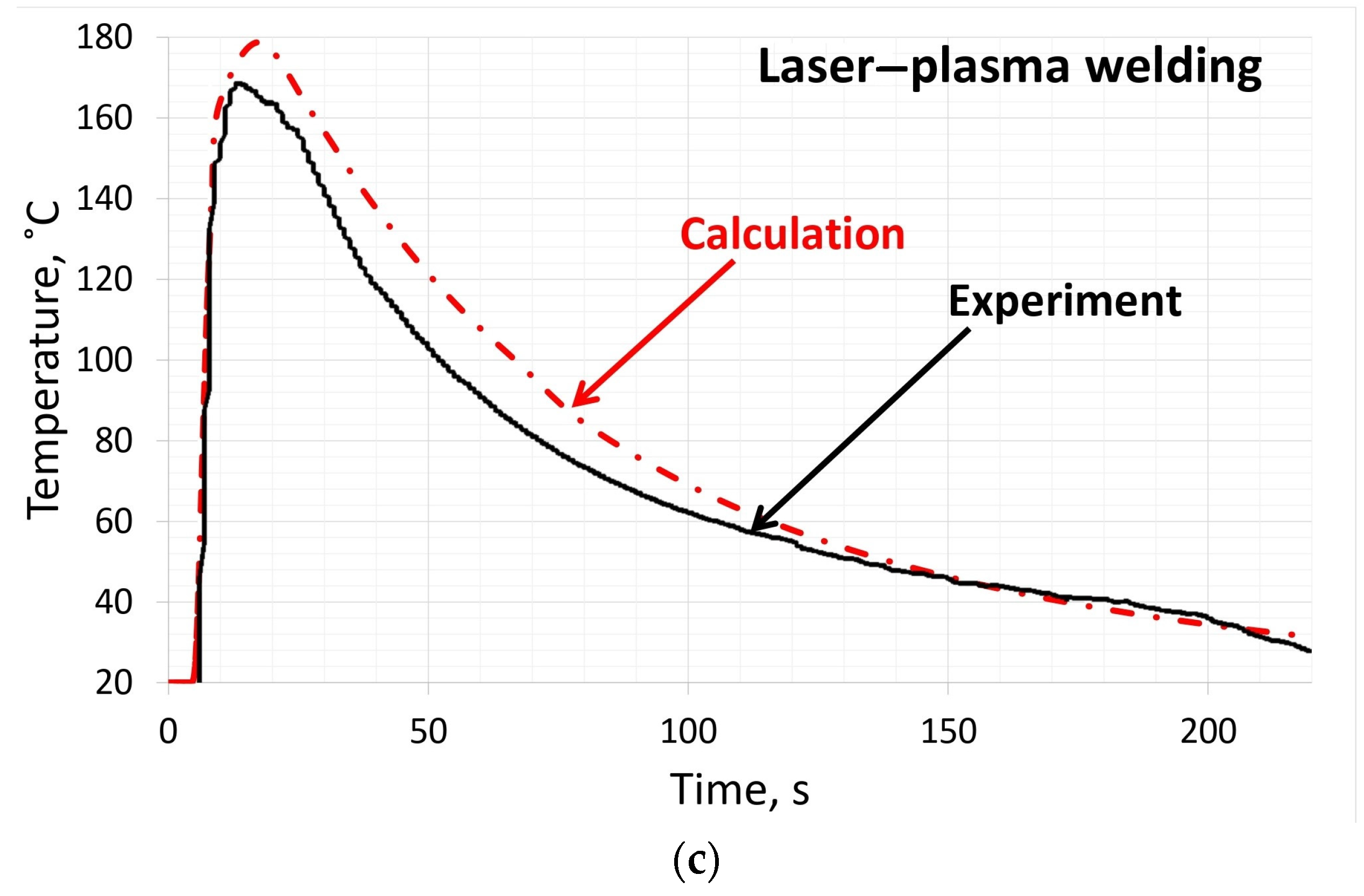




| Material | Fe | C | Si | Mn | Ni | Cr | Cu | P | S |
|---|---|---|---|---|---|---|---|---|---|
| AISI 304 steel | Base | 0.08 | 0.8 | - | 8–10 | 18–20 | 0.5–1.0 | 0.045 | 0.03 |
| Young’s Modulus, GPa | Yield Limit σ0.2, MPa | Ultimate Strength, σt, MPa | Relative Elongation, % |
|---|---|---|---|
| 193 | 300 | 654.4 | 44.45 |
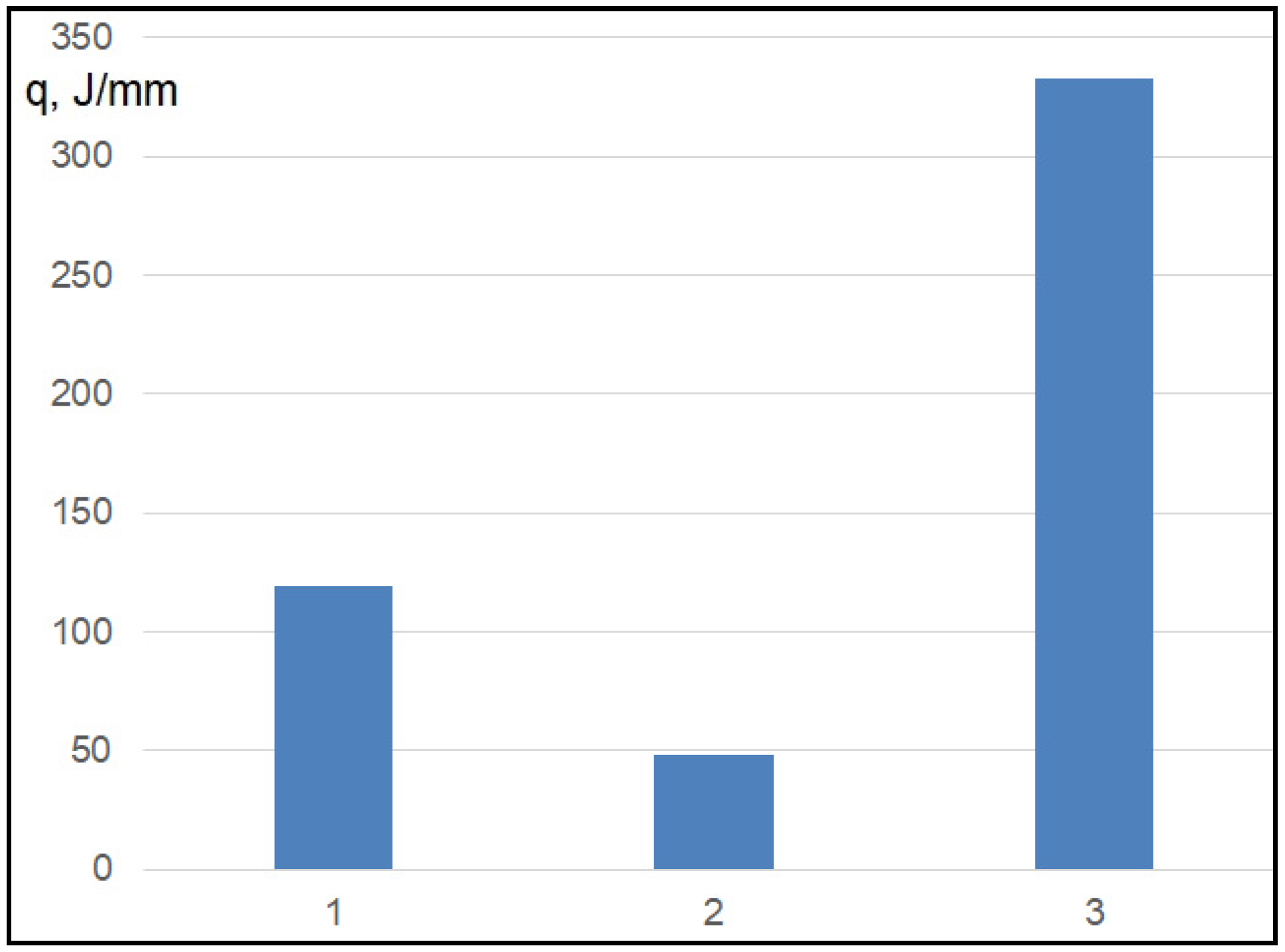
| Process | P, kW | I, A | U, V | V, m/min | ΔF, * mm | q, J/mm |
|---|---|---|---|---|---|---|
| Laser | 0.6 | - | - | 0.8 | 0.4 | 45 |
| 0.8 | 1 | 0.7 | 48 | |||
| 1.0 | 1.2 | 1.0 | 50 | |||
| Plasma | - | 70 | 19.8 | 0.2 | - | 416 |
| 80 | 20.8 | 0.3 | 333 | |||
| 90 | 21.2 | 0.4 | 286 | |||
| Hybrid | 0.6 | 70 | 25.4 | 1.1 | 0.4 | 130 |
| 0.8 | 80 | 27.2 | 1.5 | 0.7 | 119 | |
| 1.0 | 90 | 28.5 | 1.7 | 1.0 | 126 |
| Process | Parameters | Zone | |||
|---|---|---|---|---|---|
| Weld | Fusion Line | HAZ | BM | ||
| Hybrid welding | h 1 × l 2, µm | (10–15) × (40–150) | (8–15) × (80–170) | - | - |
| æ 3 (l/h) | 4–10 | 10–11 | - | - | |
| Dg 4, µm | - | 8–17 Weld, 5–15 (20) HAZ,6 | 5–15 | 5–18 | |
| HV 5 0.1 | 232 | 238 | 212 | 220 | |
| Laser welding | h × l, µm | (8–15) × (30–80) | (5–10) × (50–100) | - | - |
| æ (l/h) | 3.8–5.3 | 10 | - | - | |
| Dg, µm | - | 8–16 Weld, 4–12 HAZ | 5–15 | 5–18 | |
| HV 0.1 | 190 | 253 | 237 | 241 | |
| Plasma welding | h × l, µm | (10–50) × (100–300) | (10–20) × (60–200) Weld (5–20) × (30–100) HAZ | - | - |
| æ (l/h) | 6–10 | 6–10 Weld, 5–6 HAZ | - | - | |
| Dg, µm | - | 10–20 Weld, 10–15 HAZ | 10–30 | 5–20 | |
| HV 0.1 | 248 | 220 | 208 | 231 | |
| Process | Parameters | Zone | |||
|---|---|---|---|---|---|
| Weld | Fusion Line | HAZ | BM | ||
| Laser–plasma welding | dS 1, µm | 2–10 | 2–10 | 5–15 | 3–5 |
| hTW 2, µm | 0.1–0.2 | 0.1–0.2 | - | 0.1–0.5 | |
| Laser welding | dS, µm | 6–10 2–4 × 8–12 | 2–6 | 2–4 × 5–20 | 3–5 |
| hTW, µm | 0.1–0.3 | 0.1–0.3 | - | 0.1–0.8 | |
| Plasma welding | dS, µm | 5–20 3–6 × 10–20 | 5–10 | 5–7 × 20–40 | 3–8 |
| hTW, µm | 0.1–0.5 | 0.1–0.5 | - | 0.1–0.8 | |
| Process | Weld Width, mm Face Side/Back | Pool Section in the Macrosection | Pool Section in the Calculation Model | |
|---|---|---|---|---|
| Laser | Actual | 1.6/0.5 |  |  |
| Modeled | 1.6/0.5 | |||
| Plasma | Actual | 4.2/1.5 |  |  |
| Modeled | 4/1.7 | |||
| Hybrid | Actual | 2.4/0.7 |  |  |
| Modeled | 2.5/0.5 | |||
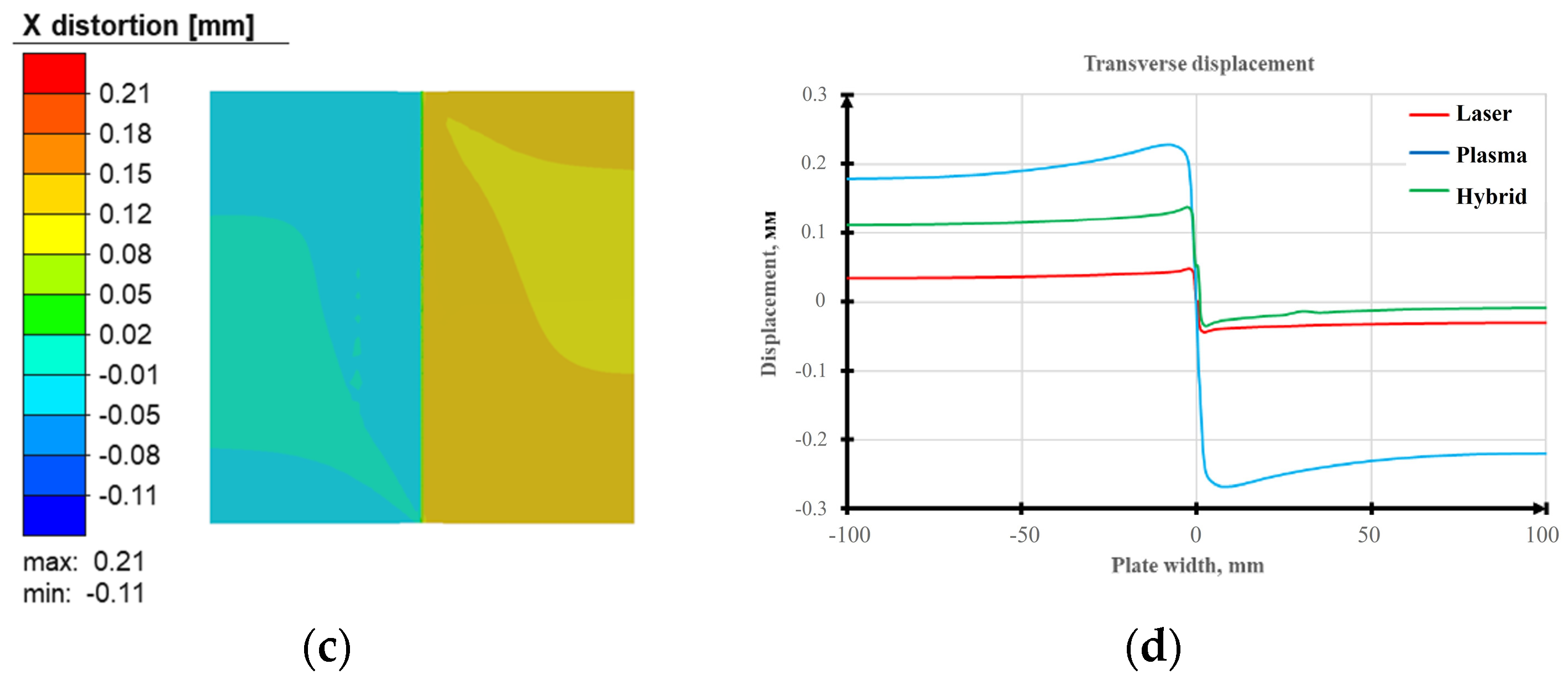
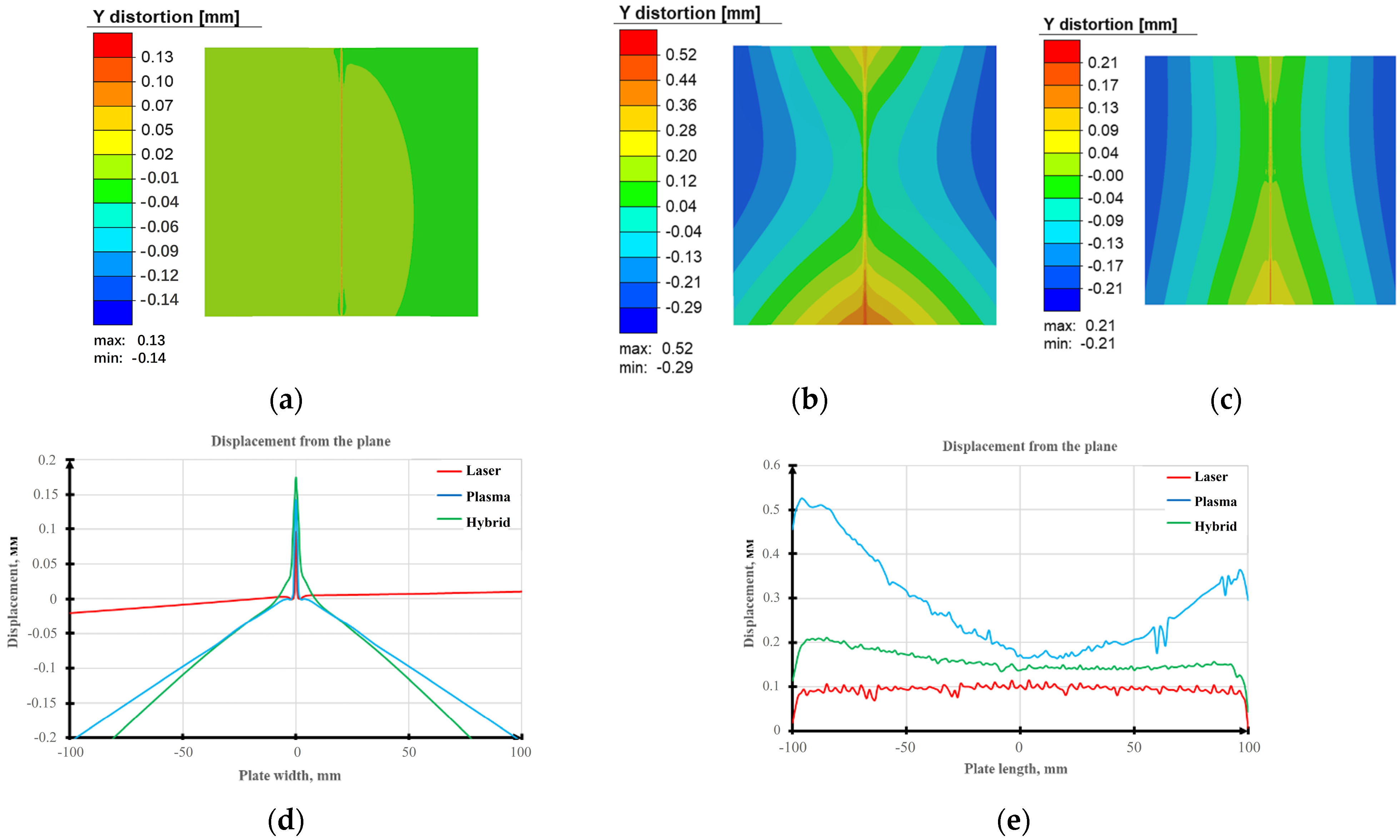
| Process | Equivalent Stresses, MPa | Displacements, mm | ||
|---|---|---|---|---|
| Maximum | Minimum | Maximum | Minimum | |
| Laser | 464.56 | 0.09 | 0.17 | 0 |
| Plasma | 461.18 | 1.29 | 0.52 | −0.29 |
| Hybrid | 464 | 0.14 | 0.2 | 0.1 |
| Welding Process | Fracture Site | Ultimate Strength σt, MPa | Relative Elongation, d % |
|---|---|---|---|
| Hybrid | Initiation and fracture in the HAZ near the fusion line | 645.6 | 51.55 |
| Laser | Initiation and fracture in the HAZ near the fusion line | 647.1 | 52.5 |
| Plasma | Initiation in the zone of fusion of the weld root with the base metal; fracture in the weld metal | 638.8 | 45.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shevchenko, V.; Korzhyk, V.; Gao, S.; Khaskin, V.; Cai, D.; Luo, Z.; Illiashenko, Y.; Kvasnytskyi, V.; Perepichay, A. Formation of Stainless Steel Welded Joints Produced with the Application of Laser and Plasma Energy Sources. Metals 2024, 14, 706. https://doi.org/10.3390/met14060706
Shevchenko V, Korzhyk V, Gao S, Khaskin V, Cai D, Luo Z, Illiashenko Y, Kvasnytskyi V, Perepichay A. Formation of Stainless Steel Welded Joints Produced with the Application of Laser and Plasma Energy Sources. Metals. 2024; 14(6):706. https://doi.org/10.3390/met14060706
Chicago/Turabian StyleShevchenko, Vitalii, Volodymyr Korzhyk, Shiyi Gao, Vladyslav Khaskin, Detao Cai, Ziyi Luo, Yevhenii Illiashenko, Viktor Kvasnytskyi, and Andrii Perepichay. 2024. "Formation of Stainless Steel Welded Joints Produced with the Application of Laser and Plasma Energy Sources" Metals 14, no. 6: 706. https://doi.org/10.3390/met14060706
APA StyleShevchenko, V., Korzhyk, V., Gao, S., Khaskin, V., Cai, D., Luo, Z., Illiashenko, Y., Kvasnytskyi, V., & Perepichay, A. (2024). Formation of Stainless Steel Welded Joints Produced with the Application of Laser and Plasma Energy Sources. Metals, 14(6), 706. https://doi.org/10.3390/met14060706








