An Overview of Estimations for the High-Cycle Fatigue Strength of Conventionally Manufactured Steels Based on Other Mechanical Properties
Abstract
1. Introduction
- “[X]” when referring to a source included in the list of references;
- “Estimation X” when referring to a proposed estimation of included in one of the tables;
- “Equation (X)” when referring to an equation in the main body of the text.
2. Estimations of the Fatigue Strength
2.1. Estimations Based on Ultimate Tensile Strength
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 1 | / | −1 | RB, UA | [15,23] | ||||
| 2 | for MPa MPa for MPa | / | / | / | / | [24] | ||
| 3 | / | −1 | RB | [23] | ||||
| 4 | / | −1 | UA | [15] | ||||
| SCM440 (AF2000) | 42CrMo4 (1.7225) | −1 | EMR | [26] | ||||
| 5 | Carbon steels normalised (ferrite/pearlite) | / | / | / | [27] | |||
| SCM440 (QT2000) | 42CrMo4 (1.7225) | −1 | US | [26] | ||||
| 6 | SCM440 (AF1600) | 42CrMo4 (1.7225) | −1 | EMR | [26] | |||
| 7 | SCM440 (QT1600) | 42CrMo4 (1.7225) | −1 | US | [26] | |||
| 8 | Carbon and low-alloy steels quenched and tempered (tempered martensite) | / | / | / | [27] | |||
| 9 | SAE 1141 | / | −1 | UA | [24] | |||
| SAE 1038 | C35E (1.1181) | |||||||
| SAE 1541 | 36Mn6 (1.1127) | |||||||
| SAE 1050 | C50 (1.0540) | |||||||
| SAE 1090 | C92D (1.0618) | |||||||
| 10 | S25C (ferrite/pearlite structure) | C25 (1.0406) | −1 | RB | / | [28] | ||
| 11 | SUS304 (austenitic structure) | X5CrNi18-10 (1.4301) | −1 | RB | / | [28] | ||
| 12 | SUS430 (ferritic structure) | X6Cr17 (1.4016) | −1 | RB | / | [28] | ||
| 13 | S35C | C35 (1.0501) | −1 | RB | / | [28] | ||
| S45C | C45 (1.0503) | |||||||
| S55C | C55 (1.0535) | |||||||
| SMn438 | 36Mn6 (1.1127) | |||||||
| SMn443 | 42Mn6 (1.1055) | |||||||
| SCr440 | 41Cr4 (1.7035) | |||||||
| SCM435 | 34CrMo4 (1.7220) | |||||||
| SCM440 | 42CrMo4 (1.7225) | |||||||
| SNC631 | 36NiCr10 (1.5736) | |||||||
| SNCM439 | 40NiCrMo6 (1.6565) | |||||||
| SNCM447 | 34CrNiMo6 (1.6582) | |||||||
| 14 | See estimation 13 | −1 | RB | [29] | ||||
| 15 | GCr15 bearing steel Low alloy steels | 100Cr6 (1.3505) | −1 | RB, US | [30] | |||
| 16 | GCr15 bearing steel Low-alloy steels | 100Cr6 (1.3505) | −1 | RB, US | [30] | |||
| 17 | SCr430B | / | 0.1 | UA | to | [31] | ||
| SAE 1055 | C55 (1.0535) | |||||||
| Fe-18Mn-0.57C TWIP | / | |||||||
| 18 | Untreated steel | 0 | UA | For MPa | [32] | |||
| 19 | 700/49 | / | −1 | RB | [33] | |||
| 20 | 900A/49 | / | −1 | RB | [33] | |||
| 21 | 900B/UIC60 | / | −1 | RB | [33] | |||
| 22 | SAE 4340 | 36CrNiMo (1.6511) | −1 | US | [34] | |||
| 23 | SAE 4340 | 36CrNiMo (1.6511) | −1 | RB | / | [34] | ||
| 24 | SAE 4140 | 42CrMo4 (1.7225) | −1 | RB | / | [34] | ||
| 25 | SAE 2340 | / | −1 | RB | / | [34] | ||
| 26 | SAE 4063 | / | −1 | RB | / | [34] | ||
| 27 | Alloy steels | / | / | to | [19] | |||
| 28 | Alloying steels | −1 | US | [19,34] | ||||
| 29 | Wrought steels | / | / | / | [34] | |||
| 30 | Ultrafine and coarse-grained low-carbon steels | / | / | / | [34] | |||
| 31 | Ductile cast steels | −1 | RB | For MPa | [25] | |||
| 32 | Ferrous powder metal materials | / | UA | : material and postprocess treatment dependent | [35] |
2.2. Estimations Based on Yield Strength
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 33 | AISI 4340 | 34CrNiMo6 (1.6511) | / | / | / | [19] | ||
| 34 | DP600 | / | −1 | UA | [36,37] | |||
| TRIP bainitic steel | ||||||||
| Al 5083 | ||||||||
| 17-4 PH stainless steel | X5CrNiCuNb16-4 (1.4542) | |||||||
| Mg alloys | ||||||||
| 35 | TMCP steels | −1 | UA | Data for converted to by Goodman equation | [38] | |||
| 36 | SAE 1141 | / | −1 | UA | [24,39] | |||
| 37 | HS 310 HS 350 HS 390 HS 450 EHS 490 EHS 590 EHS 640 EHS 690 EHD 750 HS 420 EHS 900 | / / / / / / / / / / / | 0 | UA | [40] | |||
| 38 | Mild steel | 0 | R | [32] | ||||
| DOCOL 400 BH | / | |||||||
| DOCOL 600 DL | / | |||||||
| DOCOL 600 | / | |||||||
| DOCOL 800 | / | |||||||
| 39 | 35CrMo | 34CrMo4 (1.7220) | −1 | UA | to | [42] | ||
| 40 | 700/49 | / | −1 | RB | [33] | |||
| 41 | 900A/49 | / | −1 | RB | [33] | |||
| 42 | 900B/UCI60 | / | −1 | RB | [33] |
2.3. Estimations Based on Ultimate Tensile Strength and Yield Strength
2.4. Estimations Based on Cyclic Yield Strength
2.5. Estimations Based on Vickers Hardness
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 60 | Low- or medium-strength steels | RB or UA | / | For Based on | [45,46,47] | |||
| 61 | / | / | / | / | Based on and Goodman equation | [46] | ||
| 62 | S35C | C35 (1.0501) | −1 | RT | / | [28] | ||
| S45C | C45 (1.0503) | |||||||
| S55C | C55 (1.0535) | |||||||
| SMn438 | 36Mn6 (1.1127) | |||||||
| SMn443 | 42Mn6 (1.1055) | |||||||
| SCr440 | 41Cr4 (1.7035) | |||||||
| SCM435 | 34CrMo4 (1.7220) | |||||||
| SCM440 | 42CrMo4 (1.7225) | |||||||
| SNC631 | 36NiCr10 (1.5736) | |||||||
| SNCM439 | 40NiCrMo6 (1.6565) | |||||||
| SNCM447 | 34CrNiMo6 (1.6582) | |||||||
| 63 | See estimation 62 | −1 | UA | / | [28] | |||
| 64 | See estimation 62 | −1 | RB | / | [28] | |||
| 65 | S25C | C25 (1.0406) | −1 | RB | / | [28] | ||
| S35C | C35 (1.0501) | |||||||
| S45C | C45 (1.0503) | |||||||
| S55C | C55 (1.0535) | |||||||
| SMn438 | 36Mn6 (1.1127) | |||||||
| SMn443 | 42Mn6 (1.1055) | |||||||
| SCr440 | 41Cr4 (1.7035) | |||||||
| SCM435 | 34CrMo4 (1.7220) | |||||||
| SCM440 | 42CrMo4 (1.7225) | |||||||
| SNC631 | 36NiCr10 (1.5736) | |||||||
| SNCM439 | 40NiCrMo6 (1.6565) | |||||||
| SNCM447 | 34CrNiMo6 (1.6582) | |||||||
| SUS304 | X5CrNi18-10 (1.4301) | |||||||
| SUS430 | X6Cr17 (1.4016) | |||||||
| SUS403 | X6Cr13 (1.4000) | |||||||
| 66 | S10C S15C S25C | C10E (1.1121) C15E (1.1141) C25 (1.0406) | −1 | RB | to | [48] | ||
| 67 | S30C S35C S45C (EQT) S50C (EQT) | C30 (1.0528) C35 (1.0501) C45 (1.0503) C50 (1.0540) | −1 | RB | to | [48] | ||
| 68 | S45C (Q&T) S50C (Q&T) | C45 (1.0503) C50 (1.0540) | −1 | RB | to | [48] | ||
| 69 | DIN 1.1186 DIN 1.1302 DIN 1.7218 DIN 1.7176 | C40E 30MnVS6 25CrMo4 55Cr3 | −1 | RB | to | For | [49] | |
| 70 | 35CrMo | 34CrMo4 (1.7220) | −1 | EMR | : microhardness of pearlite phase | [50] | ||
| 38MnVS | / | |||||||
| 71 | SCr430B | / | 0.1 | UA | to | [31] | ||
| SAE 1055 | C55 (1.0535) | |||||||
| Fe-18Mn-0.27C TWIP | / | |||||||
| 72 | AISI 4340 | 36CrNiMo4 (1.6511) | −1 | US | [19,34] | |||
| 73 | SUP7 | 60Si7 (1.5027) | −1 | RB | / | [19] | ||
| 74 | 4140 | 42CrMo4 (1.7225) | −1 | PB, RB | / | Residual stress in substrate Hardness at substrate’s surface | [51,52] | |
| H13 | X40CrMoV5-1 (1.2344) | |||||||
| D2 | X153CrMoV12 (1.2379) | |||||||
| ASP30 | BSt 420 S (1.0428) | |||||||
| Surface modifications: | ||||||||
| Hardening | ||||||||
| VC coating | ||||||||
| NbC coating | ||||||||
| Cr-C coating | ||||||||
| TiC coating | ||||||||
| TiN coating |
2.6. Estimations Based on Brinell Hardness
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 75 | / | −1 | RB | For Based on | [23] | |||
| 76 | SAE 1141 | / | −1 | UA | [24] | |||
| SAE 1038 | C35E (1.1181) | |||||||
| SAE 1541 | 36Mn6 (1.1127) | |||||||
| SAE 1050 | C50 (1.0540) | |||||||
| SAE 1090 | C92D (1.0618) | |||||||
| 77 | / | / | / | / | For | [19,54] | ||
| 78 | / | −1 | UA | : endurance limit factor for normal stresses (material dependent) : temperature correction for endurance limit (material dependent) : size correction factor (material dependent) : reliability correction factor | [53] |
2.7. Estimations Based on Rockwell Hardness
2.8. Estimations Based on Multiple Properties

| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 85 | AISI-SAE 4330M | / | 0 | UA | [55] | |||
| AISI-SAE 4138M | / | |||||||
| AISI-SAE 4140 | 42CrMo4 (1.7225) | |||||||
| 86 | See estimation 85 | 0 | UA | [55] | ||||
| 87 | See estimation 85 | 0 | UA | [55] | ||||
| 88 | / | / | / | / | [43] | |||
| 89 | High-strength steels | / | / | / | [19] | |||
| 90 | SAE 1141 | / | −1 | UA | [43] | |||
| SAE 1038 | C35E (1.1181) | |||||||
| SAE 1541 | 36Mn6 (1.1127) | |||||||
| SAE 1050 | C50 (1.0540) | |||||||
| SAE 1090 | C92D (1.0618) | |||||||
| 08 | / | |||||||
| 20 | / | |||||||
| 30 | / | |||||||
| 40 | / | |||||||
| 40CrNiMo | 40NiCrMo6 (1.6565) | |||||||
| 60Si2Mn | 60Si7 (1.5027) | |||||||
| 91 | Carbon and tempered steels | −1 | RB | For MPa as value in % | [25] | |||
| 92 | 100CrMnSi6-4 X0.5CuN2-2 X21CuNi2-2 C50E 42CrMo4 | (1.3520) / / (1.1206) (1.7225) | / | UA UA UA / R | [57,59] |
2.9. Estimations Based on Flaw Size
- Drilled holes with diameters from 40 to 500 µm and depths greater than 40 µm;
- Notches with depths from 5 to 300 µm;
- Circumferential cracks with a depth greater than 30 µm;
- Vickers hardness indentations with a diagonal length of 72 µm.
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 93 | S10C | C10E (1.1121) | −1 | RB | for surface flaw | [10,45,47,60] | ||
| S30C | C30 (1.0528) | for interior flaw | ||||||
| S35C | C35 (1.0501) | for flaw in contact with surface | ||||||
| S45C | C45 (1.0503) | |||||||
| S50C | C50 (1.0540) | |||||||
| YUS170 | / | Upper limit: | ||||||
| Maraging steel | ||||||||
| 70/30 brass | ||||||||
| 2017-T4 Al | 10% nonconservative for cycles | |||||||
| 94 | 60Si2Cr | 55SiCr6-3 (1.1704) | −1 | R | For interior flaw | [11,62] | ||
| 60Si2CrV | / | |||||||
| 60Si2Mn | 60Si7 (1.5027) | |||||||
| GCr15VM | / | |||||||
| GCr15ER | / | |||||||
| 95 | 60Si2CrV | / | R | For interior flaw | [61] | |||
| SUP12 | 54SiCr6 (1.7102) | |||||||
| 60Si2Mn | 60Si7 (1.5027) | |||||||
| 60Si2Cr | 55SiCr6-3 (1.1704) | |||||||
| GCr15 | 100Cr6 (1.3505) | |||||||
| NHS1 | / | |||||||
| 40CrNiMo | 40NiCrMo6 (1.6565) | |||||||
| DIN 50CrV4 | (1.2241) | |||||||
| DIN 54SiCrV6 | (1.8152) | |||||||
| DIN 54SiCr6 | (1.7102) | |||||||
| 96 | if MPa m1/2 MPa m1/2 otherwise | SUJ2 | 100Cr6 (1.3505) | / | / | / | [63] | |
| SCM435 | 34CrMo4 (1.7220) | |||||||
| SNCM439 | 40NiCrMo6 (1.6565) | |||||||
| 97 | S10C Maraging steel | C10E (1.1121) | / | RB | / | for surface flaw for interior flaw | [60] | |
| 98 | Shot-peened gear steel | / | / | / | Residual stress regarded as mean local stress | [60] | ||
| 99 | SCM440 | 42CrMo4 (1.7225) | −1 | RB | [64] | |||
| 100 | S45C | C45 (1.0503) | −1 | RB |
Idealised surface roughness (dimensions a and b) modelled as surface flaw Applied to actual surface roughness in [65] | [60] | ||
| 101 | Mild steel | −1, 0, 0.5 | / | / | l: material dependent microstructural length parameter (see Table 10) : dependent on R (see Table 11) for surface flaws for interior flaws | [46,66] | ||
| SM41B | S235JR (1.0038) | |||||||
| Low-carbon steel | ||||||||
| C45 | (1.0503) | |||||||
| 403/410 12%Cr | / | |||||||
| 17-4 PH | X5CrNiCuNb16-4 (1.4542) | |||||||
| 300 M | 41SiNiCrMoV7-6 (1.6928) | |||||||
| Alloy steel | ||||||||
| MS | / | |||||||
| AISI304 | X5CrNi18-10 (1.4301) | |||||||
| EA4T | / | |||||||
| 30Cr2Ni4MoV | / | |||||||
| 25Cr2Ni2MoV | / | |||||||
| SA387-2-22 | 12CrMo9-10 (1.7375) | |||||||
| 2.25 Cr - 1 Mo | / | |||||||
| CrMoV | / | |||||||
| 102 | SCM440 | 42CrMo4 (1.7225) | −1 | RB, UA, US | to | [67] | ||
| 103 | SCM440 | 42CrMo4 (1.7225) | 0 | UA | to | [67] | ||
| 104 | SUP7 (tempered at 430 °C) | 60Si7 (1.5027) | −1 | RB, UA, US | to | [67] | ||
| 105 | SUP7 (tempered at 500 °C) | 60Si7 (1.5027) | −1 | RB, UA, US | to | [67] | ||
| 106 | SUJ2 | 100Cr6 (1.3505) | −1 | RB, UA, US | to | [67] | ||
| 107 | SNCM439 | 40NiCrMo6 (1.6565) | −1 | RB, UA, US | to | [67] | ||
| 108 | S40C | C40 (1.0511) | −1 | RB, UA, US | to | [67] | ||
| 109 | Low-carbon steel | −1 | RB | V: volume% of nonmetallic inclusions | [71] |
| Material | Definition of l (in µm) |
|---|---|
| Ferritic steels | Ferritic grain size |
| Austenitic stainless steels | Austenitic grain size |
| Pearlitic steels | Pearlite colony size |
| Dual phase (ferritic–martensitic steels) | Ferritic grain size (with ferrite percentage higher than 50%) |
| Martensitic steels | Martensite lath widths (or packet size of martensite laths) |
| Bainitic steels | Bainite packet size |
| R | ||||
|---|---|---|---|---|
| 4.5 | 0.127 | −0.81 | ||
| 0 | 1.82 | 0.165 | 53.5 | −0.52 |
| 0.5 | 1.68 | 0.203 | 5.94 | −0.26 |
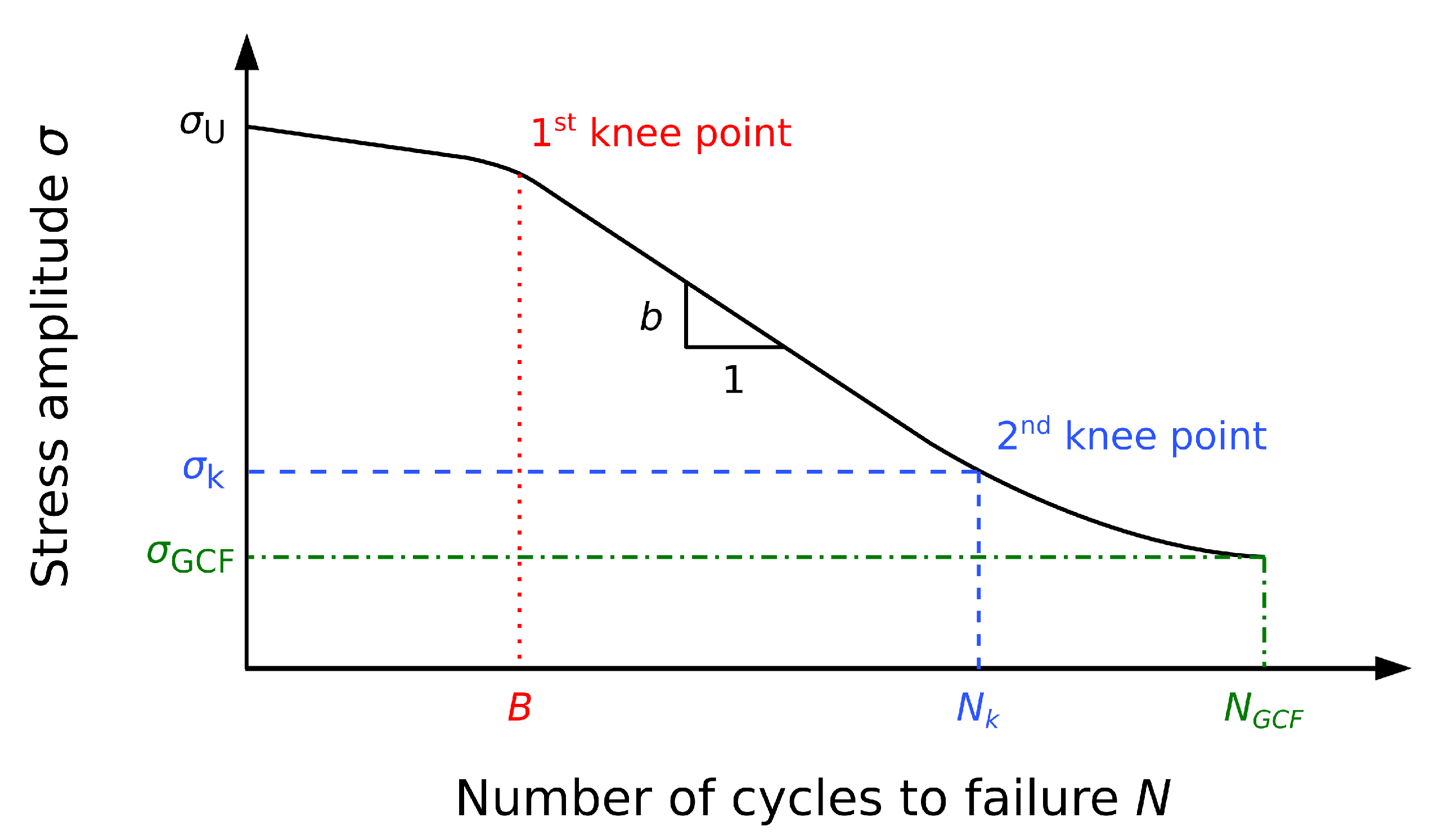
3. Estimations of the S–N Curve
3.1. Estimations Based on Murakami’s Model
- Crack initiation at an inclusion with the formation of the ODA;
- Crack propagation outside the ODA, up to the surface;
- Surface crack propagation.
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 110 | 42Cr-Mo | 42CrMo4 (1.7225) | −1 | US | to | for interior flaws for surface flaws | [12] | |
| Cr-V (60CV2) | / | |||||||
| Cr-Si (54SC6) | 54SiCr6 (1.7102) | |||||||
| Cr-Si (55SC7) | 55SiCr7 (1.7106) | |||||||
| SUP10M 10M3 | / | |||||||
| SUP10M 10M6 | / | |||||||
| SUP9 TM1 | / | |||||||
| 111 | Medium- and high-strength steels | −1 | / | to | [72] | |||
| 112 | Medium- and high-strength steels | −1 | / | to | Suitable for MPa [20] | [72] | ||
| 113 | Medium- and high-strength steels (+Al and Mg alloys) | −1 | / | to | [72] | |||
| 114 | CrMo | −1 | RB, UA | to | [20] | |||
| Cr | ||||||||
| CrSi | ||||||||
| SiMn | ||||||||
| SiCr | ||||||||
| SiCrV | ||||||||
| NiCrMo | ||||||||
| CrV | ||||||||
| MnSiCr | ||||||||
| CrMn | ||||||||
| CrNiMo | ||||||||
| SUP10M | 51CrV4 (1.8159) | |||||||
| SUJ2 | 100Cr6 (1.3505) | |||||||
| Aermet100 | / | |||||||
| SUP12 | 54SiCr6 (1.7102) | |||||||
| NSH1 | / | |||||||
| GRV | / | |||||||
| GVM | / | |||||||
| KSFA | / | |||||||
| D38MSV5S | / | |||||||
| AISI8620 | / | |||||||
| C steels | ||||||||
| 115 | See estimation 114 | −1 | RB, UA | to | [20] | |||
| 116 | / | −1 | / | to | Valid for | [73] | ||
| 117 | / | −1 | / | to | Valid for | [74] | ||
| 118 | : lower value of or | SUJ2 | 100Cr6 (1.3505) | −1 | RB, UA, US | to | Additional correlation: | [63,77] |
| SCM435 | 34CrMo4 (1.7220) | |||||||
| SNCM439 | 40NiCrMo6 (1.6565) | |||||||
| 119 | 60Si2Mn | 60Si7 (1.5027) | −1 | US | [62] | |||
| 60Si2CrV | / | |||||||
| 54SiCr6 | (1.7102) | |||||||
| 120 | SUJ2 | 100Cr6 (1.3505) | −1 | US | [78] | |||
| 121 | SCM440 | 42CrMo4 (1.7225) | −1 | RB, UA, US | to | [67] | ||
| 122 | SCM440 | 42CrMo4 (1.7225) | 0 | UA | to | [67] | ||
| 123 | SUP7 (tempered at 430 °C) | 60Si7 (1.5027) | −1 | RB, UA, US | to | [67] | ||
| 124 | SUP7 (tempered at 500 °C) | 60Si7 (1.5027) | −1 | RB, UA, US | to | [67] | ||
| 125 | SUJ2 | 100Cr6 (1.3505) | −1 | RB, UA, US | to | [67] | ||
| 126 | SNCM439 | 40NiCrMo6 (1.6565) | −1 | RB, UA, US | to | [67] | ||
| 127 | S40C | C40 (1.0511) | −1 | RB, UA, US | to | [67] | ||
| 128 | 100Cr6 | (1.3505) | −1 | US | to | [68] | ||
| 129 | S35C | C35 (1.0501) | RB, UA | to | : from estimation 93 For steels with : reduce by 20% Numerical integration required to determine fatigue life (final crack size: 1.0 or 2.0 mm) | [80] | ||
| S45C | C45 (1.0503) | |||||||
| Maraging steel | ||||||||
| Ductile cast iron FCD400 | ||||||||
| AM Ti-4Al-6V | ||||||||
| AM Inconel 718 |
3.2. Other Estimations
- : true strain at failure;
- : true stress;
- : true strain;
- : reduction in area after failure;
- : reduction in area at the onset of necking.
4. Suggestions for Future Research
5. Conclusions
Funding
Conflicts of Interest
Abbreviations
| Symbol | Physical Quantity | Unit |
| fatigue strength (stress amplitude) | MPa | |
| stress range | MPa | |
| N | number of cycles | - |
| R | stress ratio | - |
| ultimate tensile strength | MPa | |
| yield strength | MPa | |
| cyclic yield strength | MPa | |
| reduction in area | - | |
| Vickers hardness | kgf/mm2 | |
| Brinell hardness | kgf/mm2 | |
| Rockwell hardness (on different scales) | - | |
| flaw size | µm | |
| mode I threshold stress intensity factor | MPa | |
| mode I threshold stress intensity factor range | MPa | |
| mode I stress intensity factor at the maximum load in a load cycle | MPa |
References
- Findlay, S.J.; Harrison, N.D. Why aircraft fail. Mater. Today 2002, 5, 18–25. [Google Scholar] [CrossRef]
- Dieter, G.E., Jr. Mechanical Metallurgy; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1961; ISBN 07-016890-3. [Google Scholar]
- Das, A.K. Metallurgy of Failure Analysis; The McGraw-Hill Companies, Inc.: New York, NY, USA, 1997; ISBN 0-07-015804-5. [Google Scholar]
- Stephens, R.; Fatemi, A.; Stephens, R.; Fuchs, H. Metal Fatigue in Engineering; A Wiley-Interscience Publication, Wiley: Hoboken, NJ, USA, 2000; ISBN 978-0-471-51059-8. [Google Scholar]
- Gagg, C.R.; Lewis, P.R. In-service fatigue failure of engineered products and structures—Case study review. Eng. Fail. Anal. 2009, 16, 1775–1793. [Google Scholar] [CrossRef]
- Forschungskuratorium Maschinenbau. FKM Guideline: Analytical Strength Assessment; VDMA Verlag: Frankfurt, Germany, 2003; ISBN 3816304257. [Google Scholar]
- Schütz, W. A history of fatigue. Eng. Fract. Mech. 1996, 54, 263–300. [Google Scholar] [CrossRef]
- ISO 1143:2021; Metallic Materials-Rotating Bar Bending Fatigue Testing. ISO: Geneva, Switzerland, 2021.
- Fernández-Canteli, A.; Blasón, S.; Pyttel, B.; Muniz-Calvente, M.; Castillo, E. Considerations about the existence or non-existence of the fatigue limit: Implications on practical design. Int. J. Fract. 2020, 223, 189–196. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T. Factors influencing the mechanism of superlong fatigue failure in steels. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 581–590. [Google Scholar] [CrossRef]
- Liu, Y.B.; Yang, Z.G.; Li, Y.D.; Chen, S.M.; Li, S.X.; Hui, W.J.; Weng, Y.Q. On the formation of GBF of high-strength steels in the very high cycle fatigue regime. Mater. Sci. Eng. A 2008, 497, 408–415. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Berard, J.Y.; Dubarre, A.; Baudry, G.; Rathery, S.; Bathias, C. Gigacycle fatigue of ferrous alloys. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 667–672. [Google Scholar] [CrossRef]
- ISO 12107:2012; Metallic Materials-Fatigue Testing-Statistical Planning and Analysis of Data. ISO: Geneva, Switzerland, 2012.
- Li, J.; Qiu, Y.Y.; Wang, H.D.; Wang, Z.X. Evaluation of the methods for estimating the fully reversed unnotched fatigue limits of steels. Adv. Mater. Sci. Eng. 2019, 2019, 4098623. [Google Scholar] [CrossRef]
- Meggiolaro, M.A.; Castro, J.T. Statistical evaluation of strain-life fatigue crack initiation predictions. Int. J. Fatigue 2004, 26, 463–476. [Google Scholar] [CrossRef]
- Harun, M.F.; Mohammad, R. Fatigue properties of JIS H3300 C1220 copper for strain life prediction. AIP Conf. Proc. 2018, 1958, 020001. [Google Scholar] [CrossRef]
- Troshchenko, V.T.; Khamaza, L.A. Strain-life curves of steels and methods for determining the curve parameters. Part 1. Conventional methods. Strength Mater. 2010, 42, 647–659. [Google Scholar] [CrossRef]
- Tridello, A.; Niutta, C.B.; Rossetto, M.; Berto, F.; Paolino, D.S. Statistical models for estimating the fatigue life, the stress–life relation, and the P–S–N curves of metallic materials in Very High Cycle Fatigue: A review. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 332–370. [Google Scholar] [CrossRef]
- Pang, J.C.; Li, S.X.; Wang, Z.G.; Zhang, Z.F. Relations between fatigue strength and other mechanical properties of metallic materials. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 958–976. [Google Scholar] [CrossRef]
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I.; Dissanayake, R. Fatigue failure predictions for steels in the very high cycle region—A review and recommendations. Eng. Fail. Anal. 2014, 45, 421–435. [Google Scholar] [CrossRef]
- Verlag Stahlschlüssel Wegst GmbH. Online::Stahlschluessel—Key to Steel. 2023. Available online: https://www.online.stahlschluessel.de/ (accessed on 17 February 2023).
- Tóth, L.; Yarema, S.Y. Formation of the science of fatigue of metals. Part I. 1825–1870. Transl. Fiz.-Khimichna Mekhanika Mater. 2006, 42, 87–94. [Google Scholar] [CrossRef]
- Socie, D.F.; Mitchell, M.R.; Caulfield, E.M. Fundamentals of Modern Fatigue Analysis. 1978. Available online: https://fcp.mechse.illinois.edu/fcp_report026/ (accessed on 16 May 2023).
- Roessle, M.L.; Fatemi, A. Strain-controlled fatigue properties of steels and some simple approximations. Int. J. Fatigue 2000, 22, 495–511. [Google Scholar] [CrossRef]
- Andersson, H. Metal Fatigue Principles and Analyses. 2021. Available online: http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1612930&dswid=-1298 (accessed on 16 May 2023).
- Furuya, Y.; Matsuoka, S. Improvement of Gigacycle Fatigue Properties by Modified Ausforming in 1600 and 2000 MPA-Class Low-Alloy Steels. Metall. Mater. Trans. A 2022, 33A, 3421–3431. [Google Scholar] [CrossRef]
- Furuya, Y.; Nishikawa, H.; Hirukawa, H.; Nagashima, N.; Takeuchi, E. Catalogue of NIMS fatigue data sheets. Sci. Technol. Adv. Mater. 2019, 20, 1055–1072. [Google Scholar] [CrossRef]
- Nishijima, S. Basic Fatigue Properties of JIS Steels for Machine Structural Use NRIM Special Report. 1993. Available online: https://mdr.nims.go.jp/concern/publications/h989r3289 (accessed on 24 January 2023).
- Yamaguchi, K.; Abe, T.; Kobayashi, K.; Takeuchi, E.; Hirukawa, H.; Maeda, Y.; Nagashima, N.; Hayakawa, M.; Furuya, Y.; Shimodaira, M.; et al. Gigacycle fatigue data sheets for advanced engineering materials. Sci. Technol. Adv. Mater. 2007, 8, 545–551. [Google Scholar] [CrossRef][Green Version]
- Zhao, A.; Xie, J.; Sun, C.; Lei, Z.; Hong, Y. Effects of strength level and loading frequency on very-high-cycle fatigue behavior for a bearing steel. Int. J. Fatigue 2012, 38, 46–56. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, C.S. Relationship between mechanical properties and high-cycle fatigue strength of medium-carbon steels. Mater. Sci. Eng. A 2017, 690, 185–194. [Google Scholar] [CrossRef]
- Sperle, J.O. Fatigue strength of high strength dual-phase steel sheet. Int. J. Fatigue 1985, 7, 79–86. [Google Scholar] [CrossRef]
- Krumes, D.; Haračić, N.; Vitez, I.; Budi, I. Contribution to the Correlation between Fatigue Endurance and Tensile Strength of Steel. 2000. Available online: https://www.researchgate.net/publication/236942405_Contribution_to_the_correlation_between_fatigue_endurance_and_tensile_strength_of_steel (accessed on 27 January 2023).
- Pang, J.C.; Li, S.X.; Wang, Z.G.; Zhang, Z.F. General relation between tensile strength and fatigue strength of metallic materials. Mater. Sci. Eng. A 2013, 564, 331–341. [Google Scholar] [CrossRef]
- Savu, V.A.; Mourelatos, Z. Long Life Axial Fatigue Strength Models for Ferrous Powder Metals. SAE Int. J. Mater. Manuf. 2018, 11, 467–479. [Google Scholar] [CrossRef]
- Das, B.; Singh, A.; Arora, K.S.; Shome, M.; Paul, S.K. Influence of pre-straining path on high cycle fatigue performance of DP 600 steel. Int. J. Fatigue 2019, 126, 369–380. [Google Scholar] [CrossRef]
- Paul, S.K. Correlation between endurance limit and cyclic yield stress determined from low cycle fatigue test. Materialia 2020, 11, 100695. [Google Scholar] [CrossRef]
- Zhang, D.; Du, L.; Lan, L.; Gao, C.; Xiao, B. Correlation of Microstructure and Fatigue Properties of Hot-Rolled Steel Strips for Automobile Structural Application. J. Mater. Eng. Perform. 2020, 29, 4009–4017. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, P.; Zhang, Z.J.; Wang, B.; Zhang, Z.F. A practical model for efficient anti-fatigue design and selection of metallic materials: I. Model building and fatigue strength prediction. J. Mater. Sci. Technol. 2021, 70, 233–249. [Google Scholar] [CrossRef]
- Sperle, J.O.; Nilsson, T. The Application of High Strength Steels for Fatigue Loaded Structures. 1992. Available online: https://www.researchgate.net/publication/285897692_The_application_of_high_strength_steels_for_fatigue_loaded_structures (accessed on 31 January 2023).
- Sperle, J.O.; Trogen, H. Influence of yield ratio on the fatigue strength of steel sheet. Scand. J. Metall. 1989, 18, 147–154. [Google Scholar]
- Yang, M.; Gao, C.; Pang, J.; Li, S.; Hu, D.; Li, X.; Zhang, Z. High-Cycle Fatigue Behavior and Fatigue Strength Prediction of Differently Heat-Treated 35CrMo Steels. Metals 2022, 12, 688. [Google Scholar] [CrossRef]
- Li, J.; Sun, Q.; Zhang, Z.-P.; Li, C.-W.; Qiao, Y.-J. Theoretical estimation to the cyclic yield strength and fatigue limit for alloy steels. Mech. Res. Commun. 2009, 36, 316–321. [Google Scholar] [CrossRef]
- Hales, R.; Holdsworth, S.R.; O’Donnell, M.P.; Perrin, I.J.; Skelton, R.P. A Code of Practice for the determination of cyclic stress-strain data. Mater. High Temp. 2002, 19, 165–185. [Google Scholar] [CrossRef]
- Murakami, Y.; Kodama, S.; Konuma, S. Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. I: Basic fatigue mechanism and evaluation of correlation between the fatigue fracture stress and the size and location of non-metallic inclusions. Int. J. Fatigue 1989, 11, 291–298. [Google Scholar] [CrossRef]
- Rigon, D.; Meneghetti, G. Engineering estimation of the fatigue limit of wrought and defective additively manufactured metals for different load ratios. Int. J. Fatigue 2022, 154, 106530. [Google Scholar] [CrossRef]
- Murakami, Y.; Endo, M. Effects of Hardness and Crack Geometries on ΔKth of Small Cracks Emanating from Small Defects. In The Behaviour of Short Fatigue Cracks, EGF Pub. 1; Miller, K.J., de los Rios, E.R., Eds.; Mechanical Engineering Publications: London, UK, 1986; pp. 275–293. [Google Scholar]
- Mukoyama, K.; Hanaki, K.; Okada, K.; Sakaida, A.; Sugeta, A.; Nishikawa, I.; Ueno, A.; Sakai, T. A study on estimation of S–N curves for structural steels based on their static mechanical properties. Adv. Mater. Res. 2014, 891–892, 1639–1644. [Google Scholar] [CrossRef]
- Mortezaei, S.; Mashreghi, A.R. The Effect of Interaction Between Hardness, Inclusion and Microstructures on the Fatigue Behavior of Steel. J. Metall. Mater. Eng. 2017, 28, 23–36. [Google Scholar]
- Gao, C.; Yang, M.Q.; Pang, J.C.; Li, S.X.; Zou, M.D.; Li, X.W.; Zhang, Z.F. Abnormal relation between tensile and fatigue strengths for a high-strength low-alloy steel. Mater. Sci. Eng. A 2022, 832, 142418. [Google Scholar] [CrossRef]
- Saruki, K.; Hotta, S.; Fujita, H.; Arai, T. Fatigue strength of steels with thin hard coating. Thin Solid Films 1989, 181, 395. [Google Scholar] [CrossRef]
- Hotta, S.; Saruki, K.; Arai, T. Endurance limit of thin hard-coated steels in bending fatigue. Surf. Coat. Technol. 1994, 70, 121–129. [Google Scholar] [CrossRef]
- McKelvey, S.A.; Lee, Y.L.; Barkey, M.E. Stress-based uniaxial fatigue analysis using methods described in FKM-guideline. J. Fail. Anal. Prev. 2012, 12, 445–484. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Q.; Luo, A.A.; Fu, P.; Peng, L. Fatigue strength dependence on the ultimate tensile strength and hardness in magnesium alloys. Int. J. Fatigue 2015, 80, 468–476. [Google Scholar] [CrossRef]
- Martínez, A.; Jaimes, A.; Serna, A.; Uribe, I. Development of a correlation to estimate the fatigue strength for steels based on low-cost tests. Ciencia Tecnología y Futuro 2010, 4, 71–81. [Google Scholar] [CrossRef]
- Hassan, A.D. A new prediction of the fatigue limit based on Brinell hardness and ultimate strength for high strength steels. Int. J. Energy Environ. 2018, 9, 77–84. [Google Scholar]
- Görzen, D.; Ostermayer, P.; Lehner, P.; Blinn, B.; Eifler, D.; Beck, T. A New Approach to Estimate the Fatigue Limit of Steels Based on Conventional and Cyclic Indentation Testing. Metals 2022, 12, 1066. [Google Scholar] [CrossRef]
- Schwich, H.; Görzen, D.; Blinn, B.; Beck, T.; Bleck, W. Characterization of the precipitation behavior and resulting mechanical properties of copper-alloyed ferritic steel. Mater. Sci. Eng. A 2020, 772, 138807. [Google Scholar] [CrossRef]
- Görzen, D.; Schwich, H.; Blinn, B.; Bleck, W.; Beck, T. Influence of different precipitation states of Cu on the quasi-static and cyclic deformation behavior of Cu alloyed steels with different carbon contents. Int. J. Fatigue 2020, 136, 105587. [Google Scholar] [CrossRef]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–758. [Google Scholar] [CrossRef]
- Liu, Y.B.; Yang, Z.G.; Li, Y.D.; Chen, S.M.; Li, S.X.; Hui, W.J.; Weng, Y.Q. Dependence of fatigue strength on inclusion size for high-strength steels in very high cycle fatigue regime. Mater. Sci. Eng. A 2009, 517, 180–184. [Google Scholar] [CrossRef]
- Liu, Y.B.; Li, Y.D.; Li, S.X.; Yang, Z.G.; Chen, S.M.; Hui, W.J.; Weng, Y.Q. Prediction of the S–N curves of high-strength steels in the very high cycle fatigue regime. Int. J. Fatigue 2010, 32, 1351–1357. [Google Scholar] [CrossRef]
- Chapetti, M.D.; Tagawa, T.; Miyata, T. Ultra-long cycle fatigue of high-strength carbon steels part II: Estimation of fatigue limit for failure from internal inclusions. Mater. Sci. Eng. A 2003, 356, 236–244. [Google Scholar] [CrossRef]
- Song, S.H.; Choi, B.H. Fatigue characteristics and fatigue limit prediction of an induction case hardened Cr-Mo steel alloy. Mater. Sci. Eng. A 2003, 361, 15–22. [Google Scholar] [CrossRef]
- Itoga, H.; Tokaji, K.; Nakajima, M.; Ko, H.N. Effect of surface roughness on step-wise S–N characteristics in high strength steel. Int. J. Fatigue 2003, 25, 379–385. [Google Scholar] [CrossRef]
- Rigon, D.; Meneghetti, G. An engineering estimation of fatigue thresholds from a microstructural size and Vickers hardness: Application to wrought and additively manufactured metals. Int. J. Fatigue 2020, 139, 105796. [Google Scholar] [CrossRef]
- Furuya, Y. A new model for predicting the gigacycle fatigue strength of high-strength steels. Mater. Sci. Eng. A 2019, 743, 445–452. [Google Scholar] [CrossRef]
- Mayer, H.; Haydn, W.; Schuller, R.; Issler, S.; Furtner, B.; Bacher-Höchst, M. Very high cycle fatigue properties of bainitic high carbon-chromium steel. Int. J. Fatigue 2009, 31, 242–249. [Google Scholar] [CrossRef]
- Murakami, Y. Inclusion rating by statistics of extreme values and its application to fatigue strength prediction and quality control of materials. J. Res. Natl. Inst. Stand. Technol. 1994, 99, 345. [Google Scholar] [CrossRef]
- Beretta, S. More than 25 years of extreme value statistics for defects: Fundamentals, historical developments, recent applications. Int. J. Fatigue 2021, 151, 106407. [Google Scholar] [CrossRef]
- Lipiński, T. Effect of Non-Metallic Inclusions on the Fatigue Strength Coefficient of High-Purity Constructional Steel Heated in Industrial Conditions. Appl. Sci. 2022, 12, 9292. [Google Scholar] [CrossRef]
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I.; Dissanayake, R. Fatigue Strength Prediction Formulae for Steels and Alloys in the Gigacycle Regime. Int. J. Mater. Mech. Manuf. 2013, 1, 256–260. [Google Scholar] [CrossRef]
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I.; Dissanayake, R. Developing a full range S–N curve and estimating cumulative fatigue damage of steel elements. Comput. Mater. Sci. 2015, 96, 96–101. [Google Scholar] [CrossRef]
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I.; Dissanayake, R. Full range S–N curves for fatigue life evaluation of steels using hardness measurements. Int. J. Fatigue 2016, 82, 325–331. [Google Scholar] [CrossRef]
- ASTM E140-02; Standard Hardness Conversion Tables for Metals, Relationship Among Brinell Hardness, Vickers Hardness, Rockwell Hardness, Superficial Hardness, Knoop Hardness and Scleroscope Hardness. ASTM International: West Conshohocken, PA, USA, 2002.
- Bandara, C.S.; Siriwardane, S.C.; Dissanayake, U.I.; Dissanayake, R. Hardness-Based Non-destructive Method for Developing Location Specific S–N Curves for Fatigue Life Evaluation. J. Civ. Eng. Archit. 2016, 10, 183–191. [Google Scholar] [CrossRef]
- Chapetti, M.D. A simple model to predict the very high cycle fatigue resistance of steels. Int. J. Fatigue 2011, 33, 833–841. [Google Scholar] [CrossRef]
- Akiniwa, Y.; Miyamoto, N.; Tsuru, H.; Tanaka, K. Notch effect on fatigue strength reduction of bearing steel in the very high cycle regime. Int. J. Fatigue 2006, 28, 1555–1565. [Google Scholar] [CrossRef]
- Tanaka, K.; Akiniwa, Y. Fatigue crack propagation behaviour derived from S–N data in very high cycle regime. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 775–784. [Google Scholar] [CrossRef]
- Murakami, Y.; Endo, M. Prediction model of S–N curve without fatigue test or with a minimum number of fatigue tests. Eng. Fail. Anal. 2023, 154, 107647. [Google Scholar] [CrossRef]
- Bannantine, J.A.; Comer, J.J.; Handrock, J.L. Fundamentals of Metal Fatigue Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Derrick, C.; Fatemi, A. Correlations of fatigue strength of additively manufactured metals with hardness and defect size. Available online: https://digitalcommons.memphis.edu/etd/2369/ (accessed on 20 January 2023).
- Strzelecki, P.; Tomaszewski, T. Analytical models of the S–N curve based on the hardness of the material. Procedia Struct. Integr. 2017, 5, 832–839. [Google Scholar] [CrossRef]
- Stepanskiy, L.G. Cumulative model of very high cycle fatigue. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 513–522. [Google Scholar] [CrossRef]
- Hectors, K.; Waele, W.D. Cumulative damage and life prediction models for high-cycle fatigue of metals: A review. Metals 2021, 11, 204. [Google Scholar] [CrossRef]
- Hectors, K.; Vanspeybrouck, D.; Plets, J.; Bouckaert, Q.; Waele, W.D. Open-Access Experiment Dataset for Fatigue Damage Accumulation and Life Prediction Models. Metals 2023, 13, 621. [Google Scholar] [CrossRef]
- Hectors, K.; De Waele, W. Fatigue Block Loading Experiment Database. 2023. Available online: https://osf.io/6y5sd/ (accessed on 18 December 2023).
- He, L.; Wang, Z.L.; Akebono, H.; Sugeta, A. Machine learning-based predictions of fatigue life and fatigue limit for steels. J. Mater. Sci. Technol. 2021, 90, 9–19. [Google Scholar] [CrossRef]
- Agrawal, A.; Choudhary, A. A fatigue strength predictor for steels using ensemble data mining. In Proceedings of the International Conference on Information and Knowledge Management, Indianapolis, IN, USA, 24–28 October 2016; pp. 2497–2500. [Google Scholar] [CrossRef]
- Liu, C.; Wang, X.; Cai, W.; Yang, J.; Su, H. Prediction of the Fatigue Strength of Steel Based on Interpretable Machine Learning. Materials 2023, 16, 7354. [Google Scholar] [CrossRef] [PubMed]
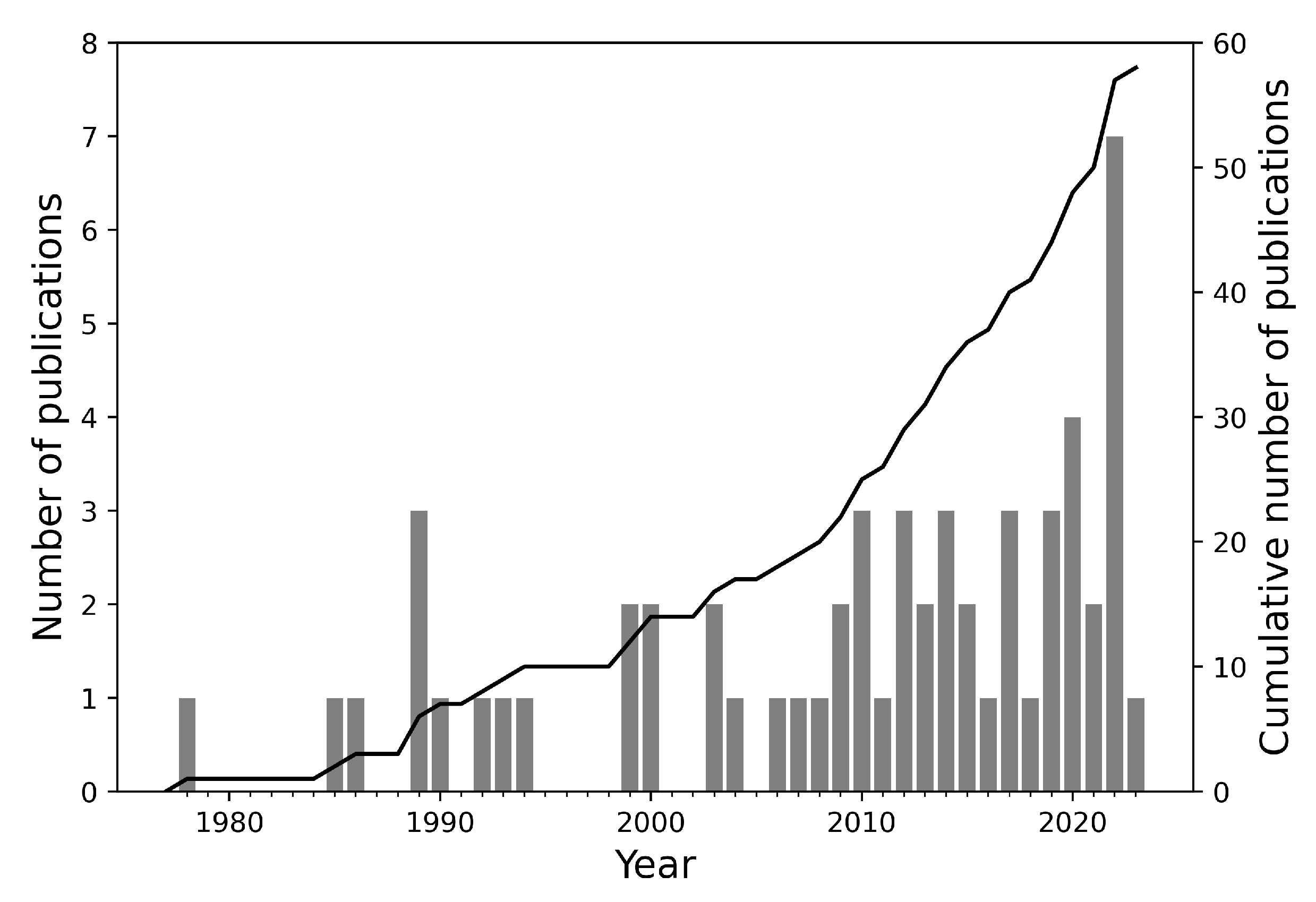

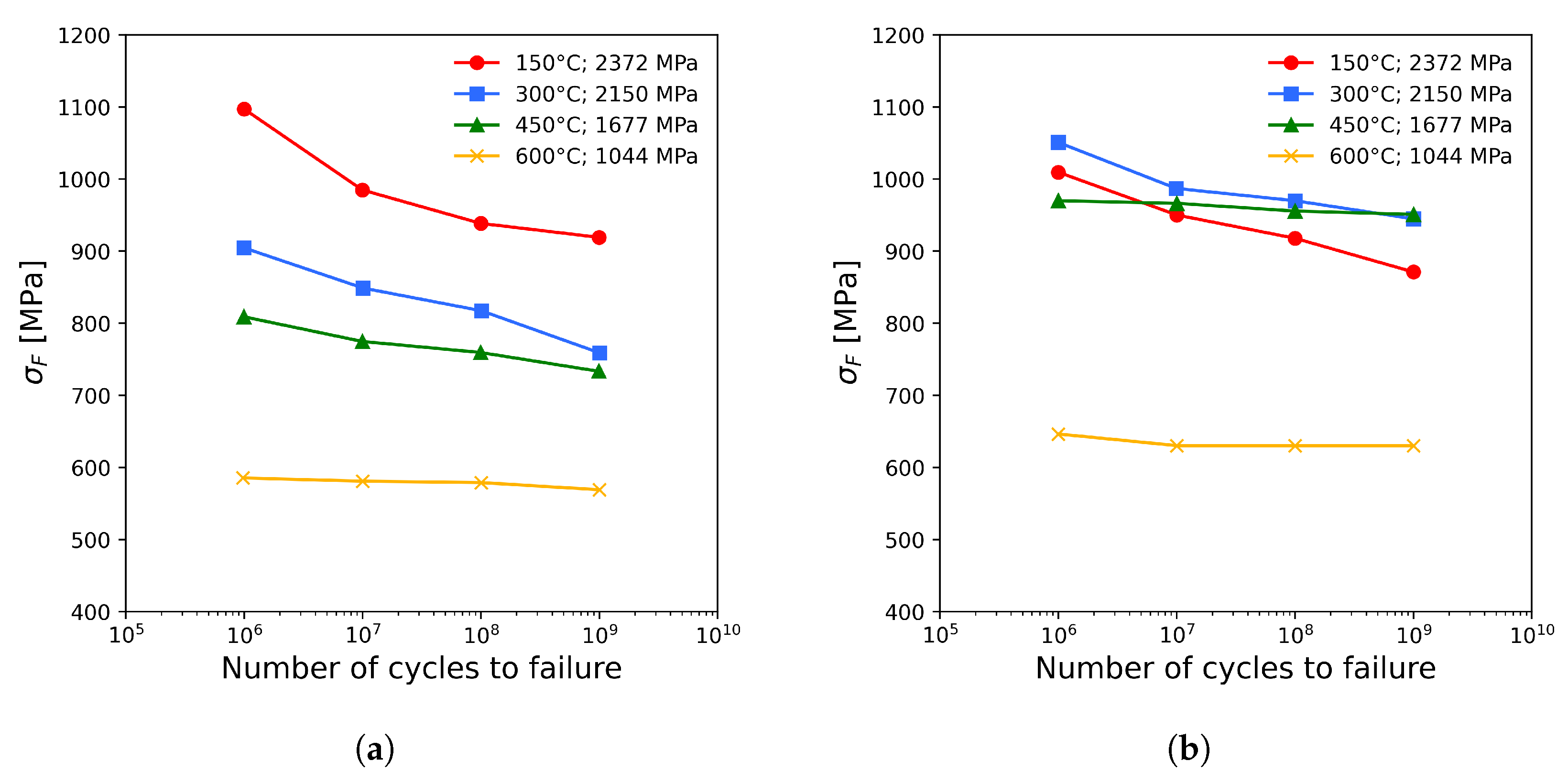



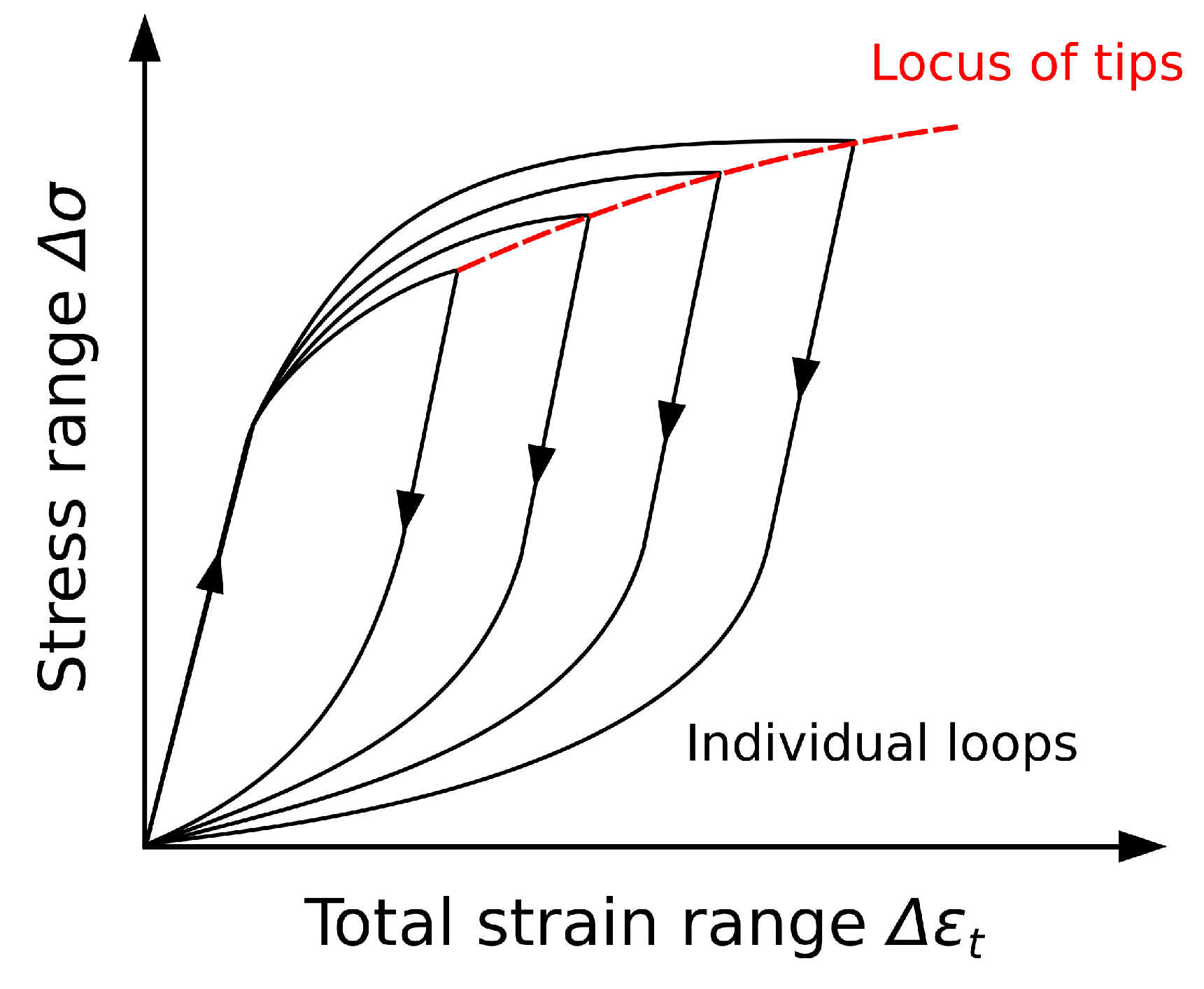
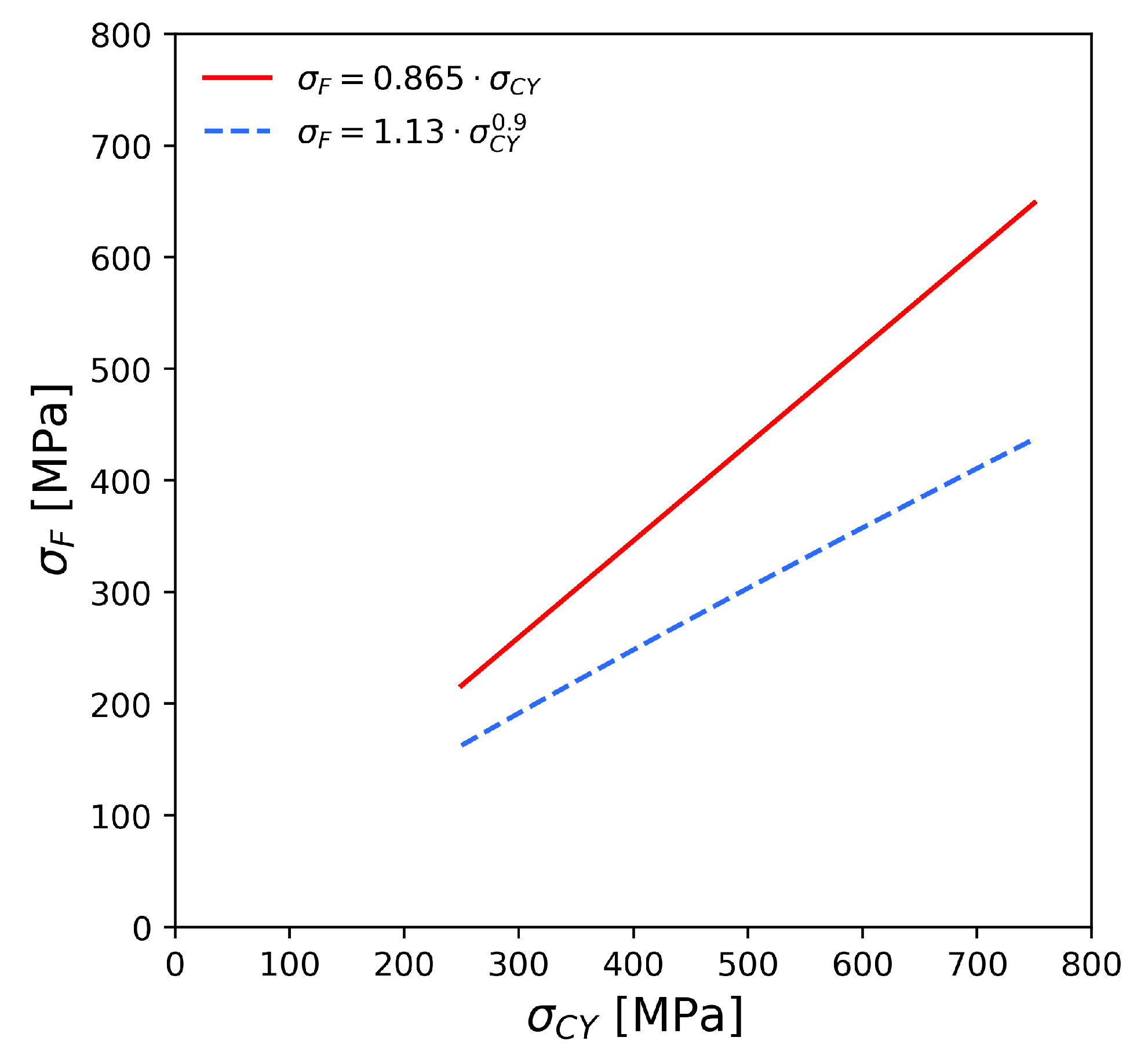
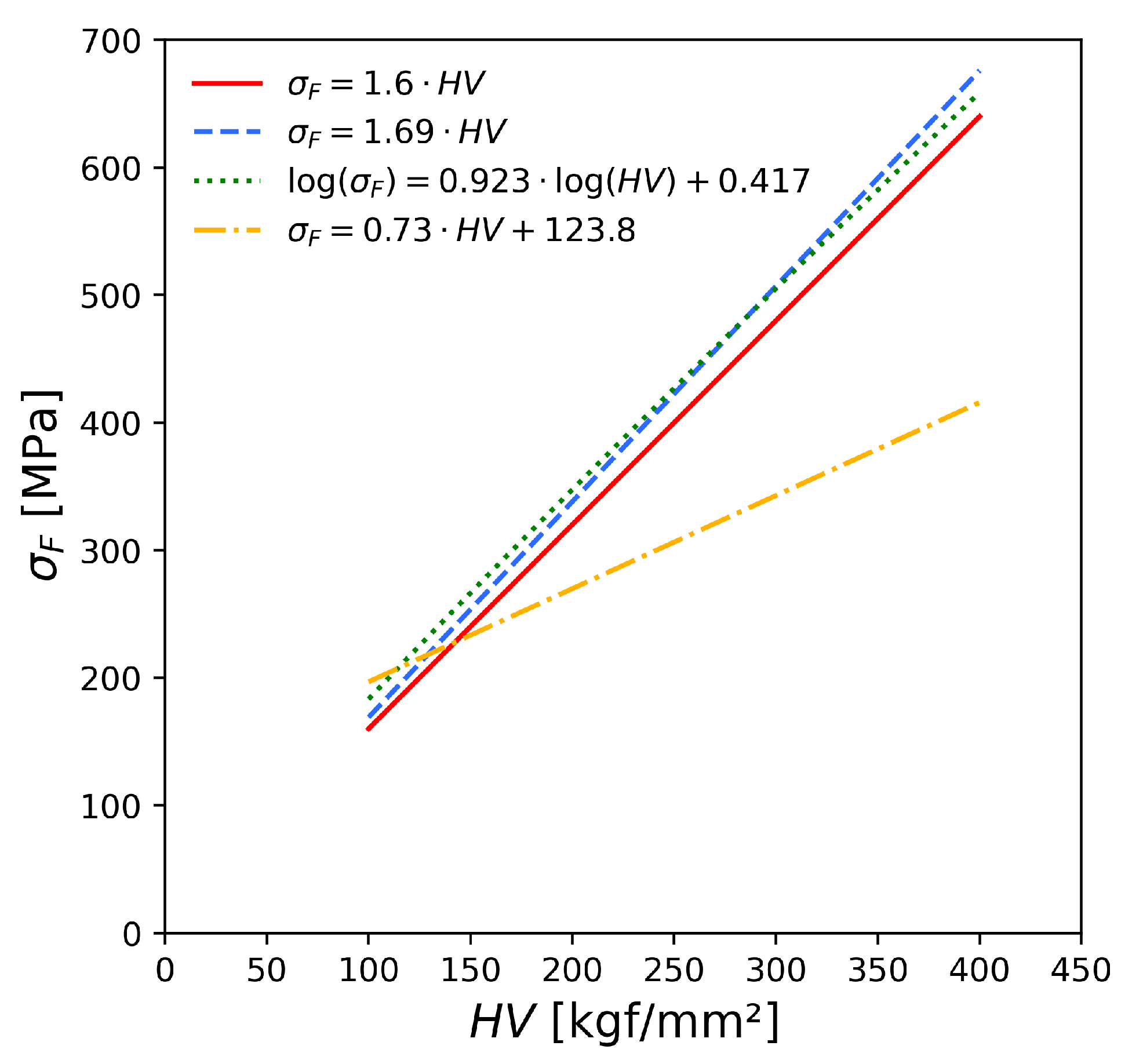
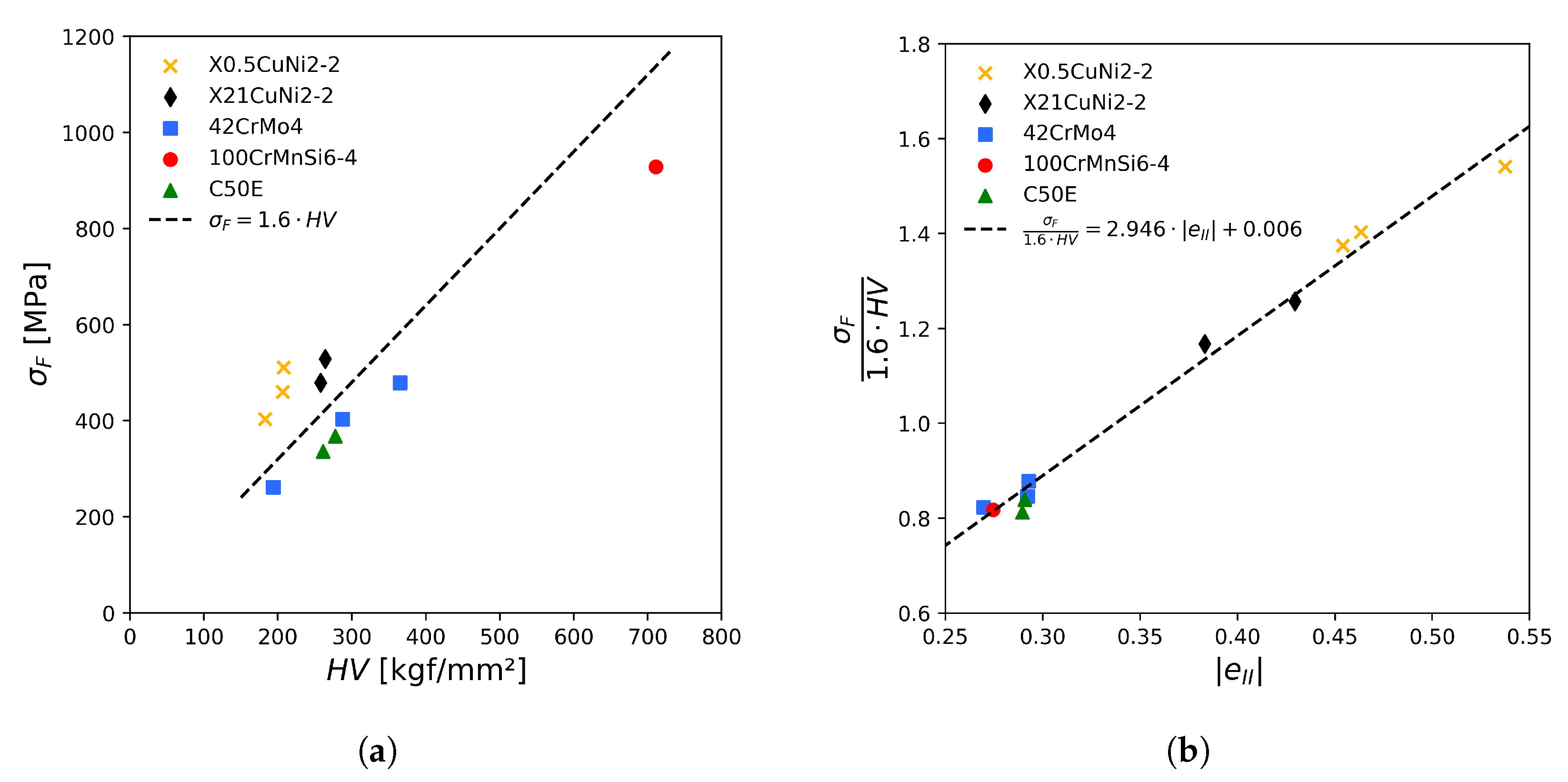
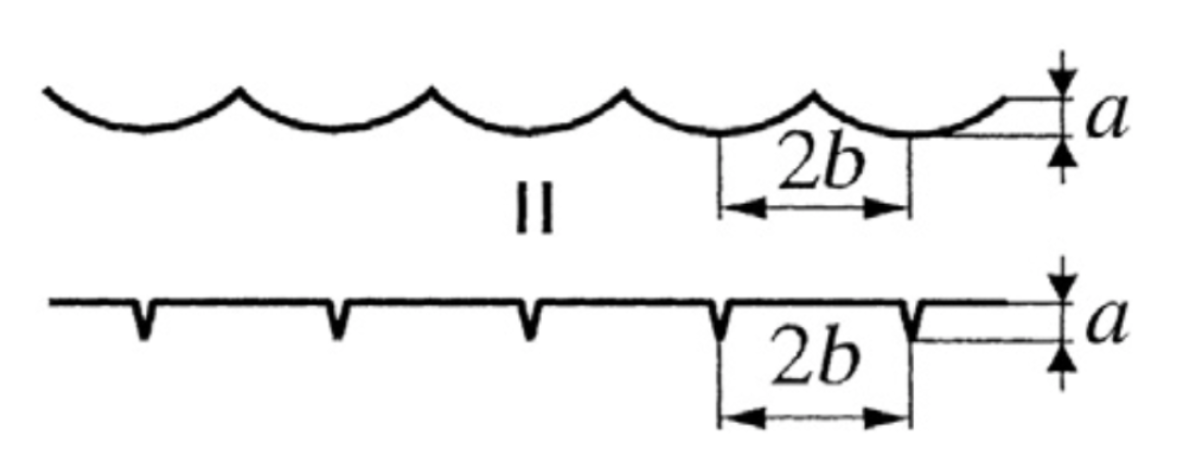

| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 43 | DOMEX 350 YP | / | 0 | R, UA | [41] | |||
| DOMEX 350 XP | / | |||||||
| DOMEX 640 XPN | / | |||||||
| DOMEX 490 XP | / | |||||||
| 44 | Low-carbon steels | −1 | RB | / | [39] | |||
| 45 | Medium- and high-carbon steels | −1 | RB | / | [39] | |||
| 46 | SPCC SPRC | DC01 (1.0330) / | 0 | UA | [39] | |||
| 47 | Si-Mn | / | −1 | RB | [39] | |||
| 48 | EN24 | 40NiCrMo6 (1.6565) | / | / | / | [39] | ||
| EN36 | / | |||||||
| 49 | EN56 | / | / | / | / | [39] | ||
| EN58 | X5CrNi18-10 (1.4301) | |||||||
| 50 | TWIP steel | −1 | UA | [39] | ||||
| 51 | TWIP steel | 0.1 | UA | [39] | ||||
| 52 | SAE1010 | C10E (1.1121) | −1 | UA | [39] | |||
| 53 | Structural steels | / | / | / | [19] |
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 54 | DP600 | / | −1 | UA | determined by 0.01% offset in the loading branch of the hysteresis loop | [37] | ||
| 55 | / | / | / | B | / | determined by 0.1% offset in the cyclic stress–strain curve | [23] | |
| 56 | SUS304 | X5CrNi18-10 (1.4301) | −1 | UA | / | determined by 0.2% offset in the cyclic stress–strain curve | [28] | |
| 57 | S25C | C25 (1.0406) | −1 | UA | / | determined by 0.2% offset in the cyclic stress–strain curve | [28] | |
| 58 | S35C | C35 (1.0501) | −1 | UA | / | determined by 0.2% offset in the cyclic stress–strain curve | [28] | |
| S45C | C45 (1.0503) | |||||||
| S55C | C55 (1.0535) | |||||||
| SMn438 | 36Mn6 (1.1127) | |||||||
| SMn443 | 42Mn6 (1.1055) | |||||||
| SCr440 | 41Cr4 (1.7035) | |||||||
| SCM435 | 34CrMo4 (1.7220) | |||||||
| SCM440 | 42CrMo4 (1.7225) | |||||||
| SNC631 | 36NiCr10 (1.5736) | |||||||
| SNCM439 | 40NiCrMo6 (1.6565) | |||||||
| SNCM447 | 34CrNiMo6 (1.6582) | |||||||
| SUS430 | X6Cr17 (1.4016) | |||||||
| SUS403 | X6Cr13 (1.4000) | |||||||
| 59 | SAE 1141 | / | −1 | UA | determined by 0.2% offset in the cyclic stress–strain curve | [43] | ||
| SAE 1038 | C35E (1.1181) | |||||||
| SAE 1541 | 36Mn6 (1.1127) | |||||||
| SAE 1050 | C50 (1.0540) | |||||||
| SAE 1090 | C92D (1.0618) | |||||||
| 08 | / | |||||||
| 20 | / | |||||||
| 30 | / | |||||||
| 40 | / | |||||||
| 40CrNiMo | 40NiCrMo6 (1.6565) | |||||||
| 60Si2Mn | 60Si7 (1.5027) |
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 79 | AISI 4340 | 36CrNiMo4 (1.6511) | −1 | US | [19,34] | |||
| 80 | SAE 4340 | 36CrNiMo4 (1.6511) | −1 | RB | / | [19] | ||
| 81 | SAE 4063 | / | −1 | RB | / | [19] | ||
| 82 | SAE 5150 | 46Cr2 (1.7006) | −1 | RB | / | [19] | ||
| 83 | SAE 4140 | 42CrMo4 (1.7225) | −1 | RB | / | [19] | ||
| 84 | Ferrous powder metal materials | / | UA | , and b: material dependent : given by Equation (14) | [35] |
| No. | Estimation | Material a | German Equivalent (Material Number) b [21] | Rc | Test Type c,d | Number of Cycles c | Notes | Ref. |
|---|---|---|---|---|---|---|---|---|
| 130 | / | −1 | / | to | For MPa | [81] | ||
| 131 | / | −1 | RB | / | For MPa | [82] | ||
| 132 | / | / | / | 1 to | Equations modified from those given in [83] | [83] | ||
| 133 | S10C | C10E (1.1121) | RB | to | [48] | |||
| S15C | C15E (1.1141) | |||||||
| S25C | C25 (1.0406) | |||||||
| 134 | S30C | C30 (1.0528) | −1 | RB | to | [48] | ||
| S35C | C35 (1.0501) | |||||||
| S45C (EQT) | C45 (1.0503) | |||||||
| S50C (EQT) | C50 (1.0540) | |||||||
| 135 | S45C (Q&T) | C45 (1.0503) | −1 | RB | to | [48] | ||
| S50C (Q&T) | C50 (1.0540) | |||||||
| 136 | / | −1 | UA | to | for body-centred cubic or face-centred cubic crystal lattice (steel and aluminium alloys) for hexagonal close-packed crystal lattice (titanium alloys) for smooth specimens | [84] | ||
| 137 | / | >0 | UA | to | for body-centred cubic or face-centred cubic crystal lattice (steel and aluminium alloys) for hexagonal close-packed crystal lattice (titanium alloys) for smooth specimens | [84] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Motte, R.; De Waele, W. An Overview of Estimations for the High-Cycle Fatigue Strength of Conventionally Manufactured Steels Based on Other Mechanical Properties. Metals 2024, 14, 85. https://doi.org/10.3390/met14010085
Motte R, De Waele W. An Overview of Estimations for the High-Cycle Fatigue Strength of Conventionally Manufactured Steels Based on Other Mechanical Properties. Metals. 2024; 14(1):85. https://doi.org/10.3390/met14010085
Chicago/Turabian StyleMotte, Robin, and Wim De Waele. 2024. "An Overview of Estimations for the High-Cycle Fatigue Strength of Conventionally Manufactured Steels Based on Other Mechanical Properties" Metals 14, no. 1: 85. https://doi.org/10.3390/met14010085
APA StyleMotte, R., & De Waele, W. (2024). An Overview of Estimations for the High-Cycle Fatigue Strength of Conventionally Manufactured Steels Based on Other Mechanical Properties. Metals, 14(1), 85. https://doi.org/10.3390/met14010085







