Local Ratcheting at the Notch Region of Non-Press-Fitted and Press-Fitted Al 7075-T6 Samples Undergoing Asymmetric Stress Cycles
Abstract
:1. Introduction
2. Kinematic Hardening Rules and Formulation
2.1. Strain Increments
2.2. The Ahmadzadeh-Varvani (A-V) Kinematic Hardening Rule
2.3. Neuber’s Rule: Relating Nominal Stress/Strain to Local Components of Stress and Strain at Notch Root
2.4. The Chaboche Kinematic Hardening Rule
3. Results and Discussion
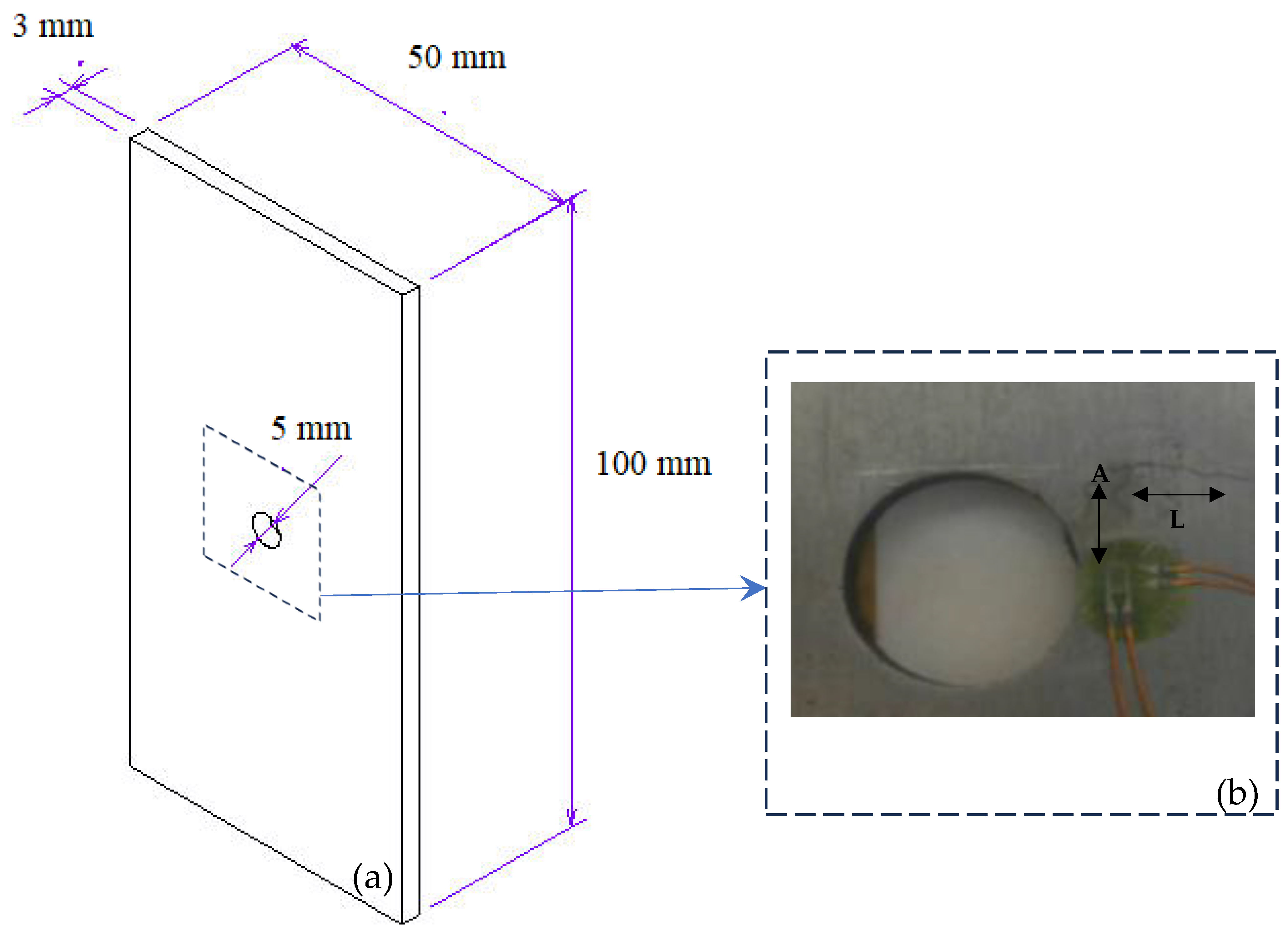
3.1. Ratcheting Data
3.2. Kinematic Hardening Rule Coefficients
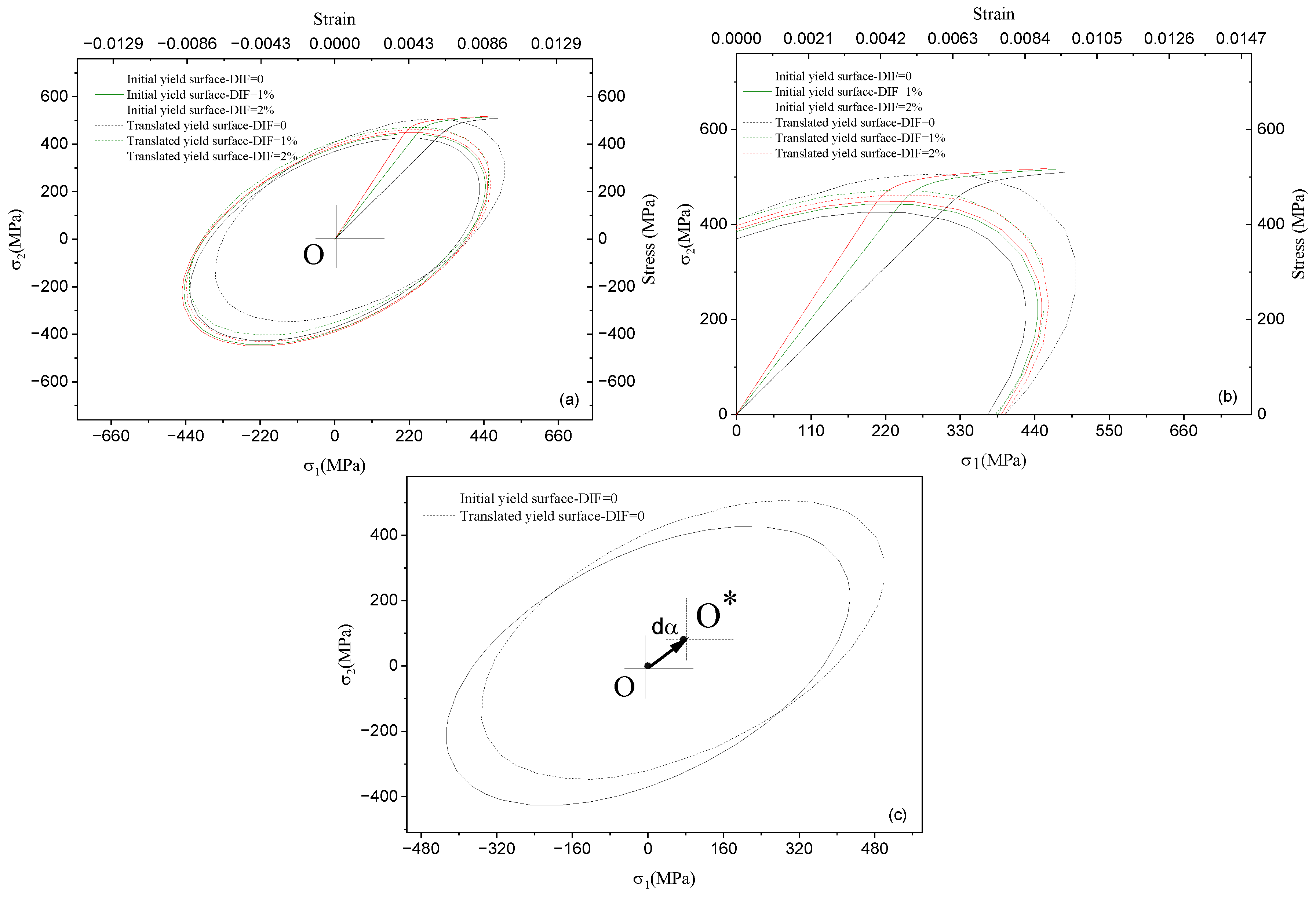
3.3. Yield Surface Evolution
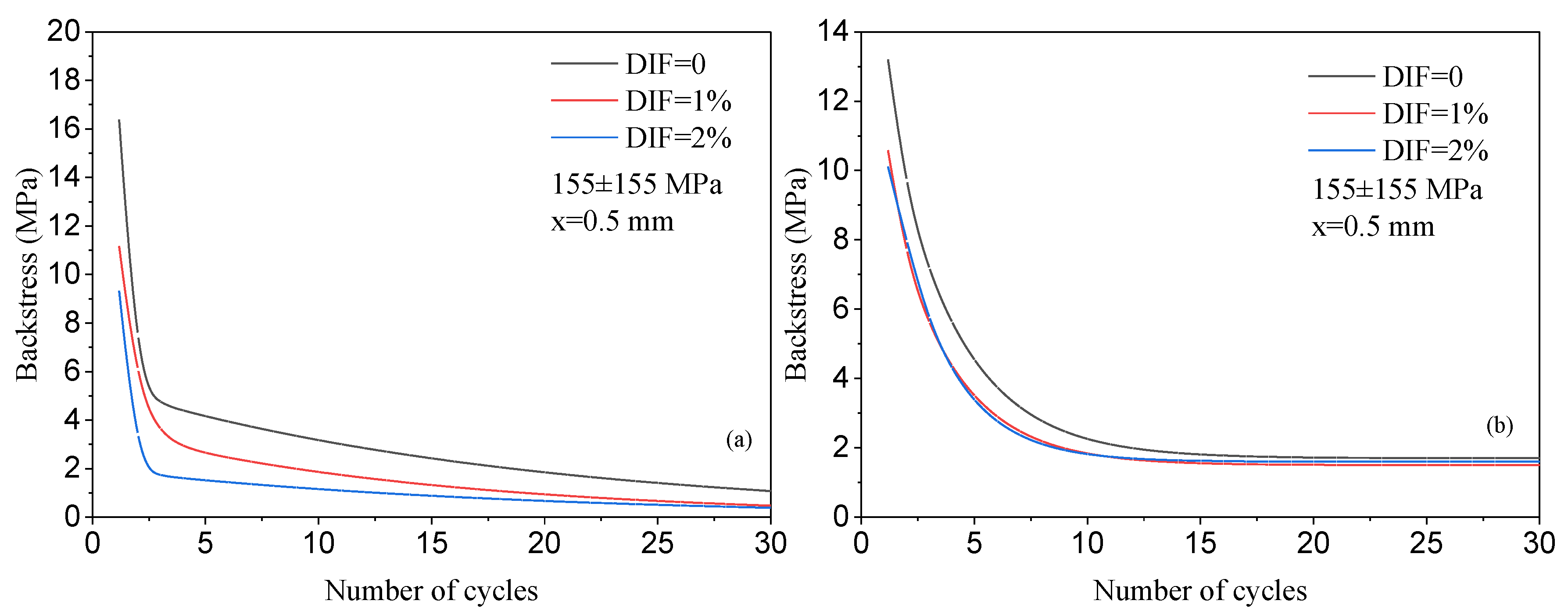
3.4. Backstress Evolution with Loading
3.5. Finite Element Analysis and Stress Distribution
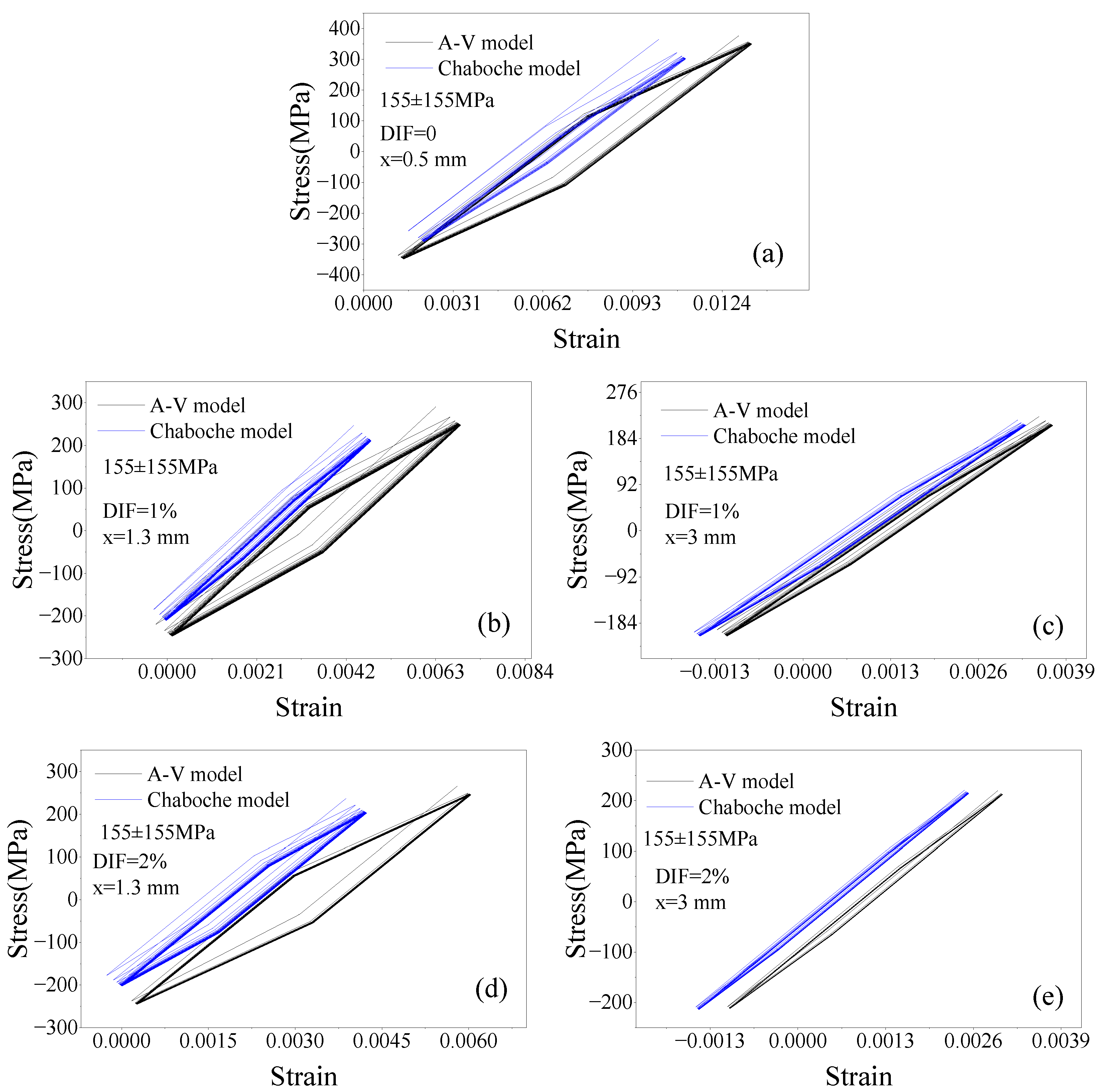
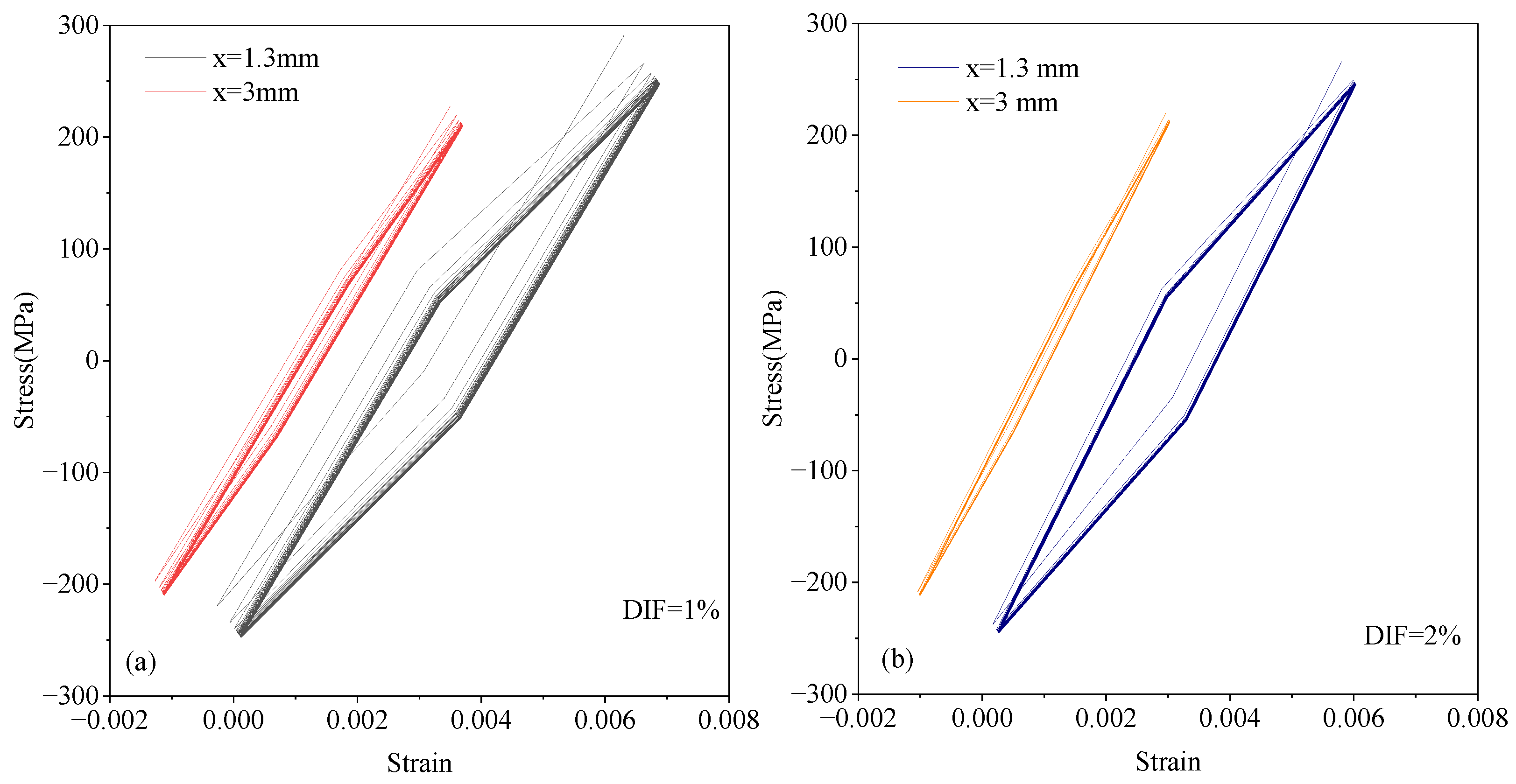
3.6. Predicted Hysteresis Loops
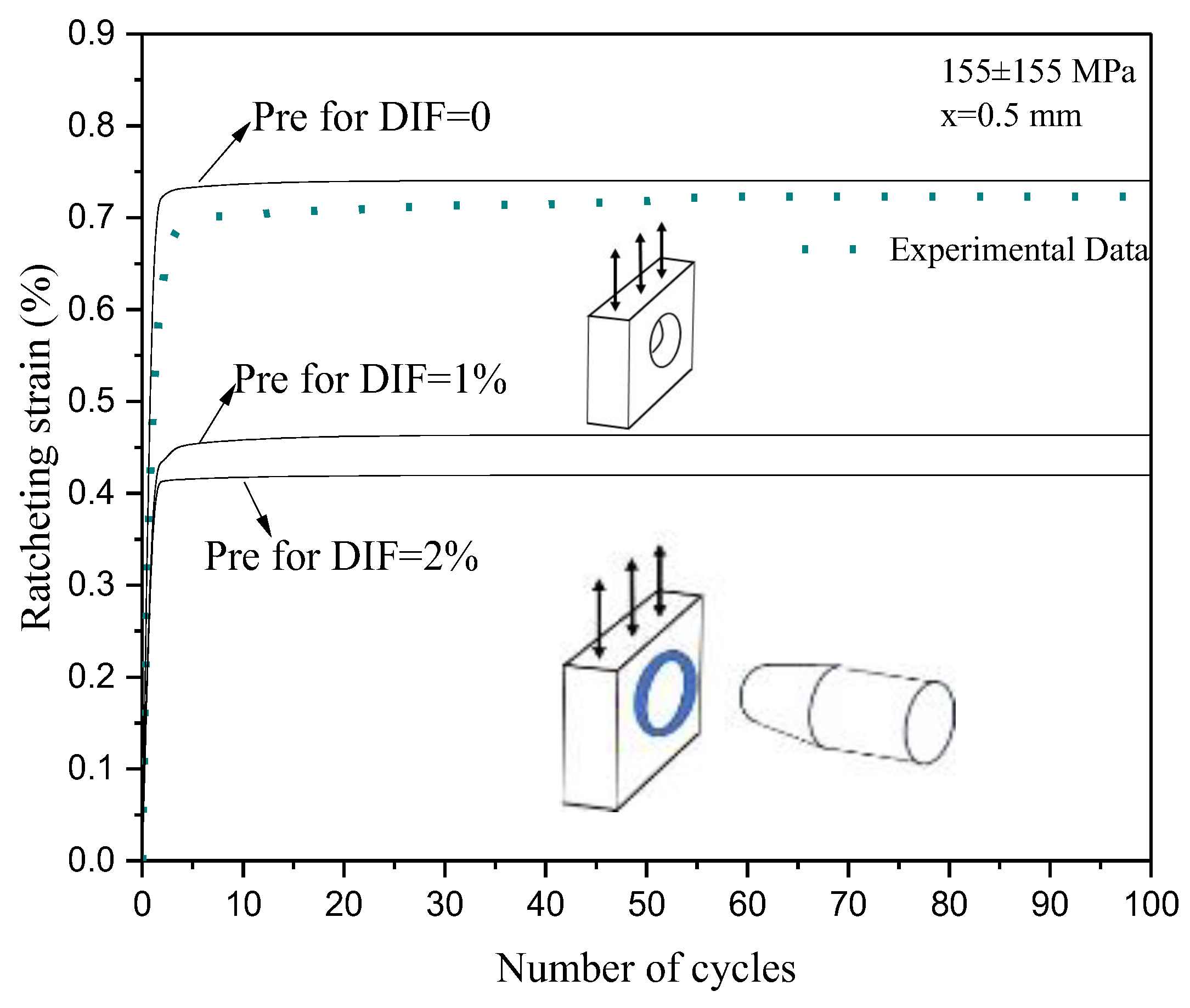
3.7. Local Ratcheting Strain Prediction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Total strain increment tensor | |
| Elastic strain increment tensor | |
| Plastic strain increment tensor | |
| E | Modulus of elasticity |
| Plastic modulus | |
| Backstress tensor | |
| Stress tensor | |
| Unit tensor | |
| Poisson’s ratio | |
| G | Shear modulus |
| Deviatoric stress tensor | |
| Initial yield strength | |
| d | Circular notch diameter |
| Coefficients of the A-V model | |
| , | Chaboche materials coefficients |
| Stress concentration factor | |
| Internal variable of the A-V model tensor | |
| Ramberg-Osgood coefficients | |
| S,e | Nominal stress and strain |
| R | Stress ratio |
| , | Stress and strain concentration factors |
| Uniaxial local stress and strain at the notch root | |
| Strain energy per unit volume at the notch root | |
| Elastic strain energy per unit volume due to the nominal remote stress |
References
- Chakherlou, T.N.; Oskouei, R.H.; Vogwell, J. Experimental and numerical investigation of the effect of clamping force on the fatigue behaviour of bolted plates. Eng. Fail. Anal. 2008, 15, 563–574. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Abazadeh, B.; Vogwell, J. The effect of bolt clamping force on the fracture strength and the stress intensity factor of a plate containing a fastener hole with edge cracks. Eng. Fail. Anal. 2009, 16, 242–253. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Vogwell, J. A novel method of cold expansion which creates near-uniform compressive tangential residual stress around a fastener hole. Fatigue Fract. Eng. Mater. Struct. 2004, 27, 343–351. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Aghdam, A.B. An experimental investigation on the effect of short time exposure to elevated temperature on fatigue life of cold expanded fastener holes. Mater. Design 2008, 29, 1504–1511. [Google Scholar] [CrossRef]
- Wang, C.; Zou, F.; Zhou, E.; Fan, Z.; Ge, E.; An, Q.; Ming, W.; Chen, M. Effect of split sleeve cold expansion on microstructure and fatigue performance of 7075-T6 aluminum alloy holes. Int. J. Fatigue 2023, 167, 107339. [Google Scholar] [CrossRef]
- Zhang, Q.; Zuo, Y. Fatigue behavior investigation of interference fitted pinned joints with extremely small edge distance. J. Mater. Eng. Perform. 2023, 21, 865–872. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Mirzajanzadeh, M.; Saeedi, K.H. Fatigue crack growth and life prediction of a single interference fitted holed plate. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 633–644. [Google Scholar] [CrossRef]
- Hassanifard, S.; Adibeig, M.R.; Mohammadpour, M.; Varvani-Farahani, A. Fatigue life of axially loaded clamped rivet-nut joints: Experiments and analyses. Int. J. Fatigue 2019, 129, 105254. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Alvandi-Tabrizi, Y.; Kiani, A. On the fatigue behavior of cold expanded fastener holes subjected to bolt tightening. Int. J. Fatigue 2011, 33, 800–810. [Google Scholar] [CrossRef]
- Kolasangiani, K.; Varvani-Farahani, A. Local ratcheting assessment of steel samples undergoing various step and block loading conditions. Theor. Appl. Fract. Mech. 2020, 107, 102533. [Google Scholar] [CrossRef]
- Shekarian, A.; Varvani-Farahani, A. Ratcheting prediction at the notch root of steel samples over asymmetric loading cycles. J. Eng. Mater. Technol. Trans. 2020, 142, 021009. [Google Scholar] [CrossRef]
- Varvani-Farahani, A. Nonlinear kinematic hardening cyclic plasticity. In Cyclic Plasticity of Metals Modeling Fundamentals and Applications; Jahed, H., Roostaei, A.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 139–174. [Google Scholar]
- Shekarian, A.; Varvani-Farahani, A. Ratcheting behavior of notched stainless-steel samples subjected to asymmetric loading cycles. J. Iron Steel Res. Int. 2021, 28, 86–97. [Google Scholar] [CrossRef]
- Shekarian, A.; Varvani-Farahani, A. Ratcheting response of SS316 steel samples with different notch shapes under various loading spectra. J. Mater. Eng. Perform. 2021, 30, 3524–3535. [Google Scholar] [CrossRef]
- Neuber, H. Theory of stress concentration for shear-strained prismatical bodies with arbitrary nonlinear stress-strain law. J. Appl. Mech. 1961, 28, 544–550. [Google Scholar] [CrossRef]
- Chaboche, J. On some modifications of kinematic hardening to improve the description of ratcheting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Ahmadzadeh, G.R.; Varvani-Farahani, A. Ratcheting assessment of materials based on the modified Armstrong—Frederick hardening rule at various uniaxial stress levels. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 1232–1245. [Google Scholar] [CrossRef]
- Wang, C.H.; Rose, L.R.F. Transient and steady-state deformation at notch root under cyclic loading. Mech. Mater. 1998, 30, 229–241. [Google Scholar]
- Hu, W.; Wang, C.H.; Barter, S. Analysis of Cyclic Mean Stress Relaxation and Strain Ratchetting Behavior of Aluminum 7050; Aeronautical and Maritime Research Lab: Melbourne, VIC, Australia, 1999. [Google Scholar]
- Rahman, S.M.; Hassan, T. Advanced cyclic plasticity models in simulating ratcheting responses of straight and elbow piping components, and notched plates. In Proceedings of the ASME Pressure Vessels and Piping Conference, Denver, CO, USA, 17–21 July 2005; pp. 421–427. [Google Scholar]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: Formulations and basic features for ratcheting behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Ohno, N.; Abdel Karim, M. Uniaxial ratcheting of 316FR steel at room temperature—Part II: Constitutive modeling and simulation. ASME J. Appl. Mech. 2000, 122, 35–41. [Google Scholar]
- Firat, M. A notch strain calculation of a notched specimen under axial-torsion loadings. Mater. Des. 2011, 32, 3876–3882. [Google Scholar] [CrossRef]
- Barkey, M.E. Calculation of Notch Strains under Multiaxial Nominal Loading. Ph.D. Thesis, Department of Theoretical and Applied Mechanics, University of Illinois at Urbana, Champaign, IL, USA, 1993. [Google Scholar]
- Liu, C.; Chen, X.; Chen, W.; Shi, L.; Su, X.; Ogonmola, O.; Shan, L. Ratcheting-fatigue behavior and life prediction of Z2CN18. 10 austenitic stainless steel elbow Int. J. Press. Vessel. Pip. 2023, 204, 104985. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, R.; Kim, K.S. On the Ohno-Wang kinematic hardening rules for multiaxial ratcheting modeling of medium carbon steel. Int. J. Plast. 2005, 21, 161–184. [Google Scholar] [CrossRef]
- Hatami, F.; Varvani-Farahani, A. Accumulation of plastic strain at notch root of steel specimens undergoing asymmetric fatigue cycles: Analysis and simulation. Materials 2023, 16, 2153. [Google Scholar] [CrossRef] [PubMed]
- Chakherlou, T.N.; Ajri, M. Strain ratcheting and stress relaxation around interference-fitted single-holed plates under cyclic loading: Experimental and numerical investigations. Fatigue Fract. Eng. Mater. Struct. 2012, 36, 327–339. [Google Scholar] [CrossRef]
- Varvani-Farahani, A. A comparative study in descriptions of coupled kinematic hardening rules and ratcheting assessment over asymmetric stress cycles. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 882–893. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; NACA Technical Note No. 902; NASA: Washington, DC, USA, 1943. [Google Scholar]
- Kolasangiani, K.; Shariati, M.; Varvani-Farahani, A. Ratcheting examination of 1045 notched steel plates under Low-High and High-Low sequences. J. Test Eval. 2021, 49, 3685–3700. [Google Scholar] [CrossRef]
- Agius, D.; Wallbrink, C.; Kourousis, K.I. Cyclic elastoplastic performance of aluminum 7075-T6 under strain- and stress-controlled loading. J. Mater. Eng. Perform. 2017, 26, 5769–5780. [Google Scholar] [CrossRef]
- Benedettia, M.; Bertob, F.; Le Bonec, L.; Santusc, C. A novel Strain-Energy-Density based fatigue criterion accounting for mean stress and plasticity effects on the medium-to-high-cycle uniaxial fatigue strength of plain and notched components. Int. J. Fatigue 2020, 133, 105397. [Google Scholar] [CrossRef]
- Benedetti, M.; Menapace, C.; Fontanari, V.; Santus, C. On the variability in static and cyclic mechanical properties of extruded 7075-T6 aluminum alloy. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2975–2989. [Google Scholar] [CrossRef]
- Zhoua, J.; Suna, Z.; Kanoutéa, P.; Retraint, D. Experimental analysis and constitutive modelling of cyclic behaviour of 316 L steels including hardening/softening and strain range memory effect in LCF regime. Int. J. Plast. 2018, 107, 54–78. [Google Scholar] [CrossRef]
- Rajaeian, M.; Parsa, M.H. Experimental analysis and constitutive modeling of cyclic behavior of 304 L stainless steel: Introduction of isotropic hardening fading effect. J. Pres V. Tech. 2023, 145, 011508. [Google Scholar] [CrossRef]
- ABAQUS User’s Manual, Version 6.13. Hibbitt, Karlsson and Sorensen. 2016. Available online: http://130.149.89.49:2080/v6.13/pdf_books/CAE.pdf (accessed on 5 July 2020).
- Neuber, H. Theory of Notch Stresses; Edwards: Ann Arbor, MI, USA, 1946. [Google Scholar]
- Chmelko, V.; Harakaľ, M.; Žlábek, P.; Margetin, M.; Ďurka, R. Simulation of stress concentrations in notches. Metals 2022, 12, 43. [Google Scholar] [CrossRef]

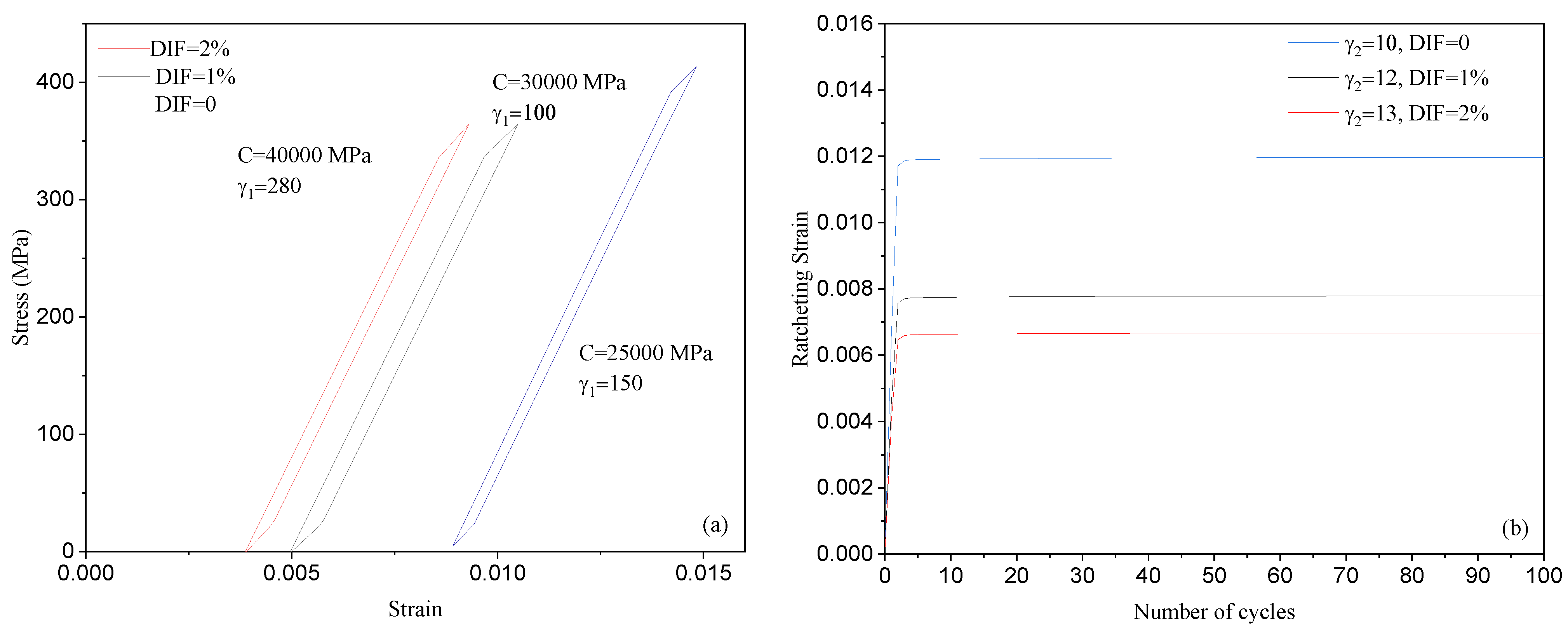




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatami, F.; Varvani-Farahani, A. Local Ratcheting at the Notch Region of Non-Press-Fitted and Press-Fitted Al 7075-T6 Samples Undergoing Asymmetric Stress Cycles. Metals 2023, 13, 1549. https://doi.org/10.3390/met13091549
Hatami F, Varvani-Farahani A. Local Ratcheting at the Notch Region of Non-Press-Fitted and Press-Fitted Al 7075-T6 Samples Undergoing Asymmetric Stress Cycles. Metals. 2023; 13(9):1549. https://doi.org/10.3390/met13091549
Chicago/Turabian StyleHatami, F., and A. Varvani-Farahani. 2023. "Local Ratcheting at the Notch Region of Non-Press-Fitted and Press-Fitted Al 7075-T6 Samples Undergoing Asymmetric Stress Cycles" Metals 13, no. 9: 1549. https://doi.org/10.3390/met13091549
APA StyleHatami, F., & Varvani-Farahani, A. (2023). Local Ratcheting at the Notch Region of Non-Press-Fitted and Press-Fitted Al 7075-T6 Samples Undergoing Asymmetric Stress Cycles. Metals, 13(9), 1549. https://doi.org/10.3390/met13091549






