Abstract
It has been known for at least 150 years that fatigue life data exhibits a considerable amount of variability. Furthermore, statistically modeling fatigue life adequately is challenging. Different empirical approaches have been used, each of which has merit; however, none is appropriate universally. Even when a sufficiently robust database exists, the scatter in the fatigue lives may be extremely large and difficult to characterize. The purpose of this work is to review traditional and more modern empirically based methodologies for estimating the statistical behavior of fatigue data. The analyses are performed on two historic sets of data for annealed aluminum wire and annealed electrolytic copper wire tested in reverse torsion fatigue. These data are readily available In publications. Specifically, the review considers a traditional method for stress-cycle (S-N) analysis which includes linear regression through load dependent medians and mean square error (MSE) confidence bounds. Another approach that is used is Weibull distribution estimation for each loading condition, from which estimations for the median behavior and confidence bounds are determined. The preferred technique is the development of a cumulative distribution functions for fatigue life, which contains aspects of traditional reliability, classical S-N, and applied loading modeling. Again, confidence bounds are estimated for this technique. Even though it is an empirical technique, there are mechanistic aspects that underlie the empiricism. This approach is suggested because the method is very robust, and the estimation is more accurate than the other methods.
1. Introduction
It is universally accepted that an essential characteristic of fatigue is variability in life data. These data often range over an order of magnitude, and sometimes even more [1]. The reasons for this scatter can be categorized as epistemic and aleatoric uncertainty. Error cannot be eliminated from experimentation, material microstructure cannot be explicitly prescribed, and processing cannot be controlled perfectly. An excellent paper on the history of fatigue was written by Schütz [2], in which, he credits Wöhler [3] as the first to implicitly consider scatter in fatigue data. One of the first times that scatter was addressed was in the book by Moore and Kommers [4]. They include the following footnote on page 168: “So far as the writers have been able to ascertain, the term “scatter” as applied to the irregularity shown by plotted test data was coined by Prof. G. B. Upton of Cornell University”.
One of the earliest research efforts to develop rich fatigue life databases is contained in the paper by Ravilly [5]. The testing procedure, microstructure, and manufacturing of those wires may not have been as controlled as is the case currently. Furthermore, the materials characterization was not performed according to modern day standards. Scatter between different applied loads and replicates for each given loading condition should be expected. These datasets are some of the very first in the open literature in which systematic experimental investigations of fatigue were conducted for statistical analysis. There were multiple stress levels for which an adequate number of replicates were performed in order to make a statistical analysis possible. Consequently, these data are considered herein to focus on statistical modeling rather than the experimental or processing techniques.
Freudenthal extensively statistically analyzed Ravilly’s data [5] in a series of publications. In [6], he considered annealed aluminum wire data, annealed Armco iron wire, and annealed electrolytic copper wire. As an aside, Armco stands for American Rolling Mill Company, which was founded in 1899. It continued operation until its purchase in 2020. In collaboration with Gumbel, Freudenthal published a paper [7] which was even more statistically orientated, using the annealed aluminum wire and annealed electrolytic copper wire data. Another paper [8] was produced using the nickel wire data and referring to the annealed aluminum wire results from the previous papers. Gumbel [9] published a paper making a few additional extensions and modifications to his previous work. Other investigators, refs. [10,11,12] for example, mention Ravilly’s data [5], but they do not perform any significant analyses with the data. In the ensuing pages, Ravilly’s data [5] will be statistically presented and analyzed. Some of this will be similar to the authors cited above, but new analyses will be shown as well.
Prior to looking at Ravilly’s data [5] specifically, it is appropriate to recall others who have contributed to statistical modeling of fatigue life. Modeling the cumulative distribution function (cdf) for fatigue life, given the applied loading conditions, is of supreme importance. There are several authors, refs. [6,13,14,15,16] for example, who use the log-normal cdf. This cdf, however, is primarily used for mathematical expediency for parameter estimation and graphical presentation. Philosophically, the log-normal cdf is not appropriate, especially for very high cycle fatigue analyses, because its hazard function decreases as fatigue life increases. A decreasing hazard function indicates that the material improves the longer it survives. Almost never does this occur in reality. Rather, the fatigue of physical components or structures leads to increasing deterioration and damage, which necessitates an increasing hazard function.
The cdf for fatigue life that has become the most commonly used is the Weibull cdf. Weibull first introduced the cdf in 1939 [17] for the strength of materials, and in 1951 [18], he extended the application to fatigue. Even though the name of the cdf is universally known as the Weibull cdf, Fréchet [19] introduced the cdf in 1927. Fisher and Tippet [20] and Gnedenko [21] proved that one of the only three possible limiting types of cdfs for the minimum of a sample of random variables is a Weibull cdf. When failure of a specimen, component, or structure is well characterized by an initial failure of the microstructure, then the Weibull cdf is the appropriate choice. The Weibull cdf has an increasing hazard function when its coefficient of variation (cv) is greater than one. Its applicability is extremely wide-ranging. Bolotin [22] advocated for the use of a Weibull cdf for the statistical modeling of fatigue. Additional examples of more recent references using a Weibull cdf for fatigue life is [23,24,25,26,27,28,29,30]. Consequently, the Weibull cdf will be the underlying cdf used herein. As an interesting aside, the printed discussion following Freudenthal’s paper [6] has several contributions from leading researchers at that time that advocate for either the log-normal cdf or the Weibull cdf. Specifically, one of the commenters is W. Weibull.
It is also necessary to make a few comments about the stress (S) versus number of cycles (N) diagrams, commonly known as an S-N diagram or graph. Similar remarks could be made about strain versus life diagrams, but since Ravilly’s data [5] will be used below, the discussion will be for S-N diagrams. One of the most-quoted papers on fatigue testing is by Wöhler [3], who is credited for introducing the S-N diagram. Frequently, it is called the Wöhler diagram. Certainly, by the time that Weibull [18] and Freudenthal [6] analyzed fatigue data, it was recognized that there was substantial variability in fatigue lives. Some authors use P-S-N to designate a probabilistic (P) S-N diagram. An excellent review of P-S-N analyses can be found in [31]. Another noteworthy article which provides a critical review of the P-S-N approach is [32]. Several other authors have indicated the significance of the P-S-N approach as a means of evaluating this relationship [33,34,35,36,37].
There have also been a number of other empirical methods used for fatigue behavior. These include Bayesian methods coupled with maximum likelihood techniques [38,39,40,41,42] and neural networks [43,44,45,46]. One of the most recent empirical approaches which has been applied to fatigue modeling is machine learning [47,48,49,50,51,52,53]. Another approach has been designated as damage mechanics, which includes effects such as load range, cycles, and geometrical features. Some recent references for this method are [54,55,56]. Since many statistical fatigue models do not include these variables explicitly, incorporating damage is warranted. The methods used herein, however, are more traditional. The suggested method developed below provides the basic structure for an advanced damage mechanics approach. Analyzing Ravilly’s data [5] with these methods may be considered in the future.
2. Materials and Methods
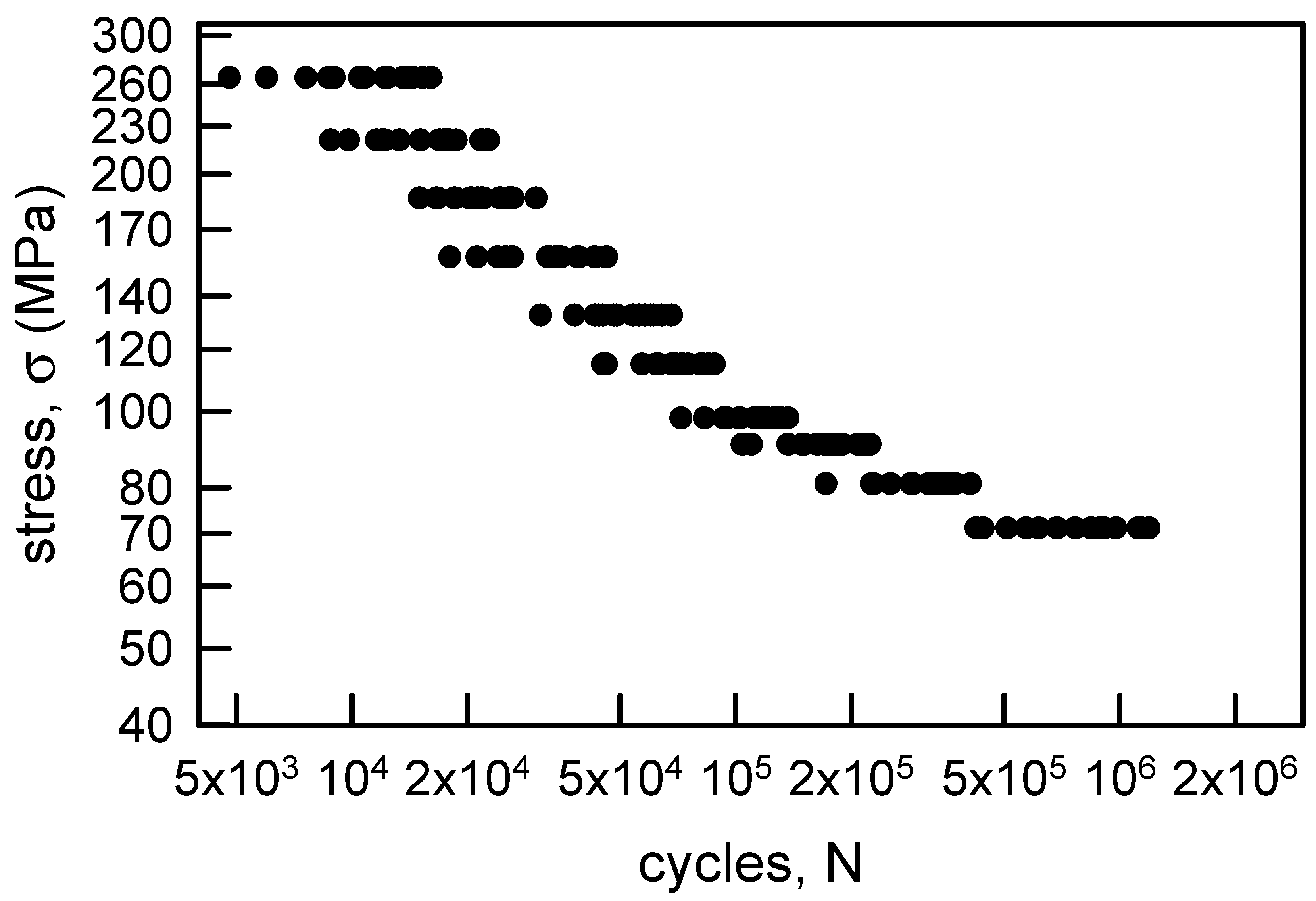
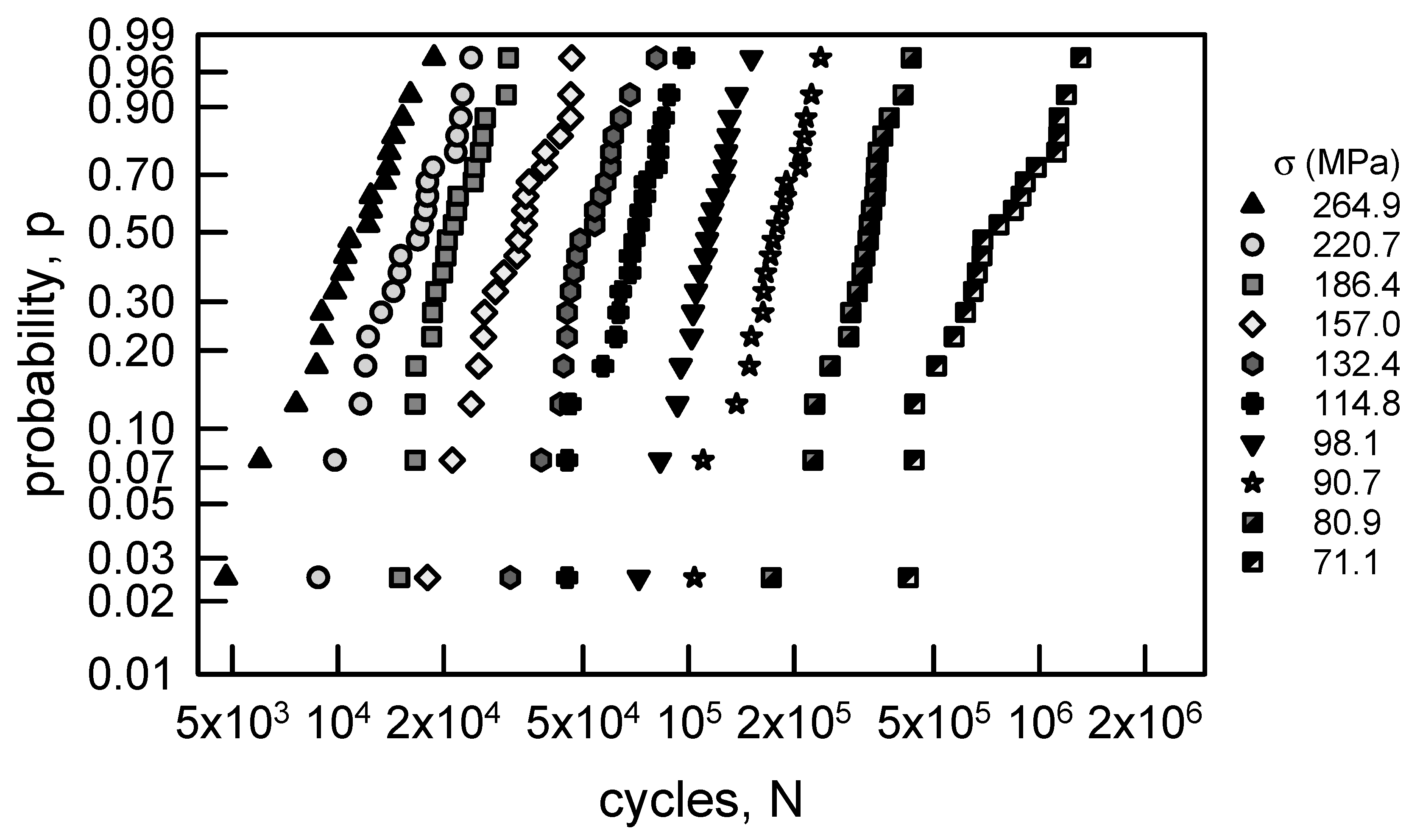
Ravilly’s paper [5] contains fatigue data for annealed aluminum wire, annealed Armco iron wire, and annealed electrolytic copper wire. The fatigue lives were obtained by using a wire fatigue testing machine where the loading is in reversed torsion for a controlled strain level. The loading is equivalent to constant stress amplitude σ fatigue loading. Also, the explicit fatigue data are presented in tabular format in Freudenthal [6]. The data considered herein will be the annealed aluminum wire data and the annealed electrolytic copper wire, both of which have 20 replicate fatigue lives for 10 different values of σ. There is sufficient data for statistical modeling and analyses. Figure 1 shows the fatigue life data for the annealed electrolytic copper wire. Both axes for the graph are natural logarithm scaling. To give further insight into the data, consider Table 1. As σ decreases, the median and average fatigue lives increase; however, there is little difference in their values. When σ = 71.1 MPa, the sample cv is the largest for the different values of σ, and when σ = 98.1 MPa, the cv is the smallest. For these fatigue life data none of the cvs is excessively large.
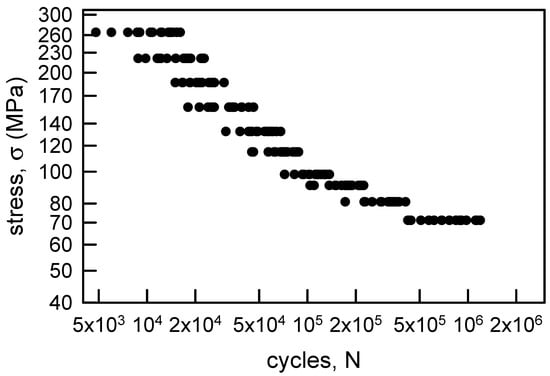
Figure 1.
S-N diagram for annealed electrolytic copper wire [6].

Table 1.
Sample properties for annealed electrolytic copper wire [6].
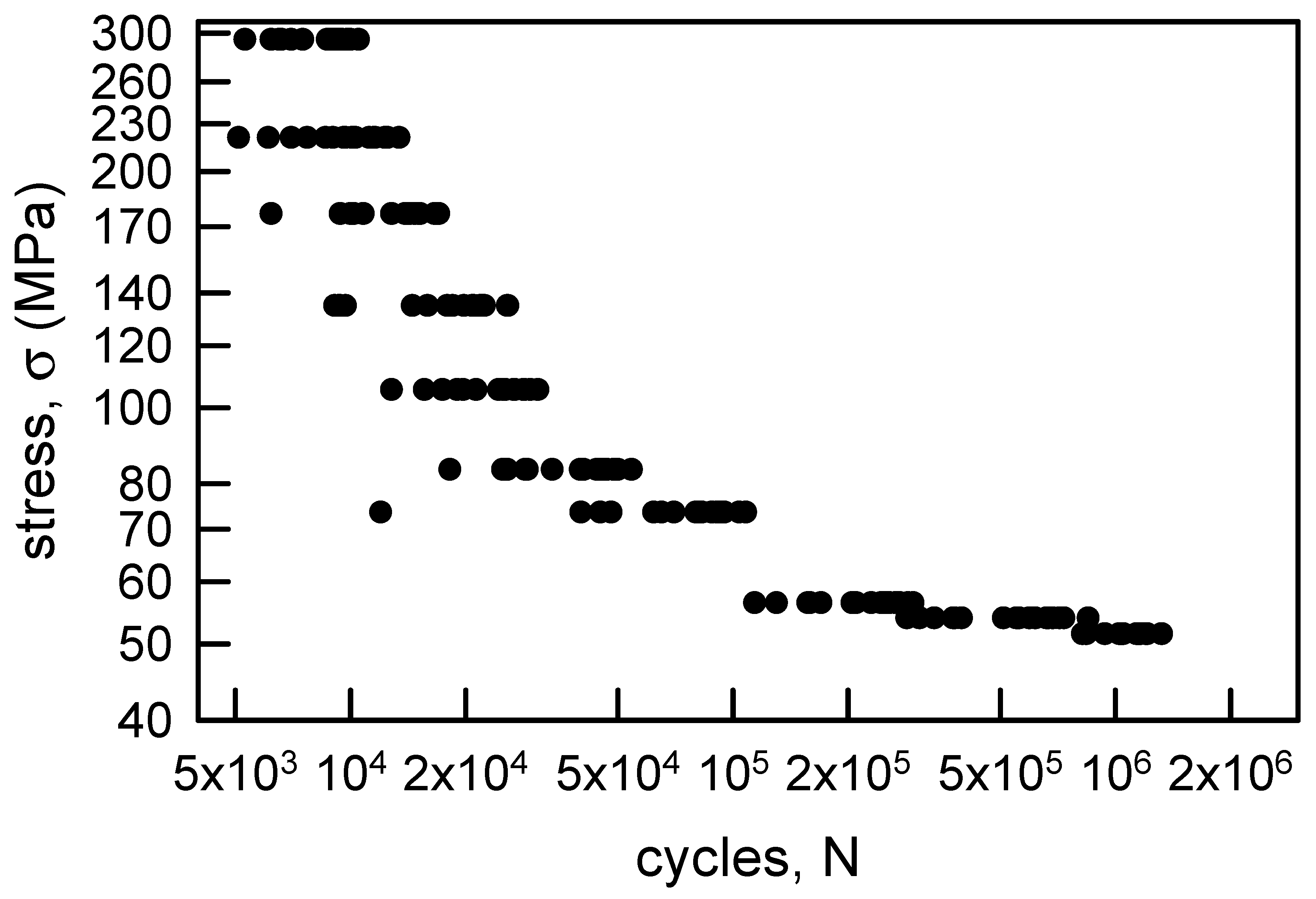
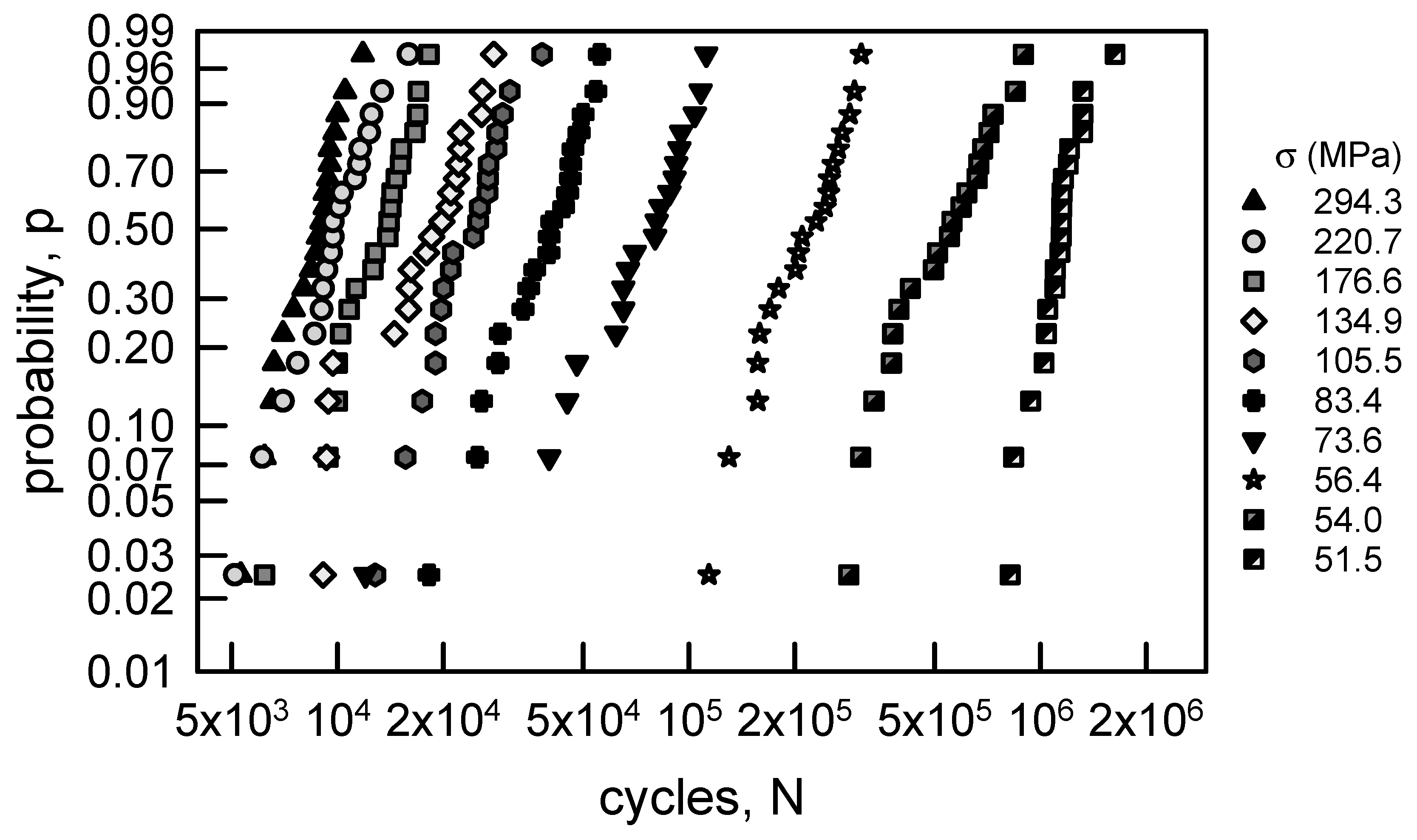
Figure 2 is similar to Figure 1 except that it contains the fatigue life data for the annealed aluminum wire. Also, Table 2 is similar to Table 1. The trends for the medians and averages for the annealed aluminum wire are comparable to those for the annealed electrolytic copper wire. The cvs, however, are not ordered. The largest cv is for σ = 73.6 MPa, and the smallest is for σ = 51.5 MPa. Typically, the amount of scatter in fatigue life data increases as the stress amplitude approaches normal operating conditions. Nevertheless, these data present an interesting statistical circumstance for modeling.
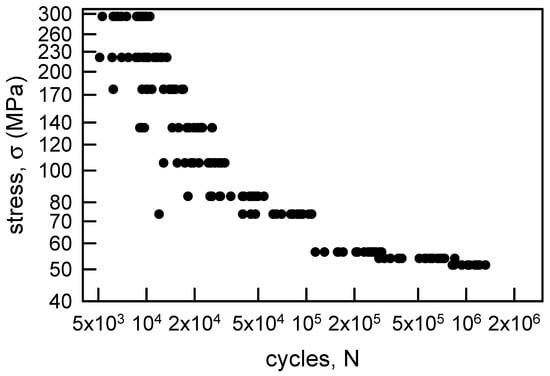
Figure 2.
S-N diagram for annealed aluminum wire [6].

Table 2.
Sample properties for annealed aluminum wire [6].
3. Results
The annealed electrolytic copper wire and the annealed aluminum wire will be analyzed below. The first analyses will be for statistical modeling of the S-N data. The next effort will be statistical modeling of the cdfs for the fatigue life for each given σ. The final investigation will be an attempt to statistically combine the S-N behavior with appropriate cdf characterizations.
3.1. S-N Modeling
3.1.1. Annealed Electrolytic Copper Wire
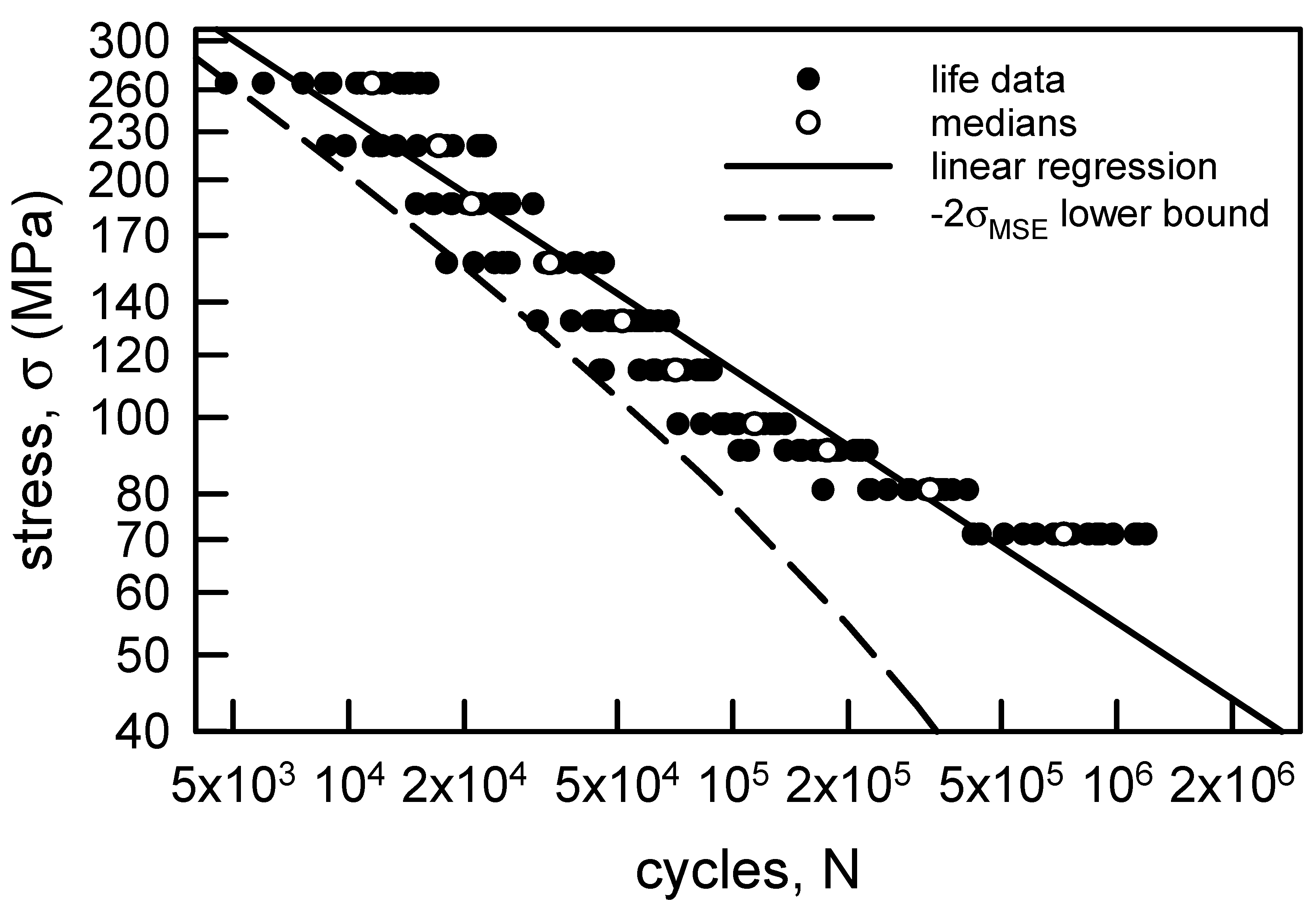
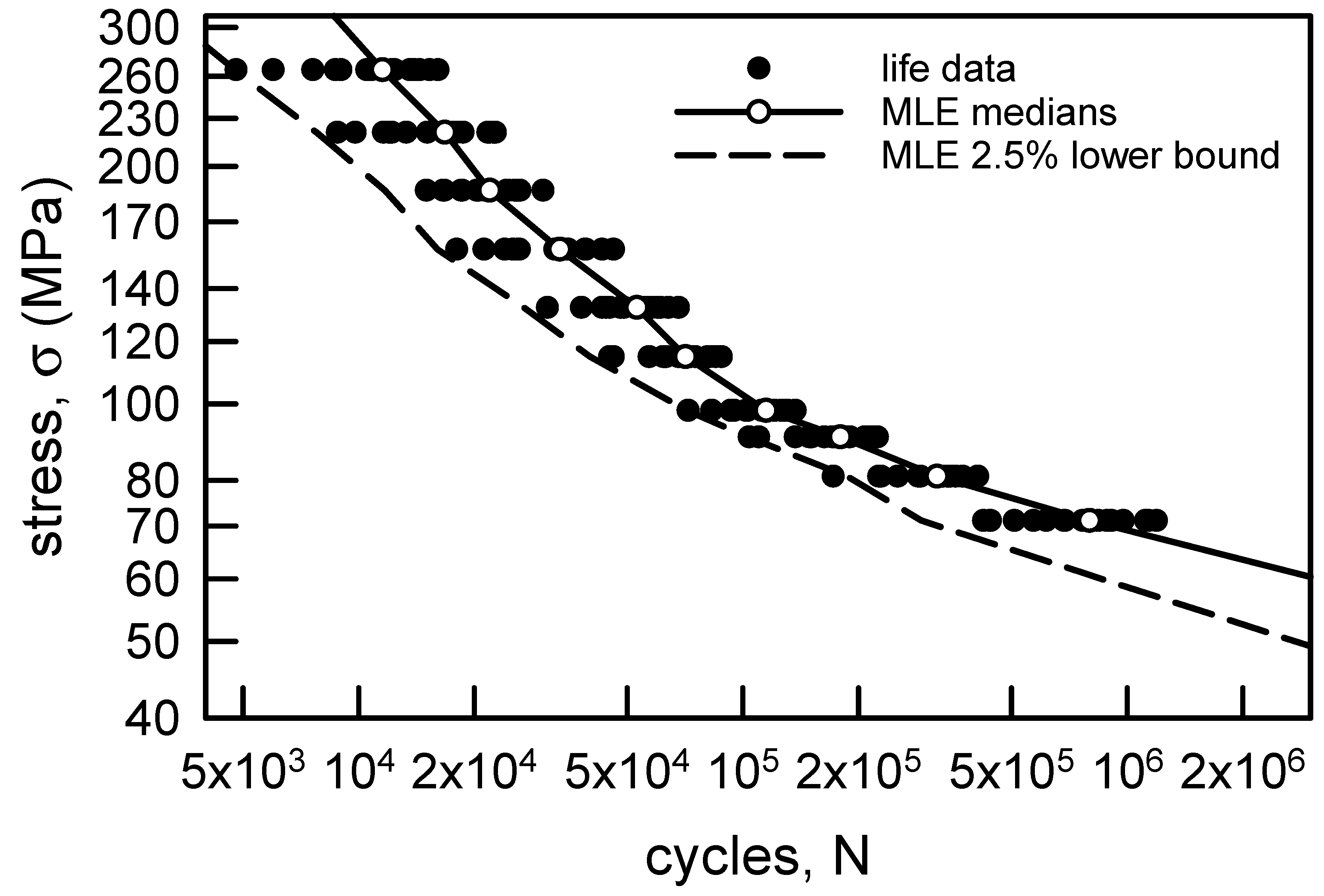
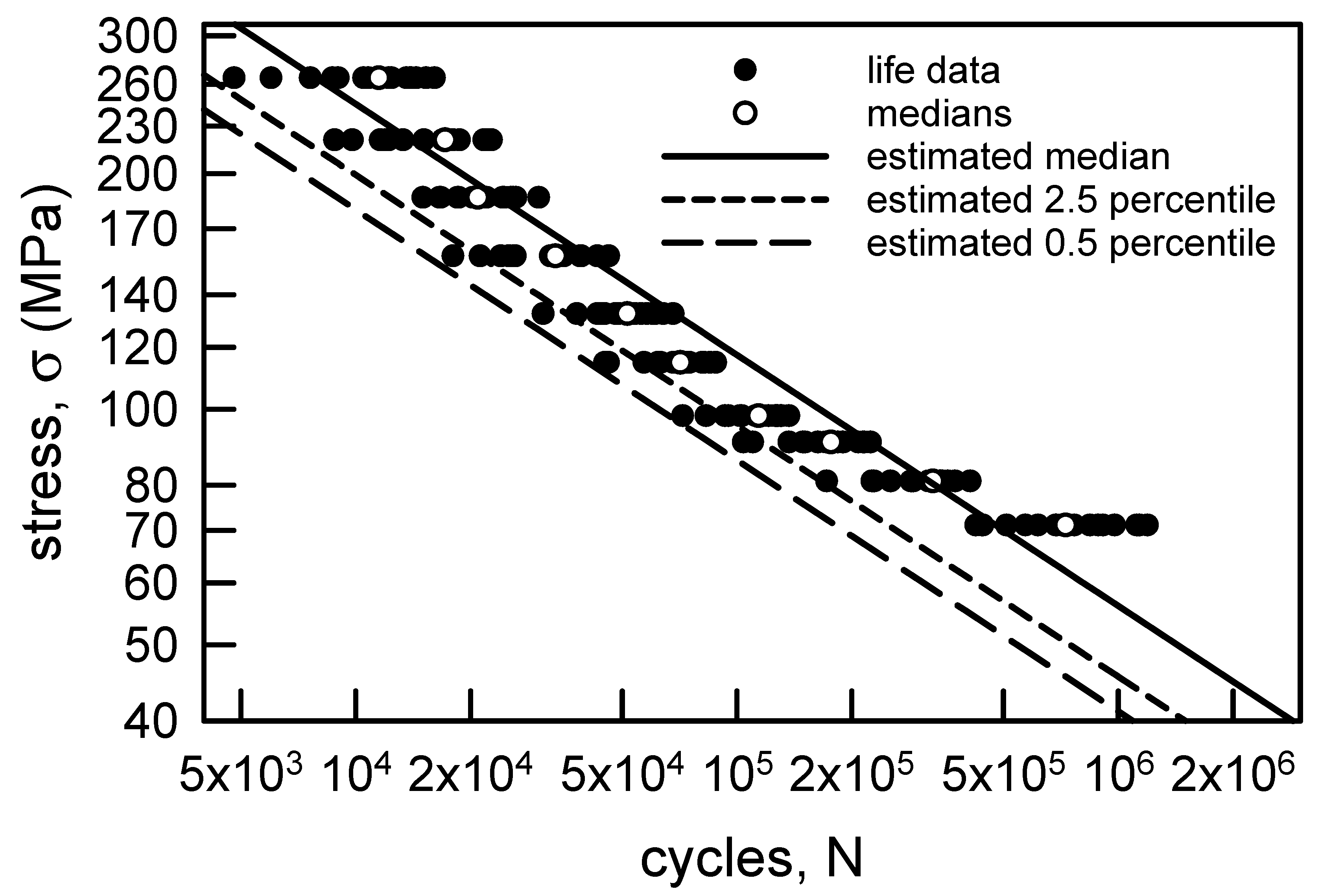
Figure 3 is identical to Figure 1 with some additions. The hollow points are the medians for each σ. Recall that the medians correspond to the 50th percentile of the sample. The solid line on Figure 3 is the linear least squares fit through the medians. The correlation coefficient r2 for the regression is 0.95, which indicates that the regression is quite good. The linear behavior on Figure 3 implies that the relationship between σ and N is given by
where m and b are the slope and intercept of the regression line, m = 0.32, and b = 6.15. Obviously, the slope is negative. The dashed line is a lower confidence bound. It is constructed by using a mean square error (MSE) analysis. The error ei is the difference between the model estimate and the data from a sample size of n. For Figure 3, the model estimate is assumed to be the linear regression. The MSE is given by
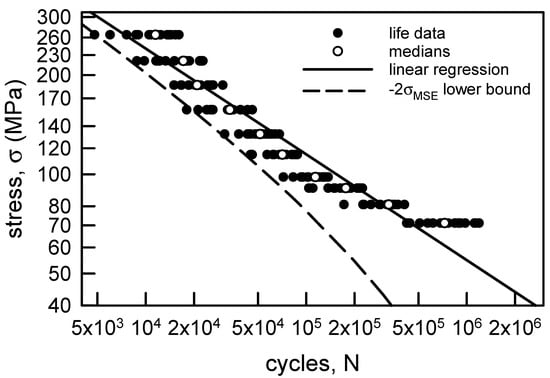
Figure 3.
S-N data for annealed electrolytic copper wire [6] with linear regression through the medians and a lower confidence bound.
The root mean square error σMSE is the square root of the MSE, and it is often used as the standard deviation to create confidence intervals. Confidence intervals can be developed by using a suitable multiple of the σMSE. One of the most common confidence intervals is constructed by adding and subtracting 2 × σMSE to the model estimate because this produces an approximation for a 95% two-sided confidence bound. A good introduction to this type of analysis is [57], and MSE is explained in detail in statistics books, for example [58]. If only 2 × σMSE is subtracted from the model estimate, then a 97.5% lower confidence bound is computed. The reason for considering just the lower bound is that the minimum life is required for design and life cycle assessment. In other words, a component or structure can be certified only up to the minimum life given a loading condition. This type of a lower confidence bound is shown on Figure 3. Notice that all of the data is greater than the lower bound, except for two data points which are on the lower bound. Also, the lower bound is reasonably close to the data except when σ = 71.1 MPa. The curvature in the lower bound as σ decreases is an indication of slightly more scatter in the fatigue lives. This nonparametric statistical analysis for the copper wire data is quite good because the median behavior is characterized well by the linear regression.
3.1.2. Annealed Aluminum Wire
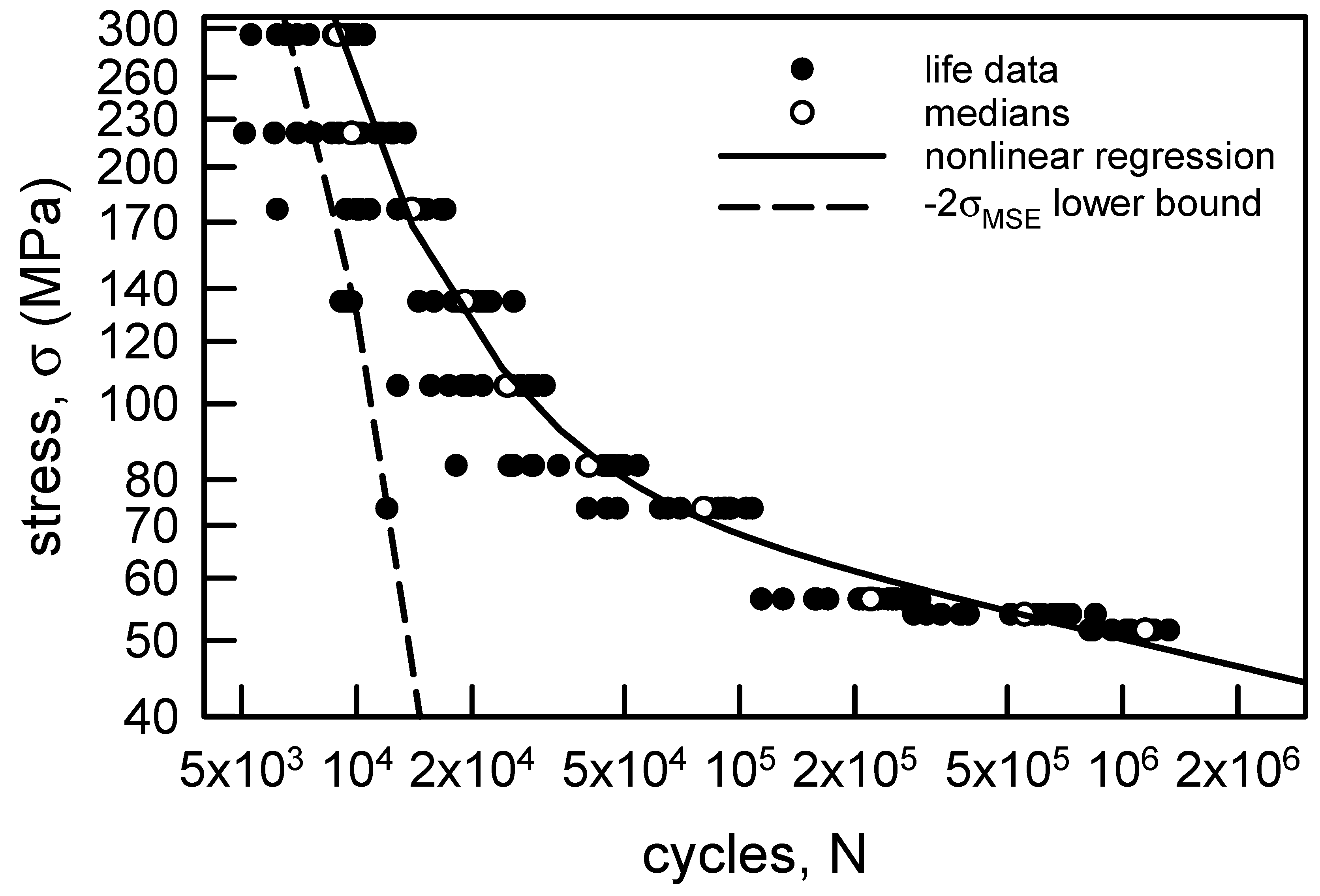
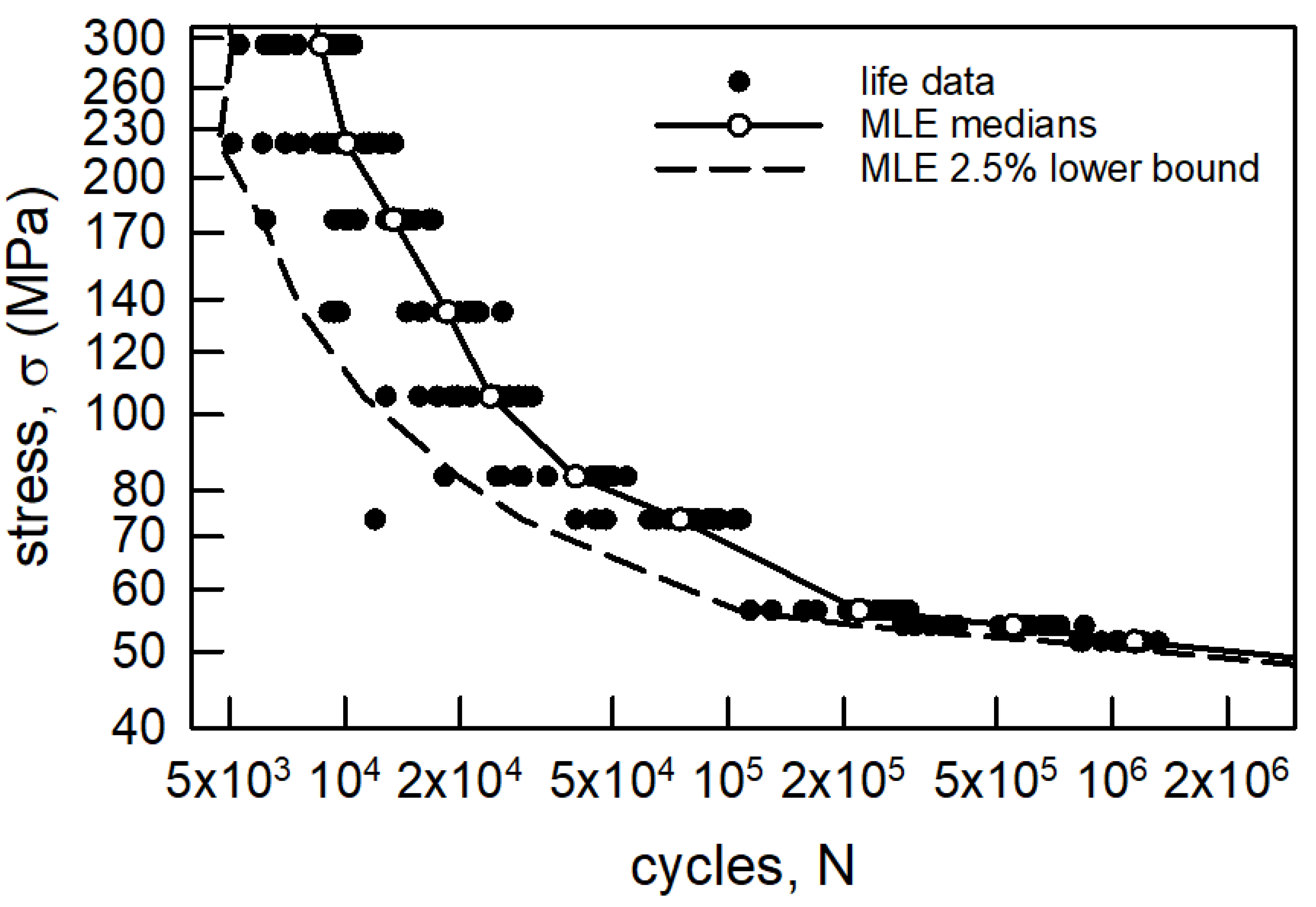
Figure 4 reproduces the S-N data from Figure 2. Again, the hollow points correspond to the medians for each σ. Clearly, a linear regression through the medians would not be an appropriate estimation of their behavior. Consequently, a nonlinear regression is needed. The equation of choice is as follows:
where a, b, c, and d are parameters to be determined. Equation (2) is similar to the shape of the Coffin–Manson model, which is designated frequently as the universal slopes method for strain life behavior [59,60]. The universal slopes method coupled with MSE analysis was used in [61] for a couple of sets of strain life data; it should be consulted for further details. Also, an equivalent form of Equation (3) was suggested in [62]. Standard nonlinear regression for Equation (3) yields the following parameter estimations: a = 1.35 × 109 MPa-cycb, b = 1.74, c = 246.3 MPa-cycd, and d = 0.115. The correlation coefficient r2 is 0.98, which indicates that the fit is excellent. Only three of the medians do not lie on the regression. The dashed line is the MSE − 2 × σMSE lower confidence bound. Obviously, the lower bound is not acceptable for the higher values of σ. There are about seven data points to the left of the lower bound. For the lowest three values of σ the lower bound is a full order of magnitude too small. While Equation (3) is an excellent representation of the medians, the MSE analysis is not acceptable. Thus, another method is required for characterization of the aluminum fatigue lives.
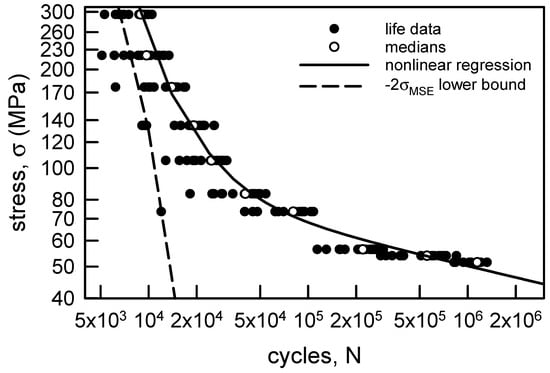
Figure 4.
S-N data for annealed aluminum wire [6] with a nonlinear regression through the medians and a lower confidence bound.
3.2. cdf Modeling
3.2.1. Annealed Electrolytic Copper Wire
The copper wire fatigue lives can be used in statistical analyses in order to estimate the cdfs given σ. The data is presented graphically on Figure 5. The graph is presented on a two-parameter Weibull probability paper, which means that a two-parameter Weibull cdf will be linear on such paper. This probability paper is selected for convenience. Also, it accentuates the lower tail behavior, which corresponds to the high reliability region. Using it does not imply that a two-parameter Weibull cdf must be used to characterize the data. The nonparametric estimate for the probability plotting points pk,n used are as follows:
where n is the sample size, and k is the index for the kth ordered data. This form for pk,n is preferred because it has the smallest MSE [63]. Visually, the data appear to be reasonably linear. Thus, the two-parameter Weibull cdf is considered to be the appropriate parametric form for characterizing these data. The two-parameter Weibull cdf F(t) is
where t represents time or cycles, α is the shape parameter, and β is the scale parameter. Graphical estimation, however, is not ideal for statistical parameter estimation. It is far better to use maximum likelihood estimation (MLE). A very efficient method for computing the MLE estimates for the parameters for the two-parameter Weibull cdf can be found in [64]. Table 3 contains the MLE estimated parameters, mean μ, and cv for each given value of σ. The hat over the parameters indicate an estimate. Also included in Table 3 are the Kolmogorov–Smirnov (KS) and Anderson–Darling (AD) goodness-of-fit values. The KS test indicates that the two-parameter Weibull cdf is acceptable for any level of significance less than 0.25. Likewise, the AD test yields the same conclusion. Therefore, the two-parameter Weibull cdfs with the MLE parameters in Table 3 are excellent characterizations of the copper wire fatigue life data.
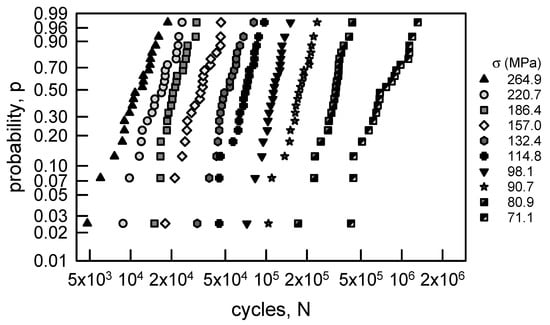
Figure 5.
Probability plot for annealed electrolytic copper wire [6]; two-parameter Weibull probability paper.

Table 3.
MLE parameter estimates for the two-parameter Weibull cdf for annealed electrolytic copper wire [6].
Figure 6 is similar to Figure 3 except that the medians are estimated from the MLE Weibull cdfs. The sample medians and the MLE estimated medians are very close in magnitude. The largest percentage difference is about 9% when σ = 71.1 MPa. The solid line is the curve through those medians. Clearly, the line is not linear, but it does follow the slight curvature of the S-N data. The 97.5% lower confidence bound is constructed by using the 2.5 percentiles from the MLE Weibull cdfs. The dashed curve is the lower bound. Because the S-N data are somewhat different for each value of σ, the MLE Weibull cdfs behave slightly differently. Thus, the lower bound is irregular in shape. It is, however, quite tight to the data, which implies that the lower bound is highly representative of the behavior. Based on the copper wire S-N data, the analysis using MLE for two-parameter Weibull cdfs is preferred to the nonparametric analysis above.
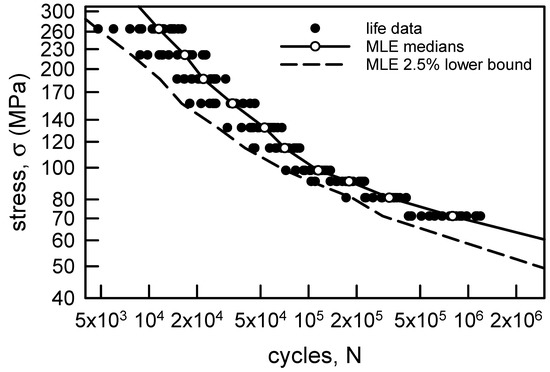
Figure 6.
S-N data for annealed electrolytic copper wire [6] with MLE estimates of medians and 2.5% probability for the median curve and a 97.5% lower confidence bound, respectively.
3.2.2. Annealed Aluminum Wire
The aluminum wire fatigue data are plotted on a two-parameter Weibull probability paper in Figure 7. The data are nearly linear for many of the values of σ; however, when σ is 134.9 MPa the data do not appear to be linear. Table 4 contains the MLE parameters and the KS and AD values, as in Table 3. The KS values imply that the MLE two-parameter Weibull cdfs are acceptable for any significance less than 0.25. The AD test infers that the MLE two-parameter Weibull cdfs are acceptable for any significance less than 0.25 for σ not equal to 134.9 or 51.5 MPa. The significance must be lower than 0.20 when σ = 134.9 MPa and less than 0.01 when σ = 51.5 MPa in order to be acceptable. This is a clear example of the difference between the KS and AD goodness-of-fit tests. The KS test is more focused on the central portion of the cdf while the AD test emphasizes the tail behavior. By careful inspection, when σ equals 134.9 or 51.5 MPa, the tails are visually different. Freudenthal and Gumbel [8] suggested that a Weibull cdf with a minimum life would be more appropriate. It should be noted that they did not use goodness-of-fit tests to validate their results. The standard three-parameter Weibull cdf is
where γ is the minimum life. Assuming that Equation (6) is appropriate for characterizing the aluminum wire fatigue data, the MLE is required. The MLE for the three-parameter Weibull is a bit more challenging. An excellent method for its computation is given in [65]. The MLE parameters are shown in Table 5. As with the other examples, the KS test infers that the three-parameter Weibull cdf is acceptable for any level of significance less than 0.25. The AD test, however, indicates that the three-parameter Weibull cdf is not acceptable when σ equals 134.9 or 73.6 MPa. For σ = 71.1 MPa the level of significance can only be 0.01. When σ is 294.3, 176.6, or 83.4 MPa, the three-parameter Weibull cdf is acceptable for only significance levels less than 0.05. All in all, it is suggested that the two-parameter Weibull cdf is preferred over the three-parameter Weibull cdf for the aluminum wire data.
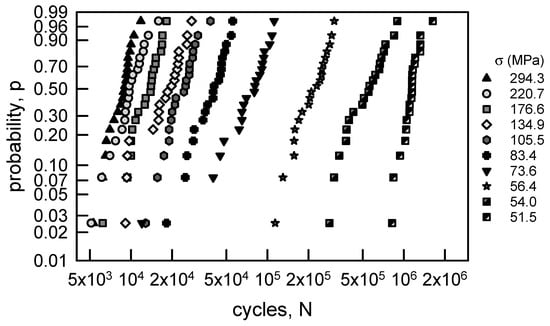
Figure 7.
Probability plot for annealed aluminum wire [6]; two-parameter Weibull probability paper.

Table 4.
MLE parameter estimates for the two-parameter Weibull cdf for annealed aluminum wire [6].

Table 5.
MLE parameter estimates for the three-parameter Weibull cdf for annealed aluminum wire [6].
In order to consider a lower confidence bound for the aluminum data, the two-parameter Weibull cdfs will be used analogously to that on Figure 6. Consider Figure 8 where the MLE estimated medians are shown. The difference between the sample medians and the MLE estimated medians is quite small. The percentage difference ranges from about 0.1% to about 7.5%. Again, the solid line is the curve through the MLE medians, and it closely follows the curvature of the S-N data. The 97.5% lower confidence bound constructed from the MLE Weibull cdfs is quite good. The only data to the left of the bound are the minimum values for σ equal to 83.4 and 73.6 MPa. The minimum value for σ = 73.6 MPa is 7500 cycles, which is so much smaller than the rest of those fatigue lives. In fact, using the MLE Weibull cdf, its probability of occurrence is only 0.00023. It causes one to wonder about its integrity. Statistically, it may be considered to be an outlier. These experiments were conducted so long ago, however, that describing this behavior would be pure speculation. Other than those two data, the lower bound is very close to the remaining data. It is suggested for engineering purposes that the analysis using MLE for two-parameter Weibull cdfs is acceptable.
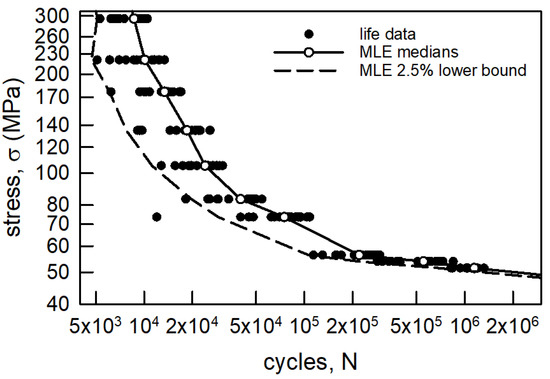
Figure 8.
S-N data for annealed aluminum wire [6] with MLE estimates of medians and 2.5% probability for the median curve and a 97.5% lower confidence bound, respectively.
3.3. Time-Dependent Modeling
3.3.1. Annealed Electrolytic Copper Wire
Coleman [66,67,68,69,70,71] developed a generalized cdf that included the time dependence of the mechanical breakdown of materials. The cdf is a natural extension of the fundamentals of reliability theory. The proposed cdf has the following form:
where Ψ(x) is the hazard function, κ(x) is the breakdown rule, and L(t) is the time dependent load function. An excellent summary of the features of Equation (7) is contained in [72]. The functional form of κ(x) in Equation (7) is heuristically mechanistically based on the material damage accumulation. Frequently, Ψ(x) is assumed to be a Weibull hazard. Since constant amplitude loading is often used for fatigue experiments, L(t) can be considered to be constant. Examples where Equation (7) has been the foundational cdf can be found in [73,74,75].
Since the two-parameter Weibull cdf is acceptable for characterizing the copper wire fatigue data, a Weibull hazard function of the form
is assumed. Here, α is the shape parameter, as in Equation (5). Because a linear regression is suitable for modeling the medians on Figure 3, a power law breakdown function given by
is considered. The parameters β and ρ are a scale and power parameter, respectively. The applied loading for the copper wire fatigue experiments was constant amplitude. Thus,
Substituting Equations (8)–(10) into Equation (7) and simplifying yields the following cdf:
The constants α, β, and ρ, are non-negative, and they are statistically estimated from the life data. It should be mentioned that the power law breakdown rule given in Equation (9) produces linear percentile curves for S-N data plotted on logarithmic versus logarithmic axes. In order to evaluate Equation (11) graphically, the ensuing transformation is considered:
For a fixed value of σ, Equation (12) is linear in ln{−ln [1 − F(t|σ)]} versus ln(t) with a slope of α. For a fixed probability, say F(t|σ) = p, Equation (12) is linear in ln(σ) versus ln(t) with a slope of −1/ρ. Given F(t|σ) and σ, after α and ρ are estimated, the final parameter in Equation (12) to be estimated is β. A detailed numerical example for this analysis can be found in [74].
In order for Equations (11) and (12) to fully represent the S-N and probability behavior, the parameters must be constant and independent of the N and σ. Equation (12) indicates that the Weibull shape parameter σ and the power law exponent ρ must be the same for all values of σ and fixed p. The MLE shape parameters given in Table 3 are reasonably close in magnitude. Thus, the estimate for α in Equations (11) and (12) is assumed to be the average of the values in Table 3, that is, = 5.09. The linear regression shown on Figure 3 can be used to estimate ρ. Equation (12) leads to the relationship that ρ is the negative reciprocal of the slope m. Thus, = 3.12. With estimates for α and ρ, β can be estimated from the S-N graph by fixing a probability, say p = 0.5, or by fixing a value for σ and using the probability graph. On Figure 3, the linear regression is very close to the median when σ = 186.4 MPa. Using these values, = 3.17 × 10−12 1/[cyc-(MPa)ρ]. Figure 9 is a facsimile of Figure 3 except that the median, the 2.5 percentile and the 0.5 percentile lines are obtained from Equations (11) and (12) with the above estimated values. The 2.5 percentile line corresponds to the 97.5% lower confidence bound, but it clearly is not appropriate as a lower bound. Several data are to the left of the line. The 0.5 percentile line, however, corresponds to a 99.5% lower confidence bound. All of the data are to the right of the bound, and it is very tight with the data. Hence, it is very acceptable as a lower confidence bound. For the copper wire fatigue data, Equation (11) is an excellent representation of the behavior.
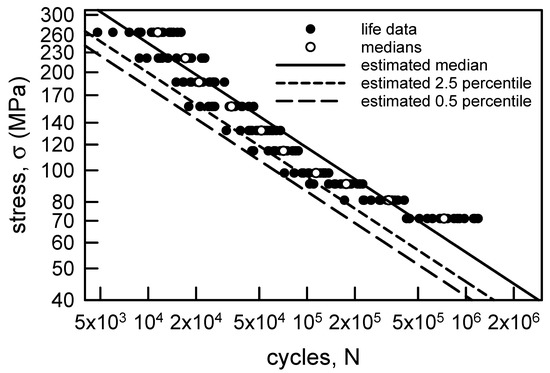
Figure 9.
S-N data for annealed electrolytic copper wire [6] with estimated median, 2.5 percentile, and 0.5 percentile lines.
3.3.2. Annealed Aluminum Wire
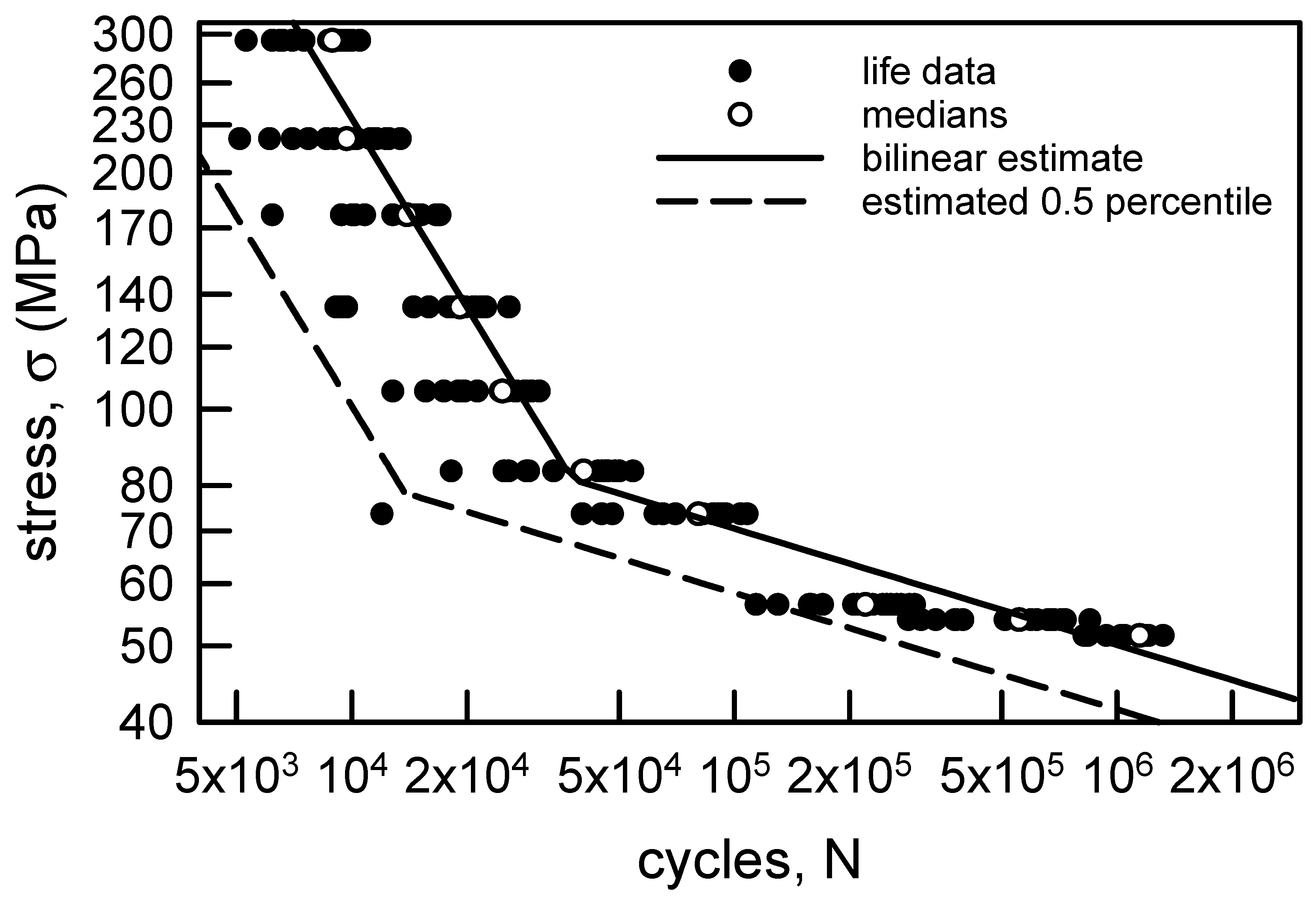
The S-N data for the aluminum wire are shown on Figure 4 with the nonlinear regression given in Equation (3). Using the nonlinear form for the median behavior in Equation (7) leads to a computationally very difficult integral. In order to make the analysis more amenable, the cdf in Equation (7) will be broken into two intervals, each of which will be assumed to be linear. Thus, the S-N data are shown with the two linear estimates for the medians on Figure 10. Specifically, the estimate is given by
where ML = −0.798, BL = 3.65 × 105 (MPa)/cycML, MH = −0.148, BH = 382.6 (MPa)/cycMH, and the subscripts L and H corresponds to the Low cyc and High cyc regions, respectively. The transition value is Nt = 39,450 cyc.
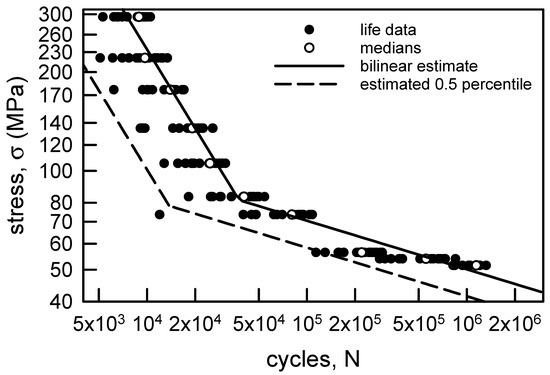
Figure 10.
S-N data for annealed aluminum wire [6] with an estimated bilinear regression for the medians and the 0.5 percentile lines.
The proposed cdf for each of the two regions is Equation (11), which assumes a Weibull hazard function, power law breakdown, and constant amplitude load. The estimated parameters are obtained similarly to those described for the copper wire above. Thus, = 4.77 and = 4.51, which are the averages of the shape parameters for the L and H regions, given in Table 4. The estimates for the power law exponents are the negative reciprocal of the appropriate slopes, that is, = 1.25 and = 6.76. The final estimates are found by considering the medians on Figure 10 when σ = 176.6 or 54.0 MPa. Thus, = 1.03 × 10−7 1/[cyc-(MPa)ρL] and = 3.23 × 10−18 1/[cyc-(MPa)ρH]. As seen in Figure 10, the 0.5 percentile line is an acceptable lower confidence bound for the L region. All the data lie to the right of the lower bound. For the H region the 0.5 percentile is an excellent lower bound for all the data except for the one value discussed above. It is impossible to determine, for data this old, why that single data is so far from the rest of the fatigue data when σ = 73.6 MPa. Nevertheless, the lower bound for the two regions seems reasonable. The 2.5 percentile lower bound is not shown because it is not acceptable, as it has several data to the left of the bound for both the L and H regions. For the aluminum wire fatigue data, Equation (11) for each region is a reasonable representation of the data.
4. Discussion
The data that were investigated herein were stress–life fatigue data for annealed aluminum wire and annealed electrolytic copper wire [5]. These historic data were selected for consideration because of the ample sample sizes of magnitude 20 produced for each of a significant number, i.e., 10, of applied stress amplitudes. These two datasets were considered because they exhibit different statistical behavior which is manifest on both the S-N graphs and the probability plots. The two sets of data were analyzed using traditional statistical S-N analysis and the MSE for lower confidence bounds. The basic conclusion is that these methodologies work quite well, if the S-N data are well behaved. This is the case for the annealed electrolytic copper wire. The annealed aluminum wire, however, has too much scatter for that modeling to be applicable.
Subsequently, the two sets of data were modeled statistically by using a two-parameter Weibull cdf. These analyses incorporated MLE and the KS and AD goodness-of-fit tests. The two-parameter Weibull cdf is an outstanding choice to characterize the annealed electrolytic copper wire data. Furthermore, the lower confidence bound estimation using the MLE Weibull estimates is extremely good as well. Again, these data are quite regular. For the annealed aluminum wire data the MLE for the two-parameter Weibull cdf is acceptable for engineering purposes. Also, the lower bound estimate is quite good, except for one data point, which may be somewhat of an outlier. Unfortunately, that single data point is not on the conservative side. Further investigation would be warranted.
The third approach for statistically analyzing the two sets of data is time-dependent modeling that merges the S-N behavior into the cdf. The cdf is built by using a hazard function, breakdown rule, and load function. The reason for this format is that the statistical parameters may be load-dependent, which leads to more generality in the modeling. For these examples, however, the parameters were assumed to be constant. The basic form of the cdf is the same as the cdf for reliability given a hazard rate. Because of the flexibility and scope of the Weibull cdf for life assessment, the hazard function was assumed to be the form of a Weibull hazard. The power law breakdown law was also well suited. Because the fatigue loading was constant amplitude, it was assumed that the loading was constant. The annealed electrolytic copper wire data is modeled extremely well by the proposed approach. As with the other statistical methods, the reason that the method works so well for the annealed electrolytic copper wire is that the data are very well behaved. The sample scatter and the median behavior for each given value of σ is relatively consistent. The annealed aluminum wire, however, is not as well behaved. In fact, the data required the use of a bilinear power law breakdown law. The estimate for the data was the best for those considered in this effort. The only caveat is that the single possible outlier is still below the lower confidence bound, but it is much closer than with the other methods used.
5. Conclusions
The efficacy and utility of the generalized cdf given in Equation (7) has been demonstrated herein. Its versatility is an underlying strength. Certainly, its use or consideration for the cdf is warranted for characterization of other sets of fatigue life data. The mathematical form of the cdf is sufficiently robust that its use is minimized only by parameter estimation. Models that explicitly incorporate stress into the cdf must be evaluated carefully. If there are minimal data for each given stress, or an insufficient number of different stresses in the experimental program, the model development is difficult. While Equation (7) is still applicable in these cases, the uncertainty in the modeling is exacerbated. Accuracy always improves as the amount of data increases. All things considered, the proposed approach has sufficient promise that further investigation and analysis is certainly warranted. Consequently, it is recommended that this cdf be considered for other life testing applications.
Funding
This research received no external funding.
Data Availability Statement
The data used herein is available in Freudenthal [6].
Conflicts of Interest
The author declares no conflict of interest.
References
- Shimokawa, T.; Hamaguchi, Y. Relationship between Fatigue Life Distribution, Notch Configuration, and S–N Curve of a 2024–T4 Aluminum Alloy. J. Eng. Mater. Technol. 1985, 107, 214–220. [Google Scholar] [CrossRef]
- Schütz, W. A History of Fatigue. Eng. Fract. Mech. 1996, 54, 263–300. [Google Scholar] [CrossRef]
- Wöhler, A. Versuche zur Ermittlung der auf die Eisenbahnwagenachsen einwirkenden Kräfte und die Widerstandsfähigkeit der Wagen-Achsen. Z. Für Bauwes. 1860, 10, 583–616. [Google Scholar]
- Moore, H.F.; Kommers, J.B. The Fatigue of Metals; McGraw-Hill: New York, NY, USA, 1927; pp. 168–170. [Google Scholar]
- Ravilly, E. Contribution a l’etude de la rupture des fils metalliques soumis à des torsions alternees. Publ. Sci. Et Tech. Du Minist. De L’air 1938, 120, 52–70. [Google Scholar]
- Freudenthal, A.M. Planning and Interpretation of fatigue Tests. In Symposium on Statistical Aspects of Fatigue; ASTM STP 121; American Society for Testing Materials: Philadelphia, PA, USA, 1951; pp. 3–13. [Google Scholar]
- Freudenthal, A.M.; Gumbel, E.J. Statistical Interpretation of Fatigue Tests. Proc. R. Soc. A 1953, 216, 309–332. [Google Scholar]
- Freudenthal, A.M.; Gumbel, E.J. Minimum Life in Fatigue. J. Am. Stat. Assoc. 1954, 49, 575–597. [Google Scholar] [CrossRef]
- Gumbel, E.J. Étude statistique de la fatigue des matériaux. Rev. De Stat. Appliquée 1957, 5, 51–86. [Google Scholar]
- Dieter, G.E.; Mehl, R.F. Investigation of the Statistical Nature of the Fatigue of Metals; Technical Note 3019; National Advisory Committee for Aeronautics: Washington, DC, USA, 1953. [Google Scholar]
- Stagg, A.M. An Investigation of the Scatter in Constant Amplitude Fatigue Test Results of Aluminium Alloys 2024 and 7075; Ministry of Technology, Aeronautical Research Council: Current Papers 1093; Her Majesty’s Stationery Office: London, UK, 1970. [Google Scholar]
- Kesling, G.D.; Whittaker, I.C. A Simulation Model of Railroad Reliability. Simulation 1985, 44, 168–180. [Google Scholar] [CrossRef]
- Ratnaparkhi, M.V.; Park, W.J. Lognormal Distribution-Model for Fatigue Life and Residual Strength of Composite Materials. IEEE Trans. Rel. 1986, 35, 312–315. [Google Scholar] [CrossRef]
- Zheng, X.-L.; Lü, B.; Jiang, H. Determination of Probability Distribution of Fatigue Strength and Expressions of P-S-N Curves. Eng. Fract. Mech. 1995, 50, 483–491. [Google Scholar] [CrossRef]
- Ramamurty, R.P.; Rajesh, S.; Satyanarayana, B.; Ramji, K. Statistical Analysis of Fatigue Life Data of A356.2-T6 Aluminum Alloy. Tech Sci. Press SDHM 2011, 7, 139–152. [Google Scholar]
- Bazaras, Ž.; Lukoševičius, V. Statistical Assessment of Low-Cycle Fatigue Durability. Symmetry 2022, 14, 1205. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Theory of the Strength of Materials. Ing. Vetenskaps. Handl. 1939, 151, 1–45. [Google Scholar]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. Trans. ASME 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Fréchet, M. Sur la loi de probabilité de l’écart maximum. Ann. De La Société Pol. De Math. 1927, 6, 93–116. [Google Scholar]
- Fisher, R.A.; Tippett, L.H.C. Limiting Forms of the Frequency Distribution of the Largest or Smallest Member of a Sample. Proc. Cambridge Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Gnedenko, B.V. Sur la Distribution Limite du Terme Maximum d’une Série Aléatoire. Ann. Math. 1943, 44, 423–453. [Google Scholar] [CrossRef]
- Bolotin, V.V. Statistical Methods in Structural Mechanics; Holden-Day, Inc.: San Francisco, CA, USA, 1969; pp. 71–77. [Google Scholar]
- Strzelecki, P. Determination of Fatigue Life for Low Probability of Failure for Different Stress Levels using 3-parameter Weibull Distribution. Int. J. Fatigue 2021, 145, 106080. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Gao, Q.; Wang, J.N. An Approach for Determining an Appropriate Assumed Distribution of Fatigue Life Under Limited Data. Reliab. Eng. Syst. Saf. E 2000, 67, 1–7. [Google Scholar] [CrossRef]
- Tosha, K.; Ueda, D.; Shimoda, H.; Shimizu, S. A Study on P-S-N Curve for Rotating Bending Fatigue Test for Bearing Steel. Tribol. Trans. 2008, 51, 166–172. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Liu, H.B. Weibull Modeling of the Probabilistic S-N Curves for Rolling Contact Fatigue. Int. J. Fatigue 2014, 66, 47–54. [Google Scholar] [CrossRef]
- Kracík, J.; Strnadel, B. A Statistical Model for Lifespan Prediction of Large Steel Structures. Eng. Struct. 2018, 176, 20–27. [Google Scholar] [CrossRef]
- Lan, C.; Bai, N.; Yang, H.; Liu, C.; Li, H.; Spencer, B.F. Weibull Modeling of the Fatigue Life for Steel Rebar Considering Corrosion Effects. Int. J. Fatigue 2018, 111, 134–143. [Google Scholar] [CrossRef]
- Hoole, J.; Sartor, P.; Booker, J.; Cooper, J.; Gogouvitis, X.V.; Schmidt, R.K. Systematic Sstatistical Characterisation of Stress-Life Datasets Using 3-Parameter Distributions. Int. J. Fatigue 2019, 129, 105216. [Google Scholar] [CrossRef]
- Diniz, B.D.C.; Júnior, R.C.S.F. Study of the Fatigue Behavior of Composites Using Modular ANN with the Incorporation of a Posteriori Failure Probability. Int. J. Fatigue 2020, 131, 105357. [Google Scholar] [CrossRef]
- Barbosa, J.F.; Correia, J.A.F.O.; Júnior, R.C.S.F.; Zhu, S.-P.; De Jesus, A.M.P. Probabilistic S-N Fields Based on Statistical Distributions Applied to Metallic and Composite Materials: State of the Art. Adv. Mech. Eng. 2019, 11, 1687814019870395. [Google Scholar] [CrossRef]
- Lia, C.; Wua, S.; Zhang, J.; Xie, L.; Zhang, Y. Determination of the Fatigue P-S-N Curves—A Critical Review and Improved Backward Statistical Inference Method. Int. J. Fatigue 2020, 139, 105789. [Google Scholar] [CrossRef]
- Hanaki, S.; Yamashita, M.; Uchida, H.; Zako, M. On Stochastic Evaluation of S-N Data Based on Fatigue Strength Distribution. Int. J. Fatigue 2010, 32, 605–609. [Google Scholar] [CrossRef]
- Fouchereau, R.; Celeux, G.; Pamphile, P. Probabilistic Modeling of S-N Curve. Int. J. Fatigue 2014, 68, 217–223. [Google Scholar] [CrossRef]
- Júnior, R.C.S.F.; Belísio, A.S. Probabilistic S-N Curves Using Exponential and Power Laws Equations. Compos. Part B Eng. 2014, 56, 582–590. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, P.; Zhang, Z.J.; Liu, R.; Zhang, Z.F. New Method for Determining P-S-N Curves in Terms of Equivalent Fatigue Lives. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2340–2353. [Google Scholar] [CrossRef]
- Shimizu, S.; Tosha, K.; Tsuchiya, K. New Data Analysis of Probabilistic Stress-Life (P-SN) Curve and Its Application for Structural Materials. Int. J. Fatigue 2010, 32, 565–575. [Google Scholar] [CrossRef]
- Ling, J.; Pan, J. A Maximum Likelihood Method for Estimating P-S-N Curves. Int. J. Fatigue 1997, 19, 415–419. [Google Scholar] [CrossRef]
- Leonetti, D.; Maljaars, J.; Snijder, H.H.B. Fitting Fatigue Test Data with a Novel S-N Curve Using Frequentist and Bayesian Inference. Int. J. Fatigue 2017, 105, 128–143. [Google Scholar] [CrossRef]
- Guida, M.; Penta, F. A Bayesian Analysis of Fatigue Data. Struct. Saf. 2010, 32, 64–76. [Google Scholar] [CrossRef]
- Liu, X.W.; Lu, D.G.; Hoogenboom, P.C.J. Hierarchical Bayesian Fatigue Data Analysis. Int. J. Fatigue 2017, 100, 418–428. [Google Scholar] [CrossRef]
- Liu, X.W.; Lu, D.G. Survival Analysis of Fatigue Data: Application of Generalized Linear Models and Hierarchical Bayesian Model. Int. J. Fatigue 2018, 117, 39–46. [Google Scholar] [CrossRef]
- Júnior, R.C.S.F.; Neto, A.D.D.; Aquino, E.M.F. Building of Constant Life Diagrams of Fatigue Using Artificial Neural Networks. Int. J. Fatigue 2005, 27, 746–751. [Google Scholar] [CrossRef]
- Bučar, T.; Nagode, M.; Fajdiga, M. A Neural Network Approach to Describing the Scatter of S-N Curves. Int. J. Fatigue 2006, 28, 311–323. [Google Scholar] [CrossRef]
- Barbosa, J.F.; Correia, J.A.F.O.; Júnior, R.C.S.F.; Jesus, A.M.P.D. Fatigue Life Prediction of Metallic Materials Considering Mean Stress Effects by Means of an Artificial Neural Network. Int. J. Fatigue 2020, 135, 105527. [Google Scholar] [CrossRef]
- Jimenez-Martinez, M. Fatigue of Offshore Structures: A Review of Statistical Fatigue Damage Assessment for Stochastic Loadings. Int. J. Fatigue 2020, 132, 105327. [Google Scholar] [CrossRef]
- Zhan, Z.; Li, H. Machine Learning Based Fatigue Life Prediction with Effects of Additive Manufacturing Process Parameters for Printed SS 316L. Int. J. Fatigue 2021, 142, 105941. [Google Scholar] [CrossRef]
- Luo, Y.W.; Zhang, B.; Feng, X.; Song, Z.M.; Qi, X.B.; Li, C.P.; Chen, G.F.; Zhang, G.P. Pore-Affected Fatigue Life Scattering and Prediction of Additively Manufactured Inconel 718: An Investigation Based on Miniature Specimen Testing and Machine Learning Approach. Mater. Sci. Eng. A 2021, 802, 140693. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Y. Probabilistic Physics-Guided Machine Learning for Fatigue Data Analysis. Expert Syst. Appl. 2021, 168, 114316. [Google Scholar] [CrossRef]
- Hooda, R.; Joshi, V.; Shah, M. A Comprehensive Review of Approaches to Detect Fatigue Using Machine Learning Techniques. Chronic Dis. Transl. Med. 2021, in press. [CrossRef]
- Zhang, J.; Zhu, J.; Guo, W.; Guo, W. A Machine Learning-Based Approach to Predict the Fatigue Life of Three-Dimensional Cracked Specimens. Int. J. Fatigue 2022, 159, 106808. [Google Scholar] [CrossRef]
- Braun, M.; Kellner, L.; Schreiber, S.; Ehlers, S. Prediction of Fatigue Failure in Small-Scale Butt-Welded Joints with Explainable Machine Learning. Procedia Struct. 2022, 38, 182–191. [Google Scholar] [CrossRef]
- Zhan, Z.; Ao, N.; Hu, Y.; Liu, C. Defect-Induced Fatigue Scattering and Assessment of Additively Manufactured 300M-AerMet100 Steel: An Investigation Based on Experiments and Machine Learning. Eng. Fract. Mech. 2022, 264, 108352. [Google Scholar] [CrossRef]
- Qian, G.; Lei, W.-S. A Statistical Model of Fatigue Failure Incorporating Effects of Specimen Size and Load Amplitude on Fatigue Life. Philos. Mag. A Mater. Sci. 2019, 99, 2089–2125. [Google Scholar] [CrossRef]
- Ai, Y.; Zhu, S.P.; Liao, D.; Correia, J.A.F.O.; Souto, C.; De Jesus, A.M.P.; Keshtegar, B. Probabilistic Modeling of Fatigue Life Distribution and Size Effect of Components with Random Defects. Int. J. Fatigue 2019, 126, 165–173. [Google Scholar] [CrossRef]
- Huang, J.; Meng, Q.; Zhan, Z.; Hu, W.; Shen, F. Damage Mechanics-Based Approach to Studying Effects of Overload on Fatigue Life of Notched Specimens. Int. J. Damage Mech. 2019, 28, 538–565. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Average Error (MAE)?—Arguments Against Avoiding RMSE in the Literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Ross, S. Introduction to Probability and Statistics for Engineers and Scientists, 4th ed.; Elsevier: London, UK, 2009. [Google Scholar]
- Manson, S.S. A Simple Procedure for Estimating High-Temperature Low-Cycle Fatigue. Exp. Mech. 1968, 8, 349–355. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Practical Implementation of the Double Linear Damage Rule and Damage Curve Approach for Treating Cumulative Fatigue Damage. Int. J. Fract 1981, 17, 169–192. [Google Scholar] [CrossRef]
- Harlow, D.G. Low Cycle Fatigue: Probability and Statistical Modeling of Fatigue Life. In Proceedings of the ASME 2014 Pressure Vessels and Piping Conference, Anaheim, CA, USA, 20–24 July 2014; PVP2014-28114, V06BT06A045. ISBN 978-0-7918-4604-9. [Google Scholar]
- Klemenc1, J.; Podgornik, B. An Improved Model for Predicting the Scattered S-N Curves. J. Mech. Eng./Stroj. Vestn. 2019, 65, 265–275. [Google Scholar] [CrossRef]
- Mann, N.R.; Schafer, R.E.; Singpurwalla, N.D. Methods for Statistical Analysis of Reliability and Life Data; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Harlow, D.G. The Effect of Proof-Testing on the Weibull Distribution. J. Mater. Sci. 1989, 24, 1467–1473. [Google Scholar] [CrossRef]
- Harlow, D.G. Fatigue Life Estimation with Censored Data. Int. J. Fatigue 2020, 141, 105899. [Google Scholar] [CrossRef]
- Coleman, B.D. Time Dependence of Mechanical Breakdown Phenomena. J. Appl. Phys. 1956, 27, 862–866, Erratum in J. Appl. Phys. 1957, 28, 1514. [Google Scholar] [CrossRef]
- Coleman, B.D. Time Dependence of Mechanical Breakdown in Bundles of Fibers. I. Constant Total Load. J. Appl. Phys. 1957, 28, 1058–1064. [Google Scholar] [CrossRef]
- Coleman, B.D.; Marquardt, D.W. Time Dependence of Mechanical Breakdown in Bundles of Fibers. II. The Infinite Ideal Bundle under Linearly Increasing Loads. J. Appl. Phys. 1957, 28, 1065–1067. [Google Scholar] [CrossRef]
- Coleman, B.D. Statistics and Time Dependence of Mechanical Breakdown in Fibers. J. Appl. Phys. 1958, 29, 968–983. [Google Scholar] [CrossRef]
- Coleman, B.D.; Marquardt, D.W. Time Dependence of Mechanical Breakdown in Bundles of Fibers. IV. Infinite Ideal Bundle under Oscillating Loads. J. Appl. Phys. 1958, 29, 1091–1099. [Google Scholar] [CrossRef]
- Coleman, B.D. Time Dependence of Mechanical Breakdown in Bundles of Fibers. V. Fibers of Class A-2. J. Appl. Phys. 1959, 30, 720–724. [Google Scholar] [CrossRef]
- Phoenix, S.L. Stochastic Strength and Fatigue of Fiber Bundles. Int. J. Fract. 1978, 13, 327–344. [Google Scholar] [CrossRef]
- Harlow, D.G. Probability Versus Statistical Modeling: Examples from Fatigue Life Prediction. Int. J. Reliab. Qual. 2005, 12, 535–550. [Google Scholar] [CrossRef]
- Harlow, D.G. Generalized Probability Distributions for Accelerated Life Modeling. SAE Int. J. Mater. Manuf. 2011, 4, 980–991. [Google Scholar] [CrossRef]
- Harlow, D.G. Fatigue Life Modeling Using Nitinol Data. In Proceedings of the ASME 2020 Pressure Vessels & Piping Conference, Virtual, 3 August 2020; Volume 83815, p. V001T01A025. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).