Effect of Minor Ce Substitution for Pr on the Glass Formability and Magnetocaloric Effect of a Fe88Zr4Pr4B4 Metallic Glass
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
- (i)
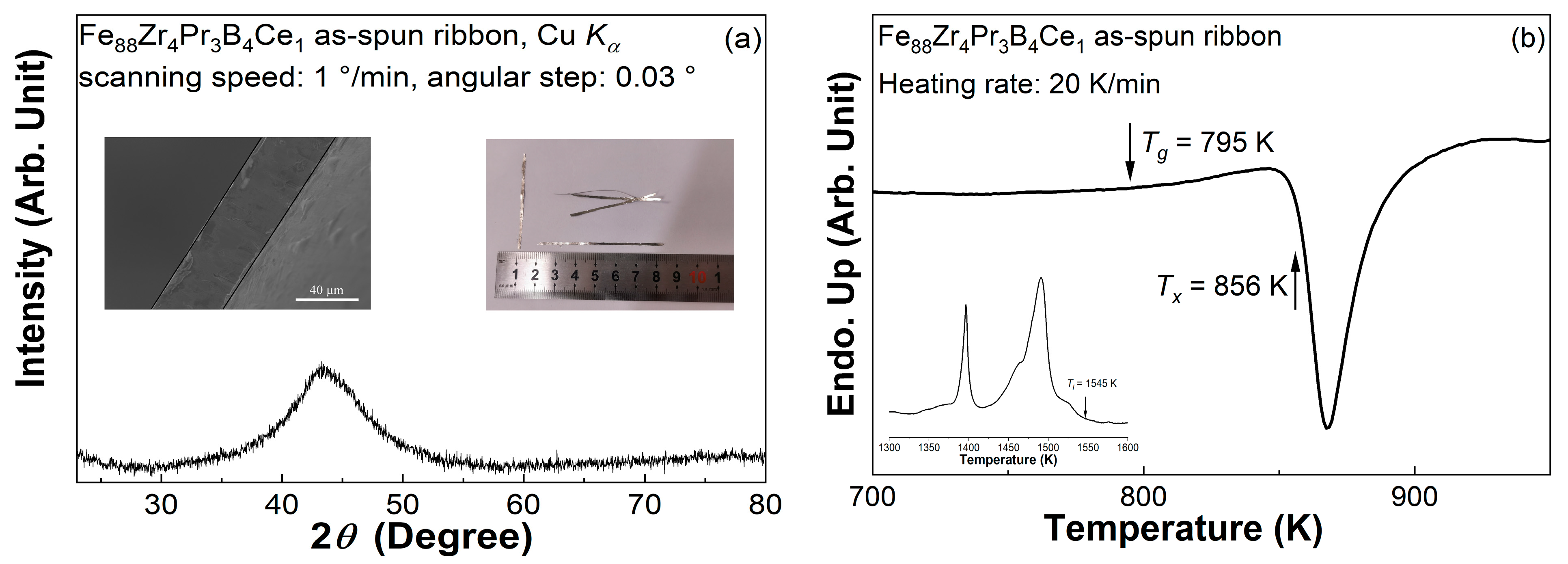
- The Trg and γ indicate that the minor Ce substitution for Pr does not obviously change the glass formability of the Fe88Zr4Pr4B4 MG, but the glass formability of both the two ribbons is enough to vitrify them into glassy ribbon.
- (ii)
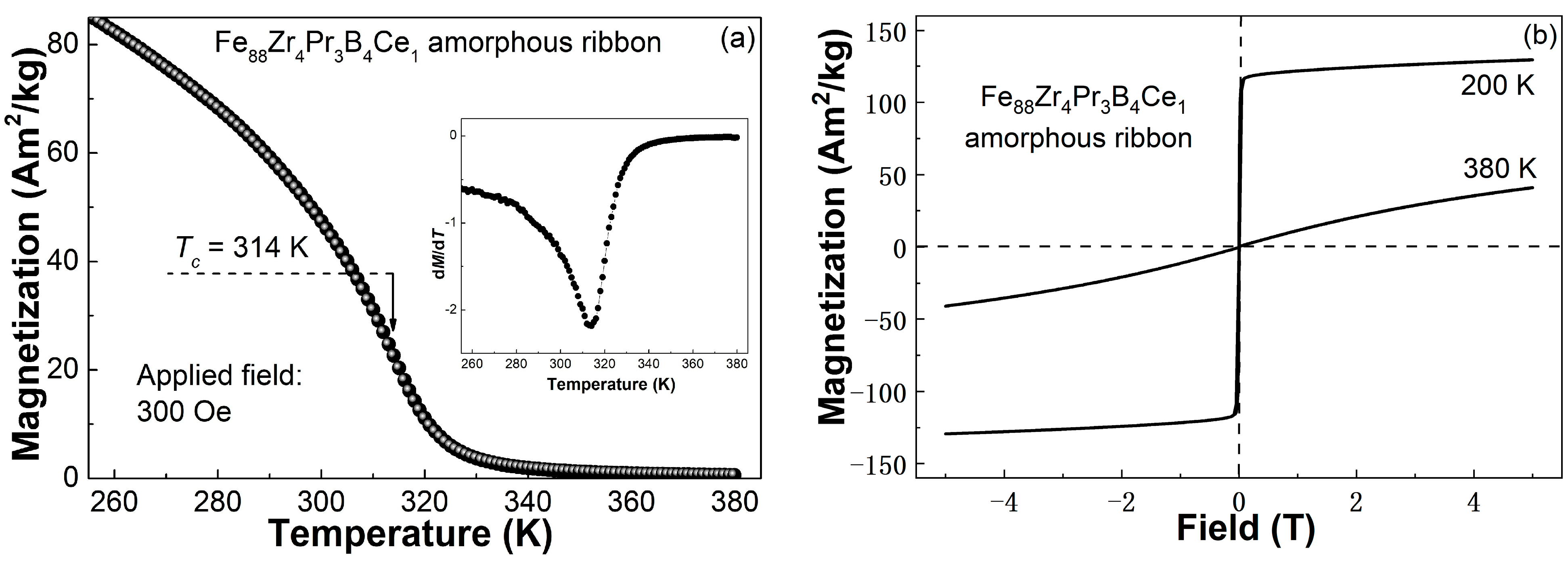
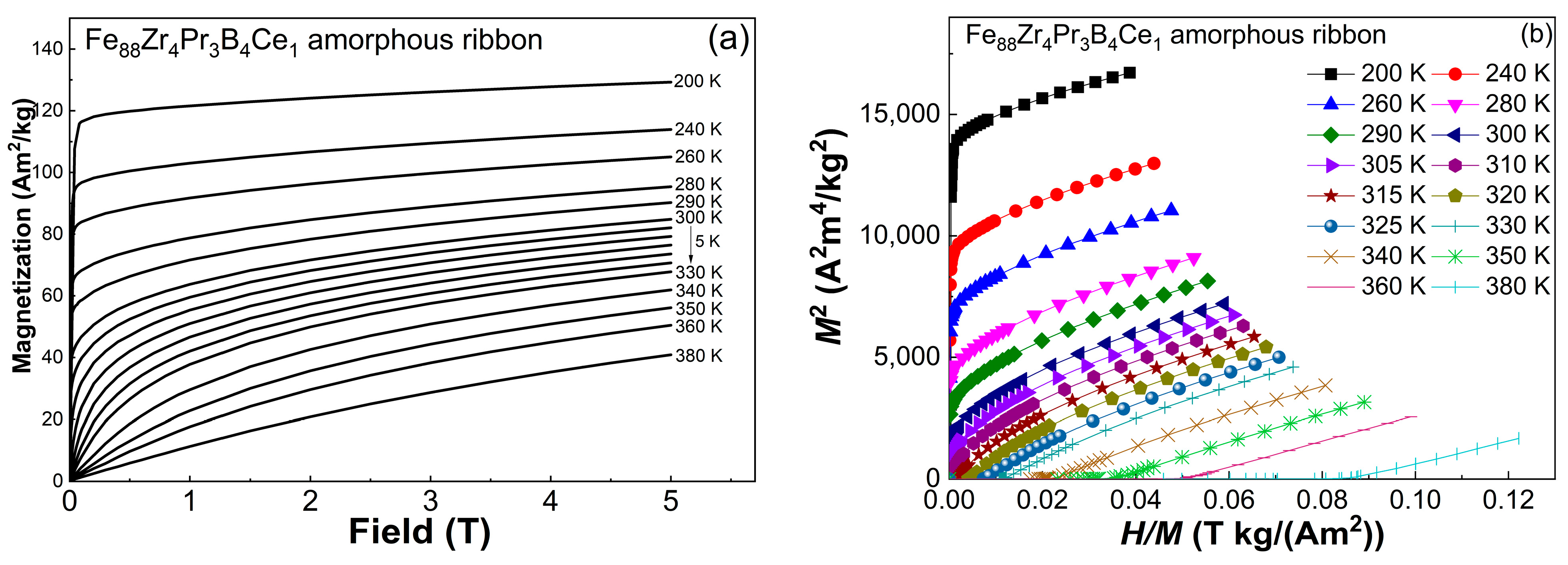
- The Tc of the Fe88Zr4Pr3B4Ce1 ribbon decreases by 9 K compared with the Fe88Zr4Pr4B4 MG, which may be closely related to the antiferromagnetic coupling of the Ce atom with the Fe atom. The Fe88Zr4Pr3B4Ce1 MG ribbon shows typical soft magnetic characteristics of fully amorphous alloys but slightly lower Ms than that of the Fe88Zr4Pr4B4 MG at 200 K. The M2-H/M plots at various temperatures indicate the typical SOMPT feature of the Fe88Zr4Pr3B4Ce1 MG.
- (iii)
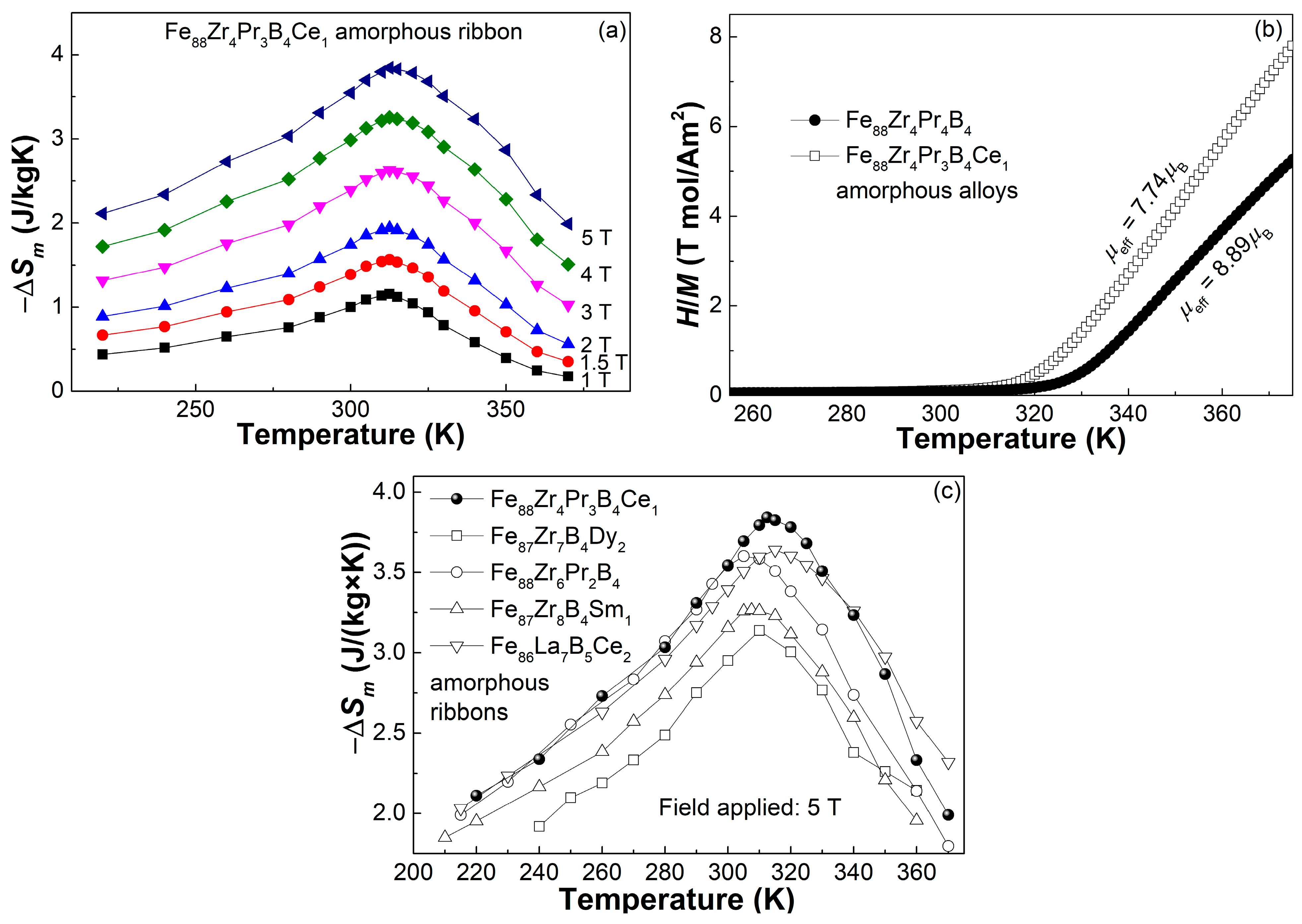
- According to the Maxwell Equation, the −ΔSmpeak of the Fe88Zr4Pr3B4Ce1 ribbon reaches 3.84 J/(kg × K) under 5 T at 312.5 K, which is slightly lower than that of the Fe88Zr4Pr4B4 MG but still higher than the −ΔSmpeak near 310 K of other amorphous alloys and even high entropy alloys reported in literature.
- (iv)
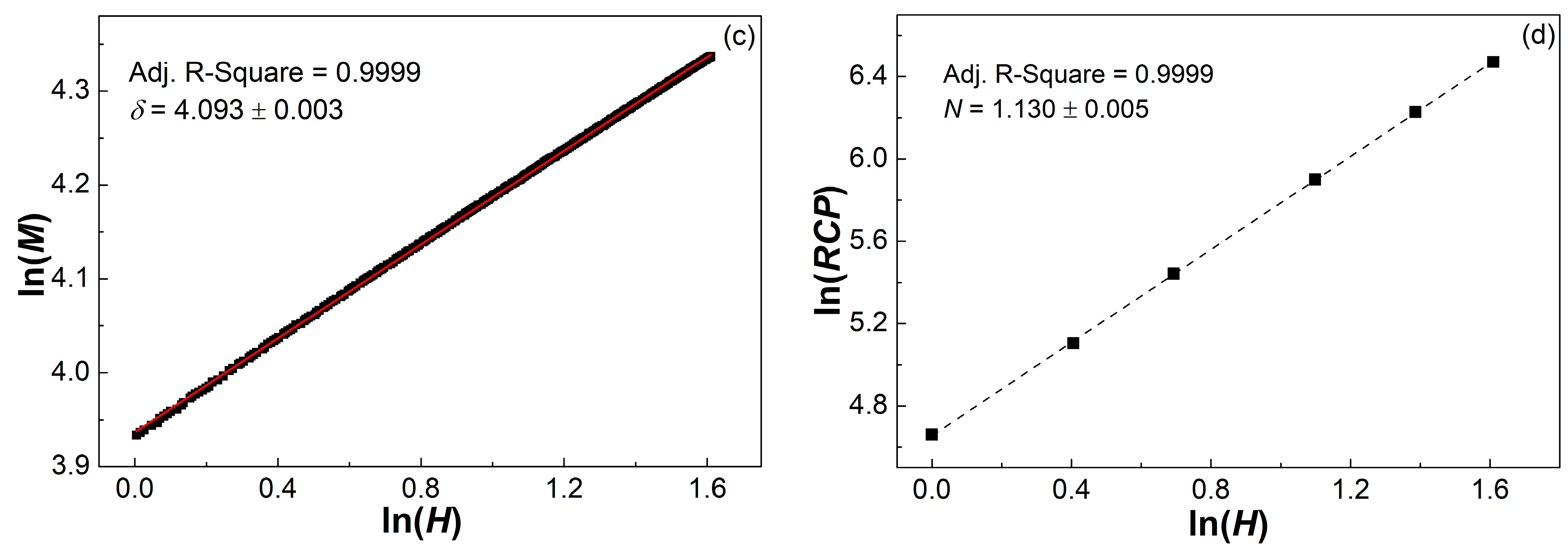
- The n-T curve, the minimum n value and the normalized universal curve of the Fe88Zr4Pr3B4Ce1 MG ribbon also indicate the typical magnetocaloric behaviors of fully amorphous alloys. The values of n and N obtained by the KF method deviate slightly from those obtained by the linear fitting of the field dependence of −ΔSmpeak and RCP, which may be due to the error in multiple derivation of the KF method.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gschneidner, K.A., Jr.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479. [Google Scholar] [CrossRef]
- Yu, B.F.; Gao, Q.; Zhang, B.; Meng, X.Z.; Chen, Z. Review on research of room temperature magnetic refrigeration. Int. J. Refrig. 2003, 26, 622–636. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K. Magnetocaloric Materials. Annu. Rev. Mater. Sci. 2000, 30, 387–429. [Google Scholar] [CrossRef]
- De Oliveira, N.A.; von Ranke, P.J. Theoretical aspects of the magnetocaloric effect. Phys. Rep. 2010, 489, 89–159. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494. [Google Scholar] [CrossRef]
- Wada, H.; Morikawa, T.; Taniguchi, K.; Shibata, T.; Yamada, Y.; Akishige, Y. Giant magnetocaloric effect of MnAs1-xSbx in the vicinity of first-order magnetic transition. Phys. B Condens. Matter 2003, 328, 114–116. [Google Scholar] [CrossRef]
- Yao, J.; Wang, P.; Mozharivskyj, Y. Tuning Magnetic and Structural Transitions through Valence Electron Concentration in the Giant Magnetocaloric Gd5-xEuxGe4 Phases. Chem. Mater. 2012, 24, 552–556. [Google Scholar] [CrossRef]
- Hashimoto, T.; Kuzuhara, T.; Sahashi, M.; Inomata, K.; Tomokiyo, A.; Yayama, H. New application of complex magnetic materials to the magnetic refrigerant in an Ericsson magnetic refrigerator. J. Appl. Phys. 1987, 62, 3873–3878. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Ingale, B.; Conde, A. The Magnetocaloric Effect and Magnetic Refrigeration Near Room Temperature: Materials and Models. Annu. Rev. Mater. Res. 2012, 42, 305–342. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, W.H. Magnetocaloric effect in rare-based bulk metallic glasses. J. Alloys Compd. 2010, 495, 209–216. [Google Scholar] [CrossRef]
- Ma, L.Y.; Gan, L.H.; Chan, K.C.; Ding, D.; Xia, L. Achieving a table-like magnetic entropy change across the ice point of water with tailorable temperature range in Gd-Co-based amorphous hybrids. J. Alloys Compd. 2017, 723, 197–200. [Google Scholar] [CrossRef]
- Wu, C.; Ding, D.; Xia, L.; Chan, K.C. Achieving tailorable magneto-caloric effect in the Gd-Co binary amorphous alloys. AIP Adv. 2016, 6, 035302. [Google Scholar] [CrossRef]
- Bingham, N.S.; Wang, H.; Qin, F.; Peng, H.X.; Sun, J.F.; Franco, V.; Srikanth, H.; Phan, M.H. Excellent magnetocaloric properties of melt-extracted Gd-based amorphous microwires. Appl. Phys. Lett. 2012, 101, 102407. [Google Scholar] [CrossRef]
- Tang, B.Z.; Xie, H.X.; Li, D.M.; Xia, L.; Yu, P. Microstructure and its effect on magnetic and magnetocaloric properties of the Co50Gd50-xFex glassy ribbons. J. Non-Cryst. Solids 2020, 533, 119935. [Google Scholar] [CrossRef]
- Wang, X.; Tang, B.Z.; Wang, Q.; Yu, P.; Ding, D.; Xia, L. Co50Gd48-xFe2Nix amorphous alloys with high adiabatic temperature rise near the hot end of a domestic magnetic refrigerator. J. Non-Cryst. Solids 2020, 544, 120146. [Google Scholar] [CrossRef]
- Tang, B.Z.; Liu, X.P.; Li, D.M.; Yu, P.; Xia, L. Effect of Ni substitution on the formability and magnetic properties of Gd50Co50 amorphous alloy. Chin. Phys. B 2020, 29, 056401. [Google Scholar] [CrossRef]
- Álvarez, P.; Sánchez Llamazares, J.L.; Gorria, P.; Blanco, J.A. Enhanced refrigerant capacity and magnetic entropy flattening using a two-amorphous FeZrB(Cu) composite. Appl. Phys. Lett. 2011, 99, 232501. [Google Scholar] [CrossRef]
- Lai, J.W.; Zheng, Z.G.; Zhong, X.C.; Franco, V.; Montemayor, R.; Liu, Z.W.; Zeng, D.C. Table-like magnetocaloric effect of Fe88-xNdxCr8B4 composite materials. J. Magn. Magn. Mater. 2015, 390, 87–90. [Google Scholar] [CrossRef]
- Yu, P.; Zhang, J.Z.; Xia, L. Effect of boron on the magneto-caloric effect in Fe91-xZr9Bx (x = 3, 4, 5) amorphous alloys. J. Mater. Sci. 2017, 52, 13948–13955. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Tang, B.Z.; Ding, D.; Cui, L.; Xia, L. Magnetic and magneto-caloric properties of the amorphous Fe92− xZr8Bx ribbons. Materials 2020, 13, 5334. [Google Scholar] [CrossRef]
- Mishra, D.; Gurram, M.; Reddy, A.; Perumal, A.; Saravanan, P.; Srinivasan, A. Enhanced soft magnetic properties and magnetocaloric effect in B substituted amorphous Fe–Zr alloy ribbons. Mater. Sci. Eng. B 2010, 175, 253–260. [Google Scholar] [CrossRef]
- Wu, Y.B.; Wang, Q.; Tang, B.Z.; Pan, L.L.; Ding, D.; Xia, L. Outstanding glass formability and magneto-caloric effect of a Fe85Co3Zr5B4Nb3 metallic glass. J. Non-Cryst. Solids 2021, 566, 120885. [Google Scholar] [CrossRef]
- Chen, L.S.; Zhang, J.Z.; Wen, L.; Yu, P.; Xia, L. Outstanding magnetocaloric effect of Fe88−xZr8B4Smx (x = 0, 1, 2, 3) amorphous alloys. Sci. China Phys. Mech. Astron. 2018, 61, 056121. [Google Scholar]
- Wang, Q.; Ding, D.; Tang, B.Z.; Yu, P.; Chan, K.C.; Xia, L. Excellent magnetocaloric performance of a Fe88Zr4Pr4B4 amorphous alloy and its amorphous hybrids. Intermetallics 2023, 161, 107982. [Google Scholar] [CrossRef]
- Wang, P.J.; Wang, Q.; Zheng, S.H.; Zhu, L.Z.; Ding, D.; Tang, B.Z.; Yu, P.; Yao, J.L.; Xia, L. Improvement of Curie temperature and magnetic entropy change of a Fe88Zr8B4 metallic glass by minor Nd substitution. J. Non-Cryst. Solids 2023, 611, 122347. [Google Scholar] [CrossRef]
- Guo, D.Q.; Yuan, Y.D.; Chan, K.C. The effect of different minor additions on the magneto-caloric effect of FeZrB metallic ribbons near room temperature. J. Magn. Magn. Mater. 2018, 446, 12–17. [Google Scholar] [CrossRef]
- Li, X.; Pan, Y. Magnetocaloric effect in Fe-Zr-B-M (M = Ni, Co, Al, and Ti) amorphous alloys. J. Appl. Phys. 2014, 116, 093910. [Google Scholar] [CrossRef]
- Fang, Y.K.; Yeh, C.C.; Hsieh, C.C.; Wang, C.W.; Chang, H.W.; Chang, W.C.; Li, X.M.; Li, W. Magnetocaloric effect in Fe–Zr–B–M (M = Mn, Cr, and Co) amorphous systems. J. Appl. Phys. 2009, 105, 07A910. [Google Scholar] [CrossRef]
- Gan, L.H.; Ma, L.Y.; Tang, B.Z.; Ding, D.; Xia, L. Effect of Co substitution on the glass forming ability and magnetocaloric effect of Fe88Zr8B4 amorphous alloys. Sci. China Phys. Mech. Astron. 2017, 60, 076121. [Google Scholar] [CrossRef]
- Li, A.L.; Wang, Q.; Tang, B.Z.; Yu, P.; Ding, D.; Xia, L. Magnetocaloric effect of the Fe87M8B5 (M = Zr, Ce) amorphous alloys. Mater. Sci. Eng. B 2022, 286, 116033. [Google Scholar] [CrossRef]
- Mozharivskyj, Y. Preparation of magnetocaloric materials. In Comprehensive Inorganic Chemistry III, 3rd ed.; Reedijk, J., Poeppelmeier, K.R., Eds.; Elsevier Ltd.: Amsterdam, The Netherlands, 2023; Volume 5, pp. 178–198. [Google Scholar]
- Turnbull, D. Under what conditions can a glass be formed? Contemp. Phys. 1969, 10, 473–488. [Google Scholar] [CrossRef]
- Lu, Z.P.; Liu, C.T. A new glass-forming ability criterion for bulk metallic glasses. Acta Mater. 2002, 50, 3501–3512. [Google Scholar] [CrossRef]
- Banerjee, B.K. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Arrott, A.S. Generalized Curie-Weiss law. Phys. Rev. B 1985, 31, 2851. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Zhu, J.; Hao, Z.H.; Hao, W.X.; Mo, Z.J.; Li, L.W. Tunable magnetic phase transition and magnetocaloric effect in the rare-earth-free Al-Mn-Fe-Co-Cr high-entropy alloys. Mater. Des. 2023, 229, 111894. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Xu, P.; Zhu, J.; Yan, S.M.; Zhang, J.C.; Li, L.W. The emergence of considerable room temperature magnetocaloric performances in the transition metal high-entropy alloys. Mater. Today Phys. 2023, 32, 101031. [Google Scholar] [CrossRef]
- Peng, J.X.; Tang, B.Z.; Wang, Q.; Bai, C.; Wu, Y.; Chen, Q.X.; Li, D.M.; Ding, D.; Xia, L.; Guo, X.L.; et al. Effect of heavy rare-earth (Dy, Tb, Gd) addition on the glass-forming ability and magneto-caloric properties of Fe89Zr7B4 amorphous alloy. J. Alloys Compd. 2022, 925, 166707. [Google Scholar] [CrossRef]
- Wang, C.H.; Wang, Q.; Tang, B.Z.; Zhou, X.; Ding, D.; Xia, L. Achieve good magneto-caloric response near the ambient temperature in a Fe86La7B5Ce2 amorphous ribbon. J. Magn. Magn. Mater. 2022, 547, 168954. [Google Scholar] [CrossRef]
- Wood, M.E.; Potter, W.H. General analysis of magnetic refrigeration and its optimization using a new concept: Maximization of refrigerant capacity. Cryogenics 1985, 25, 667–683. [Google Scholar] [CrossRef]
- Dubenko, I.; Ali, N.; Stadler, S.; Zhukov, A.; Zhukova, V.; Hernando, B.; Prida, V.; Prudnikov, V.; Gan’shina, E.; Granovsky, A. Magnetic, magnetocaloric, magnetotransport, and magneto-optical properties of Ni–Mn–In-Based Heusler alloys: Bulk, ribbons, and microwires. Nov. Funct. Magn. Mater. Springer Ser. Mater. Sci. 2016, 231, 41–83. [Google Scholar]
- Pathak, A.K.; Dubenko, I.; Stadler, S.; Ali, N. Magnetic and magnetocaloric properties of Gd6X2Si3 (X = Ni, Co) and Ln6Co2Si3 (Ln = Pr, La). J. Appl. Phys. 2011, 109, 07A913. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Conde, A. Field dependence of the magnetocaloric effect in materials with a second order phase transition: A master curve for the magnetic entropy change. Appl. Phys. Lett. 2006, 89, 222512. [Google Scholar] [CrossRef]
- Fisher, M.E. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 1967, 30, 615–730. [Google Scholar] [CrossRef]
- Kouvel, J.S.; Fisher, M.E. Detailed Magnetic Behavior of Nickel Near its Curie Point. Phys. Rev. 1964, 136, A1626. [Google Scholar] [CrossRef]
- Gębara, P.; Hasiak, M. Investigation of critical behavior in the vicinity of ferromagnetic to paramagnetic phase transition in the Fe75Mo8Cu1B16 alloy. J. Appl. Phys. 2018, 124, 083904. [Google Scholar] [CrossRef]
- Hiroyoshi, H.; Hoshi, A.; Nakagawa, Y. Arrott-Noakes plots near the Curie temperature of Fe3Pt: Ordered and disordered alloys in high magnetic fields. J. Appl. Phys. 1982, 53, 2453–2455. [Google Scholar] [CrossRef]
- Oesterreicher, H.; Parker, F.T. Magnetic cooling near Curie temperatures above 300 K. J. Appl. Phys. 1984, 55, 4334–4338. [Google Scholar] [CrossRef]
- Franco, V.; Conde, A. Scaling laws for the magnetocaloric effect in second order phase transitions: From physics to applications for the characterization of materials Lois d’échelle gouvernant l’effet magnétocalorique des transitions de phase de seconde ordre: De la physique aux applications permettant de caractériser les matériaux. Int. J. Refrig. 2010, 33, 465–473. [Google Scholar]
- Widom, B. Equation of State in the Neighborhood of the Critical Point. J. Chem. Phys. 1965, 43, 3898–3905. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Conde, A. The influence of Co addition on the magnetocaloric effect of Nanoperm-type amorphous alloys. J. Appl. Phys. 2006, 100, 064307. [Google Scholar] [CrossRef]
- Dan’kov, S.Y.; Tishin, A.M.; Pecharsky, V.K.; Gschneidner, K.A., Jr. Magnetic phase transitions and the magnetothermal properties of gadolinium. Phys. Rev. B 1998, 57, 3478–3490. [Google Scholar] [CrossRef]
- Nikitin, S.A.; Myalikgulyev, G.; Tishin, A.M.; Annaorazov, M.P.; Asatryan, K.A.; Tyurin, A.L. The magnetocaloric effect in Fe49Rh51 compound. Phys. Lett. A 1990, 148, 363–366. [Google Scholar] [CrossRef]
- Zheng, S.H.; Wang, Q.; Zhu, L.Z.; Wang, P.J.; Ding, D.; Tang, B.Z.; Yu, P.; Yao, J.L.; Xia, L. Excellent Magnetocaloric Performance of the Fe87Ce13-xBx (x = 5, 6, 7) Metallic Glasses and Their Composite. Materials 2023, 16, 4393. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.-Z.; Wang, Q.; Zheng, S.-H.; Wang, P.-J.; Ding, D.; Tang, B.-Z.; Yu, P.; Yao, J.-L.; Xia, L. Effect of Minor Ce Substitution for Pr on the Glass Formability and Magnetocaloric Effect of a Fe88Zr4Pr4B4 Metallic Glass. Metals 2023, 13, 1531. https://doi.org/10.3390/met13091531
Zhu L-Z, Wang Q, Zheng S-H, Wang P-J, Ding D, Tang B-Z, Yu P, Yao J-L, Xia L. Effect of Minor Ce Substitution for Pr on the Glass Formability and Magnetocaloric Effect of a Fe88Zr4Pr4B4 Metallic Glass. Metals. 2023; 13(9):1531. https://doi.org/10.3390/met13091531
Chicago/Turabian StyleZhu, Li-Ze, Qiang Wang, Shu-Hui Zheng, Peng-Jie Wang, Ding Ding, Ben-Zhen Tang, Peng Yu, Jin-Lei Yao, and Lei Xia. 2023. "Effect of Minor Ce Substitution for Pr on the Glass Formability and Magnetocaloric Effect of a Fe88Zr4Pr4B4 Metallic Glass" Metals 13, no. 9: 1531. https://doi.org/10.3390/met13091531
APA StyleZhu, L.-Z., Wang, Q., Zheng, S.-H., Wang, P.-J., Ding, D., Tang, B.-Z., Yu, P., Yao, J.-L., & Xia, L. (2023). Effect of Minor Ce Substitution for Pr on the Glass Formability and Magnetocaloric Effect of a Fe88Zr4Pr4B4 Metallic Glass. Metals, 13(9), 1531. https://doi.org/10.3390/met13091531






