Modified Voce-Type Constitutive Model on Solid Solution State 7050 Aluminum Alloy during Warm Compression Process
Abstract
:1. Introduction
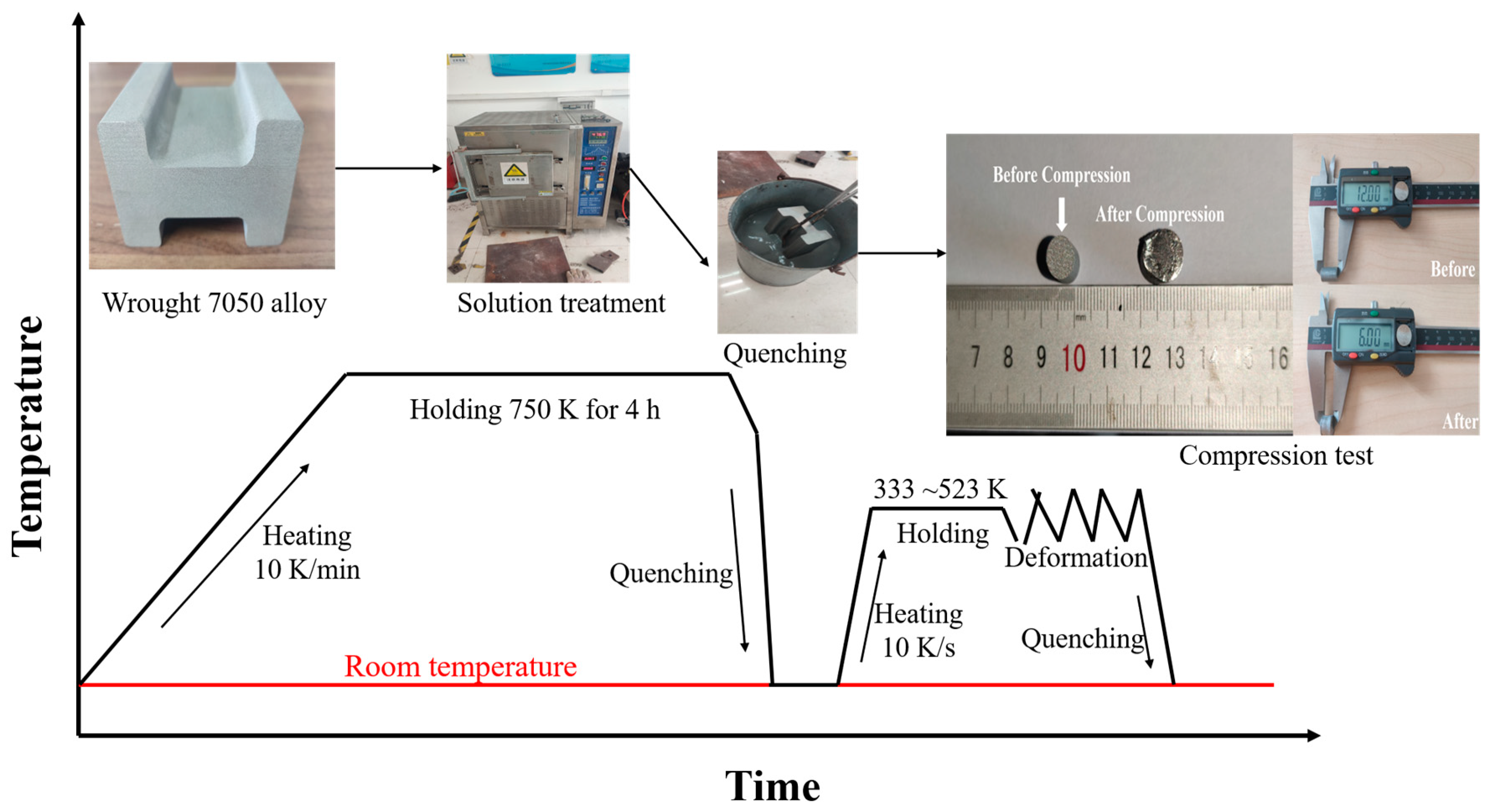
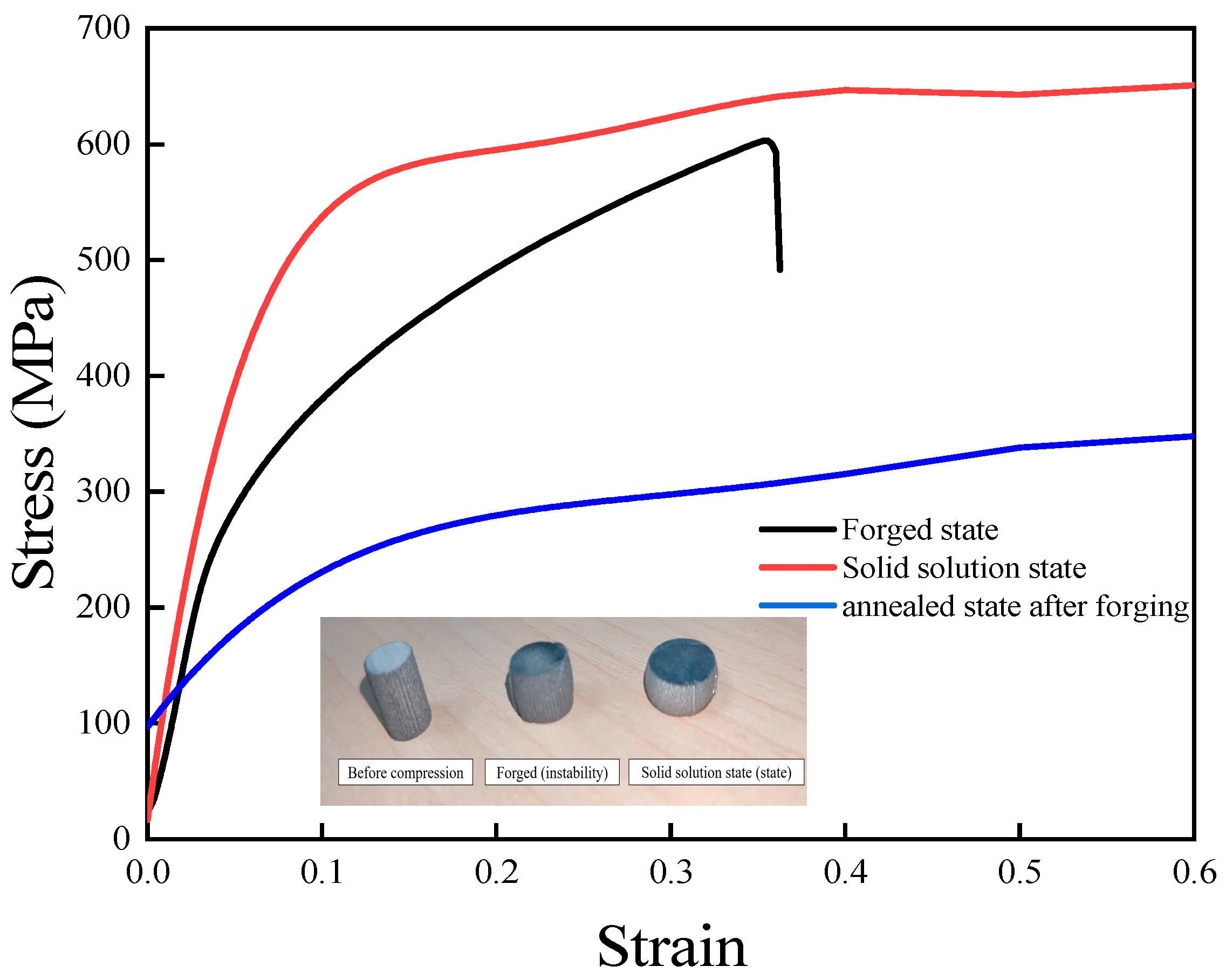
2. Materials and Methods
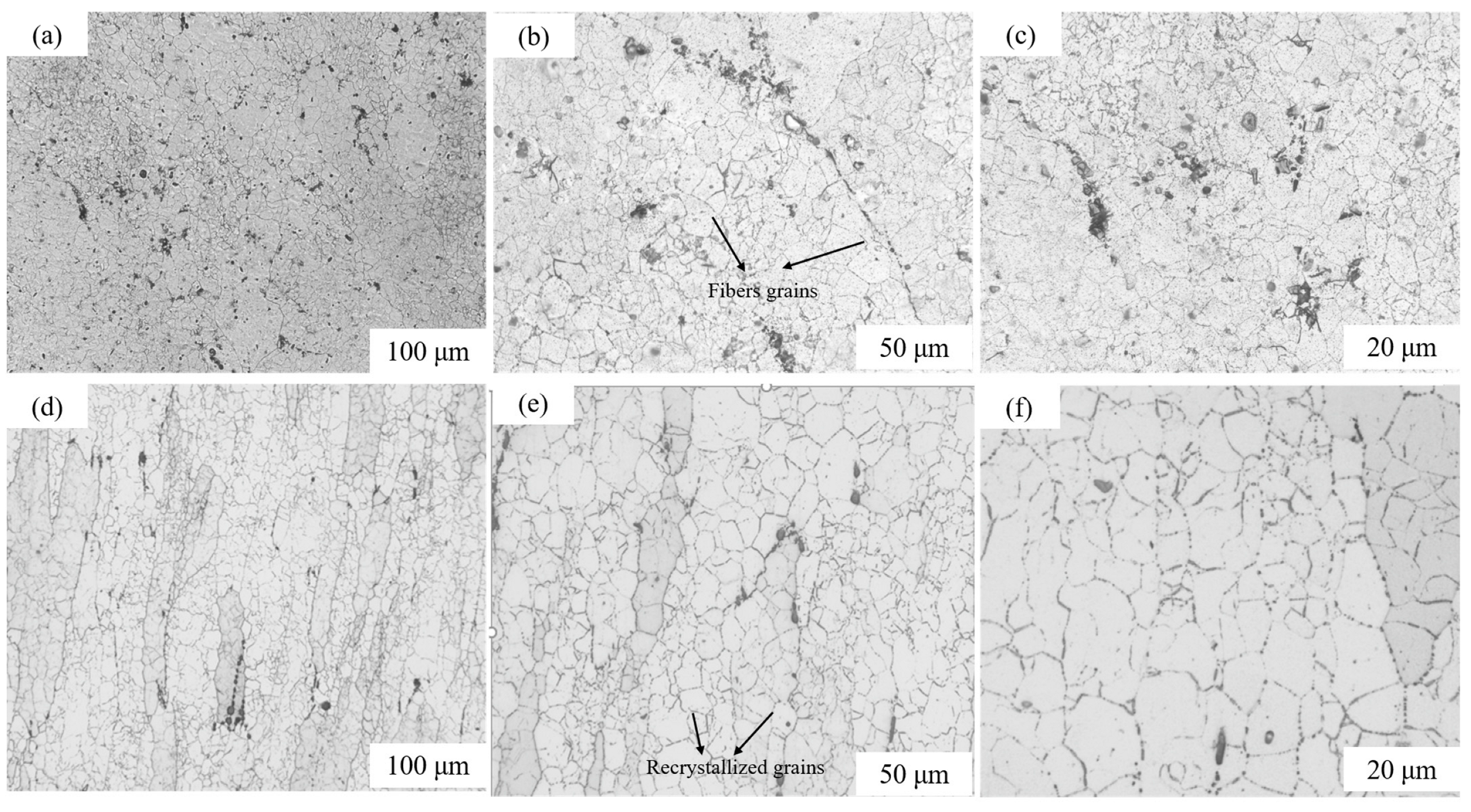
3. Results and Discussion
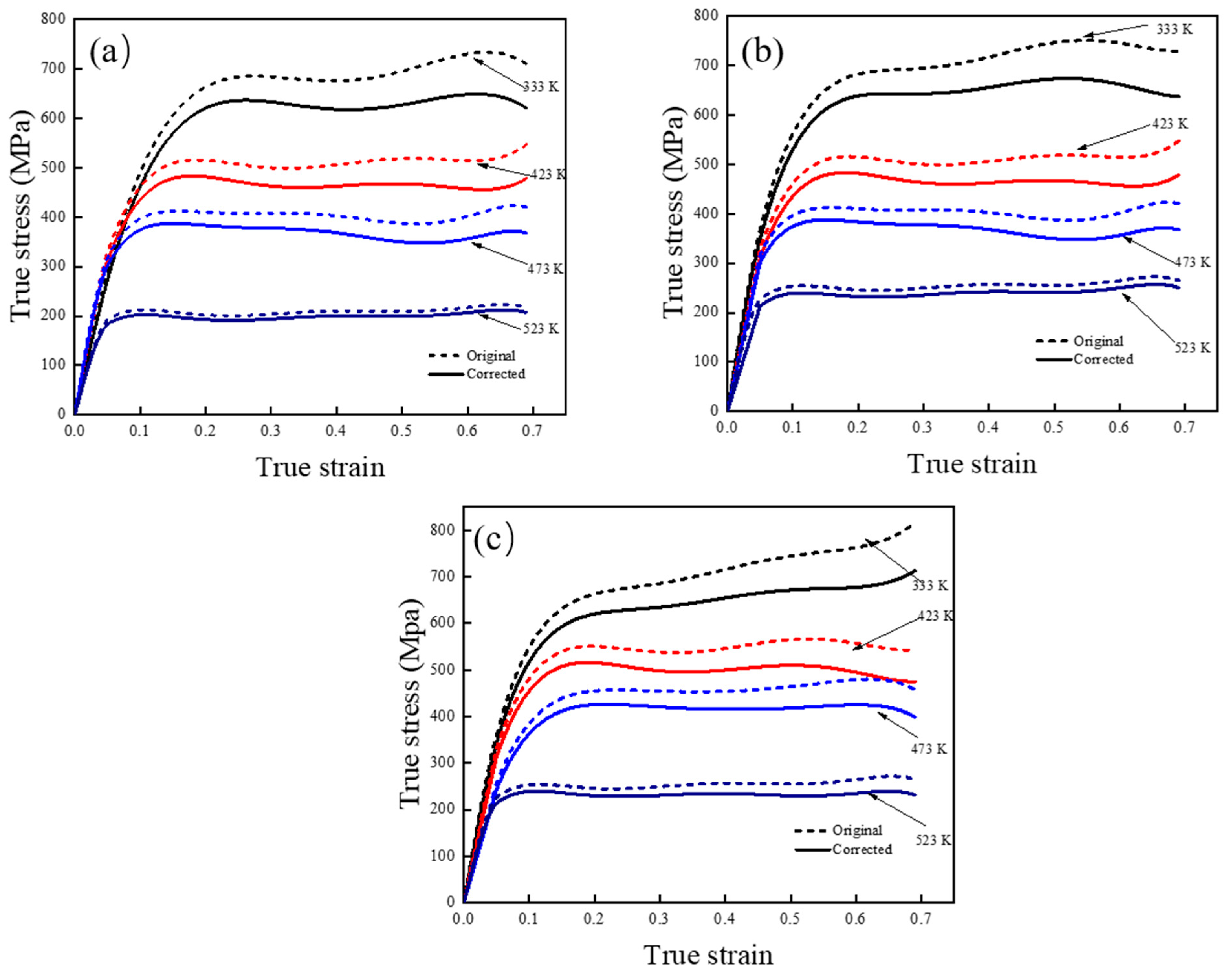
3.1. Flow Behavior
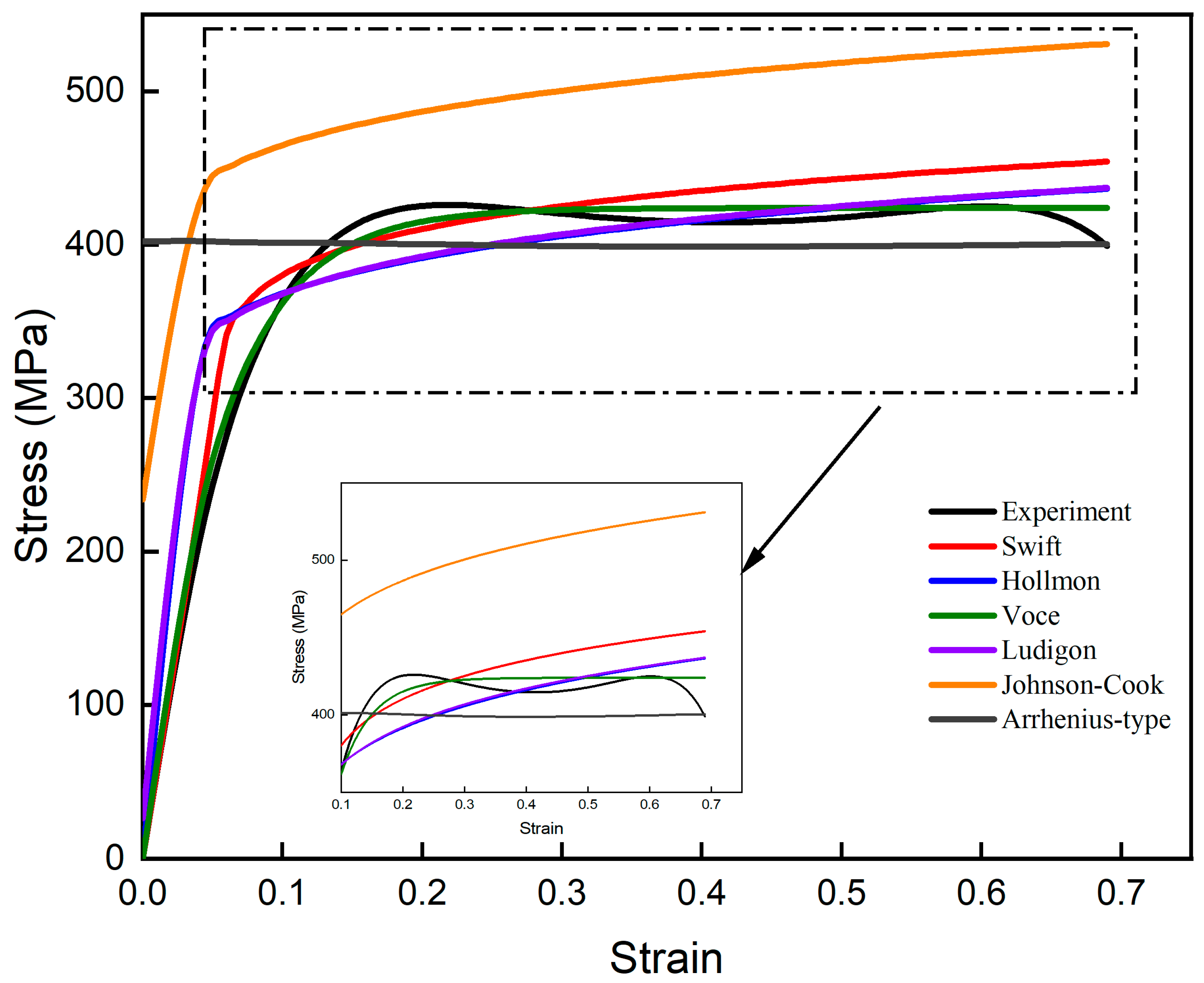
3.2. Construction and Comparison of Constitutive Models
3.2.1. Voce-Type with Softening Coefficient
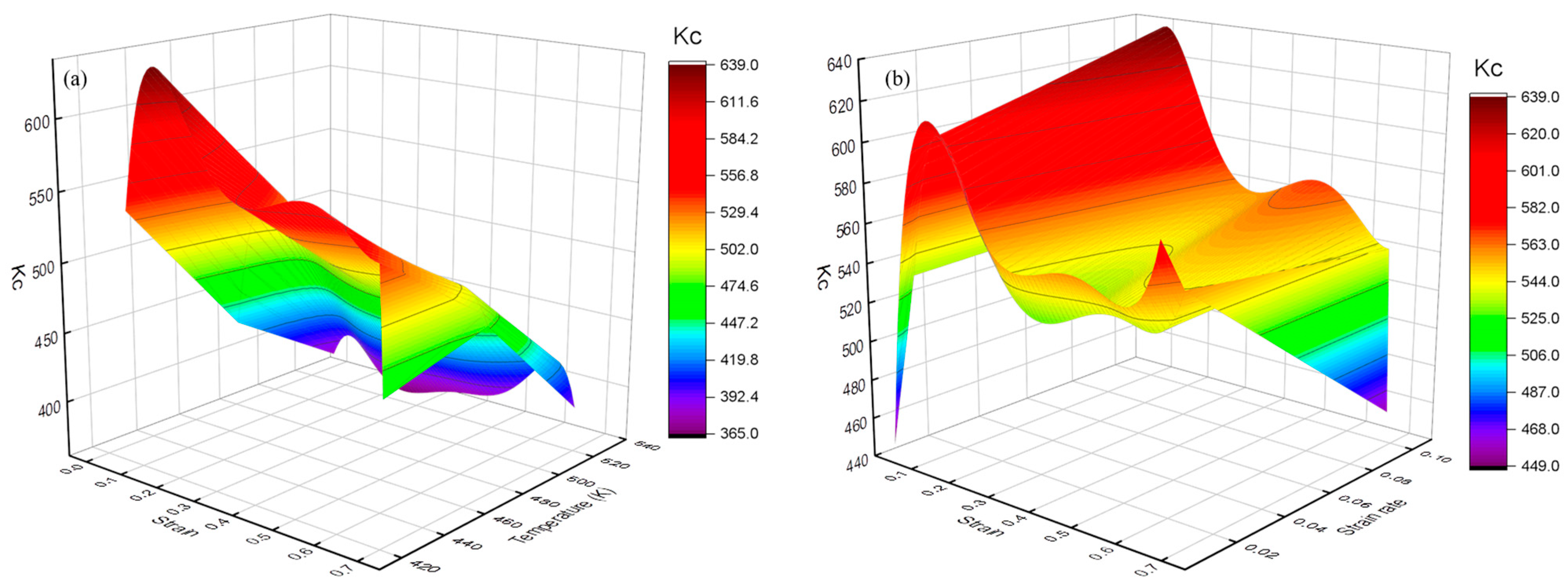
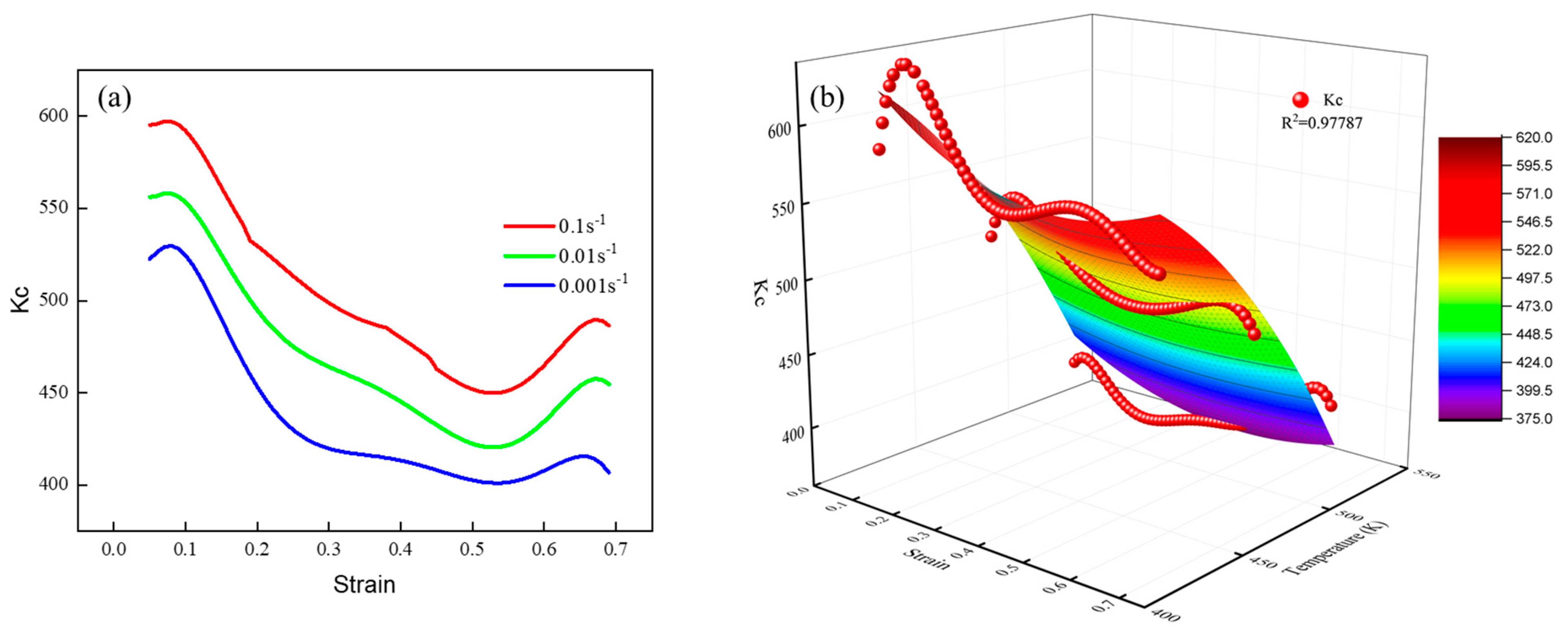
3.2.2. Modified Voce-Type Model with Variable Parameters
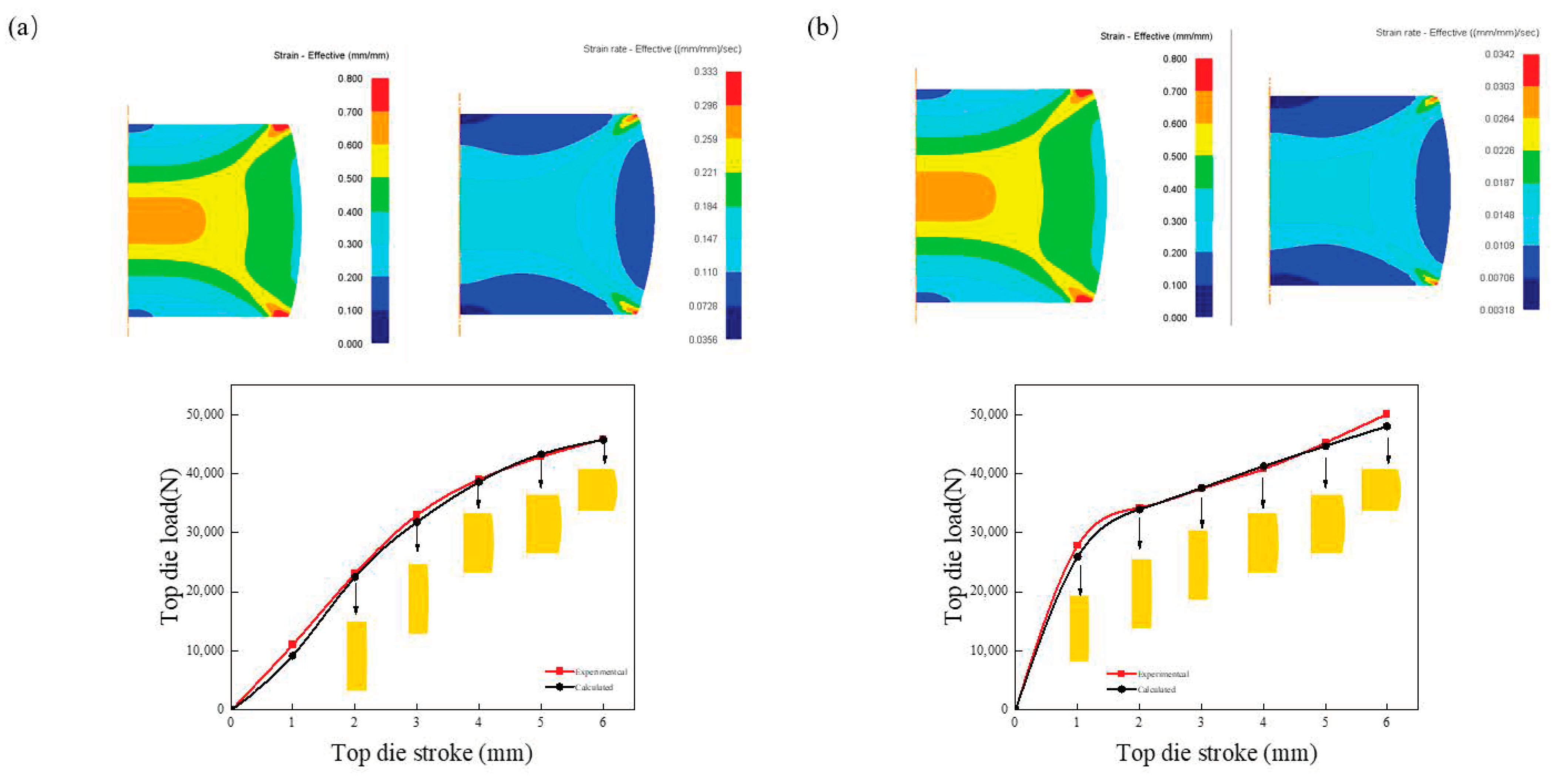
3.3. Constitutive Model Evaluation and Application
4. Conclusions
- (1)
- The Voce-type model has better precision of warm compression behavior for solid solution-state 7050 alloy than the unsaturated models;
- (2)
- The prediction accuracy of the conventional Voce model with softening coefficient on solid solution-state alloys during the warm compression process is not very high. In the conventional Voce model, the material parameters are regarded as independent of the deformation parameters. However, the parameters are variable due to microstructure deformation mechanism evolution, which decreases simulation accuracy;
- (3)
- The modified model has good predictability for warm compression behavior for solid solution-state 7050 alloy. The fitting and FEA results indicate the validity of a modified Voce-type constitutive model with variable parameters and friction correction in the warm compression process. The modified Voce-type constitutive model can be applied to the warm forge process design of the 7050 alloy in its solid solution state.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, D.; Xu, R.; Li, J.; Huang, W.; Wang, J.; Liu, Y.; Zhao, L.; Li, C.; Zhang, H. Microstructure Evolution Behavior of Spray-Deposited 7055 Aluminum Alloy During Hot Deformation. Metals 2022, 11, 1982. [Google Scholar] [CrossRef]
- Wei, S.L.; Feng, Y.; Zhang, H.; Xu, C.T.; Wu, Y. Influence of Aging on Microstructure, Mechanical Properties and Stress Corrosion Cracking of 7136 Aluminum Alloy. J. Cent. South Univ. 2021, 28, 2687–2700. [Google Scholar] [CrossRef]
- Wu, C.H.; Feng, D.; Ren, J.J.; Zang, Q.H.; Li, J.C.; Liu, S.D.; Zhang, X.M. Effect of Non-Isothermal Retrogression and Re-Ageing On through-Thickness Homogeneity of Microstructure and Properties of Al-8Zn-2Mg-2Cu Alloy Thick Plate. J. Cent. South Univ. 2022, 29, 960–972. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Gong, H.; Wu, Y. Effect of Cold Pressing and Aging on Reduction and Evolution of Quenched Residual Stress for Al-Zn-Mg-Cu T-Type Rib. Appl. Sci. 2021, 11, 5439. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Y.; Li, L.; Chen, B.; Tian, H. Assessment of Residual Stress of 7050-T7452 Aluminum Alloy Forging Using the Contour Method. Mater. Sci. Eng. A 2015, 644, 61–68. [Google Scholar] [CrossRef]
- Xu, L.; Zhan, L.; Xu, Y.; Liu, C.; Huang, M. Thermomechanical Pretreatment of Al-Zn-Mg-Cu Alloy to Improve Formability and Performance During Creep-Age Forming. J. Mater. Process. Technol. 2021, 293, 117089. [Google Scholar] [CrossRef]
- Koc, M.; Culp, J.; Altan, T. Prediction of Residual Stresses in Quenched Aluminum Blocks and their Reduction through Cold Working Processes. J. Mater. Process. Tech. 2006, 174, 342–354. [Google Scholar] [CrossRef]
- Rometsch, P.A.; Zhang, Y.; Knight, S. Heat Treatment of 7Xxx Series Aluminium Alloys—Some Recent Developments. Trans. Nonferrous Met. Soc. China 2014, 24, 15. [Google Scholar] [CrossRef]
- Zhang, C.; Chu, X.; Guines, D.; Leotoing, L.; Ding, J.; Zhao, G. Dedicated linear–Voce model and its application in Dedicated Linear-Voce Model and its Application in Investigating Temperature and Strain Rate Effects on Sheet Formability of Aluminum Alloys. Mater. Des. 2014, 67, 522–530. [Google Scholar] [CrossRef]
- Hartloper, A.R.; de Castro e Sousa, A.; Lignos, D.G. Constitutive Modeling of Structural Steels: Nonlinear Isotropic/Kinematic Hardening Material Model and its Calibration. J. Struct. Eng. 2021, 147. [Google Scholar] [CrossRef]
- Sung, J.H.; Kim, J.H.; Wagoner, R.H. A Plastic Constitutive Equation Incorporating Strain, Strain-Rate, and Temperature. Int. J. Plast. 2010, 26, 1746–1771. [Google Scholar] [CrossRef]
- Wu-Jiao, L.F.N.T. Effect of Solution Treatment Time on Mechanical Properties and Corrosion Resistance of Extruded 7050 Aluminum Alloy. Trans. Mater. Heat Treat. 2021, 42, 10. [Google Scholar]
- Li, P.Y.; Xiong, B.Q.; Zhang, Y.A.; Li, Z.H.; Zhu, B.H.; Wang, F.; Liu, H.W. Quench Sensitivity and Microstructure Character of High Strength Aa7050. Trans. Nonferrous Met. Soc. China 2012, 22, 268–274. [Google Scholar] [CrossRef]
- Feng, D.; Wang, G.; Chen, H.; Zhang, X. Effect of Grain Size Inhomogeneity of Ingot on Dynamic Softening Behavior and Processing Map of Al-8Zn-2Mg-2Cu Alloy. Met. Mater. Int. 2016, 24, 195–204. [Google Scholar] [CrossRef]
- Robson, J.D.; Prangnell, P.B. Predicting Recrystallised Volume Fraction in Aluminium Alloy 7050 Hot Rolled Plate. Met. Sci. J. 2002, 18, 607–614. [Google Scholar] [CrossRef]
- Fan, X. Homogenization of 7050 Plates by a Novel Differential Temperature Rolling. Mater. Manuf. Process. 2018, 33, 1822–1829. [Google Scholar] [CrossRef]
- Han, N.M.; Zhang, X.M.; Liu, S.D.; He, D.G.; Zhang, R. Effect of Solution Treatment on the Strength and Fracture Toughness of Aluminum Alloy 7050. J. Alloys Compd. 2011, 509, 4138–4145. [Google Scholar] [CrossRef]
- Juan, Y.; Niu, G.; Jiang, H.; Yang, J.; Tang, W.; Dai, Y.; Yang, Y.; Zhang, J. Influence of Solution Heat Treatment on Strength and Fracture Toughness of Aluminum Alloy 7050. J. Cent. South Univ. 2012, 43, 855–863. [Google Scholar]
- Li, C.; Wang, H.; Wang, W.; Ye, C.; Jin, Z.; Zhang, X.; Zhang, H.; Jia, L. Effect of Solution Treatment on Recrystallization, Texture and Mechanical Properties of 7a65-T74 Aluminum Alloy Super-Thick Hot Rolled Plate. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2022, 37, 460–469. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, J.; Xiao, X.; Li, S.; Cui, M.; Zhang, P.; Long, S.; Zhang, J. Microstructural Evolution and Hardness Responses of 7050 Al Alloy During Processing. Materials 2022, 15, 5629. [Google Scholar] [CrossRef]
- Amit, B. Mechanical Properties and Working of Metals and Alloys; Springer: Singapore, 2018. [Google Scholar]
- Chen, S.; Chen, K.; Peng, G.; Chen, X.; Ceng, Q. Effect of Heat Treatment on Hot Deformation Behavior and Microstructure Evolution of 7085 Aluminum Alloy. J. Alloys Compd. 2012, 537, 338–345. [Google Scholar] [CrossRef]
- Gasson, C.P. Light Alloys: From Traditional Alloys to Nanocrystals—Fourth Edition. Aeronaut. J. 2006, 110, 394–395. [Google Scholar] [CrossRef]
- Lu, J.; Song, Y.; Hua, L.; Zheng, K.; Dai, D. Thermal Deformation Behavior and Processing Maps of 7075 Aluminum Alloy Sheet Based on Isothermal Uniaxial Tensile Tests. J. Alloys Compd. 2018, 767, 856–869. [Google Scholar] [CrossRef]
- Zhu, R.H.; Qing LI, U.; Li, J.F.; Chen, Y.L.; Zhang, X.H.; Zheng, Z.Q. Flow Curve Correction and Processing Map of 2050 Al–Li Alloy. Trans. Nonferrous Met. Soc. China 2018, 28, 404–414. [Google Scholar] [CrossRef]
- Luo, J.; Li, M.Q.; Ma, D.W. The Deformation Behavior and Processing Maps in the Isothermal Compression of 7a09 Aluminum Alloy. Mater. Sci. Eng. A 2012, 532, 548–557. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, Y.; Tang, J.; Zhang, J. Influence of Strain Rate on Hot Deformation Behavior and Recrystallization Behavior Under Isothermal Compression of Al-Zn-Mg-Cu Alloy. J. Alloys Compd. 2019, 809, 151788. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Y.X.; Gong, H.; Wang, K. Modification of Constitutive Model and Evolution of Activation Energy On 2219 Aluminum Alloy During Warm Deformation Process. Trans. Nonferrous Met. Soc. China 2019, 29, 448–459. [Google Scholar] [CrossRef]
- Jiang, F.; Tang, J.; Fu, D.; Huang, J.; Zhang, H. A Correction to the Stress–Strain Curve During Multistage Hot Deformation of 7150 Aluminum Alloy Using Instantaneous Friction Factors. J. Mater. Eng. Perform. 2018, 27, 3083–3090. [Google Scholar] [CrossRef]
- Wu, D.X.; Long, S.; Li, S.S.; Zhou, Y.T.; Wang, S.Y.; Dai, Q.W.; Lin, H.T. Hot Deformation Behavior of Homogenized Al-7.8Zn-1.65Mg-2.0Cu (Wt.%) Alloy. J. Mater. Eng. Perform. 2022, 32, 3431–3442. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile Deformation. Met. Technol. 1945, 12, 268–290. [Google Scholar]
- Swift, H.W. Plastic Instability Under Plane Stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Ludwigson, D. Modified Stress-Strain Relation for Fcc Metals and Alloys. Metall. Trans. 1971, 2, 2825. [Google Scholar] [CrossRef]
- Voce, E. The Relationship Between Stress and Strain for Homogeneous Deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Verlinden, B.; Suhadi, A.; Delaey, L. A Generalized Constitutive Equation for an Aa6060 Aluminium Alloy. Scr. Metall. Mater. 1993, 28, 1441–1446. [Google Scholar] [CrossRef]
- Pelaccia, R.; Santangelo, P.E. A Homogeneous Flow Model for Nitrogen Cooling in the Aluminum-Alloy Extrusion Process. Int. J. Heat Mass Transf. 2022, 195, 1–14. [Google Scholar] [CrossRef]
- Shi, S.X.; Liu, X.S.; Zhang, X.Y.; Zhou, K.C. Comparison of Flow Behaviors of Near Beta Ti-55511 Alloy During Hot Compression Based on Sca and Bpann Models. Trans. Nonferrous Met. Soc. China 2021, 31, 1665–1679. [Google Scholar] [CrossRef]
- Nourani, M.; Milani, A.S.; Yannacopoulos, S. On the Effect of Different Material Constitutive Equations in Modeling Friction Stir Welding: A Review and Comparative Study on Aluminum 6061. Int. J. Adv. Eng. Technol. 2014, 7, 1–20. [Google Scholar]
- Koc, P.; Atok, B. Computer-Aided Identification of the Yield Curve of a Sheet Metal After Onset of Necking. Comput. Mater. Sci. 2004, 31, 155–168. [Google Scholar] [CrossRef]
- Ye, J.H.; Chen, M.H.; Wang, N.; Xie, L.S. Flow Stress Model of 2a12 Aluminum Alloy Based on Modified Voce Model. Trans. Mater. Heat Treat. 2019, 40, 170–176. [Google Scholar]
- Wei, G.; Peng, X.; Hadadzadeh, A.; Mahmoodkhani, Y.; Xie, W.; Yang, Y.; Wells, M.A. Constitutive Modeling of Mg-9Li-3Al-2Sr-2Y at Elevated Temperatures. Mech. Mater. 2015, 89, 241–253. [Google Scholar] [CrossRef]
- Jedrasiak, P.; Shercliff, H. Finite Element Analysis of Small-Scale Hot Compression Testing—Sciencedirect. J. Mater. Sci. Technol. 2021, 76, 174–188. [Google Scholar] [CrossRef]
- Zhang, J.S.; Xia, Y.F.; Quan, G.Z.; Wang, X.; Zhou, J. Thermal and Microstructural Softening Behaviors During Dynamic Recrystallization in 3Cr20Ni10W2 Alloy. J. Alloys Compd. 2018, 743, 464–478. [Google Scholar] [CrossRef]
- Padhi, P.C.; Mahapatra, S.S.; Yadav, S.N.; Tripathy, D.K. Multi-Objective Optimization of Wire Electrical Discharge Machining (Wedm) Process Parameters Using Weighted Sum Genetic Algorithm Approach. J. Adv. Manuf. Syst. 2016, 15, 85–100. [Google Scholar] [CrossRef]
- Long, S.; Xia, Y.-F.; Wang, P.; Zhou, Y.-T.; Gong-Ye, F.-J.; Zhou, J.; Zhang, J.-S.; Cui, M.-L. Constitutive Modelling, Dynamic Globularization Behavior and Processing Map for Ti-6Cr-5Mo-5V-4Al Alloy During Hot Deformation. J. Alloys Compd. 2019, 796, 65–76. [Google Scholar] [CrossRef]
- Wu, D.; Long, S.; Wang, S.; Li, S.S.; Zhou, Y.T. Constitutive Modelling with a Novel Two-Step Optimization for an Al-Zn-Mg-Cu Alloy and its Application in Fea. Mater. Res. Express 2021, 8, 116511. [Google Scholar] [CrossRef]





| Cr | Cu | Fe | Mg | Mn | Si | Ti | Zn | Al |
|---|---|---|---|---|---|---|---|---|
| 0.04 | 2.0 | 0.16 | 1.90 | 0.10 | 0.126 | 0.06 | 5.7 | Bal |
| Polynomial Order | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 0.97787 | 0.99201 | 0.995424 | 0.99999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, H.; Xia, Y.; Pan, C.; Li, Y. Modified Voce-Type Constitutive Model on Solid Solution State 7050 Aluminum Alloy during Warm Compression Process. Metals 2023, 13, 989. https://doi.org/10.3390/met13050989
Teng H, Xia Y, Pan C, Li Y. Modified Voce-Type Constitutive Model on Solid Solution State 7050 Aluminum Alloy during Warm Compression Process. Metals. 2023; 13(5):989. https://doi.org/10.3390/met13050989
Chicago/Turabian StyleTeng, Haihao, Yufeng Xia, Chenghai Pan, and Yan Li. 2023. "Modified Voce-Type Constitutive Model on Solid Solution State 7050 Aluminum Alloy during Warm Compression Process" Metals 13, no. 5: 989. https://doi.org/10.3390/met13050989
APA StyleTeng, H., Xia, Y., Pan, C., & Li, Y. (2023). Modified Voce-Type Constitutive Model on Solid Solution State 7050 Aluminum Alloy during Warm Compression Process. Metals, 13(5), 989. https://doi.org/10.3390/met13050989





