Abstract
Crystallization is a major challenge in metallic glass production, and predictive models may aid the development of controlled microstructures. This work describes a modeling strategy of nucleation, growth and the dissolution of crystals in a multicomponent glass-forming system. The numerical model is based on classical nucleation theory in combination with a multicomponent diffusion-controlled growth model that is valid for high supersaturation. The required thermodynamic properties are obtained by coupling the model to a CALPHAD database using the Al-Cu-Zr system as a demonstrator. The crystallization of intermetallic phases from the undercooled liquid phase were simulated under isothermal as well as rapid heating and cooling conditions (). The obtained time–temperature transformation and continuous-heating/cooling transformation diagrams agree satisfactorily with the experimental data over a wide temperature range, thereby, demonstrating the predictability of the modeling approach. A comparison of the simulation results and experimental data is discussed.
1. Introduction
Metallic glasses (MG) possess an amorphous atomic structure, which result in an unique combination of material properties, including high specific strength, a high elastic strain limit, high mechanical resilience, high corrosion resistance and excellent soft magnetic properties []. The amorphous atomic structure of metallic glasses is obtained by cooling the molten material fast enough to bypass crystallization. Crystallization is, in general, not desired as it forms at the expense of the amorphous structure. However, partial crystallization resulting in MG-crystalline composites can, in some cases, be favorable as this combines the properties of the crystalline and the amorphous material [].
This has, for example, been demonstrated by the application of nanocrystalline-amorphous Fe-based soft magnetic alloys with a unique combination of high permeability and saturation flux density [,]. Another example is the improved ductility of Zr-based MG composites, in which the ductile crystalline particles inhibit the propagation of shear bands in the brittle amorphous matrix [,,]. Whether the purpose is to achieve glass formation or control the extent of the crystalline volume fraction obtained from thermal processing, the technological and industrial importance of predictive crystallization modeling in metallic glasses is significant.
Early works on the modeling of nucleation and growth of crystals in glass-forming alloys are found in Uhlmann [], Morris [] and Gránásy []. Uhlmann derived expressions based on classical nucleation and growth theory (CNT) in combination with Johnson–Mehl–Avrami–Kolmogorov kinetics to compute time–temperature transformation (TTT) diagrams and predict the critical cooling rates of different glass-forming systems []. The approach by Uhlmann has been adopted in many works with various thermodynamic and kinetic modifications.
Morris combined the approach by Uhlmann with the thermodynamic model developed by Thompson and Spaepen [] to model crystallization in the Ni-Si-B system. Gránásy made use of the driving force for crystallization calculated from the measured specific heat capacities of the liquid and crystalline phases to compute the crystallization kinetics of metallic glass []. More recently, Ge et al. [] combined Uhlmann kinetics and CALPHAD databases to predict the glass-forming ability of various Cu-Zr and Cu-Zr-Ti alloys.
Similarly, Yang et al. [] performed calculations of the glass-forming ability in the Cu-Zr system but also considered the effect of heterogeneous nucleation. A common denominator in the above mentioned works, and in others [,,], is the assumption of polymorphic conditions for which the composition of the particle and the matrix phase are assumed equal. The transformation is then governed by the rate of atomic attachment at the interface and the coupling between crystal growth and the diffusional transport of alloying elements to the particle–matrix interface is neglected.
As discussed by Inoue et al. [] and Köster et al. [], polymorphic crystallization in metallic glasses is actually quite rare, and more often, multiple phases form of different composition than the parent matrix phase for which the growth rate is dictated by the diffusional fluxes of the partitioning elements. Reports of partitioning crystallization in Zr-, Fe-, Al- and Mg-based glass-forming systems are found in [,,,,,,,].
Baricco and Palumbo performed modeling of partitioning growth in the Fe-B and Al-Ni-Ce glass-forming systems using CALPHAD databases and the DICTRA software [,]. Nestler et al. simulated the dendritic growth of crystals in metallic glass using the phase-field method []. However, the above mentioned approaches only considered growth and not nucleation.
Nucleation and growth are concomitant processes, and in order to fully describe the crystallization process, a model describing concurrent nucleation, diffusion-controlled growth and the dissolution of particles should be considered. Ideally, it should also be applicable to arbitrary thermal conditions such that it can be used to simulate crystallization during non-isothermal processing. This task can be achieved by numerically solving the temporal evolution of the crystal size-distribution using appropriate models for partitioning nucleation and growth in glass-forming systems.
In this work, the modeling of the nucleation, growth and dissolution of crystals in the Al-Cu-Zr glass-forming system is performed. The model is based on classical nucleation theory combined with the model of multicomponent diffusion-controlled growth developed by Chen [] and implemented within the numerical Kampmann and Wagner (NKW) scheme proposed by Myhr and Grong []. The model is coupled to a CALPHAD database of the Al-Cu-Zr system [], which allows for evaluation of the composition- and temperature-dependent thermodynamic properties and accounts for the non-ideal mixing, characteristic of glass-forming liquids.
The formation of intermetallic phases are simulated during heating and cooling at high rates, as well as isothermal conditions. The capability of the modeling approach is demonstrated by comparison with the experimentally obtained time–temperature transformation and continuous-heating/cooling transformation (CHT/CCT) diagrams.
2. Modeling Methodology
In the following, the modeling methodology is presented. The equations governing nucleation and growth are presented in Section 2.1 and Section 2.2, followed by a description of the thermodynamic properties in Section 2.3. The numerical scheme is described in Section 2.4. Before proceeding, we first summarize the core assumptions adopted in the model: (i) the crystalline particles are of spherical shape, and the interface between the particles and the matrix is sharp; (ii) the growth of the particles is entirely controlled by diffusion in the matrix; (iii) the local equilibrium adjusted by the Gibbs–Thomson effect holds at the particle–matrix interface; (iv) the diffusivity of the alloying elements are equal in the matrix, and cross-diffusion between the elements is neglected; (v) the molar volumes of the particles and the matrix are equal; and (vi) nucleation occurs at a steady-state rate.
2.1. Nucleation
According to classical nucleation theory, the change in energy required to form a spherical particle with radius r is described by [],
where is the chemical driving force between the particle and the matrix per unit mole, is the molar volume of the particle, and is the interfacial energy per unit area. In Equation (1), and describe the thermodynamic competition between the bulk energy release and the energy cost for the creation of the interface. The Gibbs energy change then shows a maximum for , when r is equal to the critical radius , and
where is the corresponding maximum of , also known as the nucleation barrier.
For the evaluation of , the maximum chemical driving force approach is adopted []. In this procedure, it is assumed that a particle of phase forms with an unknown composition in an infinitely large matrix of phase and known composition . To obtain the values of and , the maximum difference between the tangent plane to the Gibbs energy of the phase and the Gibbs energy of the phase is evaluated using []
where is the molar Gibbs energy of the particle evaluated at , and n denotes the number of elements in the system. The first term involves the chemical potential and describes the tangent plane of the molar Gibbs energy of the matrix phase evaluated at . The thermodynamic models of the particle and matrix phases are described in Section 2.3.
The nucleation barrier is used to evaluate the steady-state nucleation rate as given by []
where T is the temperature, is the number of nucleation sites per unit volume, which is assumed to be equal to the number of atoms per unit volume in the system, i.e., where is the Avogadro constant, and is the molar volume of the amorphous alloy. Z is the Zeldovic factor, for which a spherical particle is evaluated as
and is the condensation rate, taken as []
where is the atomic jump distance, and is the effective diffusion coefficient in the matrix phase.
The diffusivity of glass-forming liquids is commonly estimated using the Stokes–Einstein Equation [], which relates the effective diffusion coefficient of the metallic liquid to the viscosity as follows
where is the temperature-dependent viscosity of the liquid phase. Several empirical expressions has been proposed for the viscosity, which can be fitted to the measured data. One of the more recent is the Blodgett–Egami–Nussinov–Kelton (BENK) expression, which provides a good fit using only one fitting parameter. The BENK equation can be expressed as []
where and are universal fitting constants, independent of alloy composition, is a reduced temperature, is the Heaviside step function and . The universal scaling temperature is related to the glass-transition temperature by . The high temperature viscosity constant is obtained by fitting Equation (10) to the data provided by Hembree [].
2.2. Growth
In the case of diffusion-controlled growth, the growth rate is governed by the diffusional fluxes at the interface between the spherical particle and the matrix, which depends on the composition gradient in front of the interface. This constitutes a moving boundary value problem, which has to be solved numerically []. Chen et al. proposed an approximate solution of the growth rate of a spherical particle, which avoids in solving the full diffusion field and is valid for high supersaturation []. Here, we employ the model by Chen et al. under the assumption of equal diffusivity. The assumptions is made because of the scarcity of reported diffusivity data in the Al-Cu-Zr system. Instead, the effective diffusion coefficient is used. The growth rate is expressed as
where K is dependent on the matrix supersaturation S. For low supersaturation , then , and the well known expression of is obtained. In the case of a high supersaturation , the dependence is given by
where denotes the error function. For equal diffusivity, the supersaturation becomes identical for each element and can be expressed as
where is the composition in the matrix, i.e., the same as in Equation (4), , and are the compositions at the interface on the matrix side and particle side, respectively. Equations (11)–(13) constitute a moving boundary value problem with unknown boundary conditions, and . Assume local equilibrium at the interface, and the required additional relationships between and are obtained as
where and are the chemical potentials of the bulk matrix and particle phase, respectively. These are evaluated from the thermodynamic models described in Section 2.3. The second term on the right hand side in Equation (14) considers the curvature-induced pressure on the spherical particle, known as the Gibbs–Thomson effect.
2.3. Thermodynamics
To evaluate the thermodynamic quantities for nucleation and growth, suitable thermodynamic models are required. In this work, the thermodynamic database of the Al-Cu-Zr system made by Zhou et al. [] is adopted. In the assessment by Zhou et al. [], the molar Gibbs energy of the liquid (matrix) phase is described using a substitutional solution model
where is the molar Gibbs energy of the pure elements [], and R is the gas constant. The first two terms in Equation (15) represent an ideal substitutional solution with non-interacting elements. Glass-forming metallic liquids show strong non-ideal interactions and are stabilized by negative enthalpies of mixing among the constituent elements []. Hence, the excess Gibbs energy is included in Equation (15) and is expressed as
where and are the binary and ternary Redlich–Kister polynomials describing the temperature-dependent non-ideal interactions. For a more detailed description of the Redlich–Kister polynomials, the reader is referred to [,].
In a similar manner, in [], the molar Gibbs energy of the intermetallic (particle) phase is treated as a line compound , with substitutional mixing of and on the first sublattice and a fixed composition of on the second sublattice. The molar Gibbs energy of formula unit is expressed as
where are the site fractions of on the first sublattice, is the molar Gibbs energy when the first sublattice is occupied by only one element and is the binary Redlich–Kister polynomial included in the excess Gibbs energy.
Interfacial Energy
One inherent difficulty in the application of classical nucleation theory is the interfacial energy. The nucleation rate is sensitive to the interfacial energy because of the exponential dependence on the nucleation barrier in Equation (5). Since the interfacial energy is not easily measured, it is often chosen within acceptable known ranges to provide a good fit to experimental observations of nucleation [,]. This ad hoc procedure might, however, attribute uncertainties in the experimental nucleation data or adhere other physical processes to the value of the interfacial. Hence, a theoretical determination of the interfacial energy is preferred. In this work, we employ the model proposed by Turnbull et al. [], which predicts the interfacial energy from thermodynamic data. According to the model, the interfacial energy at the melting point is estimated as
where is the difference in the molar enthalpy of fusion between the solid and liquid phase at the melting point, which is evaluated from the CALPHAD database.
Nucleation in metallic glasses occurs at large undercoolings, and the size of critical nuclei is expected to be very small. At critical sizes close to the atomic length scale, the sharp interface assumption of classical nucleation theory is known to break down, resulting in an over-predicted nucleation barrier []. One way to relax the sharp interface assumptions is by introducing a size correction factor [,]. Tolman developed the following expression for the size-dependent interfacial energy []
where is a characteristic length-scale. Following the suggestion by Kozeschnik [], this value is taken as where is the distance to the nearest atomic neighbor, estimated using the position of the first peak in the radial pair distribution function of the amorphous material.
2.4. Numerical Scheme
The numerical scheme used in this work stems from the work by Kampmann and Wagner [], who developed the idea that a continuous size distribution can be subdivided into size classes with an associated number of particles. The temporal evolution of the distribution can then be followed by calculating the evolution of each size class.
Myhr and Grong adopted a different technique []: instead of tracking the evolution of the size class, they tracked the evolution of the particle number density on a fixed grid. This was done by using the so-called “upwind scheme”, in which the flux of particles between neighboring size classes is calculated from the number density distribution and the growth rate of each size class. Following this approach, the particle number density (number of particles per volume) of size class i after a timestep is solved using
where and are the width and growth rate of size class i, respectively, and is the Heaviside step function (1 if and 0 otherwise). denotes the particle number density of size class i from the previous timestep. Once the particle-size distribution is updated, the matrix composition of each element i is calculated using
where is the volume fraction of the particles, is the initial composition, and is the particle composition.
By combining the NKW scheme with the models for the nucleation and growth rate described in Section 2.1 and Section 2.2, the evolution in the particle-density distribution, volume fraction and changes in matrix composition can be computed. The scheme is summarized as follows:
The simulations are initiated with for each size class on a grid that consists of 500 size classes ranging from to . To reduce the computational cost, the size classes are represented on a logarithmic grid. This weights the discretization to the nano-sized regime where a finer grid is required because of the high growth rate and also reduces the total number of grid points. To ensure numerical stability, particles are not allowed to move more than one size class, providing the following constraint []
which implies that the timestep is dictated by the growth rate of the particles and may therefore vary during the simulation.
Another computational cost is induced by the solution of the thermodynamic equilibrium at the interface in Step 2, which requires that a non-linear equation system involving six unknowns (, and S) has to be solved for each size class. This is remedied by using the solution from the previous timestep as an initial guess, which not only greatly reduces the number of iterations required but also solves the equation system when the accumulated change in matrix composition becomes above some threshold value set to . Further, particles contained in size classes with are removed from the size distribution as these particles are smaller than the critical size and are assumed to dissolve.
3. Results and Discussions
The presented modeling methodology is applied to simulate the formation and growth of intermetallic phases from an undercooled liquid. The nominal composition of the liquid phase is selected as , which serves as a pseudo-ternary representation of the commercially available alloy AMZ4 () []. Alloy AMZ4 is selected since the formation of crystalline phases have been identified with X-ray diffraction [,], and the TTT-diagram has been measured over a wide temperature range [,]. Further, alloy AMZ4 has received great attention as a material for laser powder bed fusion processing [].
The material parameters used in addition to the CALPHAD database are summarized in Table 1. In Section 3.1, the calculated chemical driving forces and nucleation and growth rates are presented and discussed, followed by the predicted TTT- and CCT/CHT-diagrams in Section 3.2.

Table 1.
The material parameters used in the simulations.
3.1. Nucleation and Growth Rates
The computed chemical driving force of the phase (space group P6/mmm) at a matrix composition of and is illustrated in Figure 1a. The calculated chemical driving force for different intermetallic phases are shown as a function of temperature in Figure 1b. As seen in Figure 1b, the phase with the highest driving force is (space group I4/mmm). At temperatures close to the glass transition, the phase has the second highest driving force. It is reasonable to assume that the phases with the highest driving force would crystallize first. The phase has also been confirmed to form in AMZ4 as well as the metallic glass [,]. In the study on AMZ4, the formation of the phase was identified as well, which agrees with the high driving force at low temperatures in Figure 1. The calculated values of the interfacial energy at the melting point, , using Equation (18) are for and for , respectively, and are used in the following computations.
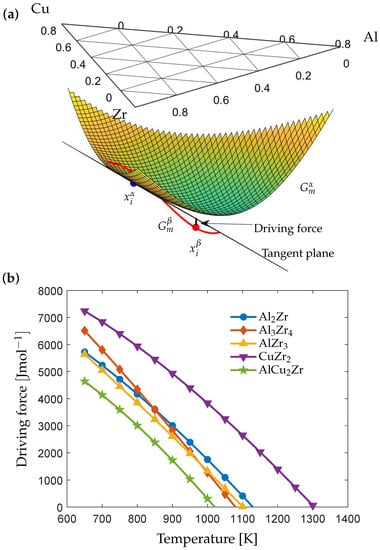
Figure 1.
(a) Gibbs energy curves and the chemical driving force of the phase at K (Computed using Equation (4)). (b) Intermetallic phases with the highest chemical driving force in at low temperatures.
Figure 2a shows the computed growth rate as a function of particle size for the phase from a matrix of composition at . The growth rate is zero at the critical size when the particle is in equilibrium with the matrix () after which it increases drastically upon reaching a maximum value and finally decreases gradually. As seen in Figure 2b,c, the drastic increase in growth rate is caused by the Gibbs–Thomson effect, which influences the chemical equilibrium at the interface and the composition gradient that drives the transformation.
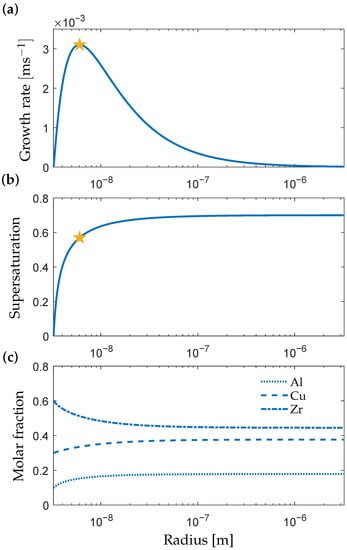
Figure 2.
(a) Growth rate v, (b) supersaturation S and (c) molar fraction at the matrix side as a function of the particle size during growth of at . The stars indicate the maximum growth rate.
Beyond the maximum growth rate, the Gibbs–Thomson effect fades, and the supersaturation approach a constant value. The growth rate then decreases proportional to (1/r) as the diffusional distance of the depletion zone extends further into the matrix. The supersaturation reaches a value of S = 0.7 at large particle sizes; this value is lower at temperatures close to the melting point and increases with undercooling. The high supersaturation indicates a significant deviation from chemical equilibrium between the matrix and particle phases, which is expected for a deeply undercooled metallic liquid.
The maximum growth rate of the and phases are shown together with the calculated nucleation rates in Figure 3. The nucleation and growth rates are higher for the phase at all temperatures because of the higher driving force as shown in Figure 1. At lower temperatures, the nucleation rate of the phase approaches the value of the phase, which suggests that the could form in conjunction with the phase at temperatures close to the glass transition, which is in agreement with the experimental observations [,].
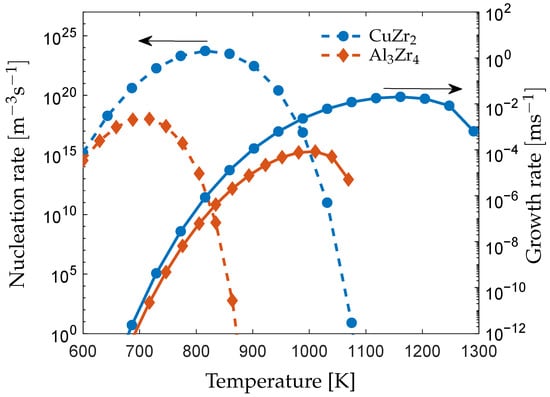
Figure 3.
The nucleation rate (dashed line, left scale) and maximum growth rate (solid line, right scale) of the and phases from a matrix composition of .
The growth rate of the phase shows a maximum of at an undercooling of , which is comparable to experimental measurements on crystallization in the alloy, where a maximum growth rate of at an undercooling of was reported []. The large difference in the nucleation and growth rates between the and phases at elevated temperatures translates into a much higher rate of crystallization of the phase and suggests that the formation of the phase is the main crystallization mechanism in the alloy.
3.2. Predicted Transformation Diagrams
Transformation diagrams can provide valuable information regarding resistance to the crystallization of metallic glasses. Such diagrams can be used to assess the critical time during thermal processing to avoid or achieve a certain volume fraction of crystals. For casting processes, the cooling rate is the most critical factor; however, for other manufacturing processes, such as thermoplastic formation and additive manufacturing, annealing and heating are of considerable interest. The model described in Section 2 is, therefore, used to simulate crystallization under isothermal as well as heating and cooling conditions.
The times to obtain a crystalline volume fraction of , and of the phase from a matrix of composition are shown in Figure 4. Two TTT-diagrams are presented, one obtained from isothermal simulations at the crystallization temperature (dark blue) and one from heating at a rate of followed by holding at (red). For comparison, the TTT-diagram measured upon heating at the same rate (green) and cooling (purple) by flash differential scanning calorimetry (DSC) in [] is included as well as the low-temperature DSC data from [] (light blue).
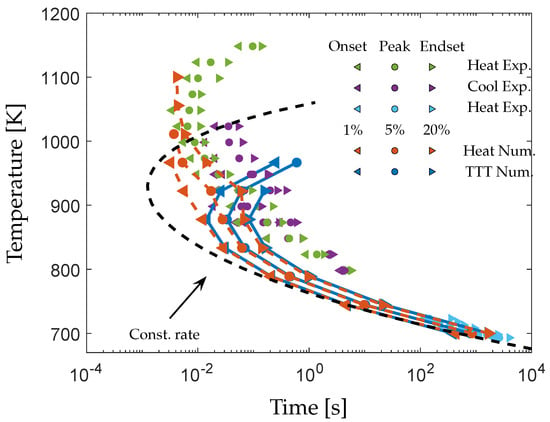
Figure 4.
Numerically obtained TTT-diagrams of the phase from a matrix composition of during heating followed by holding (red) and isothermal simulations (dark blue). The onset, peak and endset of the flash DSC measurements on AMZ4 obtained upon heating (green) and cooling (purple) followed by holding as presented in [] are included for comparison. Low-temperature DSC measurements on AMZ4 are also included []. The black dashed line shows the computed TTT-diagram using the maximum growth rate from Figure 3 as a constant rate.
A quantitative comparison of the TTT-diagrams is difficult as the representative crystalline volume fractions of the DSC peaks are unclear. Nevertheless, the qualitative agreement between the diagrams is good. The simulated TTT-diagrams follow the experimental data over a wide temperature range, which indicates that the predicted nucleation and growth rates are reasonable.
The simulated and the measured TTT-diagrams display an asymmetry between the diagrams obtained upon heating and cooling/isothermal. This is a consequence of the difference in the maximum rate between nucleation and growth. As shown in Figure 3, the maximum nucleation rate occurs at a lower temperature than the maximum growth rate. Thus, heating from the glassy state results in the formation of more nuclei prior to reaching . At low , this effect is negligible as the transformation is dictated by the high nucleation rate, and the diagrams coincide.
However, at higher , the effect becomes significant, and a simulated particle density of is obtained upon heating in comparison to under isothermal conditions at . Consequently, the time to obtain a crystalline volume fraction of at is drastically reduced from to upon heating. This shows that the modeling methodology is capable of predicting the different degrees of crystallization depending on the thermal history. This is a feature of importance in teh modeling of non-isothermal processes, such as additive manufacturing.
The asymmetry between heating and cooling also stresses the importance of the growth mode. For polymorphous growth, the growth rate increases asymptotically as a function of particle size towards a constant value [,], while for diffusion-controlled growth, the growth rate decreases following at large particle sizes (see Figure 2) caused by the depletion of solute elements.
Thus, a polymorphic growth mode results in the more rapid growth of particles formed during heating, which can have a significant effect on the rate of crystallization during cycling thermal processing []. This effect is demonstrated in Figure 4 where TTT-diagrams constructed using the maximum growth rate from Figure 3 as a constant rate are included (black dashed line). The size dependence of the diffusion-controlled growth rate results in longer crystallization times at elevated temperatures where growth has a larger effect on the transformation.
Continuous heating and cooling experiments using DSC are often performed to evaluate crystallization onset temperatures as a measure of alloy glass-forming ability and thermal stability. These are useful for understanding the isochronal crystallization behavior and can be used to obtain measurements of the critical cooling/heating rates.
The modeling of crystallization can be used in a similar manner. Figure 5 shows the numerically determined crystallization onsets for and crystalline volume fraction of the phase from an matrix of composition at various heating and cooling rates. Measured from [,] on AMZ4 are also included. According to the simulations, the critical cooling and heating rates () are upon cooling and upon heating, respectively. The large difference between and further confirms that the model captures the asymmetry in crystallization upon heating and cooling as previously discussed. In general, the crystallization onset temperature from the simulations and the experiments follows the same trend with respect to the applied heating/cooling rate.
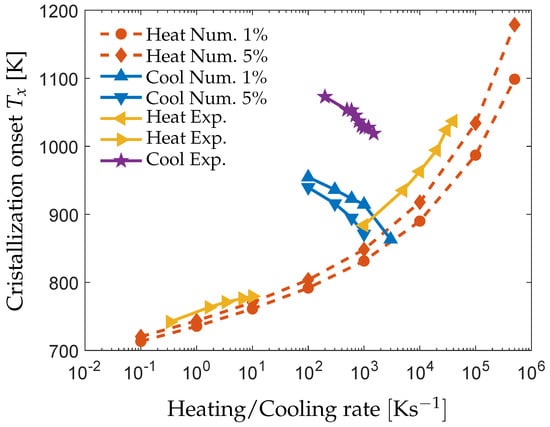
Figure 5.
The numerically obtained crystallization temperatures of the phase from a matrix composition of during continuous heating (red) and cooling (dark blue) rates. The experimentally measured onset temperatures upon heating (yellow) and cooling (purple) [,].
The predicted critical cooling and heating rates of and are higher than the reported critical rates of upon cooling and upon heating [], especially in the case for heating. The large discrepancy in the heating rate is possibly related to the assumption of steady-state nucleation. At high cooling rates, transient nucleation effects may lower the nucleation rate by several orders of magnitude below the steady-state nucleation rate, especially at lower temperatures [,].
These effects remain upon heating of the material, for which the nucleation rate at lower temperatures shows a more pronounced effect on the overall rate of crystallization in comparison to cooling. This would result in the formation of less nuclei upon heating and a lower value of . Further, a difference in order of is observed in between the simulations and experiments upon cooling in Figure 5.
The experiments in [] where performed on industrial grade AMZ4, which contains a relatively high content of oxygen. Oxygen impurity is known to significantly decrease the undercooling of Zr-based MGs as oxygen-enriched crystals form and serve as heterogeneous nucleation sites for further crystallization [,,]. In the cooling simulations, no nuclei are present prior to cooling, and a large difference in undercooling between simulations and experiments is therefore expected.
The associated values of the residual particle density N, mean radius and crystalline volume fraction f from the critical cooling/heating simulations are shown in Table 2. Cooling at resulted in a high density of very fine nanocrystals but no substantial crystalline volume fraction. Such glass has recently been termed self-doped glass (SDG) and shows an accelerated crystallization process upon heating []. To verify this, heating simulations at were performed using the particle-size distribution from continuous cooling simulations at as well as as initial conditions.

Table 2.
The reported experimental and computed critical cooling and heating rates as well as the predicted associated residual particle density N, mean radius and crystalline volume fraction f.
The results are presented in Table 3. The material cooled and heated at showed no crystallization. In contrast, the material cooled at followed by heating at showed pronounced crystallization resulting from the growth of pre-existing nanocrystals. As a result, is required to avoid crystallization upon heating of the self-doped glass, which is in agreement with recent experimental findings []. As shown in Table 2 and Table 3, the particle density of the self-doped glass decreased by roughly two orders of magnitude because of the particle dissolution upon heating.

Table 3.
The computed residual particle density N, mean radius and crystalline volume fraction f obtained from cooling at given followed by heating at .
This happens when the critical size changes more rapidly with temperature than the particle-size distribution. Therefore, a high is required to fully dissolve the nuclei upon heating. These results demonstrate the role of the different, but equally important, contributions of nucleation, growth and dissolution during sequential cooling and heating of metallic glasses. It also shows that numerical models that tracks the evolution of particle-size distribution can capture these mechanisms and be a powerful tool to model crystallization during non-isothermal processing of metallic glasses.
4. Conclusions
A modeling strategy describing the nucleation, growth and dissolution of intermetallic crystals in the Al-Cu-Zr glass-forming system was presented. The model is coupled to a CALPHAD database, thereby, allowing for composition- and temperature-dependent thermodynamic properties and accounting for non-ideal mixing interactions of the deeply undercooled liquid phase. The diffusion-controlled growth rate was obtained by solving the non-linear equilibrium equations at the interface between the matrix and the particle. The model allows for solubility in both the solid and liquid phases and is valid under high supersaturation.
The modeling strategy can be used to predict the particle number density distribution, volume fraction and changes in composition as a function of time for a certain phase during a specific heat treatment. The capability of the model was studied by application to crystallization in the Al-Cu-Zr system. The crystallization of intermetallic phases from the undercooled liquid phase were simulated under isothermal as well as non-isothermal conditions.
The model accurately predicted the asymmetry in the critical heating/cooling rate and the formation, growth and dissolution during cooling and heating. The obtained time–temperature transformation and continuous-cooling/heating transformation diagrams agree satisfactorily with the experimental data over a wide temperature range, thus, demonstrating the predictability of the modeling approach.
Author Contributions
Conceptualization, A.E. and M.F.; methodology, A.E. and M.F.; software, A.E.; validation, A.E.; formal analysis, A.E.; investigation, A.E.; resources, M.F.; data curation, A.E.; writing—original draft preparation, A.E.; writing—review and editing, A.E. and M.F.; visualization, A.E.; supervision, M.F.; project administration, M.F.; funding acquisition, M.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was performed with financial support from the Swedish Foundation for Strategic Research (SSF) through the project Additive Manufacturing–Development of Process and Material [grant number GMT14-0048]; and the strategic innovation program LIGHTer provided by Vinnova, Sweden’s Innovation Agency [grant number 2020-04526].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MG | Metallic glass |
| CALPHAD | Computer Coupling of Phase Diagrams and Thermochemistry |
| CNT | Classical nucleation theory |
| TTT | Time temperature transformation |
| CHT | Continuous heating transformation |
| CCT | Continuous cooling transformation |
| NKW | Numerical Kampmann–Wagner |
| DSC | Differential scanning calorimetry |
References
- Suryanarayana, C.; Inoue, A. Bulk Metallic Glasses, 1st ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Qiao, J.; Jia, H.; Liaw, P.K. Metallic glass matrix composites. Mater. Sci. Eng. R Rep. 2016, 100, 1–69. [Google Scholar] [CrossRef] [Green Version]
- Gheiratmand, T.; Hosseini, H.R. Finemet nanocrystalline soft magnetic alloy: Investigation of glass forming ability, crystallization mechanism, production techniques, magnetic softness and the effect of replacing the main constituents by other elements. J. Magn. Magn. Mater. 2016, 408, 177–192. [Google Scholar] [CrossRef]
- Li, F.C.; Liu, T.; Zhang, J.Y.; Shuang, S.; Wang, Q.; Wang, A.D.; Wang, J.G.; Yang, Y. Amorphous–nanocrystalline alloys: Fabrication, properties, and applications. Mater. Today Adv. 2019, 4, 100027. [Google Scholar] [CrossRef]
- Inoue, A.; Fan, C.; Saida, J.; Zhang, T. High-strength Zr-based bulk amorphous alloys containing nanocrystalline and nanoquasicrystalline particles. Sci. Technol. Adv. Mater. 2000, 1, 73–86. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Zhang, W.; Xie, G.Q.; Louzguine-Luzgin, D.V.; Inoue, A. Stable flowing of localized shear bands in soft bulk metallic glasses. Acta Mater. 2010, 58, 904–909. [Google Scholar] [CrossRef]
- Uhlmann, D.R. A Kinetic Treatment of Glass Formation. J. Non-Cryst. Solids 1972, 7, 337–348. [Google Scholar] [CrossRef]
- Morris, D.G. Glass formation and crystallisation in NiSiB alloys-I. Glass formation-test of the “avoidance of crystallisation” approach. Acta Metall. 1983, 31, 1479–1489. [Google Scholar] [CrossRef]
- Gránásy, L. Quantitative analysis of the classical nucleation theory on glass- forming alloys. J. Non-Cryst. Solids 1993, 158, 514–518. [Google Scholar] [CrossRef]
- Thompson, C.V.; Spaepen, F. On the approximation of the free energy change on crystallization. Acta Metall. 1979, 27, 1855–1859. [Google Scholar] [CrossRef]
- Ge, L.; Hui, X.; Wang, E.R.; Chen, G.L.; Arroyave, R.; Liu, Z.K. Prediction of the glass forming ability in Cu-Zr binary and Cu-Zr-Ti ternary alloys. Intermetallics 2008, 16, 27–33. [Google Scholar] [CrossRef]
- Yang, W.; Liu, F.; Liu, H.; Wang, H.F.; Chen, Z.; Yang, G.C. Glass forming ability in Cu – Zr binary alloy: Effect of nucleation mode. J. Alloys Compd. 2009, 484, 702–707. [Google Scholar] [CrossRef]
- Tanner, L.E.; Ray, R. Metallic glass formation and properties in Zr and Ti alloyed with Be-I the binary Zr-Be and Ti-Be systems. Acta Metall. 1979, 27, 1727–1747. [Google Scholar] [CrossRef]
- Masuhr, A.; Waniuk, T.A.; Busch, R.; Johnson, W.L. Time Scales for Viscous Flow, Atomic Transport, and Crystallization in the Liquid and Supercooled Liquid States of Zr41.2Ti13.8Cu12.5Ni10.0Be22.5. Phys. Rev. Lett. 1988, 61, 2291–2293. [Google Scholar]
- Ericsson, A.; Pacheco, V.; Sahlberg, M.; Lindwall, J.; Hallberg, H.; Fisk, M. Transient nucleation in selective laser melting of Zr-based bulk metallic glass. Mater. Des. 2020, 195, 108958. [Google Scholar] [CrossRef]
- Köster, U.; Herold, U. Crystallization of metallic glasses. In Glassy Metals 1; Springer: Berlin/Heidelberg, Germany, 1981; pp. 225–259. [Google Scholar] [CrossRef]
- Inoue, A.; Kawase, D.; Tsai, A.P. Stability and transformation to crystalline phases of amorphous Zr-Al-Cu alloys with significant supercooled liquid region. Mater. Sci. Eng. A 1994, 178, 255–263. [Google Scholar] [CrossRef]
- Hono, K.; Zhang, Y.; Tsai, A.P.; Inoue, A.; Sakurai, T. Solute partitioning in partially crystallized Al-Ni-Cu(-Cu) metallic glass. Scr. Metall. 1995, 32, 191–196. [Google Scholar] [CrossRef]
- Pekarskaya, E.; Löffler, J.F.; Johnson, W.L. Microstructural studies of crystallization of a Zr-based bulk metallic glass. Acta Mater. 2003, 51, 4045–4057. [Google Scholar] [CrossRef]
- Fan, C.; Yue, X.; Inoue, A.; Liu, C.T.; Shen, X.; Liaw, P.K. Recent topics on the structure and crystallization of al-based glassy alloys. Mater. Res. 2019, 22, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Xiao, H.; Li, S.; Xu, L.; Zhao, B.; Zhai, Q.; Gao, Y. Revealing the crystallization kinetics and phase transitions in Mg65Zn30Ca5 metallic glass by nanocalorimetry. J. Alloys Compd. 2021, 899, 163353. [Google Scholar] [CrossRef]
- Baricco, M.; Palumbo, M. Thermodynamic and kinetic modelling of primary crystallisation in amorphous alloys. J. Metastable Nanocrystalline Mater. 2004, 20–21, 415–424. [Google Scholar] [CrossRef]
- Palumbo, M.; Baricco, M. Modelling of primary bcc-Fe crystal growth in a Fe85B15 amorphous alloy. Acta Mater. 2005, 53, 2231–2239. [Google Scholar] [CrossRef]
- Nestler, B.; Danilov, D.; Bracchi, A.; Huang, Y.L.; Niermann, T.; Seibt, M.; Schneider, S. A metallic glass composite: Phase-field simulations and experimental analysis of microstructure evolution. Mater. Sci. Eng. A 2007, 452–453, 8–14. [Google Scholar] [CrossRef]
- Chen, Q.; Jeppsson, J.; Ågren, J. Analytical treatment of diffusion during precipitate growth in multicomponent systems. Acta Mater. 2008, 56, 1890–1896. [Google Scholar] [CrossRef]
- Myhr, O.R.; Grong, O. Modelling of non-isothermal transformations in alloys containing a particle distribution. Acta Mater. 2000, 48, 1605–1615. [Google Scholar] [CrossRef]
- Zhou, C.; Guo, C.; Li, C.; Du, Z. Thermodynamic assessment of the phase equilibria and prediction of glass-forming ability of the Al–Cu–Zr system. J. Non-Cryst. Solids 2017, 461, 47–60. [Google Scholar] [CrossRef]
- Kelton, K.F.; Greer, A. Nucleation in Condensed Matter: Applications in Materials and Biology, 1st ed.; Pergamon: Oxford, UK, 2010. [Google Scholar] [CrossRef]
- Rheingans, B.; Mittemeijer, E.J. Modelling precipitation kinetics: Evaluation of the thermodynamics of nucleation and growth. Calphad Comput. Coupling Phase Diagr. Thermochem. 2015, 50, 49–58. [Google Scholar] [CrossRef]
- Philippe, T.; Bonvalet, M.; Blavette, D. Kinetic theory of diffusion-limited nucleation. J. Chem. Phys. 2016, 144, 204501. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Blodgett, M.E.; Egami, T.; Nussinov, Z.; Kelton, K.F. Proposal for universality in the viscosity of metallic liquids. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Hembree, W. High Temperature Rheology of Zr-Based Bulk Metallic Glass Forming Liquids. Doctorial Thesis, Universität des Saarlandes, Saarbrücken, Germany, 2015. [Google Scholar]
- Kozeschnik, E. Modeling Solid-State Precipitation; Momentum Press: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Dinsdale, A.T. Sgte data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Palumbo, M.; Battezzati, L. Thermodynamics and kinetics of metallic amorphous phases in the framework of the CALPHAD approach. Calphad Comput. Coupling Phase Diagr. Thermochem. 2008, 32, 295–314. [Google Scholar] [CrossRef]
- Lukas, H.L.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The Calphad Method; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Du, Q.; Poole, W.J.; Wells, M.A. A mathematical model coupled to CALPHAD to predict precipitation kinetics for multicomponent aluminum alloys. Acta Mater. 2012, 60, 3830–3839. [Google Scholar] [CrossRef]
- Turnbull, D. Correlation of Liquid-Solid Interfacial Energies Calculated from Supercooling of Small Droplets. J. Chem. Phys. 1950, 18, 769. [Google Scholar] [CrossRef]
- Gránásy, L.; Tóth, G.I.; Warren, J.A.; Podmaniczky, F.; Tegze, G.; Rátkai, L.; Pusztai, T. Phase-field modeling of crystal nucleation in undercooled liquids—A review. Prog. Mater. Sci. 2019, 106, 100569. [Google Scholar] [CrossRef]
- Tolman, R.C. The effect of droplet size on surface tension. J. Chem. Phys. 1949, 17, 333–337. [Google Scholar] [CrossRef] [Green Version]
- Kampmann, R.; Wagner, R. Decomposition of Alloys: The Early Stages. (Chapter Kinetics of Precipitation in Metastable Binary Alloys—Theory and Application to Cu-1.9 at % and Ni-14 at% Al). 1984. Available online: https://www.sciencedirect.com/science/article/pii/B9780080316512500185?via%3Dihub (accessed on 15 May 2022).
- Perez, M.; Dumont, M.; Acevedo-Reyes, D. Implementation of classical nucleation and growth theories for precipitation. Acta Mater. 2008, 56, 2119–2132. [Google Scholar] [CrossRef]
- Heraeus AMLOY Technologies. Material datasheet: AMLOY-ZR01. Available online: https://www.heraeus.com/media/media/group/media_group/products/amorphous_metals/datasheets_1/Datasheet_AMLOY-ZR01~2.pdf (accessed on 15 May 2022).
- Pacheco, V.; Karlsson, D.; Marattukalam, J.J.; Stolpe, M.; Hjörvarsson, B.; Jansson, U.; Sahlberg, M. Thermal stability and crystallization of a Zr-based metallic glass produced by suction casting and selective laser melting. J. Alloys Compd. 2020, 825, 153995. [Google Scholar] [CrossRef]
- Ericsson, A.; Pacheco, V.; Marattukalam, J.J.; Dalgliesh, R.M.; Rennie, A.R.; Fisk, M.; Sahlberg, M. Crystallization of a Zr-based metallic glass produced by laser powder bed fusion and suction casting. J.-Non-Cryst. Solids 2021, 571, 120891. [Google Scholar] [CrossRef]
- Sohrabi, N.; Schawe, J.E.; Jhabvala, J.; Löffler, J.F.; Logé, R.E. Critical crystallization properties of an industrial-grade Zr-based metallic glass used in additive manufacturing. Scr. Mater. 2021, 199, 113861. [Google Scholar] [CrossRef]
- Sohrabi, N.; Jhabvala, J.; Log, R.E. Additive Manufacturing of Bulk Metallic Glasses—Process, Challenges and Properties: A Review. Metals 2021, 11, 1279. [Google Scholar] [CrossRef]
- Best, J.P.; Evenson, Z.; Yang, F.; Dippel, A.C.; Stolpe, M.; Gutowski, O.; Hasib, M.T.; Li, X.; Kruzic, J.J. Structural periodicity in laser additive manufactured Zr-based bulk metallic glass. Appl. Phys. Lett. 2019, 115, 031902. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, L.M.; Ma, M.Z.; Binder, S.; Volkmann, T.; Herlach, D.M.; Wang, J.S.; Xue, Q.G.; Tian, Y.J.; Liu, R.P. Diffusion-controlled crystal growth in deeply undercooled melt on approaching the glass transition. Phys. Rev. B-Condens. Matter Mater. Phys. 2011, 83. [Google Scholar] [CrossRef] [Green Version]
- Ericsson, A.; Fisk, M.; Hallberg, H. Modeling of nucleation and growth in glass-forming alloys using a combination of classical and phase-field theory. Comput. Mater. Sci. 2019, 165, 167–179. [Google Scholar] [CrossRef]
- Kelton, K.F.; Greer, A. Transient nucleation effects in glass formation. J. Non-Cryst. Solids 1986, 79, 295–309. [Google Scholar] [CrossRef]
- Ouyang, D.; Zhang, P.; Zhang, C.; Liu, L. Understanding of crystallization behaviors in laser 3D printing of bulk metallic glasses. Appl. Mater. Today 2021, 23, 100988. [Google Scholar] [CrossRef]
- Lin, X.; Johnson, W.; Rhim, W. Effect of Oxygen Impurity on Crystallization of an Undercooled Bulk Glass Forming Zr-Ti-Cu-Ni-Al Alloy. Mater. Trans. 1997, 38, 473–477. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.T.; Chisholm, M.F.; Miller, M.K. Oxygen impurity and microalloying effect in a Zr-based bulk metallic glass alloy. Intermetallics 2002, 10, 1105–1112. [Google Scholar] [CrossRef]
- Jonas, I.; Hembree, W.; Yang, F.; Busch, R.; Meyer, A. Industrial grade versus scientific pure: Influence on melt properties. Appl. Phys. Lett. 2018, 112, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Schawe, J.E.; Löffler, J.F. Existence of multiple critical cooling rates which generate different types of monolithic metallic glass. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).