Molecular Dynamics Simulations of Xe Behaviors at the Grain Boundary in UO2
Abstract
:1. Introduction
2. Simulation Method
2.1. Interatomic Potential
2.2. Model Building
2.3. MD Simulation Setup
3. Results
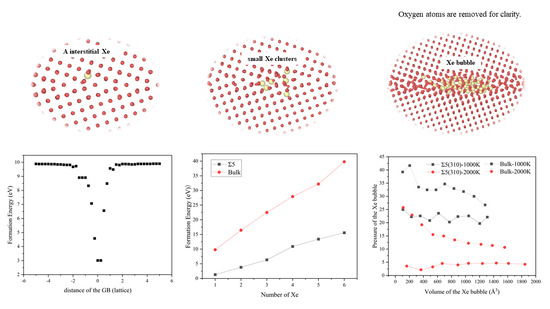
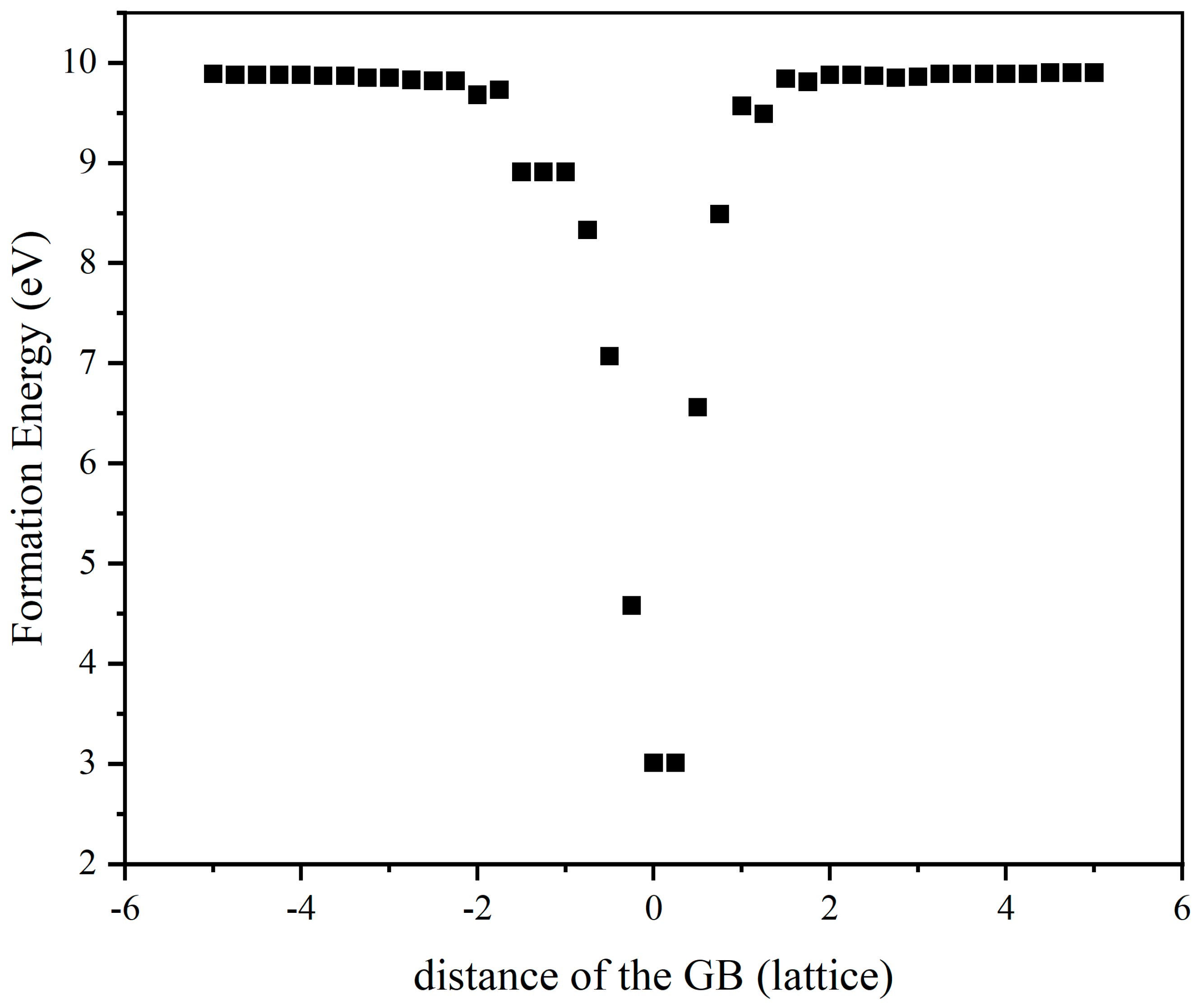
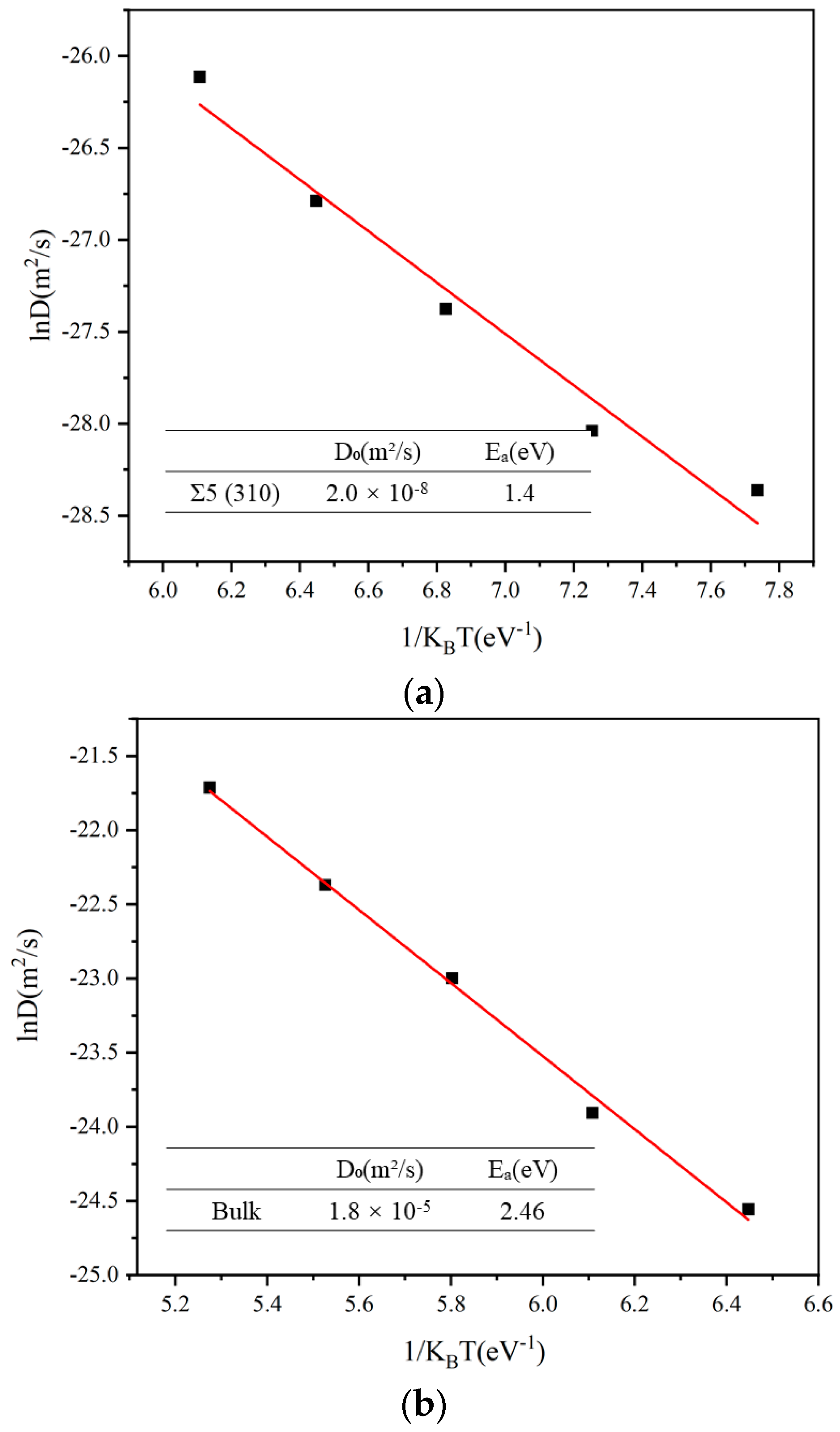
3.1. Formation Energy and Diffusion Behavior of a Single Xe Atom at the GB
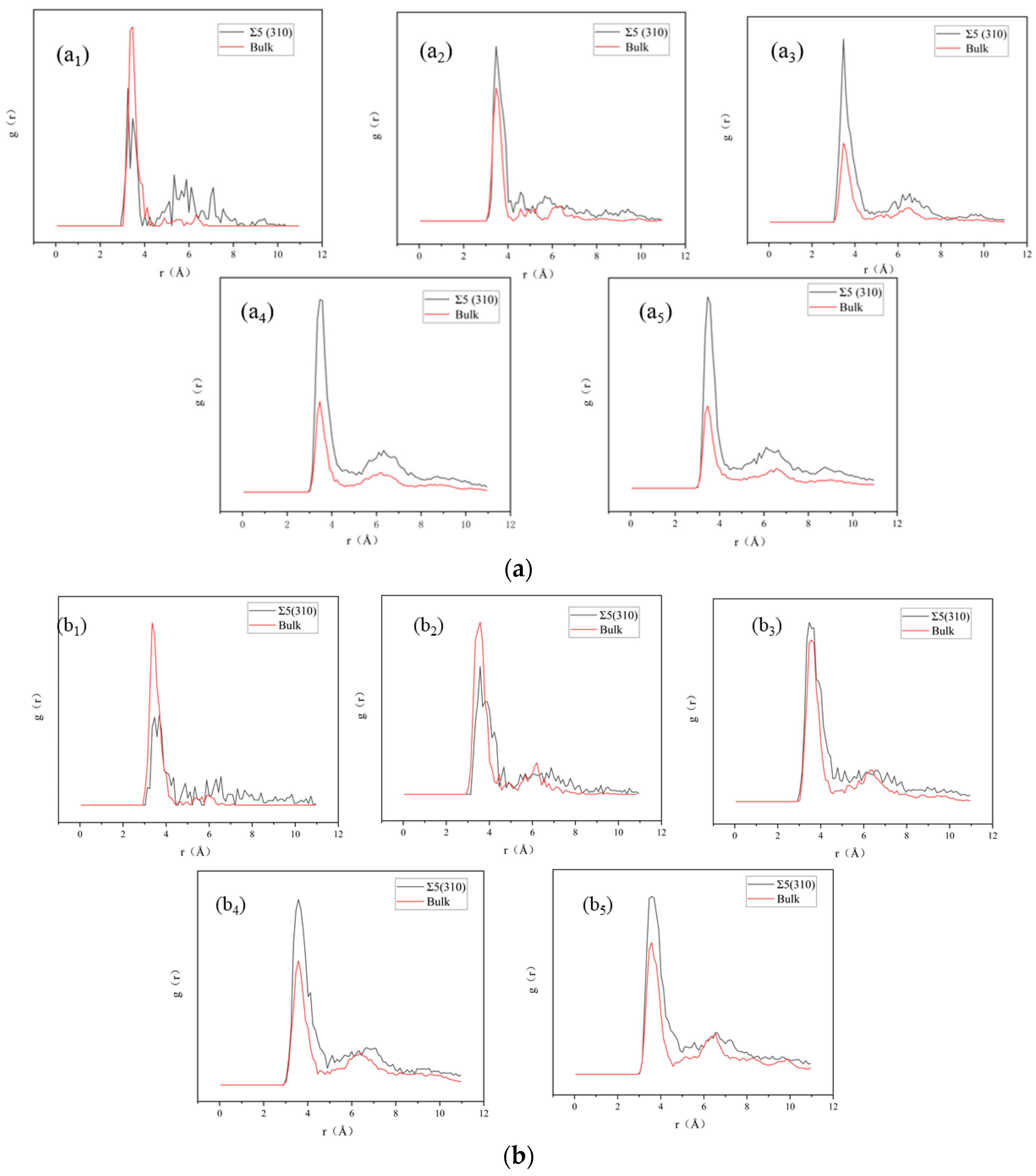
3.2. Formation Energies of Small Xe Clusters at the GB
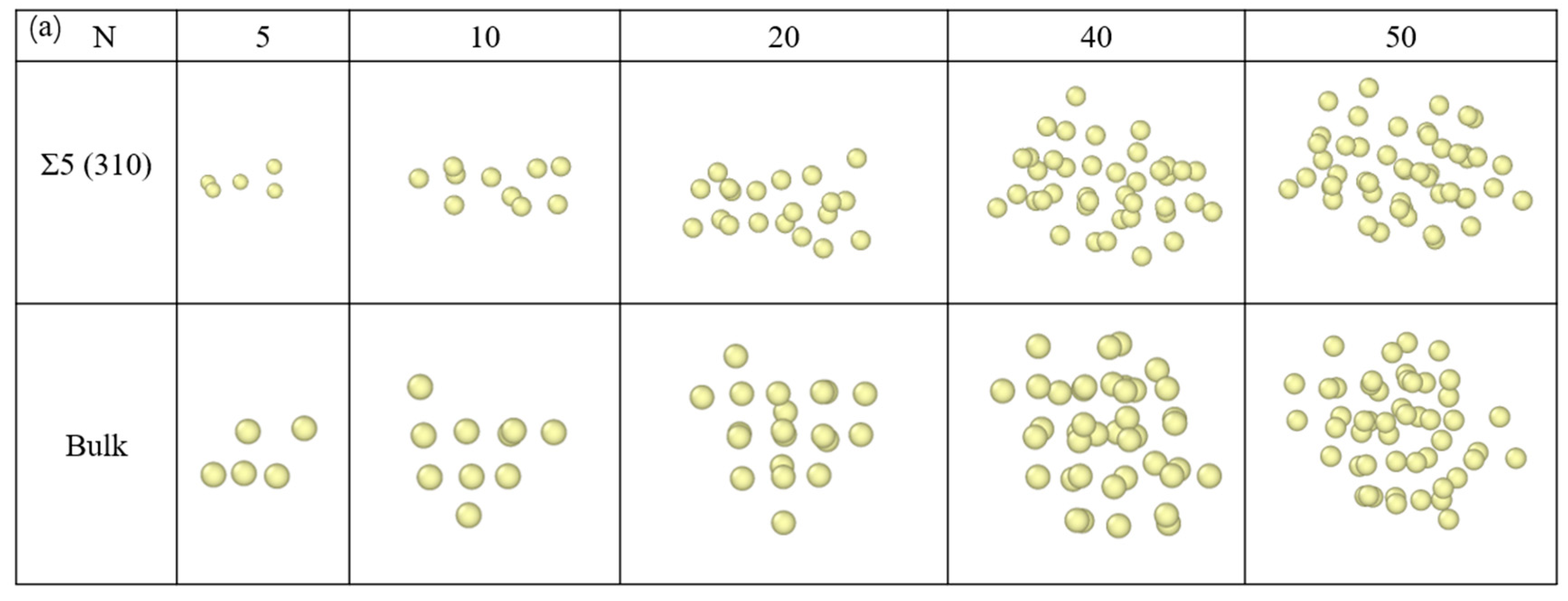
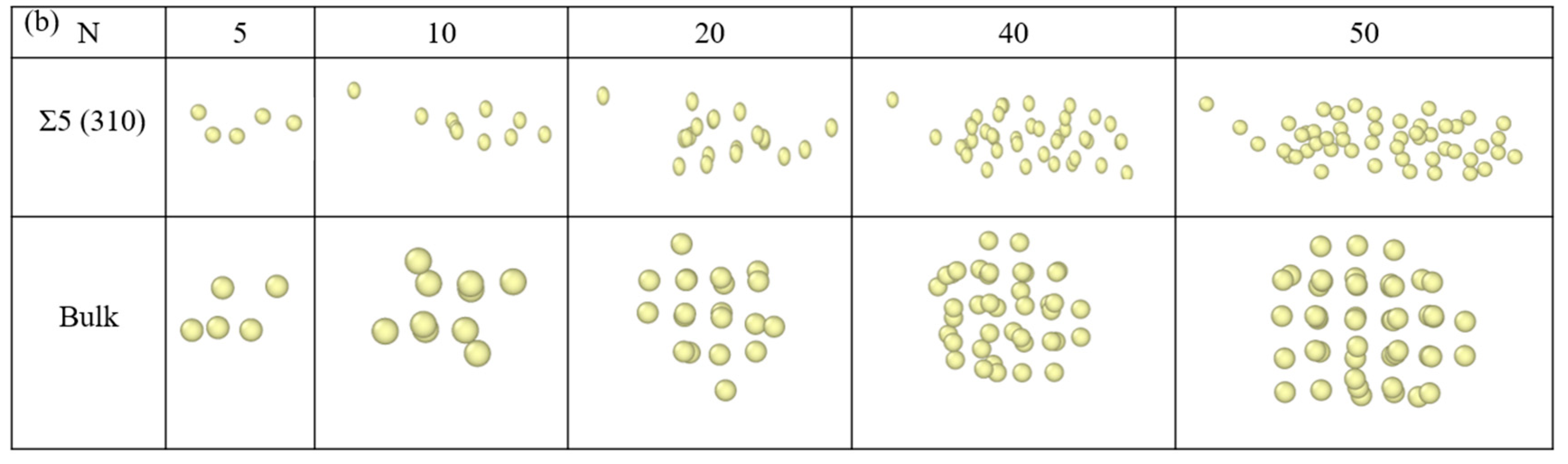
3.3. Nucleation of Xe Bubbles at the GB
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Atomic Energy Agency. Thermophysical Properties Database of Materials for Light Water Reactors and Heavy Water Reactors; IAEA TECDOC Series No. 1496; International Atomic Energy Agency: Vienna, Austria, 2006. [Google Scholar]
- Turnbull, J. The distribution of intragranular fission gas bubbles in UO2 during irradiation. J. Nucl. Mater. 1971, 38, 203–212. [Google Scholar] [CrossRef]
- Yang, L.; Wirth, B. Evolution of pressurized xenon bubble and response of uranium dioxide matrix: A molecular dynamics study. J. Nucl. Mater. 2021, 544, 152730. [Google Scholar] [CrossRef]
- Xiao-Feng, T.; Chong-Sheng, L.; Zheng-He, Z.; Tao, G. Molecular dynamics simulation of collective behaviour of Xe in UO2. Chin. Phys. B 2010, 19, 057102. [Google Scholar] [CrossRef]
- Olander, D.R. Fundamental Aspects of nuclear Reactor Fuel Elements; TID-26711-Pl (Atomic Energy Commission, 1976); California University: Berkeley, CA, USA, 1976. [Google Scholar] [CrossRef]
- Jeon, B.; Asta, M.; Valone, S.M.; Gronbech-Jensen, N. Simulation of ion-track ranges in uranium oxide. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 2688–2693. [Google Scholar] [CrossRef] [Green Version]
- Govers, K.; Lemehov, S.; Verwerft, M. On the solution and migration of single Xe atoms in uranium dioxide–An interatomic potentials study. J. Nucl. Mater. 2010, 405, 252–260. [Google Scholar] [CrossRef]
- Liu, X.-Y.; Andersson, D. Molecular dynamics study of fission gas bubble nucleation in UO2. J. Nucl. Mater. 2015, 462, 8–14. [Google Scholar] [CrossRef] [Green Version]
- Nerikar, P.V.; Rudman, K.; Desai, T.G.; Byler, D.; Unal, C.; McClellan, K.J.; Phillpot, S.R.; Sinnott, S.B.; Peralta, P.; Uberuaga, B.P. Grain boundaries in uranium dioxide: Scanning electron microscopy experiments and atomistic simulations. J. Am. Ceram. Soc. 2011, 94, 1893–1900. [Google Scholar] [CrossRef]
- Ray, I.; Thiele, H. Transmission electron microscopy study of fission product behaviour in high burnup UO2. J. Nucl. Mater. 1992, 188, 90–95. [Google Scholar] [CrossRef]
- Djourelov, N.; Marchand, B.; Marinov, H.; Moncoffre, N.; Pipon, Y.; Nédélec, P.; Toulhoat, N.; Sillou, D. Variable energy positron beam study of Xe-implanted uranium oxide. J. Nucl. Mater. 2013, 432, 287–293. [Google Scholar] [CrossRef]
- Sabathier, C.; Vincent, L.; Garcia, P.; Garrido, F.; Carlot, G.; Thome, L.; Martin, P.; Valot, C. In situ TEM study of temperature-induced fission product precipitation in UO2. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2008, 266, 3027–3032. [Google Scholar] [CrossRef]
- Niemiec, M.; Gadomski, A.; Łuczka, J.; Schimansky-Geier, L. Phase transformation kinetics in d-dimensional grains-containing systems: Diffusion-type model. Phys. A Stat. Mech. Its Appl. 1998, 248, 365–378. [Google Scholar] [CrossRef]
- Gadomski, A. Kinetic Approach to the Nucleation-and-Growth Phase Transition in Complex Systems. Nonlinear Phenom. Complex Syst. Minsk. 2000, 3, 321–352. [Google Scholar]
- Tschopp, M.A.; Horstemeyer, M.; Gao, F.; Sun, X.; Khaleel, M. Energetic driving force for preferential binding of self-interstitial atoms to Fe grain boundaries over vacancies. Scr. Mater. 2011, 64, 908–911. [Google Scholar] [CrossRef] [Green Version]
- Lejcek, P. Grain Boundary Segregation in Metals; Springer Science & Business Media: Cham, Switzerland, 2010; Volume 136. [Google Scholar]
- Van Brutzel, L.; Vincent-Aublant, E. Grain boundary influence on displacement cascades in UO2: A molecular dynamics study. J. Nucl. Mater. 2008, 377, 522–527. [Google Scholar] [CrossRef]
- Zhang, Y.; Millett, P.C.; Tonks, M.R.; Bai, X.-M.; Biner, S.B. Molecular dynamics simulations of intergranular fracture in UO2 with nine empirical interatomic potentials. J. Nucl. Mater. 2014, 452, 296–303. [Google Scholar] [CrossRef]
- Williams, N.R.; Molinari, M.; Parker, S.C.; Storr, M.T. Atomistic investigation of the structure and transport properties of tilt grain boundaries of UO2. J. Nucl. Mater. 2015, 458, 45–55. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Gao, N.; Hu, W.; Xiao, S.; Gao, F.; Deng, H. Atomistic simulations of the interaction between transmutation-produced Re and grain boundaries in tungsten. Comput. Mater. Sci. 2020, 173, 109412. [Google Scholar] [CrossRef]
- Gao, N.; Ghoniem, A.; Gao, X.; Luo, P.; Wei, K.; Wang, Z. Molecular dynamics simulation of Cu atoms interaction with symmetrical grain boundaries of BCC Fe. J. Nucl. Mater. 2014, 444, 200–205. [Google Scholar] [CrossRef]
- Li, X.; Liu, W.; Xu, Y.; Liu, C.; Fang, Q.; Pan, B.; Chen, J.-L.; Luo, G.-N.; Wang, Z. An energetic and kinetic perspective of the grain-boundary role in healing radiation damage in tungsten. Nucl. Fusion 2013, 53, 123014. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Govers, K.; Lemehov, S.; Hou, M.; Verwerft, M. Comparison of interatomic potentials for UO2. Part I: Static calculations. J. Nucl. Mater. 2007, 366, 161–177. [Google Scholar] [CrossRef]
- Cooper, M.; Rushton, M.; Grimes, R. A many-body potential approach to modelling the thermomechanical properties of actinide oxides. J. Phys. Condens. Matter 2014, 26, 105401. [Google Scholar] [CrossRef]
- Jelea, A.; Pellenq, R.-M.; Ribeiro, F. An atomistic modeling of the xenon bubble behavior in the UO2 matrix. J. Nucl. Mater. 2014, 444, 153–160. [Google Scholar] [CrossRef]
- Thompson, A.E.; Meredig, B.; Wolverton, C. An improved interatomic potential for xenon in UO2: A combined density functional theory/genetic algorithm approach. J. Phys. Condens. Matter 2014, 26, 105501. [Google Scholar] [CrossRef]
- Brillant, G.; Gupta, F.; Pasturel, A. Fission products stability in uranium dioxide. J. Nucl. Mater. 2011, 412, 170–176. [Google Scholar] [CrossRef]
- Chartier, A.; Van Brutzel, L.; Freyss, M. Atomistic study of stability of xenon nanoclusters in uranium oxide. Phys. Rev. B 2010, 81, 174111. [Google Scholar] [CrossRef]
- Yun, Y.; Kim, H.; Kim, H.; Park, K. Atomic diffusion mechanism of Xe in UO2. J. Nucl. Mater. 2008, 378, 40–44. [Google Scholar] [CrossRef]
- Basak, C.; Sengupta, A.; Kamath, H. Classical molecular dynamics simulation of UO2 to predict thermophysical properties. J. Alloy. Compd. 2003, 360, 210–216. [Google Scholar] [CrossRef]
- Geng, H.; Chen, Y.; Kaneta, Y.; Kinoshita, M. Molecular dynamics study on planar clustering of xenon in UO2. J. Alloy. Compd. 2008, 457, 465–471. [Google Scholar]
- Morelon, N.-D.; Ghaleb, D.; Delaye, J.-M.; Van Brutzel, L. A new empirical potential for simulating the formation of defects and their mobility in uranium dioxide. Philos. Mag. 2003, 83, 1533–1555. [Google Scholar]
- Cooper, M.; Kuganathan, N.; Burr, P.; Rushton, M.; Grimes, R.; Stanek, C.; Andersson, D. Development of Xe and Kr empirical potentials for CeO2, ThO2, UO2 and PuO2, combining DFT with high temperature MD. J. Phys. Condens. Matter 2016, 28, 405401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scheiber, D.; Pippan, R.; Puschnig, P.; Romaner, L. Ab initio calculations of grain boundaries in bcc metals. Model. Simul. Mater. Sci. Eng. 2016, 24, 035013. [Google Scholar] [CrossRef]
- Zheng, H.; Li, X.-G.; Tran, R.; Chen, C.; Horton, M.; Winston, D.; Persson, K.A.; Ong, S.P. Grain boundary properties of elemental metals. Acta Mater. 2020, 186, 40–49. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, T. Grain boundary engineering: Historical perspective and future prospects. J. Mater. Sci. 2011, 46, 4095–4115. [Google Scholar] [CrossRef]
- Randle, V. Grain boundary engineering: An overview after 25 years. Mater. Sci. Technol. 2010, 26, 253–261. [Google Scholar] [CrossRef]
- Lee, S.B.; Sigle, W.; Kurtz, W.; Rühle, M. Temperature dependence of faceting in Σ5 (310)[001] grain boundary of SrTiO3. Acta Mater. 2003, 51, 975–981. [Google Scholar] [CrossRef]
- He, H.; Ma, S.; Wang, S. Survey of Grain Boundary Energies in Tungsten and Beta-Titanium at High Temperature. Materials 2021, 15, 156. [Google Scholar] [CrossRef]
- Borde, M.; Germain, A.; Bourasseau, E. Molecular dynamics study of UO2 symmetric tilt grain boundaries around [001] axis. J. Am. Ceram. Soc. 2021, 104, 2879–2893. [Google Scholar] [CrossRef]
- Galvin, C.O.; Cooper, M.W.D.; Fossati, P.; Stanek, C.R.; Grimes, R.W.; Andersson, D. Pipe and grain boundary diffusion of He in UO2. J. Phys. Condens. Matter 2016, 28, 405002. [Google Scholar] [CrossRef]
- Bourasseau, E.; Mouret, A.; Fantou, P.; Iltis, X.; Belin, R.C. Experimental and simulation study of grain boundaries in UO2. J. Nucl. Mater. 2019, 517, 286–295. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Dillon, S.J.; Harmer, M.P. Multiple grain boundary transitions in ceramics: A case study of alumina. Acta Mater. 2007, 55, 5247–5254. [Google Scholar] [CrossRef]
- Sheppard, D.; Terrell, R.; Henkelman, G. Optimization methods for finding minimum energy paths. J. Chem. Phys. 2008, 128, 134106. [Google Scholar] [CrossRef] [Green Version]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef] [Green Version]
- Henkelman, G.; Jónsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef] [Green Version]
- Rycroft, C.H.; Grest, G.S.; Landry, J.W.; Bazant, M.Z. Analysis of granular flow in a pebble-bed nuclear reactor. Phys. Rev. E 2006, 74, 021306. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Gao, F.; Kurtz, R.J.; Zu, X.; Peng, S.; Long, X.; Zhou, X. Effects of local structure on helium bubble growth in bulk and at grain boundaries of bcc iron: A molecular dynamics study. Acta Mater. 2015, 97, 86–93. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Gao, F.; Deng, H.-Q.; Liu, B.; Hu, W.-Y.; Sun, X. Migration of defect clusters and xenon-vacancy clusters in uranium dioxide. Int. J. Mod. Phys. B 2014, 28, 1450120. [Google Scholar] [CrossRef]
- Thompson, A.E.; Wolverton, C. First-principles study of noble gas impurities and defects in UO2. Phys. Rev. B 2011, 84, 134111. [Google Scholar] [CrossRef]
- Yun, Y.; Eriksson, O.; Oppeneer, P.M.; Kim, H.; Park, K. First-principles theory for helium and xenon diffusion in uranium dioxide. J. Nucl. Mater. 2009, 385, 364–367. [Google Scholar] [CrossRef]
- Ichinomiya, T.; Uberuaga, B.P.; Sickafus, K.E.; Nishiura, Y.; Itakura, M.; Chen, Y.; Kaneta, Y.; Kinoshita, M. Temperature accelerated dynamics study of migration process of oxygen defects in UO2. J. Nucl. Mater. 2009, 384, 315–321. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Y.-H.; Zhou, H.-B.; Deng, H.; Lu, G.-H. Segregation and aggregation of rhenium in tungsten grain boundary: Energetics, configurations and strengthening effects. J. Nucl. Mater. 2020, 528, 151867. [Google Scholar] [CrossRef]
- Parfitt, D.C.; Grimes, R.W. Predicting the probability for fission gas resolution into uranium dioxide. J. Nucl. Mater. 2009, 392, 28–34. [Google Scholar] [CrossRef]
- Nogita, K.; Une, K. High resolution TEM observation and density estimation of Xe bubbles in high burnup UO2 fuels. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1998, 141, 481–486. [Google Scholar] [CrossRef]
- White, R.J. The development of grain-face porosity in irradiated oxide fuel. J. Nucl. Mater. 2004, 325, 61–77. [Google Scholar] [CrossRef]


| Basak/Geng | Morelon/Chartier | Basak/IPR | Morelon/IPR | CRG/IPR | CRG/Cooper | DFT | |
|---|---|---|---|---|---|---|---|
| 22.73 | 11.94 | 9.68 | 8.32 | 9.79 | 11.70 | 9.73 [27] 9.71 [28] 9.7–12.0 [26] | |
| 5.76 | 5.31 | 1.84 | 0.70 | 1.72 | 3.60 | 2.0–5.8 [26] 1.95 [28] | |
| 20.55 | 9.31 | 8.41 | 7.17 | 7.96 | 8.26 | 7.5–9.1 [26] 7.85 [28] | |
| 5.32 | 4.98 | 1.52 | 0.61 | 1.56 | 2.96 | 1.6 [26] 1.55 [28] | |
| 20.77 | Unstable | 11.89 | 10.76 | 10.29 | 12.27 | 11.33 [29] | |
| (1) | 4.82 | 4.33 | 0.91 | 0.48 | 0.95 | 1.99 | 1.06 [27] 1.2 [29] |
| (2) | 4.92 | 4.77 | 1.53 | 0.67 | 1.68 | 3.02 | 1.83 [27] 1.8 [29] |
| (3) | 5.02 | 4.70 | 1.81 | 0.65 | 1.89 | 3.45 | 1.94 [27] 2.3 [29] |
| 3.46 | 2.79 | 0.19 | 0.16 | 0.18 | 0.59 | 0.27 [27] | |
| 0.76 | 0.84 | 5.54 | 3.28 | 4.32 | 1.91 | 4.48 [30] |
| N | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| (eV) | 1.3 | 3.8 | 6.34 | 10.91 | 13.41 | 15.59 |
| (eV) | 9.79 | 16.44 | 22.49 | 27.92 | 32.19 | 39.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Wang, Z.; Wang, L.; Chen, Y.; Liu, Z.; Wang, Q.; Wu, L.; Deng, H. Molecular Dynamics Simulations of Xe Behaviors at the Grain Boundary in UO2. Metals 2022, 12, 763. https://doi.org/10.3390/met12050763
Xia Y, Wang Z, Wang L, Chen Y, Liu Z, Wang Q, Wu L, Deng H. Molecular Dynamics Simulations of Xe Behaviors at the Grain Boundary in UO2. Metals. 2022; 12(5):763. https://doi.org/10.3390/met12050763
Chicago/Turabian StyleXia, Yaping, Zhen Wang, Li Wang, Yangchun Chen, Zhixiao Liu, Qingqing Wang, Lu Wu, and Huiqiu Deng. 2022. "Molecular Dynamics Simulations of Xe Behaviors at the Grain Boundary in UO2" Metals 12, no. 5: 763. https://doi.org/10.3390/met12050763
APA StyleXia, Y., Wang, Z., Wang, L., Chen, Y., Liu, Z., Wang, Q., Wu, L., & Deng, H. (2022). Molecular Dynamics Simulations of Xe Behaviors at the Grain Boundary in UO2. Metals, 12(5), 763. https://doi.org/10.3390/met12050763